System of linear equations

수학(mathematics)에서, 선형 방정식의 시스템(system of linear equations) (또는 선형 시스템(linear system))은 변수(variable)의 같은 집합을 포함하는 하나 이상의 선형 방정식(linear equation)의 모음입니다.^[1]^[2]^[3]^[4]^[5] 예를 들어,

{\begin{alignedat}{7}3x&&\;+\;&&2y&&\;-\;&&z&&\;=\;&&1&\\2x&&\;-\;&&2y&&\;+\;&&4z&&\;=\;&&-2&\\-x&&\;+\;&&{\tfrac {1}{2}}y&&\;-\;&&z&&\;=\;&&0&\end{alignedat}}

는 세 변수 $x, y, z$ 에서 세 방정식의 시스템입니다. 선형 시스템에 대한 해(solution)는 모든 방정식이 동시에 만족시키게 됨을 만족하는 변수에 대한 값의 할당입니다. 위의 시스템에 대한 해(solution)는 다음으로 제공됩니다:

{\begin{alignedat}{2}x&\,=\,&1\\y&\,=\,&-2\\z&\,=\,&-2\end{alignedat}}

왜냐하면 그것은 모든 세 방정식을 유효하게 만들기 때문입니다. 단어 "시스템"은 방정식이 개별적이 아니라, 집합적으로 고려되어야 함을 가리킵니다.

수학에서, 선형 시스템의 이론은 선형 대수(linear algebra)의 기초 및 기본 부분이며, 현대 수학의 대부분 부분에서 사용되는 주제입니다. 해를 찾는 계산적 알고리듬(algorithm)은 수치적 선형 대수(numerical linear algebra)의 중요한 부분이고, 공학(engineering), 물리학(physics), 화학(chemistry), 컴퓨터 과학(computer science), 및 경제학(economics)에서 중요한 역할을 합니다. 비-선형 방정식의 시스템(system of non-linear equations)은 선형 시스템 (선형화(linearization)를 참조하십시오)으로 종종 근사(approximated)될 수 있으며, 상대적으로 복잡한 시스템(complex system)의 수학적 모델(mathematical model) 또는 컴퓨터 모의실험(computer simulation)을 만들 때 도움되는 기술입니다.

매우 자주, 방정식의 계수는 실수(real) 또는 복소수(complex number)이고, 해는 숫자의 같은 집합에서 찾아지지만, 이론 및 알고리듬은 임의의 필드(field)에서 계수와 해에 대해 적용합니다. 정수(integer)의 링(ring)과 같은 정수 도메인(integral domain), 또는 다른 대수적 구조(algebraic structure)의 해에 대해, 다른 이론이 개발되어 왔습니다; 링에 걸쳐 선형 방정식(Linear equation over a ring)을 참조하십시오. 정수 선형 프로그래밍(Integer linear programming)은 (많이 있을 때) "최상의" 정수 해를 찾는 방법의 모음입니다. 그뢰브너 기저(Gröbner basis) 이론은 계수와 미지수가 다항식(polynomial)일 때 알고리듬을 제공합니다. 역시 비유 기하학(tropical geometry)은 보다 특수한 구조에서 선형 대수의 한 예제입니다.

Elementary examples

Trivial example

하나의 미지수에서 하나의 방정식의 시스템

2x=4

은 다음 해를 가집니다:

x=2.

어쨌든, 선형 시스템은 공통적으로 적어도 두 방정식을 가지는 것으로 여겨집니다.

Simple nontrivial example

비-자명한 선형 시스템의 가장-간단한 종류는 두 방정식과 두 변수를 포함합니다:

{\begin{alignedat}{5}2x&&\;+\;&&3y&&\;=\;&&6&\\4x&&\;+\;&&9y&&\;=\;&&15&.\end{alignedat}}

그러한 시스템을 푸는 한 가지 방법은 다음입니다. 먼저, $y$ 의 관점에서 $x$ 에 대해 위쪽 방정식을 푸십시오:

x=3-{\frac {3}{2}}y.

이제 x에 대한 이 표현 아래쪽 방정식에 대입(substitute)하십시오:

4\left(3-{\frac {3}{2}}y\right)+9y=15.

이것은 오직 변수 $y$ 를 포함하는 하나의 방정식을 초래합니다. 풀면 $y=1$ 을 제공하고, 이것을 $x$ 에 대한 방정식에 다시 대입하면 $x=3/2$ 를 산출합니다. 이 방법은 추가적인 변수를 가진 시스템으로 일반화됩니다 (아래의 "System of linear equations § Elimination of variables" 또는 기초 대수학(elementary algebra)에 대한 기사를 참조하십시오).

General form

n 미지수를 갖는 m 선형 방정식의 일반적인 시스템은 다음으로 쓸 수 있습니다:

{\begin{aligned}a_{11}x_{1}+a_{12}x_{2}+\cdots +a_{1n}x_{n}&=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\cdots +a_{2n}x_{n}&=b_{2}\\&\ \ \vdots \\a_{m1}x_{1}+a_{m2}x_{2}+\cdots +a_{mn}x_{n}&=b_{m},\end{aligned}}

여기서 $x_{1},x_{2},\ldots ,x_{n}$ 는 미지수, $a_{11},a_{12},\ldots ,a_{mn}$ 는 시스템의 계수이고, $b_{1},b_{2},\ldots ,b_{m}$ 는 상수항입니다.

종종 계수와 미지수는 실수(real) 또는 복소수(complex number)이지만, 추상 대수적 구조(algebraic structure)의 다항식과 원소와 같이 정수(integer)와 유리수(rational number)가 역시 보입니다.

Vector equation

하나의 극단적인 유용한 관점은 각각의 미지수가 선형 조합에서 열 벡터(column vector)에 대해 가중이라는 것입니다.

x_{1}{\begin{bmatrix}a_{11}\\a_{21}\\\vdots \\a_{m1}\end{bmatrix}}+x_{2}{\begin{bmatrix}a_{12}\\a_{22}\\\vdots \\a_{m2}\end{bmatrix}}+\cdots +x_{n}{\begin{bmatrix}a_{1n}\\a_{2n}\\\vdots \\a_{mn}\end{bmatrix}}={\begin{bmatrix}b_{1}\\b_{2}\\\vdots \\b_{m}\end{bmatrix}}

이것은 벡터 공간(vector space) (또는 일반적으로 모듈(module))의 모든 언어와 이론을 가지기 위해 가져옴을 허용합니다. 예를 들어, 왼쪽 변에 대한 벡터의 모든 가능한 선형 조합의 모음은 스팬(span)으로 불리고, 그 방정식은 오른쪽-변 벡터가 단지 해당 스팬 이내에 있을 때 해를 가집니다. 만약 해당 범위 이내의 모든 각 벡터가 주어진 왼쪽-변 벡터의 선형 조합으로 정확히 하나의 표현을 가지면, 임의의 해는 고유합니다. 임의의 사건에서, 그 스팬은 정확히 하나의 표현을 보장하는 선형적으로 독립(linearly independent) 벡터의 기저(basis)를 가집니다; 그리고 해당 기초에서 벡터의 숫자 (그것의 차원(dimension))는 m 또는 n보다 클 수 없지만, 더 작을 수 있습니다. 이것은 만약 우리가 m 독립 벡터를 가지면, 해가 오른쪽-변에 상관없이 보장되고, 그렇지 않으면 보장되지 않기 때문에 중요합니다.

Matrix equation

벡터 방정식은 다음 형식의 행렬(matrix) 방정식과 동등합니다:

A\mathbf {x} =\mathbf {b}

여기서 A는 m×n 행렬, x는 n 엔트리를 갖는 열 벡터(column vector)이고, b는 m 엔트리를 갖는 열 벡터입니다.

A={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{bmatrix}},\quad \mathbf {x} ={\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{bmatrix}},\quad \mathbf {b} ={\begin{bmatrix}b_{1}\\b_{2}\\\vdots \\b_{m}\end{bmatrix}}

스팬에 대해 기저에서 벡터의 숫자는 이제 행렬의 랭크(rank)로 표현됩니다.

Solution set

선형 시스템의 해는 각 방정식이 만족시키는 변수 x₁, x₂, ..., x_n에 값의 할당입니다. 모든 가능한 해의 집합(set)은 해 집합(solution set)이라고 불립니다.

선형 시스템은 세 가능한 방법의 임의의 하나에서 작동합니다:

시스템은 무한하게 많은 해를 가집니다.
시스템은 단일 유일한 해를 가집니다.
시스템은 해를 가지지 않습니다.

Geometric interpretation

두 변수 (x와 y)를 포함하는 시스템에 대해, 각 선형 방정식은 xy-평면(plane) 위의 한 직선(line)을 결정합니다. 선형 시스템에 대한 해는 방정식의 모두를 만족시켜야 하기 때문에, 해 집합은 이들 직선의 교점(intersection)이고, 따라서 직선, 단일 점, 또는 빈 집합(empty set) 중 하나입니다.

세 변수에 대해, 각 선형 방정식은 삼-차원 공간(three-dimensional space)에서 평면(plane)을 결정하고 해 집합은 이들 평면의 교차입니다. 따라서 해 집합은 평면, 직선, 또는 단일 점, 또는 빈 집합일 수 있습니다. 예를 들어, 세 평행 평면은 공통 점을 가지지 않기 때문에, 그들의 방정식의 해 집합은 빈 것입니다; 한 점에서 교차하는 세 평면 방정식의 해 집합은 단일 점입니다; 만약 세 평면이 두 점을 통과하면, 그들의 방정식은 적어도 두 공통 해를 가집니다; 실제로 해 집합은 무한이고 이들 점을 통과하는 모든 직선으로 구성됩니다.^[6]

n 변수에 대해, 각 선형 방정식은 n-차원 공간(n-dimensional space)에서 초평면(hyperplane)을 결정합니다. 해 집합은 이들 초평면의 교차이고, 플랫(flat)이며, 이것은 n보다 작은 임의의 차원을 가질 수 있습니다.

General behavior

일반적으로, 선형 시스템의 행동은 방정식의 숫자와 미지수의 숫자 사이의 관계에 의해 결정됩니다. 여기서, "일반적으로" 다른 행동은 방정식의 계수의 특정 값에 대해 발생할 수 있음을 의미합니다.

일반적으로, 미지수보다 더 작은 방정식을 가진 시스템은 무한하게 많은 해를 가지지만, 해를 가지지 않을 수 있습니다. 그러한 시스템은 미달-결정된 시스템(underdetermined system)으로 알려져 있습니다.
일반적으로, 같은 숫자의 방정식과 미지수를 가진 시스템은 단일 고유한 해를 가집니다.
일반적으로, 미지수보다 더 많은 방정식을 가진 시스템은 해를 가지지 않습니다. 그러한 시스템은 초과-결정된 시스템(overdetermined system)으로 알려져 있습니다.

첫 번째 경우에서, 해 집합의 차원(dimension)은, 일반적으로, n − m과 같으며, 여기서 n은 변수의 숫자이고 m은 방정식의 숫자입니다.

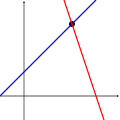
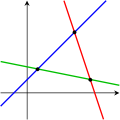
다음 그림은 두 변수의 경우에서 이 삼분법을 묘사합니다:


One equation	Two equations	Three equations

첫 번째 시스템은 무한하게 많은 해, 즉 파란 직선 위의 모든 점을 가집니다. 두 번째 시스템은 단일 고유한 해, 즉 두 직선의 교점을 가집니다. 세 번째 시스템은 해를 가지지 않는데, 왜냐하면 세 직선은 공통 점을 공유하지 않기 때문입니다.

위의 그림은 오직 가장 공통적인 경우 (일반적인 경우)를 보여줌을 기억해야 합니다. 두 방정식과 두 미지수의 시스템에 대해 (만약 두 직선이 평행하면) 해를 갖지 않는 것, 또는 세 방정식과 두 미지수의 시스템에 대해 (만약 세 직선이 단일 점에서 교차하면) 풀-수-있는 것이 가능합니다.

선형 방정식의 시스템은 만약 방정식이 선형적으로 독립(linearly dependent), 또는 만약 그것이 불일치(inconsistent)이고 미지수보다 더 많은 방정식을 가지지 않으면, 일반적인 경우와 다르게 작동합니다.

Properties

Independence

선형 시스템의 방정식은 만약 방정식의 어떤 것이 다른 방정식으로부터 대수적으로 도출될 수 없으면 독립(independent)입니다. 방정식이 독립일 때, 각 방정식은 변수에 대한 새로운 정보가 포함되고, 방정식의 임의의 것을 제거하면 해 집합의 크기가 증가합니다. 선형 방정식에 대해, 논리적 독립성은 선형 독립(linear independence)과 같습니다.

예를 들어, 방정식

3x+2y=6\;\;\;\;{\text{and}}\;\;\;\;6x+4y=12

은 독립이 아닙니다 — 그들은 2의 인수로 스케일될 때 같은 방정식이고, 그들은 동일한 그래프를 생성할 것입니다. 이것은 선형 방정식의 시스템에서 동등성의 예제입니다.

보다 복잡한 예제에 대해, 방정식

{\begin{alignedat}{5}x&&\;-\;&&2y&&\;=\;&&-1&\\3x&&\;+\;&&5y&&\;=\;&&8&\\4x&&\;+\;&&3y&&\;=\;&&7&\end{alignedat}}

은 독립이 아닌데, 왜냐하면 세 번째 방정식은 다른 둘의 합이기 때문입니다. 사실, 세 방정식의 임의의 하나는 다른 둘로부터 도출될 수 있고, 방정식의 임의의 하나는 해 집합에 영향을 미침없이 제거될 수 있습니다. 이들 방정식의 그래프는 한 점에서 교차하는 세 직선입니다.

Consistency

선형 시스템이 만약 해를 가지지 않으면 불일치(inconsistent)이고, 그렇지 않으면 그것은 일치(consistent)라고 말합니다. 시스템이 불-일치일 때, 방정식으로부터 모순(contradiction)을 도출하는 것이 가능하며, 항상 명제 0 = 1로 다시-쓸 수 있습니다.

예를 들어, 방정식

3x+2y=6\;\;\;\;{\text{and}}\;\;\;\;3x+2y=12

은 불일치입니다. 사실, 두 번째 방정식으로부터 첫 번째 방정식을 빼고 결과의 양쪽 변에 1/6을 곱함으로써, 우리는 0 = 1을 얻습니다. xy-평면 위에 이들 방정식의 그래프는 평행(parallel) 직선의 쌍입니다.

세 선형 방정식에 대해, 심지어 그들의 임의의 둘이 함께 일치이더라도, 불일치되는 것이 가능합니다. 예를 들어, 방정식

{\begin{alignedat}{7}x&&\;+\;&&y&&\;=\;&&1&\\2x&&\;+\;&&y&&\;=\;&&1&\\3x&&\;+\;&&2y&&\;=\;&&3&\end{alignedat}}

은 불일치입니다. 처음 두 방정식을 더하면 3x + 2y = 2을 제공하며, 이것은 0 = 1를 산출하기 위해 세 번째 방정식으로부터 빼질 수 있습니다. 이들 방정식의 임의의 둘은 공통 해를 가집니다. 같은 현상은 방정식의 임의의 숫자에 대해 발생할 수 있습니다.

일반적으로, 불일치는 만약 시스템에서 방정식의 왼쪽 변이 선형적으로 종속이면 발생하고, 상수 항은 종속 관계를 만족시키지 않습니다. 왼쪽 변이 선형적으로 독립인 방정식의 시스템은 항상 일치입니다.

루셰–카펠리 정리(Rouché–Capelli theorem)에 따르면, 그것을 또 다른 방법에 넣으면, 방정식의 임의의 시스템 (초과-결정된 또는 그렇지 않은 것)은 만약 증가된 행렬(augmented matrix)의 랭크(rank)가 계수 행렬(coefficient matrix)의 랭크보다 더 크면 불일치입니다. 만약, 다른 한편으로, 이들 두 행렬의 랭크가 같으면, 시스템은 적어도 하나의 해를 가져야 합니다. 그 해가 고유한 것과 랭크가 변수의 숫자와 같은 것은 필요충분 조건입니다. 그렇지 않으면 일반적인 해는 k 자유 매개-변수를 가지며, 여기서 k는 변수의 숫자와 랭크 사이의 차이입니다; 따라서 그러한 경우에서, 해의 무한대가 있습니다. 방정식 시스템의 랭크 (즉, 증가된 행렬의 랭크)는 [변수의 숫자] + 1보다 절대 높을 수 없으며, 이것은 방정식의 임의의 숫자를 가진 시스템은 많아야 [변수의 숫자] + 1과 같은 독립 방정식(independent equation)의 숫자를 가지는 시스템으로 항상 줄일 수 있음을 의미합니다.

Equivalence

변수의 같은 집합을 사용하는 두 선형 시스템은 만약 두 번째 시스템에서 방정식의 각각이 첫 번째 시스템에서 방정식으로부터 대수적으로 도출될 수 있고, 그 반대도 마찬가지이면, 동등(equivalent)입니다. 두 시스템은 만약 둘 다가 불일치 또는 그들의 각각의 각 방정식이 다른 시스템의 방정식의 선형 조합이면 동등입니다. 두 선형 시스템이 동등한 것과 그들이 같은 해 집합을 가지는 것은 필요충분 조건임을 따릅니다.

Solving a linear system

선형 방정식의 시스템을 푸는(solving) 여러 알고리듬(algorithm)이 있습니다.

Describing the solution

해 집합이 유한일 때, 단일 원소로 줄어듭니다. 이 경우에서, 고유한 해는 왼쪽 변이 미지수의 이름이고 오른쪽 변이 대응하는 값인, 예를 들어 $(x=3,\;y=-2,\;z=6)$ , 방정식의 수열에 의해 묘사됩니다. 미지수에 대한 순서는 고정, 예를 들어 알파벳 순서(alphabetical order)로 고정되어 있을 때, 해는 이전 예제에 대해 $(3,\,-2,\,6)$ 와 같은 값의 벡터(vector)로 설명될 수 있습니다.

무한한 숫자의 해를 갖는 집합을 설명하기 위해, 전형적으로 변수의 일부는 자유 (또는 독립 또는 매개-변수)로 지정되며, 그들은 임의의 값을 취하는 것을 허용되지만, 남아있는 변수는 자유 변수의 값에 종속임을 의미합니다.

예를 들어, 다음 시스템을 생각해 보십시오:

{\begin{alignedat}{7}x&&\;+\;&&3y&&\;-\;&&2z&&\;=\;&&5&\\3x&&\;+\;&&5y&&\;+\;&&6z&&\;=\;&&7&\end{alignedat}}

이 시스템에 대한 해 집합은 다음 방정식에 의해 설명될 수 있습니다:

x=-7z-1\;\;\;\;{\text{and}}\;\;\;\;y=3z+2{\text{.}}

여기서 z는 자유 변수이지만, x와 y는 z에 대해 종속입니다. 해 집합에서 임의의 점은 z에 대해 값을 먼저 선택하고, 그런-다음 x와 y에 대해 대응하는 값을 계산함으로써 구할 수 있습니다.

각 자유 변수는 해 공간 일 자유도(degree of freedom)를 제공하며, 그것의 숫자는 해 집합의 차원(dimension)과 같습니다. 예를 들어, 위의 방정식에 대해 해 집합은 직선인데, 왜냐하면 해 집합에서 한 점은 매개-변수 z의 값을 지정함으로써 선택될 수 있습니다. 더 높은 차수의 무한 해는 평면, 또는 더 높은-차원의 집합을 묘사할 수 있습니다.

자유 변수에 대해 다른 선택은 같은 해 집합의 다른 설명으로 이어질 수 있습니다. 예를 들어, 위의 방정식에 대한 해는 다음과 같이 대안적으로 설명될 수 있습니다:

y=-{\frac {3}{7}}x+{\frac {11}{7}}\;\;\;\;{\text{and}}\;\;\;\;z=-{\frac {1}{7}}x-{\frac {1}{7}}{\text{.}}

여기서 x는 자유 변수이고, y와 z는 종속입니다.

Elimination of variables

선형 방정식의 시스템을 푸는 가장 간단한 방법은 변수를 반복적으로 제거하는 것입니다. 이 방법은 다음과 같이 설명될 수 있습니다:

첫 번째 방정식에서, 다른 것들의 관점에서 변수의 하나에 대해 풉니다.
이 표현을 남아있는 방정식에 대입하십시오. 이것은 하나의 더 적은 방정식과 하나의 더 적은 미지수를 갖는 방정식의 시스템을 산출합니다.
시스템이 단일 선형 방정식으로 줄어들 때까지 반복하십시오.
이 방정식을 풀고, 그런-다음 전체 해가 구해질 때까지 역순-대입하십시오.

예를 들어, 다음 방정식을 생각해 보십시오:

{\begin{alignedat}{7}x&&\;+\;&&3y&&\;-\;&&2z&&\;=\;&&5&\\3x&&\;+\;&&5y&&\;+\;&&6z&&\;=\;&&7&\\2x&&\;+\;&&4y&&\;+\;&&3z&&\;=\;&&8&\end{alignedat}}

첫 번째 방정식을 x에 대해 풀면 x = 5 + 2z − 3y를 제공하고, 이것을 두 번째와 세 번째 방정식에 대입하면 다음을 산출합니다:

{\begin{alignedat}{5}-4y&&\;+\;&&12z&&\;=\;&&-8&\\-2y&&\;+\;&&7z&&\;=\;&&-2&\end{alignedat}}

이들 방정식의 첫 번째를 y에 대해 풀면 y = 2 + 3z을 산출하고, 이것을 두 번째 방정식에 대입하면 z = 2를 산출합니다. 우리는 이제 다음을 가집니다:

{\begin{alignedat}{7}x&&\;=\;&&5&&\;+\;&&2z&&\;-\;&&3y&\\y&&\;=\;&&2&&\;+\;&&3z&&&&&\\z&&\;=\;&&2&&&&&&&&&\end{alignedat}}

z = 2를 두 번째 방정식에 대입하면 y = 8를 제공하고, z = 2와 y = 8을 첫 번째 방정식을 대입하면 x = −15를 산출합니다. 그러므로, 해 집합은 단일 점 (x, y, z) = (−15, 8, 2)입니다.

Row reduction

행 축소법 (역시 가우스 소거법으로 알려짐)에서, 선형 시스템은 증가된 행렬로 표현됩니다:

\left[{\begin{array}{rrr|r}1&3&-2&5\\3&5&6&7\\2&4&3&8\end{array}}\right]{\text{.}}

이 행렬은 그런-다음 기본 행 연산(elementary row operations)을 사용하여 그것이 감소된 행 사다리꼴 형식(reduced row echelon form)에 도달할 때까지 수정됩니다. 기본 행 연산의 세 가지 유형이 있습니다:

유형 1: 두 행의 위치를 서로 바꿉니다.

유형 2: 행에 비-영 스칼라(scalar)를 곱합니다.

유형 3: 한 행에 또 다른 행의 스칼라 배수를 더합니다.

이러한 연산은 거꾸로-할-수-있기 때문에, 생성된 증가된 행렬은 원래와 동등한 선형 시스템을 항상 나타냅니다.

증강된 행렬을 행-감소하기 위해 여러 특정 알고리듬이 있으며, 그것의 가장 간단한 것은 가우스 소거법(Gaussian elimination) 및 가우스-요르단 소거법(Gauss-Jordan elimination)입니다. 다음 계산은 위 행렬에 적용된 가우스-요르단 소거법을 보여줍니다:

{\begin{aligned}\left[{\begin{array}{rrr|r}1&3&-2&5\\3&5&6&7\\2&4&3&8\end{array}}\right]&\sim \left[{\begin{array}{rrr|r}1&3&-2&5\\0&-4&12&-8\\2&4&3&8\end{array}}\right]\sim \left[{\begin{array}{rrr|r}1&3&-2&5\\0&-4&12&-8\\0&-2&7&-2\end{array}}\right]\sim \left[{\begin{array}{rrr|r}1&3&-2&5\\0&1&-3&2\\0&-2&7&-2\end{array}}\right]\\&\sim \left[{\begin{array}{rrr|r}1&3&-2&5\\0&1&-3&2\\0&0&1&2\end{array}}\right]\sim \left[{\begin{array}{rrr|r}1&3&-2&5\\0&1&0&8\\0&0&1&2\end{array}}\right]\sim \left[{\begin{array}{rrr|r}1&3&0&9\\0&1&0&8\\0&0&1&2\end{array}}\right]\sim \left[{\begin{array}{rrr|r}1&0&0&-15\\0&1&0&8\\0&0&1&2\end{array}}\right].\end{aligned}}

마지막 행렬은 기약 사다리꼴 형식이고, 시스템 x = −15, y = 8, z = 2을 나타냅니다. 변수의 대수적 소거법에 대한 이전 섹션에서 예제와 비교하면 이들 두 방법은 실제로 같음을 보여줍니다; 차이점은 계산이 쓰이는 방법에 있습니다.

Cramer's rule

크라메르의 규칙(Cramer's rule)은 선형 방정식의 시스템의 해에 대해 명시적 공식이며, 각 변수는 두 행렬식(determinant)의 몫에 의해 제공됩니다. 예를 들어, 다음 시스템

{\begin{alignedat}{7}x&\;+&\;3y&\;-&\;2z&\;=&\;5\\3x&\;+&\;5y&\;+&\;6z&\;=&\;7\\2x&\;+&\;4y&\;+&\;3z&\;=&\;8\end{alignedat}}

에 대한 해는 다음에 의해 제공됩니다:

x={\frac {\,\left|{\begin{matrix}5&3&-2\\7&5&6\\8&4&3\end{matrix}}\right|\,}{\,\left|{\begin{matrix}1&3&-2\\3&5&6\\2&4&3\end{matrix}}\right|\,}},\;\;\;\;y={\frac {\,\left|{\begin{matrix}1&5&-2\\3&7&6\\2&8&3\end{matrix}}\right|\,}{\,\left|{\begin{matrix}1&3&-2\\3&5&6\\2&4&3\end{matrix}}\right|\,}},\;\;\;\;z={\frac {\,\left|{\begin{matrix}1&3&5\\3&5&7\\2&4&8\end{matrix}}\right|\,}{\,\left|{\begin{matrix}1&3&-2\\3&5&6\\2&4&3\end{matrix}}\right|\,}}.

각 변수에 대해, 분모는 계수의 행렬(matrix of coefficients)의 행렬식이지만, 분자는 하나의 열이 상수 항의 벡터에 의해 대체된 행렬의 행렬식입니다.

비록 크라메르의 규칙은 이론적으로 중요하지만, 큰 행렬에 대해 실질적인 가치가 거의 없는데, 왜냐하면 큰 행렬의 계산은 다소 번거롭기 때문입니다. (실제로, 큰 행렬식은 행 축소를 사용하여 가장 쉽게 계산됩니다.) 게다가, 크라메르의 규칙은 매우 낮은 수치적 속성을 가지며, 만약 연산이 무-경계 정밀도로 합리적인 산술에서 수행되지 않으면, 심지어 작은 시스템에서도 안정적으로 푸는 것에 적합하지 않습니다.^{[citation needed]}

Matrix solution

만약 방정식 시스템이 행렬 형식 $A\mathbf {x} =\mathbf {b}$ 에서 표현되면, 전체 해 집합은 행렬 형식에서 역시 표현될 수 있습니다. 만약 행렬 A가 정사각 행렬 (m 행과 n=m 열을 가짐)이고 전체 랭크이면 (모든 m 행이 독립임), 시스템은 다음에 의해 고유한 해를 가집니다:

\mathbf {x} =A^{-1}\mathbf {b}

여기서 $A^{-1}$ 는 A의 역(inverse)입니다. 보다 일반적으로, m = n 여부에 관계없이 및 A의 랭크에 관계없이, 모든 해는 (만약 존재한다면) $A^{+}$ 로 표시되는 A의 무어-펜로즈 유사역행렬(Moore-Penrose pseudoinverse)을 사용하여, 다음과 같이, 주어집니다:

\mathbf {x} =A^{+}\mathbf {b} +(I-A^{+}A)\mathbf {w}

여기서 $\mathbf {w}$ 는 모든 가능한 n×1 벡터에 걸쳐 미치는 자유 매개-변수의 벡터입니다. 존재하기 위한 임의의 해에 대해 필요 및 충분 조건은 $\mathbf {w} =\mathbf {0}$ 을 사용하여 얻어진 잠재적 해는 $A\mathbf {x} =\mathbf {b}$ — 즉, $AA^{+}\mathbf {b} =\mathbf {b} .$ 임을 만족시키는 것입니다. 만약 이 조건이 유지되지 않으면, 방정식 시스템은 불-일치이고 해를 가지지 않습니다. 만약 그 조건이 유지되면, 그 시스템이 일치되고 적어도 하나의 해가 존재합니다. 예를 들어, 위에서-언급된 경우에서 A가 정사각 행렬이고 전체 랭크이며, $A^{+}$ 는 단순히 $A^{-1}$ 와 같고 일반적인 해 방정식은 이전에 언급된 것처럼 $\mathbf {x} =A^{-1}\mathbf {b} +(I-A^{-1}A)\mathbf {w} =A^{-1}\mathbf {b} +(I-I)\mathbf {w} =A^{-1}\mathbf {b}$ 으로 단순화되며, 여기서 $\mathbf {w}$ 는 해에서 완전히 제거되며, 오직 단일 해를 남깁니다. 다른 경우에서, 그러나, $\mathbf {w}$ 가 유지되고 따라서 자유 매개-변수 벡터 $\mathbf {w}$ 의 잠재적 값의 무한대는 방정식의 해의 무한대를 제공합니다.

Other methods

셋 또는 넷 방정식을 가진 시스템은 손으로 쉽게 풀 수 있지만 (크라코비아(Cracovian)를 참조하십시오), 컴퓨터는 더 큰 시스템에 대해 종종 사용됩니다. 선형 방정식의 시스템을 푸는 표준 알고리듬은 약간의 수정과 함께 가우스 소거법을 기반으로 합니다. 첫째, 부정확한 결과로 이어질 수 있는, 작은 숫자에 의한 나눗셈을 피하는 것이 본질적입니다. 이것은 만약 필요하다면 방정식을 다시-정렬하는, 피벗팅(pivoting)으로 알려진 과정으로 행해질 수 있습니다. 둘째, 그 알고리듬은 가우스 소거법을 정확하게 수행하지는 않지만, 행렬 A의 LU 분해(LU decomposition)를 계산합니다. 이것은 대개 조직적 도구이지만, 만약 우리가 같은 행렬 A이지만 다른 행렬 b를 갖는 여러 시스템을 풀어야 한다면 훨씬 빠릅니다.

만약 행렬 A가 어떤 특별한 구조를 가지면, 이것은 더 빠르고 더 정확한 알고리듬을 얻기 위해 이용될 수 있습니다. 예를 들어, 대칭(symmetric) 양수-한정 행렬(positive definite matrix)을 갖는 시스템은 숄레스키 분해(Cholesky decomposition)와 함께 두 배 빠르게 해결될 수 있습니다. 레빈슨 재귀(Levinson recursion)는 퇴플리츠 행렬(Toeplitz matrix)의 빠른 방법입니다. 특별한 방법은 많은 영 원소를 가진 행렬 (소위 희소 행렬(sparse matrices))에 역시 존재하며, 이것은 종종 응용에 보입니다.

완전히 다른 접근법이 매우 큰 시스템에 대해 종종 취해지며, 그렇지 않으면 너무 많은 시간 또는 메모리가 소요될 것입니다. 그 아이디어는 해에 대한 초기 근사로 시작하고 (이것은 전혀 정확하지 않아도 됩니다), 여러 단계로 이 근사를 변경하여 참 해에 더 가깝게 그것을 가져가는 것입니다. 일단 근사가 충분히 정확하면, 이것은 시스템에 대한 해로 여겨집니다. 이것은 반복적인 방법(iterative method)의 클래스로 이어집니다.

선형 방정식 시스템에 대한 양자 알고리듬(quantum algorithm for linear systems of equations)이 역시 있습니다.^[7]

Homogeneous systems

선형 방정식의 시스템은 만약 상수 항의 모두가 영이면 동차(homogeneous)입니다:

{\begin{alignedat}{7}a_{11}x_{1}&&\;+\;&&a_{12}x_{2}&&\;+\cdots +\;&&a_{1n}x_{n}&&\;=\;&&&0\\a_{21}x_{1}&&\;+\;&&a_{22}x_{2}&&\;+\cdots +\;&&a_{2n}x_{n}&&\;=\;&&&0\\\vdots \;\;\;&&&&\vdots \;\;\;&&&&\vdots \;\;\;&&&&&\,\vdots \\a_{m1}x_{1}&&\;+\;&&a_{m2}x_{2}&&\;+\cdots +\;&&a_{mn}x_{n}&&\;=\;&&&0.\\\end{alignedat}}

동차 시스템은 다음 형식의 행렬 방정식과 동등합니다:

A{\textbf {x}}={\textbf {0}}

여기서 A는 m × n 행렬, x는 n 엔트리를 갖는 열 벡터이고, 0은 m 엔트리를 갖는 영 벡터(zero vector)입니다.

Homogeneous solution set

모든 각 동차 시스템은 영 (또는 지명한) 해로 알려진 적어도 이상의 해를 가지며, 이것은 변수의 각각에 영의 값을 할당함으로써 얻습니다. 만약 그 시스템이 비-특이 행렬(non-singular matrix) ( $det(A) \neq 0$ )을 가지면, 그것은 역시 유일한 해입니다. 만약 그 시스템이 특이 행렬이면, 해의 무한 숫자를 갖는 해 집합이 있습니다. 이 해 집합은 다음 추가적인 속성을 가집니다:

만약 u와 v가 동차 시스템에서 해를 나타내는 두 벡터(vectors)이면, 벡터 합 u + v는 역시 그 시스템에 대한 해입니다.
만약 u가 동차 시스템에 대한 해를 나타내는 벡터이고, r이 임의의 스칼라(scalar)이면, ru는 역시 그 시스템에 대한 해입니다.

이들은 해 집합에 대해 Rⁿ의 선형 부분-공간(linear subspace)이 되기 위해 필요한 정확하게 그 속성입니다. 특히, 동차 시스템에 대한 해 집합은 해당하는 행렬 A의 널 공간(null space)과 같은 것입니다. 동차 시스템에 대한 수치적 해는 특이값 분해(singular value decomposition)로 구할 수 있습니다.

Relation to nonhomogeneous systems

선형 시스템에 대한 해와 해당하는 동차 시스템에 대한 해 사이에 밀접한 관계가 있습니다:

A{\textbf {x}}={\textbf {b}}\qquad {\text{and}}\qquad A{\textbf {x}}={\textbf {0}}{\text{.}}

구체적으로 특별히, 만약 p가 선형 시스템 Ax = b에 대한 임의의 특정 해이면, 전체 해 집합은 다음과 같이 설명될 수 있습니다:

\left\{{\textbf {p}}+{\textbf {v}}:{\textbf {v}}{\text{ is any solution to }}A{\textbf {x}}={\textbf {0}}\right\}.

기하학적으로, 이것은 Ax = b에 대해 해 집합이 Ax = 0에 대해 해 집합의 평행-이동(translation)이라고 말합니다. 구체적으로 특별히, 첫 번째 시스템에 대해 플랫(flat)은 벡터 p에 의해 동차 시스템에 대해 선형 부분-공간(linear subspace)을 평행-이동함으로써 얻어질 수 있습니다.

이 추론은 만약 시스템 Ax = b가 적어도 하나의 해를 가지면 오직 적용됩니다. 이것이 발생하는 것과 벡터 b가 선형 변환(linear transformation) A의 이미지(image)에 놓이는 것은 필요충분 조건입니다.

Notes

^ Anton (1987, p. 2)
^ Beauregard & Fraleigh (1973, p. 65)
^ Burden & Faires (1993, p. 324)
^ Golub & Van Loan (1996, p. 87)
^ Harper (1976, p. 57)
^ Charles G. Cullen (1990). Matrices and Linear Transformations. MA: Dover. p. 3. ISBN 978-0-486-66328-9.
^ Quantum algorithm for solving linear systems of equations, by Harrow et al..

References

Anton, Howard (1987), Elementary Linear Algebra (5th ed.), New York: Wiley, ISBN 0-471-84819-0
Beauregard, Raymond A.; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Company, ISBN 0-395-14017-X
Burden, Richard L.; Faires, J. Douglas (1993), Numerical Analysis (5th ed.), Boston: Prindle, Weber and Schmidt, ISBN 0-534-93219-3
Golub, Gene H.; Van Loan, Charles F. (1996), Matrix Computations (3rd ed.), Baltimore: Johns Hopkins University Press, ISBN 0-8018-5414-8
Harper, Charlie (1976), Introduction to Mathematical Physics, New Jersey: Prentice-Hall, ISBN 0-13-487538-9

External links

Media related to System of linear equations at Wikimedia Commons

[1] Anton (1987, p. 2)

[2] Beauregard & Fraleigh (1973, p. 65)

[3] Burden & Faires (1993, p. 324)

[4] Golub & Van Loan (1996, p. 87)

[5] Harper (1976, p. 57)

[Linear_Matrices-6] Charles G. Cullen (1990). Matrices and Linear Transformations. MA: Dover. p. 3. ISBN 978-0-486-66328-9.

[Quantum_algorithm_for_solving_linear_systems_of_equations_by_Harrow_et_al.-7] Quantum algorithm for solving linear systems of equations, by Harrow et al..

[1]

[2]

[3]

[4]

[5]

[6]

[7]