Basis (linear algebra)

수학(mathematics)에서, 벡터 공간(vector space) $V$ 에서 벡터의 집합(set) $B$ 는 만약 $V$ 의 모든 각 원소가 $B$ 의 원소의 유한 선형 조합(linear combination)으로 고유한 방법에서 쓸 수 있으면 기저(basis)라고 불립니다. 이 선형 조합의 계수는 $B$ 에 관한 벡터의 성분(구성 요소, components) 또는 좌표(coordinates)라고 참조됩니다. 기저의 원소는 기저 벡터(basis vectors)라고 불립니다.

동등하게, 집합 $B$ 는 만약 그것의 원소가 선형적으로 독립(linearly independent)이고 $V$ 의 모든 각 원소가 $B$ 의 원소의 선형 조합(linear combination)이면 기저입니다.^[1] 다시 말해서, 기저는 선형적으로 독립적인 스팬하는 집합(spanning set)입니다.

벡터 공간은 여러 기저를 가질 수 있습니다; 어쨌든 모든 기저는 벡터 공간의 차원(dimension of the vector space)이라고 불리는 같은 숫자의 원소를 가집니다.이 기사는 주로 유한-차원 벡터 공간을 다룹니다. 어쨌든, 많은 원칙이 무한-차원 벡터 공간에도 유효합니다.

Definition

필드(field) $F$ (예를 들어, 실수 $R$ 또는 복소수 $C$ )에 걸쳐 벡터 공간(vector space) $V$ 의 기저 $B$ 는 $V$ 를 스팬(span)하는 $V$ 의 선형적으로 독립 부분집합(subset)입니다. 이것은 $V$ 의 부분집합 $B$ 는 만약 그것이 다음 두 조건을 만족시키면 기저임을 의미합니다:

선형 독립(linear independence): $B$ 의 모든 각 유한(finite) 부분집합 $\{\mathbf {v} _{1},\dotsc ,\mathbf {v} _{m}\}$ 에 대해, 만약 $F$ 에서 일부 $F$ 에 대해 $c_{1}\mathbf {v} _{1}+\cdots +c_{m}\mathbf {v} _{m}=\mathbf {0}$ 이면, $c_{1}=\cdots =c_{m}=0$ 입니다;
스팬하는 속성(spanning property): $V$ 에서 모든 각 벡터 $v$ 에 대해, $\mathbf {v} =a_{1}\mathbf {v} _{1}+\cdots +a_{n}\mathbf {v} _{n}$ 임을 만족하는 $F$ 에서 $a_{1},\dotsc ,a_{n}$ 와 $B$ 에서 $\mathbf {v} _{1},\dotsc ,\mathbf {v} _{n}$ 를 선택할 수 있습니다.

스칼라(scalars) $a_{i}$ 는 기저 $B$ 에 대한 벡터 $v$ 의 좌표라고 불리고, 첫 번째 속성에 의해 그것들은 고유하게 결정됩니다.

유한(finite) 기저를 가지는 벡터 공간은 유한-차원(finite-dimensional)이라고 불립니다. 이 경우에서, 유한 부분집합은 위의 정의에서 선형 독립성을 확인하기 위해 $B$ 자체로 취할 수 있습니다.

예를 들어 방향(orientation)을 논의할 때, 또는 기저 원소를 명시적으로 참조하지 않고 기저에 관한 벡터의 스칼라 계수를 고려할 때 기저 벡터에 대한 순서화(ordering)를 가지는 것이 종종 편리하거나 심지어 필요하기도 합니다. 이 경우에서, 순서화는 각 계수를 해당 기본 원소에 연결하기 위해 필요합니다. 이 순서화는 기저 원소에 번호-지정함으로써 수행될 수 있습니다. 순서가 선택되었음을 강조하기 위해, 순서화된 기저(ordered basis)에 대해 이야기하며, 이는 따라서 단순히 구조화되지 않은 집합(set)이 아니라, 수열(sequence), 인덱스된 가족(indexed family) 또는 유사한 것입니다. 아래의 § Ordered bases and coordinates를 참조하십시오.

Examples

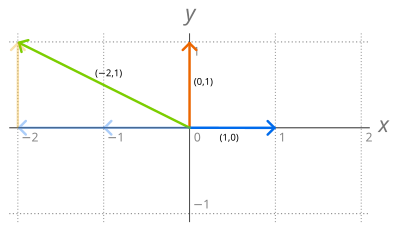
실수의 순서화된 쌍(ordered pairs)의 집합 $R 2$ 은 성분-별 덧셈 $(a,b)+(c,d)=(a+c,b+d)$ 과 스칼라 곱셈 $\lambda (a,b)=(\lambda a,\lambda b),$ 의 연산 아래에서 벡터 공간이며, 여기서 $\lambda$ 는 임의의 실수입니다. 이 벡터 공간의 단순 기저는 두 벡터 $e 1 = (1, 0)$ 와 $e 2 = (0, 1)$ 로 구성됩니다. 이들 벡터는 기저 (표준 기저라고 함)를 형성하는데 왜냐하면 $R 2$ 의 임의의 벡터 $v = (a, b)$ 가 고유하게 다음과 같이 쓸 수 있기 때문입니다: $\mathbf {v} =a\mathbf {e} _{1}+b\mathbf {e} _{2}.$ $(1, 1)$ 과 $(-1, 2)$ 와 같은 $R 2$ 의 다른 선형적으로 독립 벡터 쌍도 $R 2$ 의 기저를 형성합니다. 보다 일반적으로, 만약 $F$ 가 필드(field)이면, $F$ 의 원소의 $n$ -튜플( $n$ -tuples)의 집합 $F^{n}$ 은 유사하게 정의된 덧셈과 스칼라 곱셈에 대해 벡터 공간입니다. 다음을 $\mathbf {e} _{i}=(0,\ldots ,0,1,0,\ldots ,0)$ 1을 가지는 $i$ 번째를 제외하고 모든 성분이 0과 같은 $n$ -튜플이라고 놓습니다. 그런-다음 $\mathbf {e} _{1},\ldots ,\mathbf {e} _{n}$ 은 $F^{n}$ 의 기저이며, 이는 $F^{n}$ 의 표준 기저(standard basis)라고 불립니다. 다른 예제는 다항식 링(polynomial rings)에 의해 제공됩니다. 만약 $F$ 가 필드이면, $F$ 에서 계수를 갖는 하나의 불확정(indeterminate) $X$ 에서 모든 다항식(polynomials)의 모음 $F [X]$ 는 $F$ -벡터 공간입니다. 이 공간에 대해 한 기저는 모든 단항식(monomials)으로 구성된 단항 기저(monomial basis) $B$ 입니다: $B=\{1,X,X^{2},\ldots \}.$ 각 차수의 정확하게 하나의 다항식이 있음을 만족하는 다항식의 임의의 집합 (예를 들어, 베른슈타인 기저 다항식(Bernstein basis polynomials) 또는 체비쇼프 다항식(Chebyshev polynomials))도 기저입니다. (그러한 다항식 집합은 다항식 순서열(polynomial sequence)이라고 불립니다.) 그러나 이 형식의 것이 아닌 $F [X]$ 에 대해 많은 기저도 있습니다.

Properties

유한 기저의 많은 속성은 임의의 벡터 공간 $V$ 에 대해, 유한 스팬하는 집합(spanning set) $S$ 와 $V$ 의 $n$ 원소의 선형적으로 독립(linearly independent) 집합 $L$ 이 주어지면, $S$ 의 잘 선택된 $n$ 원소를 $L$ 을 포함하는 스패닝 집합을 얻기 위해, $S$ 에 있는 그것이 다른 원소를 가지고, $S$ 와 같은 원소의 숫자를 가지는 $L$ 의 원소로 대체할 수 있음을 말하는 슈타이니츠 교환 보조정리(Steinitz exchange lemma)에서 비롯됩니다.

슈타이니츠 교환 보조정리에서 초래하는 대부분의 속성은 유한 스팬하는 집합이 없을 때 참으로 유지되지만, 무한 경우에서 그것의 증명은 일반적으로 선택의 공리(axiom of choice) 또는 극단필터 보조정리(ultrafilter lemma)와 같은 더 약한 형식을 요구합니다.

만약 $V$ 가 필드 $F$ 에 걸쳐 벡터 공간이면, 다음입니다:

만약 $L$ 이 스팬하는 집합 $S \subseteq V$ 의 선형적으로 독립 부분집합이면, 다음을 만족하는 기저 $B$ 가 있습니다: $L\subseteq B\subseteq S.$
$V$ 는 기저를 가집니다 (이것은 $L$ 이 빈 집합(empty set)이고, $S = V$ 인 선행 속성입니다).
$V$ 의 모든 기저는 같은 카디널리티(cardinality)를 가지며, 이는 $V$ 의 차원(dimension)이라고 불립니다. 이것이 차원 정리(dimension theorem)입니다.
생성 집합 $S$ 가 $V$ 의 기저인 것과 그것이 최소인 것은 필요충분 조건이며, 즉, $S$ 의 적절한 부분집합(proper subset)도 $V$ 의 생성 집합이 아닙니다.
선형적으로 독립 집합 $L$ 이 기저인 것과 그것이 최대인 것은 필요충분 조건이며, 즉, 그것은 선형적으로 독립 집합의 적절한 부분집합이 아닙니다.

만약 $V$ 가 차원 $n$ 의 벡터 공간이면, 다음입니다:

$n$ 개의 원소를 갖는 $V$ 의 부분집합이 기저인 것과 그것이 선형적으로 독립인 것은 필요충분 조건입니다.
$n$ 개의 원소를 갖는 $V$ 의 부분집합이 기저인 것과 그것이 $V$ 의 스팬하는 집합인 것은 필요충분 조건입니다.

Coordinates

$V$ 를 필드 $F$ 에 걸쳐 유한 차원 $n$ 의 벡터 공간이라고 놓고, 다음을 $V$ 의 기저라고 놓습니다: $B=\{\mathbf {b} _{1},\ldots ,\mathbf {b} _{n}\}$ 기저의 정의에 의해, $V$ 에서 모든 각 $v$ 는 고유한 방식에서 다음과 같이 쓸 수 있습니다: $\mathbf {v} =\lambda _{1}\mathbf {b} _{1}+\cdots +\lambda _{n}\mathbf {b} _{n},$ 여기서 계수 $\lambda _{1},\ldots ,\lambda _{n}$ 는 스칼라 (즉, $F$ 의 원소)이며, 이는 $B$ 에 걸쳐 $v$ 의 좌표(coordinates)라고 불립니다. 어쨌든, 계수의 집합에 대해 이야기하면, 계수와 기저 원소 사이의 대응 관계가 손실되고, 여러 벡터가 같은 계수의 집합을 가질 수 있습니다. 예를 들어, $3\mathbf {b} _{1}+2\mathbf {b} _{2}$ 와 $2\mathbf {b} _{1}+3\mathbf {b} _{2}$ 는 계수 ${2, 3}$ 의 같은 집합을 가지지만, 서로 다릅니다. 그러므로 순서화된 기저(ordered basis)로 작업하는 것이 편리한 경우가 많습니다; 이것은 전형적으로 기저 원소를 첫 번째 자연수로 인덱싱(indexing)함으로써 수행됩니다. 그런-다음, 벡터의 좌표는 유사하게 인덱싱된 수열(sequence)을 형성하고, 벡터는 좌표의 수열에 의해 완전히 특성화됩니다. 순서화된 기저는 좌표를 정의하는 기저를 허용하는 데이터의 수열을 참조하기 위해 다양한 맥락에서 공통적으로 사용되는 단어, 프레임(frame)이라고도 불립니다.

평소와 같이, $F^{n}$ 을 $F$ 의 원소의 $n$ -튜플( $n$ -tuples)의 집합이라고 놓습니다. 이 집합은 성분-별로 정의된 덧셈과 스칼라 곱셈을 갖는 $F$ -벡터 공간입니다. 다음 맵은 $\varphi :(\lambda _{1},\ldots ,\lambda _{n})\mapsto \lambda _{1}\mathbf {b} _{1}+\cdots +\lambda _{n}\mathbf {b} _{n}$ 벡터 공간 $F^{n}$ 에서 $V$ 위로의 선형 동형(linear isomorphism)입니다. 다시 말해서, $F^{n}$ 은 $V$ 의 좌표 공간(coordinate space)이고 $n$ -튜플 $\varphi ^{-1}(\mathbf {v} )$ 는 $v$ 의 좌표 벡터(coordinate vector)입니다.

$\mathbf {b} _{i}$ 의 $\varphi$ 에 의한 역 이미지(inverse image)는 1을 가지는 $i$ 번째를 제외하고 모든 성분이 0인 $n$ -튜플 $\mathbf {e} _{i}$ 입니다. $\mathbf {e} _{i}$ 는 $F^{n}$ 의 순서화된 기저를 형성하며, 이는 표준 기저(standard basis) 또는 정식의 기저(canonical basis)라고 불립니다. 순서화된 기저 $B$ 는 $F^{n}$ 의 정식의 기저의 $\varphi$ 에 의한 이미지입니다.

모든 각 순서화된 기저는 $F^{n}$ 의 정식의 기저의 선형 동형에 의한 이미지이고, $F^{n}$ 에서 $V$ 위로의 모든 각 선형 동형은 $F^{n}$ 의 정식의 기저를 $V$ 의 주어진 순서화된 기저 위로 매핑하는 동형으로 정의될 수 있다는 것이 앞의 내용에서 이어집니다. 다시 말해서, $V$ 의 순서화된 기저 또는 $F^{n}$ 에서 $V$ 위로의 선형 동형을 정의하는 것과 같습니다.

Change of basis

$V$ 를 필드 $F$ 에 걸쳐 차원 $n$ 의 벡터 공간이라고 놓습니다. $V$ 의 두 개의 (순서화된) 기저 $B_{\text{old}}=(\mathbf {v} _{1},\ldots ,\mathbf {v} _{n})$ 와 $B_{\text{new}}=(\mathbf {w} _{1},\ldots ,\mathbf {w} _{n})$ 가 주어지면, $B_{\mathrm {new} }$ 에 관한 좌표의 관점에서 $B_{\mathrm {old} }$ 에 관한 벡터 $x$ 의 좌표를 표현하는 것이 종종 유용합니다. 이것은 아래에 설명된 기저-의-변경 공식(change-of-basis formula)에 의해 수행될 수 있습니다. 아래첨자 "old"와 "new"는 $B_{\mathrm {old} }$ 와 $B_{\mathrm {new} }$ 를 각각 이전 기저(old basis)와 새로운 기저(new basis)라고 지칭하는 것이 일반적이기 때문에 선택되었습니다. 이전 좌표를 새로운 좌표의 관점에서 설명하는 것이 유용한데, 왜냐하면 일반적으로 이전 좌표와 관련된 표현(expressions)을 가지고, 새로운 좌표의 관점에서 동등한 표현을 얻기를 원하기 때문입니다; 이것은 이전 좌표를 새로운 좌표의 관점에서 표현에 의해 대체함으로써 얻습니다.

전형적으로, 새로운 기저 벡터는 이전 기저에 걸쳐 좌표에 의해 주어집니다. 즉, $\mathbf {w} _{j}=\sum _{i=1}^{n}a_{i,j}\mathbf {v} _{i}.$ 만약 $(x_{1},\ldots ,x_{n})$ 와 $(y_{1},\ldots ,y_{n})$ 는 각각 이전 기저와 새로운 기저에 걸쳐 벡터 $x$ 의 좌표이며, 기저-의-변경 공식은 $i = 1, ..., n$ 에 대해 다음과 같습니다: $x_{i}=\sum _{j=1}^{n}a_{i,j}y_{j},$ 이 공식은 행렬(matrix) 표기법으로 간결하게 쓸 수 있습니다. $A$ 를 $a_{i,j}$ 의 행렬이라고 놓고, 다음을 $X={\begin{bmatrix}x_{1}\\\vdots \\x_{n}\end{bmatrix}}\quad {\text{and}}\quad Y={\begin{bmatrix}y_{1}\\\vdots \\y_{n}\end{bmatrix}}$ 각각 이전 기저와 새로운 기저에서 $v$ 의 좌표의 열 벡터(column vectors)라고 놓으면, 좌표를 변경하기 위한 공식은 다음과 같습니다: $X=AY.$

공식은 두 가지 기저에서 벡터 $x$ 의 분해를 고려함으로써 입증될 수 있습니다: 우리는 다음을 가집니다, $\mathbf {x} =\sum _{i=1}^{n}x_{i}\mathbf {v} _{i},$ 및 $\mathbf {x} =\sum _{j=1}^{n}y_{j}\mathbf {w} _{j}=\sum _{j=1}^{n}y_{j}\sum _{i=1}^{n}a_{i,j}\mathbf {v} _{i}=\sum _{i=1}^{n}\left(\sum _{j=1}^{n}a_{i,j}y_{j}\right)\mathbf {v} _{i}.$

기저-의-변경 공식은 기저, 여기서 $B_{\text{old}}$ 에 걸쳐 벡터의 분해의 고유성에서 발생합니다; 즉, $i = 1, ..., n$ 에 대해, 다음입니다: $x_{i}=\sum _{j=1}^{n}a_{i,j}y_{j},$

Related notions

Free module

만약 벡터 공간의 정의에서 발생하는 필드를 링(ring)으로 대체하면, 모듈(module)의 정의를 얻습니다. 모듈에 대해, 선형 독립성(linear independence)과 스팬하는 집합(spanning sets)은 벡터 공간에 대해 정확히 정의되지만, "생성하는 집합(generating set)"은 "스팬하는 집합"보다 더 공통적으로 사용됩니다.

벡터 공간과 마찬가지로, 모듈의 기저(basis)는 생성하는 집합이기도 한 선형적으로 독립 부분집합입니다. 벡터 공간의 이론과의 주요 차이점은 모든 각 모듈이 기저를 가지는 것은 아니라는 것입니다. 기저를 가지는 모듈은 자유 모듈(free module)이라고 불립니다. 자유 모듈은 자유 분해(free resolutions)를 통해 비-자유 모듈의 구조를 설명하는 데 사용될 수 있으므로 모듈 이론에서 토대적인 역할을 합니다.

정수에 걸쳐 모듈은 아벨 그룹(abelian group)과 정확하게 같은 것입니다. 따라서 정수에 걸쳐 자유 모듈은 역시 자유 아벨 그룹입니다. 자유 아벨 그룹은 다른 링에 걸쳐 모듈에 의해 공유되지 않는 특정 속성을 가집니다. 구체적으로 특별히, 자유 아벨 그룹의 모든 각 부분그룹은 자유 아벨 그룹이고, 만약 $G$ 가 유한하게 생성된 자유 아벨 그룹 $H$ (즉, 유한 기저를 가지는 아벨 그룹)의 부분그룹이면, $a_{1}\mathbf {e} _{1},\ldots ,a_{k}\mathbf {e} _{k}$ 가 일부 비-영 정수 $a_{1},\ldots ,a_{k}$ 에 대해 $G$ 의 기저임을 만족하는 $H$ 의 기저 $\mathbf {e} _{1},\ldots ,\mathbf {e} _{n}$ 와 정수 $0 \leq k \leq n$ 가 있습니다. 자세한 내용에 대해, Free abelian group § Subgroups을 참조하십시오.

Analysis

실수 또는 복소수에 걸쳐 무한-차원 벡터 공간의 맥락에서, 하멜 기저(Hamel basis, 게오르크 하멜(Georg Hamel)의 이름을 따서 지음^[2]) 또는 대수적 기저(algebraic basis)라는 용어는 이 기사에서 정의된 기저를 참조하는 데 사용될 수 있습니다. 이것은 무한-차원 벡터 공간이 여분의 구조가 부여될 때 존재하는 "기저"의 다른 개념과 구별하기 위한 것입니다. 가장 중요한 대안은 힐베르트 공간(Hilbert spaces) 위의 직교 기저(orthogonal bases), 샤우데르 기저(Schauder bases), 및 노름 선형 공간(normed linear spaces) 위의 마르쿠세비치 기저(Markushevich bases)입니다. 유리수의 필드 Q에 걸쳐 벡터 공간으로 본 실수 R의 경우에서, 하멜 기저는 셀-수-없는 것이고, 특히 연속체의 카디널리티(cardinality)를 가지며, 이는 세는-숫자(cardinal number) $2^{\aleph _{0}}$ 이며, 여기서 $\aleph _{0}$ 는 가장 작은 무한 세는-수자, 정수의 세는-숫자입니다.

다른 개념의 공통적인 특징은 그것들이 공간을 생성하기 위해 기저 벡터의 무한 선형 조합을 허용한다는 것입니다. 이것은, 물론, 무한한 합이 토폴로지적 벡터 공간(topological vector spaces) – 예를 들어, 힐베르트 공간(Hilbert spaces), 바나흐 공간(Banach spaces), 또는 프레셰 공간(Fréchet spaces)을 포함하는 벡터 공간의 큰 클래스에 대한 경우와 같이 이들 공간 위에 의미 있게 정의되어야 함을 요구합니다.

무한-차원 공간에 대해 다른 유형의 기저를 선호하는 것은 하멜 기저가 바나흐 공간에서 "너무 커지게" 된다는 사실에 의해 정당화됩니다: 만약 X가 완비(complete)인 무한-차원 노름 벡터 공간이면 ((즉, X는 바나흐 공간), X의 임의의 하멜 기저는 반드시 셀-수-없는(uncountable) 것입니다. 이것이 베르 카테고리 정리(Baire category theorem)의 결과입니다. 완비성과 마찬가지로 무한 차원은 이전 주장에서 치명적인 가정입니다. 실제로, 유한-차원 공간은 정의에 의해 유한 기저를 가지고 셀-수-있는 하멜 기저를 가지는 무한 차원 (비-완비) 노름 공간이 있습니다. 노름 ${\textstyle \|x\|=\sup _{n}|x_{n}|}$ 을 갖는 오직 유한하게 많은 비-영 원소를 가지는 실수의 수열(sequences) $x=(x_{n})$ 의 공간, $c_{00}$ 를 생각해 보십시오. 1과 같은 유일한 하나의 비-영 원소를 가지는 수열로 구성된 표준 기저(standard basis)는 셀-수-있는 하멜 기저입니다.

Example

푸리에 급수(Fourier series)의 연구에서, 함수 ${1} \cup { sin(nx), cos(nx) : n = 1, 2, 3, ... }$ 는 구간 위에 제곱-적분가능인 구간 [0, 2π] 위에 모든 (실수 또는 복소-값) 함수, 즉, 다음을 만족시키는 함수 f의 (실수 또는 복소수) 벡터 공간의 "직교 기저"임을 압니다: $\int _{0}^{2\pi }\left|f(x)\right|^{2}\,dx<\infty .$

함수 ${1} \cup { sin(nx), cos(nx) : n = 1, 2, 3, ... }$ 는 선형적으로 독립이고, [0, 2π] 위에 제곱-적분가능인 모든 각 함수 f는 적절한 (실수 또는 복소수) 계수 a_k, b_k에 대해, 다음이라는 의미에서 그것들의 "무한 선형 조합"입니다: $\lim _{n\to \infty }\int _{0}^{2\pi }\left|a_{0}+\sum _{k=1}^{n}\left(a_{k}\cos \left(kx\right)+b_{k}\sin \left(kx\right)\right)-f(x)\right|^{2}dx=0$

그러나 많은^[3] 제곱-적분가능 함수가 이들 기저 함수의 유한 선형 조합으로 나타낼 수 없으며, 따라서 하멜 기저를 구성하지 않습니다. 이 공간의 모든 각 하멜 기저는 셀-수-있는 함수의 무한 집합보다 훨씬 더 큽니다. 이런 종류의 공간의 하멜 기저는 전형적으로 유용하지 않지만, 이들 공간의 직교-정규 기저(orthonormal bases)는 푸리에 해석(Fourier analysis)에서 필수적입니다.

Geometry

아핀 공간(affine space), 투영 공간(projective space), 볼록 집합(convex set), 및 원뿔(cone)의 기하학적 개념은 기저(basis)의 관련된 개념을 가집니다.^[4] n-차원 아핀 공간에 대해 아핀 기저(affine basis)는 일반 선형 위치(general linear position)에서 $n+1$ 점입니다. 투영 기저(projective basis)는 차원 n의 투영 공간에서, 일반적인 위치에서 $n+2$ 점입니다. 폴리토프의 볼록 기저(convex basis)는 그것의 볼록 껍질(convex hull)의 꼭짓점의 집합입니다. 원뿔 기저(cone basis)는^[5] 다각형 원뿔의 가장자리에 의한 한 점으로 구성됩니다. Hilbert basis (linear programming)도 참조하십시오.

Random basis

르베그 측정에 관한 n-차원 공에서 등분포와 같이 확률 밀도 함수(probability density function)를 갖는 $R n$ 에서 확률 분포(probability distribution)에 대해, $n$ 개의 무작위적이고 독립적으로 선택된 벡터가 확률 일을 갖는 기저를 형성한다는 것을 보여줄 수 있으며, 이는 $R n$ 에서 $n$ 개의 선형적으로 종속 벡터 $x 1$ , ..., $x n$ 이 방정식 $det[x 1 \dots x n] = 0$ (열 $x i$ 를 갖는 행렬의 영 행렬식)을 만족시켜야 하고, 비-자명한 다항식의 영들의 집합이 영 측정을 가져야 한다는 사실로 인한 것입니다. 이 관찰은 무작위 기저를 근사화하는 기술로 이어져 왔습니다.^[6]^[7]

높은 차원에서, 두 개의 독립적인 확률 벡터는 높은 확률로 거의 직교하고, 모두가 주어진 높은 확률로 쌍-별 거의 직교인 독립 확률 벡터의 숫자는 차원과 함께 지수적으로 증가합니다. 보다 정확하게, n-차원 공에서 등분포를 생각해 보십시오. 공에서 N개의 독립 확률 벡터를 선택합니다 (그것들은 독립적이고 동일하게 분포됩니다). θ를 작은 양수라고 놓습니다. 그런-다음 다음에 대해

N\leq e^{\frac {\varepsilon ^{2}n}{4}}[-\ln(1-\theta )]^{\frac {1}{2}}

(Eq. 1)

$N$ 개의 확률 벡터는 확률이 $1 - θ$ 를 갖는 모두 쌍-별 ε-직교입니다.^[7] 이 $N$ 은 충분하게 큰 $n$ 에 대해 차원 $n$ 과 $N\gg n$ 과 함께 지수적으로 증가합니다. 확률 기저의 이러한 속성은 소위 측정 농도 현상(measure concentration phenomenon)의 징후입니다.^[8]

그림 (오른쪽)은 차원 n의 함수로서 n-차원 입방체 $[-1, 1] n$ 에서 독립적으로 무작위로 표본화된 벡터의 쌍-별 거의 직교 체인의 길이 N의 분포를 보여줍니다. 한 점이 먼저 입방체에서 무작위로 선택됩니다. 두 번째 점은 같은 입방체에서 무작위로 선택됩니다. 만약 벡터 사이의 각도가 $π/2 \pm 0.037π/2$ 내에 있으면, 벡터가 유지됩니다. 다음 단계에서, 새로운 벡터가 같은 입방체에서 생성되고, 이전에 생성된 벡터와의 각도가 평가됩니다. 만약 이들 각도가 $π/2 \pm 0.037π/2$ 내에 있으면, 벡터가 유지됩니다. 그 과정은 거의 직교성의 체인이 끊어질 때까지 반복되고, 그러한 쌍-별 거의 직교 벡터의 숫자 (체인의 길이)가 기록됩니다. 각 n에 대해, 20 쌍-별 거의 직교 체인이 각 차원에 대해 수치적으로 구성되었습니다. 이들 체인의 길이 분포가 표시됩니다.

Proof that every vector space has a basis

$V$ 를 일부 필드 $F$ 에 걸쳐 임의의 벡터 공간이라고 놓습니다. $X$ 를 $V$ 의 모든 선형적으로 독립 부분집합의 집합이라고 놓습니다.

집합 $X$ 는 빈 집합이 $V$ 의 독립적인 부분집합이기 때문에 비-빈이고, 그것은 보통 $\subseteq$ 에 의해 표시되는 포함에 의한 부분적으로 순서화된(partially ordered) 것입니다.

$Y$ 를 $\subseteq$ 에 의해 전체적으로 순서화된 $X$ 의 부분집합이라고 놓고, $L Y$ 를 $Y$ 의 모든 원소 (이는 $V$ 의 자체의 특정 부분집합)의 합집합이라고 놓습니다.

$(Y, \subseteq)$ 가 전체적으로 순서화되어 있으므로, $L Y$ 의 모든 각 유한 부분집합은 $V$ 의 선형적으로 독립 부분집합인 $Y$ 의 원소의 부분 집합이고, 따라서 $L Y$ 는 선형적으로 독립입니다. 따라서 $L Y$ 는 $X$ 의 원소입니다. 그러므로, $L Y$ 는 $(X, \subseteq)$ 에서 $Y$ 의 위쪽 경계입니다: 그것은 $Y$ 의 모든 각 원소를 포함하는 $X$ 의 원소입니다.

$X$ 가 비-빈이고, $(X, \subseteq)$ 의 모든 각 전체적으로 순서화된 부분집합은 $X$ 에서 위쪽 경계를 가지기 때문에, 조온의 보조정리(Zorn's lemma)는 $X$ 가 최대한의 원소를 가진다고 주장합니다. 다시 말해서, $X$ 의 일부 원소 $L$ 에 대해 $L max \subseteq L$ 일 때마다 $L = L max$ 라는 조건을 만족시키는 $X$ 의 일부 원소 $L max$ 가 존재합니다.

이제 $L max$ 가 $V$ 의 기저임을 증명하는 것이 남아 있습니다. $L max$ 가 $X$ 에 속하므로, 우리는 $L max$ 가 $V$ 의 선형적으로 독립 부분집합임을 이미 알고 있습니다.

만약 $L max$ 의 스팬에 있지 않는 $V$ 의 일부 벡터 $w$ 가 있으면, $w$ 도 $L max$ 의 원소가 아닙니다. $L w = L max \cup {w}$ 라고 놓습니다. 이 집합은 $X$ 의 원소이며, 즉, 그것은 $V$ 의 선형적으로 독립 부분집합입니다 (왜냐하면 $w$ 는 $L max$ 의 스팬 안에 있지 않고, $L max$ 는 독립적이기 때문입니다). $L max \subseteq L w$ 이고 $L max \neq L w$ 이므로 (왜냐하면 $L w$ 는 $L max$ 에 포함되지 않은 벡터 $w$ 를 포함하기 때문에), 이것은 $L max$ 의 최대성과 모순됩니다. 따라서 이것은 $L max$ 가 $V$ 를 스팬함을 보여줍니다.

따라서 $L max$ 는 선형적으로 독립적이고 $V$ 를 스팬합니다. 그것은 따라서 $V$ 의 기저이고, 이것은 모든 각 벡터 공간이 기저를 가짐을 입증합니다.

이 증명은 선택의 공리(axiom of choice)에 동등한 조온의 보조정리에 의존합니다. 반대로, 만약 모든 각 벡터 공간이 기저를 가지면 선택의 공리가 참이라는 것이 입증되었습니다.^[9] 따라서 두 주장은 동등합니다.

Notes

^ Halmos, Paul Richard (1987). Finite-Dimensional Vector Spaces (4th ed.). New York: Springer. p. 10. ISBN 978-0-387-90093-3.
^ Hamel 1905
^ Note that one cannot say "most" because the cardinalities of the two sets (functions that can and cannot be represented with a finite number of basis functions) are the same.
^ Rees, Elmer G. (2005). Notes on Geometry. Berlin: Springer. p. 7. ISBN 978-3-540-12053-7.
^ Kuczma, Marek (1970). "Some remarks about additive functions on cones". Aequationes Mathematicae. 4 (3): 303–306. doi:10.1007/BF01844160. S2CID 189836213.
^ Igelnik, B.; Pao, Y.-H. (1995). "Stochastic choice of basis functions in adaptive function approximation and the functional-link net". IEEE Trans. Neural Netw. 6 (6): 1320–1329. doi:10.1109/72.471375. PMID 18263425.
^ ^a ^b ^c Gorban, Alexander N.; Tyukin, Ivan Y.; Prokhorov, Danil V.; Sofeikov, Konstantin I. (2016). "Approximation with Random Bases: Pro et Contra". Information Sciences. 364–365: 129–145. arXiv:1506.04631. doi:10.1016/j.ins.2015.09.021. S2CID 2239376.
^ Artstein, Shiri (2002). "Proportional concentration phenomena of the sphere" (PDF). Israel Journal of Mathematics. 132 (1): 337–358. CiteSeerX 10.1.1.417.2375. doi:10.1007/BF02784520. S2CID 8095719.
^ Blass 1984

References

General references

Blass, Andreas (1984), "Existence of bases implies the axiom of choice" (PDF), Axiomatic set theory, Contemporary Mathematics volume 31, Providence, R.I.: American Mathematical Society, pp. 31–33, ISBN 978-0-8218-5026-8, MR 0763890
Brown, William A. (1991), Matrices and vector spaces, New York: M. Dekker, ISBN 978-0-8247-8419-5
Lang, Serge (1987), Linear algebra, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96412-6

Historical references

Banach, Stefan (1922), "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)" (PDF), Fundamenta Mathematicae (in French), 3: 133–181, doi:10.4064/fm-3-1-133-181, ISSN 0016-2736
Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) (in German)
Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics) (in French), Paris: Hermann
Dorier, Jean-Luc (1995), "A general outline of the genesis of vector space theory", Historia Mathematica, 22 (3): 227–261, doi:10.1006/hmat.1995.1024, MR 1347828
Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (in French), Chez Firmin Didot, père et fils
Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (in German), reprint: Hermann Grassmann. Translated by Lloyd C. Kannenberg. (2000), Extension Theory, Kannenberg, L.C., Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2031-5
Hamel, Georg (1905), "Eine Basis aller Zahlen und die unstetigen Lösungen der Funktionalgleichung f(x+y)=f(x)+f(y)", Mathematische Annalen (in German), 60 (3), Leipzig: 459–462, doi:10.1007/BF01457624, S2CID 120063569
Hamilton, William Rowan (1853), Lectures on Quaternions, Royal Irish Academy
Möbius, August Ferdinand (1827), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) (in German), archived from the original on 2009-04-12
Moore, Gregory H. (1995), "The axiomatization of linear algebra: 1875–1940", Historia Mathematica, 22 (3): 262–303, doi:10.1006/hmat.1995.1025
Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (in Italian), Turin{{citation}}: CS1 maint: location missing publisher (link)

External links

Instructional videos from Khan Academy
- Introduction to bases of subspaces
- Proof that any subspace basis has same number of elements
"Linear combinations, span, and basis vectors". Essence of linear algebra. August 6, 2016. Archived from the original on 2021-11-17 – via YouTube.
"Basis", Encyclopedia of Mathematics, EMS Press, 2001 [1994]

[1] Halmos, Paul Richard (1987). Finite-Dimensional Vector Spaces (4th ed.). New York: Springer. p. 10. ISBN 978-0-387-90093-3.

[2] Hamel 1905

[3] Note that one cannot say "most" because the cardinalities of the two sets (functions that can and cannot be represented with a finite number of basis functions) are the same.

[4] Rees, Elmer G. (2005). Notes on Geometry. Berlin: Springer. p. 7. ISBN 978-3-540-12053-7.

[5] Kuczma, Marek (1970). "Some remarks about additive functions on cones". Aequationes Mathematicae. 4 (3): 303–306. doi:10.1007/BF01844160. S2CID 189836213.

[6] Igelnik, B.; Pao, Y.-H. (1995). "Stochastic choice of basis functions in adaptive function approximation and the functional-link net". IEEE Trans. Neural Netw. 6 (6): 1320–1329. doi:10.1109/72.471375. PMID 18263425.

[GorbanTyukin2016-7] Gorban, Alexander N.; Tyukin, Ivan Y.; Prokhorov, Danil V.; Sofeikov, Konstantin I. (2016). "Approximation with Random Bases: Pro et Contra". Information Sciences. 364–365: 129–145. arXiv:1506.04631. doi:10.1016/j.ins.2015.09.021. S2CID 2239376.

[8] Artstein, Shiri (2002). "Proportional concentration phenomena of the sphere" (PDF). Israel Journal of Mathematics. 132 (1): 337–358. CiteSeerX 10.1.1.417.2375. doi:10.1007/BF02784520. S2CID 8095719.

[9] Blass 1984

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]