Subgroup

Original article: w:Subgroup

For other uses, see Subgroup (disambiguation).

그룹 이론(group theory), 수학(mathematics)의 한 가지에서, 이항 연산(binary operation) ∗ 아래에서 그룹(group) G가 주어지면, G의 부분집합(subset) H는 만약 H도 연산 ∗ 아래에서 그룹을 형성하면 G의 부분그룹이라고 불립니다. 보다 정확하게, H는 만약 H × H에 대한 ∗의 제한(restriction)이 H 위에 그룹 연산이면 G의 부분그룹입니다. 이것은 종종 H ≤ G로 표시되며, "H는 G의 부분그룹이다"라고 읽습니다.

임의의 그룹의 자명한 부분그룹(trivial subgroup)은 항등 원소로만 구성된 부분그룹 {e}입니다.

그룹 G의 적절한 부분그룹(proper subgroup)은 G의 적절한 부분집합 (즉, H ≠ G)인 부분그룹 H입니다. 이것은 종종 표기법적으로 H < G에 의해 표시되며 "H는 G의 적절한 부분그룹이다"라고 읽습니다. 일부 저자는 역시 자명한 그룹을 적절한 것 (즉, H ≠ {e})에서 제외합니다.

만약 H가 G의 부분그룹이면, G는 때때로 H의 초과그룹(overgroup)이라고 불립니다.

같은 정의는 G가 임의적인 반그룹(semigroup)일 때 보다 일반적으로 적용되지만, 이 기사는 그룹의 부분그룹만 다룰 것입니다.

Subgroup tests

G가 그룹이고, H가 G의 부분집합이라고 가정합니다. 지금은, G의 그룹 연산이 병치에 의해 표시되는 곱셈적으로 작성된다고 가정합니다.

• 그런-다음 H가 G의 부분그룹인 것과 H가 비-빈이고 곱과 역 아래에서 닫힌(closed) 것은 필요충분 조건입니다. 곱 아래에서 닫힘(Closed under products)은 H에서 모든 각 a와 b에 대해 곱 ab가 H 안에 있음을 의미합니다. 역 아래에서 닫힘(Closed under inverses)은 H에서 모든 각 a에 대해, 역 a⁻¹가 H 안에 있음을 의미합니다. 이들 두 조건은 하나로, 즉 H에 있는 모든 각 a와 b에 대해 원소 ab⁻¹가 H 안에 있다는 것으로 결합될 수 있지만, 두 개의 닫힘 조건을 개별적으로 테스트하는 것이 더 자연스럽고 보통 더 쉽습니다.
• H가 유한한 것일 때, 그 테스트는 단순화될 수 있습니다: H가 부분그룹인 것과 그것이 비-빈이고 곱 아래에 닫혀 있는 것은 필요충분 조건입니다. 이들 조건 단독으로 H의 모든 각 원소 a가 H의 유한한 순환 부분그룹, 말하자면 차수 n을 생성하고, 그런-다음 a의 역은 aⁿ⁻¹이라는 것을 의미합니다.

만약 그룹 연산이 대신 덧셈에 의해 표시되면, 곱 아래에서 닫힘은 H에서 모든 각 a와 b에 대해, 합 a+b가 H 안에 있는 조건으로 대체되어야 하고, 역 아래에서 닫힘은 H에서 모든 각 a에 대해, 역 −a는 H 안에 있다는 조건에 의해 대체되어야 합니다.

Basic properties of subgroups

• 부분그룹의 항등원(identity)은 그룹의 항등원입니다: 만약 G가 항등원 e_G를 갖는 그룹이고, H가 항등원 e_H를 갖는 G의 부분그룹이면, e_H = e_G입니다.
• 부분그룹에 있는 원소의 역(inverse)은 그룹에 있는 원소의 역입니다: 만약 H가 그룹 G의 부분그룹이고, a와 b가 ab = ba = e_H임을 만족하는 H의 원소이면, ab = ba = e_G입니다.
• 만약 H가 G의 부분그룹이면, H의 각 원소 a를 자신에게 보내는 포함 맵 H → G는 준동형(homomorphism)입니다.
• G의 부분그룹 A와 B의 교집합(intersection)은 다시 G의 부분그룹입니다. 예를 들어, 덧셈 아래에서 R²에서 x-축과 y-축의 교차점은 자명한 부분그룹입니다. 보다 일반적으로, G의 부분그룹의 임의적인 모음의 교집합은 G의 부분그룹입니다.
• 부분그룹 A와 B의 합집합(union)이 부분그룹인 것과 A ⊆ B 또는 B ⊆ A인 것은 필요충분 조건입니다. 비-예제: 2Z ∪ 3Z는 Z의 부분그룹이 아닌데, 왜냐하면 2와 3은 이 부분집합의 원소이지만 그 합, 5는 그 부분집합에 있지 않기 때문입니다. 마찬가지로, R²에서 x-축과 y-축의 합집합은 R²의 부분그룹이 아닙니다.
• 만약 S가 G의 부분집합이면, S를 포함하는 가장 작은 부분그룹, 즉 S를 포함하는 모든 부분그룹의 교집합이 존재합니다; 그것은 ⟨S⟩에 의해 표시되고 S에 의해 생성된 부분그룹이라고 불립니다. G의 원소가 ⟨S⟩ 안에 있는 것과 그것이 S의 원소와 그 역의 유한 곱–반복될 수 있음–인 것은 필요충분 조건입니다.
• 그룹 G의 모든 각 원소 a는 순환 부분그룹 ⟨a⟩를 생성합니다. 만약 ⟨a⟩가 일부 양의 정수 n에 대해 Z/nZ (정수 모드 n)과 동형적이면, n은 aⁿ = e인 가장 작은 양의 정수이고, n은 a의 차수(order)라고 불립니다. 만약 ⟨a⟩가 Z와 동형적이면, a는 무한 차수(infinite order)를 가진다고 말합니다.
• 임의의 주어진 그룹의 부분그룹은 부분그룹의 격자(lattice of subgroups)라고 불리는 포함 아래에서 완비 격자(complete lattice)를 형성합니다. (여기서 하한( infimum)은 보통의 집합-이론적 교집합이지만, 부분그룹의 집합의 상한(supremum)은 집합-이론적 합집합 자체가 아니라 부분그룹의 집합-이론적 합집합에 의해 생성된 부분그룹입니다.) 만약 e가 G의 항등원이면, 자명한 그룹 {e}는 G의 최소(minimum) 부분그룹이고, 반면에 최대(maximum) 부분그룹은 그룹 G 자체입니다.

G is the group $\mathbb {Z} /8\mathbb {Z}$, the integers mod 8 under addition. The subgroup H contains only 0 and 4, and is isomorphic to $\mathbb {Z} /2\mathbb {Z}$. There are four left cosets of H: H itself, 1+H, 2+H, and 3+H (written using additive notation since this is an additive group). Together they partition the entire group G into equal-size, non-overlapping sets. The index [G : H] is 4.

Cosets and Lagrange's theorem

Main articles: Coset and Lagrange's theorem (group theory)

부분그룹 H와 G에서 일부 a가 주어지면, 우리는 왼쪽 코셋(coset) aH = {ah : h in H}를 정의합니다. a는 역-가능이기 때문에, φ(h) = ah에 의해 주어진 맵 φ : H → aH는 전단사(bijection)입니다. 더욱이, G의 모든 각 원소는 H의 정확하게 하나의 왼쪽 코셋에 포함됩니다; 왼쪽 코셋은 동치 관계(equivalence relation) a₁ ~ a₂인 것과 a₁⁻¹a₂가 H 안에 있는 것은 필요충분 조건에 해당하는 동치 클래스입니다. H의 왼쪽 코셋의 숫자는 G에서 H의 인덱스(index)라고 불리고 [G : H]에 의해 표시됩니다.

라그랑주의 정리(Lagrange's theorem)는 유한 그룹 G와 부분그룹 H에 대해 다음과 같이 말합니다:

$[G:H]={|G| \over |H|}$

여기서 |G|와 |H|는 각각 G와 H의 차수(orders)를 나타냅니다. 특히, G의 모든 각 부분그룹의 차수 (및 G의 모든 각 원소의 차수)는 |G|의 약수(divisor)여야 합니다.

오른쪽 코셋(Right cosets)은 유사하게 정의됩니다: Ha = {ha : h in H}. 그것들은 역시 적절한 동치 관계에 대해 동치 클래스이고 그것들의 숫자는 [G : H]와 같습니다.

만약 G에서 모든 각 a에 대해 aH = Ha이면, H는 정규 부분그룹(normal subgroup)이라고 말합니다. 인덱스 2의 모든 각 부분그룹은 정규적입니다: 왼쪽 코셋과 역시 오른쪽 코셋은 단순히 부분그룹과 그것의 여집합입니다. 보다 일반적으로, 만약 p가 유한 그룹 G의 차수를 나누는 가장 낮은 소수이면, 인덱스 p의 임의의 부분그룹 (존재하는 경우)은 정규적입니다.

Example: Subgroups of Z₈

G를 그것의 원소가 다음과 같은 순환 그룹(cyclic group) Z₈이라고 놓습니다:

$G=\left\{0,4,2,6,1,5,3,7\right\}$

그리고 그것의 그룹 연산은 덧셈 모듈로 8(addition modulo 8)입니다. 그것의 케일리 테이블(Cayley table)은 다음과 같습니다:

+	0	4	2	6	1	5	3	7
0	0	4	2	6	1	5	3	7
4	4	0	6	2	5	1	7	3
2	2	6	4	0	3	7	5	1
6	6	2	0	4	7	3	1	5
1	1	5	3	7	2	6	4	0
5	5	1	7	3	6	2	0	4
3	3	7	5	1	4	0	6	2
7	7	3	1	5	0	4	2	6

이 그룹은 두 개의 비-자명한 부분그룹을 가집니다: ■ J = {0, 4} 및 ■ H = {0, 4, 2, 6} , 여기서 J는 H의 부분그룹이기도 합니다. H에 대한 케일리 테이블이 G에 대한 케일리 테이블의 꼭대기-왼쪽 사분면입니다; J에 대한 케일리 테이블은 H에 대한 케일리 테이블의 꼭대기-왼쪽 사분면입니다. 그룹 G는 순환적(cyclic)이고, 그것의 부분그룹도 마찬가지입니다. 일반적으로, 순환 그룹의 부분그룹도 순환적입니다.

Example: Subgroups of S₄

S₄를 4개 원소의 대칭 그룹(symmetric group)이라고 놓습니다. 아래는 원소의 숫자에 따라 내림차순으로 나열된 S₄의 모든 부분그룹입니다.

24 elements

전체 그룹 S₄는 차수 24의 S₄의 부분그룹입니다. 그것의 케일리 테이블은 다음과 같습니다:

The symmetric group S4 showing all permutations of 4 elements

All 30 subgroups Simplified Hasse diagrams of the lattice of subgroups of S4

12 elements

The alternating group A₄ showing only the even permutations

Subgroups:

8 elements

Dihedral group of order 8 Subgroups:

Dihedral group of order 8 Subgroups:

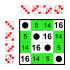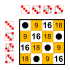Dihedral group of order 8 Subgroups: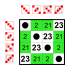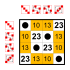

6 elements

Symmetric group S3 Subgroup:

Symmetric group S3 Subgroup:

Symmetric group S3 Subgroup:

Symmetric group S3 Subgroup:

4 elements

Klein four-group

Klein four-group

Klein four-group

Klein four-group

Cyclic group Z4

Cyclic group Z4

Cyclic group Z4

3 elements

Cyclic group Z3

Cyclic group Z3

Cyclic group Z3

Cyclic group Z3

2 elements

S₄에서 차수 2의 각 원소 s는 차수 2의 부분그룹 $\{1,s\}$를 생성합니다. 그러한 원소는 9개입니다: ${\binom {4}{2}}=6$ 전치(transpositions) (2-순환) 및 세 원소 (12)(34), (13)(24), (14)(23).

1 element

자명한 부분그룹(trivial subgroup)은 S₄에서 차수 1의 고유한 부분그룹입니다.

Other examples

• 짝수 정수는 정수 링(integer ring) Z의 부분그룹 2Z를 형성합니다: 두 개의 짝수 정수의 합은 짝수이고, 짝수 정수의 음수는 짝수입니다.
• 링 $R$에서 아이디얼(ideal)은 $R$의 덧셈 그룹의 부분그룹입니다.
• 벡터 공간(vector space)의 선형 부분공간(linear subspace)은 벡터의 덧셈 그룹의 부분그룹입니다.
• 아벨 그룹(abelian group)에서, 유한 차수(order)의 원소는 꼬임 부분그룹(torsion subgroup)이라고 불리는 부분그룹을 형성합니다.

See also

• Cartan subgroup
• Fitting subgroup
• Stable subgroup
• Fixed-point subgroup

References

• Jacobson, Nathan (2009), Basic algebra, vol. 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1.
• Hungerford, Thomas (1974), Algebra (1st ed.), Springer-Verlag, ISBN 9780387905181.
• Artin, Michael (2011), Algebra (2nd ed.), Prentice Hall, ISBN 9780132413770.
• Dummit, David S.; Foote, Richard M. (2004). Abstract algebra (3rd ed.). Hoboken, NJ: Wiley. ISBN 9780471452348. OCLC 248917264.
• Gallian, Joseph A. (2013). Contemporary abstract algebra (8th ed.). Boston, MA: Brooks/Cole Cengage Learning. ISBN 978-1-133-59970-8. OCLC 807255720.
• Kurzweil, Hans; Stellmacher, Bernd (1998). Theorie der endlichen Gruppen. Springer-Lehrbuch. doi:10.1007/978-3-642-58816-7.
• Ash, Robert B. (2002). Abstract Algebra: The Basic Graduate Year. Department of Mathematics University of Illinois.