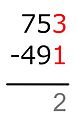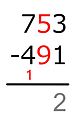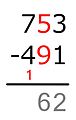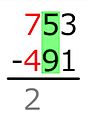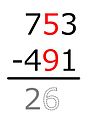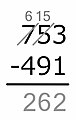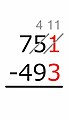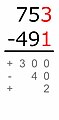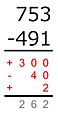Subtraction

Original article: w:Subtraction

"5 − 2 = 3" (verbally, "five minus two equals three")

Placard outside a shop in Bordeaux advertising subtraction of 20% from the price of the second perfume purchased.

뺄셈(subtraction)은 모음으로부터 대상을 제거하는 연산을 나타내는 산술 연산(arithmetic operation)입니다. 뺄셈의 결과는 차이(difference)이라고 불립니다. 뺄셈은 음의 부호(minus sign), −에 의해 의미됩니다. 예를 들어, 인접한 그림에서, 5 − 2 사과가 있습니다—5 사과에서 2 사과를 제거함을 의미하며, 전체 3 사과를 초래합니다. 그러므로, 5와 2의 차이는 3입니다. 즉, 5 − 2 = 3입니다. 주로 산술(arithmetic)에서 자연수와 관련되지만, 뺄셈은 음수(negative number), 분수(fractions), 무리수(irrational number), 벡터(vectors), 십진수, 함수, 및 행렬을 포함한 다양한 종류의 대상을 사용하여 물리 및 추상적 양을 제거하거나 감소시키는 것을 역시 나타낼 수 있습니다.

뺄셈은 여러 가지 중요한 패턴을 따릅니다. 그것은 반-교환적(anticommutative)이며, 순서를 바꾸는 것은 답의 부호가 바뀌는 것을 의미합니다. 그것은 역시 결합적(associative)이 아니며, 우리가 둘보다 많은 것을 뺄 때, 뺄셈이 수행되는 순서가 중요함을 의미합니다. 0은 덧셈의 항등원(additive identity)이기 때문에, 그것의 뺄셈은 숫자를 바꾸지 않습니다. 뺄셈은 덧셈(addition) 및 곱셈(multiplication)과 같은, 관련된 연산을 관련하여 예측-가능한 규칙을 역시 순종합니다. 이들 규칙의 모두는, 정수(integers)의 뺄셈부터 시작하고 실수(real number)와 그것 이상을 통해 일반화된 것으로, 입증(proven)될 수 있습니다. 이들 패턴을 따르는 일반적인 이항 연산(binary operations)은 추상 대수학(abstract algebra)에서 연구됩니다.

자연수에서 뺄셈을 수행하는 것은 가장 간단한 수치 임무 중에 하나입니다. 아주 작은 숫자의 뺄셈은 어린 아이들에게 접근될 수 있습니다. 초등 교육(primary education)에서, 학생들은 십진법(decimal) 시스템에서, 한 자릿수부터 시작하여 더 어려운 문제를 점진적으로 해결하기 위해서, 숫자를 빼는 것을 배웁니다.

고급 대수학 및 컴퓨터 대수학(computer algebra)에서, A − B와 같은 뺄셈을 포함하는 표현은 덧셈 A + (−B)에 대해 속기 표기법으로 일반적으로 취급됩니다. 따라서, A − B는 두 항, 즉 A와 −B를 포함합니다. 이것은 결합성(associativity) 및 교환성(commutativity)의 더 쉬운 사용을 허용합니다.

Notation and terminology

Subtraction of numbers 0–10. Line labels = minuend. X axis = subtrahend. Y axis = difference.

뺄셈은 보통 항 사이에, 즉, 중위 표기법(infix notation)에서, 음의 기호(minus sign) "−"를 사용하여 쓰입니다; 그 결과는 같음 기호(equals sign)로 표시됩니다. 예를 들어,

$2-1=1$ (pronounced as "two minus one equals one")

$4-2=2$ (pronounced as "four minus two equals two")

$6-3=3$ (pronounced as "six minus three equals three")

$4-6=-2$ (pronounced as "four minus six equals negative two")

비록 기호가 나타나지 않을지라도, 역시 뺄셈이 "이해되는" 상황이 있습니다:

• 빨간색에서 더 낮은 숫자를 갖는, 두 숫자의 열은, 열에서 더 낮은 숫자가, 선 아래에서, 밑에 쓰인 차이를 갖는 빼진 것임을 보통 나타냅니다.

공식적으로, 빼는 숫자는 감수(subtrahend)로 알려져 있지만, 그것으로부터 빼지게 되는 숫자는 피감수(minuend)입니다. 그 결과는 차이입니다.

이 용어의 모두는 라틴어(Latin)에서 파생되었습니다. "뺄셈(Subtraction)"은 라틴어 동사(verb) subtrahere로부터 파생된 영어(English) 단어이며, 이것은 차례로 sub "from under" 및 trahere "to pull"의 합성어(compound)입니다. 따라서, 빼는 것은 draw from below는 것, 또는 take away는 것입니다. 동명사(gerundive) 접미사(suffix) -nd를 사용하는 것은 "subtrahend", "thing to be subtracted"을 초래합니다. 마찬가지로, minuere로부터 "감소 또는 줄이는 것"에서, 우리는 "줄어드는 것"을 의미하는 "minuend"를 얻습니다.

Of integers and real numbers

Integers

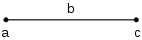
왼쪽 끝에 a로 이름이 붙고 오른쪽 끝에 c로 이름이 붙은 길이(length) b의 선분(line segment)을 생각해 보십시오. a에서 시작하여, 오른쪽으로 c에 도달하기 위해 b 걸음을 취합니다. 오른쪽으로 이 이동은 덧셈(addition)에 의해 수학적으로 모델링됩니다:

a + b = c.

c로부터, 다시 a로 돌아가기 위해 왼쪽으로 b 걸음을 취합니다. 왼쪽으로 이 이동은 뺄셈에 의해 모델링됩니다:

c − b = a.

이제, 선분에 숫자 1, 2, 및 3을 갖는 이름을 붙입니다. 위치 3으로부터, 3에 머무르기 위해 왼쪽으로 걸음을 옮기지 않으므로, 3 − 0 = 3입니다. 위치 1을 얻기 위해 왼쪽으로 2 걸음을 취하므로, 3 − 2 = 1입니다. 이 그림은 위치 3의 왼쪽으로 3 걸음 이동 후 일어날 일을 설명하기에는 부적절합니다. 그러한 연산을 나타내기 위해, 직선이 확장되어야 합니다.

임의의 자연수(natural number)를 빼기 위해, 우리는 모든 각 자연수 (0, 1, 2, 3, 4, 5, 6, ...)를 포함하는 직선으로 시작합니다. 3으로부터, 0을 얻기 위해 왼쪽으로 3 걸음을 취하므로, 3 − 3 = 0입니다. 그러나, 3 − 4는 여전히 불가능한데, 왜냐하면 그것은 직선을 벗어나기 때문입니다. 자연수는 뺄셈에 대해 유용한 문맥은 아닙니다.

그 해는 정수(integer) 숫자 직선(number line) (..., −3, −2, −1, 0, 1, 2, 3, ...)을 고려하는 것입니다. 이 방법, 3으로부터 −1을 얻기 위해 왼쪽으로 4 걸음을 취합니다:

3 − 4 = −1.

Natural numbers

자연수(natural numbers)의 뺄셈은 닫혀(closed)있지 않습니다 : 차이는 만약 빼는 숫자가 빼지는 숫자보다 크거나 같지 않으면 자연수가 아닙니다. 예를 들어, 26은 11로부터 자연수를 얻기 위해 빼질 수 없습니다. 그러한 경우는 다음 두 가지 접근 중 하나를 사용합니다:

1. 26은 11에서 빼질 수 없다는 결론을 내립니다; 뺄셈은 부분 함수(partial function)가 됩니다.
2. 음수(negative number)를 나타내는 정수(integer)로 답을 제공하므로, 11에서 26을 뺀 결과는 –15입니다.

Real numbers

실수의 뺄셈은 부호화된 숫자의 덧셈으로 정의됩니다. 구체적으로, 숫자는 3 − π = 3 + (−π)의 경우에서 처럼 그것의 덧셈의 역(additive inverse)을 더함으로써 빼집니다. 이것은 뺄셈과 같은 "새로운" 연산자의 도입을 피함으로써 실수의 링(ring)을 "단순"하게 유지하는 데 도움이 됩니다. 보통, 링은 그것에 정의된 오직 두 연산을 가집니다; 정수의 경우에서, 이것들은 덧셈과 곱셈입니다. 링은 이미 덧셈 역의 개념을 가지지만, 그것은 구별되는 뺄셈 연산의 임의의 개념을 가지지 않으므로, 뺄셈으로 부호화된 덧셈의 사용은–아무것도 증명할 필요없이–링 공리의 응용을 뺄셈에 허용합니다.

Properties

Anticommutativity

뺄셈은 반-교환적(anti-commutative)이며, 만약 우리가 차이에서 항을 왼쪽-에서-오른쪽으로 거꾸로 하면, 그 결과는 원래 결과의 음수임을 의미합니다. 기호적으로, 만약 a와 b가 임의의 두 숫자이면, 다음입니다:

a − b = −(b − a).

Non-associativity

뺄셈은 비-결합적(non-associative)이며, 이것은 우리가 반복된 뺄셈을 정의하려고 시도할 때 나타납니다. 일반적으로, 다음 표현은

"a − b − c"

(a − b) − c 또는 a − (b − c) 중 하나를 의미하는 것으로 정의될 수 있지만, 이들 두 가능성은 다른 답으로 이어집니다. 이 문제를 해결하기 위해, 우리는 다른 결과를 산출하는 다른 순서를 갖는 연산의 순서(order of operations)를 수립해야 합니다.

Predecessor

정수의 맥락에서, 일(one)의 뺄셈은 역시 특별한 역할을 합니다: 임의의 정수 a에 대해, 정수 (a − 1)는 a보다 작은 가장 큰 정수이며, 역시 a의 이전수로 알려져 있습니다.

Units of measurement

킬로그램(kilogram) 또는 파운드(pound)와 같은 측정의 단위를 갖는 두 숫자를 뺄 때, 그것들은 같은 단위를 가져야 합니다. 대부분의 경우에서, 차이는 원래 숫자와 같은 단위를 가집니다.

Percentages

백분율(percentage)에서 변화는 적어도 두 형식, 백분율 변화(percentage change) 및 백분율 점수(percentage point) 변화에서 보고될 수 있습니다. 백분율 변화는 두 양 사이의 상대적 변화를 백분율로 나타내지만, 백분율 점수 변화는 단순히 두 백분율을 뺌으로써 얻어진 숫자입니다.

예제로써, 공장에서 만든 위젯의 30%가 결함이라고 가정합니다. 6 개월 후, 위젯의 20%가 결함이 있습니다. 백분율 변화는 20% − 30%/30% = −1/3 = −33+1/3%이지만, 백분열 점수 변화는 −10 백분율 점수입니다.

In computing

여수의 방법(method of complements)은 오직 양수의 덧셈을 사용하여 한 숫자를 다른 숫자로부터 빼기 위해 사용되는 기법입니다. 이 방법은 기계식 계산기(mechanical calculator)에서 공통적으로 사용되었었고, 현대 컴퓨터(computers)에서 여전히 사용됩니다.

이진 자릿수	일의 여수
0	1
1	0

이진수 y (빼는 숫자)를 또 다른 숫자 x (빼지는 숫자)에서 빼기 위해, y의 일의 여수가 x에 더하고 일이 그 합에 더합니다. 그 결과의 선행 숫자 "1"은 그때에 버립니다.

여수의 방법은 이진법 (밑수 2)에서 특히 유용한데 왜냐하면 일의 보수는 각 비트를 거꾸로 함으로써 ("0"을 "1"로 바꾸고 그 반대도 마찬가지) 매우 쉽게 얻어지기 때문입니다. 그리고 이의 여수를 얻기 위해 1을 더하는 것은 최소 유효숫자 비트로의 올림을 모의실험함으로써 행해질 수 있습니다. 예를 들어:

  01100100  (x, equals decimal 100)
- 00010110  (y, equals decimal 22)

다음 합이 됩니다:

  01100100  (x)
+ 11101001  (ones' complement of y)
+        1  (to get the two's complement)
——————————
 101001110

첫수 "1"을 버리면 답을 제공합니다: 01001110 (십진수 78과 같습니다)

The teaching of subtraction in schools

초등 학교(elementary school)에서 뺄셈을 가르치는 데 사용되는 방법은 국가마다 다르고, 국가 내에서, 다른 방법이 다른 시간에 채택됩니다. 미국에서 전통 수학(traditional mathematics)으로 알려진 수학에서, 특정 과정은 여러-자릿수 정수와 함께 사용하기 위해 1학년 말 (또는 2학년 동안)에 학생들에게 가르쳐지고, 4학년 또는 5학년에서 분수의 십진 표현(decimal representations(을 포함하기 위해 확장됩니다.

In America

현재 거의 모든 미국 학교는 빌림 또는 재그룹화 (분해 알고리듬)을 사용하여 뺄셈의 방법과 목발이라고 불리는 표시의 시스템을 가르칩니다. 비록 빌림의 방법이 이전 교과서에서 알려지고 출판되어 왔지만, 윌리엄 브라우넬(William A. Brownell)이—목발이 이 방법을 사용하여 학생들에게 유익하다고 주장한—연구를 발표한 후 미국 학교에서 목발의 사용이 확산되었습니다. 이 시스템은 그 당시 미국에서 사용되는 다른 뺄세의 방법을 대체하여, 빠르게 적용되었습니다.

In Europe

일부 유럽 학교는, 역시 덧셈 방법으로 알려진, 오스트리아 방법으로 불리는 뺄셈의 방법을 사용합니다. 이 방법에서 빌림이 없습니다. 국가마다 변화를 가한, 역시 목발 (기억을 돕기 위한 표시)이 있습니다.

Comparing the two main methods

이들 두 방법 둘 다는 자리 값에 의한 한 자릿수 뺄셈의 과정으로 뺄셈을 나눕니다. 최하위 유효숫자 자릿수로 시작하여, 빼지는 숫자로부터

m_k m_k−1 ... m₁

빼는 숫자의 뺄셈:

s_j s_j−1 ... s₁,

여기서 각 s_i와 m_i는 자릿수이며, s_i가 m_i를 초과하지 않는 한, m₁ − s₁, m₂ − s₂, 등을 써내려 감으로써 진행합니다. 그렇지 않으면, m_i가 10씩 증가하고 일부 다른 자릿수는 이 증가를 바로잡기 위해 수정됩니다. 미국식 방법은 빼지는 숫자 자릿수 m_i+1을 1씩 줄이려고 시도함으로써 바로잡습니다 (또는 그것으로부터 빌리기 위한 비-영 자릿수가 있을 때까지 왼편 쪽으로 빌림을 계속합니다). 유럽식 방법은 빼는 숫자 자릿수 s_i+1을 1씩 증가시킴으로써 바로잡습니다.

예제: 704 − 512.

${\begin{array}{rrrr}&\color {Red}-1\\&C&D&U\\&7&0&4\\&5&1&2\\\hline &1&9&2\\\end{array}}{\begin{array}{l}{\color {Red}\longleftarrow {\rm {carry}}}\\\\\longleftarrow \;{\rm {Minuend}}\\\longleftarrow \;{\rm {Subtrahend}}\\\longleftarrow {\rm {Rest\;or\;Difference}}\\\end{array}}$

빼지는 숫자는 704이고, 빼는 숫자는 512입니다. 빼지는 숫자 자릿수는 m₃ = 7, m₂ = 0 및 m₁ = 4입니다. 빼는 숫자 자릿수는 s₃ = 5, s₂ = 1 및 s₁ = 2입니다. 일의 자리에서 시작하여, 4는 2보다 작지 않으므로 차이 2가 결과의 일의 자리에 내려씁니다. 십의 자리에서, 0은 1보다 작으므로, 0은 10으로 증가되고, 1과 차이는 9이며, 십의 자리에 내려씁니다. 미국식 방법은 빼지는 숫자에서 백 자리를 1씩 줄이으로써 십의 증가를 바로잡습니다. 즉, 7은 관통해서 긋고 6으로 대체합니다. 뺄셈은 그런-다음 백 자리에서 진행이며, 여기서 6은 5보다 작지 않으므로, 그 차이는 결과의 백의 자리에 내려서 쓰입니다. 우리는 이제 모두 끝냈고, 그 결과는 192입니다.

오스트리아의 방법은 7을 6으로 줄이지 않습니다. 오히려, 그것은 빼는 숫자 백의 자릿수를 1씩 증가시킵니다. 작은 표시가 이 숫자 자릿수 근처 또는 아래에 만들어집니다 (학교에 따라 다릅니다). 그런-다음 뺄셈은 1씩 증가하고, 5가 그것에 더해져서, 7이 되는 숫자를 물음으로써 진행됩니다. 그 답은 1이고, 결과의 백의 자리에 내려서 쓰입니다.

학생이 항상 미국식 방식으로 머릿속 뺄셈 테이블을 사용한다는 점에서 추가적인 미묘함이 있습니다. 오스트리아의 방법은 종종 학생을 덧셈 테이블을 반대로 사용하도록 권장합니다. 위의 예제에서, 1을 5에 더하고, 6을 얻고, 7로부터 그것을 빼는 대신에, 학생은 1씩 증가하고, 5가 그것에 더해지고, 7이 되는 숫자를 고려하도록 요청받습니다.

Subtraction by hand

Austrian method

예제:

• 
  1 + ... = 3
• 
  차이는 줄 아래에 쓰입니다.
• 
  9 + ... = 5
  요구된 합 (5)은 너무 작습니다.
• 
  따라서, 우리는 그것에 10을 더하고 빼는 숫자에서 다음 높은 자리 아래에 1을 써넣습니다.
• 
  9 + ... = 15
  이제 우리는 이전처럼 차이를 구할 수 있습니다.
• 
  (4 + 1) + ... = 7
• 
  차이는 줄 아래에 쓰입니다.
• 
  전체 차이.

Subtraction from left to right

예제:

• 
  7 − 4 = 3
  이 결과는 오직 연필로 씁니다.
• 
  빼지는 숫자의 다음 자릿수가 빼는 숫자보다 더 작기 때문에, 우리는 연필로-쓴-숫자에서 1을 빼고 머릿속으로 다음 숫자에 10을 더합니다.
• 
  15 − 9 = 6
• 
  빼지는 숫자에서 다음 자릿수가 빼는 숫자보다 더 작지 않기 때문에, 우리는 이 숫자를 유지합니다.
• 
  3 − 1 = 2

American method

이 방법에서, 빼는 숫자의 각 자릿수가 오른쪽에서 왼쪽으로 시작하여 그것 위의 숫자에서 빼집니다. 만약 맨 위 숫자가 너무 작아서 그것으로부터 맨 아래 숫자를 빼면, 우리는 그것에 10을 더합니다; 이 10은 왼쪽에서 맨 위 자릿수에서 "빌려오는" 것이며, 우리는 그것으로부터 1을 뺍니다. 그런-다음 우리는, 모든 각 자릿수가 빼질 때까지, 다음 자릿수를 빼고 필요에 따라 빌려오는 것으로 이동합니다.

예제:

• 
  3 − 1 = ...
• 
  우리는 줄 아래에 차이를 씁니다.
• 
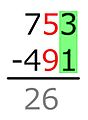
  5 − 9 = ...
  빼는 숫자 (5)는 너무 작습니다!
• 
  따라서, 우리는 그것에 10을 더합니다. 10은 왼쪽으로 자릿수로부터 "빌려오며", 이것은 1씩 감소합니다.
• 
  15 − 9 = ...
  이제 뺄셈은 작동하고, 우리는 선 아래에 차이를 씁니다.
• 
  6 − 4 = ...
• 
  우리는 줄 아래에 차이를 씁니다.
• 
  전체 차이.

Trade first

모든 빌림이 모두 뺄셈 전에 행재지는 미국식 방법의 변형입니다.

예제:

• 
  1 − 3 = 불가능.
  우리는 1에 10을 더합니다. 10이 가까운 5에서 "빌려온" 것이며, 5는 1만큼 낮아집니다.
• 
  4 − 9 = 불가능.
  따라서 우리는 단계 1에서 처럼 진행합니다.
• 
  오른쪽에서 왼쪽으로 작동합니다:
  11 − 3 = 8
• 
  14 − 9 = 5
• 
  6 − 4 = 2

Partial differences

부분 차이 방법은 빌림 또는 올림이 일어나지 않기 때문에 다른 수직 뺄셈 방법과 다릅니다. 그들 자리에서, 우리는 빼지는 숫자가 빼는 숫자보다 크거나 작은지에 따라 양 또는 음의 기호를 놓습니다. 부분 차이의 합이 전체 차이입니다.

예제:

• 
  더 작은 숫자가 더 큰 것으로부터 빼집니다:
  700 − 400 = 300
  빼지는 숫자가 빼는 숫자보다 더 크기 때문에, 이 차이는 양의 기호를 가집니다.
• 
  더 작은 숫자가 더 큰 것으로부터 빼집니다:
  90 − 50 = 40
  빼지는 숫자가 빼는 숫자보다 더 작기 때문에, 이 차이는 음의 기호를 가집니다..
• 
  더 작은 숫자가 더 큰 것으로부터 빼집니다:
  3 − 1 = 2
  빼지는 숫자가 빼는 숫자보다 더 크기 때문에, 이 차이는 양의 기호를 가집니다.
• 
  +300 − 40 + 2 = 262

Nonvertical methods

Counting up

자릿수마다 차이를 찾는 대신에, 우리가 빼는 숫자와 빼지는 숫자 사이의 숫자를 셀 수 있습니다.

예제: 1234 − 567 = 다음 단계로 구할 수 있습니다:

• 567 + 3 = 570
• 570 + 30 = 600
• 600 + 400 = 1000
• 1000 + 234 = 1234

전체 차이를 얻기 위해 각 단계로부터 값을 더합니다: 3 + 30 + 400 + 234 = 667.

Breaking up the subtraction

암기 산술에 대해 유용한 또 다른 방법은 뺄셈을 작은 단계로 나누는 것입니다.

예제: 1234 − 567 = 다음 방법에서 해결될 수 있습니다:

• 1234 − 500 = 734
• 734 − 60 = 674
• 674 − 7 = 667

Same change

같은 변화 방법은 빼지는 숫자와 빼는 숫자에서 같은 숫자를 더하거나 빼는 것이 답을 변경하지 않는다는 사실을 사용합니다. 우리는 단순히 빼는 숫자에서 영을 얻기 위해 필요한 양을 더합니다.

예제:

"1234 − 567 =" 다음처럼 해결될 수 있습니다:

• 1234 − 567 = 1237 − 570 = 1267 − 600 = 667

See also

• Decrement
• Elementary arithmetic
• Method of complements
• Negative number
• Plus and minus signs

Bibliography

• Brownell, W.A. (1939). Learning as reorganization: An experimental study in third-grade arithmetic, Duke University Press.
• Subtraction in the United States: An Historical Perspective, Susan Ross, Mary Pratt-Cotter, The Mathematics Educator, Vol. 8, No. 1 (original publication) and Vol. 10, No. 1 (reprint.) PDF

External links

• "Subtraction", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Printable Worksheets: Subtraction Worksheets, One Digit Subtraction, Two Digit Subtraction, Four Digit Subtraction, and More Subtraction Worksheets
• Subtraction Game at cut-the-knot
• Subtraction on a Japanese abacus selected from Abacus: Mystery of the Bead