Cross product

Original article: w:Cross product

This article is about the cross product of two vectors in three-dimensional Euclidean space. For other uses, see Cross product (disambiguation).

수학(mathematics)에서, 교차 곱(cross product) 또는 벡터 곱(vector product) (또는 기하학적 중요성을 강조하기 위해 간혹 방향화된 넓이 곱(directed area product))은 삼-차원 방향화된 유클리드 벡터 공간 (여기서 $E$로 나타냄)에서 두 벡터의 이항 연산이고, 기호 $\times$로 표시됩니다. 두 선형적으로 독립 벡터 $\mathbf {a}$와 $\mathbf {b}$가 주어지면, 벡터 곱, $\mathbf {a} \times \mathbf {b}$는 $\mathbf {a}$와 $\mathbf {b}$에 모두 수직(perpendicular)인 벡터이고, 따라서 그것들을 포함하는 평면에 법선(normal)입니다. 그것은 수학, 물리학, 공학, 및 컴퓨터 프로그래밍에서 많은 응용을 가집니다. 그것은 점 곱(dot product) (투영 곱(projection product))과 혼동해서는 안됩니다.

만약 두 벡터가 같은 방향을 가가지거나 서로 정확히 반대 방향을 가지면 (즉, 그것들이 선형적으로 독립이 아니면), 또는 둘 중 하나가 영 길이를 가지면, 그것들의 벡터 곱은 영입니다. 보다 일반적으로, 곱의 크기는 두 벡터를 인접한 두 변으로 가지는 평행사변형의 넓이와 같습니다; 특히 두 개의 수직 벡터의 곱의 크기는 그것들 길이의 곱입니다.

교차 곱은 반-교환적(anticommutative) (즉, $\mathbf {a} \times \mathbf {b} =-\mathbf {b} \times \mathbf {a}$)이고 덧셈에 걸쳐 분배적(distributive)입니다 (즉, $\mathbf {a} \times (\mathbf {b} +\mathbf {c} )=\mathbf {a} \times \mathbf {b} +\mathbf {a} \times \mathbf {c}$). 교차 곱과 함께 공간 $E$는 실수에 걸쳐 대수이며, 이는 교환적도 아니고 결합적도 아니지만, 리 괄호인 교차 곱을 갖는 리 대수입니다.

점 곱과 마찬가지로, 그것은 유클리드 공간의 메트릭(metric)에 의존하지만, 점 곱과는 달리, 그것은 공간의 방향(orientation)이나 "손모양(handedness)"의 선택에 따라 달라집니다 (이것은 방향화된 공간이 필요한 이유입니다). 교차 곱과 관련하여, 벡터의 외부 곱(exterior product)은 임의적인 차원 (이중벡터 또는 2-형식 결과를 포함)에서 사용될 수 있고 공간의 방향과 무관합니다.

그 곱은 전통적인 3-차원 교차 곱과 마찬가지로, n 차원에서 n − 1 벡터의 곱을 취하여 그것들 모든 벡터에 수직인 벡터를 생성할 수 있는 방향과 메트릭 구조를 사용하여 다양한 방식으로 일반화할 수 있습니다. 그러나 그 곱이 벡터 결과를 갖는 비-자명한 이항 곱으로 제한되면, 그것은 오직 3차원과 7차원에서 존재합니다. 그러나 7차원에서 교차-곱은 어쨌든 바람직하지 않은 속성 (예를 들어, 야코비 항등식을 충족하지 못함)을 가지므로, 수학적 물리학에서 다중-차원 시공간과 같은 양을 나타내는 데 사용되지 않습니다. (다른 차원에 대해서는 아래의 § Generalizations를 참조하십시오.)

The cross product with respect to a right-handed coordinate system

Definition

Finding the direction of the cross product by the right-hand rule

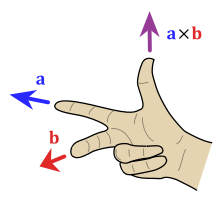
두 벡터 a와 b의 교차 곱은 삼-차원 공간에서만 정의되고 a × b로 표시됩니다. 물리학(physics)과 응용 수학(applied mathematics)에서, 쐐기 표기법 a ∧ b는 종종 벡터 곱이라는 이름과 함께 사용되지만, 순수 수학에서는 그러한 표기법이 보통 n 차원에 대해 벡터 곱의 추상화, 바로 외부 곱에 대해 예약되어 있습니다.

교차 곱 a × b는 a와 b 모두에 수직 (직교)인 벡터 c로 정의되며, 방향은 오른손 법칙에 의해 주어지고 크기는 벡터가 스팬하는 평행사변형(parallelogram)의 넓이와 같습니다.

교차 곱은 다음 공식으로 정의됩니다:

$\mathbf {a} \times \mathbf {b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\sin(\theta )\ \mathbf {n}$

여기서:

• θ는 a와 b를 포함하는 평면에서 그것들 사이의 각도(angle)입니다 (따라서, 그것은 0°와 180° 사이에 있습니다).
• ‖a‖와 ‖b‖는 벡터 a와 b의 크기(magnitudes)입니다.
• 그리고 n은 a와 b를 포함하는 평면에 수직인 단위 벡터(unit vector)이며, 순서화된 집합 (a, b, n)이 양수적으로-방향화(positively-oriented)됨을 만족하는 방향을 가집니다.

만약 벡터 a와 b가 평행이면 (즉, 그것들 사이의 각도 θ가 0° 또는 180°이면), 위의 공식에 의해, a와 b의 교차 곱은 영 벡터(zero vector) 0입니다.

Direction

The cross product a × b (vertical, in purple) changes as the angle between the vectors a (blue) and b (red) changes. The cross product is always orthogonal to both vectors, and has magnitude zero when the vectors are parallel and maximum magnitude ‖a‖‖b‖ when they are orthogonal.

벡터 n의 방향은 공간의 선택된 방향에 따라 달라집니다. 관례적으로, 그것은 오른손 두 번째 손가락을 a 방향으로, 가운데 손가락을 b 방향으로 가리키는 오른손 규칙에 의해 주어집니다. 그런-다음, 벡터 n이 엄지에서 나옵니다 (옆 그림 참조). 이 규칙을 사용하면 교차 곱은 반-교환적(anti-commutative)이라는 것을 의미합니다; 즉, b × a = −(a × b)입니다. 두 번째 손가락을 먼저 b 쪽으로 향하게 하고, 그런-다음 가운데 손가락으로 a 쪽으로 향하게 함으로써, 엄지 손가락이 반대 방향으로 강제되어, 곱 벡터의 부호가 반전됩니다.

교차 곱 연산자는 공간의 방향에 따라 달라지므로, 일반적으로 두 벡터의 교차 곱은 "참" 벡터가 아니라, 유사-벡터(pseudovector)입니다. 자세한 내용에 대해 § Handedness을 참조하십시오.

Names and origin

According to Sarrus's rule, the determinant of a 3×3 matrix involves multiplications between matrix elements identified by crossed diagonals

1842년에, 윌리엄 로완 해밀턴(William Rowan Hamilton)은 쿼터니언(quaternions) 대수와 비-교환 해밀턴 곱을 발견했습니다. 특히, 두 벡터의 해밀턴 곱 (즉, 영 스칼라 부분을 갖는 순수 쿼터니언)가 수행될 때, 스칼라 부분과 벡터 부분을 갖는 쿼터니언이 생성됩니다. 이 해밀턴 곱의 스칼라 부분과 벡터 부분은 두 벡터의 점 곱과 교차 곱의 음수에 해당합니다.

1881년에,조사이어 윌러드 깁스(Josiah Willard Gibbs)와, 독립적으로 올리버 헤비사이드(Oliver Heaviside)는 각각 마침표 (a ⋅ b)와 "×" (a × b)를 사용하여 점 곱과 교차 곱 모두에 대한 표기법을 도입했습니다.

1877년에, 점 곱의 결과는 스칼라(scalar)이고 반면 교차 곱의 결과는 벡터(vector)라는 사실을 강조하기 위해, 윌리엄 킹던 클리퍼드(William Kingdon Clifford)는 두 연산에 대해 스칼라 곱(scalar product)과 벡터 곱(vector product)이라는 대안적인 이름을 만들었습니다. 이들 대안적인 이름은 문헌에서 여전히 널리 사용됩니다.

교차 표기법 (a × b)과 교차 곱이라는 이름은 모두 a × b의 각 스칼라 성분(scalar component)이 a와 b의 비-대응하는 성분을 곱함으로써 계산된다는 사실에서 영감을 얻었을 수 있습니다. 반대로, 점 곱 a ⋅ b는 a와 b의 해당 성분 사이의 곱셈을 포함합니다. 아래에서 설명하는 것처럼, 교차 곱은 특별한 3×3 행렬의 행렬식의 형식으로 표현될 수 있습니다. 사뤼스의 규칙(Sarrus's rule)에 따르면, 이것은 교차 대각선으로 식별되는 행렬 원소 사이의 곱셈을 포함합니다.

Computing

Coordinate notation

Standard basis vectors (i, j, k, also denoted e₁, e₂, e₃) and vector components of a (a_x, a_y, a_z, also denoted a₁, a₂, a₃)

만약 (i, j, k)가 양수적으로 방향화된 직교-정규 기저이면, 기저 벡터는 다음 방정식을 만족시킵니다:

${\begin{alignedat}{2}\mathbf {\color {blue}{i}} &\times \mathbf {\color {red}{j}} &&=\mathbf {\color {green}{k}} \\\mathbf {\color {red}{j}} &\times \mathbf {\color {green}{k}} &&=\mathbf {\color {blue}{i}} \\\mathbf {\color {green}{k}} &\times \mathbf {\color {blue}{i}} &&=\mathbf {\color {red}{j}} \end{alignedat}}$

이는 교차 곱의 반-교환성(anticommutativity)에 의해 다음임을 의미합니다:

${\begin{alignedat}{2}\mathbf {\color {red}{j}} &\times \mathbf {\color {blue}{i}} &&=-\mathbf {\color {green}{k}} \\\mathbf {\color {green}{k}} &\times \mathbf {\color {red}{j}} &&=-\mathbf {\color {blue}{i}} \\\mathbf {\color {blue}{i}} &\times \mathbf {\color {green}{k}} &&=-\mathbf {\color {red}{j}} \end{alignedat}}$

교차 곱의 반-교환성 (및 선형 독립성의 명백한 결여)은 역시 다음임을 의미합니다:

$\mathbf {\color {blue}{i}} \times \mathbf {\color {blue}{i}} =\mathbf {\color {red}{j}} \times \mathbf {\color {red}{j}} =\mathbf {\color {green}{k}} \times \mathbf {\color {green}{k}} =\mathbf {0}$ (the zero vector).

이들 상등은, 교차 곱의 분배성과 선형성과 함께 (위의 정의에서 쉽게 따르지는 않지만), 두 벡터 a와 b의 교차 곱을 결정하기에 충분합니다. 각 벡터는 표준 기저 벡터에 평행한 3개의 직교 성분의 합으로 정의될 수 있습니다:

${\begin{alignedat}{3}\mathbf {a} &=a_{1}\mathbf {\color {blue}{i}} &&+a_{2}\mathbf {\color {red}{j}} &&+a_{3}\mathbf {\color {green}{k}} \\\mathbf {b} &=b_{1}\mathbf {\color {blue}{i}} &&+b_{2}\mathbf {\color {red}{j}} &&+b_{3}\mathbf {\color {green}{k}} \end{alignedat}}$

그것들의 교차 곱 a × b는 분배성을 사용하여 확장될 수 있습니다:

${\begin{aligned}\mathbf {a} \times \mathbf {b} ={}&(a_{1}\mathbf {\color {blue}{i}} +a_{2}\mathbf {\color {red}{j}} +a_{3}\mathbf {\color {green}{k}} )\times (b_{1}\mathbf {\color {blue}{i}} +b_{2}\mathbf {\color {red}{j}} +b_{3}\mathbf {\color {green}{k}} )\\={}&a_{1}b_{1}(\mathbf {\color {blue}{i}} \times \mathbf {\color {blue}{i}} )+a_{1}b_{2}(\mathbf {\color {blue}{i}} \times \mathbf {\color {red}{j}} )+a_{1}b_{3}(\mathbf {\color {blue}{i}} \times \mathbf {\color {green}{k}} )+{}\\&a_{2}b_{1}(\mathbf {\color {red}{j}} \times \mathbf {\color {blue}{i}} )+a_{2}b_{2}(\mathbf {\color {red}{j}} \times \mathbf {\color {red}{j}} )+a_{2}b_{3}(\mathbf {\color {red}{j}} \times \mathbf {\color {green}{k}} )+{}\\&a_{3}b_{1}(\mathbf {\color {green}{k}} \times \mathbf {\color {blue}{i}} )+a_{3}b_{2}(\mathbf {\color {green}{k}} \times \mathbf {\color {red}{j}} )+a_{3}b_{3}(\mathbf {\color {green}{k}} \times \mathbf {\color {green}{k}} )\\\end{aligned}}$

이것은 a × b를 i, j, 또는 k에 정렬된 벡터를 포함하는 9개의 간단한 교차 곱의 합으로 분해하는 것으로 해석될 수 있습니다. 이들 9개의 교차 곱 각각은 서로 평행하거나 직교하기 때문에 다루기 쉬운 두 벡터에서 연산합니다. 이 분해에서, 위에서-언급한 상등(equalities)을 사용하고 동류항을 수집함으로써, 다음을 얻습니다:

${\begin{aligned}\mathbf {a} \times \mathbf {b} ={}&\quad \ a_{1}b_{1}\mathbf {0} +a_{1}b_{2}\mathbf {\color {green}{k}} -a_{1}b_{3}\mathbf {\color {red}{j}} \\&-a_{2}b_{1}\mathbf {\color {green}{k}} +a_{2}b_{2}\mathbf {0} +a_{2}b_{3}\mathbf {\color {blue}{i}} \\&+a_{3}b_{1}\mathbf {\color {red}{j}} \ -a_{3}b_{2}\mathbf {\color {blue}{i}} \ +a_{3}b_{3}\mathbf {0} \\={}&(a_{2}b_{3}-a_{3}b_{2})\mathbf {\color {blue}{i}} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {\color {red}{j}} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {\color {green}{k}} \\\end{aligned}}$

이는 결과 벡터 s = s₁i + s₂j + s₃k = 의 세 스칼라 성분(scalar components)이 다음임을 의미합니다:

${\begin{aligned}s_{1}&=a_{2}b_{3}-a_{3}b_{2}\\s_{2}&=a_{3}b_{1}-a_{1}b_{3}\\s_{3}&=a_{1}b_{2}-a_{2}b_{1}\end{aligned}}$

열 벡터(column vectors)를 사용하여, 다음과 같은 결과를 나타낼 수 있습니다:

${\begin{bmatrix}s_{1}\\s_{2}\\s_{3}\end{bmatrix}}={\begin{bmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\end{bmatrix}}$

Matrix notation

Use of Sarrus's rule to find the cross product of a and b

교차 곱은 형식적(formal) 행렬식으로도 표현될 수 있습니다:

$\mathbf {a\times b} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{vmatrix}}$

이 행렬식은 사뤼스의 규칙(Sarrus's rule) 또는 여인수 전개(cofactor expansion)를 사용하여 계산될 수 있습니다. 사뤼스의 규칙을 사용하면, 다음과 같이 전개됩니다:

${\begin{aligned}\mathbf {a\times b} &=(a_{2}b_{3}\mathbf {i} +a_{3}b_{1}\mathbf {j} +a_{1}b_{2}\mathbf {k} )-(a_{3}b_{2}\mathbf {i} +a_{1}b_{3}\mathbf {j} +a_{2}b_{1}\mathbf {k} )\\&=(a_{2}b_{3}-a_{3}b_{2})\mathbf {i} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k} .\end{aligned}}$

대신 첫 번째 행을 따라 여인수(cofactor) 전개를 사용하면, 다음으로 전개됩니다:

${\begin{aligned}\mathbf {a\times b} &={\begin{vmatrix}a_{2}&a_{3}\\b_{2}&b_{3}\end{vmatrix}}\mathbf {i} -{\begin{vmatrix}a_{1}&a_{3}\\b_{1}&b_{3}\end{vmatrix}}\mathbf {j} +{\begin{vmatrix}a_{1}&a_{2}\\b_{1}&b_{2}\end{vmatrix}}\mathbf {k} \\&=(a_{2}b_{3}-a_{3}b_{2})\mathbf {i} -(a_{1}b_{3}-a_{3}b_{1})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k} ,\end{aligned}}$

이는 결과 벡터의 성분을 직접 제공합니다.

Using Levi-Civita tensors

• 임의의 기저에서, 교차 곱 $a\times b$는 텐서 공식 $E_{ijk}a^{i}b^{j}$에 의해 제공되며, 여기서 $E_{ijk}$는 공변 레비-치비타(Levi-Civita) 텐서입니다 (인덱스 위치에 주목하십시오). 그것은 여기에 주어진 본질적인 공식에 해당합니다.
• 공간과 같은 방향을 가지는 직교-정규 기저에서, $a\times b$는 유사-텐서 공식 $\varepsilon _{ijk}a^{i}b^{j}$에 의해 제공되며, 여기서 $\varepsilon _{ijk}$는 레비-치비타 기호입니다 (이는 유사-텐서입니다). 그것은 일상적인 물리학에 사용되는 공식이지만, 이 특별한 기저 선택에 대해서만 작동합니다.
• 임의의 직교-정규 기저에서, $a\times b$는 유사-텐서 공식 $(-1)^{B}\varepsilon _{ijk}a^{i}b^{j}$에 의해 지정되며, 여기서 $(-1)^{B}=\pm 1$은 기저가 공간과 같은 방향인지 여부를 나타냅니다.

후자의 공식은 직교-정규 기저를 뒤집을 때 공간의 방향을 변경하지 않아도 됩니다.

Properties

Geometric meaning

See also: Triple product

Figure 1. The area of a parallelogram as the magnitude of a cross product

Figure 2. Three vectors defining a parallelepiped

교차 곱의 크기(magnitude)는 a와 b를 변으로 가지는 평행사변형(parallelogram)의 양수 넓이(area)로 해석될 수 있습니다 (그림 1 참조): $$\left\|\mathbf {a} \times \mathbf {b} \right\|=\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\left|\sin \theta \right|.$$

실제로, 교차 곱과 점 곱의 조합인 스칼라 세-쌍 곱(scalar triple product)을 사용함으로써 a, b, 및 c를 가장자리로 가지는 평행-육면체(parallelepiped)의 부피 V를 계산할 수도 있습니다 (그림 2 참조):

$\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} ).$

스칼라 세-쌍 곱의 결과가 음수일 수 있으므로, 평행-육면체의 부피는 그것의 절댓값으로 지정됩니다:

$V=|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|.$

교차 곱의 크기는 그것의 인수 사이 각도의 사인에 의해 변하기 때문에, 교차 곱은 점 곱이 평행성(parallelism)의 측정인 것과 같은 방법으로 직각도(perpendicularity)의 측정으로 생각될 수 있습니다. 두 개의 단위 벡터(unit vectors)가 주어지면, 교차 곱은 만약 두 벡터가 수직이면 1의 크기를 가지고 평행이면 0의 크기를 가집니다. 두 단위 벡터의 점 곱은 정반대로 동작합니다: 그것은 단위 벡터가 수직이면 영이고 평행이면 1입니다.

단위 벡터는 두 가지 편리한 항등식을 가능하게 합니다: 두 단위 벡터의 점 곱은 두 단위 벡터 사이의 각도의 코사인 (양수 또는 음수일 수 있음)을 생성합니다. 두 단위 벡터의 교차 곱의 크기는 사인 (항상 양수임)을 산출합니다.

Algebraic properties

Cross product scalar multiplication. Left: Decomposition of b into components parallel and perpendicular to a. Right: Scaling of the perpendicular components by a positive real number r (if negative, b and the cross product are reversed).

Cross product distributivity over vector addition. Left: The vectors b and c are resolved into parallel and perpendicular components to a. Right: The parallel components vanish in the cross product, only the perpendicular components shown in the plane perpendicular to a remain.

The two nonequivalent triple cross products of three vectors a, b, c. In each case, two vectors define a plane, the other is out of the plane and can be split into parallel and perpendicular components to the cross product of the vectors defining the plane. These components can be found by vector projection and rejection. The triple product is in the plane and is rotated as shown.

만약 두 벡터의 교차 곱이 영 벡터이면 (즉, a × b = 0), 입력 중 하나 또는 둘 다 영 벡터 (a = 0 또는 b = 0)이거나 그렇지 않으면 두 벡터 사이의 각도의 사인이 영이 되도록 (θ = 0° 또는 θ = 180°이고 sin θ = 0) 그것들이 평행 또는 역평행 (a ∥ b)입니다.

벡터의 자기 교차 곱은 영 벡터입니다:

$\mathbf {a} \times \mathbf {a} =\mathbf {0} .$

교차 곱은 is 반-교환적(anticommutative)이고,

$\mathbf {a} \times \mathbf {b} =-(\mathbf {b} \times \mathbf {a} ),$

덧셈에 걸쳐 분배적(distributive)이고,

$\mathbf {a} \times (\mathbf {b} +\mathbf {c} )=(\mathbf {a} \times \mathbf {b} )+(\mathbf {a} \times \mathbf {c} ),$

다음이 되도록 스칼라 곱셈과 호환적입니다:

$(r\,\mathbf {a} )\times \mathbf {b} =\mathbf {a} \times (r\,\mathbf {b} )=r\,(\mathbf {a} \times \mathbf {b} ).$

그것은 결합적(associative)이지 않지만, 야코비 항등식(Jacobi identity)을 만족시킵니다:

$\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )+\mathbf {b} \times (\mathbf {c} \times \mathbf {a} )+\mathbf {c} \times (\mathbf {a} \times \mathbf {b} )=\mathbf {0} .$

분배성, 선형성, 및 야코비 항등식은 벡터 덧셈과 교차 곱과 함께 R³ 벡터 공간이 리 대수(Lie algebra), 삼-차원에서 실수 직교 그룹(orthogonal group)의 리 대수, SO(3)를 형성함을 보여줍니다. 교차 곱은 취소 법칙(cancellation law)을 따르지 않습니다; 즉, a × b = a × c (a ≠ 0)이 b = c를 의미하지 않고, 다음임을 의미합니다:

${\begin{aligned}\mathbf {0} &=(\mathbf {a} \times \mathbf {b} )-(\mathbf {a} \times \mathbf {c} )\\&=\mathbf {a} \times (\mathbf {b} -\mathbf {c} ).\\\end{aligned}}$

이것은 b와 c가 취소되는 경우일 수 있지만, 추가적으로 a와 b − c가 평행인 경우일 수 있습니다; 즉, 그것들은 스케일 인수 t에 의해 관련되어, 어떤 스칼라 t에 대해 다음으로 이어집니다:

$\mathbf {c} =\mathbf {b} +t\,\mathbf {a} .$

만약, 위와 같은 a × b = a × c이고 a ≠ 0에 더하여, a ⋅ b = a ⋅ c인 경우이면,

${\begin{aligned}\mathbf {a} \times (\mathbf {b} -\mathbf {c} )&=\mathbf {0} \\\mathbf {a} \cdot (\mathbf {b} -\mathbf {c} )&=0,\end{aligned}}$

b − c는 동시에 a와 평행 (교차 곱이 0의 경우)과 수직 (점 곱이 0의 경우)일 수 없으므로, b와 c가 취소되는 경우여야 합니다: b = c.

기하학적 정의에서, 교차 곱은 a × b에 의해 정의된 축에 대한 적절한 회전(rotations) 아래에서 불변입니다. 수식에서:

$(R\mathbf {a} )\times (R\mathbf {b} )=R(\mathbf {a} \times \mathbf {b} )$, where $R$ is a rotation matrix with $\det(R)=1$.

보다 일반적으로, 교차 곱은 행렬(matrix) 변환 아래에서 다음 항등식을 따릅니다:

$(M\mathbf {a} )\times (M\mathbf {b} )=(\det M)\left(M^{-1}\right)^{\mathrm {T} }(\mathbf {a} \times \mathbf {b} )=\operatorname {cof} M(\mathbf {a} \times \mathbf {b} )$

여기서 $M$은 3-x-3 행렬(matrix)이고 $\left(M^{-1}\right)^{\mathrm {T} }$는 역(inverse)의 전치(transpose)이고 $\operatorname {cof}$는 여인수 행렬(cofactor matrix)입니다. 만약 $M$이 회전 행렬이면 이 공식이 전자로 어떻게 축소되는지 쉽게 알 수 있습니다. 만약 $M$이 일반 교차 곱 $\mathbf {a} \times \mathbf {b}$에 적용된 3-x-3 대칭 행렬이면, 다음 관계가 참을 유지합니다:

$M(\mathbf {a} \times \mathbf {b} )=\operatorname {Tr} (M)(\mathbf {a} \times \mathbf {b} )-\mathbf {a} \times M\mathbf {b} +\mathbf {b} \times M\mathbf {a}$

두 벡터의 교차 곱은 벡터를 행으로 2 × 3 행렬의 널 공간(null space)에 놓입니다:

$\mathbf {a} \times \mathbf {b} \in NS\left({\begin{bmatrix}\mathbf {a} \\\mathbf {b} \end{bmatrix}}\right).$

두 교차 곱의 합에 대해, 다음 항등식이 유지됩니다:

$\mathbf {a} \times \mathbf {b} +\mathbf {c} \times \mathbf {d} =(\mathbf {a} -\mathbf {c} )\times (\mathbf {b} -\mathbf {d} )+\mathbf {a} \times \mathbf {d} +\mathbf {c} \times \mathbf {b} .$

Differentiation

Main article: Vector-valued function § Derivative and vector multiplication

미분 미적분의 곱 규칙(product rule)은 임의의 쌍선형 연산에 적용되고, 따라서 교차 곱에도 적용됩니다:

${\frac {d}{dt}}(\mathbf {a} \times \mathbf {b} )={\frac {d\mathbf {a} }{dt}}\times \mathbf {b} +\mathbf {a} \times {\frac {d\mathbf {b} }{dt}},$

여기서 a와 b는 실수 변수 t에 의존하는 벡터입니다.

Triple product expansion

Main article: Triple product

교차 곱은 세-쌍 곱의 두 가지 형식으로 사용됩니다. 세 벡터의 스칼라 세-쌍 곱(scalar triple product)은 다음과 같이 정의됩니다:

$\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} ),$

그것은 가장자리 a, b, 및 c를 갖는 평행-육면체(parallelepiped)의 부호화된 부피이고 이를테면 벡터는 위 순서화의 짝수 순열(even permutation)인 임의의 순서로 사용될 수 있습니다. 따라서 다음은 같습니다:

$\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} ),$

벡터 세-쌍 곱(vector triple product)은 한 벡터와 또 다른 벡터의 교차 곱의 결과의 교차 곱을 의미하고, 다음과 같은 공식에 의해 점 곱과 관련됩니다:

${\begin{aligned}\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {c} \cdot \mathbf {a} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )\\(\mathbf {a} \times \mathbf {b} )\times \mathbf {c} =\mathbf {b} (\mathbf {c} \cdot \mathbf {a} )-\mathbf {a} (\mathbf {b} \cdot \mathbf {c} )\end{aligned}}$

기억법(mnemonic) "BAC minus CAB"는 오른쪽 구성원의 벡터 순서를 기억하는 데 사용됩니다. 이 공식은 벡터 계산을 단순화하기 위해 물리학(physics)에서 사용됩니다. 그래디언트(gradients)와 관련하여 벡터 미적분(vector calculus)을 유용한 특별한 경우는 다음과 같습니다:

${\begin{aligned}\nabla \times (\nabla \times \mathbf {f} )&=\nabla (\nabla \cdot \mathbf {f} )-(\nabla \cdot \nabla )\mathbf {f} \\&=\nabla (\nabla \cdot \mathbf {f} )-\nabla ^{2}\mathbf {f} ,\\\end{aligned}}$

여기서 ∇²는 벡터 라플라스(vector Laplacian) 연산자입니다.

다른 항등원은 교차 곱을 스칼라 세-쌍 곱과 관련시킵니다:

${\begin{aligned}(\mathbf {a} \times \mathbf {b} )\times (\mathbf {a} \times \mathbf {c} )&=(\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} ))\mathbf {a} \\(\mathbf {a} \times \mathbf {b} )\cdot (\mathbf {c} \times \mathbf {d} )&=\mathbf {b} ^{\mathrm {T} }\left(\left(\mathbf {c} ^{\mathrm {T} }\mathbf {a} \right)I-\mathbf {c} \mathbf {a} ^{\mathrm {T} }\right)\mathbf {d} \\&=(\mathbf {a} \cdot \mathbf {c} )(\mathbf {b} \cdot \mathbf {d} )-(\mathbf {a} \cdot \mathbf {d} )(\mathbf {b} \cdot \mathbf {c} )\end{aligned}}$

여기서 $I$ 는 항등 행렬입니다.

Alternative formulation

교차 곱과 점 곱은 다음에 의해 관련됩니다:

$\left\|\mathbf {a} \times \mathbf {b} \right\|^{2}=\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}.$

오른쪽 변은 벡터에 의해 정의된 평행사변형 넓이의 제곱, a와 b의 그람 행렬식(Gram determinant)입니다. 이 조건은 점 곱의 크기를 결정합니다. 즉, 점 곱이 두 벡터 사이의 각도 θ의 관점에서 다음과 같이 정의되기 때문에:

$\mathbf {a\cdot b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\cos \theta ,$

위의 주어진 관계는 다음과 같이 다시 작성할 수 있습니다:

$\left\|\mathbf {a\times b} \right\|^{2}=\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}\left(1-\cos ^{2}\theta \right).$

피타고라스의 삼각형 항등식(Pythagorean trigonometric identity)을 호출하여, 다음을 얻습니다:

$\left\|\mathbf {a} \times \mathbf {b} \right\|=\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\left|\sin \theta \right|,$

이는 θ의 관점에서 표현된 교차 곱의 크기이며, a와 b에 의해 정의된 평행사변형의 넓이와 같습니다 (위의 정의 참조).

이 요구 사항과 교차 곱이 성분 a와 b에 직교한다는 속성의 조합은 교차 곱의 대안적인 정의를 제공합니다.

Lagrange's identity

다음 관계는:

$\left\|\mathbf {a} \times \mathbf {b} \right\|^{2}\equiv \det {\begin{bmatrix}\mathbf {a} \cdot \mathbf {a} &\mathbf {a} \cdot \mathbf {b} \\\mathbf {a} \cdot \mathbf {b} &\mathbf {b} \cdot \mathbf {b} \\\end{bmatrix}}\equiv \left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}.$

오른쪽 변과 관련된 또 다른 관계, 즉 다음과 같이 표현된 라그랑주의 항등식(Lagrange's identity)과 비교될 수 있습니다:

$\sum _{1\leq i<j\leq n}\left(a_{i}b_{j}-a_{j}b_{i}\right)^{2}\equiv \left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a\cdot b} )^{2}\ ,$

여기서 a와 b는 n-차원 벡터일 수 있습니다. 이것은 역시 표면에 대한 리만 부피 형식(Riemannian volume form)이 벡터 미적분학에서 표면 원소(surface element)라는 것을 보여줍니다. n = 3인 경우에서, 이들 두 방정식을 조합하면 그것의 성분의 측면에서 교차 곱의 크기에 대한 표현을 초래합니다:

${\begin{aligned}&\left\|\mathbf {a} \times \mathbf {b} \right\|^{2}\equiv \sum _{1\leq i<j\leq 3}\left(a_{i}b_{j}-a_{j}b_{i}\right)^{2}\\\equiv {}&\left(a_{1}b_{2}-b_{1}a_{2}\right)^{2}+\left(a_{2}b_{3}-a_{3}b_{2}\right)^{2}+\left(a_{3}b_{1}-a_{1}b_{3}\right)^{2}\ .\end{aligned}}$

같은 결과가 다음에서 발견된 교차 곱의 성분을 사용하여 직접 발견됩니다:

$\mathbf {a} \times \mathbf {b} \equiv \det {\begin{bmatrix}{\hat {\mathbf {i} }}&{\hat {\mathbf {j} }}&{\hat {\mathbf {k} }}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{bmatrix}}.$

R³에서, 라그랑주의 방정식은 쿼터니언 대수(quaternion algebra)에서 노름의 곱셈성 |vw| = |v||w|의 특별한 경우입니다.

그것은 또 다른 공식, 때때로 라그랑주의 항등식이라고도 불리는 특별한 경우이며, 코시–비네 항등식(Binet–Cauchy identity)의 삼-차원 사례입니다:

$(\mathbf {a} \times \mathbf {b} )\cdot (\mathbf {c} \times \mathbf {d} )\equiv (\mathbf {a} \cdot \mathbf {c} )(\mathbf {b} \cdot \mathbf {d} )-(\mathbf {a} \cdot \mathbf {d} )(\mathbf {b} \cdot \mathbf {c} ).$

만약 a = c 및 b = d이면, 이것은 위의 공식으로 단순화됩니다.

Infinitesimal generators of rotations

교차 곱은 R³에서 회전(rotations)의 무한소 생성기를 편리하게 설명합니다. 구체적으로, 만약 n이 R³에서 단위 벡터이고 R(φ, n)은 n에 의해 지정된 원점을 통해 축에 대한 회전을 나타내며, 각도 φ (라디안에서, n의 끝에서 볼 때 반-시계방향으로 측정됨)을 가지면, R³에서 모든 각 벡터 x에 대해 다음과 같습니다:

$\left.{d \over d\phi }\right|_{\phi =0}R(\phi ,{\boldsymbol {n}}){\boldsymbol {x}}={\boldsymbol {n}}\times {\boldsymbol {x}}$

따라서 n을 갖는 교차 곱은 n에 대한 회전의 무한소 생성기를 설명합니다. 이들 무한소 생성기는 회전 그룹 SO(3)의 리 대수(Lie algebra) so(3)를 형성하고, 우리는 교차 곱을 갖는 리 대수 R³가 리 대수 so(3)에 동형적이라는 결과를 얻습니다.

Alternative ways to compute

Conversion to matrix multiplication

벡터 교차 곱은 역시 반-대칭 행렬(skew-symmetric matrix)과 벡터의 곱으로 표현될 수 있습니다: $${\begin{aligned}\mathbf {a} \times \mathbf {b} =[\mathbf {a} ]_{\times }\mathbf {b} &={\begin{bmatrix}\,0&\!-a_{3}&\,\,a_{2}\\\,\,a_{3}&0&\!-a_{1}\\-a_{2}&\,\,a_{1}&\,0\end{bmatrix}}{\begin{bmatrix}b_{1}\\b_{2}\\b_{3}\end{bmatrix}}\\\mathbf {a} \times \mathbf {b} ={[\mathbf {b} ]_{\times }}^{\mathrm {\!\!T} }\mathbf {a} &={\begin{bmatrix}\,0&\,\,b_{3}&\!-b_{2}\\-b_{3}&0&\,\,b_{1}\\\,\,b_{2}&\!-b_{1}&\,0\end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}},\end{aligned}}$$ 여기서 위첨자 ^T 는 전치(transpose) 연산을 참조하고, [a]_×는 다음에 의해 정의됩니다: $$[\mathbf {a} ]_{\times }{\stackrel {\rm {def}}{=}}{\begin{bmatrix}\,\,0&\!-a_{3}&\,\,\,a_{2}\\\,\,\,a_{3}&0&\!-a_{1}\\\!-a_{2}&\,\,a_{1}&\,\,0\end{bmatrix}}.$$

벡터 a에 대해 반-대칭 행렬의 열 [a]_×,i는 단위 벡터(unit vectors)로 교차 곱을 계산함으로써 얻을 수 있습니다. 즉, $$[\mathbf {a} ]_{\times ,i}=\mathbf {a} \times \mathbf {{\hat {e}}_{i}} ,\;i\in \{1,2,3\}$$ 또는 $$[\mathbf {a} ]_{\times }=\sum _{i=1}^{3}\left(\mathbf {a} \times \mathbf {{\hat {e}}_{i}} \right)\otimes \mathbf {{\hat {e}}_{i}} ,$$ 여기서 $\otimes$ 는 밖의 곱(outer product) 연산자입니다.

역시, 만약 a가 교차 곱으로 자체 표현되면: $$\mathbf {a} =\mathbf {c} \times \mathbf {d}$$ 다음과 같습니다: $$[\mathbf {a} ]_{\times }=\mathbf {d} \mathbf {c} ^{\mathrm {T} }-\mathbf {c} \mathbf {d} ^{\mathrm {T} }.$$

Proof by substitution

교차 곱의 평가가 다음과 같이 제공됩니다: $$\mathbf {a} =\mathbf {c} \times \mathbf {d} ={\begin{pmatrix}c_{2}d_{3}-c_{3}d_{2}\\c_{3}d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}\end{pmatrix}}$$ 따라서, 왼쪽 변은 다음과 같습니다: $$[\mathbf {a} ]_{\times }={\begin{bmatrix}0&c_{2}d_{1}-c_{1}d_{2}&c_{3}d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}&0&c_{3}d_{2}-c_{2}d_{3}\\c_{1}d_{3}-c_{3}d_{1}&c_{2}d_{3}-c_{3}d_{2}&0\end{bmatrix}}$$ 이제, 오른쪽 변에 대해, $$\mathbf {c} \mathbf {d} ^{\mathrm {T} }={\begin{bmatrix}c_{1}d_{1}&c_{1}d_{2}&c_{1}d_{3}\\c_{2}d_{1}&c_{2}d_{2}&c_{2}d_{3}\\c_{3}d_{1}&c_{3}d_{2}&c_{3}d_{3}\end{bmatrix}}$$ 그리고 그것의 전치는 다음입니다: $$\mathbf {d} \mathbf {c} ^{\mathrm {T} }={\begin{bmatrix}c_{1}d_{1}&c_{2}d_{1}&c_{3}d_{1}\\c_{1}d_{2}&c_{2}d_{2}&c_{3}d_{2}\\c_{1}d_{3}&c_{2}d_{3}&c_{3}d_{3}\end{bmatrix}}$$ 오른쪽 변의 평가는 다음을 제공합니다: $$\mathbf {d} \mathbf {c} ^{\mathrm {T} }-\mathbf {c} \mathbf {d} ^{\mathrm {T} }={\begin{bmatrix}0&c_{2}d_{1}-c_{1}d_{2}&c_{3}d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}&0&c_{3}d_{2}-c_{2}d_{3}\\c_{1}d_{3}-c_{3}d_{1}&c_{2}d_{3}-c_{3}d_{2}&0\end{bmatrix}}$$ 비교는 왼쪽 변이 오른쪽 변과 같음을 보여줍니다.

이 결과는 기하학적 대수(geometric algebra)를 사용하여 더 높은 차원으로 일반화될 수 있습니다. 특히 임의의 차원에서, 이중벡터는 반-대칭 행렬로 식별될 수 있으므로, 반-대칭 행렬과 벡터 사이의 곱은 이중벡터와 벡터의 곱의 등급-1 부분과 동등합니다. 삼-차원에서 이중-벡터가 벡터에 이중이므로, 그 곱은 벡터 이중 대신 이중-벡터를 갖는 교차 곱과 동등합니다. 더 높은 치수에서, 그 곱이 여전히 계산될 수 있지만 이중-벡터는 더 많은 자유도를 가지고 벡터와 동등하지 않습니다.

이 표기법은 예를 들어 epipolar geometry에서 작업하기가 훨씬 쉽습니다.

교차 곱의 일반적인 속성에서, 다음임이 즉시 따릅니다:$$[\mathbf {a} ]_{\times }\,\mathbf {a} =\mathbf {0}$$   그리고   $$\mathbf {a} ^{\mathrm {T} }\,[\mathbf {a} ]_{\times }=\mathbf {0}$$ 그리고 [a]_×가 반-대칭이라는 사실로부터 다음임이 따릅니다: $$\mathbf {b} ^{\mathrm {T} }\,[\mathbf {a} ]_{\times }\,\mathbf {b} =0.$$

위에서-언급된 세-쌍 곱 전개 (bac–cab 규칙)는 이 표기법을 사용하여 쉽게 입증될 수 있습니다.

위에서 언급한 바와 같이, 교차 곱을 갖는 리 대수 R³는 리 대수 so(3)에 동형적이기 때문에, 그것의 원소는 3×3 반-대칭 행렬로 식별될 수 있습니다. 맵 a → [a]_×는 R³와 so(3) 사이의 동형을 제공합니다. 이 맵 아래에서, 3-벡터의 교차 곱은 3x3 반-대칭 행렬의 교환자(commutator)에 해당합니다.

Matrix conversion for cross product with canonical base vectors

$i$-번째 정식의 기저 벡터를 $\mathbf {e} _{i}\in \mathbf {R} ^{3\times 1}$로 나타내면, $\mathbf {e} _{i}$를 갖는 일반 벡터 $\mathbf {v} \in \mathbf {R} ^{3\times 1}$의 교차 곱은 $\mathbf {v} \times \mathbf {e} _{i}=\mathbf {C} _{i}\mathbf {v}$에 의해 주어지며, 여기서 $$\mathbf {C} _{1}={\begin{bmatrix}0&0&0\\0&0&1\\0&-1&0\end{bmatrix}},\quad \mathbf {C} _{2}={\begin{bmatrix}0&0&-1\\0&0&0\\1&0&0\end{bmatrix}},\quad \mathbf {C} _{3}={\begin{bmatrix}0&1&0\\-1&0&0\\0&0&0\end{bmatrix}}$$ 이들 행렬은 다음 속성을 공유합니다: $\mathbf {C} _{i}^{\textrm {T}}=-\mathbf {C} _{i}$ (반-대칭); 양쪽 대각합과 행렬식은 영입니다; ${\text{rank}}(\mathbf {C} _{i})=2$; $\mathbf {C} _{i}\mathbf {C} _{i}^{\textrm {T}}=\mathbf {P} _{\mathbf {e} _{i}}^{^{\perp }}$ (아래 참조); 벡터 $\mathbf {v} \neq \mathbf {0}$의 직교 투영 행렬(orthogonal projection matrix)은 $\mathbf {P} _{\mathbf {v} }=\mathbf {v} \left(\mathbf {v} ^{\textrm {T}}\mathbf {v} \right)^{-1}\mathbf {v} ^{T}$에 의해 제공됩니다. 직교 여 위로의 투영 행렬은 $\mathbf {P} _{\mathbf {v} }^{^{\perp }}=\mathbf {I} -\mathbf {P} _{\mathbf {v} }$에 의해 주어지며, 여기서 $\mathbf {I}$는 항등 행렬입니다. $\mathbf {v} =\mathbf {e} _{i}$의 특별한 경우에 대해, 다음임을 입증할 수 있습니다: $$\mathbf {P} _{\mathbf {e} _{1}}^{^{\perp }}={\begin{bmatrix}0&0&0\\0&1&0\\0&0&1\end{bmatrix}},\quad \mathbf {P} _{\mathbf {e} _{2}}^{^{\perp }}={\begin{bmatrix}1&0&0\\0&0&0\\0&0&1\end{bmatrix}},\quad \mathbf {P} _{\mathbf {e} _{3}}^{^{\perp }}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix}}$$ 직교 투영 행렬의 다른 속성에 대해, 투영 (선형 대수)를 참조하십시오.

Index notation for tensors

교차 곱은 대안적으로 레비-치비타 텐서(Levi-Civita tensor) E_ijk와 점 곱 η^mi의 관점에서 정의될 수 있으며, 이는 텐서 응용에 대한 벡터 표기법을 변환하는 데 유용합니다:

$\mathbf {c} =\mathbf {a\times b} \Leftrightarrow \ c^{m}=\sum _{i=1}^{3}\sum _{j=1}^{3}\sum _{k=1}^{3}\eta ^{mi}E_{ijk}a^{j}b^{k}$

여기서 인덱스(indices) $i,j,k$는 벡터 성분에 해당합니다. 교차 곱의 이러한 특성화는 종종 아인슈타인 합 규칙(Einstein summation convention)을 사용하여 다음과 같이 보다 컴팩트하게 표현됩니다:

$\mathbf {c} =\mathbf {a\times b} \Leftrightarrow \ c^{m}=\eta ^{mi}E_{ijk}a^{j}b^{k}$

이것에서 반복된 인덱스는 값 1에서 3에 걸쳐 합합니다.

양수적으로-방향화된 직교-정규 기저에서 η^mi = δ^mi (크로네커 델타) 및 $E_{ijk}=\varepsilon _{ijk}$ (레비-치비타 기호). 그 경우에서, 이 표현은 교차 곱의 반-대칭 표현의 또 다른 형식입니다:

$[\varepsilon _{ijk}a^{j}]=[\mathbf {a} ]_{\times }.$

고전적인 역학에서: 레비-치비타 기호를 사용함으로써 교차 곱을 표현하면 물리적 시스템이 등방적일 때 기계적 대칭이 분명해질 수 있습니다. (예제: 삼-차원에서 자유롭게 진동 할 수 있는, 삼 차원에서 잠재적으로 훅의 법칙에 있는 입자를 고려해 보십시오; 이 차원 중 어느 것도 어떤 의미에서도 "특별한"것이 아니므로, 대칭은 교차-곱-표현된 각 운동량에 있으며, 이는 위에서 언급한 레비-치비타 표현에 의해 분명합니다).

Mnemonic

Mnemonic to calculate a cross product in vector form

"Xyzzy (mnemonic)" redirects here. For other uses, see Xyzzy.

단어 "xyzzy"는 교차 곱의 정의를 기억하기 위해 사용될 수 있습니다.

만약 다음이면

$\mathbf {a} =\mathbf {b} \times \mathbf {c}$

여기서:

$\mathbf {a} ={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}},\ \mathbf {b} ={\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\end{bmatrix}},\ \mathbf {c} ={\begin{bmatrix}c_{x}\\c_{y}\\c_{z}\end{bmatrix}}$

다음과 같습니다:

$a_{x}=b_{y}c_{z}-b_{z}c_{y}$

$a_{y}=b_{z}c_{x}-b_{x}c_{z}$

$a_{z}=b_{x}c_{y}-b_{y}c_{x}.$

두 번째와 세 번째 방정식은 단순히 아래첨자를 수직적으로 회전, x → y → z → x함으로써 첫 번째 방정식에서 얻을 수 있습니다. 물론, 문제는 첫 번째 방정식을 기억하는 방법이고, 이 목적을 위해 두 가지 옵션을 사용할 수 있습니다: 사뤼스의 스킴 (i를 포함하는 것)의 관련 두 가지 대각선을 기억하거나, xyzzy 수열을 기억하는 것입니다.

사뤼스의 스킴에서 첫 번째 대각선은 위에서-언급된 3×3 행렬의 주요 대각선(main diagonal)일 뿐이므로, xyzzy라는 단어의 처음 세 글자는 매우 쉽게 기억될 수 있습니다.

Cross visualization

위의 기억법 장치와 유사하게, 방정식에서 두 벡터 사이에 "교차로" 또는 X로 시각화될 수 있습니다. 이것은 올바른 교차 곱 공식을 기억하는 데 도움이 될 수 있습니다.

만약 다음이면

$\mathbf {a} =\mathbf {b} \times \mathbf {c}$

다음과 같습니다:

$\mathbf {a} ={\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\end{bmatrix}}\times {\begin{bmatrix}c_{x}\\c_{y}\\c_{z}\end{bmatrix}}.$

만약 우리가 $a_{x}$에 대한 공식을 얻기를 원하면, 우리는 공식에서 $b_{x}$와 $c_{x}$를 버리고, 그 다음 두 개의 성분을 내립니다:

$a_{x}={\begin{bmatrix}b_{y}\\b_{z}\end{bmatrix}}\times {\begin{bmatrix}c_{y}\\c_{z}\end{bmatrix}}.$

$a_{y}$에 대해 이 작업을 수행할 때, 그 다음 두 개의 원소는 z 성분 뒤에 x 성분이 오도록 행렬을 "둘러싸야" 합니다. 명확히 하기 위해, $a_{y}$에 대해 이 작업을 수행할 때, 그 다음 두 개의 성분이 (해당 순서대로) z와 x여야 합니다. $a_{z}$에 대해, 그 다음 두 개의 성분은 x와 y로 취해져야 합니다.

$a_{y}={\begin{bmatrix}b_{z}\\b_{x}\end{bmatrix}}\times {\begin{bmatrix}c_{z}\\c_{x}\end{bmatrix}},\ a_{z}={\begin{bmatrix}b_{x}\\b_{y}\end{bmatrix}}\times {\begin{bmatrix}c_{x}\\c_{y}\end{bmatrix}}$

그런-다음 $a_{x}$에 대해, 교차 연산자를 왼쪽의 원소에서 오른쪽의 원소를 가리키는 것으로 시각화하면, 왼쪽의 첫 번째 원소를 가져와 오른쪽 행렬에서 교차가 가리키는 원소를 간단히 곱할 수 있습니다. 그런-다음 왼쪽 아래에 있는 다음 원소를 빼고, 여기에서도 교차 표시가 가리키는 원소를 곱합니다. 이것은 우리의 $a_{x}$ 공식을 초래합니다 –

$a_{x}=b_{y}c_{z}-b_{z}c_{y}.$

우리는 이것을 $a_{y}$와 $a_{z}$에 대해 관련 공식을 구성하기 위해 같은 방법으로 수행할 수 있습니다.

Applications

교차 곱은 다양한 상황에서 응용을 가집니다. 예를 들어, 그것은 계산적 기하학, 물리학, 및 공학에 사용됩니다. 전체가 아닌 예시 목록은 다음과 같습니다.

Computational geometry

교차 곱은 삼-차원 공간에서 서로로부터 두 개의 꼬인 직선 (같은 평면에 있지 않은 직선)의 거리 계산에 나타납니다.

교차 곱은 컴퓨터 그래픽에서 자주 수행되는 작업, 삼각형 또는 다각형의 법선을 계산하기 위해 사용될 수 있습니다. 예를 들어, 다각형 내의 한 점에 대한 다각형의 굴곡 (시계 방향 또는 반 시계 방향)은 (바퀴 살과 같은) 다각형을 삼각 측량하고 각 각도의 부호를 추적하기 위해 교차 곱을 사용하여 (살 사이의) 각도를 합산하여 계산될 수 있습니다.

평면의 계산적 기하학(computational geometry)에서, 교차 곱은 세 점 $p_{1}=(x_{1},y_{1}),$ $p_{2}=(x_{2},y_{2})$, 및 $p_{3}=(x_{3},y_{3})$에 의해 정의되는 예각(acute angle)의 부호를 결정하기 위해 사용됩니다. 그것은 두 쌍의 점 $(p_{1},p_{2})$과 $(p_{1},p_{3})$에 의해 정의된 두 개의 공통-평면 벡터(vectors)의 교차 곱의 방향 (위쪽 또는 아래쪽)에 해당합니다. 예각의 부호는 다음 식의 부호입니다:

$P=(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1}),$

이는 두 벡터의 교차 곱의 부호화된 길이입니다.

"오른손" 좌표 시스템에서, 만약 그 결과가 0이면, 점들이 공선형(collinear)에 있습니다; 만약 그것이 양수이면, 세 점은 $p_{1}$을 중심으로 $p_{2}$에서 $p_{3}$까지 양의 회전 각도를 구성하고, 그렇지 않으면 음의 각도를 구성합니다. 또 다른 관점에서 볼 때, $P$의 부호는 $p_{3}$가 직선 $p_{1},p_{2}$의 왼쪽에 있는지 또는 오른쪽에 있는지를 알려줍니다.

교차 곱은 사면체(tetrahedron) 또는 평행-육면체(parallelepiped)와 같은 다면체(polyhedron)의 부피를 계산하기 위해 사용됩니다.

Angular momentum and torque

주어진 원점에 대한 입자의 각 운동량(angular momentum) L은 다음과 같이 정의됩니다:

$\mathbf {L} =\mathbf {r} \times \mathbf {p} ,$

여기서 r은 원점에 관한 입자의 위치 벡터이고, p는 입자의 선형 운동량입니다.

같은 방법으로, 점 A 주변의 점 B에 가해지는 힘 F_B의 모멘트(moment) M은 다음과 같이 주어집니다:

$\mathbf {M} _{\mathrm {A} }=\mathbf {r} _{\mathrm {AB} }\times \mathbf {F} _{\mathrm {B} }\,$

역학에서, 힘(force)의 모멘트(moment)은 토크(torque)라고도 하고 $\mathbf {\tau }$로 표시됩니다.

위치 r,, 선형 운동량 p, 및 힘 F는 모두 참(true) 벡터이므로, 각 운동량 L과 힘 M의 모멘트는 유사-벡터(pseudovectors) 또는 축 벡터(axial vectors)입니다.

Rigid body

교차 곱은 강체 운동의 설명에 자주 나타납니다. 강체(rigid body)의 두 점 P와 Q는 다음과 같이 관련될 수 있습니다:

$\mathbf {v} _{P}-\mathbf {v} _{Q}={\boldsymbol {\omega }}\times \left(\mathbf {r} _{P}-\mathbf {r} _{Q}\right)\,$

여기서 $\mathbf {r}$은 점의 위치, $\mathbf {v}$는 속도이고 ${\boldsymbol {\omega }}$는 몸체의 각 속도(angular velocity)입니다.

위치 $\mathbf {r}$과 속도 $\mathbf {v}$는 참(true) 벡터이므로, 각 속도 ${\boldsymbol {\omega }}$는 유사-벡터(pseudovector) 또는 축 벡터(axial vector)입니다.

Lorentz force

See also: Lorentz force

교차 곱은 움직이는 전하 q_e가 겪는 로렌츠 힘(Lorentz force)을 설명하는 데 사용됩니다:

$\mathbf {F} =q_{e}\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)$

속도 v, 힘 F, 및 전기장 E는 모두 참(true) 벡터이므로, 자기장 B는 유사-벡터(pseudovector)입니다.

Other

벡터 미적분(vector calculus)에서, 교차 곱은 벡터 연산자(vector operator) 컬(curl)에 대한 공식을 정의하기 위해 사용됩니다.

행렬 곱셈의 관점에서 교차 곱을 다시 작성하는 트릭은 특히 일치 구속 조건을 도출할 때 에피폴라(epipolar)와 다중-보기 기하학에서 자주 나타납니다.

As an external product

The cross product in relation to the exterior product. In red are the orthogonal unit vector, and the "parallel" unit bivector.

교차 곱은 외부 곱의 관점에서 정의될 수 있습니다. 그것은 삼-차원 이외의 외부 곱(external product)으로 일반화될 수 있습니다. 이 관점은 교차 곱의 자연스러운 기하학적 해석을 허용합니다. 외부 대수(exterior algebra)에서, 두 벡터의 외부 곱은 이중-벡터입니다.이중-벡터는 벡터가 방향화된 선분 원소와 거의 같은 방법으로 방향화된 평면 원소입니다. 두 벡터 a와 b가 주어지면, 이중-벡터 a ∧ b를 a와 b에 의해 스팬된 평행사변형으로 볼 수 있습니다. 교차 곱은 다음과 같이 이중-벡터 a ∧ b의 호지 별(Hodge star)을 취하여 2-벡터를 벡터에 매핑하여 얻습니다:

$a\times b=\star (a\wedge b).$

이것은 이중-벡터에 "수직"인 방향화된 다중-차원 원소로 생각될 수 있습니다. 삼-차원에서만, 방향화된 1차원 원소(벡터)가 나오는 반면, 예를 들어 4차원에서는 이중-벡터의 호지 이중이 이차원 (이중벡터)입니다. 따라서 3차원에서만 a와 b의 벡터 교차 곱을 이중-벡터 a ∧ b에 대한 벡터 이중으로 정의할 수 있습니다; 그것은 이중-벡터에 수직이고, 좌표 시스템의 손모양에 따라 방향이 달라지고, a ∧ b가 단위 이중-벡터에 상대적으로 가지는 크기와 단위 법선 벡터에 대해 같은 크기를 가집니다.

Handedness

Consistency

물리 법칙을 방정식으로 쓸 때, 손모양을 포함한 좌표 시스템을 임의적으로 선택할 수 있습니다. 고려되어야 할 모든 변환 아래에서 양 측이 동일하게 동작하지 않는 방정식을 절대 작성하지 않도록 주의해야 합니다. 예를 들어, 방정식의 한 측이 두 개의 극 벡터(polar vectors)의 교차 곱이면, 결과가 축 벡터(axial vector)라는 점을 고려해야 합니다. 따라서, 일관성을 위해, 나머지 한 측도 축 벡터여야 합니다. 보다 일반적으로, 교차 곱의 결과는 피연산자의 유형 (극 벡터 또는 축 벡터)에 따라 극 벡터 또는 축 벡터가 될 수 있습니다. 즉, 극 벡터와 축 벡터는 교차 곱의 응용 아래에서 다음과 같은 방법으로 상호 연관됩니다:

• polar vector × polar vector = axial vector
• axial vector × axial vector = axial vector
• polar vector × axial vector = polar vector
• axial vector × polar vector = polar vector

또는 기호적으로

• polar × polar = axial
• axial × axial = axial
• polar × axial = polar
• axial × polar = polar

교차 곱도 극 벡터일 수 있기 때문에, 거울 이미지 변환으로 방향이 변경되지 않을 수 있습니다. 이것은 피연산자 중 하나가 극 벡터이고 다른 하나가 축 벡터 (예를 들어, 두 극 벡터의 교차 곱)이면, 위의 관계에 따라 발생합니다. 예를 들어, 3개의 극 벡터를 포함하는 벡터 세-쌍 곱(vector triple product)은 극 벡터입니다.

외부 대수를 사용하여 손모양-없는 접근이 가능합니다.

The paradox of the orthonormal basis

(i, j,k)를 직교-정규 기저라고 놓습니다. 벡터 i, j, 및 k는 공간의 방향에 의존하지 않습니다. 그것들은 어떠한 방향이 없이도 정의될 수 있습니다. 그것들은 따라서 축 벡터가 될 수 없습니다. 그러나 i와 j가 극 벡터이면 k는 i × j = k 또는 j × i = k에 대한 축 벡터입니다. 이것은 역설입니다.

"축(axial)" 및 "극(polar)"은 물리적 벡터에 대한 물리적 한정어입니다; 즉, 속도나 자기장과 같은 물리적 양을 나타내는 벡터입니다. 벡터 i, j, 및 k는 수학적 벡터이며, 축도 극도 아닙니다. 수학에서, 두 벡터의 교차-곱은 벡터입니다. 모순이 없습니다.

Generalizations

교차 곱을 더 높은 차원으로 일반화하는 여러 가지 방법이 있습니다.

Lie algebra

Main article: Lie algebra

교차 곱은 가장 단순한 리 곱 중 하나로 볼 수 있고, 따라서 리 대수(Lie algebras)에 의해 일반화되며, 다중-선형성, 반-대칭, 및 야코비 항등식의 공리를 만족시키는 이항 곱으로 공리화됩니다. 많은 리 대수가 존재하고, 그것들의 연구는 리 이론(Lie theory)이라고 불리는 수학의 주요 분야입니다.

예를 들어, 하이젠베르크 대수(Heisenberg algebra)는 $\mathbf {R} ^{3}$ 위에 또 다른 리 대수 구조를 제공합니다. 기저 $\{x,y,z\},$에서, 그 곱은 $[x,y]=z,[x,z]=[y,z]=0$입니다.

Quaternions

Further information: quaternions and spatial rotation

교차 곱은 쿼터니언(quaternions)의 관점에서 설명될 수도 있습니다. 일반적으로, 만약 벡터 [a₁, a₂, a₃]가 쿼터니언 a₁i + a₂j + a₃k로 표현되면, 두 벡터의 교차 곱은 그것들의 곱을 쿼터니언으로 취하고 결과의 실수 부분을 삭제함으로써 얻을 수 있습니다. 실수 부분은 두 벡터의 점 곱의 부정입니다.

Octonions

See also: Seven-dimensional cross product and Octonion

7차원 벡터에 대한 교차 곱은 쿼터니언 대신 옥토니언(octonions)을 사용함으로써 같은 방법으로 얻을 수 있습니다. 다른 차원에서 두 벡터의 비-자명한 벡터-값 교차 곱의 비-존재는 유일한 노름화된 나눗셈 대수(normed division algebras)는 차원 1, 2, 4, 및 8을 갖는 대수라는 후르비츠의 정리(Hurwitz's theorem) 결과와 관련이 있습니다.

Exterior product

Main articles: Exterior algebra and Comparison of vector algebra and geometric algebra § Cross and exterior products

일반적인 차원에서, 특히 벡터를 생성하는 이항 교차 곱의 직접적인 유사점은 없습니다. 어쨌든, 두 벡터의 외부 곱이 이제 보통의 벡터 대신 2-벡터라는 점을 제외하면 유사한 속성을 가지는 외부 곱이 있습니다. 위에서 언급한 바와 같이, 교차 곱은 호지 별(Hodge star) 연산자를 사용하여 2-벡터를 벡터에 매핑함으로써 삼 차원에서 외부 곱으로 해석될 수 있습니다. 외부 곱의 호지 이중은 (n − 2)-벡터를 생성하며, 이는 임의의 차원에서 교차 곱의 자연스러운 일반화입니다.

외부 곱과 점 곱은 (합을 통해) 결합되어 기하 대수에서 기하 곱(geometric product)을 형성할 수 있습니다.

External product

위에서 언급한 바와 같이, 교차 곱은 외부 곱의 호지 이중으로 삼-차원에서 해석될 수 있습니다. 임의의 유한 n 차원에서, n − 1 벡터의 외부 곱의 호지 이중은 벡터입니다. 따라서, 이항 연산 대신, 임의적인 유한 차원에서, 교차 곱은 주어진 n − 1 벡터의 외부 곱의 호지 이중으로 일반화됩니다. 이 일반화는 외부 곱(external product)이라고 불립니다.

Commutator product

Main articles: Geometric algebra § Extensions of the inner and exterior products, Cross product § Cross product and handedness, and Cross product § Lie algebra

대수의 삼-차원 벡터 공간(vector space)을 삼-차원 기하 대수의 2-벡터 (1-벡터가 아님) 부분-대수(subalgebra)로 해석하면, 여기서 $\mathbf {i} =\mathbf {e_{2}} \mathbf {e_{3}}$,$\mathbf {j} =\mathbf {e_{1}} \mathbf {e_{3}}$, 및 $\mathbf {k} =\mathbf {e_{1}} \mathbf {e_{2}}$, 교차 곱은 정확하게 기하 대수에서 교환자 곱(commutator product)에 해당하고 둘 다 같은 기호 $\times$를 사용합니다. 교환자 곱은 기하 대수에서 2-벡터 $A$와 $B$에 대해 다음과 같이 정의됩니다:

$A\times B={\tfrac {1}{2}}(AB-BA)$

여기서 $AB$는 기하 곱입니다.

교환자 곱은 삼 차원에서 임의적인 다중-벡터(multivectors)로 일반화될 수 있으며, 그 결과 다중-벡터는 등급(grades) 1 (1-벡터/참 벡터) 및 2 (2-벡터/유사-벡터) 원소로만 구성됩니다. 두 1-벡터의 교환자 곱은 실제로 외부 곱과 같고 2-벡터를 산출하는 반면, 1-벡터와 2-벡터의 교환자는 참 벡터를 산출하며, 대신 기하 대수에서 왼쪽과 오른쪽 수축(left and right contractions)에 해당합니다. 두 2-벡터의 교환자 곱은 상응하는 동등한 곱을 가지지 않으며, 이는 교환자 곱이 2-벡터에 대해 먼저 정의되는 이유입니다. 더욱이, 3개의 2-벡터의 교환자 세-쌍 곱은 벡터 대수에서 같은 3개의 유사-벡터의 벡터 세-쌍 곱(vector triple product)과 같습니다. 어쨌든, 기하 대수에서 3개의 1-벡터의 교환자 세-쌍 곱은 대신 벡터 대수에서 같은 3개의 참 벡터의 벡터 세-쌍 곱(vector triple product)의 음수(negative)입니다.

더 높은 차원으로의 일반화는 더 높은 차원의 기하 대수에서 2-벡터의 같은 교환자 곱에 의해 제공되지만, 2-벡터는 더 이상 유사-벡터가 아닙니다. 삼차원에서 2-벡터의 교환자 곱/교차 곱이 가장 간단한 리 대수에 해당하는 것처럼, 교환자 곱을 갖춘 고차원 기하 대수의 2-벡터 부분-대수도 리 대수에 해당합니다. 역시 삼차원에서와 마찬가지로, 교환자 곱은 임의적인 다중-벡터로 더 일반화될 수 있습니다.

Multilinear algebra

다중-선형 대수(multilinear algebra)의 맥락에서, 교차 곱은 3-차원 부피 형식에서 얻은 (1,2)-텐서 (혼합된 텐서, 특히 쌍선형 맵), 인덱스를 올림으로써 (0,3)-텐서로 볼 수 있습니다.

구체적으로, 3-차원 부피 형식은 이들 3개의 벡터에 의해 주어진 행렬의 행렬식을 취함으로써 곱 $V\times V\times V\to \mathbf {R}$을 정의합니다. 이중성(duality)에 의해, 이것은 $V\times V\to V^{*}$ 함수와 동등하고, (임의의 두 입력을 고정하면 세 번째 입력을 평가함으로써 $V\to \mathbf {R}$ 함수를 제공) 안의 곱 (예를 들어 점 곱; 보다 일반적으로, 비-퇴화 쌍-선형 형식)의 존재에서, 우리는 동형 $V\to V^{*}$을 가지고, 따라서 이것은 교차 곱인 맵 $V\times V\to V$을 생성합니다: (0,3)-텐서 (3개의 벡터 입력, 스칼라 출력)은 "인덱스를 올림"으로써 (1,2)-텐서 (2개의 벡터 입력, 1개의 벡터 출력)로 변환되었습니다.

위의 대수를 기하학으로 번역하면, 함수 $V\to \mathbf {R}$를 정의하는 함수 "$(a,b,-)$로 정의된 평행-육면체의 부피" (여기서 처음 두 벡터는 고정되고 마지막은 입력임)는 벡터를 갖는 점 곱으로 고유하게 표현될 수 있습니다: 이 벡터는 교차 곱 $a\times b$입니다. 이러한 관점에서, 교차 곱은 스칼라 세-쌍 곱, $\mathrm {Vol} (a,b,c)=(a\times b)\cdot c$으로 정의됩니다.

같은 방법으로, 더 높은 차원에서 $(0,n)$-텐서인 n-차원 부피 형식의 인덱스를 올림으로써 일반화된 교차 곱을 정의할 수 있습니다. 교차 곱의 가장 직접적인 일반화는 다음 중 하나를 정의하는 것입니다:

• $(1,n-1)$-텐서, 이는 입력으로 $n-1$ 벡터를 취하고, 출력으로 1 벡터를 제공합니다 – $(n-1)$-항 벡터-값 곱, 또는
• $(n-2,2)$-텐서, 이는 입력으로 2 벡터를 취하고 출력으로 랭크 n − 2의 반-대칭 텐서(skew-symmetric tensor)을 제공합니다 – 랭크 n − 2 텐서 값을 갖는 이항 곱. 역시 출력 k에 대해 $(k,n-k)$-텐서를 정의할 수 있습니다.

이들 곱은 모두 다중-선형 및 반-대칭적이고, 행렬식 및 패리티(parity)의 관점에서 정의될 수 있습니다.

$(n-1)$-항 곱은 다음처럼 설명될 수 있습니다: $\mathbf {R} ^{n}$에서 $n-1$ 벡터 $v_{1},\dots ,v_{n-1}$가 주어지면, 그것들의 일반화된 교차 곱 $v_{n}=v_{1}\times \cdots \times v_{n-1}$을 다음과 같이 정의할 수 있습니다:

• $v_{i}$에 의해 정의된 초평면에 수직,
• 크기는 $v_{i}$에 의해 정의되는 평행-다면체의 부피이며, $v_{i}$의 그람 행렬식으로 계산될 수 있습니다,
• $v_{1},\dots ,v_{n}$가 양수적으로 방향화되도록 방향화됩니다.

이것은 인덱스의 순환 순열에 대해 $e_{1}\times \cdots \times e_{n-1}=e_{n}$, $e_{2}\times \cdots \times e_{n}=e_{1},$ 등으로 평가되는 고유한 다중-선형, 교대하는 곱입니다.

좌표에서, Rⁿ에서 교차 곱의 이 $(n-1)$-항 유사체에 대해 공식을 다음과 같이 제공할 수 있습니다:

$\bigwedge _{i=0}^{n-1}\mathbf {v} _{i}={\begin{vmatrix}v_{1}{}^{1}&\cdots &v_{1}{}^{n}\\\vdots &\ddots &\vdots \\v_{n-1}{}^{1}&\cdots &v_{n-1}{}^{n}\\\mathbf {e} _{1}&\cdots &\mathbf {e} _{n}\end{vmatrix}}.$

이 공식은 기저 벡터의 행이 행렬식에서 첫 번째 행이 아니라 마지막 행이라는 점을 제외하면 R³에서 정규 교차 곱에 대한 행렬식과 구조가 동일합니다. 이것에 대한 이유는 순서화된 벡터 (v₁, ..., v_n−1, Λ^n–1
_i=0v_i)가 (e₁, ..., e_n)에 관해 양수적으로 방향(orientation)을 가짐을 보장하는 것입니다. 만약 n이 홀수이면, 이 수정은 값을 변경하지 않고 그대로 두므로, 이 규칙은 이항 곱의 통상적인 정의와 일치합니다. 어쨌든, n이 짝수인 경우에서, 이 구별이 유지되어야 합니다. 이 $(n-1)$-항 형식은 벡터 교차 곱과 같은 많은 속성을 가집니다: 그것은 인수에서 교대하고 선형이고, 각 인수에 수직이고, 크기는 인수로 묶인 영역의 초부피를 제공합니다. 그리고 벡터 교차 곱과 마찬가지로, 인수의 쐐기 곱의 호지 이중으로 좌표 독립적인 방법으로 정의될 수 있습니다. 더욱이, 곱 $[v_{1},\ldots ,v_{n}]:=\bigwedge _{i=0}^{n}v_{i}$은 Filippov 항등식을 만족합니다:

$[[x_{1},\ldots ,x_{n}],y_{2},\ldots ,y_{n}]]=\sum _{i=1}^{n}[x_{1},\ldots ,x_{i-1},[x_{i},y_{2},\ldots ,y_{n}],x_{i+1},\ldots ,x_{n}],$

그리고 따라서 Rⁿ⁺¹에 n-리 대수의 구조를 부여합니다 (의 명제 1 참조).

History

1773년에, 조제프-루이 라그랑주(Joseph-Louis Lagrange)는 삼차원에서 사면체(tetrahedron)를 연구하기 위해 점 곱과 교차 곱 모두의 성분 형식을 사용했습니다.

1843년에, 윌리엄 로언 해밀턴(William Rowan Hamilton)은 쿼터니언 곱과 함께 벡터와 스칼라라는 용어를 도입했습니다. 두 개의 쿼터니언 [0, u]와 [0, v]가 주어지면, 여기서 u와 v는 R³에서 벡터이며, 그것들의 쿼터니언 곱은 [−u ⋅ v, u × v]으로 요약될 수 있습니다. 제임스 클러크 맥스웰(James Clerk Maxwell)은 해밀턴의 쿼터니언 도구를 사용하여 그의 유명한 전자기 방정식(electromagnetism equations)을 개발했고, 이러한 이유와 다른 이유로 한동안 쿼터니언은 물리 교육의 필수적인 부분이었습니다.

1844년에, 헤르만 그라스만(Hermann Grassmann)은 2차원이나 3차원에 묶이지 않은 기하 대수를 발표했습니다. 그라스만은 [uv]로 표시되는 교차 곱을 포함하여 여러 곱을 개발합니다. (역시 참조: exterior algebra.)

1853년에, 그라스만과 동시대인, 오귀스탱-루이 코시(Augustin-Louis Cauchy)는 방정식을 풀기 위해 사용되고 교차 곱과 같은 곱셈 속성을 가지는 대수적 키에 대한 논문을 발표했습니다.

1878년에, 윌리엄 킹던 클리퍼드(William Kingdon Clifford)는 vector product이라는 용어가 증언되었든 Elements of Dynamic을 출판했습니다. 그 책에서, 이 두 벡터의 곱은 두 벡터가 두 변인 평행사변형(parallelogram)의 넓이(area)와 같은 크기와 평면에 수직인 방향을 갖는 것으로 정의됩니다. (역시 참조: Clifford algebra.)

1881년 강의 노트에서, 깁스(Gibbs)는 교차 곱을 $u\times v$로 표현하고 이를 skew product이라고 부릅니다. 1901년에, 깁스의 학생, 에드윈 비드웰 윌슨(Edwin Bidwell Wilson)은 이들 강의 노트를 편집하고 교과서 Vector Analysis으로 확장했습니다. 윌슨은 skew product이라는 용어를 유지하지만, cross produc과 vector product이라는 대안적인 용어가 더 자주 사용되는 것을 관찰합니다.

1908년에, 체사레 부랄리-포르티(Cesare Burali-Forti)와 로베르토 마르콜롱고(Roberto Marcolongo)는 벡터 곱 표기법 u ∧ v을 도입했습니다. 기호 $\times$는 이미 곱셈(multiplication)과 데카르트 곱(cartesian product)을 나타내기 위해 사용되기 때문에 이것은 오늘날까지 프랑스와 기타 지역에서 사용됩니다.

See also

• Cartesian product – a product of two sets
• Geometric algebra: Rotating systems
• Multiple cross products – products involving more than three vectors
• Multiplication of vectors
• Quadruple product
• × (the symbol)

Bibliography

• Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing. p. 134. ISBN 978-0-486-67766-8.
• Crowe, Michael J. (1994). A History of Vector Analysis. Dover. ISBN 0-486-67910-1.
• E. A. Milne (1948) Vectorial Mechanics, Chapter 2: Vector Product, pp 11 –31, London: Methuen Publishing.
• Wilson, Edwin Bidwell (1901). Vector Analysis: A text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs. Yale University Press.
• T. Levi-Civita; U. Amaldi (1949). Lezioni di meccanica razionale (in Italian). Bologna: Zanichelli editore.

External links

• "Cross product", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• A quick geometrical derivation and interpretation of cross products
• An interactive tutorial created at Syracuse University – (requires java)
• W. Kahan (2007). Cross-Products and Rotations in Euclidean 2- and 3-Space. University of California, Berkeley (PDF).
• The vector product, Mathcentre (UK), 2009