Cross section (geometry)

기하학(geometry)과 과학(science)에서, 교차 단면(cross section)은 삼-차원 공간에 있는 고체와 평면, 또는 고-차원 공간에 있는 아날로그의 비-빈 교차점(intersection)입니다. 대상을 조각으로 자르는 것은 많은 평행 교차-단면을 생성합니다. 2개의 축에 평행한, 즉, 이들 축에 의해 결정된 평면에 평행한 삼-차원 공간에서 교차-단면의 경계는 윤곽선(contour line)이라고 참조됩니다; 예를 들어, 만약 평면이 지면과 평행한 융기-부조 지도(raised-relief map)의 산을 통해 자르면, 결과는 같은 고도(elevation)의 산 표면 위에 있는 점을 표시하는 이-차원 공간에서 윤곽선입니다.

테크니컬 드로잉(technical drawing)에서, 대상을 교차하는 평면 위로 그것의 투영인 교차-단면은 -3차원 대상의 내부 배열을 이-차원으로 묘사하기 위해 사용되는 공통적인 도구입니다. 그것은 전통적으로 사용되는 재료의 유형을 나타내는 크로스해칭 스타일로 크로스해칭됩니다.

컴퓨터 축 단층 촬영(computed axial tomography)과 함께, 컴퓨터는 x-레이 데이터에서 교차-단면을 구성할 수 있습니다.

Definition

만약 평면이 고체 (3-차원 대상)와 교차하면, 평면과 고체에 공통되는 영역은 고체의 교차-단면(cross-section)이라고 불립니다.^[1] 고체의 교차-단면을 포함하는 평면은 절단 평면(cutting plane)이라고 참조됩니다.

고체의 교차-단면의 모양은 고체에 대한 절단 평면의 방향에 따라 달라질 수 있습니다. 예를 들어, 공의 모든 교차-단면은 디스크이지만,^[2] 정육면체의 교차-단면은 절단 평면이 정육면체와 어떻게 관련되어 있는지에 따라 달라집니다. 만약 절단 평면이 정육면체의 마주보는 두 면의 중심을 연결하는 직선에 수직이면, 교차-단면은 정사각형이 되지만, 만약 절단 평면이 정육면체의 마주보는 꼭짓점을 연결하는 대각선에 수직이면, 교차-단면은 점, 삼각형, 또는 육각형일 수 있습니다.

Plane sections

관련된 개념은 평면과 표면의 교차의 곡선인 평면 단면(plane section)의 개념입니다.^[3] 따라서, 평면 단면은 절단 평면에서 고체의 교차-단면의 경계입니다.

만약 삼-차원 공간에서 표면이 두 변수의 함수, 즉, $z = f (x, y)$ 에 의해 정의되면, 좌표 평면 (두 좌표 축에 의해 결정된 평면)에 평행한 절단 평면에 의한 평면 단면은 수준 곡선(level curves) 또는 등분선(isolines)이라고 합니다.^[4] 보다 구체적으로, $z = k$ ( $xy$ -평면에 평행한 평면) 형식의 방정식을 갖는 평면을 절단하면 응용 분야에서 종종 윤곽선(contour lines)이라고 불리는 평면 단면을 생성합니다.

Mathematical examples of cross sections and plane sections

다면체(polyhedron)의 교차 단면은 다각형(polygon)입니다.

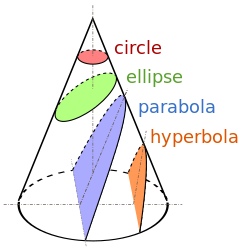
원뿔 단면 – 원, 타원, 포물선, 및 쌍곡선 – 은 왼쪽 다이어그램에서 볼 수 있듯이 다양한 다른 각도에서 절단 평면을 갖는 원뿔의 평면 단면입니다.

타원면체(ellipsoid)의 중심을 통과하는 임의의 교차-단면은 타원 영역을 형성하지만, 해당하는 평면 단면은 그것의 표면에서 타원입니다. 이것들은 절단 평면이 대칭 축에 수직(perpendicular)일 때 각각 디스크와 원으로 퇴화됩니다. 더 일반적으로, 이차-초곡면(quadric)의 평면 단면은 원뿔 단면입니다.^[5]

두 밑면 사이에 연장된 단단한 직각 원형 원기둥의 교차-단면은 만약 교차-단면이 원기둥의 밑면에 평행하면 디스크이거나, 만약 그것이 밑면에 평행하지도 않고 수직이지도 않으면 타원 영역 (오른쪽 그림 참조)입니다. 만약 절단 평면이 밑면에 수직이면, 그것이 원기둥에 접하지 않은 한 직사각형 (표시되지 않음)으로 구성되며, 이 경우에서 단일 선분입니다.

원기둥(cylinder)이라는 용어는 고체 원기둥의 옆쪽 표면을 의미할 수도 있습니다 (원기둥 참조). 만약 원기둥이 이런 의미로 사용되면, 위의 단락은 다음과 같이 읽힐 것입니다: 유한 길이의 수직 원형 원기둥의 평면 단면은^[6] 절단 평면이 원기둥의 대칭 축에 수직이면 원이고, 그것이 해당 축에 평행도 아니고 수직도 아니면 타원입니다. 만약 절단 평면이 축에 평행하면 절단 평면이 원기둥에 접하지 않은 한 평면 단면은 한 쌍의 평행한 선분으로 구성되며, 이 경우에서 평면 단면은 단일 선분입니다.

A graph of

z = x 2 + xy + y 2

. For the partial derivative at (1, 1, 3) that leaves

y

constant, the corresponding tangent line is parallel to the

xz

-plane.

A plane section of the above graph showing the level curve in the

xz

-plane at

y = 1

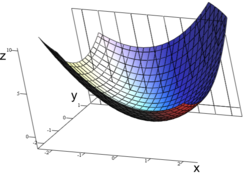
평면 단면은 그림과 같이 인수 중 하나와 관련하여 함수의 부분 도함수(partial derivative)를 시각화하기 위해 사용될 수 있습니다. $z = f (x, y)$ 라고 가정합니다. $x$ 에 관한 $f (x, y)$ 의 부분 도함수를 취하여, 고정된 $y$ 값에서 함수 $f$ 의 평면 단면을 $x$ 에 대해서만 $z$ 의 수준 곡선을 그리기 위해 취할 수 있습니다; 그런-다음 $x$ 에 관한 부분 도함수는 결과로 생성되는 2차원 그래프의 기울기입니다.

In related subjects

절단 평면이 변수 중 하나의 고정된 값에 있는 두 확률 변수의 확률 밀도 함수의 평면 단면은 나머지 다른 변수의 조건부 밀도 함수 (평면 단면을 정의하는 고정 값에 대한 조건부)입니다. 만약 대신 평면 단면이 밀도의 고정 값에 대해 취해지면, 결과는 등-밀도 윤곽선(iso-density contour)입니다. 정규 분포(normal distribution)에 대해, 이들 윤곽선은 타원입니다.

경제학(economics)에서, 생산 함수(production function) $f (x, y)$ 는 전형적으로 노동과 물적 자본과 같은 다양한 투입량 $x$ 와 $y$ 에 의해 생산될 수 있는 산출량을 지정합니다. 기업이나 사회의 생산 함수는 삼-차원 공간에 그려질 수 있습니다. 만약 평면 단면이 $xy$ -평면에 평행하게 취해지면, 결과는 평면 단면의 높이에 의해 주어진 산출량의 수준을 초래하는 노동과 자본 사용의 다양한 조합을 보여주는 등량곡선(isoquant)입니다. 대안적으로, 만약 생산 함수의 평면 단면은 $y$ 의 고정된 수준에서—즉, $xz$ -평면에 평행하게—취해지면, 결과는 다른 입력 $y$ 의 고정된 값과 조합된 한 입력의 다양한 사용 $x$ 값 각각에서 얼마나 많은 출력을 생성할 수 있는지 보여주는 이-차원 그래프입니다.

역시 경제학에서, 세는-숫자 또는 순서-숫자 효용 함수 $u (w, v)$ 는 두 재화의 양 $w$ 와 $v$ 를 소비함으로써 얻은 소비자의 만족 정도를 나타냅니다. 만약 효용 함수의 평면 단면이 주어진 높이 (효용의 수준)에서 취해지면, 이-차원 결과는 모두 지정된 수준의 효용을 제공하는 두 재화의 소비된 총양 $w$ 와 $v$ 의 다양한 대안적인 조합을 보여주는 무차별 곡선(indifference curve)입니다.

Area and volume

카발리에리의 원리(Cavalieri's principle)에 따르면 같은 넓이의 해당 교차-단면을 갖는 고체는 같은 부피를 가집니다.

특정 각도에서 볼 때 물체의 교차-단면 넓이 ( $A'$ )는 해당 각도에서 물체의 직교 투영의 총 넓이입니다. 예를 들어, 높이 h이고 반지름 r의 원기둥은 중심 축을 따라 볼 때 $A'=\pi r^{2}$ 을 가지고, 직교 방향에서 볼 때 $A'=2rh$ 를 가집니다. 반지름 r의 구는 임의의 각도에서 볼 때 $A'=\pi r^{2}$ 를 가집니다. 보다 일반적으로, $A'$ 는 다음 표면 적분을 평가함으로써 계산될 수 있습니다:

A'=\iint \limits _{\mathrm {top} }d\mathbf {A} \cdot \mathbf {\hat {r}} ,

여기서 $\mathbf {\hat {r}}$ 은 보는 방향을 따라 뷰어를 향하는 단위 벡터이고, $d\mathbf {A}$ 는 바깥쪽을-가리키는 법선을 갖는 표면 원소이고, 적분은 뷰어의 관점에서 "볼 수 있는" 표면의 부분, 오직 최상단 표면에 걸쳐 취합니다. 볼록한 몸체에 대해, 뷰어의 관점에서 물체를 통과하는 각 반직선은 두 개의 표면만 교차합니다. 그러한 물체에 대해, 적분은 (상수 벡터 필드 $\mathbf {\hat {r}}$ 에 적용된 발산 정리(Divergence Theorem)에 의해 요구하는 것처럼 물체의 "꼭대기"와 "바닥"이 빼지 않도록) 피적분의 절댓값을 취하고 2로 나눔으로써 전체 표면 ( $A$ )에 걸쳐 취할 수 있습니다:

A'={\frac {1}{2}}\iint \limits _{A}|d\mathbf {A} \cdot \mathbf {\hat {r}} |

In higher dimensions

고체의 교차-단면과 유사하게, $n$ -차원 공간에서 $n$ -차원 물체의 교차-단면은 물체와 초평면 ( $(n - 1)$ -차원 부분공간)의 비-빈 교차점입니다. 이 개념은 때때로 고차원 공간의 측면을 시각화하는 데 사용되어 왔습니다.^[7] 예를 들어, 4-차원 물체가 3-차원 공간을 통과하면, 4-차원 물체의 3-차원 교차-단면을 볼 수 있습니다. 특히, 3-공간을 통과하는 4-공 (초구)은 최대로 증가하고 그런-다음 전이하는 동안 크기에서 감소하는 3-공으로 나타납니다. 이 동적 물체 (3-공간의 관점에서 볼 때)는 4-공의 일련의 교차-단면입니다.

Examples in science

지질학(geology)에서, 행성 내부의 구조는 종종 오른쪽에서 지구의 교차-단면에서와 같이 행성의 중심을 통과하는 행성의 교차-단면 다이어그램을 사용하여 설명됩니다.

교차-단면은 왼쪽에 표시된 것처럼 기관의 내부 구조를 설명하기 위해 해부학(anatomy)에서 종종 사용됩니다.

왼쪽에 표시된 나무 줄기의 교차-단면은 나무의 나이와 그 환경의 시간적 속성을 찾기 위해 사용될 수 있는 나이테(growth rings)를 나타냅니다.

Notes

^ Swokowski 1983, p. 296
^ in more technical language, the cross-sections of a 3-ball are 2-balls
^ Albert 2016, p. 38
^ Swokowski 1983, p. 716
^ Albert 2016, p. 117
^ these cylinders are open, they do not contain their bases
^ Stewart 2001, p. 59

References

Albert, Abraham Adrian (2016) [1949], Solid Analytic Geometry, Dover, ISBN 978-0-486-81026-3
Stewart, Ian (2001), Flatterland / like flatland, only more so, Persus Publishing, ISBN 0-7382-0675-X
Swokowski, Earl W. (1983), Calculus with analytic geometry (Alternate ed.), Prindle, Weber & Schmidt, ISBN 0-87150-341-7

[1] Swokowski 1983, p. 296

[2] re technical language, the cross-sections of a 3-ball are 2-balls

[3] Albert 2016, p. 38

[4] Swokowski 1983, p. 716

[5] Albert 2016, p. 117

[6] these cylinders are open, they do not contain their bases

[7] Stewart 2001, p. 59

[1]

[2]

[3]

[4]

[5]

[6]

[7]