Cube (algebra)

Original article: w:Cube (algebra)

"Third power" redirects here. For the band, see Third Power.

"Cubed" redirects here. For other uses, see Cube (disambiguation).

"³" redirects here. Its literal meaning is the numeral "3" in superscript.

y = x³ for values of 1 ≤ x ≤ 25.

산술(arithmetic)과 대수(algebra)에서, 숫자 n의 큐브(cube)는 세 번째 거듭제곱(power), 즉, n의 셋을 함께 곱한 것의 결과입니다. 숫자 또는 임의의 다른 수학적 표현(mathematical expression)의 세제곱은 위첨자 3, 예를 들어 2³ = 8 또는 (x + 1)³에 의해 표시됩니다.

세제곱은 역시 숫자를 그것의 제곱(square)에 곱한 것입니다:

n³ = n × n × n.

세제곱 함수는 하나의 숫자를 그것의 세제곱에 매핑하는 함수(function) x ↦ x³입니다 (종종 y = x³로 표시됩니다). 그것은 다음처럼 홀수 함수(odd function)입니다:

(−n)³ = −(n³).

기하학적 정육면체(geometric cube)의 부피(volume)는 그것의 변 길이의 세제곱이며, 그 이름을 낳습니다. 그것의 세제곱이 n인 숫자를 찾는 것으로 구성되는 역(inverse) 연산은 n의 세제곱근을 추출하는 것이라고 불립니다. 그것은 주어진 부피의 정육면체의 변을 결정합니다. 그것은 역시 n에 1/3의 거듭제곱을 올립니다.

세제곱 함수의 그래프(graph)는 삼차 포물선(cubic parabola)으로 알려져 있습니다. 세제곱 함수는 홀수 함수이기 때문에, 이 곡선은 원점에 대칭의 중심(center of symmetry)이 있지만, 대칭 축(axis of symmetry)은 없습니다.

In integers

세제곱 숫자(cube number), 또는 완전 세제곱(perfect cube), 또는 때때로 단지 세제곱(cube)은 정수(integer)의 세제곱인 숫자입니다. 비-음의 60³까지 완전 세제곱은 다음입니다 (OEIS에서 수열 A000578):

03 =	0
13 =	1	113 =	1331	213 =	9261	313 =	29,791	413 =	68,921	513 =	132,651
23 =	8	123 =	1728	223 =	10,648	323 =	32,768	423 =	74,088	523 =	140,608
33 =	27	133 =	2197	233 =	12,167	333 =	35,937	433 =	79,507	533 =	148,877
43 =	64	143 =	2744	243 =	13,824	343 =	39,304	443 =	85,184	543 =	157,464
53 =	125	153 =	3375	253 =	15,625	353 =	42,875	453 =	91,125	553 =	166,375
63 =	216	163 =	4096	263 =	17,576	363 =	46,656	463 =	97,336	563 =	175,616
73 =	343	173 =	4913	273 =	19,683	373 =	50,653	473 =	103,823	573 =	185,193
83 =	512	183 =	5832	283 =	21,952	383 =	54,872	483 =	110,592	583 =	195,112
93 =	729	193 =	6859	293 =	24,389	393 =	59,319	493 =	117,649	593 =	205,379
103 =	1000	203 =	8000	303 =	27,000	403 =	64,000	503 =	125,000	603 =	216,000

기하학적으로 말하면, 양의 정수 m 완전 세제곱인 것과 m개의 단단한 단위 정육면체를 더 큰 단단한 정육면체로 배열하는 것은 필요충분(iff) 조건입니다. 예를 들어, 27개의 작은 정육면체는 3 × 3 × 3 = 27이므로 루빅스 큐브(Rubik's Cube) 모양을 갖는 하나의 큰 정육면체로 배열될 수 있습니다.

연속된 정수의 세제곱 사이의 차이는 다음과 같이 표현할 수 있습니다:

n³ − (n − 1)³ = 3(n − 1)n + 1.

또는

(n + 1)³ − n³ = 3(n + 1)n + 1.

음의 정수의 세제곱은 음수이므로, 최소 완전 세제곱은 없습니다. 예를 들어, (−4) × (−4) × (−4) = −64입니다.

Base ten

완전 제곱(perfect squares)과 달리, 완전 세제곱은 마지막 두 자릿수에 대해 작은 가능성의 숫자를 가지지 않습니다. 5로 나뉠 수 있는 세제곱을 제외하고, 여기에 오직 25, 75, 및 00가 마지막 두 자리가 될 수 있으며, 홀수 마지막 숫자를 갖는 임의의 자릿수의 쌍은 완전 세제곱의 마지막 숫자로 나타날 수 있습니다. 짝수(even) 세제곱과 함께, 오직 00에 대해 상당한 제한이 있으며, o2, e4, o6, 및 e8은 완전 세제곱의 마지막 두 자리가 될 수 있습니다 (여기서 o는 임의의 홀수 자릿수를 의미하고 e는 임의의 짝수 자릿수를 의미합니다). 일부 세제곱 숫자는 역시 제곱수이기도 합니다; 예를 들어, 64는 제곱수 (8 × 8)와 세제곱수 (4 × 4 × 4)입니다. 이것이 발생하는 것과 그 숫자가 완전 여섯 번째 거듭제곱 (이 경우 2⁶)인 것은 필요충분 조건입니다.

각 세 번째 거듭제곱의 마지막 자릿수는 다음입니다:

0

1

8

7

4

5

6

3

2

9

어쨌든, 모든 완전 세제곱이 자릿수 근(digital root) 1, 8, 또는 9를 가져야 하기 때문에, 대부분의 숫자는 완전 세제곱이 아님을 쉽게 보여줍니다. 즉, 그들의 값 모듈로(modulo) 9는 오직 0, 1, 및 8일 수 있습니다. 게다가, 임의의 숫자의 세제곱의 자릿수 근은 3으로 나눠질 때 그 수가 제공하는 나머지에 의해 결정될 수 있습니다:

• 만약 숫자 x가 3으로 나뉘면, 그것의 세제곱은 자릿수 근 9를 가집니다; 즉,

  ${\text{if}}\quad x\equiv 0{\pmod {3}}\quad {\text{then}}\quad x^{3}\equiv 0{\pmod {9}}{\text{ (actually}}\quad 0{\pmod {27}}{\text{)}};$

• 만약 그것이 3으로 나뉠 때 1의 나머지를 가지면, 그것의 세제곱은 자릿수 근 1을 가집니다; 즉,

  ${\text{if}}\quad x\equiv 1{\pmod {3}}\quad {\text{then}}\quad x^{3}\equiv 1{\pmod {9}};$

• 만약 그것이 3으로 나뉠 때 2의 나머지를 가지면, 그것의 세제곱은 자릿수 근 8을 가집니다; 즉,

  ${\text{if}}\quad x\equiv 2{\pmod {3}}\quad {\text{then}}\quad x^{3}\equiv 8{\pmod {9}}.$

Waring's problem for cubes

Main article: Waring's problem

모든 각 양의 정수는 9개 (또는 그 미만)의 양수 세제곱의 합으로 쓸 수 있습니다. 예를 들어, 23은 9개 미만의 양수 세제곱의 합으로 쓸 수 없기 때문에 아홉 세제곱의 이 높은 극한은 줄어들 수 없습니다:

23 = 2³ + 2³ + 1³ + 1³ + 1³ + 1³ + 1³ + 1³ + 1³.

Sums of three cubes

Main article: Sums of three cubes

±4 모듈로 9와 일치(congruent)하지 않는 모든 각 정수 (양수 또는 음수)는 무한하게 많은 방법으로 셋의 (양수 또는 음수) 세제곱의 합으로 쓸 수 있다고 추측됩니다. 예를 들어, $6=2^{3}+(-1)^{3}+(-1)^{3}$. ±4 모듈로 9에 일치하는 정수는 셋의 세제곱의 합으로 쓸 수 없기 때문에 제외됩니다.

그러한 합이 알려져 있지 않은 가장 작은 그러한 정수는 114입니다. 2019년 9월에, 알려진 3-세제곱 합이 없는 이전의 가장 작은 정수, 42는 다음 방정식을 만족시키는 것으로 나타났습니다:

$42=(-80538738812075974)^{3}+80435758145817515^{3}+12602123297335631^{3}.$

$x^{3}+y^{3}+z^{3}=n$에 대한 하나의 해는 n ≤ 78에 대해 아래 테이블에 제공되고, n은 4 또는 5 모듈로 9에 일치하지 않습니다. 선택된 해는 원시 (gcd(x, y, z) = 1)인 것이고, 형식 $c^{3}+(-c)^{3}+n^{3}=n^{3}$ 또는 $(n+6nc^{3})^{3}+(n-6nc^{3})^{3}+(-6nc^{2})^{3}=2n^{3}$의 것이 아니고 (왜냐하면 그것들은 무한한 해의 가족이기 때문), |z| 및 |y|에 대해 최소 값을 가집니다 (이 순서로 테스트되었습니다).

더 작은 n 값에 대한 해에서 비-원시 해를 간단하게 추론할 수 있으므로 오직 원시 해가 선택됩니다. 예를 들어, n = 24에 대해, 해 $2^{3}+2^{3}+2^{3}=24$는 해 $1^{3}+1^{3}+1^{3}=3$의 모든 항에 $8=2^{3}$을 곱함으로써 초래됩니다. 그러므로, 이것은 선택되는 또 다른 해입니다. 유사하게, n = 48에 대해, 해 (x, y, z) = (-2, -2, 4)는 제외되고, 이것이 선택된 해 (x, y, z) = (-23, -26, 31)입니다.

Primitive solutions for n from 1 to 78
n	x	y	z		n	x	y	z
1	9	10	−12		39	117367	134476	−159380
2	1214928	3480205	−3528875		42	12602123297335631	80435758145817515	−80538738812075974
3	1	1	1		43	2	2	3
6	−1	−1	2		44	−5	−7	8
7	0	−1	2		45	2	−3	4
8	9	15	−16		46	−2	3	3
9	0	1	2		47	6	7	−8
10	1	1	2		48	−23	−26	31
11	−2	−2	3		51	602	659	−796
12	7	10	−11		52	23961292454	60702901317	−61922712865
15	−1	2	2		53	−1	3	3
16	−511	−1609	1626		54	−7	−11	12
17	1	2	2		55	1	3	3
18	−1	−2	3		56	−11	−21	22
19	0	−2	3		57	1	−2	4
20	1	−2	3		60	−1	−4	5
21	−11	−14	16		61	0	−4	5
24	−2901096694	−15550555555	15584139827		62	2	3	3
25	−1	−1	3		63	0	−1	4
26	0	−1	3		64	−3	−5	6
27	−4	−5	6		65	0	1	4
28	0	1	3		66	1	1	4
29	1	1	3		69	2	−4	5
30	−283059965	−2218888517	2220422932		70	11	20	−21
33	−2736111468807040	−8778405442862239	8866128975287528		71	−1	2	4
34	−1	2	3		72	7	9	−10
35	0	2	3		73	1	2	4
36	1	2	3		74	66229832190556	283450105697727	−284650292555885
37	0	−3	4		75	4381159	435203083	−435203231
38	1	−3	4		78	26	53	−55

Fermat's Last Theorem for cubes

Main article: Fermat's Last Theorem

방정식 x³ + y³ = z³은 정수에서 비-자명한 (즉, xyz ≠ 0) 해를 가지지 않습니다. 사실, 그것은 아인슈타인 정수(Eisenstein integers)에서 해를 가지지 않습니다.

이들 명제 둘 다는 역시 방정식 x³ + y³ = 3z³에 대해 참입니다.

Sum of first n cubes

첫 번째 n 세제곱의 합은 제곱된 n번째 삼각형 숫자(triangle number)입니다:

$1^{3}+2^{3}+\dots +n^{3}=(1+2+\dots +n)^{2}=\left({\frac {n(n+1)}{2}}\right)^{2}.$

Visual proof that 1³ + 2³ + 3³ + 4³ + 5³ = (1 + 2 + 3 + 4 + 5)².

증명. Charles Wheatstone (1854)는 합에서 각 세제곱을 연속적인 홀수의 집합으로 확장함으로써 특히 간단한 유도를 제공합니다. 그는 다음 항등식을 부여하는 것으로 시작합니다:

$n^{3}=\underbrace {\left(n^{2}-n+1\right)+\left(n^{2}-n+1+2\right)+\left(n^{2}-n+1+4\right)+\cdots +\left(n^{2}+n-1\right)} _{n{\text{ consecutive odd numbers}}}.$

해당 항등식은 다음 방법에서 삼각형 숫자(triangular numbers) $T_{n}$과 관련되어 있습니다:

$n^{3}=\sum _{k=T_{n-1}+1}^{T_{n}}(2k-1),$

따라서 $n^{3}$를 형성하는 피합수는 $(n-1)^{3}$까지 모든 이전 값 $1^{3}$를 형성하는 것들 바로 다음에 시작합니다. 이 속성을 또 다른 잘-알려진 항등식과 함께 적용하면:

$n^{2}=\sum _{k=1}^{n}(2k-1),$

우리는 다음 유도를 얻습니다:

${\begin{aligned}\sum _{k=1}^{n}k^{3}&=1+8+27+64+\cdots +n^{3}\\&=\underbrace {1} _{1^{3}}+\underbrace {3+5} _{2^{3}}+\underbrace {7+9+11} _{3^{3}}+\underbrace {13+15+17+19} _{4^{3}}+\cdots +\underbrace {\left(n^{2}-n+1\right)+\cdots +\left(n^{2}+n-1\right)} _{n^{3}}\\&=\underbrace {\underbrace {\underbrace {\underbrace {1} _{1^{2}}+3} _{2^{2}}+5} _{3^{2}}+\cdots +\left(n^{2}+n-1\right)} _{\left({\frac {n^{2}+n}{2}}\right)^{2}}\\&=(1+2+\cdots +n)^{2}\\&={\bigg (}\sum _{k=1}^{n}k{\bigg )}^{2}.\end{aligned}}$

Visual demonstration that the square of a triangular number equals a sum of cubes.

보다 최근의 수학 문헌에서, Stein (1971)은 항등식의 기하학적 증명을 형성하기 위해 이들 숫자의 직사각형-세는 해석을 사용합니다 (역시 Benjamin, Quinn & Wurtz 2006을 참조하십시오); 그는 그것이 역시 귀납법에 의해 쉽게 (그러나 정보가 없게) 증명될 수 있다는 것을 관찰하고, Toeplitz (1963)는 "흥미로운 고대 아랍어 증명"을 제공한다고 말합니다. Kanim (2004)은 순수한 시각적 증명을 제공하고, Benjamin & Orrison (2002)은 둘의 추가 증명을 제공하고, Nelsen (1993)은 일곱의 기하학적 증명을 제공합니다.

예를 들어, 처음 5 세제곱의 합은 5번째 삼각형 숫자의 제곱입니다,

$1^{3}+2^{3}+3^{3}+4^{3}+5^{3}=15^{2}$

유사한 결과는 처음 y 홀수(odd) 세제곱의 합에 대해 제공될 수 있습니다:

$1^{3}+3^{3}+\dots +(2y-1)^{3}=(xy)^{2}$

그러나 x, y는 음의 펠 방정식(Pell equation) x² − 2y² = −1을 만족시켜야 합니다. 예를 들어, y = 5와 29에 대해, 다음이고, 이런 식으로 계속됩니다:

$1^{3}+3^{3}+\dots +9^{3}=(7\cdot 5)^{2}$

$1^{3}+3^{3}+\dots +57^{3}=(41\cdot 29)^{2}$

역시, 모든 각 짝수(even) 완전 숫자(perfect number)는, 가장 낮은 것을 제외, 처음 2^p−1/2
홀수 세제곱 (p = 3, 5, 7, ...)의 합입니다:

$28=2^{2}(2^{3}-1)=1^{3}+3^{3}$

$496=2^{4}(2^{5}-1)=1^{3}+3^{3}+5^{3}+7^{3}$

$8128=2^{6}(2^{7}-1)=1^{3}+3^{3}+5^{3}+7^{3}+9^{3}+11^{3}+13^{3}+15^{3}$

Sum of cubes of numbers in arithmetic progression

One interpretation of Plato's number, 3³ + 4³ + 5³ = 6³

그것의 합이 세제곱인 산술 진행(arithmetic progression)에서 숫자의 세제곱의 예제가 있습니다:

$3^{3}+4^{3}+5^{3}=6^{3}$

$11^{3}+12^{3}+13^{3}+14^{3}=20^{3}$

$31^{3}+33^{3}+35^{3}+37^{3}+39^{3}+41^{3}=66^{3}$

이때, 첫 번째 숫자는 때때로 신비한 플라톤의 숫자(Plato's number)로 식별됩니다. 공통 차이 d와 초기 세제곱 a³를 갖는 산술 진행에서 숫자의 n 세제곱의 합을 찾는 공식 F는,

$F(d,a,n)=a^{3}+(a+d)^{3}+(a+2d)^{3}+\cdots +(a+dn-d)^{3}$

다음에 의헤 제공됩니다:

$F(d,a,n)=(n/4)(2a-d+dn)(2a^{2}-2ad+2adn-d^{2}n+d^{2}n^{2})$

다음에 대한 매개변수적 해는

$F(d,a,n)=y^{3}$

d = 1의 특별한 경우, 또는 연속적인 세제곱에 대해 알려져 있지만, 오직 산발적 해는 d = 2, 3, 5, 7, 11, 13, 37, 39, 등과 같은 정수 d > 1에 대해 알려져 있습니다.

Cubes as sums of successive odd integers

홀수 정수 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, ...의 수열에서, 첫 번째 하나는 세제곱 (1 = 1³)입니다. 다음 두 개의 합은 다음 세제곱 (3 + 5 = 2³)입니다; 다음 세 개의 합은 다음 세제곱 (7 + 9 + 11 = 3³)입니다; 그리고 이런 식으로 계속됩니다.

In rational numbers

모든 각 양의 유리수(rational number)는 세 개의 양의 유리수 세제곱의 합이고, 둘의 유리수 세제곱의 합이 아닌 유리수가 있습니다.

In real numbers, other fields, and rings

Further information: cubic function

y = x³ plotted on a Cartesian plane

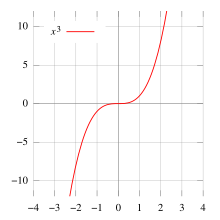
실수(real number)에서, 세제곱 함수는 순서를 유지합니다: 더 큰 숫자가 더 큰 세제곱을 가집니다. 다시 말해서, 세제곱은 (엄격하게) 단조적으로 증가(monotonically increase)합니다. 역시, 그 코도메인(codomain)은 전체 실수 직선(real line)입니다: 함수 x ↦ x³ : R → R는 전사(surjection)입니다 (모든 가능한 값을 취합니다). 오직 셋의 숫자가 자신의 세제곱과 같습니다: −1, 0, 및 1. 만약 −1 < x < 0 또는 1 < x이면, x³ > x입니다. 만약 x < −1 또는 0 < x < 1이면, x³ < x입니다. 모든 앞서 언급한 속성은 실수의 임의의 더 높은 홀수 거듭제곱 (x⁵, x⁷, ...)에도 적용됩니다. 상등과 부등식(inequalities)은 역시 임의의 순서화된 링(ordered ring)에서 참입니다.

닮은(similar) 유클리드 입체(solids)의 부피는 그것들의 선형 크기의 세제곱과 관련됩니다.

복소수(complex number)에서, 순수 허수(purely imaginary)의 세제곱은 역시 순수 허수입니다. 예를 들어, i³ = −i입니다.

x³의 도함수(derivative)는 3x²과 같습니다.

세제곱은 때때로 p ≠ 1 (mod 3)인 그러한 소수 p에 대해 F_p에서 처럼 다른 필드(fields)에 전서 속성을 가지지만, 반드시 그런 것은 아닙니다: 위의 유리수를 갖는 반대예제를 참조하십시오. 역시 F₇에서 오직 셋의 원소 0, ±1가 총 일곱의 완전 세제곱입니다. −1, 0, 및 1은 어디에서나 완전 세제곱이고 필드의 유일한 원소는 고유한 세제곱과 같습니다:x³ − x = x(x − 1)(x + 1).

History

큰 숫자의 세제곱을 결정하는 것은 많은 고대 문명에서 매우 공통적이었습니다. 메소포타미아 수학자들은 구 바빌로니아(Old Babylonian) 시대 (기원전 20세기에서 16세기)까지 세제곱과 세제곱근을 계산하기 위한 테이블을 갖는 설형 태블릿을 만들었습니다. 삼차 방정식은 고대 그리스 수학자 디오판토스(Diophantus)에게 알려져 있었습니다. 알렉산드리아의 히이로(Hero of Alexandria)는 서기 1세기에 세제곱근을 계산하는 방법을 고안했습니다. 삼차 방정식을 풀고 세제곱근을 추출하는 방법은 기원전 2세기경에 편집되고 기원후 3세기에 유 휘(Liu Hui)에 의해 논평된 중국 수학 텍스트, The Nine Chapters on the Mathematical Art에 나타납니다.

See also

• Cabtaxi number
• Cubic equation
• Doubling the cube
• Euler's sum of powers conjecture
• Fifth power (algebra)
• Fourth power
• Kepler's laws of planetary motion#Third law
• Monkey saddle
• Perfect power
• Taxicab number

References

• Hardy, G. H.; Wright, E. M. (1980). An Introduction to the Theory of Numbers (Fifth ed.). Oxford: Oxford University Press. ISBN 978-0-19-853171-5.
• Wheatstone, C. (1854), "On the formation of powers from arithmetical progressions", Proceedings of the Royal Society of London, 7: 145–151, Bibcode:1854RSPS....7..145W, doi:10.1098/rspl.1854.0036.