Parallel (geometry)

Original article: w:Parallel (geometry)

This article is about the geometry concept. For other uses, see Parallel (disambiguation).

"Parallel lines" and "Parallel line" redirect here. For other uses, see Parallel lines (disambiguation).

Line art drawing of parallel lines and curves.

기하학(geometry)에서, 평행 직선(parallel lines)은 임의의 점에서 교차(intersect)하지 않는 공통-평면(coplanar) 직진 직선(lines)입니다. 평행 평면(parallel planes)은 같은 삼-차원 공간(three-dimensional space)에서 결코 만나지 않는 평면(planes)입니다. 평행 곡선(parallel curve)은 서로 접촉(touch)하지 않거나 교차하지 않고 고정된 최소 길이를 유지하는 곡선(curve)입니다. 삼-차원 유클리드 공간에서, 한 점을 공유하지 않은 한 직선과 한 평면은 역시 평행이라고 말합니다. 어쨌든, 둘의 비-공평면 직선은 꼬인 직선(skew lines)이라고 불립니다.

평행 직선은 유클리드(Euclid)의 평행 공준(parallel postulate)의 주제입니다. 평행성은 주로 아핀 기하학(affine geometries)의 속성이고 유클리드 기하학(Euclidean geometry)은 기하학의 이 유형의 특별한 예제입니다. 쌍곡선 기하학(hyperbolic geometry)과 같은 일부 다른 기하학에서, 직선은 평행성으로 참조되는 유사한 속성을 가질 수 있습니다.

Symbol

평행 기호는 $\parallel$입니다. 예를 들어, $AB\parallel CD$는 직선 AB가 직선 CD와 평행임을 나타냅니다.

유니코드(Unicode) 문자 집합에서, "평행"과 "평행 아님" 기호는, 각각, 코드점 U+2225 (∥)과 U+2226 (∦)을 가집니다. 게다가, U+22D5 (⋕)는 "같고 평행한" 관계를 나타냅니다.

같은 기호는 전기 공학에서 이진 함수 (병렬 연산자(parallel operator))에 대해 사용됩니다. 그것은 노름(norm)을 나타내는 이중-수직-줄 괄호와 마찬가지로 여러 프로그래밍 언어에서 논리적 또는 연산자 (||)와 구별됩니다.

Euclidean parallelism

Two lines in a plane

Conditions for parallelism

As shown by the tick marks, lines a and b are parallel. This can be proved because the transversal t produces congruent corresponding angles $\theta$, shown here both to the right of the transversal, one above and adjacent to line a and the other above and adjacent to line b.

유클리드 공간(Euclidean space)에서 평행한 직선 l과 m이 주어지면, 다음 속성은 동등합니다:

1. 직선 m 위의 모든 각 점은 직선 l에서 정확하게 같은 (최소) 거리에 위치됩니다 등거리 직선).
2. 직선 m은 직선 l과 같은 평면에 있지만 l과 교차하지 않습니다 (직선들이 양쪽 방향에서 무한대(infinity)로 연장됨을 기억하십시오).
3. 직선 m과 l이 둘 다 같은 평면에서 세 번째 직선 (횡단(transversal))에 의해 교차될 때, 횡단과 교차의 대응하는 각도(corresponding angles)는 합동(congruent)입니다.

이것들은 동등 속성이기 때문에, 그것들 중 임의의 하나가 유클리드 공간에서 평행 직선의 정의로 취할 수 있지만, 첫 번째와 세 번째 속성은 측정을 포함하고, 따라서, 두 번째 속성보다 "더 복잡합니다". 따라서, 두 번째 속성은 보통 유클리드 기하학에서 평행 직선의 정의하는 속성으로 선택되는 속성입니다. 다른 속성들은 유클리드의 평행 공준(Euclid's Parallel Postulate)의 결과입니다. 역시 측정을 포함하는 또 다른 속성은 서로 평행한 직선은 같은 그래디언트(gradient) (기울기)를 가진다는 것입니다.

History

평면에서 만나지 않은 한 쌍의 직선으로 평행 직선의 정의는 유클리드의 원론(Euclid's Elements)의 책 I에서 정의 23으로 나타납니다. 대안적인 정의는 종종 평행 공준(parallel postulate)을 증명하기 위한 시도의 일부로 다른 그리스인들에 의해 논의되었습니다. 프로크로스(Proclus)는 등거리 직선으로 평행 직선의 정의를 포세이도니오스(Posidonius)에게 기인하고 비슷한 맥락에서 제미노스(Geminus)를 인용합니다. 심플리치오(Simplicius)는 역시 포세이도니오스의 정의와 마찬가지로 철학자 아가니스(Aganis)에 의한 그것의 수정을 언급합니다.

19세기 말에, 영국에서, 유클리드의 원론은 여전히 중등학교에서 표준 교과서였습니다. 기하학의 전통적인 처리는 투영 기하학(projective geometry)과 비-유클리드 기하학(non-Euclidean geometry)의 새로운 발전에 의해 변화해야 한다는 압력을 받고 있었으므로, 기하학의 가르침에 대해 몇 가지 새로운 교과서가 이 시기에 쓰였습니다. 이들 개혁 교과서 사이의 주요 차이점은 그들 자체 사이와 그들과 유클리드 사이 둘 다에서 평행 직선의 처리입니다. 이들 개혁 교과서는 그것들의 비평이 없지는 않았고 그 중 한 명, 찰스 도지슨(Charles Dodgson) (일명 루이스 캐럴(Lewis Carroll))은 희곡, Euclid and His Modern Rivals을 썼으며, 이것에서 이들 교과서는 비난을 받았습니다.

초기 개혁 교과서 중 하나는 1868년의 제임스 모리스 윌슨(James Maurice Wilson)의 Elementary Geometry였습니다. 윌슨은 방향의 원시 개념(primitive notion) 위에 평행 직선의 정의를 기초로 했습니다. 빌헬름 킬링(Wilhelm Killing)에 따르면, 그 아이디어는 라이프니츠(Leibniz)로 거슬러 올라갈 수 있습니다. 윌슨은, 그것이 원시이기 때문에 방향을 정의없이, 그의 여섯 번째 정의, "서로 만나는 두 직선은 다른 방향을 가지고, 그것들의 방향의 차이는 그것들 사이의 각도이다"와 같은 다른 정의에서 용어를 사용합니다. 정의 15에서, 그는 이런 방법에서 평행 직선을 도입했습니다; "같은 방향을 가지지만, 같은 직선의 일부가 아닌 직선은 평행 직선이라고 불립니다." 오거스터스 드 모르간(Augustus De Morgan)은 이 교과서를 검토하고 주로 이 정의와 윌슨이 평행 직선에 대한 것을 증명하기 위해 사용했었던 방법에 근거하여 그것을 실패로 선언했습니다. 도지슨은 역시 그의 희곡 (2막, 장면 VI § 1)의 상당 부분을 윌슨의 평행의 처리를 비난하기 위해 할애합니다. 윌슨은 이 개념을 그의 교과서의 세 번째 이상 버전에서 편집했습니다.

평행 직선의 정의에 대해 대체로 사용했었던, 다른 개혁자들에 의해 제안된 다른 속성은 그다지 좋지 않았습니다. 도지슨에 의해 지적되었던 대로 주요 어려움은 이러한 방법에서 그것들을 사용하기 위해 시스템에 더해지는 추가적인 공리를 요구한다는 것이었습니다. 프랜시스 커스버트슨(Francis Cuthbertson)에 의해 1874년 그의 교과서 Euclidean Geometry에서 설명되었던, 포세이도니오스의 등거리 직선 정의는 직선의 한 변 위에 고정된 주어진 거리에서 발견되는 점이 직선을 형성하는 것으로 보여야 하는 문제를 겪고 있습니다. 이것은 증명될 수 없고 사실로 가정되어야 합니다. W. D. Cooley에 의한 그의 1860년 교과서, The Elements of Geometry, simplified and explained에서 사용된 횡단 속성에 의해 형성된 대응하는 각도는 만약 하나의 횡단이 일치하는 대응하는 각도에서 한 쌍의 직선을 만나면 모든 횡단이 마찬가지로 그래햐 한다는 사실의 증명을 요구합니다. 다시 말하지만, 새로운 공리가 이 명제를 정당화하기 위해 필요됩니다.

Construction

위의 세 가지 속성은 평행 직선의 세 가지 다른 구성 방법으로 이어집니다.

The problem: Draw a line through a parallel to l.

• 
  Property 1: Line m has everywhere the same distance to line l.
• 
  Property 2: Take a random line through a that intersects l in x. Move point x to infinity.
• 
  Property 3: Both l and m share a transversal line through a that intersect them at 90°.

Distance between two parallel lines

Main article: Distance between two lines

유클리드 평면에서 평행 직선은 등거리(equidistant)이기 때문에, 두 평행 직선 사이의 고유한 거리가 있습니다. 둘의 비-수직, 비-수평 평행 직선의 방정식이 주어지면,

$y=mx+b_{1}\,$

$y=mx+b_{2}\,,$

그 두 직선 사이의 거리는 평행 직선에 공통된 수직선 위에 놓이는 두 점 (각 직선에 하나씩)을 찾고 그들 사이의 거리를 계산함으로써 구할 수 있습니다. 직선이 기울기 m을 가지므로, 공통 수직선은 기울기 −1/m을 가질 것이고 우리는 방정식 y = −x/m을 갖는 직선을 공통 수직선으로 취할 수 있습니다. 다음 선형 시스템을 풀면

${\begin{cases}y=mx+b_{1}\\y=-x/m\end{cases}}$

및

${\begin{cases}y=mx+b_{2}\\y=-x/m\end{cases}}$

그 점의 좌표를 얻을 수 있습니다. 선형 방정식에 대한 해는 다음 점입니다:

$\left(x_{1},y_{1}\right)\ =\left({\frac {-b_{1}m}{m^{2}+1}},{\frac {b_{1}}{m^{2}+1}}\right)\,$

및

$\left(x_{2},y_{2}\right)\ =\left({\frac {-b_{2}m}{m^{2}+1}},{\frac {b_{2}}{m^{2}+1}}\right).$

이들 공식은 심지어 평행 직선이 수평이면 (즉, m = 0이면), 여전히 정확한 점 좌표를 제공합니다. 그 점 사이의 거리는 다음입니다:

$d={\sqrt {\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}}={\sqrt {\left({\frac {b_{1}m-b_{2}m}{m^{2}+1}}\right)^{2}+\left({\frac {b_{2}-b_{1}}{m^{2}+1}}\right)^{2}}}\,,$

이것은 다음으로 줄어듭니다:

$d={\frac {|b_{2}-b_{1}|}{\sqrt {m^{2}+1}}}\,.$

그 직선이 직선의 방정식의 일반 형식에 의해 주어지면 (수평 및 수직 직선이 포함됨):

$ax+by+c_{1}=0\,$

$ax+by+c_{2}=0,\,$

그것들의 거리는 다음으로 표현될 수 있습니다:

$d={\frac {|c_{2}-c_{1}|}{\sqrt {a^{2}+b^{2}}}}.$

Two lines in three-dimensional space

교차하지 않는 같은 삼-차원 공간(three-dimensional space)에서 두 직선은 평행할 필요가 없습니다. 오직 그것들이 공통 평면에 있으면 그것들은 평행이라고 불립니다; 그렇지 않으면 그것들은 꼬인 직선(skew lines)이라고 불립니다.

삼-차원 공간에서 둘의 구별되는 직선 l과 m이 평행인 것과 직선 m 위에 한 점 P에서 직선 l 위의 가장 가까운 점까지의 거리가 직선 m 위의 P 위치와 무관한 것은 필요충분(iff) 조건입니다. 이것은 결코 꼬인 직선에 대해 유지되지 않습니다.

A line and a plane

삼-차원 공간에서 직선 m과 평면 q, 해당 평면에 놓이지 않은 직선이 평행인 것과 그것들이 교차하지 않는 것은 필요충분 조건입니다.

동등하게, 그것들이 평행인 것과 지선 m 위의 한 점 P에서 평면 q에서 가장 가까운 점까지의 거리가 직선 m 위의 P의 위치와 무관한 것은 필요충분 조건입니다.

Two planes

평행 직선이 같은 평면에 위치되어야 하는 사실과 유사하게, 평행한 평면은 같은 삼-차원 공간에 놓여야 하고 공통 점을 포함하지 않습니다.

둘의 구별되는 평면 q와 r이 평행인 것과 평면 q에서 한 점 P로부터 평면 r에서 가장 가까운 점까지의 거리가 평면 q에서 P의 위치와 무관한 것은 필요충분 조건입니다. 이것은 만약 두 평면이 같은 삼-차원 공간에 있지 않으면 결코 유지하지 않을 것입니다.

Extension to non-Euclidean geometry

비-유클리드 기하학(non-Euclidean geometry)에서, (직선) 선보다 측지선(geodesic)에 대해 이야기하는 것이 더 공통적입니다. 측지선은 주어진 기하학에서 두 점 사이의 최단 경로입니다. 물리학에서, 이것은 입자가 만약 힘이 그것에 가해지지 않으면 따라가는 경로로 해석될 수 있습니다. 비-유클리드 기하학 (타원(elliptic) 또는 쌍곡선 기하학(hyperbolic geometry))에서, 위에서 언급한 세 가지 유클리드 속성은 동등 않고 오직 두 번째 속성이 있는데 (직선 m은 직선 l과 같은 평면에 있지만 l과 교차하지 않음), 왜냐하면 그것은 측정이 필요하지 않으므로 비유클리드 기하학에서 유용하기 때문입니다. 일반 기하학에서, 위의 세 가지 속성은 각각 세 가지 유형의 곡선, 등거리 곡선(equidistant curves), 평행 측지선(parallel geodesics), 및 공통 수직선을 공유하는 측지선(geodesics sharing a common perpendicular)을 제공합니다.

Hyperbolic geometry

See also: hyperbolic geometry

Intersecting, parallel and ultra parallel lines through a with respect to l in the hyperbolic plane. The parallel lines appear to intersect l just off the image. This is just an artifact of the visualisation. On a real hyperbolic plane the lines will get closer to each other and 'meet' in infinity.

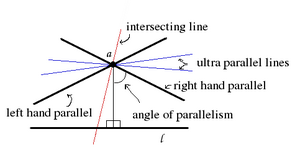
유클리드 기하학에서, 두 측지선이 교차되거나 평행될 수 있지만, 쌍곡선 기하학에서, 세 가지 가능성이 있습니다. 같은 평면에 속하는 두 측지선은 다음 중 하나일 수 있습니다:

1. 교차하는(intersecting), 만약 그것들이 그 평면에서 공통 점에서 교차하면,
2. 평행(parallel), 만약 그것들이 그 평면에서 교차하지 않지만, 무한대에서 점 (아이디얼 점(ideal point))에서 공통 극한으로 수렴하면, 또는
3. 극단 평행(ultra parallel), 만약 그것들이 무한대에서 공통 극한 점을 가지지 않으면.

문헌에서, 극단 평행 측지선은 종종 비-교차하는(non-intersecting) 것이라고 불립니다. 무한대에서 교차하는 측지선은 극한하는 평행(limiting parallel)이라고 불립니다.

직선 l 위에 있지 않은 한 점을 통한 그림에서와 같이 직선 l의 각 방향 아이디얼 점(ideal point)에 대해 하나씩 둘의 극한하는 평행(limiting parallel) 직선이 있습니다. 그것들은 직선 l과 교차하는 직선과 직선 l에 극단 평행인 직선을 분리합니다.

극단 평행 직선은 단일 공통 수직선 (극단평행 정리(ultraparallel theorem))을 가지고, 이 공통 수직선의 양쪽 편에서 발산합니다.

Spherical or elliptic geometry

See also: Spherical geometry and Elliptic geometry

On the sphere there is no such thing as a parallel line. Line a is a great circle, the equivalent of a straight line in spherical geometry. Line c is equidistant to line a but is not a great circle. It is a parallel of latitude. Line b is another geodesic which intersects a in two antipodal points. They share two common perpendiculars (one shown in blue).

구형 기하학(spherical geometry)에서, 모든 측지선은 큰 원(great circles)입니다. 큰 원은 구를 둘의 같은 반구(hemispheres)로 나누고 모든 큰 원은 서로 교차합니다. 따라서, 모든 측지선이 교차하기 때문에, 주어진 측지선에 평행한 측지선이 없습니다. 구 위의 등거리 곡선은 지구 위의 위도(latitude)선과 유사한 위도의 평행이라고 불립니다. 위도의 평행은 구의 중심을 통과하는 평면에 평행한 평면과 구의 교차에 의해 생성될 수 있습니다.

Reflexive variant

만약 l, m, n이 셋의 구별되는 직선이면, $l\parallel m\ \land \ m\parallel n\ \implies \ l\parallel n$입니다.

이 경우에서, 평행성은 전이 관계(transitive relation)입니다. 어쨌든, l = n 경우에서, 중첩된 직선은 유클리드 기하학에서 평행으로 고려되지 않습니다. 평행 직선 사이의 이항 관계(binary relation)는 분명하게 대칭 관계(symmetric relation)입니다. 유클리드의 신념에 따르면, 평행성은 반사 관계(reflexive relation)가 아니고 따라서 동치 관계(equivalence relation)에 실패합니다. 그럼에도 불구하고, 아핀 기하학(affine geometry)에서 평행 직선의 연필(pencil)은 평행성이 동치 관계인 직선의 집합에서 동치 클래스(equivalence class)로 취합니다.

이것을 끝맺기 위해, 에밀 아르틴(Emil Artin) (1957)은 두 직선이 만약 그것들이 공통으로 모두를 가지거나 전혀 없을 때 평행인 평행성의 정의를 채택했습니다. 그런-다음 직선은 반사와 전이 속성이 이러한 유형의 평행성에 속하도록 자체적으로 평행이며, 직선의 집합 위에 동치 관계를 생성합니다. 투사 기하학(incidence geometry)의 연구에서, 평행성의 이 변형은 아핀 평면(affine plane)에서 사용됩니다.

See also

• Clifford parallel
• Concurrent lines
• Limiting parallel
• Parallel curve
• Ultraparallel theorem

References

• Heath, Thomas L. (1956), The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.), New York: Dover Publications

(3 vols.): ISBN 0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3). Heath's authoritative translation plus extensive historical research and detailed commentary throughout the text.

• Richards, Joan L. (1988), Mathematical Visions: The Pursuit of Geometry in Victorian England, Boston: Academic Press, ISBN 0-12-587445-6
• Wilson, James Maurice (1868), Elementary Geometry (1st ed.), London: Macmillan and Co.
• Wylie Jr., C. R. (1964), Foundations of Geometry, McGraw–Hill

Further reading

• Papadopoulos, Athanase; Théret, Guillaume (2014), La théorie des parallèles de Johann Heinrich Lambert : Présentation, traduction et commentaires, Paris: Collection Sciences dans l'histoire, Librairie Albert Blanchard, ISBN 978-2-85367-266-5

External links

• Constructing a parallel line through a given point with compass and straightedge