Bisection

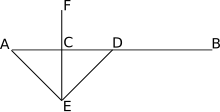
Line DE bisects line AB at D, line EF is a perpendicular bisector of segment AD at C, and line EF is the interior bisector of right angle AED

기하학(geometry)에서, 이등분(bisection)은 무언가를 두 개의 같은 또는 일치(congruent)하는 부분으로의 분할이며, 보통 이등분선(bisector)이라고 불리는, 직선(line)에 의해 분할됩니다. 이등분선의 가장 자주 고려되는 유형은 선분 이등분선(segment bisector) (주어진 선분(segment)의 중간 점을 통과하는 직선)과 각도 이등분선(angle bisector) (각(angle)의 정점을 통과하여, 각을 두 개의 같은 각으로 나누는 직선)입니다.

삼-차원 공간(three-dimensional space)에서, 이등분은 보통 평면에 의해 행해지며, 역시 이등분면(bisector) 또는 이등분하는 평면(bisecting plane)이라고 불립니다.

Line segment bisector

선분(line segment) 이등분선은 선분의 중간점(midpoint)을 통과합니다. 특히 중요한 것은 선분의 수직(perpendicular) 이등분선이며, 그것의 이름에 따라, 선분을 직각(right angle)에서 만납니다. 선분의 수직 이등분선은 역시 그것의 각 점이 선분의 끝점에서 등거리(equidistant)에 있다는 속성을 가집니다. 그러므로, 보로노이 다이어그램(Voronoi diagram) 경계는 그러한 직선 또는 평면의 분절로 구성됩니다.

고전 기하학에서, 이등분은 단순한 컴퍼스와 직선자 구성(compass and straightedge construction)이며, 그것의 가능성은 같은 반지름과 다른 중심의 원(circle)을 그리는 능력에 달려 있습니다. 선분은 같은 반지름의 교차하는 원을 그림으로써 이등분되며, 그것의 중심은 선분의 끝점이고 각 원은 하나의 끝점을 통과함을 만족합니다. 그 두 원의 교차하는 점에 의해 결정되는 직선은 선분의 수직 이등분선인데, 왜냐하면 그것은 그것의 중심에서 선분을 가로지르기 때문입니다. 이 구성은 실제로 주어진 점에서 주어진 직선에 수직인 직선을 구성할 때 사용됩니다: 그것의 중심이 해당 점인 임의적인 원을 그리면, 그것은 둘보다 많은 점에서 직선과 교차하고, 구성될 수직은 직선을 이들 두 점에 의해 정의된 선분을 이등분하는 것입니다.

브라마굽타의 정리(Brahmagupta's theorem)는 만약 순환 사변형(cyclic quadrilateral)이 직교(orthodiagonal)이면 (즉, 수직(perpendicular) 대각선(diagonals)을 가짐), 대각선의 교차의 점에서 변에 수직이 항상 반대 변을 이등분한다는 말합니다.

대수적으로, 끝점 $P_{1}(x_{1},y_{1})$ 과 $P_{2}(x_{2},y_{2})$ 을 갖는 선분의 수직 이등분선은 다음 방정식에 의해 제공됩니다:

y=m(x-x_{3})+y_{3}

, where

m=-{\frac {x_{2}-x_{1}}{y_{2}-y_{1}}}

,

x_{3}={\tfrac {1}{2}}(x_{1}+x_{2})

, and

y_{3}={\tfrac {1}{2}}(y_{1}+y_{2})

.

Angle bisector

Bisection of an angle using a compass and straightedge

각도(angle) 이등분선은 각도를 같은(equal) 측정을 갖는 값으로 두 각도로 나눕니다. 각도는 오직 하나의 이등분선을 가집니다. 각도 이등분선의 각 점은 각도의 변에서 등거리에 있습니다.

각도의 내부 이등분선(interior 또는 internal bisector)은 180° 미만의 각도를 두 같은 각도로 나누는 직선, 반-직선(half-line), 또는 선분입니다. 외부 이등분선(exterior 또는 external bisector)은, 원래 각도를 형성하는 한 변과 다른 변의 연장에 의해 형성된, 보충 각도(supplementary angle) (180°에서 원래 각도를 뺀 값)를 두 개의 같은 각도로 나누는 직선입니다.^[1]

직선자와 컴퍼스(straightedge and compass)와 함께 각도를 이등분하기 위해, 우리는 그것의 중심이 꼭짓점인 원을 그립니다. 그 원은 각 다리에 하나씩 두 점에서 각도를 만납니다. 이들 점의 각각을 중심으로 사용하여, 같은 크기의 두 원을 그립니다. 원의 교차점 (두 점)은 각도 이등분선인 직선을 결정합니다.

이 구성의 정확성의 증명은 문제의 대칭에 의존하여 상당히 직관적입니다. 각도의 삼등분(trisection of an angle) (그것을 셋의 같은 부분으로 나누는 것)은 컴퍼스와 자 단독으로 달성될 수 없습니다 (이것은 피에르 방첼(Pierre Wantzel)에 의해 처음 입증되었습니다).

각도의 내부와 외부 이등분선은 수직(perpendicular)입니다. 만약 각도가 $l_{1}x+m_{1}y+n_{1}=0$ 과 $l_{2}x+m_{2}y+n_{2}=0$ 으로 대수적으로 주어진 두 직선에 의해 형성되면, 내부와 외부 이등분선은 다음 두 방정식에 의해 제공됩니다:^[2]^: p.15

{\frac {l_{1}x+m_{1}y+n_{1}}{\sqrt {l_{1}^{2}+m_{1}^{2}}}}=\pm {\frac {l_{2}x+m_{2}y+n_{2}}{\sqrt {l_{2}^{2}+m_{2}^{2}}}}.

Triangle

Concurrencies and collinearities

삼각형(triangle)의 내부 각도 이등분선은 오른쪽 그림에서 볼 수 있듯이 삼각형의 내-중심(incenter)이라고 불리는 점에서 공점(concurrent)입니다.

두 외부 각도(exterior angle)의 이등분선과 다른 내부 각도(interior angle)의 이등분선은 공점입니다.^[3]^: p.149

세 개의 교차점은, 반대 연잔된 변을 갖는 외부 각도 이등분선의 각각, 같은 직선 위(collinear)에 있습니다 (서로 같은 직선 위에 떨어집니다).^[3]^{: p. 149}

셋의 교차 점, 내부 각도 이등분선과 반대쪽 변 사이의 그것들 중 둘과 다른 외부 각도 이등분선과 연장된 반대쪽 변 사이의 세 번째 것은 같은-직선-위에 있습니다.^[3]^{: p. 149}

Angle bisector theorem

각도 이등분 정리는 삼각형(triangle)의 변이 반대편 각도를 이등분하는 직선으로 나뉘는 두 선분의 상대적 길이(length)와 관련시킵니다. 그것은 그것들의 상대 길이를 삼각형의 다른 두 변의 상대 길이와 같게 합니다.

Lengths

만약 삼각형의 변 길이가 $a,b,c$ , 반-둘레는 $s=(a+b+c)/2$ 이고, A가 변 $a$ 의 반대편 각도이면, 각도 A의 내부 이등분선의 길이는 다음입니다:^[3]^{: p. 70}

{\frac {2{\sqrt {bcs(s-a)}}}{b+c}},

또는 삼각법적 항에서,^[4]

{\frac {2bc}{b+c}}\cos {\frac {A}{2}}.

만약 삼각형 ABC에서 각도 A의 내부 이등분선이 길이 $t_{a}$ 를 가지고 이 이등분선이 A 반대쪽 변을 길이 m과 n의 선분으로 나누면, 다음입니다:^[3]^: p.70

t_{a}^{2}+mn=bc

여기서 b와 c는 꼭짓점 B와 C의 반대쪽 변 길이입니다; 그리고 A 반대쪽 변은 비율 b:c에서 나뉩니다.

만약 각도 A, B, 및 C의 내부 이등분선이 길이 $t_{a},t_{b},$ 및 $t_{c}$ 를 가지면, 다음입니다:^[5]

{\frac {(b+c)^{2}}{bc}}t_{a}^{2}+{\frac {(c+a)^{2}}{ca}}t_{b}^{2}+{\frac {(a+b)^{2}}{ab}}t_{c}^{2}=(a+b+c)^{2}.

일치하지 않는 두 삼각형은 셋의 내부 각도 이등분 길이의 같은 집합을 공유하지 않습니다.^[6]^[7]

Integer triangles

유리 각도 이등분선을 가진 정수 삼각형(integer triangles with a rational angle bisector)이 존재합니다.

Quadrilateral

볼록(convex) 사변형(quadrilateral)의 내부 각도 이등분선은 순환 사변형(cyclic quadrilateral)을 형성하거나 (즉, 인접한 각도 이등분선의 넷의 교차점이 일치-순환(concyclic)입니다),^[8] 또는 그것들은 공점(concurrent)입니다. 후자의 경우에서, 사변형은 접하는 사변형(tangential quadrilateral)입니다.

Rhombus

마름모(rhombus)의 각 대각선은 반대 각도를 이등분합니다.

Ex-tangential quadrilateral

밖의-접하는 사변형(ex-tangential quadrilateral)의 밖의-중심은 여섯 각도 이등분선의 교차에 놓입니다. 이것들은 두 개의 반대편 꼭짓점 각도에서 내부 각도 이등분선, 다른 두 꼭짓점 각도에서 외부 각도 이등분선 (보충 각도 이등분선), 및 반대쪽 변의 연장선(extensions of opposite sides)이 교차하는 곳에서 형성된 각도에서 외부 각도 이등분선입니다.

Parabola

임의의 점에서 포물선(parabola)에 대한 접선(tangent)은 그 점을 초점에 연결하는 직선과 그 점에서 방향선에 수직(perpendicular)인 직선 사이의 각도를 이등분합니다.

Bisectors of the sides of a polygon

Triangle

Medians

삼각형의 세 중앙선(medians)의 각각은 하나의 꼭짓점(vertex)과 반대쪽 변의 중간점을 통과하는 선분이므로, 그것은 해당 변을 이등분합니다 (일반적으로 수직이 아닙니다). 세 중앙선은 삼각형의 도형-중심(centroid)이라고 불리는 점에서 서로 교차하며, 도형-중심은 만약 삼각형이 균등 밀도를 가지면 그것의 질량의 중심(center of mass)입니다; 따라서 삼각형의 도형-중심과 그것의 꼭짓저 중 하나를 통과하는 임의의 직선은 반대쪽 변을 이등분합니다. 도형-중심은 임의의 한 변의 중앙점보다 반대쪽 꼭짓점에 두 배 가깝습니다.

Perpendicular bisectors

삼각형의 변의 내부 수직(perpendicular) 이등분선은 해당 변을 수직으로 이등분하는 직선의 삼각형 위와 내부에 완전히 떨어지는 선분입니다. 삼각형의 세 변의 셋의 수직 이등분선은 둘레-중심(circumcenter) (세 꼭짓점을 통과하는 원의 중심)에서 교차합니다. 따라서 삼각형의 둘레-중심을 통과하고 한 변에 수직인 임의의 직선은 해당 변을 이등분합니다.

예각 삼각형(acute triangle)에서, 둘레-중심은 둘의 가장 짧은 변의 내부 수직 이등분선을 같은 비율로 나눕니다. 둔각 삼각형(obtuse triangle)에서, 둘의 가장 짧은 변의 수직 이등분선 (그것들의 반대쪽 삼각형 변을 넘어 둘레-중심까지 연장됨)은 같은 비율로 그것들 각각의 교차하는 삼각형 변에 의해 나뉩니다.^[9]^{: Corollaries 5 and 6}

임의의 삼각형에 대해 내부 수직 이등분선은 $p_{a}={\tfrac {2aT}{a^{2}+b^{2}-c^{2}}},$ $p_{b}={\tfrac {2bT}{a^{2}+b^{2}-c^{2}}},$ 및 $p_{c}={\tfrac {2cT}{a^{2}-b^{2}+c^{2}}}$ 에 의해 제공되며, 여기서 변은 $a\geq b\geq c$ 이고 넓이는 $T$ 입니다.^[9]^{: Thm 2}

Quadrilateral

볼록(convex) 사변형(quadrilateral)의 둘의 이-중앙선(bimedians)은 반대쪽 변의 중간점을 연결하는 선분이며, 따라서 각각 두 변을 이등분합니다. 대각선의 중간점을 연결하는 둘의 이-중앙선과 선분은 "꼭짓점 도형-중심(vertex centroid)"라고 불리는 점에서 공점이고 이 점에 의해 모두 이등분됩니다.^[10]^: p.125

볼록 사변형의 넷의 "적도(maltitudes)"는 반대쪽 변의 중간점을 통해 변에 수직이며, 따라서 후자의 변을 이등분합니다. 만약 사변형이 순환(cyclic)이면 (원에 내접되면), 이들 적도는 "반-중심(anticenter)"이라고 불리는 공통 점에서 공점(concurrent)합니다 (공통 점에서 모두 만납니다).

브라마굽타의 정리(Brahmagupta's theorem)는 만약 순환 사변형이 직교(orthodiagonal)이면 (즉, 수직(perpendicular) 대각선(diagonals)을 가지면), 대각선의 교차의 점에서 변에 수직이 항상 반대쪽 변을 이등분한다고 말합니다.

수직 이등분선 구성(perpendicular bisector construction)는 또 다른 사변형의 변의 수직 이등분선에서 사변형을 형성합니다.

Area bisectors and perimeter bisectors

Triangle

삼각형(triangle)의 넓이(area)를 이등분하는 무한개의 직선이 있습니다. 그것들 중 셋은 삼각형의 중앙선(medians) (변의 중간점과 반대쪽 꼭짓점을 연결함)이고, 이것들은 삼각형의 도형-중심(centroid)에서 공점(concurrent)입니다; 실제로, 그것들은 도형-중심을 통과하는 유일한 넓이 이등분선입니다. 셋의 다른 넓이 이등분선은 삼각형의 변과 평행합니다; 이것들의 각각은 다른 두면을 교차하여 비율 ${\sqrt {2}}+1:1$ 과 함께 그것들을 선분으로 나눕니다.^[11] 이들 여섯 직선은 동시에 공점 셋입니다: 셋의 중앙선이 공점인 것 외에도, 임의의 하나의 중앙선이 둘의 변-평행 넓이 이등분선과 공점입니다.

넓이 이등분선의 무한대의 봉투(envelope)는 델토이드(deltoid)입니다 (델토이드의 외부에 오목한 곡선에 의해 연결된 셋의 꼭짓점을 갖는 그림으로 광범위하게 정의되며, 내부 점을 비-볼록 집합으로 만듭니다).^[11] 델토이드의 꼭짓점은 중앙선의 중간점에 있습니다; 델토이드 내부의 모든 점은 셋의 다른 넓이 이등분선 위에 있지만, 그것의 외부의 모든 점은 단 하나 위에 있습니다. [1] 델토이드의 변은 삼각형의 연장된 변에 점근적(asymptotic)인 쌍곡선(hyperbola)의 호입니다.^[11] 삼각형의 면적에 대한 넓이 이등분선의 봉투의 넓이의 비율은 모든 삼각형에 대해 불변이고, ${\tfrac {3}{4}}\log _{e}(2)-{\tfrac {1}{2}},$ 즉, 0.019860...와 같거나 2%보다 작습니다.

삼각형의 클리버(cleaver)는 삼각형의 둘레(perimeter)를 이등분하는 선분으고 셋의 변 중 하나의 중간점에 하나의 끝 점을 가집니다. 셋의 클리버는 중앙 삼각형(medial triangle)의 내원(incircle)인 슈피커 원의 중심(center of the Spieker circle)에서 공점(concur)입니다 (모두 통과합니다). 클리버는 각도 이등분선에 평행합니다.

삼각형의 스플리터(splitter)는 삼각형의 셋의 꼭짓점 중 하나에 하나의 끝점을 가지고 둘레를 이등분하는 선분입니다. 셋의 스플리터는 삼각형의 나겔 점(Nagel point)에서 공점입니다.

삼각형의 넓이와 그것의 둘레 둘 다를 반으로 나누는 삼각형을 통과하는 임의의 직선은 삼각형의 내-중심 (그것의 내원(incircle)의 중심)을 통과합니다. 임의의 주어진 삼각형에 대해 이것들 중 하나, 둘 또는 셋이 있습니다. 내-중심을 통과하는 직선이 넓이 또는 둘레 중 하나를 이등분하는 것과 그것이 역시 다른 것을 이등분하는 것은 필요충분 조건입니다.^[12]

Parallelogram

평행사변형(parallelogram)의 중간점을 통과하는 임의의 직선은 넓이와 둘레를 이등분합니다.^[13]

Circle and ellipse

원 또는 다른 타원의 모든 넓이 이등분선과 둘레 이등분선은 중심을 통과하고, 중심을 통과하는 임의의 현(chord)은 넓이와 둘레를 이등분합니다. 원의 경우에서 그것들은 원의 지름(diameter)입니다.

Bisectors of diagonals

Parallelogram

평행사변형의 대각선(diagonal)은 서로 이등분합니다.

Quadrilateral

만약 사변형의 대각선을 연결하는 선분이 두 대각선을 이등분하면, 이 선분 (뉴턴 직선(Newton Line))은 꼭짓점 도형-중심(vertex centroid)에 의해 자체로 이등분됩니다.

Volume bisectors

주어진 비율에서 사면체의 둘의 반대쪽 가장자리를 나누는 평면은 역시 같은 비율로 사면체의 부피를 나눕니다. 따라서 사면체의 이-중앙선 (반대쪽 가장자리의 중간점의 연결자)을 포함하는 임의의 평면은 사면체의 부피를 이등분합니다.^[14]^[15]^{: pp.89–90}

References

^ Weisstein, Eric W. "Exterior Angle Bisector." From MathWorld--A Wolfram Web Resource.
^ Spain, Barry. Analytical Conics, Dover Publications, 2007 (orig. 1957).
^ ^a ^b ^c ^d ^e Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929).
^ Oxman, Victor. "On the existence of triangles with given lengths of one side and two adjacent angle bisectors", Forum Geometricorum 4, 2004, 215–218. http://forumgeom.fau.edu/FG2004volume4/FG200425.pdf
^ Simons, Stuart. Mathematical Gazette 93, March 2009, 115-116.
^ Mironescu, P., and Panaitopol, L., "The existence of a triangle with prescribed angle bisector lengths", American Mathematical Monthly 101 (1994): 58–60.
^ Oxman, Victor, "A purely geometric proof of the uniqueness of a triangle with prescribed angle bisectors", Forum Geometricorum 8 (2008): 197–200.
^ Weisstein, Eric W. "Quadrilateral." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Quadrilateral.html
^ ^a ^b Mitchell, Douglas W. (2013), "Perpendicular Bisectors of Triangle Sides", Forum Geometricorum 13, 53-59. http://forumgeom.fau.edu/FG2013volume13/FG201307.pdf
^ Altshiller-Court, Nathan, College Geometry, Dover Publ., 2007.
^ ^a ^b ^c Dunn, J. A., and Pretty, J. E., "Halving a triangle," Mathematical Gazette 56, May 1972, 105-108.
^ Kodokostas, Dimitrios, "Triangle Equalizers," Mathematics Magazine 83, April 2010, pp. 141-146.
^ Dunn, J. A., and J. E. Pretty, "Halving a triangle", Mathematical Gazette 56, May 1972, p. 105.
^ Weisstein, Eric W. "Tetrahedron." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Tetrahedron.html
^ Altshiller-Court, N. "The tetrahedron." Ch. 4 in Modern Pure Solid Geometry: Chelsea, 1979.

External links

The Angle Bisector at cut-the-knot
Angle Bisector definition. Math Open Reference With interactive applet
Line Bisector definition. Math Open Reference With interactive applet
Perpendicular Line Bisector. With interactive applet
Animated instructions for bisecting an angle and bisecting a line Using a compass and straightedge
Weisstein, Eric W. "Line Bisector". MathWorld.

This article incorporates material from Angle bisector on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

[1] Weisstein, Eric W. "Exterior Angle Bisector." From MathWorld--A Wolfram Web Resource.

[2] Spain, Barry. Analytical Conics, Dover Publications, 2007 (orig. 1957).

[Johnson-3] Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929).

[4] Oxman, Victor. "On the existence of triangles with given lengths of one side and two adjacent angle bisectors", Forum Geometricorum 4, 2004, 215–218. http://forumgeom.fau.edu/FG2004volume4/FG200425.pdf

[5] Simons, Stuart. Mathematical Gazette 93, March 2009, 115-116.

[6] Mironescu, P., and Panaitopol, L., "The existence of a triangle with prescribed angle bisector lengths", American Mathematical Monthly 101 (1994): 58–60.

[7] Oxman, Victor, "A purely geometric proof of the uniqueness of a triangle with prescribed angle bisectors", Forum Geometricorum 8 (2008): 197–200.

[8] Weisstein, Eric W. "Quadrilateral." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Quadrilateral.html

[Mitchell-9] Mitchell, Douglas W. (2013), "Perpendicular Bisectors of Triangle Sides", Forum Geometricorum 13, 53-59. http://forumgeom.fau.edu/FG2013volume13/FG201307.pdf

[Altshiller-Court-10] Altshiller-Court, Nathan, College Geometry, Dover Publ., 2007.

[Dunn-11] Dunn, J. A., and Pretty, J. E., "Halving a triangle," Mathematical Gazette 56, May 1972, 105-108.

[12] Kodokostas, Dimitrios, "Triangle Equalizers," Mathematics Magazine 83, April 2010, pp. 141-146.

[13] Dunn, J. A., and J. E. Pretty, "Halving a triangle", Mathematical Gazette 56, May 1972, p. 105.

[14] Weisstein, Eric W. "Tetrahedron." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Tetrahedron.html

[15] Altshiller-Court, N. "The tetrahedron." Ch. 4 in Modern Pure Solid Geometry: Chelsea, 1979.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]