Parabola

Original article: w:Parabola

For other uses, see Parabola (disambiguation).

Part of a parabola (blue), with various features (other colours). The complete parabola has no endpoints. In this orientation, it extends infinitely to the left, right, and upward.

The parabola is a member of the family of conic sections.

수학(mathematics)에서, 포물선(parabola)은 거울-대칭적(mirror-symmetrical)이고 근사적으로 U-모양(shape)인 평면 곡선(plane curve)입니다. 그것은 여러 다른 표면적으로 틀린 수학적(mathematical) 설명에 적합하고, 모두는 정확히 같은 곡선을 정의하는 것으로 입증될 수 있습니다.

포물선의 한 설명은 한 점(point) (초점(focus))과 한 직선(line) (방향선(directrix))을 포함합니다. 초점은 방향선 위에 놓이지 않습니다. 포물선은 그 평면에서 방향선과 초점 둘 다로부터 등거리(equidistant)에 있는 점들의 자취(locus of points)입니다. 포물선의 다른 설명은 직각 원형 원뿔형 표면(conical surface)과 원뿔형 표면에 접(tangent)하는 또 다른 평면(plane)에 평행(parallel)한 평면의 교차점에서 만들어진 원뿔 표면(conic section)과 같습니다.

방향선에 수직이고 초점을 통과하는 직선 (즉, 중간을 통과해서 포물선을 절반으로 나누는 직선)은 "대칭의 축(axis of symmetry)"으로 불립니다. 대칭축과 교차하는 포물선 위의 점은 "꼭짓점(vertex)"으로 불리고 포물선이 가장 예리하게 변하는 점입니다. 대칭축을 따라 측정된, 꼭짓점과 초점 사이의 거리눈 "초점 거리(focal length)"입니다. "래투스 렉텀(latus rectum)"은 방향선과 평행하고 초점을 통과하는 포물선의 현(chord)입니다. 포물선은 위, 아래, 왼쪽, 오른쪽 또는 어떤 다른 임의의 방향으로 열릴 수 있습니다. 임의의 포물선은 위치를 조정하고 크기를 조정해서 임의의 다른 포물선에 정확하게 겹칠 수 있습니다—즉, 모든 포물선은 기하학적으로 닮음(similar)입니다.

포물선은, 만약 그들이 빛(light)을 반사하는(reflect) 물질로 만들어지면, 포물선의 대칭축과 평행을 이루고 오목한 면에 부딪히는 빛은, 포물선 위의 반사가 일어나는 점과 관계없이, 그의 초점에 반사되는 속성을 가집니다. 반대로, 초점에 있는 점 광원으로부터 발생하는 빛은 평행("collimated") 반직선으로 반사되어, 포물선의 대칭축과 평행하게 나아갑니다. 같은 현상은 소리(sound) 및 다른 파동과 함께 발생합니다. 이 반사 속성은 포물선의 많은 실용적인 사용의 기초입니다.

포물선은, 포물선 안테나(parabolic antenna) 또는 포물선 마이크로폰(parabolic microphone)에서부터 자동차 전조등 반사기와 탄도 미사일(ballistic missiles) 설계에 이르기까지, 많은 중요한 응용을 가집니다. 그들은 물리학(physics), 공학(engineering), 및 많은 다른 분야에서 자주 사용됩니다.

History

Parabolic compass designed by Leonardo da Vinci

원뿔 단면에 대한 최초의 알려진 연구는 기원전 4세기에서 메나이크모스(Menaechmus)에 의한 것이었습니다. 그는 포물선을 사용하여 정육면체 두 배(doubling the cube)의 문제를 해결하는 방법을 발견했습니다. (그 해는, 어쨌든, 컴퍼스-와-직선자 구성(compass-and-straightedge construction)의 요구 사항을 충족하지 못합니다.) 포물선과 선분으로 둘러싸인 넓이, 소위 "포물선 구획"은, 기원전 3세기, 그의 The Quadrature of the Parabola에서, 소진의 방법(method of exhaustion)으로 아르키메테스(Archimedes)에 의해 계산되었습니다. 이름 "포물선"은 원뿔 단면의 많은 속성을 발견한 |아폴로니우스(Apollonius)에 기인됩니다. 그것은 "응용"을 의미하는데, 아폴로니우스가 증명한 것처럼, 이 곡선과 연결을 가지는, "넓이의 적용" 개념을 언급합니다. 포물선과 다른 원뿔 단면의 초점–방향선 속성은 파푸스(Pappus)에 기인합니다.

갈릴레오(Galileo)는 발사체의 경로가, 중력으로 인한 균일한 가속도의 결과로, 포물선을 따른다는 것을 보였습니다.

포물선 반사기(parabolic reflector)는 이미지를 생성할 수 있다는 아이디어는 반사 망원경(reflecting telescope)의 발명 이전에 이미 잘 알려져 있었습니다. 디자인은, 르네 데카르트(René Descartes), 마랭 메르센(Marin Mersenne), 및 제임스 그레고리 (James Gregory)를 포함하는 많은 수학자(mathematician)에 의해 17세기 초–중반에서 제안되었습니다. 아이작 뉴턴(Isaac Newton)은 1668년에 최초의 반사 망원경(first reflecting telescope)을 만들었을 때, 그는 제조의 어려움때문에 포물면 거울을 건너 뛰고, 구면 거울(spherical mirror)을 선택합니다. 포물면 거울은 가장 현대적인 반사 망원경 및 위성 접시(satellite dish) 및 레이더(radar) 수신기에서 사용됩니다.

Definition as a locus of points

포물선은 유클리드 평면에서 점의 집합 (점의 자취(locus of points))로 기하학적으로 정의될 수 있습니다:

• 포물선은, 임의의 점 $P$에 대해, 고정된 점 $F$, 초점에 대한 거리 $|PF|$가 고정된 직선 $l$, 방향선에 대한 거리와 같은 것을 만족하는 점의 집합입니다.

$\{P:|PF|=|Pl|\}.$

초점 $F$에서 방향선 $l$으로 수직의 중간점 $V$는 꼭짓점(vertex)으로 불리고, 직선 $FV$는 포물선의 대칭의 축(axis of symmetry)입니다.

In a cartesian coordinate system

Axis of symmetry parallel to the y axis

Parabola: Definition, p: semi-latus rectum

Parabola: axis parallel to y axis

Parabola: general case

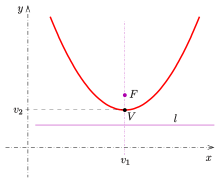
만약 우리가, $F=(0,f),\ f>0$ 및 방향선이 방정식 $y=-f$을 만족하는, 데카르트 좌표(Cartesian coordinates)를 도입하면, 우리는 점 $P=(x,y)$에 대해 $|PF|^{2}=|Pl|^{2}$으로부터 방정식 $x^{2}+(y-f)^{2}=(y+f)^{2}$을 획득합니다. $y$에 대해 풀면 다음을 산출합니다:

$y={\frac {1}{4f}}x^{2}.$

이 포물선은 (위로 열려있는) U-자 모양입니다.

초점을 통한 수평 현 (열린 단면의 그림을 참조하십시오)은 래투스 렉텀(latus rectum)으로 불립니다; 그것의 절-반은 반-래투스 렉텀(semi-latus rectum)입니다. 래투스 렉텀은 방향선과 평행합니다. 반-래투스 렉텀은 문자 $p$로 지정됩니다. 그림으로부터 우리는 다음을 얻습니다:

$p=2f.$

래투스 렉텀은 다른 두 원뿔형 – 타원과 쌍곡선에 대해 비슷하게 정의됩니다. 래투스 렉텀은 방향선과 평행한 월뿔 단면의 초점을 통해 그려진 직선이 곡선에 의해 양쪽 방식으로 끝납니다. 임의의 경우에 대해, $p$는 꼭짓점에서 진동하는 원(osculating circle)의 반지름입니다. 포물선에 대해, 반-래투스 렉텀, $p$는 방향선으로부터 초점의 거리입니다. 매개-변수 $p$를 사용하면, 포물선의 방정식은 다음으로 다시-쓸 수 있습니다:

$x^{2}=2py.$

보다 일반적으로, 만약 꼭짓점은 $V=(v_{1},v_{2})$, 초점 $F=(v_{1},v_{2}+f)$, 및 방향선 $y=v_{2}-f$이면, 우리는 다음 방정식을 획득합니다:

$y={\frac {1}{4f}}(x-v_{1})^{2}+v_{2}={\frac {1}{4f}}x^{2}-{\frac {v_{1}}{2f}}x+{\frac {v_{1}^{2}}{4f}}+v_{2}.$

주의

1. $f<0$의 경우에서, 포물선은 아래쪽으로 열린 것을 가집니다.
2. 축이 y-축에 평행하다는 가정은 우리에게 포물선을 차수 2의 다항식(polynomial)의 그래프로 여기는 것을 허용하고, 반대로: 차수 2의 임의의 다항식의 그래프는 포물선입니다 (다음 섹션을 참조하십시오).
3. 만약 우리가 $x$와 $y$를 서로-바꾸면, 우리는 형식 $y^{2}=2px$의 방정식을 얻습니다. 이들 포물선은 (만약 $p<0$이면) 왼쪽으로 열리거나 (만약 $p>0$이면) 오른쪽으로 열립니다.

General case

만약 초점은 $F=(f_{1},f_{2})$이고 방향선 $ax+by+c=0$이면, 우리는 다음 방정식을 획득합니다:

${\frac {(ax+by+c)^{2}}{a^{2}+b^{2}}}=(x-f_{1})^{2}+(y-f_{2})^{2}$

(방정식의 왼쪽 변은 거리 $|Pl|$를 계산하기 위해 직선의 헤세 법선 형식(Hesse normal form)을 사용합니다).

일반적인 위치에서 포물선의 매개-변수 방정식(parametric equation)에 대해 § As the affine image of the unit parabola를 참조하십시오.

포물선의 음 방정식(implicit equation)은, $b^{2}-4ac=0$를 만족하는 또는, 동등하게, $ax^{2}+bxy+cy^{2}$가 선형 다항식(linear polynomial)의 제곱인 것을 만족하는, 차수 이의 기약 다항식(irreducible polynomial)에 의해 정의됩니다:

$ax^{2}+bxy+cy^{2}+dx+ey+f=0$.

As a graph of a function

Parabolas $y=ax^{2}$

이전 섹션은 꼭짓점으로 원점이고 대칭축으로 y-축을 갖는 포물선이 다음 함수의 그래프로 여길 수 있음을 보여줍니다:

$f(x)=ax^{2}{\text{ with }}a\neq 0.$

$a>0$에 대해 포물선은 위로 열린 것이고, $a<0$에 대해 아래로 열린 것입니다 (그림을 참조하십시오). 위의 섹션으로부터 우리는 다음을 얻습니다:

• 초점은 $\left(0,{\frac {1}{4a}}\right)$입니다,
• 초점 거리 ${\frac {1}{4a}}$, 반-래투스 렉텀은 $p={\frac {1}{2a}}$입니다,
• 꼭짓점은 $(0,0)$입니다,
• 방향선은 방정식 $y=-{\frac {1}{4a}}$을 가집니다,
• 점 $(x_{0},ax_{0}^{2})$에서 접선(tangent)은 방정식 $y=2ax_{0}x-ax_{0}^{2}$을 가집니다.

$a=1$에 대해, 포물선은 방정식 $y=x^{2}$을 가진 단위 포물선(unit parabola)입니다. 그의 초점은 $\left(0,{\tfrac {1}{4}}\right)$이고, 반-래투스 렉텀 $p={\tfrac {1}{2}}$, 및 방향선은 방정식 $y=-{\tfrac {1}{4}}$을 가집니다.

차수 2의 일반적인 방정식은 다음입니다:

$f(x)=ax^{2}+bx+c{\text{ with }}a,b,c\in \mathbb {R} ,\ a\neq 0$.

제곱식을 완성(Completing the square)하는 것은 다음을 산출합니다:

$f(x)=a\left(x+{\frac {b}{2a}}\right)^{2}+{\frac {4ac-b^{2}}{4a}},$

이것은 다음과 함께 포물선의 방정식입니다:

• 축 $x=-{\frac {b}{2a}}$ (y-축에 평행합니다),
• 초점 거리 ${\frac {1}{4a}}$, 반-래투스 렉텀 $p={\frac {1}{2a}}$,
• 꼭짓점 $V=\left(-{\frac {b}{2a}},{\frac {4ac-b^{2}}{4a}}\right)$,
• 초점 $F=\left(-{\frac {b}{2a}},{\frac {4ac-b^{2}+1}{4a}}\right)$,
• 방향선 $y={\frac {4ac-b^{2}-1}{4a}}$,
• y-축을 교차하는 포물선의 점은 좌표 $(0,c)$를 가지고,
• y-축 위의 점에서 접선은 방정식 $y=bx+c$을 가집니다.

Similarity to the unit parabola

When the parabola $\color {blue}{y=2x^{2}}$ is uniformly scaled by factor 2, the result is the parabola $\color {red}{y=x^{2}}$

유클리드 평면에서 두 대상은 만약 우리가 닮음(similarity), 즉 강성 운동 (평행-이동(translations)과 회전(rotations)) 및 균등 스케일링(uniform scaling)의 임의 합성(composition)에 의해 다른 대상으로 변환될 수 있으면, 닮은(similar) 것입니다.

꼭짓점 $V=(v_{1},v_{2})$를 가진 포물선 ${\mathcal {P}}$은 꼭짓점으로 원점을 가진 것에서 평행-이동 $(x,y)\to (x-v_{1},y-v_{2})$에 의해 변환될 수 있습니다. 원점을 중심으로 적절한 회전은 그런-다음 대칭축으로 y-축을 갖는 것으로 포물선을 변환할 수 있습니다. 그러므로 포물선 ${\mathcal {P}}$는 방정식 $y=ax^{2},\ a\neq 0$을 가진 포물선으로 강성 운동에 의해 변환될 수 있습니다. 그러한 포물선은 방정식 $y=x^{2}$을 가진 균등 스케일링(uniform scaling) $(x,y)\to (ax,ay)$에 의해 단위 포물선으로 변환될 수 있습니다. 따라서, 임의의 포물선은 닮음에 의해 단위 포물선으로 매핑될 수 있습니다.

닮은 삼각형을 사용하는, 합성(synthetic) 접근법은 이 결과를 수립하기 위해 역시 사용될 수 있습니다.

일반적인 결과는 두 개의 원뿔 단면 (필수적으로 같은 유형)이 닮은 것인 것과 그들이 같은 이심률을 가지는 것은 필요충분 조건입니다. 따라서, 오직 원 (모두 이심률 0을 가짐)이 포물선 (모두 이심률 1을 가짐)과 함께 이 속성을 공유하며, 반면에 일반적인 타원과 쌍곡선은 그렇지 않습니다.

$(x,y)\to \left(x,{\tfrac {y}{a}}\right)$을 만족하는 포물선 $y=ax^{2}$를 단위 포물선 위로 매핑하는 다른 간단한 아핀 변환이 있습니다. 그러나 이 매핑은 닮음이 아니고, 단지 모든 포물선이 아핀적으로 동등함을 보입니다 (§ As the affine image of the unit parabola을 참조하십시오).

As a special conic section

Pencil of conics with a common vertex

대칭축으로 x-축, 원점 (0, 0)에 하나의 꼭짓점 및 같은 반-래투스 렉텀 $p$를 가진 원뿔 단면(conic section)의 연필(pencil)은 다음 방정식으로 나타낼 수 있습니다:

$y^{2}=2px+(e^{2}-1)x^{2},\quad e\geq 0,$

이때 $e$ 이심률(eccentricity)에 따라,

• $e=0$에 대해, 원뿔형은 원입니다 (연필의 진동하는 원),
• $0<e<1$에 대해, 타원,
• $e=1$에 대해, 방정식 $y^{2}=2px$을 가진 포물선,
• $e>1$에 대해, 쌍곡선 (그림을 참조하십시오).

In polar coordinates

Pencil of conics with a common focus

만약 p > 0이면, 방정식 $y^{2}=2px$ (오른쪽으로 열린)을 가진 포물선은 다음 극(polar) 표현을 가집니다:

$r=2p{\frac {\cos \varphi }{\sin ^{2}\varphi }},\quad \varphi \in \left[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right]\setminus \{0\}$

($r^{2}=x^{2}+y^{2},\ x=r\cos \varphi$).

그의 꼭짓점은 $V=(0,0)$이고, 그의 초점은 $F=\left({\tfrac {p}{2}},0\right)$입니다.

만약 우리가 원점을 초점으로 이동하면, 즉, $F=(0,0)$이면, 우리는 다음 방정식을 얻습니다:

$r={\frac {p}{1-\cos \varphi }},\quad \varphi \neq 2\pi k.$

주의 1: 이 극 형식을 역하는 것은 포물선이 심장형(cardioid)의 역(inverse)임을 보입니다.

주의 2: 두 번째 극 형식은 초점 $F=(0,0)$을 가진 원뿔형의 연필의 특별한 경우입니다 (그림을 참조하십시오):

$r={\frac {p}{1-e\cos \varphi }}$ ($e$는 이심률입니다).

Conic section and quadratic form

Diagram, description, and definitions

Cone with cross-sections

다이어그램은 그의 축 AV를 가진 원뿔(cone)을 나타냅니다. 점 A는 그의 꼭대기(apex)입니다. 분홍색으로 표시된, 원뿔의 경사진 교차-단면(cross-section)은, 원뿔의 변에서 처럼, 같은 각도 θ만큼 축에서 기울어집니다. 원뿔 단면으로 포물선의 정의에 따르면, 이 분홍색 교차-단면 EPD의 경계는 포물선입니다.

원뿔의 축에 수직인 교차-단면은 포물선의 꼭짓점 P를 통과합니다. 이 교차-단면은 원형이지만, 다이어그램에 표시된 것처럼, 비스듬히 볼 때 타원형(elliptical)으로 나타납니다. 그의 중심은 V이고, PK는 지름입니다. 우리는 그것의 반지름 r이라고 부를 것입니다.

축에 대한 또 다른 수직, 원뿔의 원형 교차-단면은 직전에 설명한 것보다 꼭대기 A에서 더 멀어집니다. 그것은 현(chord) DE를 가지며, 포물선이 원과 교차(intersection)하는 점에 연결됩니다. 또 다른 현 BC는 DE의 수직 이등분(perpendicular bisector)이고 결과적으로 원의 지름입니다. 이들 두 현 및 포물선의 대칭축 PM 모두는 점 M에서 교차합니다.

D와 E를 제외한, 모든 레이블된 점은 공통-평면(coplanar) 위에 있습니다. 그것들은 전체 그림의 대칭 평면 안에 있습니다. 이것은, 위에서 언급하지 않은, 점 F를 포함합니다. 그것은, § Position of the focus에서, 아래에 정의되고 논의됩니다.

DM와 EM x의 길이, 및 PM y의 길이라고 부를 것입니다.

Derivation of quadratic equation

BM 및 CM의 길이는 다음입니다:

${\overline {\mathrm {BM} }}=2y\sin \theta$ (삼각형 BPM은 이등변(isosceles)인데, 왜냐하면 ${\overline {PM}}\parallel {\overline {AC}}\implies \angle PMB=\angle ACB=\angle ABC$이기 때문입니다),

${\overline {\mathrm {CM} }}=2r$ (PMCK는 평행사변형(parallelogram)입니다).

현 BC 및 DE 위의 교차하는 현 정리(intersecting chords theorem)를 사용하면, 우리는 다음을 얻습니다:

${\overline {\mathrm {BM} }}\cdot {\overline {\mathrm {CM} }}={\overline {\mathrm {DM} }}\cdot {\overline {\mathrm {EM} }}.$

치환하면:

$4ry\sin \theta =x^{2}.$

다시-정렬하면:

$y={\frac {x^{2}}{4r\sin \theta }}.$

임의의 주어진 원뿔과 포물선에 대해, r과 θ는 상수이지만, x와 y는 수평 교차-단면 BECD가 만들어지는 것에서 임의의 높이에 의존하는 변수입니다. 이 마지막 방정식은 이들 변수 사이의 관계를 보여줍니다. 그들은, 그의 원점으로 P를 가진 분홍색 평면의 시스템에서, 점 D와 E의 데카르트 좌표(Cartesian coordinates)로 해석될 수 있습니다. x는 방정식에서 제곱된 것이므로, D와 E가 y-축의 대변 위에 있다는 사실은 중요하지 않습니다. 만약 수평 교차-단면이 원뿔의 꼭대기로부터 위 또는 아래, 향하거나 멀어지게 움직이면, D와 E는, 방정식에서 보인 x와 y 사이의 관계를 유지하는, 포물선을 따라 움직입니다. 포물형 곡선은, 그러므로, 방정식이 충족시키는 점의 자취(locus)이며, 그것을 방정식에서 이차 함수의 데카르트 그래프(Cartesian graph)를 만듭니다.

Focal length

이전 섹션(preceding section)에서, 만약 포물선이 원점에 꼭짓점을 가지면, 및 만약 그것이 양의 y-방향으로 열리면, 그의 방정식은 y = x²/4f이며, 여기서 f는 초점 길이임을 입증했습니다. 이것을 위의 마지막 방정식과 비교하면, 원뿔에서 포물선의 초점 길이가 r sin θ임을 알 수 있습니다.

Position of the focus

위 다이어그램에서, 점 V는 포물선의 꼭짓점에서 원뿔의 축까지 수선의 발(foot of the perpendicular)입니다. 점 F는 점 V에서 포물선의 평면까지 수선의 발입니다. 대칭에 의해, F는 포물선의 대칭축 위에 있습니다. 각도 VPF는 θ에 대한 여각(complementary)이고, 각도 PVF는 각도 VPF에 대한 여각이므로, 각도 PVF는 θ입니다. PV의 길이는 r이므로, 포물선의 꼭짓점으로부터 F의 거리는 r sin θ입니다. 그것은 위에서 보였는데, 이 거리는 포물선의 초점 길이와 같으며, 이것은 꼭짓점에서 초점까지 거리입니다. 초점과 점 F는, 그러므로, 같은 직선을 따라 꼭짓점에서 똑같이 떨어져 있으며, 이는 그들이 같은 점임을 의미합니다. 따라서, 위에서 정의한 점 F는 포물선의 초점입니다.

이 토론은 원뿔 단면으로 포물선의 정의로부터 시작되었지만, 그것은 이제 이차 함수의 그래프로 설명되어집니다. 이것은 이들 두 설명이 동등한 것임을 보여줍니다. 그들 둘 다는 정확히 같은 모양의 곡선을 정의합니다.

Alternative proof with Dandelin spheres

Parabola (red): side projection view and top projection view of a cone with a Dandelin sphere

대안적인 증명은 당들랭 구(Dandelin spheres)를 사용하여 행해질 수 있습니다. 그것은 계산없이 작동하고 오직 기본 기하학적 고려-사항을 사용합니다 (아래 유도를 참조하십시오).

수직으로부터 기울기가 원뿔의 생성선(generatrix) (일명 생성기 직선, 꼭대기와 원뿔 표면 위의 한 점을 포함하는 직선) $m_{0}$와 같은, 평면 $\pi$에 의한 똑바른 원뿔의 교차는 포물선입니다 (다이어그램에서 빨간색 곡선입니다).

이 생성선 $m_{0}$는 평면 $\pi$에 평행한 원뿔의 유일한 생성선입니다. 그렇지 않으면, 만약 교차하는 평면에 평행 한 두 생성선이 있으면, 교차 곡선은 쌍곡선(hyperbola)이 될 것입니다 (또는 만약 두 생성선이 교차하는 평면이면, 퇴화 쌍곡선(degenerate hyperbola)이 될 것입니다). 만약 교차하는 평면에 평행한 생성선이 없으면, 교차 곡선은 타원(ellipse) 또는 원(circle) (또는 하나의 점(a point))이 될 것입니다.

평면 $\sigma$를 원뿔의 수직축과 직선 $m_{0}$을 포함하는 평면으로 놓습니다. 수직으로부터 평면 $\pi$의 기울기는 직선 $m_{0}$과 같은데, 변에서 봤을 때 (즉, 평면 $\pi$는 평면 $\sigma$에 수직입니다) $m_{0}\parallel \pi$임을 의미합니다.

포물선의 방향선 속성을 입증하기 위해 (위의 § Definition as a locus of points를 참조하십시오), 우리는 당들랭 구(Dandelin spheres) $d$를 사용하며, 이것은 원 $c$를 따라 원뿔 및 점 $F$에서 평면 $\pi$에 닿는 구입니다. 원 $c$을 포함하는 평면은 직선 $l$에서 평면 $\pi$와 교차합니다. 평면 $\pi$, 당들랭 구 $d$ 및 원뿔로 구성되는 시스템에서 거울 대칭(mirror symmetry)이 있습니다 (대칭 평면(plane of symmetry)은 $\sigma$입니다).

원 $c$를 포함하는 평면은 평면 $\sigma$와 수직이고 $\pi \perp \sigma$이므로, 그들의 교차 직선 $l$은 반드시 평면 $\sigma$와 역시 수직입니다. 직선 $m_{0}$는 평면 $\sigma$ 안에 있으므로, $l\perp m_{0}$입니다.

$F$가 포물선의 초점이고, $l$이 포물선의 방향선인 것을 밝힐 것입니다.

1. $P$를 교차 곡선의 임의의 점으로 놓습니다.
2. $P$를 포함하는 원뿔의 생성선(generatrix)은 점 $A$에서 원 $c$와 교차합니다.
3. 선분 ${\overline {PF}}$ 및 ${\overline {PA}}$은 구 $d$에 접하고, 그러므로 같은 길이입니다.
4. 생성선 $m_{0}$은 점 $D$에서 원 $c$와 교차합니다. 선분 ${\overline {ZD}}$ 및 ${\overline {ZA}}$은 구 $d$에 접하고, 그러므로 같은 길이입니다.
5. 직선 $q$를 $m_{0}$와 평행하고 점 $P$를 통과하는 직선으로 놓습니다. $m_{0}\parallel \pi$이고, 점 $P$는 평면 $\pi$ 안에 있으므로, 직선 $q$는 반드시 평면 $\pi$ 안에 있습니다. $m_{0}\perp l$이므로, 우리는 마찬가지로 $q\perp l$임을 압니다.
6. 점 $B$를 직선 $l$에 대한 점 $P$로부터 수선의 발로 놓습니다. 즉, ${\overline {PB}}$는 직선 $q$의 부분이고, 그러므로 ${\overline {PB}}\parallel {\overline {ZD}}$입니다.
7. 절편 정리(intercept theorem)와 ${\overline {ZD}}={\overline {ZA}}$로부터, 우리는 ${\overline {PA}}={\overline {PB}}$임을 압니다. ${\overline {PA}}={\overline {PF}}$이므로, 우리는 ${\overline {PF}}={\overline {PB}}$임을 아는데, 이것은 초점 $P$로부터 $F$까지 거리는 $P$로부터 방향선 $l$까지 거리와 같음을 의미합니다.

Proof of the reflective property

Reflective property of a parabola

반사 속성은, 만약 포물선이 빛을 반사할 수 있으면, 대칭 축에 평행하게 움직여 그것에 들어가는 빛은 초점을 향해 반사된다고 말합니다. 이것은 빛이 반직선으로 이동한다는 가정에 기반한 기하학적 광학(geometrical optics)에서 파생됩니다. 다음의 증명에서, 포물선 위의 모든 각 점은 초점 및 방향선으로부터 등거리에 있다는 사실은 공리로 취합니다.

포물선 y = x²를 생각해 보십시오. 모든 포물선은 비슷하므로, 이 간단한 경우는 모든 다른 것을 나타냅니다. 다이어그램의 오른쪽은 이 포물선의 일부를 보여줍니다.

Construction and definitions

점 E는 좌표 (x, x²)와 함께 포물선 위의 임의의 점입니다. 초점은 F, 꼭짓점은 A (원점),및 직선 FA (y-축)은 대칭-축입니다. 직선 EC는 대칭-축에 평행하고 D에서 x-축과 교차합니다. 점 C는 방향선 위에 위치합니다 (혼란을 최소화하기 위해, 그것은 표시하지 않습니다). 점 B는 선분 FC의 중점입니다.

Deductions

대칭축을 따라 측정된, 꼭짓점 A는 초점 F와 방향선으로부터 등거리에 있습니다. 절편 정리(intercept theorem)에 따르면, C가 방향선이므로, F와 C의 y-좌표는 절댓값이 같고 부호가 반대입니다. B는 FC의 중점이므로, 그의 y-좌표는 0이며, 따라서 그것은 x-축 위에 놓입니다. 그의 x-좌표는 E, D, 및 C 좌표의 절반, 즉, x/2입니다. 직선 BE의 기울기는 ED와 BD의 길이의 몫이며, 이것은 x²/x/2 = 2x입니다. 그러나, 2x는 역시 E에서 포물선의 기울기 (첫 번째 도함수)입니다. 그러므로, 직선 BE는 E에서 포물선에 접합니다.

거리 EF와 EC는 같은데 왜냐하면 E가 포물선 위에 있고, F가 초점이고 C는 방향선 위에 있기 때문입니다. 그러므로, B는 FC의 중점이므로, 삼각형 △FEB 및 △CEB는 합동 (세 변이 같음)이므로, 이것은 α로 표시된 각도가 일치함을 의미합니다. (E 위의 각도는 각도 ∠BEC와 수직적으로 반대입니다.) 이것은 포물선에 들어가고 대칭축에 평행하게 움직이는 E에 도달하는 빛의 반직선이 직선 BE에 의해 반사될 것이므로, 그것은, 다이어그램에서 빨간색으로 표시된 것처럼, 직선 EF를 따라 움직이는 것을 의미합니다 (직선이 어떻게든지 빛을 반사할 수 있음을 가정합니다). BE는 E에서 포물선에 접하므로, 같은 반사는 E에서 포물선의 무한소 호에 의해 행해질 것입니다. 그러므로, 포물선에 들어가고 포물선의 대칭축에 평행하게 움직이는 E에 도달하는 빛은 포물선에 의해 그의 초점을 향해 반사됩니다.

점 E는 특별한 특성을 가지지 않습니다. 반사된 빛에 대한 이 결론은, 다이어그램의 왼쪽에 표시된 것처럼, 포물선 위의 모든 점에 적용됩니다. 이것은 반사하는 특성입니다.

Other consequences

위의 논증에서 간단히 추론될 수 있는 다른 정리들이 있습니다.

Tangent bisection property

위의 증명과 첨부 다이어그램은 접선 BE가 각도 ∠FEC를 이등분한다는 것을 보여줍니다. 다시 말해, 임의의 점에서 포물선에 접선은 초점을 그 점에 연결한 직선과 방향선에 수직인 직선 사이의 각도를 이등분합니다.

Intersection of a tangent and perpendicular from focus

Perpendicular from focus to tangent

삼각형 △FBE 및 △CBE가 합동이므로, FB는 접선 BE에 수직입니다. B는 꼭짓점에서 포물선에 접하는 x-축 위에 있으므로, 그것은 포물선에 대한 임의의 접선과 초점으로부터 그 접선으로 직각 사이의 교차의 점이 꼭짓점에 포물선에 직선 위에 놓이는 것을 따릅니다. 애니메이션 다이어그램 및 페달 곡선(pedal curve)을 참조하십시오.

Reflection of light striking the convex side

만약 빛이 직선 CE를 따라 움직이면, 그것은 대칭축에 평행하게 움직이고 E에서 포물선의 볼록한 면에 부딪칩니다. 그것은 위의 다이어그램에서 분명하고 이 빛은, 선분 FE의 연장선을 따라, 초점에서 직접 멀어지게 반사됩니다.

Alternative proofs

Parabola and tangent

반사 및 접하는 이등분 속성의 위의 증명은 미적분학의 직선을 사용합니다. 여기에 기하학적 증명이 제시됩니다.

이 다이어그램에서, F는 포물선의 초점이고, T와 U는 그의 방향선 위에 놓입니다. P는 포물선 위의 임의의 점입니다. PT는 방향선에 수직이고, 직선 MP는 각도 ∠FPT를 이등분합니다. Q는 포물선의 또 다른 점이며, QU가 방향선에 수직입니다. 우리는 FP = PT 및 FQ = QU임을 알고 있습니다. 분명하게, QT > QU이므로, QT > FQ입니다. 이등분선 MP 위의 모든 점은 F와 T로부터 등거리에 있지만, Q는 T보다 F에 더 가깝습니다. 이것은, Q가 MP의 왼쪽, 즉 초점으로 그것의 같은 쪽 위에 있음을 의미합니다. 같은 것은 만약 Q가 포물선 위의 다른 곳 (점 P를 제외함)에 위치되면, 참인 것이므로, 점 P를 제외한 전체 포물선은 MP의 초점 쪽에 있습니다. 그러므로, MP는 P에서 포물선에 접하는 것입니다. 그것은 각도 ∠FPT를 이등분하므로, 이것은 접선의 이등분 속성을 입증합니다.

마지막 단락의 논리는 반사하는 속성의 위의 증명을 수정하기 위해 적용될 수 있습니다. 그것은 만약 각도 α가 같으면, 직선 BE가 E에서 포물선에 접하는 것임을 효과적으로 증명합니다. 반사하는 속성은 이전에서 보인 것으로 따릅니다.

Pin and string construction

Parabola: pin string construction

초점과 방향선에 의한 포물선의 정의는 압정과 끈의 도움으로 그것을 그리는 것에 사용될 수 있습니다:

1. 포물선의 초점 $F$와 방향선 $l$을 선택하십시오.
2. 삼각자의 삼각형을 취하고 길이 $|AB|$를 가진 끈을 준비하십시오 (그림을 참조하십시오).
3. 삼각형의 점 $A$에 끈의 하나의 끝 및 초점 $F$에 다른 끝을 핀으로 고정하십시오.
4. 직각의 두 번째 가장자리는 방향선을 따라 자유롭게 미끄러지도록 삼각형을 배치하십시오.
5. 연필을 잡고 끈을 삼각자 옆에 단단히 고정하십시오.
6. 방향선을 따라 삼각자을 움직이면서, 연필은 포물선의 호를 그리는데, 왜냐하면 $|PF|=|PB|$이기 때문입니다 (포물선의 정의를 참조하십시오).

Properties related to Pascal's theorem

포물선은 무한대 $g_{\infty }$의 직선 – $Y_{\infty }$에서 접선입니다 – 위에 점 $Y_{\infty }$을 가진 비-퇴화된 투영 원뿔형의 아핀 부분으로 여길 수 있습니다. 파스칼 정리(Pascal's theorem)의 5-, 4- 및 3- 점 퇴화는 적어도 하나의 접선을 다루는 원뿔형의 속성입니다. 만약 우리가 이 접선을 무한대에 직선으로 여기고 그의 접점을 y-축의 무한대에 점으로 여기면, 우리는 포물선에 대해 세 명제를 얻습니다.

포물선의 다음 속성은 용어 연결, 교차, 평행와 함께 오직 다루어지는데, 이것들은 닮음(similarities)의 불변입니다. 그래서, 그것은 방정식 $y=x^{2}$을 가진 단위 포물선에 대해 임의의 속성을 증명하기 위해 충분합니다.

4-points property

4-points property of a parabola

임의의 포물선은 방정식 $y=ax^{2}$에 의해 적절한 좌표 시스템에서 설명될 수 있습니다.

• $P_{1}=(x_{1},y_{1}),\ P_{2}=(x_{2},y_{2}),\ P_{3}=(x_{3},y_{3}),\ P_{4}=(x_{4},y_{4})$를 포물선의 네 점, $Q_{2}$를 $x=x_{2}$와 가름선 $P_{1}P_{4}$의 교차로 놓고, $Q_{1}$을 $x=x_{1}$과 가름선 $P_{2}P_{3}$의 교차로 놓습니다 (그림을 참조하십시오). 그런-다음 가름선 $P_{3}P_{4}$는 직선 $Q_{1}Q_{2}$와 평행합니다.

(직선 $x=x_{1}$ 및 $x=x_{2}$은 포물선의 축과 평행합니다.)

증명: 단위 포물선 $y=x^{2}$에 대해 직접 계산.

응용: 포물선의 4-점 속성은 점 $P_{4}$의 구성에 대해 사용될 수 있지만, $P_{1},P_{2},P_{3}$ 및 $Q_{2}$는 주어집니다.

주의: 포물선의 4-점 속성은 파스칼의 정리의 5-점 퇴화의 아핀 버전입니다.

3-points–1-tangent property

3-points–1-tangent property

$P_{0}=(x_{0},y_{0}),P_{1}=(x_{1},y_{1}),P_{2}=(x_{2},y_{2})$를 방정식 $y=ax^{2}$을 가진 포물선의 세 점 및 $Q_{2}$를 직선 $x=x_{2}$와 가름선 $P_{0}P_{1}$의 교차 및 $Q_{1}$을 직선 $x=x_{1}$과 가름선 $P_{0}P_{2}$의 교차로 놓습니다 (그림을 참조하십시오). 그런-다음 점 $P_{0}$에서 접선은 직선 $Q_{1}Q_{2}$에 평행합니다. (직선 $x=x_{1}$ 및 $x=x_{2}$는 포물선의 축에 평행합니다.)

증명: 단위 포물선 $y=x^{2}$에 대해 수행될 수 있습니다. 짧은 계산은 보여줍니다: 직선 $Q_{1}Q_{2}$는 기울기 $2x_{0}$를 가지면, 이것은 점 $P_{0}$에서 접선의 기울기입니다.

응용 포물선의 3-점-1-접선-속성은 점 $P_{0}$에서 접선의 구성에 사용될 수 있지만, $P_{1},P_{2},P_{0}$는 주어집니다.

주의: 포물선의 3-점-1-접선-속성은 파스칼의 정리의 4-점-퇴화의 아핀 버전입니다.

2-points–2-tangents property

2-points–2-tangents property

$P_{1}=(x_{1},y_{1}),\ P_{2}=(x_{2},y_{2})$를 방정식 $y=ax^{2}$를 가진 포물선의 두 점, $Q_{2}$를 직선 $x=x_{2}$와 점 $P_{1}$에서 접선의 교차, 및 $Q_{1}$를 직선 $x=x_{1}$과 점 $P_{2}$에서 접선의 교차로 놓습니다 (그림을 참조하십시오). 그런-다음 가름선 $P_{1}P_{2}$는 직선 $Q_{1}Q_{2}$에 평행합니다. (직선 $x=x_{1}$ 및 $x=x_{2}$는 포물선의 축에 평행합니다.)

증명: 단위 포물선 $y=x^{2}$에 대해 직접 계산.

응용: 포물선의 2-점–2-접선 속성은, 만약 $P_{1},P_{2}$ 및 $P_{1}$에서 접선이 주어지면, 점 $P_{2}$에서 포물선의 접선의 구성에 대해 사용될 수 있습니다.

주의 1: 포물선의 2-점–2-접선 속성은 파스칼의 정리의 3-점 퇴화의 아핀 버전입니다.

주의 2: 포물선의 2-점–2-접선 속성은 포물선의 다음 속성과 절대 혼동되어서는 안되며, 이것은 2 점과 2 접선을 역시 다루지만, 파스칼의 정리와 관련되지 않습니다.

Axis direction

Construction of the axis direction

위의 명제는, 점 $Q_{1},Q_{2}$를 구성하기 위해, 포물선의 축 방향에 대한 지식을 전제로 합니다. 다음 속성은 오직 두 주어진 점과 그들의 접선에 의해 점 $Q_{1},Q_{2}$를 결정하고, 그 결과는, 직선 $Q_{1}Q_{2}$가 포물선의 축에 평행하다는 것입니다.

다음을 놓습니다:

1. $P_{1}=(x_{1},y_{1}),\ P_{2}=(x_{2},y_{2})$를 포물선 $y=ax^{2}$의 두 점, 및 $t_{1},t_{2}$를 그들의 접선;
2. $Q_{1}$을 접선 $t_{1},t_{2}$의 교차,
3. $Q_{2}$를 $P_{2}$를 통한 $t_{1}$에 평행한 직선과 $P_{1}$을 통한 $t_{2}$에 평행한 직선의 교차 (그림을 참조하십시오).

그런-다음 직선 $Q_{1}Q_{2}$은 포물선의 축에 평행하고 방정식 $x=(x_{1}+x_{2})/2$을 가집니다.

증명: 단위 포물선 $y=x^{2}$에 대해 (위의 속성과 마찬가지로) 행해질 수 있습니다.

응용: 이 속성은, 만약 두 점과 그들의 접선이 주어지면, 포물선의 축의 방향을 결정하기 위해 사용될 수 있습니다. 대안적인 방법은 두 평행 현의 중점을 결정하기 위한 것으로써, 평행 현에 대한 섹션을 참조하십시오.

주의: 이 속성은 비-퇴화 원뿔형의 두 원근 삼각형(perspective triangles)의 이론의 아핀 버전입니다.

Steiner generation

Parabola

Steiner generation of a parabola

슈타이너(Steiner)는 비-퇴화 원뿔형 구성에 대해 다음 절차를 확립했습니다 (슈타이너 원뿔형(Steiner conic)을 참조하십시오):

• 두 점 $U,V$에서 직선의 두 연필(pencils) $B(U),B(V)$ (각각, $U$와 $V$를 포함하는 모든 직선) 및 $B(U)$를 $B(V)$ 위로 투영이지만 원근이 아닌 매핑 $\pi$가 주어지면, 대응하는 직선의 교차 점은 비-퇴화 투영 원뿔 단면을 형성합니다.

이 절차는 포물선 $y=ax^{2}$ 위의 점의 간단한 구성에 대해 사용될 수 있습니다:

• 꼭짓점 $S(0,0)$에서 연필 및 y-축에 평행한 직선 $\Pi _{y}$의 집합을 생각해 보십시오.

1. $P=(x_{0},y_{0})$를 포물선 위의 점, 및 $A=(0,y_{0})$, $B=(x_{0},0)$를 놓습니다.
2. 선분 ${\overline {BP}}$은 n개의 같은 간격 선분으로 나뉘고, 이 나눗셈은 선분 ${\overline {AP}}$ 위로 (방향 $BA$에서) 투영됩니다 (그림을 참조하십시오). 이 투영은 연필 $S$에서 연필 $\Pi _{y}$ 위로의 투영 매핑을 야기합니다.
3. 직선 $SB_{i}$와 y-축에 평행한 i-번째 것의 교차는 포물선 위의 점입니다.

증명: 직접 계산.

주의: 슈타이너의 생성은 타원(ellipse)과 쌍곡선(hyperbola)에 대해 역시 유용합니다.

Dual parabola

Dual parabola and Bezier curve of degree 2 (right: curve point and division points $Q_{0},Q_{1}$ for parameter $t=0.4$)

이중 포물선은 보통의 포물선의 접선의 집합으로 구성됩니다.

원뿔형의 슈타이너 생성은 점과 직선의 의미를 바꿈으로써 이중 원뿔형의 생성에 적용될 수 있습니다:

• 두 직선 $u,v$에 대한 두 점 집합, 및 이들 점 집합 사이의 투영이지만 원근이 아닌 매핑 $\pi$가 주어진 것으로 놓으면, 대응하는 점의 연결하는 직선은 비-퇴화 이중 원뿔형을 형성합니다.

이중 포물선의 원소를 생성하기 위해, 우리는 다음으로 시작합니다:

1. 한 직선 위에 있지 않은 세 점 $P_{0},P_{1},P_{2}$,
2. 직선 부분 ${\overline {P_{0}P_{1}}}$ 및 ${\overline {P_{1}P_{2}}}$를 각각 $n$ 같은 간격 선분으로 나누고 그림에서 보이는 것처럼 숫자를 더하십시오.
3. 그런-다음 직선 $P_{0}P_{1},P_{1}P_{2},(1,1),(2,2),\dotsc$은 포물선의 접선, 그러므로 이중 포물선의 원소입니다.
4. 포물선은 제어 점 $P_{0},P_{1},P_{2}$을 가진 차수 2의 베지에 곡선(Bezier curve)입니다.

증명은 차수 2의 베지에 곡선에 대해 드 캐스텔쥬 알고리듬(de Casteljau algorithm)의 결과입니다.

Inscribed angles and the 3-point form

Inscribed angles of a parabola

방정식 $y=ax^{2}+bx+c,\ a\neq 0$을 가진 포물선은 다른 x-좌표를 갖는 세 점 $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$에 의해 고유하게 결정됩니다. 계수 $a,b,c$를 결정하기 위한 보통 절차는 방정식에 그 점 좌표를 대입하는 것입니다. 그 결과는 세 방정식의 선형 시스템이며, 이것은, 예를 들어, 가우스 소거법(Gaussian elimination) 또는 크라메르의 규칙(Cramer's rule)에 의해 해결될 수 있습니다. 대안적인 방법은 포물선에 대해 내접-각 이론(inscribed angle theorem)을 사용합니다.

다음에서, 두 직선의 각도는 포물선의 방향선에 관한 직선의 기울기 차이에 의해 측정될 것입니다. 즉, 방정식 $y=ax^{2}+bx+c$의 포물선에 대해, 방정식 $y=m_{1}x+d_{1},\ y=m_{2}x+d_{2}$의 두 직선 사이의 각도는 $m_{1}-m_{2}$에 의해 측정됩니다.

원에 대해 내접-각 정리(inscribed angle theorem)와 유사하게, 우리는 포물선에 대해 내접-각 정리(inscribed angle theorem for parabolas)를 가집니다:

다른 x-좌표를 가진 네 점 $P_{i}=(x_{i},y_{i}),\ i=1,\ldots ,4$ (그림을 참조)이 방정식 $y=ax^{2}+bx+c$을 가진 포물선 위에 있는 것과 $P_{3}$ 및 $P_{4}$에서 각도가, 위에서 정의된 것처럼, 같은 측정을 가지는 것은 필요충분 조건입니다. 즉,

${\frac {y_{4}-y_{1}}{x_{4}-x_{1}}}-{\frac {y_{4}-y_{2}}{x_{4}-x_{2}}}={\frac {y_{3}-y_{1}}{x_{3}-x_{1}}}-{\frac {y_{3}-y_{2}}{x_{3}-x_{2}}}.$

(증명: 직접 계산: 만약 점들이 포물선 위에 있고, 우리는 방정식 $y=ax^{2}$을 가지는 것으로 좌표를 평행-이동할 수 있으면, 우리는, 만약 점들이 포물선 위에 있으면, ${\frac {y_{i}-y_{j}}{x_{i}-x_{j}}}=x_{i}+x_{j}$을 가집니다.)

결론은 다른 x-좌표를 가진 세 점 $P_{i}=(x_{i},y_{i}),\ i=1,2,3$에 의해 결정된 포물선의 (${\color {green}x},{\color {red}y}$에서) 방정식은 다음과 같다는 것입니다 (만약 두 x-좌표가 같으면, 그 점들을 통과하는, x-축에 평행한 방향선을 가진 포물선은 없습니다):

${\frac {{\color {red}y}-y_{1}}{{\color {green}x}-x_{1}}}-{\frac {{\color {red}y}-y_{2}}{{\color {green}x}-x_{2}}}={\frac {y_{3}-y_{1}}{x_{3}-x_{1}}}-{\frac {y_{3}-y_{2}}{x_{3}-x_{2}}}.$

${\color {green}x}$에 따라 분모를 곱함으로써, 우리는 다음의 보다 표준 형식을 얻습니다:

$(x_{1}-x_{2}){\color {red}y}=({\color {green}x}-x_{1})({\color {green}x}-x_{2})\left({\frac {y_{3}-y_{1}}{x_{3}-x_{1}}}-{\frac {y_{3}-y_{2}}{x_{3}-x_{2}}}\right)+(y_{1}-y_{2}){\color {green}x}+x_{1}y_{2}-x_{2}y_{1}.$

Pole–polar relation

Parabola: pole–polar relation

적절한 좌표 시스템에서, 임의의 포물선은 방정식 $y=ax^{2}$에 의해 설명될 수 있습니다. 점 $P_{0}=(x_{0},y_{0}),\ y_{0}=ax_{0}^{2}$에서 접선의 방정식은 다음입니다:

$y=2ax_{0}(x-x_{0})+y_{0}=2ax_{0}x-ax_{0}^{2}=2ax_{0}x-y_{0}.$

우리는 포물선의 점의 집합을 접선의 집합 위로의 다음 방정식을 얻습니다:

$(x_{0},y_{0})\to y=2ax_{0}x-y_{0}$.

분명히, 이 함수는 $\mathbb {R} ^{2}$의 점과 방정식 $y=mx+d,\ m,d\in \mathbb {R}$을 가진 직선 사이의 전단사에 대한 $\mathbb {R} ^{2}$의 모든 점의 집합 위로 확장될 수 있습니다. 역 매핑은 다음입니다:

직선 $y=mx+d$ → 점 $({\tfrac {m}{2a}},-d)$.

이 관계는 포물선의 극점-극선 관계(pole–polar relation)로 불리는데, 여기서 그 점은 극점이고, 해당하는 직선은 그의 극선입니다.

계산에 의해, 우리는 포물선의 극점-극선 관계의 다음 속성을 점검합니다:

• 포물선 위의 점 (극점)에 대해, 극선은 그 점에서 접선입니다 (그림을 참조하십시오: $P_{1},\ p_{1}$).
• 포물선 밖의 극점 $P$에 대해, 포물선과 그의 극선의 교점은 $P$를 통과하는 두 접선의 접점입니다 (그림을 참조하십시오: $P_{2},\ p_{2}$).
• 포물선 안의 점에 대해, 극선은 포물선과 공통으로 점을 가지지 않습니다 (그림을 참조하십시오: $P_{3},\ p_{3}$ 및 $P_{4},\ p_{4}$).
• 두 극선 (예를 들어, $p_{3},p_{4}$)의 교점은 그들의 극점 (예제에서: $P_{3},P_{4}$)의 연결하는 직선의 극점입니다.
• 포물선의 초점과 방향선은 극점-극선 쌍입니다.

주의: 극점–극선 관계는 타원과 쌍곡선에 대해 역시 존재합니다.

Tangent properties

Two tangent properties related to the latus rectum

대칭의 직선이 점 Q에서 포물선과 교차하게 놓고, 점 F로 초점 및 f로 점 Q로부터 거리를 나타내기 놓습니다. 초점을 통해 대칭의 직선에 직각을 이루고 점 T에서 포물선을 교차하도록 놓습니다. 그런-다음 (1) F으로부터 T까지 거리는 2f이고, (2) 점 T에서 포물선에 대한 접선이 45 ° 각도에서 대칭의 직선을 교차합니다.

Perpendicular tangents intersect on the directrix

Orthoptic property

Main article: Orthoptic (geometry)

만약 포물선에 대한 두 접선이 서로 수직이면, 그들은 방향선 위에 교차합니다. 반대로, 방향선 위에 교차하는 두 접선은 수직입니다.

Lambert's theorem

포물선에 대한 세 접선은 삼각형을 형성하도록 놓습니다. 람베르트의(Lambert's) 정리는 포물선의 초점은 삼각형의 둘레-원(circumcircle) 위에 놓인다고 말합니다.

람베르트의 정리에 대한 슈커맨의 역은, 만약 직선의 둘이 그의 초점이 삼각형의 둘레 위에 놓이는 포물선에 접하면, 세 번째 직선은 포물선에 역시 접하는 삼각형을 경계를 짓는 세 직선을 제공한다고 말합니다.

Facts related to chords

Focal length calculated from parameters of a chord

현이 대칭축에 수직인 포물선을 가로-지르고 있다고 가정합니다. 현이 포물선과 교차하는 점 사이의 현의 길이를 c 및 대칭축을 따라 측정된, 포물선의 꼭짓점으로부터 현까지 거리를 d로 놓습니다. 포물선의 초점 거리 f는 다음에 의해 제공됩니다:

$f={\frac {c^{2}}{16d}}.$

증명

데카르트 좌표의 시스템은, 포물선의 꼭짓점이 원점에 있고, 대칭축은 y-축을 만족하는 것을 사용함을 가정합니다. 포물선은 위로 열립니다. 이 기사의 다른 곳에서 처럼 다음입니다: 포물선의 방정식은 4fy = x²이며, 여기서 f는 초점 거리입니다. 현의 양의 x-끝에서, x = c/2 및 y = d입니다. 이 점은 포물선 위에 있으므로, 이들 좌표는 반드시 위의 방정식을 만족시킵니다. 그러므로, 치환에 의해, $4fd=\left({\tfrac {c}{2}}\right)^{2}$입니다. 이것으로부터, $f={\tfrac {c^{2}}{16d}}$입니다.

Area enclosed between a parabola and a chord

Parabola (magenta) and line (lower light blue) including a chord (blue). The area enclosed between them is in pink. The chord itself ends at the points where the line intersects the parabola.

포물선과 현 사이에 둘러싸인 넓이 (그림 참조하십시오)는 그것을 둘러싸는 평행사변형 넓이의 3분의 2입니다. 평행사변형의 한 변은 현이고, 대변은 포물선에 접합니다. 다른 평행 변의 기울기는 넓이와 관련이 없습니다. 종종, 여기에서 처럼, 그들은 포물선의 대칭축과 평행하게 그려지지만, 이것은 임의적입니다.

이것과 동등하지만, 세부-사항에서 다른 정리는 기원전 3세기에 아르키메데스(Archimedes)에 의해 도출되었습니다. 그는 평행사변형의 그것이 아닌 삼각형의 넓이를 사용했습니다. 포물선의 구적법(The Quadrature of the Parabola)을 참조하십시오.

만약 현은 길이 b를 가지고 포물선의 대칭축에 수직이면, 그리고 만약 포물선의 꼭짓점으로부터 현까지 수직 거리가 h이면, 평행사변형은 b와 h의 변을 가진 직사각형입니다. 포물선과 현에 의해 둘러싸인 포물형 부분의 넓이 A는 그러므로 다음입니다:

$A={\frac {2}{3}}bh.$

이 공식은 삼각형의 넓이와 비교될 수 있습니다: 1/2bh.

일반적으로, 둘러싸인 넓이는 다음으로 계산될 수 있습니다. 먼저, 포물선의 기울기가 현의 기울기와 같은 포물선 위에 그 점을 찾습니다. 이것은 미적분학, 또는 포물선의 대칭축에 평행하고 현의 중점을 통과하는 직선을 사용하여 행해질 수 있습니다. 필요한 점은 이 직선이 포물선과 교차하는 것입니다. 그런-다음, 점에서 직선까지 거리(Distance from a point to a line)에서 주어진 공식을 사용하여, 이 점에서 현까지 수직 거리를 계산하십시오. 이것에 평행사변형의 넓이를 얻기 위해 현의 길이를 곱하고, 그런-다음 요구된 둘러싸인 넓이를 얻기 위해 2/3을 곱하십시오.

Corollary concerning midpoints and endpoints of chords

Midpoints of parallel chords

위의 토론의 따름정리는, 만약 포물선이 여러 개의 평행 현을 가지면, 중점 모두는 대칭축에 평행한 직선 위에 놓인다는 것입니다. 만약 포물선에 대한 접선이 이들 현 중 임의의 것의 끝점을 통해 그려지면, 두 접선은 대칭축에 평행한 이 같은 직선 위에 교차합니다 (포물선의 축-방향(Axis-direction of a parabola)을 참조하십시오).

Arc length

만약 점 X가 초점 길이 f를 가진 포물선 위에 위치되고 p가 X에서 포물선의 대칭-축까지 수직 거리(perpendicular distance)이면, X에서 끝나는 포물선의 호(arcs)의 길이는 다음으로 f 및 p로부터 계산될 수 있는데, 그것들은 모두 같은 단위로 표현되었다고 가정합니다.

${\begin{aligned}h&={\frac {p}{2}},\\q&={\sqrt {f^{2}+h^{2}}},\\s&={\frac {hq}{f}}+f\ln {\frac {h+q}{f}}.\end{aligned}}$

이 양 s는 X와 포물선의 꼭짓점 사이의 호의 길이입니다.

X와 포물선의 다른 쪽 위의 대칭적으로 반대 점 사이의 호의 길이는 2s입니다.

수직 거리 (p)는 대칭축 (X)의 어느 쪽이 위치되어 있는지를 나타 내기 위해 양 또는 음의 부호를 부여 할 수있다. p의 부호를 바꾸면 절대 값을 변경하지 않고 h와 s의 부호가 반전됩니다. 이 수량에 부호가 있으면 포물선의 두 점 사이의 호 길이는 항상 s 값의 차이로 표시됩니다. 로그 속성을 사용하여 계산을 단순화 할 수 있습니다.

수직 거리 p는 X가 대칭축의 어느 쪽에 위치되어 있는지를 나타내기 위해 양 또는 음의 부호를 제공될 수 있습니다. p의 부호를 거꾸로 하면 그들의 절댓값 변경없이 h와 s의 부호가 거꾸로 됩니다. 만약 이들 수량이 부호화되면, 포물선 위의 임의의 두 점 사이의 호 길이는 s의 그들의 값들 사이의 차이에 의해 항상 표시됩니다. 계산은 로그의 속성을 사용함으로써 단순화될 수 있습니다:

$s_{1}-s_{2}={\frac {h_{1}q_{1}-h_{2}q_{2}}{f}}+f\ln {\frac {h_{1}+q_{1}}{h_{2}+q_{2}}}.$

이것은, 예를 들어, 포물면 반사기(parabolic reflector) 또는 포물면 집광기(parabolic trough)를 만들기 위해 필요한 재료의 크기를 계산하는 것에서 유용될 수 있습니다.

이 계산은 임의의 방향에서 포물선에 대해 사용될 수 있습니다. 그것은 대칭-축이 y-축과 평행한 상황으로 제한되지 않습니다.

A geometrical construction to find a sector area

S는 초점이고, V는 포물선 VG의 주요 꼭짓점입니다. VX를 SV에 수직으로 그립니다.

VG 위에 점 B를 취하고 B에서 VX까지 수직 BQ를 떨어뜨립니다. T에서, 만약 필요하다면, 연장되는, 교차 BQ를 수직 ST를 그립니다. B에서, J에서 VX를 교차하는, 수직 BJ를 그립니다.

포물선에 대해, 구획 VBV, 현 VB와 호 VB로 둘러싸인 넓이는 ∆VBQ / 3과 같고, 역시 $BQ={\frac {VQ^{2}}{4SV}}$입니다.

포물형 부채꼴의 넓이 SVB = ∆SVB + ∆VBQ / 3${}={\frac {SV\cdot VQ}{2}}+{\frac {VQ\cdot BQ}{6}}$입니다.

삼각형 TSB와 QBJ는 닮았으므로,

$VJ=VQ-JQ=VQ-{\frac {BQ\cdot TB}{ST}}=VQ-{\frac {BQ\cdot (SV-BQ)}{VQ}}={\frac {3VQ}{4}}+{\frac {VQ\cdot BQ}{4SV}}.$

그러므로, 포물형 부채꼴의 넓이 $SVB={\frac {2SV\cdot VJ}{3}}$이고, 위에서 구해진 것처럼, VJ의 길이로부터 구할 수 있습니다.

S, V 및 B를 통과하는 원은 역시 J를 통과합니다.

반대로, 만약 포물선 VG 위의 한 점 B가 부채꼴 SVB의 넓이가 지정된 값과 같아지도록 찾으려면, VX 위의 점 J를 결정하고 S, V 및 J를 통해 원을 구성하십시오. SJ는 지름이므로, 원의 중심은 그의 중점에 있고, 그것은 SV의 수직 이등분, SV로부터 VJ의 절반 거리 위에 놓입니다. 필요한 점 B는 이 원이 포물선과 교차하는 점입니다.

만약 몸체가 S를 향한 방향화된 역 제곱 힘으로 인한 포물선의 경로를 추적하면, 넓이 SVB는, 점 B가 앞으로 움직일 때, 일정한 비율로 증가합니다. 그것은 B가 포물선을 따라 움직일 때 J는 VX를 따라 일정한 속도로 움직이는 것을 따릅니다.

만약 SV에 수직으로 움직이는 꼭짓점에서 몸체의 속도가 v이면, J의 속도는 3v/4와 같습니다.

구성은 다음으로 반지름이 축 SV와 일치하지 않는 경우를 포함하기 위해 간단히 확장될 수 있습니다. A를 V와 B 사이의 VG 위의 고정 점, H를 A에서 SA에 직교하는 VX 위의 교점으로 놓습니다. 위에서부터, 포물형 부태꼴의 넓이 $SAB={\frac {2SV\cdot (VJ-VH)}{3}}={\frac {2SV\cdot HJ}{3}}$입니다.

반대로, 만약 넓이 SAB에 대해 점 B를 찾는 것이 요구되면, HJ로부터 점 J를 찾고 이전 처럼 B를 찾습니다. 뉴턴의 Principia의 책 1, 제안 16, 따름정리 6에 의해, 초점을 향해 방향화된 힘을 가진 포물선을 따라 움직이는 몸체의 속력은 반지름의 제곱 근에 반비례합니다. 만약 A에서 속력이 v이면, 꼭짓점에서 그것은 ${\sqrt {\frac {SA}{SV}}}v$이고, 점 J는 ${\frac {3v}{4}}{\sqrt {\frac {SA}{SV}}}$의 일정한 속력으로 움직입니다.

위의 구성은 아이작 뉴턴에 의해 고안되었고 Philosophiæ Naturalis Principia Mathematica의 책 1권에서 제안 30으로 발견될 것입니다.

Focal length and radius of curvature at the vertex

포물선의 초점 거리는 그의 꼭짓점에서 곡률의 반지름(radius of curvature)의 절반입니다.

증명

• 
  Image is inverted. AB is x axis. C is origin. O is center. A is (x, y). OA = OC = R. PA = x. CP = y. OP = (R − y). Other points and lines are irrelevant for this purpose.
• 
  The radius of curvature at the vertex is twice the focal length. The measurements shown on the above diagram are in units of the latus rectum, which is four times the focal length.
• 

반지름 R 및 (0, R)에 중심을 가진 원 위에 점 (x, y)를 생각해 보십시오. 원은 원점을 통과합니다. 만약 그 점이 원점 근처에 있으면, 피타고라스 정리(Pythagorean theorem)는 다음임을 보입니다:

${\begin{aligned}x^{2}+(R-y)^{2}&=R^{2},\\x^{2}+R^{2}-2Ry+y^{2}&=R^{2},\\x^{2}+y^{2}&=2Ry.\end{aligned}}$

그러나 만약 (x, y)가 원점에 극단적으로 가까우면, x-축이 원의 접선이기 때문에, y는 x에 비교하여 매우 작으므로, y²은 다른 항과 비교해서 무시해도 좋습니다. 그러므로, 원점에 매우 가까우면:

$x^{2}=2Ry.$ (1)

이것을 포물선과 비교하면:

$x^{2}=4fy,$ (2)

이것은 원점에 꼭짓점을 가지고, 위로 열려 있고, 초점 거리 f를 가집니다 (이 기사의 이전 섹션을 참조하십시오).

방정식 (1)과 (2)는 만약 R = 2f이면 동등합니다. 그러므로, 이것은 원점에 극단적으로 가까운 것에서 일치하기 위한 원과 포물선에 대해 조건입니다. 포물선의 꼭짓점인, 원점에서 곡률의 반지름은 초점 거리의 두 배입니다.

따름정리

구의 작은 부분인 오목 거울은 근사적으로 포물면 거울처럼 행동하며, 구의 중심과 표면 사이의 중간 점에 평행한 빛을 집중시킵니다.

As the affine image of the unit parabola

Parabola as an affine image of the unit parabola

포물선의 또 다른 정의는 아핀 변환(affine transformation)을 사용합니다:

• 임의의 포물선 방정식 $y=x^{2}$를 가진 단위 포물선의 아핀 이미지입니다.

매개-변수 표현

유클리드 평면의 아핀 변환은 형식 ${\vec {x}}\to {\vec {f}}_{0}+A{\vec {x}}$을 가지며, 여기서 $A$는 정규 행렬이고 (행렬식(determinant)은 0이 아닙니다), ${\vec {f}}_{0}$는 임의의 벡터입니다. 만약 ${\vec {f}}_{1},{\vec {f}}_{2}$는 행렬 $A$의 열 벡터이면, 단위 포물선 $(t,t^{2}),\ t\in \mathbb {R}$은 다음 포물선 위로 매핑됩니다:

${\vec {x}}={\vec {p}}(t)={\vec {f}}_{0}+{\vec {f}}_{1}t+{\vec {f}}_{2}t^{2},$

여기서

${\vec {f}}_{0}$는 포물선의 점입니다,

${\vec {f}}_{1}$는 점 ${\vec {f}}_{0}$에서 접 벡터입니다,

${\vec {f}}_{2}$는 포물선의 축에 평행입니다 (꼭짓점을 통한 대칭축).

꼭짓점

일반적으로, 두 벡터 ${\vec {f}}_{1},{\vec {f}}_{2}$는 수직이 아니고, 만약 아핀 변환이 닮음(similarity)이 아니면, ${\vec {f}}_{0}$는 꼭짓점이 아닙니다.

점 ${\vec {p}}(t)$에서 접 벡터는 ${\vec {p}}'(t)={\vec {f}}_{1}+2t{\vec {f}}_{2}$입니다. 꼭짓점에서, 접 벡터는 ${\vec {f}}_{2}$에 직교입니다. 그러므로 꼭짓점의 매개변수 $t_{0}$는 다음 방정식의 해입니다:

${\vec {p}}'(t)\cdot {\vec {f}}_{2}={\vec {f}}_{1}\cdot {\vec {f}}_{2}+2tf_{2}^{2}=0,$

이것은 다음입니다:

$t_{0}=-{\frac {{\vec {f}}_{1}\cdot {\vec {f}}_{2}}{2f_{2}^{2}}},$

그리고 꼭짓점은 다음입니다:

${\vec {p}}(t_{0})={\vec {f}}_{0}-{\frac {{\vec {f}}_{1}\cdot {\vec {f}}_{2}}{2f_{2}^{2}}}{\vec {f}}_{1}+{\frac {({\vec {f}}_{1}\cdot {\vec {f}}_{2})^{2}}{4(f_{2}^{2})^{2}}}{\vec {f}}_{2}.$

초점 거리 및 초점

초점 거리는 적절한 매개-변수 변환에 의해 결정될 수 있습니다 (이것은 포물선의 기하학적 모양을 변경하지 않습니다). 초점 거리는 다음입니다:

$f={\frac {f_{1}^{2}\,f_{2}^{2}-({\vec {f}}_{1}\cdot {\vec {f}}_{2})^{2}}{4|f_{2}|^{3}}}.$

그러므로 포물선의 초점은 다음입니다:

$F:\ {\vec {f}}_{0}-{\frac {{\vec {f}}_{1}\cdot {\vec {f}}_{2}}{2f_{2}^{2}}}{\vec {f}}_{1}+{\frac {f_{1}^{2}\,f_{2}^{2}}{4(f_{2}^{2})^{2}}}{\vec {f}}_{2}.$

암시적 표현(implicit representation)

크라메르 규칙(Cramer's rule)에 의해 $\;t,t^{2}\;$에 대해 매개-변수 표현을 푸는 것 및 $\;t\cdot t-t^{2}=0\;$을 사용하면, 우리는 암시적 표현을 얻습니다:

$\det({\vec {x}}\!-\!{\vec {f}}\!_{0},{\vec {f}}\!_{2})^{2}-\det({\vec {f}}\!_{1},{\vec {x}}\!-\!{\vec {f}}\!_{0})\det({\vec {f}}\!_{1},{\vec {f}}\!_{2})=0$.

공간에서 포물선

이 섹션에서 포물선의 정의는, 심지어 공간에서, 만약 우리가 공간에서 ${\vec {f}}\!_{0},{\vec {f}}\!_{1},{\vec {f}}\!_{2}$를 벡터인 것으로 허용하면, 임의의 포물선의 매개-변수 표현을 제공합니다.

As quadratic Bézier curve

Quadratic Bézier curve and its control points

이차 베이에 곡선(quadratic Bézier curve)은, 그것의 제어 점으로 불리는, 세 점 $P_{0}:{\vec {p}}_{0}$, $P_{1}:{\vec {p}}_{1}$ 및 $P_{2}:{\vec {p}}_{2}$에 의해 정의된 곡선 ${\vec {c}}(t)$입니다:

${\begin{aligned}{\vec {c}}(t)&=\sum _{i=0}^{2}{\binom {2}{i}}t^{i}(1-t)^{2-i}{\vec {p}}_{i}\\&=(1-t)^{2}{\vec {p}}_{0}+2t(1-t){\vec {p}}_{1}+t^{2}{\vec {p}}_{2}\\&=({\vec {p}}_{0}-2{\vec {p}}_{1}+{\vec {p}}_{2})t^{2}+(-2{\vec {p}}_{0}+2{\vec {p}}_{1})t+{\vec {p}}_{0},\quad t\in [0,1].\end{aligned}}$

이 곡선은 포물선의 호입니다 (§ As the affine image of the unit parabola를 참조하십시오).

Numerical integration

Simpson's rule: the graph of a function is replaced by an arc of a parabola

수치 적분(numerical integration)의 한 방법에서, 우리가 함수의 그래프를 포물선의 호로 대체하고 포물선 호를 적분합니다. 포물선은 세 점으로 결정됩니다. 하나의 호에 대한 공식은 다음입니다:

$\int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{6}}\cdot \left(f(a)+4f\left({\frac {a+b}{2}}\right)+f(b)\right).$

이 방법은 심프슨 공식(Simpson's rule)으로 불립니다.

As plane section of quadric

다음 이차-초곡면(quadric)은 평면 단면으로 포물선을 포함합니다:

• 타원형 원뿔(cone),
• 포물형 원기둥(cylinder),
• 타원형 포물면체(paraboloid)
• 쌍곡형 포물면체,
• 한 판의 쌍곡면체(hyperboloid),
• 두 판의 쌍곡면체.

• 
  Elliptic cone
• 
  Parabolic cylinder
• 
  Elliptic paraboloid
• 
  Hyperbolic paraboloid
• 
  Hyperboloid of one sheet
• 
  Hyperboloid of two sheets

As trisectrix

Angle trisection with a parabola

포물선은 삼단선(trisectrix)으로 사용될 수 있습니다. 즉 그것은 직선자와 컴퍼스와 함께 임의의 각도의 정확하게 삼등분(exact trisection of an arbitrary angle)을 허용합니다. 이것은 단독으로 컴퍼스-와-직선자 구성(compass-and-straightedge construction)과 함께 각도 삼등분의 불가능과 모순되지 않는데, 왜냐하면 포물선의 사용은 컴퍼스-와-직선자 구성에 대해 고전적인 규칙에서 허용되지 않습니다.

$\angle AOB$을 삼등분하기 위해, 꼭짓점 $O$가 좌표 시스템의 원점에 있는 것을 만족하는 그의 다리 $OB$를 x-축 위에 위치시킵니다. 좌표 시스템은 포물선 $y=2x^{2}$를 역시 포함합니다. 원점의 주위를 도는 반지름 1을 가진 단위 원은 각도의 다른 다리 $OA$와 교차하고, 교차의 이 점으로부터 y-축 위로 수선을 그립니다. 그 수선의 중점을 통과하는 y-축에 평행선과 $(0,1)$에서 단위 원 위의 접선은 $C$에서 교차합니다. 반지름 $OC$를 가진 $C$의 주위를 도는 원은 $P_{1}$에서 포물선과 교차합니다. $P_{1}$에서 x-축 위로의 수선은 $P_{2}$에서 단위 원과 교차하고, $\angle P_{2}OB$는 $\angle AOB$의 정확히 3분의 1입니다.

이 구성의 정확성은 $P_{1}$의 x-좌표가 $\cos(\alpha )$임을 보임으로써 알 수 있습니다. 방정식 시스템을 푸는 것은 $C$의 주위를 도는 원에 의해 제공되고 포물선은 삼차 방정식 $4x^{3}-3x-\cos(3\alpha )=0$으로 이어집니다. 삼배-각 공식(triple-angle formula) $\cos(3\alpha )=4\cos(\alpha )^{3}-3\cos(\alpha )$은 그런-다음 $\cos(\alpha )$이 해당 삼차 방정식의 실제 해임을 보입니다.

이 삼등분은 르네 데카르트(René Descartes)로 거슬러 올라가며, 그는 그것을 그의 책 La Géométrie (1637)에 묘사했습니다.

Generalizations

만약 우리가 임의의 필드(field)로 실수를 대체하면, 포물선 $y=x^{2}$의 많은 기하학적 속성은 여전히 유효합니다:

1. 직선은 최대 두 점에서 교차합니다.
2. 임의의 점 $(x_{0},x_{0}^{2})$에서, 직선 $y=2x_{0}x-x_{0}^{2}$은 접선입니다.

본질적으로 새로운 현상이, 만약 필드가 특성 2 (즉, $1+1=0$)를 가지면, 발생합니다: 접선은 모두 평행입니다.

대수 기하학(algebraic geometry)에서, 포물선은 유리 정규 곡선(rational normal curve)에 의해 일반화되며, 그것은 좌표 (x, x², x³, …, xⁿ)를 가집니다; 표준 포물선은 경우 n = 2이고, 경우 n = 3은 뒤틀린 삼차(twisted cubic)로 알려져 있습니다. 보다 일반화는, 하나보다 많은 입력 변수가 있을 때, 베로네세 다양체(Veronese variety)에 의해 제공됩니다.

이차 형식(quadratic form)의 이론에서, 포물선은 이차 형식 x² (또는 다른 스케일링)의 그래프이지만, 타원형 포물면체(elliptic paraboloid)은 양의-한정(positive-definite:양의-정부호) 이차 형식 x² + y² (또는 스케일링)의 그래프이고, 쌍곡형 포물면체(hyperbolic paraboloid)은 부정 이차 형식(indefinite quadratic form) x² − y²의 그래프입니다. 더 많은 변수에 대한 일반화는 그러한 대상을 더 산출합니다.

p의 다른 값에 대해 곡선 y = x^p는 고차 포물선(higher parabolas)으로 전통적으로 참조되고, p와 q 둘 다 양의 정수에 대해 형식 x^p = ky^q에서, 암시적으로 원래 처리되었으며, 그 형식에서 그들은 대수적 곡선인 것으로 보입니다. 이들은 x의 양의 분수 거듭제곱에 대해 명시적 공식 y = x^p/q에 해당합니다. 음의 분수 거듭제곱은 암시적(음) 방정식 x^py^q = k에 해당하고 전통적으로 고차 쌍곡선(higher hyperbolas)으로 참조됩니다. 해석적으로, x는 (x의 양수 값에 대해) 무리수 거듭제곱을 역시 올려질 수 있습니다; 해석적 속성은 x가 유리수 거듭제곱으로 올려질 때와 유사하지만, 결과 곡선은 더 이상 대수적이지 않고 대수 기하학으로 절대 해석될 수 없습니다.

In the physical world

본질적으로, 포물선의 근사와 포물면은 많은 다양한 상황에서 발견됩니다. 물리학(physics)의 역사에서 포물선의 가장 잘 알려진 예제는 공기 저항(air resistance)없이 (예를 들어, 공기 마찰(friction)을 무시하는, 공기를 통해 날아가는 공) 균등한 중력 필드(gravitational field)의 영향 아래의 운동에서 입자 또는 물체의 궤적(trajectory)입니다.

발사체의 포물형 궤도는 갈릴레오(Galileo)에 의해 17세기 초에서 실험적으로 발견되었으며, 그는 경사진 평면 위를 구르는 공으로 실험을 수행했습니다. 그는 나중에 그의 책 Dialogue Concerning Two New Sciences에서 이것을 수학적(mathematical)으로 입증했습니다. 다이빙 보드에서 뛰어 내리는 다이버와 같이, 공간으로 확장된 대상에 대해, 대상 그 자체는 그것이 회전하는 것처럼 복잡한 동작을 따르지만, 대상의 질량의 중심(center of mass)은 그럼에도 불구하고 포물선을 따라 움직입니다. 물리 세계에서 모든 경우에서 처럼, 궤적은 항상 포물선의 근사입니다. 공기 저항의 존재는, 예를 들어, 비록 낮은 속력에서 일지라도, 모양을 항상 왜곡되지만, 모양은 포물선의 좋은 근사입니다. 탄도에서 처럼, 더 높은 속력에서, 모양은 매우 왜곡되고 포물선을 닮지 않습니다.

아이작 뉴턴 경(Sir Isaac Newton)에 의해 17세기와 18세기에서 묘사된 물리학 이론에 따르면, 포물선이 발생할 수 있는 또 다른 가설적(hypothetical) 상황은, 두-몸체 궤도(two-body orbit)에서, 예를 들어, 작은 행성체 또는 태양(Sun)의 중력의 영향 아래에 다른 대상의 경로입니다. 포물형 궤도(Parabolic orbit)는 본질적으로 발생하지 않습니다; 단순한 궤도는 가장 흔하게 쌍곡선(hyperbola) 또는 타원(ellipse)과 닮았습니다. 포물형 궤도는 이상적인 궤도의 그들의 두 유형 사이의 퇴화(degenerate) 중간 경우입니다. 포물형 궤도를 따르는 대상은 그것이 도는 대상의 정확한 탈출 속도(escape velocity)에서 움직일 것입니다; 타원형(elliptical) 또는 쌍곡형(hyperbolic) 궤도에서 대상은, 각각, 탈출 속도보다 작거나 더 큰 속도로 움직입니다. 장-기간 혜성(comet)은 내부 태양 시스템를 통해 움직이는 동안 태양의 탈출 속도에 가깝게 이동하므로, 그들의 경로는 거의 포물형입니다.

포물선의 근사는 간단한 부유 다리(suspension bridge:현수교)의 주요 케이블의 모양에서 역시 발견됩니다. 부유 다리의 체인의 곡선은 항상 포물선과 쇠사슬-모양(catenary:현수선) 사이의 중간 곡선이지만, 실제로 이 곡선은 일반적으로 포물선에 더 가깝고, 계산에서 이-차 포물선이 사용됩니다. (수평 부유 데크와 같이) 균등 하중의 영향 아래에서, 기타 쇠사슬-모양 케이블은 포물선을 향해 변형됩니다. 비-탄성 체인과 달리, 영 비-응력의 길이의 자유롭게 매달리는 용수철은 포물선 모양을 취합니다. 부유-다리 케이블은 다른 힘, 예를 들어, 굽힘을 지니는 것없이 이상적으로 순수한 긴장되어 있습니다. 마찬가지로, 포물선 아치의 구조는 순전히 압축되어 있습니다.

포물면은 마찬가지로 여러 물리적 상황에서 발생합니다. 가장 잘 알려진 예제는 빛 또는 다른 형태의 전자기 방사선(electromagnetic radiation)을 공통 초점(focal point)에 집중, 또는 반대로, 초점에 점 광원으로부터 평행한 빔으로 빛을 내보내는 거울 또는 유사한 반사 장치인 포물형 반사기(parabolic reflector)입니다. 포물형 반사기의 원리는 기하학자 아르키메데스(Archimedes)에 의해 기원전 3세기에서 발견되었을 것입니다. 모호한 전설에 따르면, 그는 로마(Roman) 함대에 대항해서 시러큐스(Syracuse)를 방어하기 위한 포물형 거울을 건설했는데, 태양의 반직선을 집중시켜 로마 선단의 갑판에 불을 질렀습니다. 그 원리는 17세기 망원경(telescope)에 적용되었습니다. 오늘날, 포물형 반사기는 전세계에 걸쳐 전자-레인지(microwave) 및 위성-접시 수신 및 송신 안테나에서 공통적으로 관찰될 수 있습니다.

포물형 마이크로폰(parabolic microphone)에서, 포물형 반사기는 소리를 마이크로폰으로 집중하기 위해 사용되며, 높은 직접적 성능을 제공합니다.

포물면은 용기에 갇힌 액체의 표면에서 관찰되고 중심 축을 중심으로 회전합니다. 이 경우에서, 원심력(centrifugal force)으로 인해 액체가 용기의 벽을 올라, 포물형 표면을 형성합니다. 이것이 액체-거울 망원경(liquid-mirror telescope)의 기본 원리입니다.

항공기(Aircraft)는, 나사(NASA)의 "Vomit Comet"에서 처럼, 실험의 목적에 대해 무중력 상태(weightless state)를 만드기 위해 사용되며, 그것은 자유 낙하(free fall)에서 물체의 진로를 추적하기 위해 짧은 기간에 대해 수직 포물형 궤적을 따르며, 자유 낙하는 대부분 목적에 대해 무중력과 같은 효과를 냅니다.

미국(United States)에서, 도로의 수직 곡선(vertical curves)은 보통 설계에서 포물형입니다.

Gallery

• 
  A bouncing ball captured with a stroboscopic flash at 25 images per second. The ball becomes significantly non-spherical after each bounce, especially after the first. That, along with spin and air resistance, causes the curve swept out to deviate slightly from the expected perfect parabola.
• 
  Parabolic trajectories of water in a fountain.
• 
  The path (in red) of Comet Kohoutek as it passed through the inner Solar system, showing its nearly parabolic shape. The blue orbit is the Earth's.
• 
  The supporting cables of suspension bridges follow a curve that is intermediate between a parabola and a catenary.
• 
  The Rainbow Bridge across the Niagara River, connecting Canada (left) to the United States (right). The parabolic arch is in compression and carries the weight of the road.
• 
  Parabolic arches used in architecture
• 
  Parabolic shape formed by a liquid surface under rotation. Two liquids of different densities completely fill a narrow space between two sheets of transparent plastic. The gap between the sheets is closed at the bottom, sides and top. The whole assembly is rotating around a vertical axis passing through the centre. (See Rotating furnace)
• 
  Solar cooker with parabolic reflector
• 
  Parabolic antenna
• 
  Parabolic microphone with optically transparent plastic reflector used at an American college football game.
• 
  Array of parabolic troughs to collect solar energy
• 
  Edison's searchlight, mounted on a cart. The light had a parabolic reflector.
• 
  Physicist Stephen Hawking in an aircraft flying a parabolic trajectory to simulate zero gravity

See also

• Degenerate conic
• Parabolic dome
• Parabolic partial differential equation
• Quadratic equation
• Quadratic function
• Universal parabolic constant

Further reading

• Lockwood, E. H. (1961). A Book of Curves. Cambridge University Press.

External links

• "Parabola", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Parabola". MathWorld.
• Interactive parabola-drag focus, see axis of symmetry, directrix, standard and vertex forms
• Archimedes Triangle and Squaring of Parabola at cut-the-knot
• Two Tangents to Parabola at cut-the-knot
• Parabola As Envelope of Straight Lines at cut-the-knot
• Parabolic Mirror at cut-the-knot
• Three Parabola Tangents at cut-the-knot
• Focal Properties of Parabola at cut-the-knot
• Parabola As Envelope II at cut-the-knot
• The similarity of parabola at Dynamic Geometry Sketches, interactive dynamic geometry sketch.
• Frans van Schooten: Mathematische Oeffeningen, 1659