Pythagorean triple

Original article: w:Pythagorean triple

Animation demonstrating the simplest Pythagorean triple, 3² + 4² = 5².

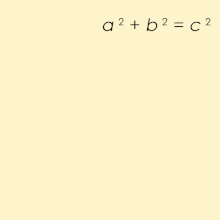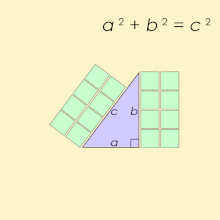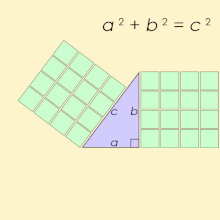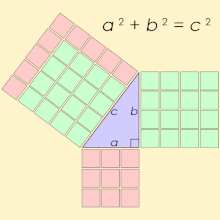
피타고라스의 세-쌍(Pythagorean triple)은, $a^{2}+b^{2}=c^{2}$를 만족하는, 세 개의 양의 정수(integer) a, b, 및 c로 구성됩니다. 그러한 세-쌍은 (a, b, c)로 공통적으로 쓰이고, 잘 알려진 예제는 (3, 4, 5)입니다. 만약 (a, b, c)가 피타고라스의 세-쌍이면, 임의의 양의 정수 k에 대해 (ka, kb, kc)도 마찬가지입니다. 원시 피타고라스 세-쌍(primitive Pythagorean triple)은 a, b, 및 c가 서로소 (즉, 1보다 큰 공통 약수를 가지지 않음)인 것입니다. 예를 들어, (3, 4, 5)는 원시 피타고라스 세-쌍이지만 (6, 8, 10)는 아닙니다. 그것의 변이 피타고라스의 세-쌍을 형성하는 삼각형은 피타고라스 삼각형(Pythagorean triangle)이라고 불리고, 반드시 직각 삼각형(right triangle)입니다.

그 이름은 모든 각 직각 삼각형이 공식 $a^{2}+b^{2}=c^{2}$를 만족시키는 변 길이를 가진다고 말하는 피타고라스의 정리(Pythagorean theorem)로부터 파생되었습니다; 따라서, 피타고라스의 세-쌍은 직각 삼각형의 세 정수 변의 길이를 나타냅니다. 어쨌든, 비-정수 변을 갖는 직각 삼각형은 피타고라스의 세-쌍을 형성하지 않습니다. 예를 들어, 변 $a=b=1$와 $c={\sqrt {2}}$를 갖는 삼각형은 직각 삼각형이지만, $(1,1,{\sqrt {2}})$는 피타고라스 세-쌍이 아닌데 왜냐하면 ${\sqrt {2}}$는 정수가 아니기 때문입니다. 더구나, ${\sqrt {2}}$는 무리수(irrational)이기 때문에, $1$과 ${\sqrt {2}}$는 정수 공통 배수를 가지지 않습니다.

피타고라스의 세-쌍은 고대 시절부터 알려져 왔습니다. 가장 오래된 알려진 기록은 기원전 1800년경의 바빌론 점토판, 플림프턴 322(Plimpton 322)에서 나온 것으로, 육십진수(sexagesimal) 숫자 시스템으로 쓰여 있습니다. 그것은 1900년 직후 에드가 제임스 뱅크스(Edgar James Banks)에 의해 발견되었고, 1922년 조지 아서 플림프턴(George Arthur Plimpton)에게 10달러에 팔렸습니다.

정수 해를 검색할 때, 방정식(equation) $a^{2}+b^{2}=c^{2}$는 디오판토스 방정식(Diophantine equation)입니다. 따라서, 피타고라스의 세-쌍은 비선형(nonlinear) 디오판토스 방정식의 가장 오래된 알려진 해 중의 하나입니다.

Examples

Scatter plot of the legs (a, b) of the first Pythagorean triples with a and b less than 6000. Negative values are included to illustrate the parabolic patterns. The "rays" are a result of the fact that if (a, b, c) is a Pythagorean triple, then so is (2a, 2b, 2c), (3a, 3b, 3c) and, more generally, (ka, kb, kc) for any positive integer k.

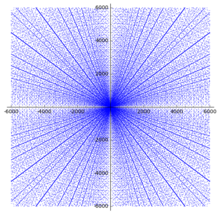
최대 100까지의 16개의 원시 피타고라스 세-쌍이 있습니다:

(3, 4, 5)	(5, 12, 13)	(8, 15, 17)	(7, 24, 25)
(20, 21, 29)	(12, 35, 37)	(9, 40, 41)	(28, 45, 53)
(11, 60, 61)	(16, 63, 65)	(33, 56, 65)	(48, 55, 73)
(13, 84, 85)	(36, 77, 85)	(39, 80, 89)	(65, 72, 97)

(6, 8, 10)과 같은 다른 작은 피타고라스 세-쌍은 원시적이지 않기 때문에 나열되지 않습니다; 예를 들어 (6, 8, 10)은 (3, 4, 5)의 배수입니다.

이들 각 점 (배수 포함)은 오른쪽의 산점도에서 방사형 직선을 형성합니다.

추가적으로, 다음은 300까지의 숫자 중에 남아있는 원시 피타고라스 세-쌍입니다:

(20, 99, 101)	(60, 91, 109)	(15, 112, 113)	(44, 117, 125)
(88, 105, 137)	(17, 144, 145)	(24, 143, 145)	(51, 140, 149)
(85, 132, 157)	(119, 120, 169)	(52, 165, 173)	(19, 180, 181)
(57, 176, 185)	(104, 153, 185)	(95, 168, 193)	(28, 195, 197)
(84, 187, 205)	(133, 156, 205)	(21, 220, 221)	(140, 171, 221)
(60, 221, 229)	(105, 208, 233)	(120, 209, 241)	(32, 255, 257)
(23, 264, 265)	(96, 247, 265)	(69, 260, 269)	(115, 252, 277)
(160, 231, 281)	(161, 240, 289)	(68, 285, 293)

Generating a triple

Main article: Formulas for generating Pythagorean triples

The primitive Pythagorean triples. The odd leg a is plotted on the horizontal axis, the even leg b on the vertical. The curvilinear grid is composed of curves of constant m − n and of constant m + n in Euclid's formula.

A plot of triples generated by Euclid's formula maps out part of the z² = x² + y² cone. A constant m or n traces out part of a parabola on the cone.

유클리드의 공식(Euclid's formula)은 m > n > 0을 갖는 정수 m과 n의 임의적인 쌍이 주어질 때 피타고라스 세-쌍을 생성하기 위한 토대적 공식입니다.그 공식은 다음 정수가 피타고라스 세-쌍을 형성한다고 말합니다:

$a=m^{2}-n^{2},\ \,b=2mn,\ \,c=m^{2}+n^{2}$

유클리드의 공식에 의해 생성된 세-쌍은 원시적인 것과 m과 n이 서로소(coprime)이고 그 중 하나가 짝수인 것은 필요충분 조건입니다. m과 n 둘 다가 홀수일 때, a, b, 및 c는 짝수일 것이고, 세-쌍은 원시적이지 않을 것입니다; 어쨌든, a, b, 및 c를 2로 나누면 m과 n이 서로소일 때 원시 세-쌍을 산출할 것입니다.

모든 각 원시 세-쌍은 (만약 a가 짝수이면, a와 b의 교환 후) 그것 중 하나가 짝수인 서로소 숫자 m, n의 고유한 쌍에서 발생합니다. 그것은 무한하게 많은 원시 피타고라스 세-쌍이 있음에서 따릅니다. 유클리드의 공식에서 나온 a, b, 및 c와 m과 n의 관계는 이 기사의 뒤 부분에서 참조됩니다.

모든 원시 세-쌍을 생성함에도 불구하고, 유클리드의 공식은 모든 세-쌍을 생성하지 않습니다—예를 들어, (9, 12, 15)는 정수 m과 n을 사용하여 생성될 수 없습니다. 이것은 공식에 추가적인 매개변수 k를 삽입함으로써 해결될 수 있습니다. 다음은 모든 피타고라스 세-쌍을 고유하게 생성할 것입니다:

$a=k\cdot (m^{2}-n^{2}),\ \,b=k\cdot (2mn),\ \,c=k\cdot (m^{2}+n^{2})$

여기서 m, n, 및 k는 m > n이고, m과 n은 서로소이고 둘 다 홀수가 아님을 갖는 양의 정수입니다.

이들 공식이 피타고라스 세-쌍을 생성한다는 것은 기본 대수(elementary algebra)를 사용하여 a² + b²를 확장하고 결과가 c²과 같은지 확인함으로써 검증될 수 있습니다. 모든 각 피타고라스의 세-쌍은 원시 세-쌍을 얻기 위해 어떤 정수 k로 나눌 수 있기 때문에, 모든 각 세-쌍은 m과 n을 갖는 공식을 사용하여 그것의 원시 짝과 그런-다음 마지막 방정식에서와 같이 k를 곱함으로써 고유하게 생성될 수 있습니다.

특정 정수 수열에서 m과 n을 선택하면 흥미로운 결과를 제공합니다. 예를 들어, 만약 m과 n이 연속적인 펠 숫자(Pell numbers)이면, a와 b는 1씩 다릅니다.

특정 속성을 갖는 세-쌍을 생성하기 위한 많은 공식이 유클리드 시대 이후로 개발되어 왔습니다.

Proof of Euclid's formula

a, b, c에 의한 유클리드 공식의 만족은 피타고라스가 될 삼각형에 대해 충분하다는 것은 양의 정수 m과 n에 대해, m > n, 공식에 의해 주어진 a, b, 및 c가 모두 양의 정수라는 사실과 다음이라는 사실에서 명백합니다:

$a^{2}+b^{2}=(m^{2}-n^{2})^{2}+(2mn)^{2}=(m^{2}+n^{2})^{2}=c^{2}.$

a, b, c가 임의의 원시 피타고라스 세-쌍에 대한 유클리드의 공식에 의해 표현되어야 하는 필요(necessity)의 증명은 다음과 같습니다. 모든 그러한 원시 세-쌍은 (a, b, c)로 쓸 수 있으며 여기서 a² + b² = c²이고 a, b, c는 서로소(coprime)입니다. 따라서 a, b, c는 쌍별 서로소입니다 (만약 소수가 이들 중 둘을 나누면, 세 번째 것도 나누어야 합니다). a와 b는 서로소이기 때문에, 그들 중 적어도 하나는 홀수이므로, 필요하다면 a와 b를 교환함으로써 a가 홀수라고 가정할 수 있습니다. 이것은 b가 짝수이고 c가 홀수임을 의미합니다 (만약 b가 홀수였으면, c는 짝수이고 c²는 4의 배수일 것이지만, a² + b²는 2 모듈로 4에 합동일 것인데, 왜냐하면 홀수 제곱은 1 모듈로 4와 합동이기 때문입니다).

$a^{2}+b^{2}=c^{2}$로부터, 우리는 $c^{2}-a^{2}=b^{2}$를 획득하고 따라서 $(c-a)(c+a)=b^{2}$입니다. 그런-다음 ${\tfrac {(c+a)}{b}}={\tfrac {b}{(c-a)}}$입니다. ${\tfrac {(c+a)}{b}}$가 유리수이기 때문에, 우리는 가장 낮은 항에서 그것을 ${\tfrac {m}{n}}$과 같게 설정했습니다. 따라서 ${\tfrac {(c-a)}{b}}={\tfrac {n}{m}}$이며, ${\tfrac {(c+a)}{b}}$의 역수입니다. 그런-다음 ${\tfrac {c}{b}}$와 ${\tfrac {a}{b}}$에 대해 풀면

${\frac {c}{b}}+{\frac {a}{b}}={\frac {m}{n}},\quad \quad {\frac {c}{b}}-{\frac {a}{b}}={\frac {n}{m}}$

다음을 제공합니다:

${\frac {c}{b}}={\frac {1}{2}}\left({\frac {m}{n}}+{\frac {n}{m}}\right)={\frac {m^{2}+n^{2}}{2mn}},\quad \quad {\frac {a}{b}}={\frac {1}{2}}\left({\frac {m}{n}}-{\frac {n}{m}}\right)={\frac {m^{2}-n^{2}}{2mn}}.$

${\tfrac {m}{n}}$이 완전하게 감소하므로, m과 n은 서로소이고, 그것들은 둘 다 짝수일 수 없습니다. 만약 그것들이 둘 다 홀수였으면, ${\tfrac {m^{2}-n^{2}}{2mn}}$의 분자는 4의 배수가 되고 (홀수 제곱은 1 모듈로 4와 합동이므로), 분모 2mn은 4의 배수가 아닐 것입니다. 4가 분자에서 최소 가능한 짝수 인수일 것이고 2는 분모에서 최대 가능한 짝수 인수일 것이므로, 이것은 a를 홀수로 정의함에도 불구하고 짝수임을 의미합니다. 따라서 m과 n 중 하나는 홀수이고 다른 하나는 짝수이고, 분모 2mn을 갖는 두 분수의 분자는 홀수입니다. 따라서 이들 분수는 완전하게 감소됩니다 (이 분모를 나누는 홀수 소수는 m과 n 중 하나를 나누지만 다른 것은 나누지 않습니다; 따라서 m² ± n²를 나누지 않습니다). 따라서 분자를 갖는 분자와 분모를 갖는 분모를 동일시하여, 다음 유클리드의 공식을 제공할 수 있습니다:

$a=m^{2}-n^{2},\ \,b=2mn,\ \,c=m^{2}+n^{2}$ with m and n coprime and of opposite parities.

더 길지만 더 평범한 증명은 Maor (2007)와 Sierpiński (2003)에서 제공됩니다. 또 다른 증명은 Diophantine equation § Example of Pythagorean triples에서, 모든 각 동차(homogeneous) 디오판토스 이차 방정식에 적용되는 일반적인 방법의 사례로 제공됩니다.

Interpretation of parameters in Euclid's formula

피타고라스 세-쌍의 변이 길이 m² − n², 2mn, 및 m² + n²을 가진다고 가정하고, 길이 m² − n²의 다리와 길이 m² + n²의 빗변(hypotenuse) 사이의 각도가 β로 표시된다고 가정합니다. 그런-다음 $\tan {\tfrac {\beta }{2}}={\tfrac {n}{m}}$이고 전체-각도 삼각 값이 $\sin {\beta }={\tfrac {2mn}{m^{2}+n^{2}}}$, $\cos {\beta }={\tfrac {m^{2}-n^{2}}{m^{2}+n^{2}}}$, 및 $\tan {\beta }={\tfrac {2mn}{m^{2}-n^{2}}}$입니다.

A variant

유클리드 공식의 다음 변형은 때때로 더 편리한데, 왜냐하면 m과 n에서 더 대칭적이기 때문입니다 (m과 n에서 같은 패리티 조건).

만약 m과 n은 m > n를 만족하는 두 개의 홀수 정수이면, 다음은

$a=mn,\ \,b={\frac {m^{2}-n^{2}}{2}},\ \,c={\frac {m^{2}+n^{2}}{2}}$

피타고라스 세-쌍을 형성하는 세 개의 정수이며, 이들이 원시적인 것과 m과 n이 서로소인 것은 필요충분 조건입니다. 반대로, 모든 각 원시 피타고라스 세-쌍은 (a와 b의 교환 후, a가 짝수이면) 서로소 홀수 정수의 고유한 쌍 m > n > 0에서 발생합니다.

Elementary properties of primitive Pythagorean triples

General properties

a < b < c (a 또는 b 중 어느 것이 짝수이고 어느 것이 홀수인지 지정하지 않음)를 갖는 원시 피타고라스 세-쌍 (a, b, c)의 속성은 다음을 포함합니다:

• ${\tfrac {(c-a)(c-b)}{2}}$는 항상 완전 제곱입니다. 그것이 필요조건일 뿐 충분조건은 아니기 때문에, 숫자의 주어진 세-쌍이 시험에 실패했을 때 피타고라스 세-쌍이 아닌지 확인하는 데 사용될 수 있습니다. 예를 들어, 세-쌍 {6, 12, 18}과 {1, 8, 9}는 각각 (c − a)(c − b)/2가 완전 제곱이라는 테스트를 통과하지만, 둘 다 피타고라스 세-쌍이 아닙니다.
• 숫자 a, b, 및 c의 세-쌍이 원시 피타고라스 세-쌍을 형성할 때, (c 빼기 짝수 다리)와 (c 빼기 홀수 다리)의 절반은 둘 다 완전 제곱입니다; 어쨌든 이것은 숫자 {1, 8, 9}는 완전 제곱 테스트를 통과하지만 1² + 8² ≠ 9²이기 때문에 피타고라스 세-쌍이 아니기 때문에 충분 조건이 아닙니다.
• a, b, c 중 많아야 하나가 제곱입니다.
• 피타고라스 세-쌍의 넓이는 자연수의 제곱이거나 제곱의 두 배입니다.
• a, b 중 정확히 하나가 2로 나눌 수 있지만 (짝수임), c는 아닙니다.
• a, b 중 정확히 하나가 3으로 나눌 수 있지만, c는 아닙니다.
• a, b 중 정확히 하나가 4으로 나눌 수 있지만, c는 아닙니다 (왜냐하면 c는 짝수가 아닙니다).
• a, b, c 중 정확히 하나가 5로 나눌 수 있습니다.
• abc를 항상 나누는 가장 큰 숫자는 60입니다.
• 2m+1 형식의 임의의 홀수는, 여기서 m은 정수이고 m>1, 원시 피타고라스 세-쌍 [PPT]의 홀수 다리가 될 수 있습니다. 아래의 almost-isosceles PPT 섹션을 참조하십시오. 어쨌든, 4로 나누어지는 짝수만이 PPT의 짝수 다리가 될 수 있습니다. 이것은 위에서 주어진 짝수 다리에 대한 유클리드의 공식(Euclid's formula)이 2mn이고 m 또는 n 중 하나가 짝수여야 하기 때문입니다.
• 빗변 c는 두 제곱의 합입니다. 이것은 모든 그것의 소수 인수가 $4n+1$ 형식의 소수여야 함을 요구합니다. 그러므로, c는 $4n+1$ 형식입니다. PPT에 대해 가능한 빗변 숫자의 수열은 (OEIS에서 수열 A008846)에서 찾을 수 있습니다.
• 넓이 (K = ab/2)는 6으로 나누어지는 합동 숫자(congruent number)입니다.
• 모든 각 피타고라스 세-쌍에서, 내원(incircle)의 반지름과 세 개의 외원의 반지름은 자연수입니다. 구체적으로, 원시 세-쌍에 대해 내원의 반지름은 r = n(m − n)이고, 변 m² − n², 2mn, 및 빗변 m² + n² 반대편에 있는 외원의 반지름은 각각 m(m − n), n(m + n), 및 m(m + n)입니다.
• 임의의 직각 삼각형에 대해, 탈레스 정리(Thales' theorem)의 전환은 둘레원(circumcircle)의 지름이 빗변과 같다고 말합니다; 따라서 원시 세-쌍에 대해, 둘레-지름은 m² + n²이고 둘레-반지름은 이것의 절반이고 따라서 유리수이지만 정수는 아닙니다 (왜냐하면 m과 n이 반대 패리티를 가지기 때문입니다).
• 피타고라스 삼각형의 넓이가 내원과 3개의 외원의 곡률(curvatures)에 곱해지면, 결과는 각각 4개의 양의 정수 w > x > y > z입니다. 정수 −w, x, y, z는 데카르트의 원 방정식(Descartes's Circle Equation)을 만족시킵니다. 동등하게, 임의의 직각 삼각형의 밖의 소디 원(outer Soddy circle)의 반지름은 그것의 반둘레와 같습니다. 밖의 소디 중심은 D에 위치되며, 여기서 ACBD는 직사각형, ACB는 직각 삼각형, AB는 빗변입니다.
• 원시 피타고라스 세-쌍을 생성하기 위한 유클리드의 공식(Euclid's formula)에 따르면, 다리 중 하나는 복합수이고 짝수여야 하기 때문에 원시 피타고라스 세-쌍의 두 변만이 동시에 소수일 수 있습니다. 어쨌든, 한 변만이 완전 거듭제곱 $p\geq 2$의 정수일 수 있는데, 왜냐하면 만약 두 변이 같은 지수 $p$를 갖는 완전 거듭제곱의 정수이면, 디오판토스 방정식(Diophantine equation) $x^{2p}\pm y^{2p}=z^{2}$에 대한 정수 해가 없다는 사실과 모순되기 때문이며, 이때 $x$, $y$, 및 $z$는 쌍별 서로소입니다.
• 빗변과 하나의 다리가 또 다른 피타고라스 삼각형의 다리인 피타고라스 삼각형은 없습니다; 이것은 페르마의 직각 삼각형 정리(Fermat's right triangle theorem)의 동등한 형식 중 하나입니다.
• 각각의 원시 피타고라스 삼각형은 넓이 K와 반-둘레(semiperimeter) s 제곱의 비율을 가지며, 즉, 자체로 고유하고 다음과 같이 제공됩니다:

${\frac {K}{s^{2}}}={\frac {n(m-n)}{m(m+n)}}=1-{\frac {c}{s}}.$

• 원시 피타고라스 삼각형은 빗변에서 정수 고도를 가지지 않습니다; 즉, 모든 각 원시 피타고라스 삼각형은 분해할 수 없습니다.
• 모든 원시 피타고라스 세-쌍의 집합은 자연스러운 방법에서 뿌리가 있는 삼항 트리(ternary tree)를 형성합니다; 원시 피타고라스 세-쌍의 트리를 참조하십시오.
• 피타고라스 삼각형의 예각(acute angles) 중 어느 것도 유리수의 각도가 될 수 없습니다. (이것은 니벤의 정리(Niven's theorem)에서 따온 것입니다.)

Special cases

게다가, 특정 추가 속성을 갖는 특수 피타고라스 세-쌍이 존재하기 위해 보장될 수 있습니다:

• 2 mod 4와 합동이 아닌 2보다 큰 모든 각 정수 (다시 말해서, 4k + 2 형식이 아닌 2보다 큰 모든 각 정수)는 원시 피타고라스 세-쌍의 일부입니다. (만약 정수가 4k 형식을 가지면, 유클리드의 공식에서 n = 1과 m = 2k를 취할 수 있습니다; 만약 정수가 2k + 1이면, n = k와 m = k + 1을 취할 수 있습니다.)
• 2보다 큰 모든 각 정수는 원시 또는 비-원시 피타고라스 세-쌍의 일부입니다. 예를 들어, 정수 6, 10, 14, 및 18은 원시 세-쌍의 일부가 아니지만, 비-원시 세-쌍 (6, 8, 10), (14, 48, 50), 및 (18, 80, 82)의 일부입니다.
• 빗변과 가장 긴 다리가 정확히 일 차이가 나는 피타고라스의 세-쌍은 무한하게 많이 존재합니다. 그러한 세-쌍은 반드시 원시적이고 형식 (2n + 1, 2n² + 2n, 2n² + 2n +1)을 가집니다. 이것은 조건이 세-쌍이 원시적이고 (m² + n²) - 2mn = 1임을 검증해야 한다는 것을 의미함을 주목함으로써 유클리드 공식으로부터 결과입니다. 이것은 (m – n)² = 1임을 의미하고, m = n + 1입니다. 위의 세-쌍의 형식은 따라서 유클리드의 공식에서 m을 n + 1로 대체한 결과입니다.
• 빗변과 가장 긴 다리가 정확히 2만큼 차이가 나는 원시 피타고라스의 세-쌍은 무한하게 많이 존재합니다. 그것들은 모두 원시적이고, 유클리드의 공식에 n = 1을 넣음으로써 얻습니다. 보다 일반적으로, 모든 각 정수 k > 0에 대해, 빗변과 홀수 다리가 2k²만큼 다른 원시 피타고라스 세-쌍이 무한하게 많이 존재합니다. 그것들은 유클리드의 공식에 n = k를 대입함으로써 얻습니다.
• 두 다리가 정확히 일만큼 다른 피타고라스의 세-쌍은 무한하게 많이 존재합니다. 예를 들어, 20² + 21² = 29²; 이것들은 ${\tfrac {m-n}{n}}$이 ${\sqrt {2}}$로 수렴할 때 유클리드의 공식에 의해 생성됩니다.
• 각각의 자연수 k에 대해, 서로 다른 빗변과 같은 넓이를 갖는 k개의 피타고라스 세-쌍이 존재합니다.
• 각각의 자연수 k에 대해, 같은 다리 a를 갖는 적어도 k개의 다른 원시 피타고라스 세-쌍이 존재하며, 여기서 a는 자연수입니다 (짝수 다리의 길이는 2mn이고, 많은 인수분해를 갖는 a를 선택하는 것으로 충분하며, 예를 들어 a = 4b, 여기서 b는 k개의 다른 홀수 소수의 곱입니다: 이것은 적어도 2^k개의 다른 원시 세-쌍을 생성합니다.
• 각각의 자연수 k에 대해, 같은 빗변을 갖는 적어도 k개의 서로 다른 피타고라스 세-쌍이 존재합니다.
• 만약 c = p^e가 소수 거듭제곱(prime power)이면, 원시 피타고라스 세-쌍 a² + b² = c²이 존재하는 것과 소수 p가 형식 4n + 1을 가지는 것은 필요충분 조건입니다; 이 세-쌍은 a와 b의 교환까지(up to) 고유합니다.
• 보다 일반적으로, 양의 정수 c가 원시 피타고라스 세-쌍의 빗변인 것과 c의 각 소수 인수가 1 모듈로 4와 합동인 것은 필요충분 조건입니다; 즉, 각 소수 인수는 4n + 1 형식을 가집니다. 이 경우에서, a < b를 갖는 원시 피타고라스 세-쌍 (a, b, c)의 개수는 2^k−1이며, 여기서 k는 c의 고유한 소수 인수의 개수입니다.
• 빗변 c와 다리의 합 a + b 둘 다에 대해 제곱 숫자를 갖는 피타고라스의 세-쌍은 무한하게 많이 존재합니다. 페르마에 따르면, 가장 작은 그러한 세-쌍은 변 a = 4,565,486,027,761; b = 1,061,652,293,520; 및 c = 4,687,298,610,289를 가집니다. 여기서 a + b = 2,372,159²이고 c = 2,165,017²입니다. 이것은 매개변수 값 m = 2,150,905과 n = 246,792를 갖는 유클리드 공식에 의해 생성됩니다.
• 빗변에서 정수 고도를 갖는 비-원시 피타고라스 삼각형이 존재합니다. 그러한 피타고라스 삼각형은 이 고도를 따라 두 개의 별도의 더 작은 피타고라스 삼각형으로 분할될 수 있기 때문에 분해-가능한(decomposable) 삼각형으로 알려져 있습니다.

Geometry of Euclid's formula

Rational points on a unit circle

3,4,5 maps to x,y point (4/5,3/5) on the unit circle

The rational points on a circle correspond, under stereographic projection, to the rational points of the line.

피타고라스 세-쌍에 대한 유클리드 공식은

$a=m^{2}-n^{2},\quad b=2mn,\quad c=m^{2}+n^{2}$

단위 원(unit circle) 위의 유리 점(rational points)의 기하학적 구조의 관점에서 이해될 수 있습니다 (Trautman 1998).

사실, 좌표 (x, y)를 갖는 데카르트 평면(Cartesian plane)에서 한 점은 x² + y² = 1이면 단위 원에 속합니다. 그 점은 만약 x와 y가 유리수(rational numbers)이면, 즉 다음임을 만족하는 서로소 정수( coprime integers) a, b, c가 있으면 유리수(rational)입니다:

${\biggl (}{\frac {a}{c}}{\biggr )}^{2}+{\biggl (}{\frac {b}{c}}{\biggr )}^{2}=1.$

두 항에 c²를 곱하면, 원 위의 유리 점이 원시 피타고라스 세-쌍과 일-대-일 대응임을 알 수 있습니다.

단위 원은 다음 매개변수 방정식(parametric equation)에 의해 정의될 수도 있습니다:

$x={\frac {1-t^{2}}{1+t^{2}}}\quad y={\frac {2t}{1+t^{2}}}.$

피타고라스 세-쌍에 대한 유클리드의 공식과 역 관계 t = y / (x + 1)는 (−1, 0)을 제외하고, 원 위의 점 (x, y)가 유리수인 것과 대응하는 t의 값이 유리수인 것은 필요충분 조건임을 의미합니다. t = y / (x + 1) = b / (a + c) = n / m은 길이 b의 삼각형 면과 반대편에 있는 각도의 절반의 탄젠트(tangent of half of the angle)이기도 합니다.

Stereographic approach

Stereographic projection of the unit circle onto the x-axis. Given a point P on the unit circle, draw a line from P to the point N = (0, 1) (the north pole). The point P′ where the line intersects the x-axis is the stereographic projection of P. Inversely, starting with a point P′ on the x-axis, and drawing a line from P′ to N, the inverse stereographic projection is the point P where the line intersects the unit circle.

유리 좌표와 원시 피타고라스 세-쌍을 갖는 단위 원 위의 점 사이에는 대응 관계가 있습니다. 이 시점에서, 유클리드의 공식은 삼각법(trigonometry)의 방법이나 동등하게 입체 투영(stereographic projection)을 사용하여 유도될 수 있습니다.

입체적 접근 방식에 대해, P′가 다음 유리 좌표를 갖는 x-축 위의 점이라고 가정합니다:

$P'=\left({\frac {m}{n}},0\right).$

그런-다음, 점 P가 다음 좌표를 가진다는 것을 기본 대수학으로 나타낼 수 있습니다:

$P=\left({\frac {2\left({\frac {m}{n}}\right)}{\left({\frac {m}{n}}\right)^{2}+1}},{\frac {\left({\frac {m}{n}}\right)^{2}-1}{\left({\frac {m}{n}}\right)^{2}+1}}\right)=\left({\frac {2mn}{m^{2}+n^{2}}},{\frac {m^{2}-n^{2}}{m^{2}+n^{2}}}\right).$

이것은 x-축의 각 유리 점(rational point)이 단위 원의 유리 점으로 넘어가는 것을 설정합니다. 단위 원의 모든 각 유리 점은 x-축의 그러한 점에서 나온다는, 그 전환은 역 입체 투영을 적용함으로써 따라옵니다. P(x, y)가 x와 y 유리수를 갖는 단위 원의 한 점이라고 가정합니다. 그런-다음 x-축 위로의 입체 투영에 의해 얻은 점 P′는 다음 좌표를 가집니다:

$\left({\frac {x}{1-y}},0\right)$

이는 유리수입니다.

대수적 기하학(algebraic geometry)의 관점에서, 단위 원 위에 있는 유리 점의 대수적 다양체(algebraic variety)는 유리수에 걸쳐 아핀 직선(affine line)에 대해 쌍유리수(birational)입니다. 따라서 단위 원은 유리 곡선(rational curve)이라고 불리고, 유리 함수를 수단으로 그 위의 (유리수) 점의 명시적 매개변수화를 가능하게 하는 것은 바로 이 사실입니다.

Pythagorean triangles in a 2D lattice

2D 격자(lattice)는 만약 임의의 하나의 점이 데카르트 원점 (0, 0)으로 선택되면, 모든 다른 점은 (x, y)에 있는 고립된 점의 규칙적 배열이며, 여기서 x와 y는 모든 양의 정수와 음의 정수에 걸쳐 있습니다. 세-쌍 (a, b, c)를 갖는 임의의 피타고라스 삼각형은 (0, 0), (a, 0), 및 (0, b) 좌표에 꼭짓점을 갖는 2D 격자 내에 그릴 수 있습니다. 삼각형의 엄격하게 경계 내에 놓이는 격자 점의 개수는 ${\tfrac {(a-1)(b-1)-\gcd {(a,b)}+1}{2}}$에 의해 지정됩니다; 원시 피타고라스 세-쌍에 대해, 이 내부 격자 개수는 ${\tfrac {(a-1)(b-1)}{2}}$입니다. 넓이 (내부 격자 개수에 경계 격자 개수의 절반을 더한 것보다 1 작은 것과 같은 픽의 정리(Pick's theorem)에 의함)은 ${\tfrac {ab}{2}}$와 같습니다.

같은 넓이를 공유하는 두 개의 원시 피타고라스 세-쌍의 첫 번째 발생은 변 (20, 21, 29), (12, 35, 37)이고 공통 영역 210을 갖는 삼각형 (OEIS에서 수열 A093536)에서 발생합니다. 같은 내부 격자 개수를 공유하는 두 개의 원시 피타고라스 세-쌍의 첫 번째 발생은 (18108, 252685, 253333), (28077, 162964, 165365)이고 내부 격자 개수 2287674594 (OEIS에서 수열 A225760)에서 발생합니다. 같은 넓이를 공유하는 세 개의 원시 피타고라스 세-쌍이 발견되었습니다: 넓이 13123110를 갖는 (4485, 5852, 7373), (3059, 8580, 9109), (1380, 19019, 19069)입니다. 아직까지, 같은 내부 격자 개수를 공유하는 세 개의 원시 피타고라스 세-쌍의 집합이 발견되지 않았습니다.

Enumeration of primitive Pythagorean triples

유클리드의 공식에 의해, 모든 원시 피타고라스 세-쌍은 $m>n>0$, $m+n$ 홀수 및 $\gcd(m,n)=1$를 갖는 정수 $m$과 $n$에서 생성될 수 있습니다. 따라서 ${\tfrac {n}{m}}$이 구간 $(0,1)$이고 $m+n$이 홀수인 원시 피타고라스 세-쌍에 유리수 (가장 낮은 항으로)의 1:1 매핑이 있습니다.

$c>b>a>0$인 원시 세-쌍 $(a,b,c)$에서 유리수 ${\tfrac {n}{m}}$으로의 역 매핑은 두 합 $a+c$와 $b+c$를 연구함으로써 달성됩니다. 이들 합계 중 하나는 $(m+n)^{2}$와 같을 수 있는 제곱이고 다른 하나는 $2m^{2}$와 같을 수 있는 제곱의 두 배입니다. 그것은 그런-다음 유리수 ${\tfrac {n}{m}}$를 결정할 수 있습니다.

원시 피타고라스 세-쌍을 열거하기 위해, 유리수는 순서화된 쌍 $(n,m)$으로 표현될 수 있고 칸토어의 쌍화 함수(Cantor's pairing function)와 같은 쌍화 함수를 사용하여 정수로 매핑될 수 있습니다. 예제는 (OEIS에서 수열 A277557)에서 볼 수 있습니다. 그것은 다음과 같이 시작합니다:

$8,18,19,32,33,34,\dots$ and gives rationals

${\tfrac {1}{2}},{\tfrac {2}{3}},{\tfrac {1}{4}},{\tfrac {3}{4}},{\tfrac {2}{5}},{\tfrac {1}{6}},\dots$ these, in turn, generate primitive triples

$(3,4,5),(5,12,13),(8,15,17),(7,24,25),(20,21,29),(12,35,37),\dots$

Spinors and the modular group

피타고라스 세-쌍은 마찬가지로 다음 형식의 정사각 행렬(square matrix)로 인코딩될 수 있습니다:

$X={\begin{bmatrix}c+b&a\\a&c-b\end{bmatrix}}.$

이 형식의 행렬은 대칭적(symmetric)입니다. 게다가, X의 행렬식(determinant)은 다음입니다:

$\det X=c^{2}-a^{2}-b^{2}\,$

여기서 (a,b,c)가 피타고라스 세-쌍일 때 정확하게 영입니다. 만약 X가 피타고라스 세-쌍에 해당하면, 행렬로서 그것은 랭크(rank) 1을 가져야 합니다.

X가 대칭적이기 때문에, 선형 대수(linear algebra)에서 결과로부터 다음 밖의 곱(outer product)이 유지됨을 만족하는 열 벡터(column vector) ξ = [m n]^T있음으로 이어집니다:

$X=2{\begin{bmatrix}m\\n\end{bmatrix}}[m\ n]=2\xi \xi ^{T}\,$

(1)

여기서 T는 행렬 전치(matrix transpose)를 나타냅니다. 벡터 ξ는 (로렌츠 그룹 SO(1, 2)에 대해) 스피너(spinor)라고 불립니다. 추상적인 용어로, 유클리드 공식은 각각의 원시 피타고라스 세-쌍이 (1)에서와 같이 정수 항목을 갖는 스피너의 자체와의 밖의 곱으로 작성될 수 있음을 의미합니다.

모듈러 그룹(modular group) Γ는 정수 항목을 갖는 2×2 행렬의 집합입니다:

$A={\begin{bmatrix}\alpha &\beta \\\gamma &\delta \end{bmatrix}}$

여기서 행렬식은 일과 같습니다: αδ − βγ = 1. 이 집합은 그룹(group)을 형성하는데, 왜냐하면 Γ에 있는 행렬의 역이 Γ에 있는 두 행렬의 곱인 것처럼 다시 Γ에 있기 때문입니다. 모듈러 그룹은 모든 정수 스피너의 모음 위에 작용합니다. 더구나, 그 그룹은 상대적으로 소수 엔터리를 갖는 정수 스피너의 모음에서 전이적입니다. [m n]^T이 상대적으로 소수 엔트리를 가지면, 다음과 같습니다:

${\begin{bmatrix}m&-v\\n&u\end{bmatrix}}{\begin{bmatrix}1\\0\end{bmatrix}}={\begin{bmatrix}m\\n\end{bmatrix}}$

여기서 u와 v는 mu + nv = 1이 되도록 (유클리드 알고리듬에 의해) 선택됩니다.

(1)에서 스피너 ξ 위에 작용함으로써, Γ의 작용은 피타고라스 세-쌍 위에 작용으로 넘어가며, 음의 구성 요소가 있을 수 있는 세-쌍을 허용한다는 조건으로 합니다. 따라서, 만약 A가 Γ에 있는 행렬이면, 다음은

$2(A\xi )(A\xi )^{T}=AXA^{T}\,$

(2)

(1)에서 행렬 X 위에 작용을 발생시킵니다. 이것은 원시 세-쌍 위에 잘-정의된 작용을 제공하지 않는데, 왜냐하면 원시 세-쌍에서 비-원시 세-쌍을 취할 수 있기 때문입니다. 이 점에서 (Trautman 1998에 따라) c > 0이고 (a,b,c)가 상대적으로 소수이거나 (a/2,b/2,c/2)가 홀수 a/2와 상대적으로 소수이면 표준(standard) 세-쌍 (a,b,c)라고 부르는 것이 편리합니다. 만약 스피너 [m n]^T이 상대적으로 소수 엔트리를 가지면, (1)에 의해 결정된 결합된 세-쌍 (a,b,c)는 표준 세-쌍입니다. 모듈러 그룹의 작용은 표준 세-쌍의 집합 위에 전이적이라는 것으로 이어집니다.

대안적으로, m이 홀수이고 n이 짝수인 m과 n의 값에 주의를 제한하십시오. Γ의 부분그룹 Γ(2)를 그룹 준동형(group homomorphism)의 커널(kernel)이라고 놓습니다:

$\Gamma =\mathrm {SL} (2,\mathbf {Z} )\to \mathrm {SL} (2,\mathbf {Z} _{2})$

여기서 SL(2,Z₂)는 정수 모듈로 2의 유한 필드 Z₂에 걸쳐 특수 선형 그룹(special linear group)입니다. 그런-다음 Γ(2)는 각 엔트리의 패리티를 보존하는 단일-모듈러 변환의 그룹입니다. 따라서 ξ의 첫 번째 엔트리가 홀수이고 두 번째 엔트리가 짝수이면, 모든 A ∈ Γ(2)에 대해 Aξ도 마찬가지입니다. 사실, 동작 (2) 아래에서, 그룹 Γ(2)는 원시 피타고라스 세-쌍의 모음에 전이적으로 동작합니다 (Alperin 2005).

그룹 Γ(2)는 그것의 생성기가 다음 행렬이면 자유 그룹(free group)입니다:

$U={\begin{bmatrix}1&2\\0&1\end{bmatrix}},\qquad L={\begin{bmatrix}1&0\\2&1\end{bmatrix}}.$

결과적으로, 모든 각 원시 피타고라스 세-쌍은 행렬 U와 L의 복사본의 곱으로 고유한 방법으로 얻을 수 있습니다.

Parent/child relationships

Main article: Tree of Pythagorean triples

Berggren (1934)의 결과에 의해, 모든 원시 피타고라스 세-쌍은 아래의 세 개의 선형 변환 T₁, T₂, T₃을 사용하여 (3, 4, 5) 삼각형에서 생성될 수 있으며, 여기서 a, b, c는 세-쌍의 변입니다:

	new side a	new side b	new side c
T1:	a − 2b + 2c	2a − b + 2c	2a − 2b + 3c
T2:	a + 2b + 2c	2a + b + 2c	2a + 2b + 3c
T3:	−a + 2b + 2c	−2a + b + 2c	−2a + 2b + 3c

다시 말해서, 모든 각 원시 세-쌍은 세 개의 추가적인 원시 세-쌍에 대한 "부모"가 됩니다. a = 3, b = 4, 및 c = 5인 초기 노드에서 시작하여, 연산 T₁은 새로운 세-쌍을 생성합니다:

(3 − (2×4) + (2×5), (2×3) − 4 + (2×5), (2×3) − (2×4) + (3×5)) = (5, 12, 13),

그리고 유사하게 T₂와 T₃는 세-쌍 (21, 20, 29)와 (15, 8, 17)를 생성합니다.

선형 변환 T₁, T₂, 및 T₃는 이차 형식(quadratic forms)의 언어로 기하학적 해석을 가집니다. 이것들은 정수에 걸쳐 x² + y² − z²의 직교 그룹(orthogonal group)을 생성하는 반사와 밀접하게 관련되어 있습니다 (그러나 같지는 않습니다).

Relation to Gaussian integers

대안적으로, 유클리드 공식은 가우스 정수(Gaussian integers)를 사용하여 분석되고 입증될 수 있습니다. 가우스 정수는 α = u + vi 형식의 복소수이며, 여기서 u와 v는 보통의 정수이고 i는 음수 일의 제곱근입니다. 가우스 정수의 단위(units)는 ±1과 ±i입니다. 보통의 정수는 유리 정수(rational integers)라고 불리고 'Z'로 표시됩니다. 가우스 정수는 Z[i]로 표시됩니다. 피타고라스 정리(Pythagorean theorem)의 오른쪽 변은 가우스 정수에서 인수화될 수 있습니다:

$c^{2}=a^{2}+b^{2}=(a+bi){\overline {(a+bi)}}=(a+bi)(a-bi).$

원시 피타고라스 세-쌍은 a와 b가 서로소(coprime), 즉, 그것들이 정수에서 소수 인수를 공유하지 않는 것입니다. 그러한 세-쌍에 대해, a 또는 b 중 하나는 짝수이고, 다른 하나는 홀수입니다; 이로부터, c도 홀수라는 결론이 나옵니다.

원시 피타고라스 세-쌍의 두 인수 z := a + bi와 z* := a − bi는 각각 가우스 정수의 제곱과 같습니다. 이것은 모든 각 가우스 정수가 단위까지(up to) 가우스 소수로 고유하게 인수화될 수 있다는 속성을 사용하여 입증될 수 있습니다. (이 고유한 인수분해는, 대략적으로 말해서, 유클리드 알고리듬 버전이 그것 위에 정의될 수 있다는 사실에서 비롯됩니다.) 증명은 세 단계를 가집니다. 첫째, a와 b가 정수에서 소수 인수를 공유하지 않으면, 그것들은 가우스 정수에서도 소수 인수를 공유하지 않습니다. (가우스 정수 g, u, 및 v를 갖는 a = gu와 b = gv라고 가정하고 g는 단위가 아닙니다. 그런-다음 u와 v는 원점을 통과하는 같은 직선 위에 놓입니다. 그러한 직선 위의 모든 가우스 정수는 일부 가우스 정수 h의 정수 배수입니다. 그러나 그때에 정수 gh ≠ ±1은 a와 b를 모두 나눕니다.) 둘째, z와 z*도 마찬가지로 가우스 정수에서 소수 인수를 공유하지 않음으로 이어집니다. 만약 그것들이 그랬었다면, 그것들의 공통 약수 δ도 z + z* = 2a와 z − z* = 2ib로 나눌 것입니다. a와 b는 서로소이기 때문에, δ가 2 = (1 + i)(1 − i) = i(1 − i)²로 나뉜다는 것을 의미합니다. 공식 c² = zz*에서, 이는 차례로 원시 피타고라스 세-쌍의 가설과 반대로 c가 짝수임을 의미합니다. 셋째, c²가 제곱이기 때문에, 그것의 인수분해에서 모든 각 가우스 소수는 두 배가 되며, 즉, 짝수 번 나타납니다. z와 z*은 소수 인수를 공유하지 않기 때문에, 이 두 배가 되는 것도 그것들에 대해 참입니다. 따라서, z와 z*는 제곱입니다.

따라서, 첫 번째 인수는 다음과 같이 쓸 수 있습니다:

$a+bi=\varepsilon \left(m+ni\right)^{2},\quad \varepsilon \in \{\pm 1,\pm i\}.$

이 방정식의 실수 부분과 허수 부분은 다음 두 공식을 제공합니다:

${\begin{cases}\varepsilon =+1,&\quad a=+\left(m^{2}-n^{2}\right),\quad b=+2mn;\\\varepsilon =-1,&\quad a=-\left(m^{2}-n^{2}\right),\quad b=-2mn;\\\varepsilon =+i,&\quad a=-2mn,\quad b=+\left(m^{2}-n^{2}\right);\\\varepsilon =-i,&\quad a=+2mn,\quad b=-\left(m^{2}-n^{2}\right).\end{cases}}$

임의의 원시 피타고라스 세-쌍에 대해, 이들 두 방정식을 만족시킴을 만족하는 정수 m과 n이 있어야 합니다. 따라서, 모든 각 피타고라스 세-쌍은 이들 정수 중 일부 선택에서 생성될 수 있습니다.

As perfect square Gaussian integers

만약 우리가 가우스 정수의 제곱을 고려하면, 우리는 가우스 정수의 완전 제곱을 나타내는 유클리드의 공식을 다음과 같이 직접 해석을 얻습니다.

$(m+ni)^{2}=(m^{2}-n^{2})+2mni.$

가우스 정수가 유클리드 도메인이고 가우스 정수 $p$에 대해, $|p|^{2}$은 항상 제곱이라는 사실을 사용하여, 빗변이 소수이면 피타고라스 세-쌍이 소수 가우스 정수의 제곱에 해당함을 보여줄 수 있습니다.

만약 가우스 정수가 소수가 아니면, $|p|^{2}$과 $|q|^{2}$ 정수를 갖는 두 가우스 정수 $p$와 $q$의 곱입니다. 크기는 가우스 정수에서 곱하기 때문에, 곱은 $|p||q|$이어야 하며, 이는 피타고라스 세-쌍을 찾기 위해 제곱될 때 합성수이어야 합니다. 대우가 증명을 완성합니다.

Distribution of triples

A scatter plot of the legs (a,b) of the first Pythagorean triples with a and b less than 4500.

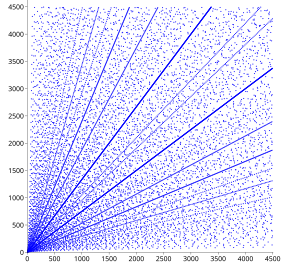
피타고라스 세-쌍의 분포에 대한 많은 결과가 있습니다. 산점도에서, 많은 분명한 패턴이 이미 명백합니다. 원시 세-쌍의 다리 (a,b)가 그림에 나타날 때마다, (a,b)의 모든 정수 배수도 그림에 나타나야 하고, 이 속성은 다이어그램에서 원점으로부터 방사되는 직선 모양을 생성합니다.

산포 내에, 점의 높은 밀도와 원점에서 모든 그것들의 초점을 갖는 포물선(parabolic) 패턴의 집합이 있으며, 네 방향 모두에서 열립니다. 다른 포물선은 축에서 교차하고 45도의 입사 각도로 축에서 반사되는 것처럼 보이며, 세 번째 포물선은 수직 방식으로 진입합니다. 이 사분면 내에, 원점을 중심으로 하는 각 호는 포물선의 끝과 반-래투스 렉툼(semi-latus rectum)과의 교차점 사이에 있는 포물선의 부분을 보여줍니다.

이들 패턴은 다음과 같이 설명될 수 있습니다. 만약 $a^{2}/4n$이 정수이면, (a, $|n-a^{2}/4n|$, $n+a^{2}/4n$)은 피타고라스 세-쌍입니다. (실제로 모든 각 피타고라스 세-쌍 (a, b, c)는 $n=(b+c)/2$이고 a와 b가 둘 다 홀수일 수 없기 때문에 a와 b를 교환한 후에 정수 n으로 이런 방법으로 쓸 수 있습니다.) 따라서 피타고라스 세-쌍은 $b=|n-a^{2}/4n|$으로 주어진 곡선, 즉, a-축에서 반사된 포물선과 a와 b가 서로 바뀌는 해당 곡선 위에 놓여 있습니다. 만약 a가 주어진 n에 대해 (즉, 주어진 포물선 위에) 변하면, n이 제곱이거나 제곱의 작은 배수이면 b의 정수 값이 상대적으로 자주 발생합니다. 만약 여러 그러한 값이 함께 가까이 놓이게 되면, 해당하는 포물선이 거의 일치하고, 세-쌍이 좁은 포물선 스트립에 모여 있습니다. 예를 들어, 38² = 1444, 2 × 27² = 1458, 3 × 22² = 1452, 5 × 17² = 1445, 및 10 × 12² = 1440; n ≈ 1450 주변의 해당 포물선 스트립은 산점도에서 명확하게 볼 수 있습니다.

위에서 설명된 각도 속성은 포물선의 함수형 형식에서 바로 이어집니다. 포물선은 a = 2n에서 a-축에 반사되고, 이 점에서 a에 관한 b의 도함수는 –1입니다; 따라서 입사 각도는 45°입니다. 클러스터는, 모든 세-쌍과 마찬가지로, 정수 배수로 반복되므로, 값 2n도 클러스터에 해당합니다. 해당 포물선은 b = 2n에서 직각으로 b-축과 교차하고, 따라서 a와 b의 교환에 대한 반사는 a = 2n에서 직각으로 a-축과 교차하며, 정확하게 여기서 n에 대한 포물선은 a-축에서 반사됩니다. (물론 a와 b가 서로 바뀌어도 마찬가지입니다.)

Albert Fässler와 다른 사람들은 등각 매핑의 맥락에서 이들 포물선의 중요성에 대한 통찰력을 제공합니다.

Special cases and related equations

The Platonic sequence

피타고라스 세-쌍의 보다 일반적인 구성의 경우 n = 1은 오랫동안 알려져 왔습니다. 프로크로스(Proclus)는, 유클리드의 원론의 첫 번째 책의 47번째 제안에 대한 그의 주석에서, 다음과 같이 설명합니다:

이러한 종류의 삼각형의 발견에 대한 특정 방법은, 그것들이 플라톤을 참조한 것과 피타고라스를 참조하여 또 다른 것을 전승됩니다. (후자는) 홀수부터 시작합니다. 그것은 홀수를 직각에 대한 변들 중 더 작은 것으로 만들기 때문입니다; 그런-다음 그것의 제곱을 취하고, 단위를 빼고 직각에 대한 변 중 더 큰 차이의 절반을 만듭니다; 마지막으로 이것에 단위를 더하고 따라서 남아있는 변, 빗변을 형성합니다. ...플라톤의 방법은 짝수부터 논의합니다. 주어진 짝수를 취하고 직각에 대한 변 중 하나로 만듭니다; 그런-다음 이 숫자를 이등분하고 절반을 제곱하여, 제곱에 단위를 더하여 빗변을 형성하고, 제곱에서 단위를 빼서 직각에 대해 다른 변을 형성합니다. ... 따라서 다른 방법으로 얻은 것과 같은 삼각형을 형성했습니다.

방정식 형식에서, 이것은 다음이 됩니다:

a는 홀수입니다 (피타고라스, 기원전 약,540년):

${\text{side }}a:{\text{side }}b={a^{2}-1 \over 2}:{\text{side }}c={a^{2}+1 \over 2}.$

a는 짝수입니다 (플라톤, 기원전 약 380년):

${\text{side }}a:{\text{side }}b=\left({a \over 2}\right)^{2}-1:{\text{side }}c=\left({a \over 2}\right)^{2}+1$

모든 피타고라스 세-쌍은 a를 비-정수 유리수 값을 취하도록 허용함으로써 기본 플라톤 순서열 (a, (a² − 1)/2와 (a² + 1)/2)에서 적절한 크기 조정과 함께 얻을 수 있음을 보여줄 수 있습니다. 만약 a가 순서열에서 분수 m/n으로 대체되면, 그 결과는 크기 조정 후 '표준' 세-쌍 생성기 (2mn, m² − n²,m² + n²)와 같습니다. 따라서 모든 각 세-쌍은 닮은 삼각형 (같은 세 각과 원래와 같은 비율의 변을 갖는 삼각형)을 생성하기 위해 사용될 수 있는 대응 유리수 a 값을 가집니다. 예를 들어, (56, 33, 65)의 플라톤 등가물은 a = m/n = 7/4에 의해 (a, (a² –1)/2, (a²+1)/2) = (56/32, 33/32, 65/32)로 생성됩니다. 플라톤 순서열 자체는 디오판토스 II.VIII에 설명된 '제곱 분할' 단계를 따라 유도할 수 있습니다.

The Jacobi–Madden equation

Main article: Jacobi–Madden equation

다음 방정식은,

$a^{4}+b^{4}+c^{4}+d^{4}=(a+b+c+d)^{4}$

다음과 같은 특별한 피타고라스 세-쌍과 동등합니다,

$(a^{2}+ab+b^{2})^{2}+(c^{2}+cd+d^{2})^{2}=((a+b)^{2}+(a+b)(c+d)+(c+d)^{2})^{2}$

변수에 대한 푸는 것은 타원 곡선(elliptic curve)을 포함되므로 이 방정식에 대한 무한하게 많은 해가 있습니다. 작은 것들은,

$a,b,c,d=-2634,955,1770,5400$

$a,b,c,d=-31764,7590,27385,48150$

Equal sums of two squares

$a^{2}+b^{2}=c^{2}+d^{2}$에 대한 해를 생성하기 위한 한 방법은 다음과 같이 a, b, c, d를 정수 m, n, p, q의 관점에서 매개변수화하는 것입니다:

$(m^{2}+n^{2})(p^{2}+q^{2})=(mp-nq)^{2}+(np+mq)^{2}=(mp+nq)^{2}+(np-mq)^{2}.$

Equal sums of two fourth powers

두 개의 피타고라스 세-쌍의 집합이 주어지면,

$(a^{2}-b^{2})^{2}+(2ab)^{2}=(a^{2}+b^{2})^{2}$

$(c^{2}-d^{2})^{2}+(2cd)^{2}=(c^{2}+d^{2})^{2}$

빗변이 아닌 변과 빗변의 같은 곱을 찾는 문제는,

$(a^{2}-b^{2})(a^{2}+b^{2})=(c^{2}-d^{2})(c^{2}+d^{2})$

다음과 같은 다음과 같은 방정식과 동등하다는 것을 쉽게 알 수 있습니다,

$a^{4}-b^{4}=c^{4}-d^{4}$

그리고 오일러에 의해 $a,b,c,d=133,59,158,134$로 처음 해결되었습니다. 그가 이것이 타원 곡선(elliptic curve)에서 유리 점임을 보여주었기 때문에, 무한한 숫자의 해가 있습니다. 실제로, 그는 7차 다항식 매개변수화도 발견했습니다.

Descartes' Circle Theorem

모든 변수가 제곱인 데카르트의 원 정리(Descartes' circle theorem)에 대해,

$2(a^{4}+b^{4}+c^{4}+d^{4})=(a^{2}+b^{2}+c^{2}+d^{2})^{2}$

오일러는 이것이 다음과 같은 세 개의 연립 피타고라스 세-쌍과 동등하다는 것을 보여주었습니다,

$(2ab)^{2}+(2cd)^{2}=(a^{2}+b^{2}-c^{2}-d^{2})^{2}$

$(2ac)^{2}+(2bd)^{2}=(a^{2}-b^{2}+c^{2}-d^{2})^{2}$

$(2ad)^{2}+(2bc)^{2}=(a^{2}-b^{2}-c^{2}+d^{2})^{2}$

무한한 수의 해가 있고, $a+b=c$인 특수한 경우에 대해, 그 방정식은 다음과 같이 단순화됩니다,

$4(a^{2}+ab+b^{2})=d^{2}$

이때 $a,b,c,d=3,5,8,14$와 같은 작은 해를 갖고 이진 이차 형식(binary quadratic forms)으로 풀 수 있습니다.

Almost-isosceles Pythagorean triples

피타고라스 세-쌍은 이등변(isosceles)이 아닌데, 왜냐하면 빗변과 다른 변의 비율은 ${\sqrt {2}}$이지만, ${\sqrt {2}}$는 정수 2개의 비율로 표현될 수 없기 때문입니다.

어쨌든, 다음과 같이 빗변이 아닌 변의 길이가 일만큼 다른 적분 변을 갖는 직각 삼각형이 있습니다:

$3^{2}+4^{2}=5^{2}$

$20^{2}+21^{2}=29^{2}$

그리고 무한한 수의 다른 것들이 있습니다. 그것들은 다음과 같이 완전하게 매개변수화될 수 있습니다:

$\left({\tfrac {x-1}{2}}\right)^{2}+\left({\tfrac {x+1}{2}}\right)^{2}=y^{2}$

여기서 {x, y}는 펠 방정식(Pell equation) $x^{2}-2y^{2}=-1$에 대한 해입니다.

만약 a, b, c가 이러한 유형의 원시 피타고라스 세-쌍 (PPT)의 변이면 펠 방정식의 해는 다음 재귀 공식(recursive formula)에 의해 제공됩니다:

$a_{n}=6a_{n-1}-a_{n-2}+2$ with $a_{1}=3$ and $a_{2}=20$

$b_{n}=6b_{n-1}-b_{n-2}-2$ with $b_{1}=4$ and $b_{2}=21$

$c_{n}=6c_{n-1}-c_{n-2}$ with $c_{1}=5$ and $c_{2}=29$.

이 PPT의 순서열은 PPT의 뿌리박은 삼항 트리(rooted ternary tree)의 중심 줄기를 형성합니다.

그것이 다음과 같은 더 긴 빗변이 아닌 변과 일만큼 다른 빗변일 때,

$5^{2}+12^{2}=13^{2}$

$7^{2}+24^{2}=25^{2}$

PPT a, b, c에 대해 완전한 해는 다음과 같습니다:

$a=2m+1,\quad b=2m^{2}+2m,\quad c=2m^{2}+2m+1$

그리고

$(2m+1)^{2}+(2m^{2}+2m)^{2}=(2m^{2}+2m+1)^{2}$

여기서 정수 $m>0$은 생성 매개변수입니다.

이 유형의 거의 이등변 PPT에는 모든 홀수 (1보다 큼)가 나타남을 알 수 있습니다. 이 PPT의 순서열은 PPT의 뿌리박은 삼항 트리의 오른쪽 외부 줄기를 형성합니다.

이 유형의 거의 이등변 PPT의 또 다른 속성은 그 변이 일부 정수 $K$에 대해 다음임을 만족함과 관련되어 있다는 것입니다:

$a^{b}+b^{a}=Kc$

또는 다른 말로 $a^{b}+b^{a}$는 다음에서 처럼 $c$로 나눌 수 있습니다:

$(5^{12}+12^{5})/13=18799189$.

Fibonacci numbers in Pythagorean triples

5부터 시작하여, 모든 각 두 번째 피보나치 숫자(Fibonacci number)는 정수 변을 갖는 직각 삼각형의 빗변의 길이, 또는 다른 말로, 다음 공식에서 구한 피타고라스 세-쌍의 숫자에서 가장 큰 숫자입니다:

$$(F_{n}F_{n+3})^{2}+(2F_{n+1}F_{n+2})^{2}=F_{2n+3}^{2}.$$

이 공식에서 얻은 피타고라스 삼각형의 수열은 다음 변의 길이를 가집니다:

(3,4,5), (5,12,13), (16,30,34), (39,80,89), ...

각 이들 삼각형의 중간 변은 이전 삼각형의 세 변의 합입니다.

Generalizations

피타고라스 세-쌍의 개념을 일반화하기 위한 여러 방법이 있습니다.

Pythagorean n-tuple

See also: Pythagorean quadruple

다음 전개는

$\left(m_{1}^{2}-m_{2}^{2}-\ldots -m_{n}^{2}\right)^{2}+\sum _{k=2}^{n}(2m_{1}m_{k})^{2}=\left(m_{1}^{2}+\ldots +m_{n}^{2}\right)^{2}$

m²
₁ > m²
₂ + ... + m²
_n를 갖는 양의 정수 (m₁, ..., m_n)의 임의의 튜플에 대한 피타고라스 n-튜플입니다. 피타고라스의 n-튜플은 해당 값의 최대 공통 약수로 나눔으로써 원시적으로 만들 수 있습니다.

게다가, 임의의 원시 피타고라스 n-튜플 a²
₁ + ... + a²
_n = c²은 이 접근 방식을 통해 찾을 수 있습니다. (m₁, ..., m_n) = (c + a₁, a₂, ..., a_n)을 사용하여 위 공식으로 피타고라스 n-튜플을 얻고 최대 공통 약수, 2m₁ = 2(c + a₁)로 나눕니다. 이들 (m₁, ..., m_n) 값의 최대 공통 약수로 나누면 같은 원시 피타고라스 n-튜플을 제공합니다; 그리고 m²
₁ > m²
₂ + ... + m²
_n을 만족시키는 집합-별 서로소(setwise coprime) 양의 정수 (m₁, ..., m_n)의 튜플과 원시 피타고라스 n-튜플 사이에는 일대일 대응이 있습니다.

집합-별 서로소 값 ${\vec {m}}$과 원시 피타고라스 n-튜플 사이의 관계의 예제는 다음을 포함합니다:

${\begin{aligned}{\vec {m}}=(1)&\leftrightarrow 1^{2}=1^{2}\\{\vec {m}}=(2,1)&\leftrightarrow 3^{2}+4^{2}=5^{2}\\{\vec {m}}=(2,1,1)&\leftrightarrow 1^{2}+2^{2}+2^{2}=3^{2}\\{\vec {m}}=(3,1,1,1)&\leftrightarrow 1^{2}+1^{2}+1^{2}+1^{2}=2^{2}\\{\vec {m}}=(5,1,1,2,3)&\leftrightarrow 1^{2}+1^{2}+1^{2}+2^{2}+3^{2}=4^{2}\\{\vec {m}}=(4,1,1,1,1,2)&\leftrightarrow 1^{2}+1^{2}+1^{2}+1^{2}+1^{2}+2^{2}=3^{2}\\{\vec {m}}=(5,1,1,1,2,2,2)&\leftrightarrow 1^{2}+1^{2}+1^{2}+1^{2}+2^{2}+2^{2}+2^{2}=4^{2}\end{aligned}}$

Consecutive squares

m²으로 시작하는 k개의 연속 제곱의 합 F(k,m)은 다음 공식에 의해 제공되므로,

$F(k,m)=km(k-1+m)+{\frac {k(k-1)(2k-1)}{6}}$

F(k,m)이 제곱이 되도록 값 (k, m)을 찾을 수 있으며, 예를 들어 항의 숫자가 제곱 자체인 허쉬호른에 의한 것입니다:

$m={\tfrac {v^{4}-24v^{2}-25}{48}},\;k=v^{2},\;F(m,k)={\tfrac {v^{5}+47v}{48}}$

그리고 v ≥ 5는 2 또는 3으로 나눌 수 없는 임의의 정수입니다. 가장 작은 경우 v = 5, 따라서 k = 25에 대해, 이것은 잘-알려진 루카스(Lucas)의 포탄-쌓기 문제를 산출합니다:

$0^{2}+1^{2}+2^{2}+\dots +24^{2}=70^{2}$

이는 리치 격자(Leech lattice)와 관련된다는 사실입니다.

게다가, 피타고라스 n-튜플 (n ≥ 4)에서 하나를 제외하고 모든 더해지는 숫자(addends)가 연속적이면, 다음 방정식을 사용할 수 있습니다,

$F(k,m)+p^{2}=(p+1)^{2}$

p의 두 번째 거듭제곱이 상쇄되기 때문에, 이것은 $p={\tfrac {F(k,m)-1}{2}}$에 대해 오직 선형이고 쉽게 풀릴 수 있지만, k, m은 p가 정수가 되도록 선택되어야 하며, 작은 예제는 k = 5, m = 1일 때 다음을 산출합니다,

$1^{2}+2^{2}+3^{2}+4^{2}+5^{2}+27^{2}=28^{2}$

따라서, 피타고라스 n-튜플을 생성하는 한 가지 방법은 다양한 x에 대해 다음을 사용하는 것입니다,

$x^{2}+(x+1)^{2}+\cdots +(x+q)^{2}+p^{2}=(p+1)^{2},$

여기서 q = n–2이고,

$p={\frac {(q+1)x^{2}+q(q+1)x+{\frac {q(q+1)(2q+1)}{6}}-1}{2}}.$

Fermat's Last Theorem

Main article: Fermat's Last Theorem

피타고라스 세-쌍의 개념의 일반화는 어떤 2보다 엄격히 큰 n에 대해, aⁿ + bⁿ = cⁿ임을 만족하는 양의 정수 a, b, 및 c의 세-쌍을 찾는 것입니다. 1637년 피에르 드 페르마(Pierre de Fermat)는 그러한 세-쌍이 존재하지 않는다고 주장했으며, 페르마에 의한 어떤 다른 추측보다 입증되거나 반증되는 데 시간이 오래 걸리기 때문에 페르마의 마지막 정리(Fermat's Last Theorem)로 알려지게 된 주장입니다. 첫 번째 증명은 1994년 앤드루 와일스(Andrew Wiles)에 의해 제공되었습니다.

n − 1 or n nth powers summing to an nth power

Main article: Euler's sum of powers conjecture

또 다른 일반화는 마지막 항의 n-번째 거듭제곱이 이전 항의 n-번째 거듭제곱의 합인 n + 1개의 양의 정수 순서열을 검색하는 것입니다. n의 알려진 값에 대한 가장 작은 순서열은 다음과 같습니다:

• n = 3: {3, 4, 5; 6}.
• n = 4: {30, 120, 272, 315; 353}
• n = 5: {19, 43, 46, 47, 67; 72}
• n = 7: {127, 258, 266, 413, 430, 439, 525; 568}
• n = 8: {90, 223, 478, 524, 748, 1088, 1190, 1324; 1409}

$x^{3}+y^{3}+z^{3}=w^{3}$인 n = 3 경우에 대해, 페르마 삼차(Fermat cubic)라고 불리며, 모든 해를 제공하는 일반 공식이 존재합니다.

약간 다른 일반화를 통해 (k + 1) n-번째 거듭제곱의 합이 (n − k) n-번째의 합과 같게 됩니다. 예를 들어:

• (n = 3): 1³ + 12³ = 9³ + 10³, 숫자 1729는 두 개의 서로 다른 방법으로 두 세제곱의 합으로 표현할 수 있는 가장 작은 숫자라는 하디가 라마누젠(Ramanujan)과 나눈 대화를 회상하면서 유명해졌습니다.

역시 그것들의 n-번째 거듭제곱 합이 하나의 n-번째 거듭제곱인 n − 1 양의 정수가 존재할 수 있습니다 (페르마의 마지막 정리에 따르면, n = 3에 대해 그럴 수 없습니다); 이것들은 오일러의 거듭제곱의 합 추측(Euler's sum of powers conjecture)에 대한 반대예제입니다. 알려진 가장 작은 반대예제는 다음과 같습니다:

• n = 4: (95800, 217519, 414560; 422481)
• n = 5: (27, 84, 110, 133; 144)

Heronian triangle triples

Main article: Heronian triangle

헤론 삼각형(Heronian triangle)은 공통적으로 그것의 넓이도 정수인 정수 변을 갖는 삼각형으로 정의됩니다. 그러한 삼각형의 변의 길이는 a ≤ b ≤ c에 대해 헤론 세-쌍(Heronian triple) (a, b, c)를 형성합니다. 모든 각 피타고라스 세-쌍은 헤론 세-쌍인데, 왜냐하면 다리 a, b 중 적어도 하나는 피타고라스 세-쌍에서 짝수여야 하므로, 넓이 ab/2는 정수이기 때문입니다. 모든 각 헤론 세-쌍이 피타고라스 세-쌍인 것은 아니지만, 넓이 24를 갖는 예제 (4, 13, 15)가 보여줍니다.

만약 (a, b, c)가 헤론 세-쌍이면, (ka, kb, kc)도 마찬가지이며, 여기서 k는 임의의 양의 정수입니다; 그것의 넓이는 (a, b, c) 삼각형의 정수 넓이에 k²를 곱한 정수입니다. 헤론 세-쌍 (a, b, c)는 a, b, c가 집합-별 서로소(setwise coprime)라는 조건 아래에서 원시(primitive)입니다. (원시 피타고라스 세-쌍과 함께 그것들이 쌍-별 서로소라는 더 강한 명제도 적용되지만, 원시 헤론 삼각형과 함께 예를 들어 (7, 15, 20)에서 처럼 더 강한 명제가 항상 참인 것은 아닙니다.) 다음은 가장 단순한 원시 헤론 세-쌍이지만 피타고라스 세-쌍은 아닙니다:

(4, 13, 15) with area 24

(3, 25, 26) with area 36

(7, 15, 20) with area 42

(6, 25, 29) with area 60

(11, 13, 20) with area 66

(13, 14, 15) with area 84

(13, 20, 21) with area 126

헤론의 공식(Heron's formula)에 의해, a < b < c를 갖는 양의 정수 (a, b, c)의 세-쌍에 대해 헤론이 되기 위한 추가적인 조건은 다음과 같습니다.

(a² + b² + c²)² − 2(a⁴ + b⁴ + c⁴)

또는 동등하게

2(a²b² + a²c² + b²c²) − (a⁴ + b⁴ + c⁴)

16으로 나누어지는 비-영 완전 제곱이어야 합니다.

Application to cryptography

원시 피타고라스 세-쌍은 암호화에서 무작위 순서열과 키의 생성에 사용되어 왔습니다.

See also

• Boolean Pythagorean triples problem
• Congruum
• Diophantus II.VIII
• Eisenstein triple
• Euler brick
• Heronian triangle
• Hilbert's theorem 90
• Integer triangle
• Modular arithmetic
• Nonhypotenuse number
• Plimpton 322
• Pythagorean prime
• Pythagorean quadruple
• Quadric
• Tangent half-angle formula
• Trigonometric identity

References

• Alperin, Roger C. (2005), "The modular tree of Pythagoras" (PDF), American Mathematical Monthly, 112 (9): 807–816, CiteSeerX 10.1.1.112.3085, doi:10.2307/30037602, JSTOR 30037602, MR 2179860
• Berggren, B. (1934), "Pytagoreiska trianglar", Tidskrift för Elementär Matematik, Fysik och Kemi (in Swedish), 17: 129–139
• Barning, F.J.M. (1963), "Over pythagorese en bijna-pythagorese driehoeken en een generatieproces met behulp van unimodulaire matrices" (PDF), Math. Centrum Amsterdam Afd. Zuivere Wisk. (in Dutch), ZW-011: 37
• Eckert, Ernest (1992), "Primitive Pythagorean triples", The College Mathematics Journal, 23 (5): 413–417, doi:10.2307/2686417, JSTOR 2686417
• Elkies, Noam, Pythagorean triples and Hilbert's theorem 90 (PDF)
• Heath, Thomas (1956), The Thirteen Books of Euclid's Elements Vol. 1 (Books I and II) (2nd ed.), Dover Publications, ISBN 978-0-486-60088-8
• Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: D. C. Heath and Company, LCCN 77171950
• Martin, Artemas (1875), "Rational right angled triangles nearly isosceles", The Analyst, 3 (2): 47–50, doi:10.2307/2635906, JSTOR 2635906
• McCullough, Darryl (2005), "Height and excess of Pythagorean triples" (PDF), Mathematics Magazine, 78 (1): 26–44, doi:10.1080/0025570X.2005.11953298, S2CID 1701449
• Romik, Dan (2008), "The dynamics of Pythagorean triples" (PDF), Trans. Amer. Math. Soc., 360 (11): 6045–6064, arXiv:math.DS/0406512, doi:10.1090/S0002-9947-08-04467-X, MR 2425702
• Teigen, M.G.; Hadwin, D.W. (1971), "On Generating Pythagorean Triples", The American Mathematical Monthly, 78 (4): 378–379, doi:10.2307/2316903, JSTOR 2316903
• Trautman, Andrzej (1998), "Pythagorean spinors and Penrose twistors", in S.A. Hugget; L.J. Mason; K.P. Tod; S.T. Tsou; N.M.J. Woodhouse (eds.), Geometric universe (Postscript)

External links

• Clifford Algebras and Euclid's Parameterization of Pythagorean triples
• Curious Consequences of a Miscopied Quadratic
• Discussion of Properties of Pythagorean triples, Interactive Calculators, Puzzles and Problems
• Generating Pythagorean Triples Using Arithmetic Progressions
• "Pythagorean numbers", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Interactive Calculator for Pythagorean Triples
• The negative Pell equation and Pythagorean triples
• Parameterization of Pythagorean Triples by a single triple of polynomials
• Price, H. Lee (2008), The Pythagorean Tree: A New Species, arXiv:0809.4324
• Pythagorean Triples and the Unit Circle, chap. 2–3, in "A Friendly Introduction to Number Theory" by Joseph H. Silverman, 3rd ed., 2006, Pearson Prentice Hall, Upper Saddle River, NJ, ISBN 0-13-186137-9
• Pythagorean Triples at cut-the-knot Interactive Applet showing unit circle relationships to Pythagorean Triples
• Pythagorean Triplets
• The Remarkable Incircle of a Triangle
• Solutions to Quadratic Compatible Pairs in relation to Pythagorean Triples
• Theoretical properties of the Pythagorean Triples and connections to geometry
• The Trinary Tree(s) underlying Primitive Pythagorean Triples at cut-the-knot
• Weisstein, Eric W., "Pythagorean Triple", MathWorld