Smoothness

Original article: wikipedia:Smoothness

"C infinity" redirects here. For the extended complex plane $\mathbb {C} _{\infty }$, see Riemann sphere.

"C^n" redirects here. For $\mathbb {C} ^{n}$, see Complex coordinate space.

For smoothness in number theory, see smooth number.

A bump function is a smooth function with compact support.

수학적 해석학(mathematical analysis)에서, 함수(function)의 매끄러움(smoothness)은 그것이 일부 도메인에 걸쳐 가지는 연속(continuous) 도함수(derivatives)의 숫자에 의해 측정되는 속성입니다. 최소한, 만약 함수가 어디에서나 미분-가능이면 (따라서 연속이면), 그것은 "매끄러운" 것으로 여길 수 있습니다. 다른 끝에서, 그것은 그것의 도메인(domain) 안의 모든 차수(orders)의 도함수를 역시 보유할 수 있으며, 이 경우에서 그것은 무한하게 미분-가능(infinitely differentiable)으로 말해지고 C-무한 함수 (C-infinity function 또는 $C^{\infty }$ 함수)로 참조됩니다.

Differentiability classes

미분-가능성 클래스는 그들 도함수(derivative)의 속성에 따라 함수를 분류한 것입니다. 그것은 함수에 대해 존재하는 가장 높은 도함수의 차수의 측정입니다.

실수 직선(real line) 위에 열린 집합(open set)과 실수 값을 갖는 해당 집합 위에 정의된 함수 f를 생각해 보십시오. k를 비-음의 정수(integer)라고 놓습니다. 함수 f는 만약 도함수 f′, f″, ..., f^(k)가 존재하고 연속(continuous)이면 (미분가능성) 클래스 C^k라고 말합니다 (연속성은 f^(k)를 제외한 모든 도함수에 대해 미분가능성에 의해 암시됩니다). 함수 f는 만약 그것이 모든 차수의 도함수를 가지면 무한하게 미분-가능, 매끄러운, 또는 클래스 C^∞라고 말합니다. 함수 f는 만약 r가 매끄럽고 그리고 도메인에서 임의의 점 주변의 그것의 테일러 급수(Taylor series) 전개가 그 점의 어떤 이웃에서 함수로 수렴하면 클래스 C^ω, 또는 해석적(analytic)이라고 말합니다. C^ω는 따라서 C^∞에 엄격하게 포함됩니다. 혹 함수(Bump function)는 C^∞에서 함수의 예지이지만 C^ω에서 함수는 아닙니다.

다르게 말하면, 클래스 C⁰는 모든 연속 함수로 구성됩니다. 클래스 C¹은 그의 도함수가 연속인 모든 미분-가능 함수(differentiable function)로 구성됩니다; 그러한 함수는 연속적으로 미분-가능(continuously differentiable)이라고 불립니다. 따라서 C¹ 함수는 정확하게 그의 도함수가 존재하고 클래스 C⁰의 것인 함수입니다. 일반적으로 클래스 C^k는 C⁰를 모든 연속 함수의 집합으로 선언하고, 임의의 양의 정수 k에 대해 C^k를 그의 도함수가 C^k−1에 있는 모든 미분-가능 함수의 집합으로 선언함으로써 재귀적(recursively)으로 정의될 수 있습니다. 특히, C^k는 모든 각 k > 0에 대해 C^k−1에 포함되고, 이 포함이 엄격함 (C^k ⊊ C^k−1)을 보여주는 예제가 있습니다. 무한하게 미분-가능 함수의 클래스 C^∞는 k가 비-음의 정수에 걸쳐 변화할 때 클래스 C^k의 교집합입니다.

Examples

The C⁰ function f(x) = x for x ≥ 0 and 0 otherwise.

The function g(x) = x² sin(1/x) for x > 0.

The function $f:\mathbb {R} \to \mathbb {R}$ with $f(x)=x^{2}\sin \left({\tfrac {1}{x}}\right)$ for $x\neq 0$ and $f(0)=0$ is differentiable. However, this function is not continuously differentiable.

A smooth function that is not analytic.

다음 함수는

$f(x)={\begin{cases}x&{\mbox{if }}x\geq 0,\\0&{\text{if }}x<0\end{cases}}$

연속이지만, x = 0에서 미분-가능이 아니므로, 그것은 클래스 C⁰의 것이지만, 클래스 C¹의 것은 아닙니다.

다음 함수는

$g(x)={\begin{cases}x^{2}\sin {({\tfrac {1}{x}})}&{\text{if }}x\neq 0,\\0&{\text{if }}x=0\end{cases}}$

미분-가능이면, 도함수는 다음과 같습니다:

$g'(x)={\begin{cases}-{\mathord {\cos({\tfrac {1}{x}})}}+2x\sin({\tfrac {1}{x}})&{\text{if }}x\neq 0,\\0&{\text{if }}x=0.\end{cases}}$

$\cos(1/x)$는 x → 0일 때 진동하기 때문에, $g'(x)$는 영에서 연속이 아닙니다. 그러므로, $g(x)$는 미분-가능이지만 클래스 C¹의 것은 아닙니다. 게다가, 만약 우리가 이 예제에서 $g(x)=x^{4/3}\sin(1/x)$ (x ≠ 0)를 취하면, 미분-가능 함수의 도함수가 컴팩트 집합 위에 무경계일 수 있고, 따라서, 컴팩트 집합(compact set) 위의 미분-가능 함수가 지역적으로 립시츠 연속(Lipschitz continuous)이 아닐 수 있음을 보이는 것에 사용될 수 있습니다.

다음 함수는

$f(x)=|x|^{k+1}$,

여기서 k는 짝수이며, 연속이고 모든 x에서 k-번 미분가능입니다. 그러나 x = 0에서 그것들은 (k + 1)-번 미분가능이 아니므로, 그것들은 클래스 C^k의 것이지만 클래스 C^j의 것은 아니며 여기서 j > k입니다.

지수 함수(exponential function)는 해석적이고, 따라서 클래스 C^ω가 됩니다. 삼각 함수(trigonometric function)는 역시 그들이 정의되는 곳마다 해석적입니다.

혹 함수(bump function)는

$f(x)={\begin{cases}e^{-{\frac {1}{1-x^{2}}}}&{\text{ if }}|x|<1,\\0&{\text{ otherwise }}\end{cases}}$

매끄러우므로, 클래스 C^∞의 것이지만, 그것은 x = ±1에서 해석적이 아니고, 따라서 클래스 C^ω의 것이 아닙니다. 함수 f는 컴팩트 지원(compact support)을 갖는 매끄러운 함수의 하나의 예제입니다.

Multivariate differentiability classes

$\mathbb {R} ^{n}$의 열린 집합 $U$ 위에 정의된 함수 $f:U\subset \mathbb {R} ^{n}\to \mathbb {R}$은, 만약 모든 부분 도함수(partial derivatives)가

${\frac {\partial ^{\alpha }f}{\partial x_{1}^{\alpha _{1}}\,\partial x_{2}^{\alpha _{2}}\,\cdots \,\partial x_{n}^{\alpha _{n}}}}(y_{1},y_{2},\ldots ,y_{n})$

존재하고, 모든 각 $\alpha _{1},\alpha _{2},\ldots ,\alpha _{n}$ 비-음의 정수에 대해, $\alpha =\alpha _{1}+\alpha _{2}+\cdots +\alpha _{n}\leq k$, 및 모든 각 $(y_{1},y_{2},\ldots ,y_{n})\in U$를 만족하는 것에서 연속이면, 임의의 양의 정수 $k$에 대해, $U$에서 클래스 $C^{k}$의 것이라고 말합니다. 함수 $f$는 만약 그것이 $U$ 위에 연속이면 클래스 $C$ 또는 $C^{0}$의 것이라고 말합니다.

$\mathbb {R} ^{n}$의 열린 집합 $U$ 위에 정의된, 함수 $f:U\subset \mathbb {R} ^{n}\to \mathbb {R} ^{m}$는 만약 그것의 성분의 모두가

$f_{i}(x_{1},x_{2},\ldots ,x_{n})=(\pi _{i}\circ f)(x_{1},x_{2},\ldots ,x_{n})=\pi _{i}(f(x_{1},x_{2},\ldots ,x_{n})){\text{ for }}i=1,2,3,\ldots ,m$

클래스 $C^{k}$의 것이면, 양의 정수 $k$에 대해, $U$ 위에 클래스 $C^{k}$의 것이라고 말해지며, 여기서 $\pi _{i}$는 $\pi _{i}(x_{1},x_{2},\ldots ,x_{m})=x_{i}$에 의해 정의된 자연스러운 투영(projections) $\pi _{i}:\mathbb {R} ^{m}\to \mathbb {R}$입니다. 그것은 만약 그것이 연속이면, 또는 동등하게, 만약 모든 성분 $f_{i}$가 $U$ 위에 연속이면 클래스 $C$ 또는 $C^{0}$의 것이라고 말합니다.

The space of C^k functions

D를 실수 직선의 열린 부분집합으로 놓습니다. D 위에 정의된 모든 C^k 실수-값 함수의 집합은, 다음 반-노름(seminorm)의 셀-수-있는 가족과 함께, 프레셰 벡터 공간(Fréchet vector space)입니다:

$p_{K,m}=\sup _{x\in K}\left|f^{(m)}(x)\right|$

여기서 K는 그의 합집합(union)이 D인 컴팩트 집합(compact set)의 증가하는 수열에 걸쳐 변하고, m = 0, 1, ..., k입니다.

D에 걸쳐 C^∞ 함수의 집합은 역시 프레셰 공간을 형성합니다. 우리는, m이 모든 비-음의 정수 값에 걸쳐 변경하는 것을 제외하고, 위에서 처럼 같은 반-노름을 사용합니다.

위의 공간은 특정 순서의 도함수를 가지는 함수가 필요한 응용에서 자연스럽게 발생합니다; 어쨌든, 특히 부분 미분 방정식(partial differential equation)의 연구에서, 소볼레프 공간(Sobolev space)과 함께 대신 사용하는 것이 때때로 더 유익할 수 있습니다.

Parametric continuity

용어 매개변수 연속성 및 기하학적 연속성 (Gⁿ)은 브라이언 바르스키(Brian Barsky)에 의해 도입되었으며, 곡선의 매끄러움이, 매개변수가 곡선을 추적하는 것과 함께, 속력(speed)에 대한 제한을 제거함으로써 측정될 수 있음을 보이는 것입니다.

매개변수적 연속성(Parametric continuity)은 매개변수 곡선(parametric curve)에 적용되는 개념으로, 곡선을 따라 거리와 함께 매개변수 값의 매끄러움을 설명합니다.

Definition

(매개변수) 곡선 $s:[0,1]\to \mathbb {R} ^{n}$은, 만약 $\textstyle {\frac {d^{k}s}{dt^{k}}}$가 존재하고 $[0,1]$ 위에 연속이면 클래스 C^k의 것이라고 말해지며, 여기서 끝-점 $0,1\in [0,1]$에서 도함수는 한-쪽 도함수(one sided derivatives) (즉, 오른쪽에서 $0$에서, 그리고 왼쪽에서 $1$에서)로 취합니다.

이 개념의 실용적인 응용으로써, 시간의 매개변수를 갖는 대상의 움직임을 설명하는 곡선은–대상에 대해 유한한 가속도를 가지기 위해–C¹ 연속성을 가져야 합니다. 영화를 만드는 동안 카메라의 경로의 움직임과 같이, 더 부드러운 동작에 대해, 더 높은 차수의 매개변수 연속성이 요구됩니다.

Order of continuity

Two Bézier curve segments attached that is only C⁰ continuous

Two Bézier curve segments attached in such a way that they are C¹ continuous

매개변수 연속성의 다양한 차수는 다음과 같이 설명될 수 있습니다:

• C⁰: 곡선은 연속입니다.
• C¹: 일차 도함수는 연속입니다.
• C²: 일차와 이차 도함수는 연속입니다.
• Cⁿ: 일차에서 n차 도함수는 연속입니다.

Geometric continuity

Curves with G¹-contact (circles,line)

$(1-\varepsilon ^{2})x^{2}-2px+y^{2}=0,\ p>0\ ,\varepsilon \geq 0$
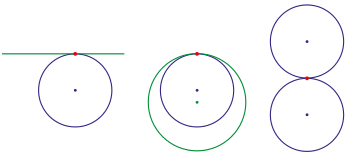
pencil of conic sections with G²-contact: p fix, $\varepsilon$ variable
($\varepsilon =0$: circle,$\varepsilon =0.8$: ellipse, $\varepsilon =1$: parabola, $\varepsilon =1.2$: hyperbola)

기하학적 또는 기하학 연속성의 개념은 주로 라이프니츠(Leibniz), 케플러(Kepler), 및 퐁슬레(Poncelet)와 같은 수학자에 의해 원뿔 단면(conic sections) (및 관련된 모양)에 적용되었습니다. 그 개념은, 대수학보다는 기하학을 통해, 매개변수 함수를 통해 표현된 것으로 연속성(continuity)의 개념을 설명하려는 초기 시도였습니다.

기하학적 연속성 뒤에 기본 아이디어는 다섯 원뿔 단면이 실제로 같은 모양의 다섯 가지 다른 버전이라는 것입니다. 타원(ellipse)은 이심률(eccentricity)이 영으로 가까워질 때 원(circle)으로 경향이고, 그것이 일에 가까워질 때 포물선(parabola)으로 경향입니다; 그리고 쌍곡선(hyperbola)은 이심률이 일을 향해 떨어질 때 포물선(parabola)으로 경향이 있습니다; 그것은 역시 직선(line)을 교차하는 경향일 수 있습니다. 따라서, 원뿔 단면 사이에 연속성이 있었습니다. 이들 아이디어는 다른 연속성의 개념으로 이어졌습니다. 예를 들어, 만약 원과 직선이 같은 모양의 두 표현이었으면, 아마도 직선은 무한 반지름(radius)의 원으로 생각될 수 있습니다. 이러한 경우에 대해, 우리는 점 $x=\infty$를 원 위의 점이 되도록 허용하고, $x=+\infty$ 및 $x=\neg \infty$에 대해 같은 것이 되도록 허용함으로써 직선을 닫히게 만들어야 합니다. 그러한 아이디어는 함수와 $\infty$의 연속성(continuity)의 현대의, 대수적으로 정의된, 아이디어를 만드는 데 유용했습니다 (자세한 것에 대해 투영적으로 확장된 실수 직선(projectively extended real line)을 참조하십시오).

Smoothness of curves and surfaces

곡선(curve) 또는 표면(surface)은 Gⁿ 연속성을 갖는 것으로 설명될 수 있으며, 여기서 n은 매끄러움의 증가하는 측정입니다. 곡선에서 한 점의 양쪽에 있는 선분을 생각해 보십시오:

• G⁰: 곡선은 결합 점에서 접합니다.
• G¹: 곡선은 결합 점에서 공통 접선(tangent) 방향을 역시 공유합니다.
• G²: 곡선은 결합 점에서 곡률의 공통 중심을 역시 공유합니다.

일반적으로, Gⁿ 연속성은 만약 그 곡선이 Gⁿ (매개변수) 연속성을 가지기 위해 다시-매개변수화될 수 있으면 존재합니다. 곡선의 재-매개변수화는 원래의 것과 기하학적으로 동일합니다; 오직 매개변수가 영향을 받습니다.

동등하게, 두 벡터 함수 f(t) 및 g(t)는 만약 f⁽ⁿ⁾(t) ≠ 0이고 스칼라 k > 0에 대해 f⁽ⁿ⁾(t) ≡ kg⁽ⁿ⁾(t)이면 (즉, 만약 두 벡터의 방향이 같지만, 크기는 그럴 필요가 없으면) Gⁿ 연속성을 가집니다.

곡선이 매끄럽게 보이기 위해 G¹ 연속성이 필요하다는 것이 분명할 수 있지만, 건축(architecture) 및 스포츠카(sports car) 디자인에서 추구하는 것과 같은 좋은 미학(aesthetics)을 위해서는, 더 높은 수준의 기하학적 연속성이 필요합니다. 예를 들어, 자체에 G² 연속성을 가지지 않으면, 차체의 굴절이 부드럽게 나타나지 않습니다.

(네 모서리에 90도 원호를 갖는) 둥근 직사각형(rounded rectangle)은 G¹ 연속성을 갖지만, G² 연속성을 가지지 않습니다. 같은 것은 가장자리에 구의 팔분체를 갖고 그것의 가장자리를 따라 사분체-원통을 갖는 둥근 정육면체(rounded cube)에 대해 참입니다. 만약 G² 연속성을 갖는 편집-가능한 곡선이 요구되면, 큐빅 스플라인(cubic splines)이 전형적으로 선택됩니다; 이들 곡선은 산업 디자인(industrial design)에서 자주 사용됩니다.

Other concepts

Relation to analyticity

모든 해석적 함수(analytic function)는 그것들이 해석되는 집합 위에서 "매끄러운" (즉, 모든 도함수 연속을 가짐) 것이지만, (위에서 언급된) 혹 함수(bump function)와 같은 예제는 그 전환이 실수 위에서 함수에 대해 참이 아님을 보여줍니다: 해석적이 아닌 매끄러운 실수 함수가 존재합니다. 임의의 점에서 매끄러운 것이지만 해석적이지 않은 함수의 간단한 예제는 푸리에 급수(Fourier series)를 수단으로 만들어질 수 있습니다; 또 다른 예제는 파비우스 함수(Jaap Fabius)입니다. 비록 그러한 함수가 규칙이라기 보다는 예외인 것처럼 보일 수 있지만, 해석적 함수가 매끄러운 함수 사이에 매우 얇게 흩어져 있는 것으로 밝혀졌습니다; 보다 엄격하게, 해석적 함수가 매끄러운 함수의 마른(meagre) 부분집합을 형성합니다. 게다가, 실수 직선의 모든 각 열린 부분집합 A에 대해, A 위에 해석적이고 다른 곳에서 그렇지 않은 매끄러운 함수가 존재합니다.

실수 직선에서 초월적 숫자(transcendental number)의 어디에나 존재하는 것의 상황과 그 상황을 비교하는 것이 유용합니다. 실수 직선과 매끄러운 함수의 집합 둘 다에서, 우리가 처음에 생각했던 예제 (대수적 숫자/유리수 및 해석적 함수)는 대부분의 경우보다 훨씬 더 잘 작동합니다: 초월적 숫자와 아무 데도 해석적 함수가 아닌 것이 완전한 측정을 가집니다. (그들의 여집합은 마른 것입니다).

이렇게 설명된 상황은 복소 미분-가능 함수와 뚜렷한 대조를 이룹니다. 만약 복소 함수가 열린 집합 위에 단지 한번 미분-가능이면, 해당 집합 위에 무한하게 미분-가능 및 해석적 둘 다입니다.

Smooth partitions of unity

주어진 닫힌 지원(support)과 함께 매끄러운 함수는 단위-구간의 매끄러운 분할(smooth partitions of unity)의 구성에서 사용됩니다 (단위-구간의 분할(partition of unity) 및 토폴로지 용어집(topology glossary)을 참조하십시오); 예를 들어, 리만 메트릭(Riemannian metric)이 그것들의 지역적 존재부터 시작하여 전역적으로 정의될 수 있음을 보여주기 위해, 이것들은 매끄러운 매니폴드(smooth manifold)의 연구에서 필수적입니다. 간단한 경우는 실수 직선 위의 혹 함수(bump function), 즉 구간 [a, b] 외부에서 값 0을 취하고 다음을 만족하는 매끄러운 함수 f의 경우입니다:

$f(x)>0\quad {\text{ for }}\quad a<x<b.\,$

직선 위에 여러 개의 겹치는 구간이 주어지면, 혹 함수는 그것들의 각각 위에, 및 전체 직선을 덮기 위해 반-무한 구간 (−∞, c] 및 [d, +∞) 위에, 함수의 합은 항상 1을 만족하도록 구성될 수 있습니다.

방금 말한 것에서, 단위-구간의 분할은 정칙 함수(holomorphic function)에 적용되지 않습니다; 존재와 해석적 연속(analytic continuation)에 상대적인 그것들의 다른 행동은 뭉치(sheaf) 이론의 뿌리 중 하나입니다. 대조적으로, 매끄러운 함수의 뭉치는 많은 토폴로지적 정보를 전달하지 않는 경향이 있습니다.

Smooth functions on and between manifolds

매끄러운 매니폴드(smooth manifold) $M$, 차원 m이, 아틀라스 ${\mathfrak {U}}=\{(U_{\alpha },\phi _{\alpha })\}_{\alpha }$와 함께 주어지면, 맵 $f:M\to \mathbb {R}$이 만약 모든 $p\in M$에 대해, $(\phi ^{-1})^{*}f=f\circ \phi ^{-1}:\phi (U)\to \mathbb {R}$로 표시된, $\phi ^{-1}$에 의해 $f$의 당김은 $\phi (p)$의 이웃에서 $\mathbb {R} ^{m}$에서 $\mathbb {R}$로의 함수로 매끄러운 것이면 M 위에 매끄러운 것입니다 (주어진 차수까지 모든 부분 도함수가 연속입니다). 매끄러움은 아틀라스(atlas)에서 p에 대한 임의의 선호된 차트(chart)에 관해 점검될 수 있는데, 왜냐하면 차트 사이의 전환 함수에 대한 매끄러움 요구 사항은 만약 $f$가 한 차트에서 p에 대해 매끄러운 것이면 아틀라스의 임의의 다른 차트에서 p에 대한 매끄러운 것일 수 있음을 보장하기 때문임을 주목하십시오. 만약 대신 $F:M\to N$가 $M$에서 n-차원 매니폴드 $N$으로의 맵이면, F가 만약, 모든 각 p ∈ M에 대해, $\psi \circ F\circ \phi ^{-1}:\phi (U)\to \psi (V)$가 R^m에서 Rⁿ으로의 함수로 매끄러운 것을 만족하는 $M$에서 p에 대한 차트 $(U,\phi )$와 $F(U)\subset V$을 갖는 $N$에서 $F(p)$에 대한 차트 $(V,\psi )$가 있으면, 매끄러운 것입니다.

매니폴드 사이의 매끄러운 맵은 접 공간(tangent spaces) 사이의 선형 맵을 유도합니다: $F:M\to N$에 대해, 각 점에서 밂(pushforward) (또는 미분)은 p에서 접 벡터를 F(p): $F_{*,p}:T_{p}M\to T_{F(p)}N$에서 접 벡터로 매핑하고, 접 다발(tangent bundle)의 수준에서, 밂은 벡터 다발 준동형(vector bundle homomorphism): $F_{*}:TM\to TN$입니다. 밂에 대한 이중은 당김이며, 이것은 $N$에 대한 코벡터에서 $M$에 대한 코벡터로 돌아가게, k-형식을 k-형식: $F^{*}:\Omega ^{k}(N)\to \Omega ^{k}(M)$으로 "당깁니다". 이 방법에서 매니폴드 사이의 매끄러운 함수는 벡터 필드(vector fields)와 미분 형식(differential forms)과 같은 지역적 데이터(local data)를 한 매니폴드에서 또 다른 매니폴드로, 또는 적분화(integration)와 같은 계산이 잘 이해되는 유클리드 공간 아래로 전송할 수 있습니다.

매끄러운 함수에 따른 이전-이미지와 밂은, 일반적으로, 추가적인 가정없이 매니폴드가 아닙니다. 정규 점의 이전-이미지 (즉, 만약 미분이 이전-이미지에서 사라지지 않으면)는 매니폴드입니다; 이것이 이전-이미지 정리(preimage theorem)입니다. 유사하게, 삽입을 따라 밂은 매니폴드입니다.

Smooth functions between subsets of manifolds

임의적인 매니폴드의 부분집합에 대해 매끄러운 맵(smooth map)의 대응하는 개념이 있습니다. 만약 f : X → Y가 그것의 도메인(domain)과 치역(range)이 각각 X ⊂ M 및 Y ⊂ N 매니폴드의 부분집합인 함수(function)이면, f는 만약 모든 p ∈ U ∩ X에 대해 F(p) = f(p)를 만족하는 모든 x ∈ X에 대해 x ∈ U를 갖는 열린 집합 U ⊂ M과 매끄러운 함수 F : U → N가 있으면 매끄러운 것이라고 말합니다.

See also

• Non-analytic smooth function
• Quasi-analytic function
• Singularity (mathematics)
• Sinuosity
• Smooth scheme
• Smooth number (number theory)
• Smoothing
• Spline