Surface (topology)

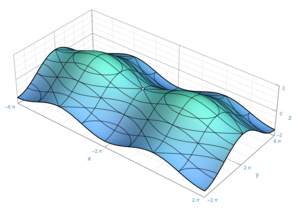
토폴로지(topology)라고 참조되는 수학의 부분에서, 표면(surface)은 이-차원 매니폴드(manifold)입니다. 일부 표면은 삼-차원 고체의 경계(boundaries)로 나타납니다; 예를 들어 구는 고체 공의 경계입니다. 다른 표면은 두 변수의 함수(functions)의 그래프로 나타납니다; 오른쪽 그림을 참조하십시오. 어쨌든, 표면은 임의의 주변 공간에 대한 참조 없이 추상적으로 정의될 수도 있습니다. 예를 들어, 클라인 병(Klein bottle)은 삼-차원 유클리드 공간(Euclidean space)에 삽입될 수 없는 표면입니다.

토폴로지적 표면은 때때로 미분 기하학(differential geometry)과 복소 해석학(complex analysis)과 같은 수학 내의 다른 분야에 그것들을 연결하는 리만 메트릭(Riemannian metric) 또는 복소 구조와 같은 추가 정보를 갖추게 됩니다. 표면의 다양한 수학적 개념은 물리적 세계에서 표면(surfaces)을 모델링하기 위해 사용될 수 있습니다.

In general

수학(mathematics)에서, 표면(surface)은 변형된 평면(plane)과 닮은 기하학적 모양입니다. 가장 친숙한 예제는 구(spheres)와 같은 보통의 삼-차원 유클리드 공간(Euclidean space) R³에서 고체 대상의 경계로 발생합니다. 표면의 정확한 정의는 상황에 의존할 수 있습니다. 전형적으로, 대수적 기하학(algebraic geometry)에서, 표면이 자체적으로 교차할 수 있고 (및 다른 특이점(singularities)을 가질 수 있음), 반면에 토폴로지와 미분 기하학(differential geometry)에서, 그것은 교차하지 않을 수 있습니다.

표면은 이-차원 공간(two-dimensional space)입니다; 이것은 표면 위에 움직이는 점이 두 방향에서 움직일 수 있음을 의미합니다 (그것은 2 자유도(degrees of freedom)를 가집니다). 다시 말해서, 거의 모든 지점 주변에는, 이-차원 좌표 시스템(coordinate system)이 정의된 좌표 패치(coordinate patch)가 있습니다. 예를 들어, 지구의 표면은 (이상적으로는) 이-차원 구(sphere)와 유사하고, 위도(latitude)와 경도(longitude)는 그것 위에 이-차원 좌표를 제공합니다 (극과 180도 자오선(180th meridian)을 따르는 것은 제외합니다).

표면의 개념은 주로 물리적 물체의 표면을 나타내는 데 물리학(physics), 공학(engineering), 컴퓨터 그래픽(computer graphics), 및 여러 기타 분야에서 널리 사용됩니다. 예를 들어, 비행기의 공기역학적(aerodynamic) 속성을 분석하는 데, 중심적인 고려 사항은 그 표면을 따라 흐르는 공기의 흐름입니다.

Definitions and first examples

(토폴로지적) 표면은 모든 각 점이 유클리드 평면 E²의 일부 열린 부분-집합(open subset)에 위상-동형적(homeomorphic) 열린 이웃(neighbourhood)을 가지는 토폴로지적 공간(topological space)입니다. 대응하는 위상-동형과 함께 그러한 이웃은 (좌표) 차트로 알려져 있습니다. 이웃이 유클리드 평면 위의 표준 좌표를 상속받는 것은 이 차트를 통해서 이루어집니다. 이들 좌표는 지역적 좌표(local coordinates)로 알려져 있고 이들 위상-동형은 표면을 지역적으로 유클리드(locally Euclidean)인 것으로 설명하도록 유도합니다.

그 주제에 대한 대부분의 저서에서, 표면은 토폴로지적 공간으로서 역시 비-빈, 두 번째-셀-수-있고, 하우스도르프라고 명시적으로 또는 암시적으로 가정하는 경우가 많습니다. 역시 고려 중인 표면이 연결된 것으로 종종 가정됩니다.

이 기사의 나머지 부분은 달리 지정하지 않은 한 표면이 비-빈, 하우스도르프, 두 번째-셀-수-있고, 연결된 것이라고 가정할 것입니다.

더 일반적으로, 경계를 갖는 (토폴로지적) 표면은 모든 각 점이 C에서 위쪽 절반-평면 H²의 클로저의 일부 열린 부분-집합으로 위상-동형적 열린 이웃(neighbourhood)을 가지는 하우스도르프 토폴로지적 공간입니다. 이들 위상-동형은 (좌표) 차트로도 알려져 있습니다. 위쪽 절반-평면의 경계는 x-축입니다. 차트를 통해 x-축에 매핑된 표면 위의 점은 경계 점(boundary point)이라고 이름-짓습니다. 그러한 점들의 모음은 필연적으로 일-매니폴드, 즉, 닫힌 곡선의 합집합인 표면의 경계(boundary)로 알려져 있습니다. 다른 한편으로, x-축 위쪽에 매핑된 점은 내부 점(interior point)입니다. 내부 점의 모음은 항상 비-빈(empty) 것인 표면의 내부(interior)입니다. 닫힌 디스크는 경계를 갖는 표면의 간단한 예제입니다. 디스크의 경계는 원입니다.

자격 부여 없이 사용되는 표면이라는 용어는 경계 없는 표면을 참조합니다. 특히, 빈 경계를 갖는 표면은 보통의 의미에서 표면입니다. 컴팩트한 빈 경계를 갖는 표면은 '닫힌' 표면이라고 알려져 있습니다. 이-차원 구, 이-차원 토러스(torus), 및 실수 투영 평면(real projective plane)은 닫힌 표면의 예제입니다.

뫼비우스 띠(Möbius strip)는 시계 방향과 반시계 방향 사이의 구별이 지역적으로 정의될 수 있지만, 전체적으로는 정의될 수 없는 표면입니다. 일반적으로, 표면이 만약 뫼비우스 띠의 위상-동형적 사본을 포함하지 않으면 방향-가능(orientable)이라고 말합니다; 직관적으로, 그것은 두 개의 구별되는 "측면"을 가집니다. 예를 들어, 구와 토러스는 방향-가능이고, 반면에 실수 투영 평면은 그렇지 않습니다 (왜냐하면 한 점이 제거된 실수 투영 평면은 열린 뫼비우스 띠로의 위상-동형적이기 때문입니다).

미분 기하학(differential geometry)과 대수적 기하학(algebraic geometry)에서, 여분의 구조가 표면의 토폴로지 위에 더합니다. 이렇게 더해진 구조는 매끄러움 구조 (표면에서 및 표면으로의 미분-가능 맵을 정의할 수 있게 함), 리만 메트릭 (표면 위에 길이와 각도를 정의할 수 있게 함), 복소 구조 (표면으로 및 표면으로의 정칙 맵을 정의할 수 있게 함—이 경우에서 표면은 리만 표면이라고 함), 또는 대수적 구조 (놓여있는 토폴로지의 관점에서만 설명될 수 없는 자체-교차점과 첨점과 같은 특이점(singularities)을 감지할 수 있게 함)가 될 수 있습니다.

Extrinsically defined surfaces and embeddings

역사적으로, 표면은 처음에 유클리드 공간의 부분-공간으로 정의되었습니다. 종종, 이들 표면은 특정 함수, 보통 다항 함수의 영(zeros)의 자취(locus)였습니다. 그러한 정의는 표면을 더 큰 (유클리드) 공간의 일부로 고려했고, 이를테면 외부적(extrinsic)이라고 이름-지었습니다.

이전 섹션에서, 표면은 특정 속성, 즉 하우스도르프와 지역적 유클리드를 갖는 토폴로지적 공간으로 정의됩니다. 이 토폴로지적 공간은 또 다른 공간의 부분-공간으로 고려되지 않습니다. 이런 의미에서, 현재 수학자들이 사용하는 정의인 위에서 주어진 정의는 본질적(intrinsic)입니다.

본질적으로 정의된 표면은 유클리드 공간의 부분-공간이라는 더해진 제약 조건을 만족시키는 것을 요구하지 않습니다. 본질적으로 정의된 일부 표면은 외부적 의미에서 표면이 아닌 것으로 보일 수 있습니다. 어쨌든, 휘트니 삽입 정리(Whitney embedding theorems)는 모든 각 표면이 사실상 유클리드 공간, 사실상 E⁴에 위상-동형적으로 삽입될 수 있다고 주장합니다: 외부적 접근과 본질적 접근은 동등한 것으로 판명되었습니다.

실제로, 방향-가능이거나 경계를 가지는 임의의 컴팩트 표면은 E³에 삽입될 수 있습니다; 다른 한편으로, 컴팩트, 비-방향-가능이고 경계 없는 실수 투영 평면은 E³에 삽입될 수 없습니다 (Gramain 참조). Boy's surface, Roman surface, 및 cross-cap을 포함한 Steiner surfaces는 E³에서 실수 투영 평면의 모델이지만, Boy 표면만이 잠긴 표면(immersed surface)입니다. 모든 이들 모델은 그것들이 자체와 교차하는 점에서 특이적입니다.

알렉산더 뿔-달린 구(Alexander horned sphere)는 2-구를 3-구로의 잘 알려진 병리적(pathological) 삽입입니다.

또 다른 공간으로 표면의 (어떤 것이라도 있다면) 선택된 삽입은 외부적 정보로 고려됩니다; 그것은 표면 자체에 필수적인 것은 아닙니다. 예를 들어, 토러스는 "표준" 방식 (이는 베이글(bagel)처럼 보임) 또는 매듭진 방식 (그림 참조)으로 E³에 삽입될 수 있습니다. 두 개의 삽입된 토러스는 위상-동형적이지만, 동위적(isotopic)은 아닙니다: 그것들은 토폴로지적으로 동등하지만, 그것들은 삽입은 그렇지 않습니다.

R²에서 더 높은 차원 Rⁿ까지의 연속, 단사 함수의 이미지(image)는 매개변수 표면(parametric surface)이라고 말합니다. 그러한 이미지는 도메인 R²의 x-방향과 y-방향이 이미지를 매개변수화하는 2개의 변수이기 때문에 그렇게 불립니다. 매개변수 표면은 토폴로지적 표면일 필요가 없습니다. 회전의 표면(surface of revolution)은 특별한 종류의 매개변수 표면으로 볼 수 있습니다.

만약 f가 그것의 그래디언트가 어디에서도 영이 아닌 R³에서 R로의 매끄러운 함수이면, f의 영들(zeros)의 자취(locus)은 암시적 표면(implicit surface)으로 알려진 표면을 정의합니다. 만약 비-사라지는 그래디언트의 조건이 버려지면, 영 자취는 특이점을 나타낼 수 있습니다.

Construction from polygons

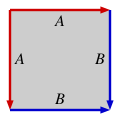
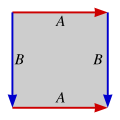
각각의 닫힌 표면은 가장자리를 쌍-별로 식별함으로써 표면의 기본 다각형(fundamental polygon)이라고 불리는 짝수의 면을 갖는 방향화된 다각형으로 구성될 수 있습니다. 예를 들어, 아래의 각 다각형에서, 일치하는 레이블 (A와 A, B와 B)를 갖는 면을 부착하여, 화살표가 같은 방향을 가리키도록 하면 표시된 표면을 생성합니다.

임의의 기본 다각형은 다음과 같이 기호적으로 작성될 수 있습니다. 임의의 꼭짓점에서 시작하고, 시작하는 꼭짓점으로 돌아갈 때까지 어느 방향으로든 다각형의 주변을 따라 진행합니다. 이 순회 동안, 가장자리가 순회 방향과 반대이면 지수에 -1을 갖는 각 가장자리의 레이블을 순서대로 기록합니다. 위의 네 가지 모델은, 위의 왼쪽에서 시작하여 시계 방향으로 횡단할 때, 다음을 산출합니다:

구: $ABB^{-1}A^{-1}$
실수 투영 평면: $ABAB$
토러스: $ABA^{-1}B^{-1}$
클라인 병: $ABAB^{-1}$ .

구와 투영 평면은 둘 다 2-각형의 몫으로 실현될 수 있고, 반면에 토러스와 클라인 병은 4-각형 (정사각형)을 요구함을 주목하십시오.

따라서 표면의 기본 다각형에서 유도된 표현은 다각형 가장자리 레이블을 생성기로 갖는 표면의 기본 그룹(fundamental group)의 표시(presentation)에서 단 하나의 관계인 것으로 밝혀졌습니다. 이것은 자이페르트-판 캄펀 정리(Seifert–van Kampen theorem)의 결과입니다.

다각형의 가장자리를 붙이는 것은 특별한 종류의 몫 공간(quotient space) 과정입니다. 몫 개념은 표면의 새로운 또는 대안적인 구성을 생성하기 위해 더 큰 일반성에서 적용될 수 있습니다. 예를 들어, 실수 투영 평면은 구 위에 반대편 모든 쌍의 점을 식별함으로써 구의 몫으로 얻을 수 있습니다. 몫의 또 다른 예제는 연결된 합입니다.

Connected sums

두 표면 M과 N의 연결된 합(connected sum)은, M # N으로 표시되며, 그것들의 각각에서 디스크를 제거하고 해당 결과 경계 구성 요소를 따라 접착함으로써 얻습니다. 디스크의 경계는 원이므로, 이들 경계 구성 요소는 원입니다. M # N의 오일러 특성(Euler characteristic) $\chi$ 는 피합수의 오일러 특성에서 2를 뺀 값의 합입니다:

\chi (M\mathbin {\#} N)=\chi (M)+\chi (N)-2.\,

구 S는 연결된 합에 대한 항등 원소(identity element)이며, S # M = M임을 의미합니다. 이것은 구에서 디스크를 삭제하면 디스크를 남기고, 접착 시 M에서 삭제된 디스크를 간단히 대체하기 때문입니다.

토러스 T와의 연결된 합계는 다른 피합수 M에 "핸들"을 부착하는 것으로도 설명됩니다. 만약 M이 방향-가능이면, T # M도 마찬가지입니다. 연결된 합은 결합적이므로, 표면의 유한 모음의 연결된 합은 잘-정의됩니다.

두 실수 투영 평면 P # P의 연결된 합은 클라인 병(Klein bottle) K입니다. 실수 투영 평면과 클라인 병의 연결된 합은 실수 투영 평면과 토러스의 연결된 합과 위상-동형적입니다; 형식에서, P # K = P # T입니다. 따라서, 세 개의 실수 투영 평면의 연결된 합은 토러스를 갖는 실수 투영 평면의 연결된 합과 위상-동형적입니다. 실수 투영 평면을 포함하는 임의의 연결된 합은 비-방향가능입니다.

Closed surfaces

닫힌 표면은 컴팩트(compact)이고 경계(boundary) 없는 표면입니다. 닫힌 표면의 예제는 구(sphere), 토러스(torus), 및 클라인 병(Klein bottle)을 포함합니다. 비-닫힌 표면의 예제는 열린 디스크 (구멍(puncture)을 갖는 구), 원기둥 (두 개의 구멍을 갖는 구), 및 뫼비우스 띠를 포함합니다.

삼-차원 공간(three-dimensional space)에 삽입된 표면이 닫혀 있는 것과 그것이 고체의 경계인 것은 필요충분 조건입니다. 임의의 닫힌 매니폴드(closed manifold)와 마찬가지로, 상속된 유클리드 토폴로지(Euclidean topology)에 관해 닫힌 유클리드 공간에 삽입된 표면이 반드시 닫힌 표면인 것은 아닙니다; 예를 들어, 경계를 포함하는 $\mathbb {R} ^{3}$ 에 삽입된 디스크는 토폴로지적으로 닫혀 있지만 닫힌 표면은 아닙니다.

Classification of closed surfaces

Some examples of orientable closed surfaces (left) and surfaces with boundary (right). Left: Some orientable closed surfaces are the surface of a sphere, the surface of a torus, and the surface of a cube. (The cube and the sphere are topologically equivalent to each other.) Right: Some surfaces with boundary are the disk surface, square surface, and hemisphere surface. The boundaries are shown in red. All three of these are topologically equivalent to each other.

닫힌 표면의 분류 정리는 임의의 연결된(connected) 닫힌 표면이 다음 세 가족 중 하나의 일부 구성원과 위상-동형적임을 나타냅니다:

구(sphere),
g ≥ 1에 대해 g 토러스의 연결된 합(connected sum),
k ≥ 1에 대해 k 실수 투영 평면(projective planes)의 연결된 합.

처음 두 가족에 있는 표면은 방향-가능(orientable)입니다. 구를 0 토러스의 연결된 합으로 고려함으로써 두 가족을 결합하는 것이 편리합니다. 관련된 토러스의 숫자 g는 표면의 속(genus)이라고 불립니다. 구와 토러스는 각각 오일러 특성 2와 0을 가지고, 일반적으로 g 토러스의 연결된 합의 오일러 특성은 2 − 2g입니다.

세 번째 가족에 있는 표면은 비-방향가능입니다. 실수 투영 평면의 오일러 특성은 1이고, 일반적으로 이것들의 k의 연결된 합의 오일러 특성은 2 − k입니다.

닫힌 표면은 두 가지 정보: 그것의 오일러 특성과 그것이 방향-가능인지 여부에 따라, 위상-동형까지, 결정됨을 따릅니다. 다시 말해서, 오일러 특성과 방향가능성은 닫힌 곡면을 위상-동형성까지 완전하게 분류합니다.

여러 개의 연결된 구성 요소(connected components)를 갖는 닫힌 표면은 각 연결 구성 요소의 클래스에 의해 분류되고, 따라서 일반적으로 표면이 연결되어 있다고 가정합니다.

Monoid structure

이 분류를 연결된 합과 연관시키면, 임의의 고정된 차원의 매니폴드가 실제로 그러하듯이, 위상-동형까지 닫힌 표면은 연결된 합의 연산 아래에서 교환적(commutative) 모노이드(monoid)를 형성합니다. 항등원은 구이고, 반면에 실수 투영 평면과 토러스는 단일 관계 P # P # P = P # T를 갖는 이 모노이드를 생성하며, 이는 K = P # P이기 때문에 P # K = P # T로 쓸 수도 있습니다. 이 관계는 때때로 (Dyck 1888)에서 그것을 입증했던 발터 폰 뒤크(Walther von Dyck)의 이름을 따서 뒤크의 정리로 알려져 있고, 삼중 교차 곡면 P # P # P는 그것에 따라서 뒤크의 표면이라고 불립니다.

기하학적으로, 토러스를 갖는 연결-합 (# T)은 양 끝을 표면의 같은 쪽에 부착된 핸들을 더하고, 반면에 클라인 병을 갖는 연결-합 (# K)은 두 끝을 방향-가능 표면의 반대쪽에 부착된 핸들을 추가합니다; 투영 평면의 존재 (# P)에서, 표면은 방향-가능이 아니므로 (측면의 개념이 없음), 토러스를 부착하는 것과 클라인 병을 부착하는 것 사이에는 차이가 없으며, 이는 관계를 설명합니다.

Proof

닫힌 표면의 분류는 1860년대부터 알려져 왔고,^[1] 오늘날 많은 증명이 존재합니다.

토포로지적 및 조합적 증명은 일반적으로 모든 각 컴팩트 2-매니폴드가 단순 복합체(simplicial complex)에 대한 위상-동형적이라는 어려운 결과에 의존하며, 이는 그 자체로 흥미로운 것입니다. 분류의 가장 공통적인 증명은 (Seifert & Threlfall 1934)이며,^[1] 이는 모든 삼각분할된 표면을 표준 형식으로 가져옵니다. 표준 형식을 피하는 단순화된 증명은 1992년경 존 콘웨이(John H. Conway)에 의해 발견되었으며, 그는 이를 "Zero Irrelevancy Proof" 또는 "ZIP 증명"이라고 불렀고 (Francis & Weeks 1999)에 제시되었습니다.

더 강력한 기하학적 결과를 산출하는 기하학적 증명은 균등화 정리(uniformization theorem)입니다. 이것은 원래 펠릭스 클라인(Felix Klein), 파울 쾨베(Paul Koebe), 및 앙리 푸앵카레(Henri Poincaré)에 의해 1880년대와 1900년대에 리만 표면에 대해서만 입증되었습니다.

Surfaces with boundary

아마도 경계를 갖는 컴팩트(Compact) 표면은 한정된 수의 구멍 (제거된 열린 디스크)을 갖는 간단히 닫힌 표면입니다. 따라서, 연결된 컴팩트 표면은 경계 구성 요소의 수와 대응하는 닫힌 표면의 속 (genus)에 의해 – 동등하게, 경계 구성 요소의 수, 방향가능성, 및 오일러 특성에 의해 분류됩니다. 컴팩트 표면의 속은 대응하는 닫힌 표면의 속으로 정의됩니다.

이러한 분류는 닫힌 표면의 분류에서 거의 즉시 따릅니다: 닫힌 표면에서 열린 디스크를 제거하면 경계 구성 요소에 대한 원을 갖는 컴팩트 표면을 산출하고, k 개의 열린 디스크를 제거하면 경계 구성 요소에 대해 k 개의 서로소 원을 갖는 컴팩트 표면을 생성합니다. 구멍의 정확한 위치는 관련이 없는데, 왜냐하면 위상-동형 그룹은 적어도 2 차원의 임의의 연결된 매니폴드 위에 k-전이적(k-transitively)으로 작용하기 때문입니다.

반대로, 컴팩트 곡면의 경계는 닫힌 1-매니폴드이고, 따라서 유한한 수의 원의 서로소 합집합입니다; 이들 원을 디스크로 채우면 (형식적으로, 원뿔을 취함) 닫힌 표면을 산출합니다.

속 g 및 k 경계 구성 요소를 갖는 고유한 컴팩트 방향-가능 표면은, 예를 들어 매핑 클래스 그룹(mapping class group)의 연구에서, 종종 $\Sigma _{g,k}$ 로 표시됩니다.

Non-compact surfaces

비-컴팩트 표면은 분류하기가 더 어렵습니다. 간단한 예제로, 비-컴팩트 표면은 닫힌 매니폴드에 (유한한 점의 집합을 제거하는) 구멍냄으로써 얻을 수 있습니다. 다른 한편으로, 컴팩트 표면의 임의의 열린 부분집합은 그 자체로 비-컴팩트 표면입니다; 예를 들어, 구에 있는 칸토어 집합(Cantor set)의 여집합을 생각해 보십시오, 달리 칸토어 트리 표면(Cantor tree surface)이라고 알려져 있습니다. 어쨌든, 모든 각 비-컴팩트 표면이 컴팩트 표면의 부분집합인 것은 아닙니다; 두 가지 정식의 반대-예제는 야곱의 사다리(Jacob's ladder)와 네스호 괴물(Loch Ness monster)이며, 이것들은 무한 지너스(genus)를 갖는 비-컴팩트 표면입니다.

비-컴팩트 표면 M은 비-빈 끝의 공간 E(M)을 가지며, 이는 비공식적으로 말하자면 표면이 "무한대로 가 버리는(go off to infinity)" 방법을 설명합니다. 공간 E(M)은 항상 칸토어 집합(Cantor set)의 닫힌 부분공간과 토폴로지적으로 동등합니다. M은 핸들의 유한하거나 셀-수-있는 무한한 숫자 N_h를 가질 수 있고, 마찬가지로 투영 평면(projective planes)의 유한하거나 셀-수-있는 무한한 숫자 N_p를 가질 수 있습니다. 만약 N_h와 N_p가 모두 유한하면, 이들 두 숫자와 끝 공간의 토폴로지적 유형은 표면 M을 토폴로지적 동등성까지 분류합니다. 만약 N_h와 N_p 중 하나 또는 둘 모두가 무한이면, M의 토폴로지적 유형은 이들 두 숫자뿐만 아니라 무한한 숫자(들)가 끝 공간에 어떻게 접근하는지에 따라 달라집니다. 일반적으로 M의 토폴로지적 유형은 무한하게 많은 핸들과 무한하게 많은 투영 평면의 극한 점, 핸들만 있는 극한 점, 투영 평면만 있는 극한 점, 및 둘 다 없는 극한 점인 E(M)의 네 부분공간에 의해 결정됩니다.^[2]

Assumption of second-countability

만약 표면의 정의에서 두-번째-셈가능성의 가정을 제거하면, 그것들 토폴로지에 대해 셀-수-있는 기저를 가지지 않는 (반드시 비-컴팩트) 토폴로지적 표면이 존재합니다. 아마도 가장 간단한 예제는 실수의 공간을 갖는 긴 직선(long line)의 데카르트 곱입니다.

그것의 토폴로지에 대해 셀-수-있는 기저를 가지지 앉지만, 그 존재를 입증하기 위해 선택의 공리를 요구하지 않은 또 다른 표면은 실수-해석적(real-analytic) 표면임을 보여주는 간단한 방정식에 의해 설명될 수 있는 프뤼퍼 매니폴드(Prüfer manifold)입니다. 프뤼퍼 매니폴드는 각 실수 x에 대해 점 (x,0) 바로 아래에 매달려 있는 하나의 추가 "혀" T_x를 갖는 위쪽 절반 평면으로 생각될 수 있습니다.

1925년에, 티보르 라도(Tibor Radó)는 모든 리만 표면 (즉, 일-차원 복소 매니폴드)이 반드시 두-번째-셀-수-있음을 입증했습니다 (라도의 정리). 대조적으로, 만약 프뤼퍼 표면 구성에서 실수를 복소수로 대체하면, 셀-수-있는 기저를 가지지 않는 이-차원 복소 매니폴드 (이는 반드시 사-차원 실수 매니폴드임)를 얻습니다.

Surfaces in geometry

정육면체(cube)의 경계와 같은 다면체(Polyhedra)는 기하학에서 만나는 첫 번째 표면 중 하나입니다. 역시 매끄러운 표면을 정의하는 것도 가능하며, 이것에서 각 점은 E²에서 일부 열린 집합에 미분-동형적(diffeomorphic)인 이웃을 가집니다. 이러한 정교함을 통해 미적분(calculus)을 표면에 적용하여 많은 결과를 입증할 수 있습니다.

두 개의 매끄러운 표면이 미분-동형적인 것과 그것들이 위상-동형적인 것은 필요충분 조건입니다. (유사한 결과는 더 높은 차원의 매니폴드에는 유지되지 않습니다.) 따라서 닫힌 표면(closed surfaces)은 그것들의 오일러 특성과 방향-가능성에 의해 미분-동형(diffeomorphism)까지 분류됩니다.

리만 메트릭을 갖춘 매끄러운 표면은 미분 기하학(differential geometry)에서 토대적으로 중요합니다. 리만 메트릭은 표면에 측지선(geodesic), 거리(distance), 각도(angle), 및 넓이의 개념을 부여합니다. 그것은 역시 각 점에서 표면이 구부러지거나 휘어지는 정도를 나타내는 가우스 곡률(Gaussian curvature)을 발생시킵니다. 곡률은 표면의 일반적인 미분-동형에 의해 보존되지 않는다는 점에서 강건한, 기하학적 속성입니다. 어쨌든, 닫힌 표면에 대해 유명한 가우스–보네 정리(Gauss–Bonnet theorem)는 전체 표면 S에 걸쳐 가우스 곡률 K의 적분이 오일러 특성에 의해 결정된다고 말합니다:

\int _{S}K\;dA=2\pi \chi (S).

이 결과는 표면의 기하학과 토폴로지 (및, 정도는 덜하지만, 더 높은 차원의 매니폴드) 사이의 깊은 관계를 보여줍니다.

기하학에서 표면이 발생하는 또 다른 방법은 복소 도메인으로 전달하는 것입니다. 복소 일-매니폴드는 매끄러운 방향화된 표면이며, 역시 리만 표면(Riemann surface)이라고 불립니다. 복소 매니폴드로 보이는 임의의 복소 비-특이 대수적 곡선(algebraic curve)은 리만 표면입니다. 사실, 모든 각 컴팩트 방향-가능 표면은 리만 표면으로 실현될 수 있습니다. 따라서 컴팩트 리만 표면은 그들의 지너스: 0, 1, 2, ...에 의해 토폴로지적으로 특성화됩니다. 다른 한편으로, 지너스는 복소 구조를 특성화하지 않습니다. 예를 들어, 저니스 1 (타원 곡선)의 비-동형적 컴팩트 리만 표면이 셀-수-없이 많습니다.

닫힌 방향화된 표면 위에 복소 구조는 표면 위에 리만 메트릭의 등각 동치 클래스(conformal equivalence classes)에 해당합니다. (푸앵카레로 인한) 균등화 정리(uniformization theorem)의 한 버전은 방향화된, 닫힌 표면 위에 임의의 리만 메트릭(Riemannian metric)이 본질적으로 상수 곡률(constant curvature)의 고유한 메트릭과 등각적으로 동등하다고 말합니다. 이것은 오일러 특성 단독으로 토폴로지적 분류보다 리만 표면의 더 미세한 분류를 제공하는 타이히뮐러 이론(Teichmüller theory)에 대한 접근 방식 중 하나에 대한 출발점을 제공합니다.

복소 표면(complex surface)은 복소 2-매니폴드이고 따라서 실수 4-매니폴드입니다; 그것은 이 기사의 의미에서 표면이 아닙니다. 복소수 이외의 필드에 걸쳐 정의된 대수적 곡선도 아니고, 실수 이외의 필드에 걸해 정의된 대수적 표면도 아닙니다.

Notes

^ ^a ^b (Francis & Weeks 1999)
^ Richards, Ian (1963). "On the classification of noncompact surfaces". Trans. Amer. Math. Soc. 106 (2): 259–269. doi:10.2307/1993768. JSTOR 1993768.

References

Dyck, Walther (1888), "Beiträge zur Analysis situs I", Math. Ann., 32 (4): 459–512, doi:10.1007/bf01443580, S2CID 118123073

Simplicial proofs of classification up to homeomorphism

Seifert, Herbert; Threlfall, William (1980), A textbook of topology, Pure and Applied Mathematics, vol. 89, Academic Press, ISBN 0126348502, English translation of 1934 classic German textbook
Ahlfors, Lars V.; Sario, Leo (1960), Riemann surfaces, Princeton Mathematical Series, vol. 26, Princeton University Press, Chapter I
Maunder, C. R. F. (1996), Algebraic topology, Dover Publications, ISBN 0486691314, Cambridge undergraduate course
Massey, William S. (1991). A Basic Course in Algebraic Topology. Springer-Verlag. ISBN 0-387-97430-X.
Bredon, Glen E. (1993). Topology and Geometry. Springer-Verlag. ISBN 0-387-97926-3.
Jost, Jürgen (2006), Compact Riemann surfaces: an introduction to contemporary mathematics (3rd ed.), Springer, ISBN 3540330658, for closed oriented Riemannian manifolds

Morse theoretic proofs of classification up to diffeomorphism

Hirsch, M. (1994), Differential topology (2nd ed.), Springer
Gauld, David B. (1982), Differential topology: an introduction, Monographs and Textbooks in Pure and Applied Mathematics, vol. 72, Marcel Dekker, ISBN 0824717090
Shastri, Anant R. (2011), Elements of differential topology, CRC Press, ISBN 9781439831601, careful proof aimed at undergraduates
Gramain, André (1984). Topology of Surfaces. BCS Associates. ISBN 0-914351-01-X. (Original 1969-70 Orsay course notes in French for "Topologie des Surfaces")
A. Champanerkar; et al., Classification of surfaces via Morse Theory (PDF), an exposition of Gramain's notes{{citation}}: CS1 maint: postscript (link)

Other proofs

Lawson, Terry (2003), Topology: a geometric approach, Oxford University Press, ISBN 0-19-851597-9, similar to Morse theoretic proof using sliding of attached handles
Francis, George K.; Weeks, Jeffrey R. (May 1999), "Conway's ZIP Proof" (PDF), American Mathematical Monthly, 106 (5): 393, doi:10.2307/2589143, JSTOR 2589143, archived from the original (PDF) on 2010-06-12, page discussing the paper: On Conway's ZIP Proof {{citation}}: External link in |postscript= (help)CS1 maint: postscript (link)
Thomassen, Carsten (1992), "The Jordan-Schönflies theorem and the classification of surfaces", Amer. Math. Monthly, 99 (2): 116–13, doi:10.2307/2324180, JSTOR 2324180, short elementary proof using spanning graphs
Prasolov, V.V. (2006), Elements of combinatorial and differential topology, Graduate Studies in Mathematics, vol. 74, American Mathematical Society, ISBN 0821838091, contains short account of Thomassen's proof

External links

Classification of Compact Surfaces in Mathifold Project
The Classification of Surfaces and the Jordan Curve Theorem in Home page of Andrew Ranicki
Math Surfaces Gallery, with 60 ~surfaces and Java Applet for live rotation viewing
Math Surfaces Animation, with JavaScript (Canvas HTML) for tens surfaces rotation viewing
The Classification of Surfaces Lecture Notes by Z.Fiedorowicz
History and Art of Surfaces and their Mathematical Models
2-manifolds at the Manifold Atlas

[fw-1] (Francis & Weeks 1999)

[2] Richards, Ian (1963). "On the classification of noncompact surfaces". Trans. Amer. Math. Soc. 106 (2): 259–269. doi:10.2307/1993768. JSTOR 1993768.

[1]

[2]