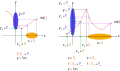Surjective function

수학(mathematics)에서, 집합(set) X에서 집합 Y로의 함수(function) f는, 만약 f의 코도메인(codomain) Y에서 모든 각 원소(element) y에 대해 f(x) = y를 만족하는 f의 도메인(domain) X에서 적어도 한 원소 x가 있으면, 전사적(surjective) (역시 위로의(onto), 또는 전사(surjection)로 알려짐)입니다.^[1]^[2]^[3] 여기서 x가 고유한(unique) 것임을 요구하지는 않습니다; 함수 f는 X의 하나 이상의 원소를 Y의 같은 원소에 매핑할 수 있습니다.

용어 전사(surjective)와 관련된 용어 단사(injective) 및 전단사(bijective)는, 이 필명으로 1935년에 시작된 현대 고급 수학의 박람회를 전시하는 일련의 책을 저술한, 주로 프랑스(French)의 20세기 수학자 그룹인, 니콜라 부르바키(Nicolas Bourbaki)^[4]^[5]에 의해 도입되었습니다. 프랑스어 단어 sur는 위에(over) 또는 ...을 넘어(above)을 의미하고, 전사 함수의 도메인의 이미지(image)가 해당 함수의 코도메인을 완전히 덮는다는 사실과 관련이 있습니다.

임의의 함수는 그의 코도메인을 그의 도메인의 이미지로 제한(restriction)함으로써 전사를 야기합니다. 모든 각 전사 함수는 오른쪽 역함수(right inverse)를 가지고, 오른쪽 역함수를 갖는 모든 각 함수는 반드시 전사입니다. 전사 함수의 합성(composition)은 항상 전사입니다. 임의의 함수는 전사와 단사로 분해될 수 있습니다.

Definition

전사 함수는 그의 이미지(image)가 그것의 코도메인(codomain)과 같은 함수(function)입니다. 동등하게, 도메인(domain) X와 코도메인 Y를 갖는 함수 f는, 만약 Y에서 모든 각 y에 대해, $f(x)=y$ 를 가진 X에서 적어도 하나의 x가 존재하면, 전사입니다.^[2] 전사는 f : X ↠ Y에서 처럼, 때때로 두-머리 오른쪽 화살표 (U+21A0 ↠ RIGHTWARDS TWO HEADED ARROW),^[6]로 표시됩니다.

기호적으로,

만약

f\colon X\rightarrow Y

이면,

f

가 만약 다음이면 전사로 말합니다:

\forall y\in Y,\,\exists x\in X,\;\;f(x)=y

.^[3]^[7]

Examples

**A non-surjective function** from domain X to codomain Y. The smaller yellow oval inside Y is the image (also called range) of f. This function is **not** surjective, because the image does not fill the whole codomain. In other words, Y is colored in a two-step process: First, for every x in X, the point f(x) is colored yellow; Second, all the rest of the points in Y, that are not yellow, are colored blue. The function f would be surjective only if there were no blue points.

임의의 집합 X에 대해, X 위에 항등 함수(identity function) id_X는 전사입니다.
f(n) = n 모드(mod) 2 (즉, 짝수(even) 정수(integer)가 0으로 홀수(odd) 정수가 1로 매핑됨)에 의해 정의된 함수 f : Z → {0,1}는 전사입니다.
f(x) = 2x + 1에 의해 정의된 함수 f : R → R는 전사 (및 심지어 전단사(bijective))인데, 왜냐하면 모든 각 실수(real number) y에 대해, 우리는 f(x) = y: 그러한 적절한 x가 (y − 1)/2을 만족하는 x를 가집니다.
f(x) = x³ − 3x에 의해 정의된 함수 f : R → R는 전사인데, 왜냐하면 임의의 실수(real number) y의 이전-이미지는 삼차 다항 방정식 x³ − 3x − y = 0의 해 집합이고, 실수 계수를 갖는 모든 각 삼차 다항식은 적어도 하나의 실수 근을 가지기 때문입니다. 어쨌든, 이 함수는 단사(injective)는 아닌데 (및 따라서 전단사(bijective)가 아님), 왜냐하면, 예를 들어, y = 2의 이전-이미지는 {x = −1, x = 2}이기 때문입니다. (사실, 모든 각 y에 대해 이 함수의 이전-이미지, −2 ≤ y ≤ 2는 하나보다 많은 원소를 가집니다.)
g(x) = x²에 의해 정의된 함수 g : R → R는 전사가 아닌데, 왜냐하면 x² = −1를 만족하는 실수 x가 없기 때문입니다. 어쨌든, (제한된 코도메인과 함께) g(x) = x²에 의해 정의된 함수 g : R → R₀⁺는 전사인데, 왜냐하면 비-음의 실수 코도메인 Y에서 모든 각 y에 대해, x² = y를 만족하는 실수 도메인 X에서 적어도 하나의 x가 있기 때문입니다.
자연 로그(natural logarithm) 함수 ln : (0,+∞) → R는 전사이고 심지어 전단사입니다 (양의 실수의 집합으로부터 모든 실수의 집합으로 매핑합니다). 그것의 역, 지수 함수(exponential function)는, 만약 도메인으로 실수의 집합과 함께 정의되면, 전사가 아닙니다 (왜냐하면 그것의 이미지는 양의 실수의 집합이기 때문입니다).
행렬 지수(matrix exponential)는 모든 n×n 행렬(matrices)의 공간에서 자체로의 매핑으로 보일 때 전사가 아닙니다. 어쨌든, 보통 모든 n×n 행렬의 공간에서 차수 n의 일반적인 선형 그룹(general linear group) (즉, 모든 n×n 역-가능한 행렬(invertible matrices)의 그룹(group))으로의 매핑으로 정의됩니다. 이 정의 아래에서, 행렬 지수는, 비록 실수 행렬에 대해 여전히 전사가 아닐지라도, 복소 행렬에 대해 전사입니다.
데카르트 곱(cartesian product) A × B에서 그것의 인수의 하나로의 투영(projection)은, 만약 나머지 다른 인수가 빈 것이 아니면, 전사입니다.
3D 비디오 게임에서, 벡터는 전사 함수를 수단으로 2D 평평한 스크린 위로 투영됩니다.

Properties

함수가 전단사(bijective)인 것과 그것이 전사 및 단사(injective) 둘 다인 것은 필요충분 조건입니다.

만약 (종종 행해지는 것처럼) 함수는 그것의 그래프(graph)와 함께 식별되면, 전사성은 함수 자체의 속성이 아니지만, 오히려 매핑(mapping)의 속성입니다.^[8] 이것은 그것의 코도메인과 함께 함수입니다. 단사성과 달리, 전사성은 단독으로 함수의 그래프로 읽을 수 없습니다.

Surjections as right invertible functions

함수 g : Y → X는 만약 Y에서 모든 각 y에 대해 f(g(y)) = y이면 (g가 f로 취소될 수 있음) 오른쪽 역함수(right inverse)라고 말합니다.. 다시 말하면, g가 만약 해당 순서에서 g와 f의 합성(composition)이 g의 도메인 Y에 대한 항등 함수(identity function)이면, f의 오른쪽 역함수입니다. 함수 g는 f의 완전한 역함수(inverse)일 필요는 없는데, 왜냐하면 나머지 다른 순서에서 합성, g o f가 f의 도메인 X에 대한 항등 함수가 아닐 수 있기 때문입니다. 다시 말해, f는 g를 취소 또는 "되돌릴"수 있지만, 그것에 의해 반드시 되돌릴 수는 없습니다.

오른쪽 역함수를 갖는 모든 각 함수는 반드시 전사입니다. 모든 각 전사 함수가 오른쪽 역함수를 갖는다는 제안은 선택의 공리(axiom of choice)와 동등합니다.

만약 f : X → Y가 전사이고 B가 Y의 부분-집합(subset)이면, f(f⁻¹(B)) = B입니다. 따라서, B는 그것의 이전-이미지 f⁻¹(B)로부터 복원될 수 있습니다.

예를 들어, 위쪽의 첫 번째 그림에서, g(C) = 4를 만족하는 일부 함수가 있습니다. 역시 f(4) = C를 만족하는 일부 함수가 있습니다. g(C)이 역시 3과 같은 것은 문제가 되지 않습니다; 오직 f가 g를 "거꾸로 되게" 하는 것이 중요합니다.

Surjections as epimorphisms

함수 f : X → Y는 전사인 것과 그것이 오른쪽-취소(right-cancellative)인 것은 필요충분 조건입니다:^[9] 임의의 함수 g,h : Y → Z가 주어지면, g o f = h o f일 때마다, g = h입니다. 이 속성은 함수와 그들의 합성(composition)의 관점에서 공식화되고 카테고리(category)의 사상(morphism)과 그들의 합성의 보다 일반적인 개념으로 일반화될 수 있습니다. 오른쪽-취소 사상은 전사-사상(epimorphism)으로 불립니다. 구체적으로, 전사 함수는 집합의 카테고리(category of sets)에서 정확하게 전사-사상입니다. 접두사 epi는 over, above, on를 의미하는 그리스 전치사 ἐπί에서 파생됩니다.

오른쪽 역함수를 가진 임의의 사상은 전사-사상이지만, 그 전환은 일반적으로 참이 아닙니다. 사상 f의 오른쪽 역함수 g는 f의 단면(section)이라고 불립니다. 오른쪽 역을 갖는 사상은 분할 전사-사상(split epimorphism)으로 불립니다.

Surjections as binary relations

도메인 X와 코도메인 Y를 갖는 임의의 함수는 그것의 함수 그래프(function graph)로 그것을 식별함으로써 X와 Y 사이의 왼쪽-전체(left-total) 및 오른쪽-고유한(right-unique) 이항 관계로 보일 수 있습니다. 도메인 X와 코도메인 Y를 갖는 전사 함수는 그런-다음 X와 Y 사이의 이항 관계, 즉, 오른쪽-고유한 및 왼쪽-전체와 오른쪽-전체(right-total) 둘 다입니다.

Cardinality of the domain of a surjection

전사 함수의 도메인의 카디널리티(cardinality)는 그것의 코도메인의 카디널리티보다 크거나 같습니다: 만약 f : X → Y가 전사 함수이면, X는 세는-숫자(cardinal number)의 의미에서 적어도 Y만큼 많은 원소를 가집니다. (증명은 Y에서 모든 y에 대해 f(g(y)) = y를 만족시키는 함수 g : Y → X가 존재함을 보이기 위해 선택의 공리(axiom of choice)에 호소합니다. g가 단사임을 쉽게 보일 수 있으며, 따라서 |Y| ≤ |X|의 형식적 정의(formal definition)가 만족됩니다.)

구체적으로 특별히, 만약 X와 Y 둘 다가 같은 숫자의 원소를 갖는 유한(finite)이면, f : X → Y가 전사인 것과 f가 단사(injective)인 것은 필요충분 조건입니다.

두 집합 X와 Y가 주어지면, 표기법 X ≤^* Y는 X가 빈 것 또는 Y에서 X 위로의 전사가 있음을 말하기 위해 사용됩니다. 선택 공리를 사용하면, 우리는 X ≤^* Y 및 Y ≤^* X가 함께 |Y| = |X|, 슈뢰더–베른슈타인 정리(Schröder–Bernstein theorem)의 변형임을 의미합니다.

Composition and decomposition

전사 함수의 합성(composition)은 항상 전사입니다: 만약 f와 g가 둘 다 전사이고, g의 코도메인이 f의 도메인과 같으면, f o g는 전사입니다. 반대로, 만약 f o g가 전사이면, f는 전사입니다 (그러나 g, 먼저 적용되는 함수는 전사일 필요는 없습니다). 이들 속성은 집합의 카테고리(category of sets)에서 전사에서 임의의 카테고리(category)의 전사-사상(epimorphism)으로 일반화됩니다.

임의의 함수는 전사와 단사(injection)로 분해될 수 있습니다: 임의의 함수 h : X → Z에 대해, h = g o f를 만족하는 전사 f : X → Y와 단사 g : Y → Z가 존재합니다. 이것을 보이기 위해, Y를 이전-이미지(preimage)의 집합 h⁻¹(z)로 정의하며, 여기서 z는 h(X) 안에 있습니다. 이들 이전-이미지는 서로소(disjoint)이고 분할(partition) X입니다. 그런-다음 f는 각 x를 포함하는 Y의 원소에 각 x를 전달하고, g는 h가 해당 점을 보내는 Z 안의 점에 Y의 각 원소를 전달합니다. 그런-다음 f는 전사인데 왜냐하면 그것이 투영 맵이고, g는 정의에 의해 단사이기 때문입니다.

Induced surjection and induced bijection

임의의 함수는 그것의 코도메인을 그것의 치역으로 제한함으로써 전사를 유도합니다. 모든 전사 함수는 모든 인수를 주어진 고정된 이미지로 매핑하는 것으로 축소함으로써 해당 도메인의 몫(quotient)에 정의된 전단사를 유도합니다. 보다 정확하게, 모든 각 전사 f : A → B는 다음처럼 전단사에 의해 따르는 투영으로 인수화될 수 있습니다. A/~를 다음 동치 관계(equivalence relation)를 따르는 것 아래에서 A의 동치 클래스(equivalence class)로 놓습니다: x ~ y인 것과 f(x) = f(y)인 것은 필요충분 조건입니다. 동등하게, A/~는 f 아래에서 모든 이전-이미지의 집합입니다. P(~) : A → A/~를 A에서 각 x를 그것의 동치 클래스 [x]_~로 보내는 투영 맵(projection map)으로 놓고, f_P : A/~ → B를 f_P([x]_~) = f(x)에 의해 주어진 잘-정의된 함수로 놓습니다. 그런-다음 f = f_P o P(~)입니다.

Space of surjections

고정된 $A$ 와 $B$ 가 주어졌을 때, 전사 $A ↠ B$ 의 집합을 형성할 수 있습니다. 이 집합의 카디널리티(cardinality)는 로타의 열두겹 방법(Twelvefold way)의 12가지 측면 중 하나이고, ${\textstyle |B|!{\begin{Bmatrix}|A|\\|B|\end{Bmatrix}}}$ 에 의해 주어지며, 여기서 ${\textstyle {\begin{Bmatrix}|A|\\|B|\end{Bmatrix}}}$ 는 두 번째 종류의 스털링 숫자(Stirling number of the second kind)를 나타냅니다.

Gallery

A non-injective surjective function (surjection, not a bijection)
An injective surjective function (bijection)
An injective non-surjective function (injection, not a bijection)
A non-injective non-surjective function (neither a bijection)

Surjective composition: the first function need not be surjective.
Non-surjective functions in the Cartesian plane. Although some parts of the function are surjective, where elements y in Y do have a value x in X such that y = f(x), some parts are not. Left: There is y₀ in Y, but there is no x₀ in X such that y₀ = f(x₀). Right: There are y₁, y₂ and y₃ in Y, but there are no x₁, x₂, and x₃ in X such that y₁ = f(x₁), y₂ = f(x₂), and y₃ = f(x₃).
Interpretation for surjective functions in the Cartesian plane, defined by the mapping f : X → Y, where y = f(x), X = domain of function, Y = range of function. Every element in the range is mapped onto from an element in the domain, by the rule f. There may be a number of domain elements which map to the same range element. That is, every y in Y is mapped from an element x in X, more than one x can map to the same y. Left: Only one domain is shown which makes f surjective. Right: two possible domains X₁ and X₂ are shown.

References

^ "The Definitive Glossary of Higher Mathematical Jargon — Onto". Math Vault. 2019-08-01. Retrieved 2019-12-07.{{cite web}}: CS1 maint: url-status (link)
^ ^a ^b "Injective, Surjective and Bijective". www.mathsisfun.com. Retrieved 2019-12-07.
^ ^a ^b "Bijection, Injection, And Surjection | Brilliant Math & Science Wiki". brilliant.org. Retrieved 2019-12-07.
^ Miller, Jeff, "Injection, Surjection and Bijection", Earliest Uses of Some of the Words of Mathematics, Tripod.
^ Mashaal, Maurice (2006). Bourbaki. American Mathematical Soc. p. 106. ISBN 978-0-8218-3967-6.
^ "Arrows – Unicode" (PDF). Retrieved 2013-05-11.
^ Farlow, S. J. "Injections, Surjections, and Bijections" (PDF). math.umaine.edu. Retrieved 2019-12-06.{{cite web}}: CS1 maint: url-status (link)
^ T. M. Apostol (1981). Mathematical Analysis. Addison-Wesley. p. 35.
^ Goldblatt, Robert (2006) [1984]. Topoi, the Categorial Analysis of Logic (Revised ed.). Dover Publications. ISBN 978-0-486-45026-1. Retrieved 2009-11-25.