Triangle inequality

수학(mathematics)에서, 삼각형 부등식(triangle inequality)은 임의의 삼각형(triangle)에 대해, 임의의 두 변의 길이의 합이 남아있는 변의 길이보다 크거나 같아야 한다고 말합니다.^[1]^[2] 이 명제는 퇴화 삼각형(degenerate triangles)의 포함을 허용하지만, 일부 저자, 특히 기본 기하학에 대해 쓰는 사람들은 이 가능성을 배제할 것이고, 따라서 상등의 가능성을 배제합니다.^[3] 만약 $x$ , $y$ , 및 $z$ 가 삼각형의 변의 길이이고, $z$ 보다 큰 변이 없으면, 삼각형 부등식은 다음임을 말합니다:

z\leq x+y,

여기서 상등은 오직 영 넓이를 갖는 삼각형의 퇴화 경우입니다. 유클리드 기하학(Euclidean geometry)과 일부 다른 기하학에서, 삼각형 부등식은 거리에 대한 정리이고, 그것은 벡터와 벡터 길이 (노름(norms))를 사용하여 쓰입니다:

\|\mathbf {x} +\mathbf {y} \|\leq \|\mathbf {x} \|+\|\mathbf {y} \|,

여기서 세 번째 변의 길이 $z$ 는 벡터 합 $x + y$ 에 의해 대체됩니다. $x$ 와 $y$ 가 실수(real number)일 때, 그것들은 $R 1$ 에서 벡터로 보일 수 있고, 삼각형 부등식은 절댓값(absolute value) 사이의 관계를 나타냅니다.

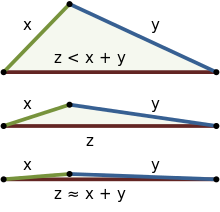
유클리드 기하학에서, 직각 삼각형(right triangle)에 대해 삼각형 부등식은 피타고라스 정리(Pythagorean theorem)의 결과이고, 일반적인 삼각형에 대해, 코사인의 법칙(law of cosines)의 결과이지만, 그것은 이들 정리 없이 입증될 수 있습니다. 부등식은 $R 2$ 또는 $R 3$ 에서 직관적으로 볼 수 있습니다. 그림은 명백한 부등식 (꼭대기)에서 시작하여 상등 (바닥)에 가까워지는 세 가지 예제를 보입니다. 유클리드 경우에서, 상등은 오직 삼각형이 하나의 $180°$ 각도와 둘의 $0°$ 각도를 가지면 발생하며, 바닥 예제에서 보이는 것처럼 셋의 꼭짓점(vertices)을 공선형(collinear)으로 만듭니다. 따라서, 유클리드 기하학에서, 두 점 사이의 가장 짧은 거리는 직선입니다.

구형 기하학(spherical geometry)에서, 두 점 사이의 가장 짧은 거리는 큰 원(great circle)의 호이지만, 구 위의 두 점 사이의 거리가 그들 끝점과의 보조 구형 선분 (즉, 중심각이 $[0, π]$ 인 선분)의 길이라는 제한이 있다는 조건 아래에서 삼각형 부등식은 유지됩니다.^[4]^[5]

삼각형 부등식은 노름(norms)의 정의하는 속성(defining property)이고 거리(distance)의 측정입니다. 이 속성은 각 특정 공간에 대해 그러한 목적으로 제안된 임의의 함수에 대한 정리로 설립되어야 합니다: 예를 들어, 실수(real number), 유클리드 공간(Euclidean space), L^p 공간 ( $p \geq 1$ ), 및 안의 곱 공간(inner product space)과 같은 공간입니다.

Euclidean geometry

유클리드는 그림에서 구성을 사용하여 평면 기하학(plane geometry)에서 거리에 대한 삼각형 부등식을 입증했습니다.^[6] 삼각형 $ABC$ 로 시작하여, 이등변 삼각형은 한 변을 $BC$ 로 하고 다른 변을 변 $AB$ 의 연장선을 따라 같은 다리 $BD$ 로 하여 구성합니다. 그런-다음 각도 $β$ 가 각도 $α$ 보다 크기가 더 크므로, 변 $AD$ 가 변 $AC$ 보다 더 길다고 주장됩니다. 그러나 $AD = AB + BD = AB + BC$ 이므로, 변 $AB$ 와 $BC$ 의 길이의 합은 $AC$ 의 길이보다 큽니다. 이 증명은 유클리드의 원론, 책 1, 제안 20에 나와 있습니다.^[7]

Mathematical expression of the constraint on the sides of a triangle

적절한 삼각형에 대해, 삼각형 부등식은, 말로 표현한 것처럼, 문자 그대로 세 가지 부등식으로 변환됩니다 (적절한 삼각형은 변 길이 $a$ , $b$ , $c$ 를 가지고 모두 양수이고 영 넓이의 퇴화 경우를 제외하는 것으로 제공됩니다):

a+b>c,\quad b+c>a,\quad c+a>b.

이 부등식 시스템의 보다 간결한 형태는 다음과 같이 표시될 수 있습니다:

|a-b|<c<a+b.

그것을 설명하는 또 다른 방법은 다음과 같습니다:

\max(a,b,c)<a+b+c-\max(a,b,c)

여기서 다음을 의미합니다:

2\max(a,b,c)<a+b+c

그리고 따라서 가장 긴 변의 길이는 반-둘레(semiperimeter)보다 작습니다.

수학적으로 동등한 공식화는 변 $a$ , $b$ , $c$ 를 갖는 삼각형의 넓이가 영보다 큰 실수여야 한다는 것입니다. 넓이에 대한 헤론의 공식(Heron's formula)은 다음과 같습니다:

{\begin{aligned}4\cdot {\text{area}}&={\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\\&={\sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2a^{2}c^{2}+2b^{2}c^{2}}}.\end{aligned}}

어는 한 넓이 표현의 관점에서, 모든 변에 부과된 삼각형 부등식은 제곱근 기호 아래의 표현이 실수이고 영보다 크다는 조건과 동등합니다 (따라서 넓이 표현은 실수이고 영보다 큽니다).

삼각형 부등식은 변 $a$ , $b$ , $c$ 를 갖는 삼각형에 대해 두 가지 더 흥미로운 제약 조건을 제공하며, 여기서 $a\geq b\geq c$ 이고

$\phi$ 는 다음과 같은 황금 비율(golden ratio)입니다:

1<{\frac {a+c}{b}}<3

1\leq \min \left({\frac {a}{b}},{\frac {b}{c}}\right)<\phi .

^[8]

Right triangle

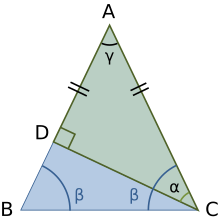
직각 삼각형의 경우에서, 삼각형 부등식은 빗변이 두 변 중 하나보다 크고 그 합보다 작다는 명제에 특화되어 있습니다.^[9]

이 정리의 두 번째 부분은 임의의 삼각형의 임의의 변에 대해 이미 위에서 설정되었습니다. 첫 번째 부분은 그림을 사용하여 설정됩니다. 그림에서, 직각 삼각형 $ADC$ 를 생각해 보십시오. 이등변 삼각형 $ABC$ 는 같은 변 $AB = AC$ 로 구성됩니다. 삼각형 공준(triangle postulate)에서, 직각 삼각형 $ADC$ 에서 각도는 다음을 만족시킵니다:

\alpha +\gamma =\pi /2\ .

마찬가지로, 이등변 삼각형 $ABC$ 에서, 각도는 다음을 만족시킵니다:

2\beta +\gamma =\pi \ .

그러므로,

\alpha =\pi /2-\gamma ,\ \mathrm {while} \ \beta =\pi /2-\gamma /2\ ,

그리고 따라서, 특히,

\alpha <\beta \ .

그것은 각도 $α$ 의 반대쪽 변 $AD$ 가 더 큰 각도 $β$ 의 반대쪽 변 $AB$ 보다 짧다는 것을 의미합니다. 그러나 $AB = AC$ 입니다. 따라서:

{\overline {\mathrm {AC} }}>{\overline {\mathrm {AD} }}\ .

비슷한 구성은 $AC > DC$ 임을 보이고, 그 정리를 수립합니다.

대안적 증명은, 역시 삼각형 공준에 기초하며, 점 $B$ 에 대해 세 가지 위치를 고려함으로써 진행됩니다:^[10] (i) 표시된 대로(증명되어야 함), 또는 (ii) $B$ 는 $D$ 와 일치합니다 (이는 이등변 삼각형이 밑변 각도와 꼭짓점 각도 $γ$ 로 두 개의 직각을 가짐을 의미하며, 이는 삼각형 공준을 위반함), 또는 마지막으로, (iii) 점 $A$ 와 $D$ 사이의 직각 삼각형에 대한 $B$ 내부 (이 경우에서 각도 $ABC$ 는 직각 삼각형 $BDC$ 의 외부 각도이고 따라서 $π /2$ 보다 크며, 이는 이등변 삼각형의 다른 밑변 각도도 $π /2$ 보다 크고 그 합이 삼각형 공준을 위반하여 $π$ 를 초과함을 의미합니다).

부등식을 수립하는 이 정리는 피타고라스의 정리(Pythagoras' theorem)에 의해 빗변의 길이의 제곱이 다른 두 변의 제곱의 합과 같다는 상등으로 개선됩니다.

Examples of use

변이 산술 진행(arithmetic progression)에 있는 삼각형을 고려하고 변을 $a$ , $a + d$ , $a + 2 d$ 라고 놓습니다. 그런-다음 삼각형 부등식은 다음임을 요구합니다:

0<a<2a+3d

0<a+d<2a+2d

0<a+2d<2a+d.

모든 이들 부등식을 만족시키려면 다음임을 요구합니다:

a>0{\text{ and }}-{\frac {a}{3}}<d<a.

^[11]

$d$ 가 $d = a /3$ 임을 만족하도록 선택될 때, 그것은 변 $3$ , $4$ , $5$ 를 갖는 피타고라스의 세-쌍(Pythagorean triple)과 항상 닮은 직각 삼각형을 생성합니다.

이제 변이 기하 진행(geometric progression)에 있는 삼각형을 고려하고 변을 $a$ , $ar$ , $ar 2$ 로 놓습니다. 그런-다음 삼각형 부등식은 다음임을 요구합니다:

0<a<ar+ar^{2}

0<ar<a+ar^{2}

0<ar^{2}<a+ar.

첫 번째 부등식은 $a > 0$ 임을 요구합니다; 결과적으로 그것은 나뉘고 제거될 수 있습니다. $a > 0$ 과 함께, 중간 부등식은 오직 $r > 0$ 임을 요구합니다. 이것은 이제 다음을 만족시키도록 필요로 하는 첫 번째와 세 번째 부등식을 남깁니다:

{\begin{aligned}r^{2}+r-1&{}>0\\r^{2}-r-1&{}<0.\end{aligned}}

이들 이차 부등식 중 첫 번째는 $r$ 을 이차 방정식 $r 2 + r - 1 = 0$ 의 양의 근의 값을 넘어선 영역의 범위에 있도록 요구하며, 즉, $r > φ - 1$ 이며 여기서 $φ$ 는 황금 비율(golden ratio)입니다. 두 번째 이차 부등식은 $r$ 을 0과 이차 방정식 $r 2 - r - 1 = 0$ 의 양의 근 사이의 범위에 있도록 요구하며, 즉, $0 < r < φ$ 입니다. 결합된 요구 사항은 $r$ 을 다음 범위로 제한하도록 초래합니다:

\varphi -1<r<\varphi \,{\text{ and }}a>0.

^[12]

공통 비율 $r$ 이 $r = \sqrt φ$ 임을 만족하도록 선택될 때, 그것은 항상 케플러 삼각형(Kepler triangle)과 닮은 직각 삼각형을 생성합니다.

Generalization to any polygon

삼각형 부등식은 수학적 귀납법(mathematical induction)에 의해 임의적인 다각형 경로로 확장될 수 있으며, 그러한 경로의 총 길이는 끝점 사이의 직선 길이보다 작지 않음을 보여줍니다. 결과적으로, 임의의 다각형 변의 길이는 항상 다른 다각형 변 길이의 합보다 작습니다.

Example of the generalized polygon inequality for a quadrilateral

변이 기하 진행(geometric progression)에 있는 사변형을 고려하고 변을 $a$ , $ar$ , $ar 2$ , $ar 3$ 라고 놓습니다. 그런-다음 일반화된 다각형 부등식은 다음임을 요구합니다:

0<a<ar+ar^{2}+ar^{3}

0<ar<a+ar^{2}+ar^{3}

0<ar^{2}<a+ar+ar^{3}

0<ar^{3}<a+ar+ar^{2}.

a > 0에 대해 이들 부등식은 다음으로 줄어듭니다:

r^{3}+r^{2}+r-1>0

r^{3}-r^{2}-r-1<0.

^[13]

이들 두 부등식의 왼쪽-변 다항식은 트리보나치 상수(tribonacci constant)와 그 역수인 근을 가집니다. 결과적으로, $r$ 은 $1/ t < r < t$ 범위로 제한되며 여기서 $t$ 는 트리보나치 상수입니다.

Relationship with shortest paths

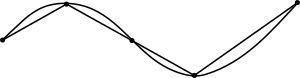
The arc length of a curve is defined as the least upper bound of the lengths of polygonal approximations.

이 일반화는 유클리드 기하학에서 두 점 사이의 가장 짧은 곡선이 직선임을 입증하기 위해 사용될 수 있습니다.

두 점 사이의 어떤 다각형 경로도 두 점 사이의 직선보다 짧지 않습니다. 이것은 곡선이 끝점 사이의 거리보다 작은 호 길이(arc length)를 가질 수 없음을 의미합니다. 정의에 의해, 곡선의 호 길이는 곡선의 모든 다각형 근삿값 길이의 최소 위쪽 경계(least upper bound)입니다. 다각형 경로에 대해 결과는 끝점 사이의 직선이 모든 다각형 근삿값 중에서 가장 짧다는 것을 보여줍니다. 곡선의 호 길이는 모든 각 다각형 근삿값의 길이보다 크거나 같기 때문에, 곡선 자체는 직선 경로보다 짧을 수 없습니다.^[14]

Converse

삼각형 부등식 정리의 전환도 참입니다: 세 개의 실수가 각각이 다른 것들의 합보다 작음을 만족하는 것이면, 이들 숫자를 한 변의 길이로 하고 양수 넓이를 갖는 삼각형이 존재합니다; 그리고 한 숫자가 다른 두 숫자의 합과 같으면, 이들 숫자를 변의 길이로 갖는 퇴화 삼각형 (즉, 영 넓이를 가짐)이 존재합니다.

두 경우 모두에서, 변의 길이가, a, b, c이면, 다이어그램에서 보인 것처럼 유클리드 평면(Euclidean plane)에 삼각형을 배치하려고 시도할 수 있습니다. 우리는 값 a, b, 및 c와 일치하는 실수 h가 존재한다는 것을 입증해야 하며, 이 경우에서 이 삼각형이 존재합니다.

피타고라스 정리(Pythagorean theorem)에 의해, 그림에 따라 $b 2 = h 2 + d 2$ 와 $a 2 = h 2 + (c - d) 2$ 를 가집니다. 이들을 빼면 $a 2 - b 2 = c 2 - 2 cd$ 을 산출합니다. 이 방정식을 사용하면 삼각형의 변의 관점에서 $d$ 를 표현할 수 있습니다:

d={\frac {-a^{2}+b^{2}+c^{2}}{2c}}.

삼각형의 높이에 대해, $h 2 = b 2 - d 2$ 임을 가집니다. $d$ 를 위에 주어진 공식으로 대체함으로써, 우리는 다음을 가집니다:

h^{2}=b^{2}-\left({\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)^{2}.

실수 h가 이를 만족시키려면, $h^{2}$ 가 비-음수여야 합니다:

b^{2}-\left({\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)^{2}\geq 0,

\left(b-{\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)\left(b+{\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)\geq 0,

\left(a^{2}-(b-c)^{2})((b+c)^{2}-a^{2}\right)\geq 0,

(a+b-c)(a-b+c)(b+c+a)(b+c-a)\geq 0,

(a+b-c)(a+c-b)(b+c-a)\geq 0,

이는 삼각형 부등식이 모든 변에 대해 만족시키면 성립합니다. 그러므로 변 a, b, c와 일치하는 실수 h가 존재하고 삼각형이 존재합니다. 만약 각 삼각형 부등식이 엄격하게(strictly) 유지되면, h > 0이고 삼각형은 비-퇴화입니다 (양의 넓이를 가집니다); 그러나 부등식 중 하나가 상등을 유지하면, 따라서 h = 0이며, 삼각형이 퇴화됩니다.

Generalization to higher dimensions

사면체(tetrahedron)의 삼각형 면의 넓이는 다른 세 삼각형 면의 넓이의 합보다 작거나 같습니다. 보다 일반적으로, 유클리드 공간에서 n-심플렉스(simplex)의 $(n - 1)$ -패싯(facet)의 초-부피는 다른 $n$ 패싯의 초-부피의 합보다 작거나 같습니다.

삼각형 부등식이 다각형 부등식으로 일반화되는 것과 마찬가지로, 임의의 차원의 심플렉스에 대해 부등식은 임의의 차원의 폴리토프(polytope)로 일반화됩니다: 폴리토프의 임의의 면의 초-부피는 남아있는 패싯의 초-부피의 합보다 작거나 같습니다.

어떤 경우에는 사면체 부등식이 삼각형 부등식의 여러 응용보다 더 강력합니다. 예를 들어, 삼각형 부등식은 유클리드 공간에서 다음 거리를 만족하는 4개의 점 $A$ , $B$ , $C$ , 및 $Z$ 의 가능성을 허용하는 것으로 보입니다:

AB = BC = CA = 26

및

AZ = BZ = CZ = 14

.

어쨌든, 그러한 거리를 갖는 점은 존재할 수 없습니다: 26–26–26 등변 삼각형 $ABC$ 의 넓이는 $169 \sqrt 3$ 이며, 이는 $39 \sqrt 3$ , 26–14–14 이등변 삼각형의 넓이 (모두 헤론의 공식으로 구함)의 3배보다 더 크므로, 배열은 사면체 부등식에 의해 금지됩니다.

Normed vector space

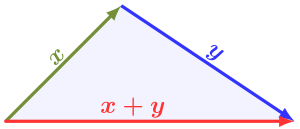
Triangle inequality for norms of vectors.

노름 벡터 공간(normed vector space) $V$ 에서, 노름(norm)의 정의하는 속성 중 하나는 다음 삼각형 부등식입니다:

\|x+y\|\leq \|x\|+\|y\|\quad \forall \,x,y\in V

즉, 두 벡터의 합(sum of two vectors)의 노름은 많아야 두 벡터의 노름의 합만큼 큽니다. 이것은 역시 부분-덧셈성(subadditivity)이라고 참조됩니다. 노름으로 행동하기 위한 제안된 함수에 대해, 그것은 이 요구 사항을 만족시켜야 합니다.^[15] 만약 노름 공간이 유클리드(euclidean), 또는, 더 일반적으로, 엄격하게 볼록(strictly convex)이면, $\|x+y\|=\|x\|+\|y\|$ 인 것과 $x$ , $y$ , 및 $x + y$ 에 의해 형성된 삼각형이 퇴화이며, 즉, $x$ 와 $y$ 가 같은 반직선 위에 있으며, 즉, $x = 0$ 또는 $y = 0$ , 또는 어떤 $α > 0$ 에 대해 $x = α y$ 인 것은 필요충분 조건입니다. 이 속성은 $1 < p < \infty$ 을 갖는 $ℓ p$ 공간과 같은 엄격하게 볼록 노름 공간을 특성화합니다. 어쨌든, 이것이 참이 아닌 노름 공간이 있습니다. 예를 들어, $ℓ 1$ 노름 (맨해튼 거리)를 갖는 평면을 고려하고 $x = (1, 0)$ 과 $y = (0, 1)$ 으로 표시합니다. 그런-다음 $x$ , $y$ , 및 $x + y$ 에 의해 형성된 삼각형은 비-퇴화이지만 다음입니다:

\|x+y\|=\|(1,1)\|=|1|+|1|=2=\|x\|+\|y\|.

Example norms

실수 직선(real line)에 대해 노름으로 절댓값. 노름이 되기 위해, 삼각형 부등식은 절댓값(absolute value)이 임의의 실수 $x$ 와 $y$ 에 대해 다음을 만족시킴을 요구합니다: $|x+y|\leq |x|+|y|,$ 이것이 그렇습니다.

증명:^[16]

-\left\vert x\right\vert \leq x\leq \left\vert x\right\vert

-\left\vert y\right\vert \leq y\leq \left\vert y\right\vert

덧셈 후에,

-(\left\vert x\right\vert +\left\vert y\right\vert )\leq x+y\leq \left\vert x\right\vert +\left\vert y\right\vert

$\left\vert b\right\vert \leq a\Leftrightarrow -a\leq b\leq a$ 라는 사실을 사용하며 (b를 x+y로 대체하고 a를 $\left\vert x\right\vert +\left\vert y\right\vert$ 로 대체하여), 우리는 다음을 가집니다:

|x+y|\leq |x|+|y|

삼각형 부등식은 개별 숫자의 크기 측면에서 두 숫자의 합 크기에 대한 최상의 위쪽 경계 추정을 결정하기 위한 수학적 해석학(mathematical analysis)에 유용합니다.

임의의 실수 $x$ 와 $y$ 에 대해 다음과 같은 반전 삼각형 부등식(reverse triangle inequality)을 사용하여 찾을 수 있는 더 낮은 추정값도 있습니다:

|x-y|\geq {\biggl |}|x|-|y|{\biggr |}.

안의 곱 공간(inner product space)에서 노름으로 안의 곱. 만약 노름이 (유클리드 공간에 대해 경우에서 처럼) 안의 곱에서 발생하면, 삼각형 부등식은 다음과 같이 코시-슈바르츠 부등식(Cauchy–Schwarz inequality)에서 따릅니다: 주어진 벡터 $x$ 와 $y$ 가 주어지고, 안의 곱을 $\langle x,y\rangle$ 로 표시하면:^[17]

$\\|x+y\\|^{2}$	$=\langle x+y,x+y\rangle$
	$=\\|x\\|^{2}+\langle x,y\rangle +\langle y,x\rangle +\\|y\\|^{2}$
	$\leq \\|x\\|^{2}+2\|\langle x,y\rangle \|+\\|y\\|^{2}$
	$\leq \\|x\\|^{2}+2\\|x\\|\\|y\\|+\\|y\\|^{2}$ (by the Cauchy–Schwarz inequality)
	$=\left(\\|x\\|+\\|y\\|\right)^{2}$ .

코시-슈바르츠 부등식이 상등으로 변하는 것과 $x$ 와 $y$ 가 선형 종속인 것은 필요충분 조건입니다. 부등식 $\langle x,y\rangle +\langle y,x\rangle \leq 2\left|\left\langle x,y\right\rangle \right|$ 이 선형적으로 종속 $x$ 와 $y$ 에 대해 상등으로 변하는 것과 벡터 $x$ 또는 $y$ 중 하나가 다른 것의 비-음의 스칼라인 것은 필요충분 조건입니다.

최종 결과의 제곱근을 취하면 삼각형 부등식을 제공합니다.

$p$ -노름( $p$ -norm): 공통적으로 사용된 노름은 p-노름입니다: $\|x\|_{p}=\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{1/p}\ ,$ 여기서 $x i$ 는 벡터 $x$ 의 구성 요소입니다. $p = 2$ 에 대해, $p$ -노름은 유클리드 노름(Euclidean norm)이 됩니다: $\|x\|_{2}=\left(\sum _{i=1}^{n}|x_{i}|^{2}\right)^{1/2}=\left(\sum _{i=1}^{n}x_{i}^{2}\right)^{1/2}\ ,$ 이는 $n$ -차원에서 피타고라스의 정리(Pythagoras' theorem)이며, 안의 곱 노름에 해당하는 매우 특별한 경우입니다. $p = 2$ 인 경우를 제외하고 $p$ -노름은 평행사변형 법칙(parallelogram law)을 만족시키지 않기 때문에 안의 곱 노름이 아닙니다. $p$ 의 일반 값에 대해 삼각형 부등식은 민코프스키의 부등식(Minkowski's inequality)이라고 불립니다.^[18] 그것은 다음과 같은 형식을 취합니다: $\|x+y\|_{p}\leq \|x\|_{p}+\|y\|_{p}\ .$

Metric space

메트릭 $d$ 를 갖는 메트릭 공간(metric space) $M$ 에서, 삼각형 부등식은 $M$ 에서 모든 $x$ , $y$ , $z$ 에 대해 거리(distance)에 대한 요구 사항입니다:

d(x,\ z)\leq d(x,\ y)+d(y,\ z)\ .

즉, $x$ 에서 $z$ 까지의 거리는 많아야 $x$ 에서 $y$ 까지의 거리와 $y$ 에서 $z$ 까지의 거리의 합만큼 커야 합니다.

삼각형 부등식은 메트릭 공간 위의 흥미로운 구조, 즉 수렴의 대부분을 담당합니다. 이것은 메트릭에 대한 남아있는 요구 사항이 비교적 단순하기 때문입니다. 예를 들어, 메트릭 공간에서 임의의 수렴 수열(convergent sequence)이 코시 수열(Cauchy sequence)이라는 사실은 삼각형 부등식의 직접적인 결과인데, 왜냐하면 $d (x n, x) < ε /2$ 와 $d (x m, x) < ε /2$ 를 만족하는 임의의 $x n$ 과 $x m$ 을 선택하면, 여기서 $ε > 0$ 가 주어지고 임의적이며 (메트릭 공간에서 극한 정의에서와 같이), 정의에 의해, 수열 ${x n}$ 이 코시 수열이 되도록, 삼각형 부등식에 의해, $d (x n, x m) \leq d (x n, x) + d (x m, x) < ε /2 + ε /2 = ε$ 입니다.

삼각형 부등식의 이 버전은 메트릭이 $d (x, y) ≔ ‖ x - y ‖$ 를 통해 유도되는 노름 벡터 공간의 경우에서 위에서 언급된 것으로 축소되며, $x - y$ 는 점 $y$ 에서 $x$ 를 가리키는 벡터입니다.

Reverse triangle inequality

반전 삼각형 부등식(reverse triangle inequality)은 위쪽 경계 대신 아래쪽 경계를 제공하는 삼각형 부등식의 기본 결과입니다. 평면 기하학에 대해, 그 명제는 다음과 같습니다:^[19]

삼각형의 한 변은 다른 두 변 사이의 차이보다 크거나 같습니다.

노름 벡터 공간의 경우에서, 그 명제는 다음과 같습니다:

{\bigg |}\|x\|-\|y\|{\bigg |}\leq \|x-y\|,

또는 메트릭 공간에 대해, $| d (y, x) - d (x, z)| \leq d (y, z)$ 입니다. 이것은 노름 $\|\cdot \|$ 와 마찬가지로 거리 함수 $d(x,\cdot )$ 는 립시츠 상수 1을 갖는 립시츠 연속(Lipschitz continuous)이고, 따라서 특히 균등 연속(uniformly continuous)임을 의미합니다.

반전 삼각형에 대해 증명은 정규 삼각형 부등식과 $\|y-x\|=\|{-}1(x-y)\|=|{-}1|\cdot \|x-y\|=\|x-y\|$ 를 사용합니다:

\|x\|=\|(x-y)+y\|\leq \|x-y\|+\|y\|\Rightarrow \|x\|-\|y\|\leq \|x-y\|,

\|y\|=\|(y-x)+x\|\leq \|y-x\|+\|x\|\Rightarrow \|x\|-\|y\|\geq -\|x-y\|,

이들 두 명제를 결합하면 다음을 제공합니다:

-\|x-y\|\leq \|x\|-\|y\|\leq \|x-y\|\Rightarrow {\bigg |}\|x\|-\|y\|{\bigg |}\leq \|x-y\|.

Triangle inequality for cosine similarity

호 길이에 대해 삼각형 부등식과 반전 삼각형 부등식에 코사인 함수를 적용하고 코사인에 대한 각도 덧셈과 뺄셈 공식을 사용함으로써, 그것은 다음임을 즉시 따릅니다:

$\operatorname {sim} (x,z)\geq \operatorname {sim} (x,y)\cdot \operatorname {sim} (y,z)-{\sqrt {\left(1-\operatorname {sim} (x,y)^{2}\right)\cdot \left(1-\operatorname {sim} (y,z)^{2}\right)}}$

및

$\operatorname {sim} (x,z)\leq \operatorname {sim} (x,y)\cdot \operatorname {sim} (y,z)+{\sqrt {\left(1-\operatorname {sim} (x,y)^{2}\right)\cdot \left(1-\operatorname {sim} (y,z)^{2}\right)}}\,.$

이러한 공식과 함께, 검사된 벡터 ${x, y}$ 의 각 쌍에 대해 $arccos(sim(x, y))$ 가 아니라 검사되는 벡터 ${x, y, z}$ 의 각 세-쌍에 대해 제곱근(square root)을 계산해야 하고, 검사된 세-쌍의 수가 검사된 쌍의 수보다 적을 때 성능이 향상될 수 있습니다.

Reversal in Minkowski space

민코프스키 공간(Minkowski space) 메트릭 $\eta _{\mu \nu }$ 는 양의-한정이 아니며. 이는 $\|x\|^{2}=\eta _{\mu \nu }x^{\mu }x^{\nu }$ 는 벡터 $x$ 가 비-영이더라도 부호를 가지거나 사라질 수 있음을 의미합니다. 더욱이, 만약 $x$ 와 $y$ 가 모두 미래의 빛 원뿔에 놓이는 시간과-같은 벡터이면, 삼각형 부등식이 반전됩니다:

\|x+y\|\geq \|x\|+\|y\|.

이러한 부등식의 물리적 예는 특수 상대성(special relativity)에서 쌍둥이 역설(twin paradox)입니다. 부등식의 같은 반전된 형식은 만약 두 벡터가 모두 과거 빛 원뿔에 놓이고, 하나 또는 둘 다가 널 벡터이면 유지됩니다. 결과는 임의의 $n\geq 1$ 에 대해 $n+1$ 차원으로 유지됩니다. 만약 $x$ 와 $y$ 에 의해 정의된 평면이 공간과 비슷하면 (따라서 유클리드 부분-공간이면), 보통의 삼각형 부등식이 유지됩니다.

Notes

^ Wolfram MathWorld – http://mathworld.wolfram.com/TriangleInequality.html
^ Mohamed A. Khamsi; William A. Kirk (2001). "§1.4 The triangle inequality in $R n$ ". An introduction to metric spaces and fixed point theory. Wiley-IEEE. ISBN 0-471-41825-0.
^ for instance, Jacobs, Harold R. (1974), Geometry, W. H. Freeman & Co., p. 246, ISBN 0-7167-0456-0
^ Oliver Brock; Jeff Trinkle; Fabio Ramos (2009). Robotics: Science and Systems IV. MIT Press. p. 195. ISBN 978-0-262-51309-8.
^ Arlan Ramsay; Robert D. Richtmyer (1995). Introduction to hyperbolic geometry. Springer. p. 17. ISBN 0-387-94339-0.
^ Harold R. Jacobs (2003). Geometry: seeing, doing, understanding (3rd ed.). Macmillan. p. 201. ISBN 0-7167-4361-2.
^ David E. Joyce (1997). "Euclid's elements, Book 1, Proposition 20". Euclid's elements. Dept. Math and Computer Science, Clark University. Retrieved 2010-06-25.
^ American Mathematical Monthly, pp. 49-50, 1954.
^ Claude Irwin Palmer (1919). Practical mathematics for home study: being the essentials of arithmetic, geometry, algebra and trigonometry. McGraw-Hill. p. 422.
^ Alexander Zawaira; Gavin Hitchcock (2009). "Lemma 1: In a right-angled triangle the hypotenuse is greater than either of the other two sides". A primer for mathematics competitions. Oxford University Press. ISBN 978-0-19-953988-8.
^ Wolfram|Alpha. "input: solve 0<a<2a+3d, 0<a+d<2a+2d, 0<a+2d<2a+d,". Wolfram Research. Retrieved 2010-09-07.
^ Wolfram|Alpha. "input: solve 0<a<ar+ar², 0<ar<a+ar², 0<ar²<a+ar". Wolfram Research. Retrieved 2010-09-07.
^ Wolfram|Alpha. "input: solve 0<a<ar+ar²+ar³, 0<ar³<a+ar+ar²". Wolfram Research. Retrieved 2012-07-29.
^ John Stillwell (1997). Numbers and Geometry. Springer. ISBN 978-0-387-98289-2. p. 95.
^ Rainer Kress (1988). "§3.1: Normed spaces". Numerical analysis. Springer. p. 26. ISBN 0-387-98408-9.
^ James Stewart (2008). Essential Calculus. Thomson Brooks/Cole. p. A10. ISBN 978-0-495-10860-3.
^ John Stillwell (2005). The four pillars of geometry. Springer. p. 80. ISBN 0-387-25530-3.
^ Karen Saxe (2002). Beginning functional analysis. Springer. p. 61. ISBN 0-387-95224-1.
^ Anonymous (1854). "Exercise I. to proposition XIX". The popular educator; fourth volume. Ludgate Hill, London: John Cassell. p. 196.

References

Pedoe, Daniel (1988). Geometry: A comprehensive course. Dover. ISBN 0-486-65812-0..
Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. ISBN 0-07-054235-X..

External links

Triangle inequality at ProofWiki

[1] Wolfram MathWorld – http://mathworld.wolfram.com/TriangleInequality.html

[Khamsi-2] Mohamed A. Khamsi; William A. Kirk (2001). "§1.4 The triangle inequality in $R n$ ". An introduction to metric spaces and fixed point theory. Wiley-IEEE. ISBN 0-471-41825-0.

[3] r instance, Jacobs, Harold R. (1974), Geometry, W. H. Freeman & Co., p. 246, ISBN 0-7167-0456-0

[Ramos-4] Oliver Brock; Jeff Trinkle; Fabio Ramos (2009). Robotics: Science and Systems IV. MIT Press. p. 195. ISBN 978-0-262-51309-8.

[Ramsay-5] Arlan Ramsay; Robert D. Richtmyer (1995). Introduction to hyperbolic geometry. Springer. p. 17. ISBN 0-387-94339-0.

[Jacobs-6] Harold R. Jacobs (2003). Geometry: seeing, doing, understanding (3rd ed.). Macmillan. p. 201. ISBN 0-7167-4361-2.

[Joyce-7] David E. Joyce (1997). "Euclid's elements, Book 1, Proposition 20". Euclid's elements. Dept. Math and Computer Science, Clark University. Retrieved 2010-06-25.

[8] American Mathematical Monthly, pp. 49-50, 1954.

[Palmer-9] Claude Irwin Palmer (1919). Practical mathematics for home study: being the essentials of arithmetic, geometry, algebra and trigonometry. McGraw-Hill. p. 422.

[Zawaira-10] Alexander Zawaira; Gavin Hitchcock (2009). "Lemma 1: In a right-angled triangle the hypotenuse is greater than either of the other two sides". A primer for mathematics competitions. Oxford University Press. ISBN 978-0-19-953988-8.

[11] Wolfram|Alpha. "input: solve 0<a<2a+3d, 0<a+d<2a+2d, 0<a+2d<2a+d,". Wolfram Research. Retrieved 2010-09-07.

[12] Wolfram|Alpha. "input: solve 0<a<ar+ar², 0<ar<a+ar², 0<ar²<a+ar". Wolfram Research. Retrieved 2010-09-07.

[13] Wolfram|Alpha. "input: solve 0<a<ar+ar²+ar³, 0<ar³<a+ar+ar²". Wolfram Research. Retrieved 2012-07-29.

[14] John Stillwell (1997). Numbers and Geometry. Springer. ISBN 978-0-387-98289-2. p. 95.

[Kress-15] Rainer Kress (1988). "§3.1: Normed spaces". Numerical analysis. Springer. p. 26. ISBN 0-387-98408-9.

[Stewart-16] James Stewart (2008). Essential Calculus. Thomson Brooks/Cole. p. A10. ISBN 978-0-495-10860-3.

[Stillwell-17] John Stillwell (2005). The four pillars of geometry. Springer. p. 80. ISBN 0-387-25530-3.

[Saxe-18] Karen Saxe (2002). Beginning functional analysis. Springer. p. 61. ISBN 0-387-95224-1.

[inequality-19] Anonymous (1854). "Exercise I. to proposition XIX". The popular educator; fourth volume. Ludgate Hill, London: John Cassell. p. 196.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

$\\|x+y\\|^{2}$	$=\langle x+y,x+y\rangle$
	$=\\|x\\|^{2}+\langle x,y\rangle +\langle y,x\rangle +\\|y\\|^{2}$
	$\leq \\|x\\|^{2}+2\|\langle x,y\rangle \|+\\|y\\|^{2}$
	$\leq \\|x\\|^{2}+2\\|x\\|\\|y\\|+\\|y\\|^{2}$ (by the Cauchy–Schwarz inequality)
	$=\left(\\|x\\|+\\|y\\|\right)^{2}$ .