Elementary algebra

{\overset {}{\underset {}{x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}}}

The quadratic formula, which is the solution to the quadratic equation

ax^{2}+bx+c=0

where

a\neq 0

. Here the symbols

a,b,c

represent arbitrary numbers, and

x

is a variable which represents the solution of the equation.

Two-dimensional plot (red curve) of the algebraic equation $y=x^{2}-x-2$

기초 대수학(elementary algebra)은, 수학(mathematics)의 주요 가지 중 하나, 대수학(algebra)의 기본 개념 중 일부를 포함합니다. 그것은 전형적으로 중등 학교(secondary school) 학생들에게 가르치고 산술(arithmetic)의 이해를 세웁니다. 산술은 지정된 숫자를 다루지만,^[1] 대수는 변수로 알려진 고정된 값없이 양을 도입합니다.^[2] 이 변수의 사용은 대수적 표기법의 사용을 수반하고 산술에서 도입된 연산자(operator)의 일반적인 규칙의 이해를 수반합니다. 추상 대수학(abstract algebra)과는 달리, 기초 대수학은 실수(real)와 복소수(complex) 영역 밖의 대수적 구조(algebraic structures)와는 관련이 없습니다.

양을 나타내기 위해 변수의 사용은 양 사이의 일반적인 관계를 공식적이고 간결하게 표현됨을 허용하고, 따라서 문제의 보다 광범위한 범위를 해결하는 것을 활성화합니다. 과학과 수학에서 많은 양적 관계는 대수적 방정식(equation)으로 표현됩니다.

Algebraic notation

대수적 표기법은 수학적 표현(mathematical expressions)을 작성하는 것에 대해 규칙과 관례, 마찬가지로 표현의 일부에 대한 이야기하는 것에 사용되는 용어를 설명합니다. 예를 들어, 표현 $3x^{2}-2xy+c$ 은 다음 구성-요소를 가집니다:

계수(coefficient)는 변수를 곱하는 숫자 값, 또는 숫자 상수를 나타내는 문자입니다 (연사자는 생략됩니다). 항(term)은 더하기 또는 빼기 연산자에 의해 다른 항과 분리될 수 있는, 더하는 숫자 또는 더해지는 숫자(addend or a summand), 계수의 그룹, 변수, 상수 및 지수입니다.^[3] 문자는 변수와 상수를 나타냅니다. 관례에 의해, 알파벳의 시작하는 것에서 문자 (예를 들어, $a,b,c$ )가 전형적으로 상수(constant)를 나타내기 위해 사용되고, 알파벳의 끝으로 향하는 그것들 (예를 들어, $x,y,z$ )는 변수(variable)를 나타내기 위해 사용됩니다.^[4] 그것들은 보통 기울임꼴로 쓰입니다.^[5]

대수적 연산은 덧셈(addition), 뺄셈(subtraction), 곱셈(multiplication), 나눗셈(division)과 지수화(exponentiation)와 같은 산술 연산(arithmetic operations)과^[6] 같은 방법으로 작동하고,^[7] 대수적 변수와 항에 적용됩니다. 곱셈 기호는 보통, 두 변수 또는 항 사이에 공백이 없거나, 계수(coefficient)가 사용될 때, 생략되고 암시됩니다. 예를 들어, $3\times x^{2}$ 는 $3x^{2}$ 로 쓰이고, $2\times x\times y$ 는 $2xy$ 로 쓸 수 있습니다.^[8]

보통 가장-높은 거듭제곱 (지수(exponent))를 갖는 항은 왼쪽에 쓰입니다. 예를 들어, $x^{2}$ 은 $x$ 의 왼쪽에 쓰입니다. 개수가 일일 때, 그것은 보통 생략됩니다 (예를 들어, $1x^{2}$ 은 $x^{2}$ 으로 쓰입니다).^[9] 지수 (거듭제곱)이 일일 때도 마찬가지입니다 (예를 들어, $3x^{1}$ 는 $3x$ 로 쓰입니다).^[10] 지수가 영일 때, 결과는 항상 1입니다 (예를 들어, $x^{0}$ 는 항상 $1$ 로 쓰입니다).^[11] 어쨌든 $0^{0}$ 은, 비-정의된 것이며, 표현에서 나타날 수 없고, 주의는 변수가 지수에서 나타날 수 있는 표현을 단순화하는 것에서 취해져야 합니다.

Alternative notation

표기법의 다른 유형은 요구된 형식이 유용하지 않을 때, 또는 오직 문자와 기호가 유용한 곳과 같은 암시될 수 없을 때 대수적 표현에 사용됩니다. 이것의 실례로서, 지수는 보통 위첨자, 예를 들어, $x^{2}$ 를 사용하여 형식화되지만, 보통 텍스트(plain text), 및 텍(TeX) 마크-업 언어에서, 캐럿(caret) 기호 "^"가 지수화를 나타내므로, $x^{2}$ 은 "x^2"으로 쓰이며,^[12]^[13] Lus와 같은 일부 프로그래밍 언어에서도 마찬가지입니다. 에이다(Ada),^[14] 포트란(Fortran),^[15] 펄(Perl),^[16] 파이선(Python)^[17] 및 루비(Ruby),^[18]와 같은 프로그래밍 언어에서, 이중 별표가 사용되므로, $x^{2}$ 은 "x**2"로 쓰입니다. 많은 프로그래밍 언어와 계산기는 곱셈 기호를 나타내기 위해 단일 별표를 사용하고,^[19] 그것은 명시적으로 사용되어야 합니다. 예를 들어, $3x$ 는 "3*x"으로 쓰입니다.

Concepts

Variables

기초 대수는 일반적인 (비-지정된) 숫자를 나타내기 위한 변수라고 불리는 문자를 도입함으로써 산술을 구축하고 확장합니다.^[20] 이것은 여러 가지 이유로 유용합니다.

변수는 값이 아직 알려지지 않은 숫자를 나타낼 수 있습니다. 예를 들어, 만약 오늘의 기온, C가 전날의 기온, P보다 20도 더 높으면, 문제는 $C=P+20$ 으로 대수적으로 설명될 수 있습니다.^[21]
변수는 관련되는 양의 값을 지정하지 것없이 일반적인 문제를 설명하는 것을 허용합니다.^[22] 예를 들어, 5분은 $60\times 5=300$ 초와 동등하다고 구체적으로 지정될 수 있습니다. 보다 일반적인 (대수적) 설명은 초의 숫자, $s=60\times m$ 을 나타낼 수 있으며, 여기서 m은 분의 숫자입니다.
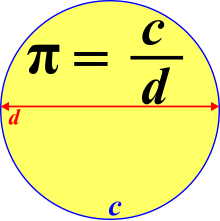
변수는 변할 수 있는 양 사이의 수학적 관계를 설명하는 것을 허용합니다.^[23] 예를 들어, 원의 둘레, c와 지름 d 사이의 관계는 $\pi =c/d$ 에 의해 설명됩니다.
변수는 일부 수학적 속성을 설명하는 것을 허용합니다. 예를 들어, 덧셈의 기본 속성은 함께 더해지는 숫자의 순서가 중요하지 않음을 나타내는 교환성(commutativity)입니다. 교환성은 대수적으로 $(a+b)=(b+a)$ 로 말합니다.^[24]

Simplifying expressions

대수적 표현은 산술 연산 (덧셈(addition), 뺄셈(subtraction), 곱셈(multiplication), 나눗셈(division) 및 지수화(exponentiation))의 기본 속성을 기반으로 평가되고 단순화될 수 있습니다. 예를 들어,

더해진 항은 계수를 사용하여 단순화됩니다. 예를 들어, $x+x+x$ 는 $3x$ 로 단순화될 수 있습니다 (여기서 3은 숫자 계수입니다).
곱해진 항은 지수를 사용하여 단순화됩니다. 예를 들어, $x\times x\times x$ 는 $x^{3}$ 로 표현됩니다.
동류 항은 함께 더합니다.^[25] 예를 들어, $2x^{2}+3ab-x^{2}+ab$ 는 $x^{2}+4ab$ 로 쓰이는데, 왜냐하면 $x^{2}$ 을 포함하는 항은 함께 더해지고, $ab$ 를 포함하는 항은 함께 더합니다.
괄호는 분배 속성(distributive property)을 사용하여 "곱해져 나옵니다". 예를 들어, $x(2x+3)$ 는 $(x\times 2x)+(x\times 3)$ 로 쓸 수 있으며, 이것은 $2x^{2}+3x$ 로 쓸 수 있습니다.
표현은 인수화될 수 있습니다. 예를 들어, $6x^{5}+3x^{2}$ 는, $3x^{2}$ 로 양쪽 항을 나눔으로써, $3x^{2}(2x^{3}+1)$ 로 쓸 수 있습니다.

Equations

방정식은 두 표현이 상등에 대해 기호, = (같음 기호(equals sign))를 사용하여 같다는 것을 나타냅니다.^[26] 가장 잘 알려진 방정식 중 하나는 직각(right angle) 삼각형의 변의 길이와 관련된 피타고라스의 법칙을 설명합니다:^[27]

c^{2}=a^{2}+b^{2}

이 방정식은 직각의 반대편 변, 빗변인 변의 길이의 제곱을 나타내는 $c^{2}$ 이 그것의 길이가 $a$ 와 $b$ 에 의해 표시되는 다른 두 변의 제곱의 합 (덧셈)과 같다는 것을 말합니다.

방정식은 두 표현이 같은 값을 가지고 같다는 것을 주장입니다. 일부 방정식은 관련된 변수의 모든 값에 대해 참입니다 (예를 들어, $a+b=b+a$ ); 그러한 방정식은 항등식(identities)이라고 불립니다. 조건부 방정식은 관련된 변수의 오직 일부 값에 대해 참입니다. 예를 들어, $x^{2}-1=8$ 는 $x=3$ 과 $x=-3$ 에 대해 오직 참입니다. 방정식을 참으로 만드는 변수의 값은 방정식의 해이고 방정식 푸는 것(equation solving)을 통해 찾아질 수 있습니다.

또 다른 방정식의 유형은 부등식입니다. 부등식은 방정식의 한쪽이 다른 쪽보다 크거나 작음을 표시하기 위해 사용됩니다. 이것에 대해 사용되는 기호는 다음입니다: $a>b$ 여기서 $>$ 는 '보다 큼'을 나타내고, $a<b$ 여기서 $<$ 은 '보다 작음'을 나타냅니다. 표준 상등 방정식과 마찬가지로, 숫자는 더해지거나, 빼지거나, 곱해지거나, 나뉠 수 있습니다. 유일한 예외는 음수로 곱하거나 나뉠 때, 부등식 기호는 뒤집어져야 한다는 것입니다.

Properties of equality

정의에 따라, 상등은 동치 관계(equivalence relation)이며, 그것은 (a) 반사적(reflexive) (예를 들어, $b=b$ ), (b) 대칭적(symmetric) (예를 들어, 만약 $a=b$ 이면 $b=a$ 입니다) (c) 전이적(transitive) (예를 들어, 만약 $a=b$ 와 $b=c$ 이면 $a=c$ 입니다) 속성을 가지는 것을 의미합니다.^[28] 그것은 역시 만약 두 기호가 같은 것에 사용되면, 하나의 기호는 첫 번째에 대한 임의의 참 명제에서 다른 기호로 대체될 수 있고 그 명제는 참으로 유지될 것이라는 중요한 속성을 만족시킵니다. 이것은 다음 속성을 의미합니다:

만약 $a=b$ 이고 $c=d$ 이면 $a+c=b+d$ 이고 $ac=bd$ 입니다;
만약 $a=b$ 이면 $a+c=b+c$ 이고 $ac=bc$ 입니다;
보다 일반적으로, 임의의 함수 $f$ 에 대해, 만약 $a=b$ 이면 $f(a)=f(b)$ 입니다.

Properties of inequality

관계 보다 작음 $<$ 과 보다 큼 $>$ 은 전이성의 속성을 가집니다:^[29]

만약 $a<b$ 이고 $b<c$ 이면 $a<c$ 입니다;
만약 $a<b$ 이고 $c<d$ 이면 $a+c<b+d$ 입니다;^[30]
만약 $a<b$ 이고 $c>0$ 이면 $ac<bc$ 입니다;
만약 $a<b$ 이고 $c<0$ 이면 $bc<ac$ 입니다.

부등식을 반전함으로써, $<$ 과 $>$ 은 서로 바꿀 수 있습니다.^[31] 예를 들어:

$a<b$ 는 $b>a$ 과 동등합니다.

Substitution

치환은 표현에서 항을 새로운 표현을 생성하기 위해 대체하는 것입니다. 표현 $a *5$ 에서 $a$ 에 대해 3을 치환하는 것은 15를 의미하는 새로운 표현 $3*5$ 를 만듭니다. 명제의 항을 치환하는 것은 새로운 명제를 만듭니다. 원래 명제가 항의 값에 관계없이 참일 때, 치환에 의해 생성된 명제는 역시 참입니다. 따라서, 정의는 기호적 항으로 만들어질 수 있고 치환을 통해 해석될 수 있습니다: 만약 $a^{2}:=a\times a$ 가 $a$ 와 자체의 곱으로 $a^{2}$ 의 정의를 의미하면, $a$ 에 대해 3을 치환하는 것은 $3^{2}$ 은 $3 \times 3 = 9$ 를 의미함을 이 명제의 독자에게 알립니다. 종종 그 명제가 항의 값과 독립적으로 참인지 여부는 알 수 없습니다. 그리고, 치환은 가능한 값에 대한 제한을 유도하는 것, 또는 명제를 어떤 조건에 아래에서 유지되는지 보여주는 것을 허용합니다. 예를 들어, 명제 $x + 1 = 0$ 취하면, 만약 $x$ 가 1로 치환되면, 이것은 거짓인 $1 + 1 = 2 = 0$ 을 의미하며, 이것은 만약 $x + 1 = 0$ 이면 $x$ 는 1이 될 수 없음을 의미합니다.

만약 $x$ 와 $y$ 가 정수(integers), 유리수(rationals), 또는 실수(real numbers)이면, $xy = 0$ 는 $x = 0$ 또는 $y = 0$ 임을 의미합니다. $abc = 0$ 를 생각해 보십시오. 그런-다음, $x$ 에 대해 $a$ 를 치환하고 $y$ 에 대해 $bc$ 를 치환하면, 우리는 $a = 0$ 또는 $bc = 0$ 임을 배웁니다. 그런-다음 우리는 다시 치환할 수 있으며, 만약 $bc = 0$ 이면 $b = 0$ 또는 $c = 0$ 임을 보이기 위해 $x = b$ 또는 $y = c$ 라고 놓습니다. 따라서, 만약 $abc = 0$ 이면, $a = 0$ 또는 ( $b = 0$ 또는 $c = 0$ )이므로, $abc = 0$ 은 $a = 0$ 또는 $b = 0$ 또는 $c = 0$ 임을 의미합니다.

만약 원래 사실이 " $ab = 0$ 가 $a = 0$ 또는 $b = 0$ 을 의미함"으로 말해졌다면, " $abc = 0$ 을 생각해 보십시오"라고 말할 때, 우리는 치환할 때 항의 충돌을 가졌을 것입니다. 그러나 위의 논리는 만약 $abc = 0$ 이면 $a = 0$ 또는 $b = 0$ 또는 $c = 0$ 이면 만약, $a = a$ 과 $b = bc$ 라고 놓는 대신에, 우리가 $a$ 에 대해 a로, $bc$ 에 대해 $b$ 를 치환하는 (및 $bc = 0$ 와 함께, $a$ 에 대해 $b$ 를 및 $b$ 에 대해 $c$ 를 치환하는) 것을 보여주는 것이 여전히 유효합니다. 이것은 명제에서 항을 치환하는 것이 명제로부터 항을 치환된 항과 같게 놓는 것과 항상 같은 것은 않음을 보여줍니다. 이 상황에서 만약 우리가 표현 $a$ 를 원래 방정식의 $a$ 항으로 치환하면, 대체된 $a$ 는 명제 " $ab = 0$ 은 $a = 0$ 또는 $b = 0$ 을 의미함"에서 $a$ 를 참조하지 않는다는 것이 분명합니다.

Solving algebraic equations

다음 섹션은 접할 수 있는 몇 가지 대수적 방정식의 유형의 예제를 배치합니다.

Linear equations with one variable

선형 방정식은, 그것들이 그려질 때, 직선을 설명하기 때문에 그렇게 불립니다. 풀기 위한 가장 간단한 방정식은 오직 하나의 변수를 가지는 선형 방정식(linear equation)입니다. 그것들은 오직 상수와 지수없는 단일 변수를 포함합니다. 예제로, 다음을 생각해 보십시오:

말로 표현한 문제: 만약 아이의 나이를 두 배하고 4를 더하면, 그 결과의 답이 12입니다. 아이는 몇 살입니까?

동등한 방정식:

2x+4=12

여기서

x

는 아이의 나이를 나타냅니다.

이 종류의 방정식을 풀기 위해, 기법은 방정식의 한쪽 변에 있는 변수를 분리하기 위해 방정식의 양쪽 변을 같은 숫자로 더하거나, 빼거나, 곱하거나 나누는 것입니다. 일단 변수가 분리되면, 방정식의 다른 쪽은 변수의 값입니다.^[32] 이 문제와 그것의 해는 다음과 같습니다:

1. 풀기 위한 방정식:	$2x+4=12$
2. 양쪽 변에서 4를 뺍니다:	$2x+4-4=12-4$
3. 이것은 아래와 같이 단순화됩니다:	$2x=8$
4. 양쪽 변을 2로 나눕니다:	${\frac {2x}{2}}={\frac {8}{2}}$
5. 이것은 해로 단순화됩니다:	$x=4$

말로 표현한 해: 아이는 4살입니다.

하나의 변수를 갖는 선형 방정식의 일반적인 형식은 다음으로 쓸 수 있습니다:

ax+b=c

같은 과정을 따라 (즉, 양쪽 변에서 $b$ 를 빼고, 그런-다음 $a$ 로 나눕니다), 일반적인 해는 $x={\frac {c-b}{a}}$ 에 의해 제공됩니다.

Linear equations with two variables

Solving two linear equations with a unique solution at the point that they intersect.

두 변수를 갖는 선형 방정식은 많은 (즉, 무한 숫자의) 해를 가집니다.^[33] 예를 들어:

말로 표현한 문제: 아버지는 그의 아들보다 22년 더 나이가 많습니다. 그들은 몇 살입니까?

동등한 방정식:

y=x+22

여기서

y

는 아버지의 나이,

x

는 아들의 나이입니다.

그것은 자체로 해결될 수 없습니다. 만약 아들의 나이가 알려지게 되면, 더 이상 두 미지수 (변수)가 없습니다. 문제는 그런-다음 바로 위에서 설명한 것처럼 풀릴 수 있는 단지 하나의 변수를 갖는 선형 방정식이 됩니다.

두 변수 (미지수)를 갖는 선형 방정식을 풀기 위해, 두 관련된 방정식을 요구합니다. 예를 들어, 만약 그것이 역시 다음과 같이 밝혀지면:

말로 표현한 문제: 10년 후에, 아버지는 그의 아들보다 두 배의 나이가 될 것입니다.
동등한 방정식: ${\begin{aligned}y+10&=2\times (x+10)\\y&=2\times (x+10)-10&&{\text{Subtract 10 from both sides}}\\y&=2x+20-10&&{\text{Multiple out brackets}}\\y&=2x+10&&{\text{Simplify}}\end{aligned}}$

이제 두 개의 관련된 선형 방정식이 있으며, 각각 두 개의 미지수를 가지며, 하나를 다른 하나로 뺌으로써 단지 하나의 변수를 갖는 선형 방정식을 생성할 수 있습니다 (취소 방법이라고 함):^[34]

{\begin{cases}y=x+22&{\text{First equation}}\\y=2x+10&{\text{Second equation}}\end{cases}}

{\begin{aligned}&&&{\text{Subtract the first equation from}}\\(y-y)&=(2x-x)+10-22&&{\text{the second in order to remove }}y\\0&=x-12&&{\text{Simplify}}\\12&=x&&{\text{Add 12 to both sides}}\\x&=12&&{\text{Rearrange}}\end{aligned}}

달리 말해서, 아들은 12살이고 아버지는 22살 더 많으므로, 그는 34살이어야 합니다. 10년 후에, 아들은 22살이 될 것이고, 아버지는 그 나이의 두 배, 44살이 될 것입니다. 이 문제는 방정식의 관련된 그림에 묘사됩니다.

이 종류의 방정식을 푸는 다른 방법에 대해, 아래, 선형 방정식의 시스템을 참조하십시오.

Quadratic equations

Quadratic equation plot of $y=x^{2}+3x-10$ showing its roots at $x=-5$ and $x=2$ , and that the quadratic can be rewritten as $y=(x+5)(x-2)$

이차 방정식은 2의 지수를 갖는 항, 예를 들어, $x^{2}$ 을 포함하고,^[35] 더 높은 지수를 갖는 항을 포함하지 않는 방정식입니다. 이름은 정사각형(제곱)을 의미하는 라틴어 quadrus에서 유래되었습니다.^[36] 일반적으로, 이차 방정식은 형식 $ax^{2}+bx+c=0$ 으로 표현할 수 있으며,^[37] 여기서 $a$ 는 영이 아닙니다 (만약 그것이 영이면, 그 방정식은 이차가 아니라 선형일 것입니다). 이것 때문에 이차 방정식은 이차 항으로 알려져 있는 항 $ax^{2}$ 을 포함해야 합니다. 그러므로, $a\neq 0$ 이고, 따라서 우리는 $a$ 로 나눌 수 있고 방정식을 다음 표준 형식으로 재배열할 수 있습니다:

x^{2}+px+q=0

여기서 $p={\frac {b}{a}}$ 이고 $q={\frac {c}{a}}$ 입니다. 이것을 풀면, 제곱식을 완성(completing the square)으로 알려진 과정에 의해, 다음 이차 공식(quadratic formula)으로 이어집니다:

x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}},

여기서 기호 "±"는 다음 둘 다가 이차 방정식의 해임을 나타냅니다:

x={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\quad {\text{and}}\quad x={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}

.

이차 방정식은 역시 인수분해(factorization)를 사용하여 풀릴 수 있습니다 (인수분해의 반대 과정은 전개(expansion)이지만, 두 선형 항(linear terms)에 대해 때때로 포일링(foiling)으로 표시됩니다). 인수화의 예제로:

x^{2}+3x-10=0,

이것은 아래와 같은 것입니다:

(x+5)(x-2)=0.

두 $x=2$ 또는 $x=-5$ 이 해가 되는 것은 영-곱 속성(zero-product property)을 따르는데, 왜냐하면 정확하게 인수 중 하나가 영(zero)과 같아야 하기 때문입니다. 모든 이차 방정식은 복소수(complex number) 시스템에서 두 해를 가질 것이지만, 실수(real number) 시스템에서 어떤 해도 가지지 않을 수 있습니다.

x^{2}+1=0

위의 방정식은 실수 해를 가지지 않는데 왜냐하면 제곱된 실수는 −1과 같지 않습니다. 때때로 이차 방정식은 다음처럼 중복도(multiplicity) 2의 근을 가집니다:

(x+1)^{2}=0.

이 방정식에 대해, −1은 중복도 2의 근입니다. 이것은 −1이 두 번 나타남을 의미하는데, 왜냐하면 방정식은 다음으로 인수화된 형식에서 다시 쓸 수 있기 때문입니다:

[x-(-1)][x-(-1)]=0.

Complex numbers

모든 이차 방정식은 복소수(complex numbers)에서, 즉, 실수, 허수, 및 실수(real number)와 허수(imaginary number)의 합을 포함하는 카테고리에서 정확히 두 해를 가집니다 (그러나 그것들은 서로 같을 수 있습니다). 복소수는 이차 방정식과 이차 공식의 가르침에서 처음으로 발생합니다. 예를 들어, 다음 이차 방정식은

x^{2}+x+1=0

다음 해를 가집니다:

x={\frac {-1+{\sqrt {-3}}}{2}}\quad \quad {\text{and}}\quad \quad x={\frac {-1-{\sqrt {-3}}}{2}}.

${\sqrt {-3}}$ 는 임의의 실수가 아니기 때문에, x에 대해 이들 두 해는 복소수입니다.

Exponential and logarithmic equations

지수 방정식은 $a>0$ 에 대해 형식 $a^{x}=b$ 을 가지는 방정식이며,^[38] 이것은 $b>0$ 일 때 다음 해를 가집니다:

X=\log _{a}b={\frac {\ln b}{\ln a}}

기초 대수적 기법은 해에 도달하기 전에 위의 방법으로 주어진 방정식을 다시-쓰기 위해 사용됩니다. 예를 들어, 만약 다음이면

3\cdot 2^{x-1}+1=10

방정식의 양쪽 변에서 1을 빼고, 그런-다음 양쪽 변을 3으로 나눔으로써, 우리는 다음을 얻습니다:

2^{x-1}=3

로그 정의로부터

x-1=\log _{2}3

또는

x=\log _{2}3+1.

로그 방정식은 $a>0$ 에 대해 형식 $log_{a}(x)=b$ 의 방정식이며, 다음 해를 가집니다:

X=a^{b}.

예를 들어, 다음이면

4\log _{5}(x-3)-2=6

방정식의 양쪽 변에 2를 더하고, 그런-다음 양쪽 변을 4로 나눔으로써, 우리는 다음을 얻습니다:

\log _{5}(x-3)=2

로그 정의로부터

x-3=5^{2}=25

이것으로부터 우리는 다음을 얻습니다:

x=28.

Radical equations

{\overset {}{\underset {}{{\sqrt[{2}]{x^{3}}}\equiv x^{\frac {3}{2}}}}}

Radical equation showing two ways to represent the same expression. The triple bar means the equation is true for all values of x

제곱근 방정식은 제곱근 기호를 포함하는 방정식이며, 이-제곱근(square root), ${\sqrt {x}},$ 세-제곱근(cube root), ${\sqrt[{3}]{x}}$ , 및 n번째 근(nth roots), ${\sqrt[{n}]{x}}$ 을 포함합니다. n번째 근은 ${\sqrt[{n}]{x}}$ 가 $x^{\frac {1}{n}}$ 와 동등하도록 지수 형식에서 다시-쓸 수 있음을 기억해 내십시오. 정규 지수 (거듭제곱)을 결합하면, ${\sqrt[{2}]{x^{3}}}$ (세제곱근된 $x$ 의 제곱근)은 $x^{\frac {3}{2}}$ 으로 다시-쓸 수 있습니다.^[39] 따라서 제곱근 방정식의 공통 형식은 ${\sqrt[{n}]{x^{m}}}=a$ ( $x^{\frac {m}{n}}=a$ 과 동등함)이며, 여기서 $m$ 과 $n$ 은 정수입니다. 그것은 실수(real) 해를 가집니다:

$n$ 이 홀수	$n$ 이 짝수 및 $a\geq 0$	$n$ 과 $m$ 이 짝수 및 $a<0$	$n$ 이 짝수, $m$ 이 홀수, 및 $a<0$
$x={\sqrt[{n}]{a^{m}}}$ 동등하게 $x=\left({\sqrt[{n}]{a}}\right)^{m}$	$x=\pm {\sqrt[{n}]{a^{m}}}$ 동등하게 $x=\pm \left({\sqrt[{n}]{a}}\right)^{m}$	$x=\pm {\sqrt[{n}]{a^{m}}}$	실수 해 없음

예를 들어, 만약 다음이면:

(x+5)^{2/3}=4

다음이고

{\begin{aligned}x+5&=\pm ({\sqrt {4}})^{3},\\x+5&=\pm 8,\\x&=-5\pm 8,\end{aligned}}

따라서 다음입니다:

x=3\quad {\text{or}}\quad x=-13

System of linear equations

두 변수를 갖는 선형 방정식의 시스템을 푸는 다른 방법이 있습니다.

Elimination method

선형 방정식의 시스템을 푸는 예제는 취소 방법을 사용하는 것입니다:

{\begin{cases}4x+2y&=14\\2x-y&=1.\end{cases}}

두 번째 방정식에서 항에 2를 곱하면:

4x+2y=14

4x-2y=2.

다음을 얻기 위해 두 방정식을 함께 더하면:

8x=16

이것은 다음으로 단순화됩니다:

x=2.

$x=2$ 가 알려진 사실이기 때문에, 그런-다음 ( $x$ 대신에 2를 사용함으로써) 원래 두 방정식의 하나에 의해 $y=3$ 임을 추론할 수 있습니다. 이 방정식에 대한 완전한 해는 그런-다음 다음입니다:

{\begin{cases}x=2\\y=3.\end{cases}}

이것은 이 특정 시스템을 풀기 위한 유일한 방법은 아닙니다; $y$ 는 $x$ 전에 해결되었습니다.

Substitution method

같은 선형 방정식의 시스템을 푸는 또 다른 방법은 대체에 의한 것입니다.

{\begin{cases}4x+2y&=14\\2x-y&=1.\end{cases}}

$y$ 에 대해 동등한 것은 두 방정식의 하나를 사용함으로써 추론될 수 있습니다. 두 번째 방정식을 사용하여:

2x-y=1

방정식의 각 변으로부터 $2x$ 를 빼면:

{\begin{aligned}2x-2x-y&=1-2x\\-y&=1-2x\end{aligned}}

그리고 양쪽 변에 −1을 곱하면:

y=2x-1.

이 $y$ 값을 원래 시스템의 첫 번째 방정식에서 사용하면:

{\begin{aligned}4x+2(2x-1)&=14\\4x+4x-2&=14\\8x-2&=14\end{aligned}}

방정식의 각 변에 2를 더하면:

{\begin{aligned}8x-2+2&=14+2\\8x&=16\end{aligned}}

이것은 다음으로 단순화됩니다:

x=2

이 값을 방정식의 하나에 사용하면, 이전 방법에서 처럼 같은 해가 얻습니다.

{\begin{cases}x=2\\y=3.\end{cases}}

이것은 이 특정 시스템을 풀기 위한 유일한 방법이 아닙니다; 이 경우에서 마찬가지로, $y$ 는 $x$ 전에 해결되었습니다.

Other types of systems of linear equations

Inconsistent systems

Plot of a quadratic equation (red) and a linear equation (blue) that do not intersect, and consequently for which there is no common solution.

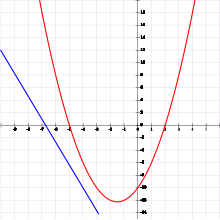
위의 예제에서, 해가 존재합니다. 어쨌든, 임의의 해를 가지지 않는 방정식의 시스템이 역시 있습니다. 그러한 시스템은 불일치(inconsistent)라고 불립니다. 명백한 예제는 다음입니다:

{\begin{cases}{\begin{aligned}x+y&=1\\0x+0y&=2\,.\end{aligned}}\end{cases}}

0≠2이므로, 시스템에서 두 번째 방정식은 해를 가지지 않습니다. 그러므로, 시스템은 해를 가지지 않습니다. 어쨌든, 모든 불일치 시스템이 한 눈에 인식되는 것은 아닙니다. 예제로서, 다음 시스템을 생각해 보십시오:

{\begin{cases}{\begin{aligned}4x+2y&=12\\-2x-y&=-4\,.\end{aligned}}\end{cases}}

두 번째 방정식의 양쪽 변에 2를 곱하고, 그것을 첫 번째 방정식에 곱하면 다음을 초래합니다:

0x+0y=4\,,

이것은 명백하게 해를 가지지 않습니다.

Undetermined systems

고유한 해 ( $x$ 와 $y$ 에 대해 고유한 값의 쌍을 의미함)를 가진 시스템과 달리, 무한하게 많은 해를 가지는 시스템이 역시 있습니다. 예를 들어:

{\begin{cases}{\begin{aligned}4x+2y&=12\\-2x-y&=-6\end{aligned}}\end{cases}}

두 번째 방정식에서 $y$ 를 분리하면:

y=-2x+6

그리고 시스템의 첫 번째 방정식에서 이 값을 사용하면:

{\begin{aligned}4x+2(-2x+6)=12\\4x-4x+12=12\\12=12\end{aligned}}

상등은 참이지만, 그것이 $x$ 에 대해 값을 제공하지는 않습니다. 실제로, 우리는 임의의 $x$ 에 대해 $y=-2x+6$ 하는 한 해가 있다는 것을 쉽게 확인할 수 있습니다 (단지 $x$ 의 일부 값을 채움으로써 확인할 수 있습니다). 이 시스템에 대해 무한한 숫자의 해가 있습니다.

Over- and underdetermined systems

선형 방정식의 숫자보다 더 많은 변수를 갖는 시스템은 미달-결정된(underdetermined) 것이라고 불립니다. 그러한 시스템은, 만약 그것이 임의의 해를 가지면, 고유한 해를 가지는 것이 아니라 무한한 해를 가집니다. 그러한 시스템의 예제는 다음입니다:

{\begin{cases}{\begin{aligned}x+2y&=10\\y-z&=2.\end{aligned}}\end{cases}}

그것을 풀려고 시도할 때, 우리는 임의의 해가 존재하면 어떤 변수를 다른 변수의 함수로 표현하는 것으로 이어지지만, 수치적으로(numerically) 모든 해를 표현할 수는 없는데 왜냐하면 만약 해가 있으면 해의 무한 숫자가 있기 때문입니다.

변수보다 방정식의 숫자가 더 많은 시스템은 초과-결정된(overdetermined) 것이라고 불립니다. 만약 초과-결정된 시스템이 임의의 해를 가지면, 필연적으로 일부 방정식은 다른 방정식의 선형 조합(linear combination)입니다.

References

Leonhard Euler, Elements of Algebra, 1770. English translation Tarquin Press, 2007, ISBN 978-1-899618-79-8, also online digitized editions^[40] 2006,^[41] 1822.
Charles Smith, A Treatise on Algebra, in Cornell University Library Historical Math Monographs.
Redden, John. Elementary Algebra. Flat World Knowledge, 2011

^ H.E. Slaught and N.J. Lennes, Elementary algebra, Publ. Allyn and Bacon, 1915, page 1 (republished by Forgotten Books)
^ Lewis Hirsch, Arthur Goodman, Understanding Elementary Algebra With Geometry: A Course for College Students, Publisher: Cengage Learning, 2005, ISBN 0534999727, 9780534999728, 654 pages, page 2
^ Richard N. Aufmann, Joanne Lockwood, Introductory Algebra: An Applied Approach, Publisher Cengage Learning, 2010, ISBN 1439046042, 9781439046043, page 78
^ William L. Hosch (editor), The Britannica Guide to Algebra and Trigonometry, Britannica Educational Publishing, The Rosen Publishing Group, 2010, ISBN 1615302190, 9781615302192, page 71
^ James E. Gentle, Numerical Linear Algebra for Applications in Statistics, Publisher: Springer, 1998, ISBN 0387985425, 9780387985428, 221 pages, [James E. Gentle page 183]
^ Horatio Nelson Robinson, New elementary algebra: containing the rudiments of science for schools and academies, Ivison, Phinney, Blakeman, & Co., 1866, page 7
^ Ron Larson, Robert Hostetler, Bruce H. Edwards, Algebra And Trigonometry: A Graphing Approach, Publisher: Cengage Learning, 2007, ISBN 061885195X, 9780618851959, 1114 pages, page 6
^ Sin Kwai Meng, Chip Wai Lung, Ng Song Beng, "Algebraic notation", in Mathematics Matters Secondary 1 Express Textbook, Publisher Panpac Education Pte Ltd, ISBN 9812738827, 9789812738820, page 68
^ David Alan Herzog, Teach Yourself Visually Algebra, Publisher John Wiley & Sons, 2008, ISBN 0470185597, 9780470185599, 304 pages, page 72
^ John C. Peterson, Technical Mathematics With Calculus, Publisher Cengage Learning, 2003, ISBN 0766861899, 9780766861893, 1613 pages, page 31
^ Jerome E. Kaufmann, Karen L. Schwitters, Algebra for College Students, Publisher Cengage Learning, 2010, ISBN 0538733543, 9780538733540, 803 pages, page 222
^ Ramesh Bangia, Dictionary of Information Technology, Publisher Laxmi Publications, Ltd., 2010, ISBN 9380298153, 9789380298153, page 212
^ George Grätzer, First Steps in LaTeX, Publisher Springer, 1999, ISBN 0817641327, 9780817641320, page 17
^ S. Tucker Taft, Robert A. Duff, Randall L. Brukardt, Erhard Ploedereder, Pascal Leroy, Ada 2005 Reference Manual, Volume 4348 of Lecture Notes in Computer Science, Publisher Springer, 2007, ISBN 3540693351, 9783540693352, page 13
^ C. Xavier, Fortran 77 And Numerical Methods, Publisher New Age International, 1994, ISBN 812240670X, 9788122406702, page 20
^ Randal Schwartz, Brian Foy, Tom Phoenix, Learning Perl, Publisher O'Reilly Media, Inc., 2011, ISBN 1449313140, 9781449313142, page 24
^ Matthew A. Telles, Python Power!: The Comprehensive Guide, Publisher Course Technology PTR, 2008, ISBN 1598631586, 9781598631586, page 46
^ Kevin C. Baird, Ruby by Example: Concepts and Code, Publisher No Starch Press, 2007, ISBN 1593271484, 9781593271480, page 72
^ William P. Berlinghoff, Fernando Q. Gouvêa, Math through the Ages: A Gentle History for Teachers and Others, Publisher MAA, 2004, ISBN 0883857367, 9780883857366, page 75
^ Thomas Sonnabend, Mathematics for Teachers: An Interactive Approach for Grades K-8, Publisher: Cengage Learning, 2009, ISBN 0495561665, 9780495561668, 759 pages, page xvii
^ Lewis Hirsch, Arthur Goodman, Understanding Elementary Algebra With Geometry: A Course for College Students, Publisher: Cengage Learning, 2005, ISBN 0534999727, 9780534999728, 654 pages, page 48
^ Lawrence S. Leff, College Algebra: Barron's Ez-101 Study Keys, Publisher: Barron's Educational Series, 2005, ISBN 0764129147, 9780764129148, 230 pages, page 2
^ Ron Larson, Kimberly Nolting, Elementary Algebra, Publisher: Cengage Learning, 2009, ISBN 0547102275, 9780547102276, 622 pages, page 210
^ Charles P. McKeague, Elementary Algebra, Publisher: Cengage Learning, 2011, ISBN 0840064217, 9780840064219, 571 pages, page 49
^ Andrew Marx, Shortcut Algebra I: A Quick and Easy Way to Increase Your Algebra I Knowledge and Test Scores, Publisher Kaplan Publishing, 2007, ISBN 1419552880, 9781419552885, 288 pages, page 51
^ Mark Clark, Cynthia Anfinson, Beginning Algebra: Connecting Concepts Through Applications, Publisher Cengage Learning, 2011, ISBN 0534419380, 9780534419387, 793 pages, page 134
^ Alan S. Tussy, R. David Gustafson, Elementary and Intermediate Algebra, Publisher Cengage Learning, 2012, ISBN 1111567689, 9781111567682, 1163 pages, page 493
^ Douglas Downing, Algebra the Easy Way, Publisher Barron's Educational Series, 2003, ISBN 0764119729, 9780764119729, 392 pages, page 20
^ Ron Larson, Robert Hostetler, Intermediate Algebra, Publisher Cengage Learning, 2008, ISBN 0618753524, 9780618753529, 857 pages, page 96
^ "What is the following property of inequality called?". Stack Exchange. November 29, 2014. Retrieved 4 May 2018.
^ Chris Carter, Physics: Facts and Practice for A Level, Publisher Oxford University Press, 2001, ISBN 019914768X, 9780199147687, 144 pages, page 50
^ Slavin, Steve (1989). All the Math You'll Ever Need. John Wiley & Sons. p. 72. ISBN 0-471-50636-2.
^ Sinha, The Pearson Guide to Quantitative Aptitude for CAT 2/ePublisher: Pearson Education India, 2010, ISBN 8131723666, 9788131723661, 599 pages, page 195
^ Cynthia Y. Young, Precalculus, Publisher John Wiley & Sons, 2010, ISBN 0471756849, 9780471756842, 1175 pages, page 699
^ Mary Jane Sterling, Algebra II For Dummies, Publisher: John Wiley & Sons, 2006, ISBN 0471775819, 9780471775812, 384 pages, page 37
^ John T. Irwin, The Mystery to a Solution: Poe, Borges, and the Analytic Detective Story, Publisher JHU Press, 1996, ISBN 0801854660, 9780801854668, 512 pages, page 372
^ Sharma/khattar, The Pearson Guide To Objective Mathematics For Engineering Entrance Examinations, 3/E, Publisher Pearson Education India, 2010, ISBN 8131723631, 9788131723630, 1248 pages, page 621
^ Aven Choo, LMAN OL Additional Maths Revision Guide 3, Publisher Pearson Education South Asia, 2007, ISBN 9810600011, 9789810600013, page 105
^ John C. Peterson, Technical Mathematics With Calculus, Publisher Cengage Learning, 2003, ISBN 0766861899, 9780766861893, 1613 pages, page 525
^ Euler's Elements of Algebra Archived 2011-04-13 at the Wayback Machine
^ Euler, Leonhard; Hewlett, John; Horner, Francis; Bernoulli, Jean; Lagrange, Joseph Louis (4 May 2018). "Elements of Algebra". Longman, Orme. Retrieved 4 May 2018 – via Google Books.

External links

Media related to Elementary algebra at Wikimedia Commons

[1] H.E. Slaught and N.J. Lennes, Elementary algebra, Publ. Allyn and Bacon, 1915, page 1 (republished by Forgotten Books)

[2] Lewis Hirsch, Arthur Goodman, Understanding Elementary Algebra With Geometry: A Course for College Students, Publisher: Cengage Learning, 2005, ISBN 0534999727, 9780534999728, 654 pages, page 2

[3] Richard N. Aufmann, Joanne Lockwood, Introductory Algebra: An Applied Approach, Publisher Cengage Learning, 2010, ISBN 1439046042, 9781439046043, page 78

[4] William L. Hosch (editor), The Britannica Guide to Algebra and Trigonometry, Britannica Educational Publishing, The Rosen Publishing Group, 2010, ISBN 1615302190, 9781615302192, page 71

[5] James E. Gentle, Numerical Linear Algebra for Applications in Statistics, Publisher: Springer, 1998, ISBN 0387985425, 9780387985428, 221 pages, [James E. Gentle page 183]

[6] Horatio Nelson Robinson, New elementary algebra: containing the rudiments of science for schools and academies, Ivison, Phinney, Blakeman, & Co., 1866, page 7

[7] Ron Larson, Robert Hostetler, Bruce H. Edwards, Algebra And Trigonometry: A Graphing Approach, Publisher: Cengage Learning, 2007, ISBN 061885195X, 9780618851959, 1114 pages, page 6

[8] Sin Kwai Meng, Chip Wai Lung, Ng Song Beng, "Algebraic notation", in Mathematics Matters Secondary 1 Express Textbook, Publisher Panpac Education Pte Ltd, ISBN 9812738827, 9789812738820, page 68

[9] David Alan Herzog, Teach Yourself Visually Algebra, Publisher John Wiley & Sons, 2008, ISBN 0470185597, 9780470185599, 304 pages, page 72

[10] John C. Peterson, Technical Mathematics With Calculus, Publisher Cengage Learning, 2003, ISBN 0766861899, 9780766861893, 1613 pages, page 31

[11] Jerome E. Kaufmann, Karen L. Schwitters, Algebra for College Students, Publisher Cengage Learning, 2010, ISBN 0538733543, 9780538733540, 803 pages, page 222

[12] Ramesh Bangia, Dictionary of Information Technology, Publisher Laxmi Publications, Ltd., 2010, ISBN 9380298153, 9789380298153, page 212

[13] George Grätzer, First Steps in LaTeX, Publisher Springer, 1999, ISBN 0817641327, 9780817641320, page 17

[14] S. Tucker Taft, Robert A. Duff, Randall L. Brukardt, Erhard Ploedereder, Pascal Leroy, Ada 2005 Reference Manual, Volume 4348 of Lecture Notes in Computer Science, Publisher Springer, 2007, ISBN 3540693351, 9783540693352, page 13

[15] C. Xavier, Fortran 77 And Numerical Methods, Publisher New Age International, 1994, ISBN 812240670X, 9788122406702, page 20

[16] Randal Schwartz, Brian Foy, Tom Phoenix, Learning Perl, Publisher O'Reilly Media, Inc., 2011, ISBN 1449313140, 9781449313142, page 24

[17] Matthew A. Telles, Python Power!: The Comprehensive Guide, Publisher Course Technology PTR, 2008, ISBN 1598631586, 9781598631586, page 46

[18] Kevin C. Baird, Ruby by Example: Concepts and Code, Publisher No Starch Press, 2007, ISBN 1593271484, 9781593271480, page 72

[19] William P. Berlinghoff, Fernando Q. Gouvêa, Math through the Ages: A Gentle History for Teachers and Others, Publisher MAA, 2004, ISBN 0883857367, 9780883857366, page 75

[20] Thomas Sonnabend, Mathematics for Teachers: An Interactive Approach for Grades K-8, Publisher: Cengage Learning, 2009, ISBN 0495561665, 9780495561668, 759 pages, page xvii

[21] Lewis Hirsch, Arthur Goodman, Understanding Elementary Algebra With Geometry: A Course for College Students, Publisher: Cengage Learning, 2005, ISBN 0534999727, 9780534999728, 654 pages, page 48

[22] Lawrence S. Leff, College Algebra: Barron's Ez-101 Study Keys, Publisher: Barron's Educational Series, 2005, ISBN 0764129147, 9780764129148, 230 pages, page 2

[23] Ron Larson, Kimberly Nolting, Elementary Algebra, Publisher: Cengage Learning, 2009, ISBN 0547102275, 9780547102276, 622 pages, page 210

[24] Charles P. McKeague, Elementary Algebra, Publisher: Cengage Learning, 2011, ISBN 0840064217, 9780840064219, 571 pages, page 49

[25] Andrew Marx, Shortcut Algebra I: A Quick and Easy Way to Increase Your Algebra I Knowledge and Test Scores, Publisher Kaplan Publishing, 2007, ISBN 1419552880, 9781419552885, 288 pages, page 51

[26] Mark Clark, Cynthia Anfinson, Beginning Algebra: Connecting Concepts Through Applications, Publisher Cengage Learning, 2011, ISBN 0534419380, 9780534419387, 793 pages, page 134

[27] Alan S. Tussy, R. David Gustafson, Elementary and Intermediate Algebra, Publisher Cengage Learning, 2012, ISBN 1111567689, 9781111567682, 1163 pages, page 493

[28] Douglas Downing, Algebra the Easy Way, Publisher Barron's Educational Series, 2003, ISBN 0764119729, 9780764119729, 392 pages, page 20

[29] Ron Larson, Robert Hostetler, Intermediate Algebra, Publisher Cengage Learning, 2008, ISBN 0618753524, 9780618753529, 857 pages, page 96

[30] "What is the following property of inequality called?". Stack Exchange. November 29, 2014. Retrieved 4 May 2018.

[31] Chris Carter, Physics: Facts and Practice for A Level, Publisher Oxford University Press, 2001, ISBN 019914768X, 9780199147687, 144 pages, page 50

[32] Slavin, Steve (1989). All the Math You'll Ever Need. John Wiley & Sons. p. 72. ISBN 0-471-50636-2.

[33] Sinha, The Pearson Guide to Quantitative Aptitude for CAT 2/ePublisher: Pearson Education India, 2010, ISBN 8131723666, 9788131723661, 599 pages, page 195

[34] Cynthia Y. Young, Precalculus, Publisher John Wiley & Sons, 2010, ISBN 0471756849, 9780471756842, 1175 pages, page 699

[35] Mary Jane Sterling, Algebra II For Dummies, Publisher: John Wiley & Sons, 2006, ISBN 0471775819, 9780471775812, 384 pages, page 37

[36] John T. Irwin, The Mystery to a Solution: Poe, Borges, and the Analytic Detective Story, Publisher JHU Press, 1996, ISBN 0801854660, 9780801854668, 512 pages, page 372

[37] Sharma/khattar, The Pearson Guide To Objective Mathematics For Engineering Entrance Examinations, 3/E, Publisher Pearson Education India, 2010, ISBN 8131723631, 9788131723630, 1248 pages, page 621

[38] Aven Choo, LMAN OL Additional Maths Revision Guide 3, Publisher Pearson Education South Asia, 2007, ISBN 9810600011, 9789810600013, page 105

[39] John C. Peterson, Technical Mathematics With Calculus, Publisher Cengage Learning, 2003, ISBN 0766861899, 9780766861893, 1613 pages, page 525

[40] Euler's Elements of Algebra Archived 2011-04-13 at the Wayback Machine

[41] Euler, Leonhard; Hewlett, John; Horner, Francis; Bernoulli, Jean; Lagrange, Joseph Louis (4 May 2018). "Elements of Algebra". Longman, Orme. Retrieved 4 May 2018 – via Google Books.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]