Equivalence class

수학(mathematics)에서, 어떤 집합(set) $S$ 의 원소가 그들 위에 정의된 (동치 관계(equivalence relation)로 공식화된) 동치의 개념을 가질 때, 우리는 집합 $S$ 를 동치 클래스(equivalence classes)로 자연스럽게 나눌 수 있습니다. 이들 동치 클래스는 원소 $a$ 와 $b$ 가 같은 동치 클래스(equivalence class)에 속하도록 구성되는 것과 그들이 동등한 것은 필요충분(iff) 조건입니다.

공식적으로, 집합 $S$ 와 $S$ 위에 동치 관계 $~$ 가 주어지면, $S$ 에서 원소 $a$ 의 동치 클래스는, $[a]$ 로 나타내며,^[1]^[2] $a$ 와 동등한 원소의 집합입니다:^[3]

\{x\in S\mid x\sim a\}

.

그것은, 동치 클래스가 $S$ 의 분할(partition)을 형성한다는, 동치 관계의 속성을 정의하는 것으로부터, 입증될 수 있습니다. 이 분할–동치 클래스의 집합–은 때때로 $~$ 에 의한 $S$ 의 몫 집합(quotient set) 또는 몫 공간(quotient space)으로 불리고, $S / ~$ 로 표시됩니다.

집합 $S$ 가 (그룹 연산(group operation) 또는 토폴로지(topology)와 같은) 어떤 구조를 가지고 동치 관계 $~$ 가 이 구조와 호환될 때, 몫 집합은 그것의 부모 집합으로부터 비슷한 구조를 종종 상속받습니다. 예제는 선형 대수에서 몫 공간(quotient spaces in linear algebra), 토폴로지에서 몫 공간(quotient spaces in topology), 몫 그룹(quotient group), 동차 공간(homogeneous space), 몫 링(quotient ring), 몫 모노이드(quotient monoid), 및 몫 카테고리(quotient categories)를 포함합니다.

Examples

만약 $X$ 가 모든 자동차의 집합이고, $~$ 가 동치 관계(equivalence relation) "무엇과 같은 색깔을 가짐"이면, 하나의 특정 동치 클래스는 모든 녹색 자동차로 구성될 것이고, $X /~$ 는 모든 자동차 색깔의 집합으로 자연스럽게 식별될 수 있습니다.
$X$ 를 평면에서 모든 직사각형의 집합으로 놓고, $~$ 를 동치 관계 "무엇과 같은 넓이를 가짐"으로 놓으면, 그때에 각 양의 실수 A에 대해, 넓이 A를 가지는 모든 직사각형의 동치 클래스가 있을 것입니다.^[4]
정수(integer)의 집합, $Z$ 위의 모듈로(modulo) 2 동치 관계를 생각해 보십시오: $x ~ y$ 를 만족하는 것과 그들의 차이 $x - y$ 가 짝수(even number)인 것은 필요충분 조건입니다. 이 관계는 정확히 두 동치 클래스를 발생시킵니다: 하나의 클래스는 모든 짝수로 구성되고, 나머지 다른 클래스는 모든 홀수로 구성됩니다. 이 관계 아래에서 동치 클래스를 나타내기 위해 클래스의 하나의 구성원 주위로 대괄호를 사용하면, $[7]$ , $[9]$ , 및 $[1]$ 모두는 $Z /~$ 의 같은 원소를 나타냅니다.^[5]
$X$ 를 비-영 $b$ 를 갖는 정수 $(a, b)$ 의 순서 쌍(ordered pairs)의 집합으로 놓고, $(a, b) ~ (c, d)$ 를 만족하는 것과 $ad = bc$ 인 것이 필요충분 조건인 $X$ 위의 동치 관계 $~$ 를 정의하면, 그때에 쌍 $(a, b)$ 의 동치 클래스는 유리수(rational number) $a / b$ 로 식별될 수 있고, 이 동치 관계와 그것의 동치 클래스는 유리수의 집합의 공식적인 정의를 제공하기 위해 사용될 수 있습니다.^[6] 같은 구성은 임의의 정수 도메인(integral domain)의 분수의 필드(field of fractions)로 일반화될 수 있습니다.
만약 $X$ 가, 말하자면, 유클리드 평면(Euclidean plane)에서, 모든 직선들로 구성되고, L ~ M이 L과 M이 평행 직선(parallel lines)임을 의미하는 것이면, 서로 평행한 직선의 집합은 직선이 그 자신과 평행으로 여겨지는 한 동치 클래스를 형성합니다. 이 상황에서, 각 동치 클래스는 무한대에 점(point at infinity)을 결정합니다.

Definition and notation

집합 $X$ 에 대한 동치 관계(equivalence relation)는 다음 세 속성을 만족시키는 $X$ 에 대한 이항 관계(binary relation) $~$ 입니다:^[7]^[8]

$X$ 에서 모든 $a$ 에 대해 $a ~ a$ (반사성(reflexivity)),
$X$ 에서 모든 $a$ 와 $b$ 에 대해 $a ~ b$ 는 $b ~ a$ 를 의미합니다 (대칭(symmetry)),
$X$ 에서 모든 $a$ 와 $b$ , 및 $c$ 에 대해 만약 $a ~ b$ 와 $b ~ c$ 이면, $a ~ c$ 입니다 (전이성(transitivity)).

원소 $a$ 의 동치 클래스는 $[a]$ 또는 $[a] ~$ 로 표시되고,^[1] $~$ 에 의해 $a$ 에 관련된 원소의 집합 $\{x\in X\mid a\sim x\}$ 으로 정의됩니다.^[3] 용어 "동치 클래스"에서 단어 "클래스"는 집합 이론(set theory)에서 정의된 것처럼 클래스(classes)를 참조하지 않으며, 어쨌든 동치 클래스는 종종 적절한 클래스(proper classes)로 판명됩니다.

동치 관계 $R$ 에 관한 $X$ 에서 모든 동치 클래스의 집합은 $X / R$ 로 표시되고, $X$ 모듈로 $R$ (또는 $R$ 에 의한 $X$ 의 몫 집합)이라고 불립니다.^[9] $X$ 에서 $X / R$ 위로의 전사 맵(surjective map) $x\mapsto [x]$ 는, 각 원소를 그것의 동치 클래스에 매핑하며, 정식 전사(canonical surjection), 또는 정식 투영 맵(canonical projection map)이라고 불립니다.

원소가 각 동치 클래스에서 (종종 암시적으로) 선택될 때, 이것은 섹션(section)이라고 불리는 단사 맵(injective map)을 정의합니다. 만약 이 섹션이 $s$ 로 표시되면, 우리는 모든 각 동치 클래스 $c$ 에 대해 $[s (c)] = c$ 를 가집니다. 원소 $s (c)$ 는 $c$ 의 대표(representative)라고 불립니다. 클래스의 임의의 원소는 적절하게 섹션을 선택함으로써 클래스의 대표로 선택될 수 있습니다.

때때로, 다른 섹션보다 더 "자연스러운" 것인 섹션이 있습니다. 이 경우에서, 대표는 정식의 대표라고 불립니다. 예를 들어, 모듈러 산술(modular arithmetic)에서, 다음과 같이 정의된 정수에 대한 동치 관계를 생각해 보십시오: 만약 $a - b$ 가 (모듈러스라고 불리는) 주어진 양의 정수 $n$ 의 배수이면 $a ~ b$ 입니다. 각 클래스는 $n$ 보다 더 작은 고유한 비-음의 정수를 포함하고, 이들 정수는 정식의 대표입니다. 클래스와 그것의 대표는, 표기법 $a mod n$ 이 클래스, 또는 그것의 정식 대표 ( $n$ 에 의한 $a$ 의 나눗셈(division)의 나머지(remainder))를 나타낼 수 있다는 사실에서 입증하는 것처럼, 다소 식별됩니다.

Properties

$X$ 의 모든 각 원소 $x$ 는 동치 클래스 $[x]$ 의 구성원입니다. 모든 각 두 동치 클래스 $[x]$ 와 $[y]$ 는 모두 같거나 서로소(disjoint)입니다. 그러므로, $X$ 의 모든 동치 클래스의 집합은 $X$ 의 분할(partition)을 형성합니다: $X$ 의 모든 각 원소는 하나와 오직 하나의 동치 클래스에 속합니다.^[10] 반대로, $X$ 의 모든 각 분할은 이런 방법으로 동치 관계에서 비롯되며, 이것에 따라 $x ~ y$ 인 것과 $x$ 와 $y$ 가 분할의 같은 집합에 속하는 것은 필요충분 조건입니다. ^[11]

그것은 다음인 것인 동치 클래스의 속성을 따릅니다:

x ~ y

if and only if

[x] = [y]

.

다른 단어에서, 만약 $~$ 가 집합 $X$ 에서 동치 관계이고, $x$ 와 $y$ 가 $X$ 의 두 원소이면, 이들 명제는 동등합니다:

$x\sim y$
$[x]=[y]$
$[x]\cap [y]\neq \emptyset .$

Graphical representation

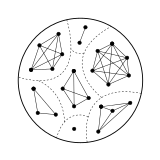
Graph of an example equivalence with 7 classes

무-방향 그래프(undirected graph)는 집합 $X$ 에서 임의의 대칭 관계(symmetric relation)와 결합될 수 있으며, 여기서 꼭짓점은 $X$ 의 원소이고, 두 꼭짓점 $s$ 와 $t$ 가 결합된 것과 $s ~ t$ 인 것은 필요충분 조건입니다. 이들 그래프 중에는 동치 관계의 그래프입니다; 그것들은 연결된 성분(connected components)이 클릭(cliques)임을 만족하는 그래프로 특성화됩니다. ^[12]

Invariants

만약 $~$ 는 $X$ 에 대한 동치 관계이고, $P (x)$ 는, $x ~ y$ 일 때마다, $P (x)$ 는 만약 $P (y)$ 가 참이면 참을 만족하는 $X$ 의 원소의 속성이면, 속성 $P$ 는 $~$ 의 불변(invariant), 또는 관계 $~$ 아래에서 잘-정의된(well-defined) 것이라고 말합니다.

빈번한 특별한 경우가 $f$ 가 $X$ 에서 또 다른 집합 $Y$ 로의 함수일 때 발생합니다; 만약 $x 1 ~ x 2$ 일 때마다 $f (x 1) = f (x 2)$ 이면, $f$ 는 $~$ 아래에서 클래스 불변, 또는 단순히 $~$ 아래에서 불변이라고 말합니다. 이것은, 예를 들어, 유한 그룹의 성격 이론에서 발생합니다. 일부 저자는 " $~$ 아래에서 불변" 대신에 " $~$ 와 호환" 또는 " $~$ 에 관계한"을 사용합니다.

임의의 함수(function) $f : X \to Y$ 자체는 $x 1 ~ x 2$ 인 것과 $f (x 1) = f (x 2)$ 인 것이 필요충분 조건임에 따라 $X$ 에 대한 동치 관계를 정의합니다. $x$ 의 동치 클래스는 $f (x)$ 에 매핑된 것을 얻는 $X$ 에서 모든 원소의 집합입니다. 즉, 클래스 $[x]$ 는 $f (x)$ 의 역 이미지(inverse image)입니다. 이 동치 관계는 $f$ 의 커널(kernel)로 알려져 있습니다.

보다 일반적으로, 함수는 ( $X$ 에 대한 동치 관계 $~ X$ 아래에서) 동치 인수를 ( $Y$ 에 대한 동치 관계 $~ Y$ 아래에서) 동치 값에 매핑할 수 있습니다. 그러한 함수는 동치 관계를 갖춘 집합의 사상(morphism)입니다.

Quotient space in topology

토폴로지(topology)에서, 몫 공간(quotient space)은 동치 클래스의 집합에 대한 토폴로지를 생성하기 위한 원래 공간의 토폴로지를 사용하여 토폴로지적 공간에 대한 동치 관계의 동치 클래스의 집합에 형성된 토폴로지적 공간(topological space)입니다.

추상 대수(abstract algebra)에서, 대수의 놓여있는 집합에 대한 합동 관계(congruence relation)는 대수학을 몫 대수(quotient algebra)라고 불리는 관계의 동치 클래스에 대한 대수를 도입하는 것을 허용합니다. 선형 대수(linear algebra)에서, 몫 공간(quotient space)은 몫 그룹(quotient group) 취함으로써 형성된 벡터 공간이며, 여기서 몫 준동형은 선형 맵(linear map)입니다. 확장에 의해, 추상 대수에서, 용어 몫 공간은 몫 모듈(quotient module), 몫 링(quotient ring), 몫 그룹(quotient group), 또는 임의의 몫 대수에 대해 사용될 수 있습니다. 어쨌든, 보다 일반적인 경우에 대한 용어의 사용은 종종 그룹 동작의 궤도와 함께 아날로그에 의해 일 수 있습니다.

집합에 대한 그룹 동작(group action)의 궤도는 집합에 대한 작용의 몫 공간으로 불릴 수 있으며, 특히 그룹 동작의 궤도가 그룹의 부분그룹의 오른쪽 코셋(coset)일 때, 이것은 왼쪽 변환에 의한 그룹에 의한 부분그룹의 작용에서 발생하며, 또는 각각 오른쪽 변환 아래에서 궤도로 왼쪽 코셋일 때입니다.

변환 작용에 의한 그룹에 작용하는, 토폴로지적 그룹의 표준의 부분그룹은 동시에 토폴로지, 추상 대수, 및 그룹 동작의 의미에서 몫 공간입니다.

비록 그 용어가 동치 클래스의 임의의 동치 관계의 집합에 대해 사용될 수 있지만, 아마도 추가적인 구조와 함께, 그 용어를 사용하는 목적은 일반적으로 집합 $X$ 에 대한 동치 관계의 유형을, $X$ 에 대한 같은 종류의 구조에서 동치 클래스의 집합에 대한 일부 구조를 유도하는 동치 관계로, 또는 그룹 동작의 궤도로, 일부 구조를 유도하는 등가 관계와 비교하는 것입니다. 동치 관계에 의해 보존되는 구조의 의미, 및 그룹 동작 아래에서 불변(invariants)의 연구 둘 다는 위에 주어진 동치 관계의 불변(invariants)의 정의로 이어집니다.

Notes

^ ^a ^b "Comprehensive List of Algebra Symbols". Math Vault. 2020-03-25. Retrieved 2020-08-30.
^ "7.3: Equivalence Classes". Mathematics LibreTexts. 2017-09-20. Retrieved 2020-08-30.
^ ^a ^b Weisstein, Eric W. "Equivalence Class". mathworld.wolfram.com. Retrieved 2020-08-30.
^ Avelsgaard 1989, p. 127
^ Devlin 2004, p. 123
^ Maddox 2002, pp. 77–78
^ Devlin 2004, p. 122
^ Weisstein, Eric W. "Equivalence Relation". mathworld.wolfram.com. Retrieved 2020-08-30.
^ Wolf 1998, p. 178
^ Maddox 2002, p. 74, Thm. 2.5.15
^ Avelsgaard 1989, p. 132, Thm. 3.16
^ Devlin 2004, p. 123

References

Avelsgaard, Carol (1989), Foundations for Advanced Mathematics, Scott Foresman, ISBN 0-673-38152-8
Devlin, Keith (2004), Sets, Functions, and Logic: An Introduction to Abstract Mathematics (3rd ed.), Chapman & Hall/ CRC Press, ISBN 978-1-58488-449-1
Maddox, Randall B. (2002), Mathematical Thinking and Writing, Harcourt/ Academic Press, ISBN 0-12-464976-9
Wolf, Robert S. (1998), Proof, Logic and Conjecture: A Mathematician's Toolbox, Freeman, ISBN 978-0-7167-3050-7

External links

Media related to Equivalence classes at Wikimedia Commons

[:0-1] "Comprehensive List of Algebra Symbols". Math Vault. 2020-03-25. Retrieved 2020-08-30.

[2] "7.3: Equivalence Classes". Mathematics LibreTexts. 2017-09-20. Retrieved 2020-08-30.

[:1-3] Weisstein, Eric W. "Equivalence Class". mathworld.wolfram.com. Retrieved 2020-08-30.

[4] Avelsgaard 1989, p. 127

[5] Devlin 2004, p. 123

[6] Maddox 2002, pp. 77–78

[7] Devlin 2004, p. 122

[8] Weisstein, Eric W. "Equivalence Relation". mathworld.wolfram.com. Retrieved 2020-08-30.

[9] Wolf 1998, p. 178

[10] Maddox 2002, p. 74, Thm. 2.5.15

[11] Avelsgaard 1989, p. 132, Thm. 3.16

[12] Devlin 2004, p. 123

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]