Frustum

Set of pyramidal right $n$ -gonal frustums
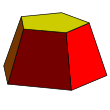Set of pyramidal right n-gonal frustums
	Examples: right pentagonal and square frustums; (n = 5 and n = 4)
Faces	n isosceles trapezoids, 2 regular n-gons
Edges	3n
Vertices	2n
Symmetry group	Cnv, [1,n], (*nn)
Dual polyhedron	convex asymmetric right n-gonal bipyramid
Properties	convex
Net
	Example: net of right trigonal frustum (n = 3)

기하학(geometry)에서, 절두체(frustum) ("morsel"에 대한 라틴어에서 유래, 복수형: frusta 또는 frustums)는 그것을 절단하는 하나 또는 두 개의 평행 평면 사이에 놓이는 고체(solid) (통상적으로 각뿔(pyramid) 또는 원뿔(cone))의 일부입니다. 그것의 밑면은 다각형(polygonal)이고 측면은 사다리꼴(trapezoidal)입니다. 오른쪽 절두체는 그것의 축에 수직으로 잘린(truncated) 직각 각뿔(right pyramid) 또는 직각 원뿔입니다.^[1]

만약 절두체가 같은 길이의 모든 가장자리 (등변 그림) 가지면, 그것은 균등 각기둥(prism)입니다.

컴퓨터 그래픽(computer graphics)에서, 보는 절두체(viewing frustum)는 화면에서 볼 수 있는 삼-차원 영역입니다. 그것은 잘린(clipped) 각뿔에 의해 형성됩니다; 특히, 절두체 컬링(frustum culling)은 숨겨진 표면 결정(hidden surface determination)의 방법입니다.

항공 우주 산업(aerospace industry)에서, 절두체는 잘린(truncated) 원뿔과 같은 형성화된 다단 로켓(multistage rocket) (예를 들어 Saturn V)의 두 단계 사이의 쌍화(fairing)입니다.

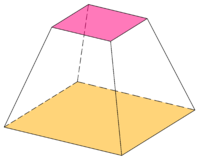
Elements, special cases, and related concepts

절두체의 축은 원래 원뿔 또는 각뿔의 축입니다. 만약 그것이 원형 밑변이면 절두체는 원형입니다; 그 축이 두 밑면에 수직이면 그것은 직각이고, 그렇지 않으면 비스듬합니다.

절두체의 높이는 두 밑면 사이의 수직 거리입니다.

원뿔과 각뿔은 절단 평면 중 하나가 (해당하는 밑면이 한 점으로 줄어들도록) 꼭대기(apex)를 통과하는 절두체의 퇴화 경우로 보일 수 있습니다. 각뿔형 절두체는 각기둥형(prismatoids)의 부분클래스입니다.

이들 합동(congruent) 밑면에서 결합된 2개의 합동 밑면을 갖는 두 개의 절두체는 이중절두체(bifrustum)를 만듭니다.

Formulas

Volume

각뿔형 정사각 절두체의 부피에 대한 공식은 13왕조(13th dynasty) (기원전 1850년경)에 쓰인 모스크바 수학 파피루스(Moscow Mathematical Papyrus)에서 불렸던 것을 고대 이집트 수학(Egyptian mathematics)에 의해 도입되었습니다:

V={\frac {h}{3}}\left(a^{2}+ab+b^{2}\right),

여기서 $a$ 와 $b$ 는 밑면과 윗면 길이이고, $h$ 는 높이입니다.

이집트인들은 잘린 정사각 각뿔의 부피에 대한 정확한 공식을 알고 있었지만, 모스크바 파피루스에는 이 방정식의 증명은 제공하지 않았습니다.

원뿔형 또는 각뿔형 절두체의 부피(volume)는 "꼭대기"를 자르기 전의 고체 부피에서 이 "꼭대기"의 부피를 뺀 것입니다:

V={\frac {h_{1}B_{1}-h_{2}B_{2}}{3}},

여기서 $B 1$ 와 $B 2$ 는 밑면과 윗면의 넓이이고, $h 1$ 과 $h 2$ 는 꼭대기에서 밑 평면과 윗 평면에 이르는 수직 거리입니다.

다음을 생각해 보십시오:

{\frac {B_{1}}{h_{1}^{2}}}={\frac {B_{2}}{h_{2}^{2}}}={\frac {\sqrt {B_{1}B_{2}}}{h_{1}h_{2}}}=\alpha ,

부피에 대한 그 공식은 이 비례성, $\alpha$ 와 오직 높이 $h 1$ 과 $h 2$ 의 세제곱의 차이(difference of the cubes)의 삼분의 1로 표현될 수 있습니다:

V={\frac {h_{1}\alpha h_{1}^{2}-h_{2}\alpha h_{2}^{2}}{3}}=\alpha {\frac {h_{1}^{3}-h_{2}^{3}}{3}}.

항등식 $a 3 - b 3 = (a - b)(a 2 + ab + b 2)$ 을 사용함으로써, 다음을 얻습니다:

V=(h_{1}-h_{2})\alpha {\frac {h_{1}^{2}+h_{1}h_{2}+h_{2}^{2}}{3}},

여기서 $h 1 - h 2 = h$ 는 절두체의 높이입니다.

$\alpha$ 를 분배하고 그것의 정의로부터 빼면, 넓이 $B 1$ 과 $B 2$ 의 헤론 평균(Heronian mean)은 다음과 같이 얻습니다:

{\frac {B_{1}+{\sqrt {B_{1}B_{2}}}+B_{2}}{3}};

대안적인 공식은 따라서 다음입니다:

V={\frac {h}{3}}\left(B_{1}+{\sqrt {B_{1}B_{2}}}+B_{2}\right).

알렉산드리아의 헤론(Heron of Alexandria)은 이 공식을 유도한 것으로 유명하고, 그것과 함께, 허수 단위(imaginary unit), 음의 일의 제곱근을 만나게 됩니다.^[2]

특히:

원형 원뿔 절두체의 부피는 다음입니다:

V={\frac {\pi h}{3}}\left(r_{1}^{2}+r_{1}r_{2}+r_{2}^{2}\right),

여기서

r 1

과

r 2

는 밑면과 윗면 반지름(radii)입니다.

밑면이 정규 $n$ -각형인 각뿔형 절두체의 부피는 다음입니다:

V={\frac {nh}{12}}\left(a_{1}^{2}+a_{1}a_{2}+a_{2}^{2}\right)\cot {\frac {\pi }{n}},

여기서

a 1

과

a 2

는 밑면 변과 윗면 변 길이입니다.

Surface area

직각 원형 원뿔 절두체에 대해^[3]^[4]

{\begin{aligned}{\text{Lateral surface area}}&=\pi \left(r_{1}+r_{2}\right)s\\&=\pi \left(r_{1}+r_{2}\right){\sqrt {\left(r_{1}-r_{2}\right)^{2}+h^{2}}}\end{aligned}}

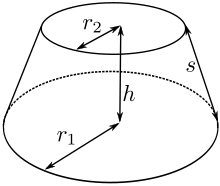
그리고

{\begin{aligned}{\text{Total surface area}}&=\pi \left(\left(r_{1}+r_{2}\right)s+r_{1}^{2}+r_{2}^{2}\right)\\&=\pi \left(\left(r_{1}+r_{2}\right){\sqrt {\left(r_{1}-r_{2}\right)^{2}+h^{2}}}+r_{1}^{2}+r_{2}^{2}\right)\end{aligned}}

여기서 $r_{1}$ 과 $r_{2}$ 는 각각 밑면과 윗면 반지름이고, $s$ 는 절두체의 경사 높이입니다.

그것의 밑면이 닮은 정규 $n$ -변 다각형(polygons)인 직각 절두체의 표면 넓이는 다음입니다:

A={\frac {n}{4}}\left[\left(a_{1}^{2}+a_{2}^{2}\right)\cot {\frac {\pi }{n}}+{\sqrt {\left(a_{1}^{2}-a_{2}^{2}\right)^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}\left(a_{1}+a_{2}\right)^{2}}}\right]

여기서 $a_{1}$ 과 $a_{2}$ 는 두 밑면의 변입니다.

Examples

Rolo brand chocolates approximate a right circular conic frustum, although not flat on top.

미국 1달러 지폐의 뒷면에, 각뿔형 절두체가 뒷면에는 섭리의 눈에 의해 둘러싸인 미국의 대인장의 뒷면에 나타나 있습니다.
지구라트(Ziggurats), 계단식 각뿔(step pyramids), 및 특정 고대 아메리카 원주민 고분은 역시 덧붙인 계단과 같은 추가 기능을 갖는 하나 이상의 각뿔의 절두체를 형성합니다.
중국 각뿔(Chinese pyramids).
일리노이 주, 시카고에 있는 John Hancock Center는 밑면이 직사각형인 절두체입니다.
워싱턴 기념비는 작은 각뿔로 덮인 좁은 정사각형-밑변 각뿔형 절두체입니다.
3D 컴퓨터 그래픽에서 보는 절두체(viewing frustum)는 각뿔형 절두체로 모델링된 가상 사진 또는 비디오 카메라의 사용 가능한 시야(field of view)입니다.
Stanislaw Lem의 단편 소설 모음 The Cyberiad의 영어 번역에서, Love and tensor algebra 시에서는 "모든 각 절두체는 원뿔이 되기를 갈망합니다"라고 주장합니다.
양동이와 전형적인 전등갓은 원뿔형 절두체의 일상적인 예입니다.
음료수 잔과 일부 우주 캡슐도 일부 예입니다.
Garsų Gaudyklė, Neringa, Lithuania
Garsų Gaudyklė 네링가, 리투아니아 사운드 캐쳐 나무 구조 또는 리투아니아의 동상.
Jordan Hall

Notes

References

^ William F. Kern, James R. Bland, Solid Mensuration with proofs, 1938, p. 67
^ Nahin, Paul. An Imaginary Tale: The story of √−1. Princeton University Press. 1998
^ "Mathwords.com: Frustum". Retrieved 17 July 2011.
^ Al-Sammarraie, Ahmed T.; Vafai, Kambiz (2017). "Heat transfer augmentation through convergence angles in a pipe". Numerical Heat Transfer, Part A: Applications. 72 (3): 197−214. doi:10.1080/10407782.2017.1372670. S2CID 125509773.

External links

[1] William F. Kern, James R. Bland, Solid Mensuration with proofs, 1938, p. 67

[2] Nahin, Paul. An Imaginary Tale: The story of √−1. Princeton University Press. 1998

[3] "Mathwords.com: Frustum". Retrieved 17 July 2011.

[4] Al-Sammarraie, Ahmed T.; Vafai, Kambiz (2017). "Heat transfer augmentation through convergence angles in a pipe". Numerical Heat Transfer, Part A: Applications. 72 (3): 197−214. doi:10.1080/10407782.2017.1372670. S2CID 125509773.

[1]

[2]

[3]

[4]