Complex analysis

Original article: wikipedia:Complex analysis

"Complex analytic" and "complex variables" redirect here. For the complex analytic class of functions, see Holomorphic function. For the study of several complex variables, see Function of several complex variables.

Not to be confused with Complexity theory.

복소 해석학(complex analysis)은, 전통적으로 복소 변수의 함수의 이론(theory of functions of a complex variable)으로 알려져 있으며, 복소수(complex numbers)의 함수(functions)를 조사하는 수학적 해석학(mathematical analysis)의 가지입니다. 그것은 대수적 기하학(algebraic geometry), 숫자 이론(number theory), 해석적 조합론(analytic combinatorics), 응용 수학(applied mathematics)을 포함하는, 수학의 많은 가지에서 유용합니다; 뿐만 아니라 유체 동역학(hydrodynamics), 열역학(thermodynamics), 및 특히 양자 역학(quantum mechanics)의 가지를 포함하는 물리학(physics)에서도 유용합니다. 확장에 의해, 복소 해석학의 사용은 핵(nuclear), 항공-우주(aerospace), 기계 공학(mechanical engineering), 및 전기 공학(electrical engineering)과 같은 공학 분야에서도 응용을 역시 가집니다.

복소 변수의 미분-가능 함수(differentiable function)는 그것의 테일러 급수와 같기 때문에 (즉, 해석적(analytic)이기 때문에), 복소 해석학은 복소 변수를 갖는 해석적 함수(analytic functions, 즉, 정칙 함수(holomorphic function))와 특별히 관련됩니다.

History

The Mandelbrot set, a fractal

복소 해석학은 18세기와 그 직전에 뿌리를 둔 수학의 고전적인 가지 중 하나입니다. 복소수와 관련된 중요한 수학자는 Euler, Gauss, Riemann, Cauchy, Weierstrass 등을 포함하고 20세기에는 더 많습니다. 복소 해석학, 특히 등각 매핑(conformal mappings)의 이론은 많은 물리적 응용을 가지고 있고 역시 해석적 숫자 이론(analytic number theory) 전체에 걸쳐 사용됩니다. 현대에서, 그것은 복소 동역학의 새로운 후원과 정칙 함수(holomorphic functions)를 반복함으로써 생성되는 프랙탈의 그림을 통해 매우 인기가 있습니다. 복소 해석학의 또 다른 중요한 응용 분야는 양자 필드 이론(quantum field theory)에서 등각 불변을 조사하는 끈 이론(string theory)입니다.

Complex functions

An exponential function Aⁿ of a discrete (integer) variable n, similar to geometric progression

복소 함수는 복소수(complex numbers)에서 복소수로의 함수(function)입니다. 다시 말해서, 그것은 복소수의 부분집합을 도메인(domain)으로, 복소수를 코도메인(codomain)으로 가지는 함수입니다. 복소 함수는 일반적으로 복소 평면(complex plane)의 비-빈 열린 부분집합(open subset)을 포함하는 도메인을 가지고 있다고 가정됩니다.

임의의 복소 함수에 대해, 도메인에서 값 $z$와 치역에서 그 이미지 $f(z)$는 실수(real) 부분과 허수(imaginary) 부분으로 분리될 수 있습니다.

$z=x+iy\quad {\text{ and }}\quad f(z)=f(x+iy)=u(x,y)+iv(x,y),$

여기서 $x,y,u(x,y),v(x,y)$는 모두 실수-값입니다.

다른 말로, 복소 함수 $f:\mathbb {C} \to \mathbb {C}$는 다음으로 분해될 수 있습니다:

$u:\mathbb {R} ^{2}\to \mathbb {R} \quad$ and $\quad v:\mathbb {R} ^{2}\to \mathbb {R} ,$

즉, 두 개의 실수 변수 ($x$, $y$)의 두 개의 실수-값 함수 ($u$, $v$)로 분해될 수 있습니다.

유사하게, 임의적인 집합(set) X에 대해 임의의 복소-값 함수 f는 두 개의 실수-값 함수(real-valued functions)의 순서화된 쌍(ordered pair): (Re f, Im f), 또는 X에서 $\mathbb {R} ^{2}$로의 벡터-값 함수(vector-valued function)로 고려될 수 있습니다.

복소-값 함수의 일부 속성 (예를 들어, 연속성)은 두 실수 변수의 벡터 값 함수의 해당하는 속성에 지나지 않습니다. 미분-가능성(differentiability)과 같은 복소 해석학의 다른 개념은 실수 함수에 대해 유사한 개념의 직접적인 일반화이지만, 매우 다른 속성을 가질 수 있습니다. 특히, 모든 각 미분-가능 복소 함수(differentiable complex function)는 해석적(analytic)이고 (다음 섹션 참조), 점의 이웃(neighborhood)에서 같은 두 개의 미분-가능 함수는 (도메인이 연결된 것이면) 그것들의 도메인의 교차점에서 같습니다. 후자의 속성은 그것의 도메인이 유한한 수의 제거된 곡선 호(curve arcs)를 갖는 전체 복소 평면인 복소 해석적 함수를 얻는 데 고유한 방법으로 모든 각 실수 해석적 함수(analytic function)를 확장을 허용하는 해석적 연속화(analytic continuation)의 원칙의 기초입니다. 복소 지수 함수(complex exponential function), 복소 로그 함수(complex logarithm functions), 및 삼각 함수(trigonometric functions)를 포함하여 많은 기본과 특수(special) 복소 함수가 이러한 방법으로 정의됩니다.

Holomorphic functions

Main article: Holomorphic function

복소 평면의 열린 부분집합(open subset) $\Omega$의 모든 각 점에서 미분-가능(differentiable)인 복소 함수는 $\Omega$ 위에 정칙적(holomorphic)이라고 말합니다. 복소 해석학의 맥락에서, $z_{0}$에서 $f$의 도함수는 다음과 같이 정의됩니다:

$f'(z_{0})=\lim _{z\to z_{0}}{\frac {f(z)-f(z_{0})}{z-z_{0}}}.$

표면적으로, 이 정의는 형식적으로 실수 함수의 도함수의 정의와 유사합니다. 어쨌든, 복소 도함수와 미분-가능 함수는 실수 함수와 상당히 다른 방법으로 동작합니다. 특히, 이 극한이 존재하려면, 복소 평면에서 $z_{0}$에 접근하는 방식에 관계없이 차이 몫의 값이 같은 복소수에 접근해야 합니다. 결과적으로, 복소 미분-가능성은 실수 미분-가능성보다 훨씬 더 강력한 의미를 가집니다. 예를 들어, 정칙 함수는 무한하게 미분-가능(infinitely differentiable)이지만, 반면에 n번째 도함수의 존재는 실수 함수에 대해 (n + 1)번째 도함수의 존재를 의미할 필요가 없습니다. 더욱이, 모든 정칙 함수는 더 강한 해석성( analyticity) 조건을 만족시키며, 함수가 그 도메인 안의 모든 각 점에서 수렴 거듭제곱 급수에 의해 지역적으로 주어진다는 것을 의미입니다. 본질적으로, 이것은 $\Omega$ 위에 정칙 함수가 $\Omega$에서 모든 각 점의 일부 이웃에서 다항식에 의해 임의적으로 잘 근사화될 수 있음을 의미합니다. 이것은 미분-가능 실수 함수와 뚜렷한 대조를 이룹니다; 어디에도 해석적이지 않은 무한하게 미분-가능 실수 함수가 있습니다. Non-analytic smooth function § A smooth function which is nowhere real analytic를 참조하십시오.

지수 함수(exponential function), 삼각 함수(trigonometric functions), 및 모든 다항 함수(polynomial functions)를 포함하는 대부분의 기본 함수는 함수 $\mathbb {C} \to \mathbb {C}$와 같이 복소 인수로 적절하게 확장되며, 전체 복소 평면에 걸쳐 정칙적이며, 그것들을 전체 함수(entire functions)로 만들고, 반면에 유리 함수 $p/q$는, 여기서 p와 q는 다항식이며, q가 영인 점을 제외하는 도메인 위에 정칙적입니다. 고립된 점 집합을 제외한 모든 곳에서 정칙적인 그러한 함수는 유리형 함수(meromorphic functions)라고 알려져 있습니다. 다른 한편으로, 함수 $z\mapsto \Re (z)$, $z\mapsto |z|$, 및 $z\mapsto {\bar {z}}$는 코시-리만 조건을 만족시키지 못하는 것으로 표시될 수 있는 것처럼 복소 평면 위의 어느 곳에서도 정칙적이 아닙니다 (아래를 참조하십시오).

정칙 함수의 중요한 속성은 코시-리만 조건(Cauchy–Riemann conditions)으로 알려진 그것들의 실수와 허수 구성 요소의 부분 도함수 사이의 관계입니다. 만약 $f(z)=f(x+iy)=u(x,y)+iv(x,y)$에 의해 정의된 $f:\mathbb {C} \to \mathbb {C}$는, 여기서 $x,y,u(x,y),v(x,y)\in \mathbb {R}$, 영역(region) $\Omega$ 위에 정칙적이면, 모든 $z_{0}\in \Omega$에 대해,

${\frac {\partial f}{\partial {\bar {z}}}}(z_{0})=0,\ {\text{where }}{\frac {\partial }{\partial {\bar {z}}}}\mathrel {:=} {\frac {1}{2}}\left({\frac {\partial }{\partial x}}+i{\frac {\partial }{\partial y}}\right).$

함수의 실수 부분과 허수 부분, u와 v의 측면에서, 이것은 방정식 쌍 $u_{x}=v_{y}$와 $u_{y}=-v_{x}$와 동등하며, 여기서 아래-첨자는 부분 미분을 나타냅니다. 어쨌든, 코시-리만 조건은 추가적인 연속성 조건 없이 정칙 함수를 특성화하지 않습니다(루만-멘코프 정리(Looman–Menchoff theorem)를 참조하십시오).

정칙 함수는 몇 가지 놀라운 특색을 보여줍니다. 예를 들어, 피카르의 정리(Picard's theorem) 는 전체 함수의 치역이 일부 $z_{0}\in \mathbb {C}$에 대해 $\mathbb {C} \setminus \{z_{0}\}$, 또는 $\{z_{0}\}$의 세 가지 가능한 형식만 취할 수 있다고 주장합니다. 다시 말해서, 만약 두 개의 구별되는 복소수 $z$와 $w$가 전체 함수 $f$의 치역에 있지 않으면, $f$는 상수 함수입니다. 더욱이, 연결된 열린 집합 위에 정칙 함수는 임의의 비-빈 열린 부분집합에 대한 그것의 제한에 의해 결정됩니다.

Conformal map

Main article: Conformal map

등각 매핑은 방향 보존을 위해 2차원에서 지역적으로 역-가능 복소 해석적(complex analytic) 함수입니다.

Application of Conformal mapping

• In aerospace engineering
• In Biomedical sciences
• In Brain mapping
• Genetic mapping
• Geodesics
• In Geometry
• In Geophysics
• In Google
• In Literature
• in Engineering
• In Electronics
• In Protein synthesis
• In Geography, in Cartography.

Major results

Color wheel graph of the function f(x) = (x² − 1)(x − 2 − i)²/x² + 2 + 2i.
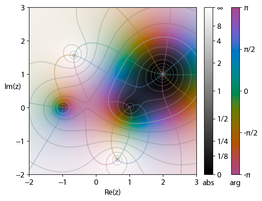
Hue represents the argument, brightness the magnitude.

복소 해석학의 핵심 도구 중 하나는 곡선 적분(line integral)입니다. 닫힌 경로에 의해 경계진 영역 내부의 모든 곳에서 정칙인 함수의 닫힌 경로 주위의 곡선 적분은 코시 적분 정리(Cauchy integral theorem)에 의해 설명되는 것처럼 항상 영입니다. 디스크 내부의 그러한 정칙 함수의 값은 디스크 경계 위에 경로 적분에 의해 계산될 수 있습니다 (코시의 적분 공식(Cauchy's integral formula)에 표시됩니다). 복소 평면에서 경로 적분은 종종 복잡한 실수 적분을 결정하기 위해 사용되고, 여기에서 다른 것 중에서 잔여의 이론이 적용 가능합니다 (윤곽 적분의 방법(methods of contour integration)을 참조하십시오). 함수의 "극점" (또는 고립된 특이점)은 함수의 값이 경계지지 않거나, "폭발"하는 점입니다. 만약 함수가 그러한 극점을 가지면, 그곳에서 함수의 잔여를 계산할 수 있으며, 이는 함수와 관련된 경로 적분을 계산하기 위해 사용될 수 있습니다; 이것이 강력한 잔여 정리(residue theorem)의 내용입니다. 본질적 특이점 근처에서 정칙 함수의 현저한 동작은 피카드의 정리(Picard's theorem)에 의해 설명됩니다. 극점만 가지지만 본질적 특이점(essential singularities)은 없는 함수는 유리형(meromorphic)이라고 불립니다. 로랑 급수(Laurent series)는 테일러 급수(Taylor series)와 동등한 복소-값이지만, 다항식과 같이 더 잘 이해되는 함수의 무한 합을 통해 특이점 근처의 함수의 동작을 연구하기 위해 사용될 수 있습니다.

전체 복소 평면에서 정칙인 경계진 함수(bounded function)는 상수여야 합니다; 이것이 리우빌의 정리(Liouville's theorem)입니다. 그것은 복소수의 필드(field)가 대수적으로 닫힌(algebraically closed) 것이라고 말하는 대수학의 기본 정리(fundamental theorem of algebra)에 대해 자연스럽고 간단한 증명을 제공하기 위해 사용될 수 있습니다.

만약 함수가 연결된(connected) 도메인 전체에서 정칙이면, 그것의 값은 더 작은 부분도메인의 값에 의해 완전하게 결정됩니다. 더 큰 도메인 위에 함수는 더 작은 도메인 위에 값에서 해석적으로 연속(analytically continued)이라고 말합니다. 이를 통해 리만 제타 함수(Riemann zeta function)와 같은 함수 정의를 확장할 수 있으며, 리만 제타 함수는 초기에 제한된 도메인에서만 거의 전체 복소 평면으로 수렴하는 무한 합의 관점에서 정의됩니다. 때때로, 자연 로그(natural logarithm)의 경우와 같이, 복소 평면에서 비-단순 연결된 도메인에 해석적으로 정칙 함수를 계속하는 것은 불가능하지만, 리만 표면(Riemann surface)으로 알려진 밀접하게 관련된 표면에서 정칙 함수를 확장하는 것은 가능합니다.

이 모든 것은 하나의 변수에서 복소 해석학을 의미합니다. 거듭제곱 급수(power series) 확장과 같은 해석적 속성이 이월되는 반면 하나의 복소 차원 (예를 들어 등각성)에서 정칙 함수의 대부분의 기하학적 속성이 이월되지 않는 하나보다 많은 복소 차원에서 복소 해석학의 매우 풍부한 이론이 있습니다. 일-차원 이론에서 가장 중요한 결과라 할 수 있는 복소 평면에서 특정 도메인의 등각 관계에 대한 리만 매핑 정리(Riemann mapping theorem)는 고차원에서는 극적으로 실패합니다.

특정 복소 공간(complex spaces)의 주요 응용은 양자 역학(quantum mechanics)에서 파동 함수(wave functions)입니다.

See also

• Hypercomplex analysis
• Vector calculus
• Complex dynamics
• List of complex analysis topics
• Monodromy theorem
• Real analysis
• Riemann–Roch theorem
• Runge's theorem

References

• Ablowitz, M. J. & A. S. Fokas, Complex Variables: Introduction and Applications (Cambridge, 2003).
• Ahlfors, L., Complex Analysis (McGraw-Hill, 1953).
• Cartan, H., Théorie élémentaire des fonctions analytiques d'une ou plusieurs variables complexes. (Hermann, 1961). English translation, Elementary Theory of Analytic Functions of One or Several Complex Variables. (Addison-Wesley, 1963).
• Carathéodory, C., Funktionentheorie. (Birkhäuser, 1950). English translation, Theory of Functions of a Complex Variable (Chelsea, 1954). [2 volumes.]
• Carrier, G. F., M. Krook, & C. E. Pearson, Functions of a Complex Variable: Theory and Technique. (McGraw-Hill, 1966).
• Conway, J. B., Functions of One Complex Variable. (Springer, 1973).
• Fisher, S., Complex Variables. (Wadsworth & Brooks/Cole, 1990).
• Forsyth, A., Theory of Functions of a Complex Variable (Cambridge, 1893).
• Freitag, E. & R. Busam, Funktionentheorie. (Springer, 1995). English translation, Complex Analysis. (Springer, 2005).
• Goursat, E., Cours d'analyse mathématique, tome 2. (Gauthier-Villars, 1905). English translation, A course of mathematical analysis, vol. 2, part 1: Functions of a complex variable. (Ginn, 1916).
• Henrici, P., Applied and Computational Complex Analysis (Wiley). [Three volumes: 1974, 1977, 1986.]
• Kreyszig, E., Advanced Engineering Mathematics. (Wiley, 1962).
• Lavrentyev, M. & B. Shabat, Методы теории функций комплексного переменного. (Methods of the Theory of Functions of a Complex Variable). (1951, in Russian).
• Markushevich, A. I., Theory of Functions of a Complex Variable, (Prentice-Hall, 1965). [Three volumes.]
• Marsden & Hoffman, Basic Complex Analysis. (Freeman, 1973).
• Needham, T., Visual Complex Analysis. (Oxford, 1997). http://usf.usfca.edu/vca/
• Remmert, R., Theory of Complex Functions. (Springer, 1990).
• Rudin, W., Real and Complex Analysis. (McGraw-Hill, 1966).
• Shaw, W. T., Complex Analysis with Mathematica (Cambridge, 2006).
• Stein, E. & R. Shakarchi, Complex Analysis. (Princeton, 2003).
• Sveshnikov, A. G. & A. N. Tikhonov, Теория функций комплексной переменной. (Nauka, 1967). English translation, The Theory Of Functions Of A Complex Variable (MIR, 1978).
• Titchmarsh, E. C., The Theory of Functions. (Oxford, 1932).
• Wegert, E., Visual Complex Functions. (Birkhäuser, 2012).
• Whittaker, E. T. & G. N. Watson, A Course of Modern Analysis. (Cambridge, 1902). 3rd ed. (1920)

External links

• Wolfram Research's MathWorld Complex Analysis Page