Inscribed angle

Original article: w:Inscribed angle

The inscribed angle θ is half of the central angle 2θ that subtends the same arc on the circle. The angle θ does not change as its vertex is moved around on the circle.

기하학(geometry)에서, 내접 각도(inscribed angle)는 두 현(chords)이 원(circle) 위에 교차할 때 원의 내부에 형성되는 각도(angle)입니다. 그것은 역시 원 위의 한 점에서 원 위의 주어진 두 점에 끼워진 각도로 정의될 수 있습니다.

동등하게, 내접 각도는 끝점을 공유하는 원의 두 현에 의해 정의됩니다.

내접 각도 정리(inscribed angle theorem)는 내접 각도의 측정(measure)을 같은 호(arc)에 끼워진 중심 각도(central angle)의 측정과 연결합니다.

내접 각도 정리는 유클리드의 원론(Euclid's Elements)의 3권에서 제안 20으로 나타납니다.

Theorem

Statement

For fixed points A and B, the set of points M in the plane for which the angle AMB is equal to α is an arc of a circle. The measure of ∠ AOB, where O is the center of the circle, is 2α.

내접 각도 정리는 원에 내접된 각도 θ가 원 위의 같은 호(arc)에 끼워진(subtend) 중심 각도 2θ의 절반이라는 것입니다. 그러므로, 그 각도는 그것의 꼭짓점(vertex)이 원 위의 다른 위치로 이동하더라도 변경되지 않습니다.

Proof

Inscribed angles where one chord is a diameter

Case: One chord is a diameter

오른쪽 그림에서 처럼, O를 원의 중심이라고 놓습니다. 원 위에 두 점을 선택하고, 그것들을 V와 A라고 부릅니다. 그것이 점 V와 지름방향으로 반대편(diametrically opposite)인 점 B에서 원과 교차하도록 직선 VO를 그리고 O를 지나 확장합니다. 그것의 꼭짓점(vertex)이 점 V이고 그것의 변이 점 A와 B를 통과하는 각도를 그립니다.

직선 OA를 그립니다. 각도 BOA는 중심 각도(central angle)입니다; 그것을 θ라고 합니다. 직선 OV와 OA 둘 다는 원의 반지름(radii)이므로, 그것들은 같은 길이를 가집니다. 그러므로, 삼각형 VOA는 이등변(isosceles)이므로, 각도 BVA (내접 각도)와 각도 VAO는 같습니다; 그것들의 각각을 ψ로 표시하도록 놓습니다.

O를 통과하는 선 VB가 직선이기 때문에, 각도 BOA와 AOV는 더해져서 180°가 됩니다. 그러므로, 각도 AOV는 180° − θ를 측정합니다.

삼각형(triangle)의 셋의 각도는 합해져서 180°이고, 삼각형 VOA의 셋의 각도는 다음과 같이 알려져 있습니다:

180° − θ

ψ

ψ.

그러므로,

$2\psi +180^{\circ }-\theta =180^{\circ }.$

양쪽 변에서 다음을 빼면

$(180^{\circ }-\theta )$

다음을 산출합니다:

$2\psi =\theta ,$

여기서 θ는 호 AB에 끼워지는 중심 각도이고 ψ는 호 AB에 끼워지는 내접 각도입니다.

Inscribed angles with the center of the circle in their interior

Case: Center interior to angle

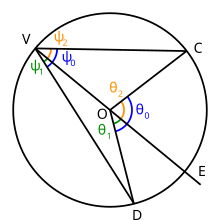
그것이 중심이 점 O인 원이 주어지면, 그 원 위에 세 점 V, C, 및 D를 선택하십시오. 직선 VC와 VD를 그리십시오: 각도 DVC는 내접 각도입니다. 이제 직선 VO를 그리고 그것이 점 E에서 원과 교차하도록 그것을 점 O를 통과하게 연장하십시오. 각도 DVC는 원 위에서 호 DC에 끼워집니다.

이 호가 그것 안에 점 E를 포함한다고 가정하십시오. 점 E는 점 V와 지름방향으로 반대편에 있습니다. 각도 DVE와 EVC는 역시 내접 각도이지만, 이들 둘 다는 원의 중심을 통과하는 한 변을 가지고, 따라서 위의 부분 1에서 정리가 그것들에 적용될 수 있습니다.

그러므로,

$\angle DVC=\angle DVE+\angle EVC.$

그런-다음, 다음이 되도록

$\psi _{0}=\psi _{1}+\psi _{2}.\qquad \qquad (1)$

다음으로 놓습니다:

$\psi _{0}=\angle DVC,$

$\psi _{1}=\angle DVE,$

$\psi _{2}=\angle EVC$.

직선 OC와 OD를 그립니다. 각도 DOC는 중심 각도이지만, 각도 DOE와 EOC도 마찬가지이고, 다음입니다:

$\angle DOC=\angle DOE+\angle EOC.$

다음이 되도록

$\theta _{0}=\theta _{1}+\theta _{2}.\qquad \qquad (2)$

다음으로 놓습니다:

$\theta _{0}=\angle DOC,$

$\theta _{1}=\angle DOE,$

$\theta _{2}=\angle EOC$.

부분 1에서 우리는 $\theta _{1}=2\psi _{1}$임과 $\theta _{2}=2\psi _{2}$임을 압니다. 이들 결과를 방정식 (2)와 결합하면 다음을 산출합니다:

$\theta _{0}=2\psi _{1}+2\psi _{2}=2(\psi _{1}+\psi _{2})$

그러므로, 방정식 (1)에 의해,

$\theta _{0}=2\psi _{0}.$

Inscribed angles with the center of the circle in their exterior

Case: Center exterior to angle

이전 경우는 이 증명의 첫 부분에서 논의된 내접 각도의 측정이 두 내접 각도의 차이인 경우를 덮어쓰기 위해 확장될 수 있습니다.

그것의 중심이 점 O인 원이 주어지면, 그 원 위에 세 점 V, C, 및 D를 선택하십시오. 직선 VC와 VD를 그리십시오: 각도 DVC는 내접 각도입니다. 이제 직선 VO를 그리고 그것이 점 E에서 원과 교차하도록 점 O를 통과하게 연장하십시오. 각도 DVC는 원 위에 호 DC에 끼워집니다.

이 호가 그 안에 점 E를 포함하지 않는다고 가정합니다. 점 E는 점 V와 지름방향에서 반대쪽입니다. 각도 EVD와 EVC도 내접 각도이지만, 이들 각도 둘 다는 원의 중심을 통과하는 한 변을 가지고, 따라서 위의 부분 1의 정리가 그것들에 적용될 수 있습니다.

그러므로,

$\angle DVC=\angle EVC-\angle EVD$.

그런-다음 다음이 되도록

$\psi _{0}=\psi _{2}-\psi _{1}.\qquad \qquad (3)$

다음으로 놓습니다:

$\psi _{0}=\angle DVC,$

$\psi _{1}=\angle EVD,$

$\psi _{2}=\angle EVC$.

직선 OC와 OD를 그리십시오. 각도 DOC는 중심 각도이지만, 각도 EOD와 EOC도 마찬가지이고, 다음입니다:

$\angle DOC=\angle EOC-\angle EOD.$

다음이 되도록

$\theta _{0}=\theta _{2}-\theta _{1}.\qquad \qquad (4)$

다음으로 놓습니다:

$\theta _{0}=\angle DOC,$

$\theta _{1}=\angle EOD,$

$\theta _{2}=\angle EOC$.

부분 1로부터 우리는 $\theta _{1}=2\psi _{1}$임과 $\theta _{2}=2\psi _{2}$임을 압니다. 이들 결과를 방정식 (4)와 결합하면 다음을 산출합니다:

$\theta _{0}=2\psi _{2}-2\psi _{1}$

그러므로, 방정식 (3)에 의해,

$\theta _{0}=2\psi _{0}.$

Corollary

유사한 논증에 의해, 현(chord)과 그것의 교차점 중 하나에서 접선(tangent) 사이의 각도는 현에 끼워진 중심 각도의 절반과 같습니다. 역시 원에 접하는 직선(Tangent lines to circles)을 참조하십시오.

Applications

내접 각도 정리(theorem)는 평면의 기본 유클리드 기하학의 많은 증명에서 사용됩니다. 정리의 특별한 경우는 지름(diameter)에 의해 끼워진 각도가 항상 90°, 즉 직각이라고 말하는 탈레스의 정리(Thales' theorem)입니다. 정리의 결과로, 순환 사변형(cyclic quadrilateral)의 반대 각도는 합해서 180°가 됩니다; 반대로, 이것이 참인 임의의 사변형은 원에 내접될 수 있습니다. 또 다른 예제로서, 내접 각도 정리는 원에 대한 점의 배율(power of a point)과 관련된 여러 정리에 대해 기초입니다. 게다가, 둘의 현이 원 안에 교차할 때, 그것들의 조각의 길이의 곱이 같다는 것을 증명하는 것을 허용합니다.

Inscribed angle theorems for ellipses, hyperbolas and parabolas

내접 각도 정리는 타원, 쌍곡선, 및 포물선에도 존재합니다. 근본적인 차이점은 각도의 측정입니다. (각도는 한 쌍의 교차하는 직선으로 고려됩니다.)

• 타원(Ellipse)
• 쌍곡선(Hyperbola)
• 포물선(Parabola)

References

• Ogilvy, C. S. (1990). Excursions in Geometry. Dover. pp. 17–23. ISBN 0-486-26530-7.
• Gellert W, Küstner H, Hellwich M, Kästner H (1977). The VNR Concise Encyclopedia of Mathematics. New York: Van Nostrand Reinhold. p. 172. ISBN 0-442-22646-2.
• Moise, Edwin E. (1974). Elementary Geometry from an Advanced Standpoint (2nd ed.). Reading: Addison-Wesley. pp. 192–197. ISBN 0-201-04793-4.

External links

• Weisstein, Eric W. "Inscribed Angle". MathWorld.
• Relationship Between Central Angle and Inscribed Angle
• Munching on Inscribed Angles at cut-the-knot
• Arc Central Angle With interactive animation
• Arc Peripheral (inscribed) Angle With interactive animation
• Arc Central Angle Theorem With interactive animation
• At bookofproofs.org