Position (geometry)

기하학(geometry)에서, 반지름 벡터(radius vector)로 역시 알려져 있는, 위치(position) 또는 위치 벡터(postion vector 또는 location vector)는 임의의 참조 원점(origin) O에 관련하여 공간에서 점(point) P의 위치를 나타내는 유클리드 벡터(Euclidean vector)입니다. 보통 x, r, 또는 s로 표시하며, 그것은 O에서 P까지의 직선 선분에 해당합니다. 달리 말해서, 그것은 원점을 P로 매핑하는 변위(displacement) 또는 변환(translation)입니다:^[1]

\mathbf {r} ={\overrightarrow {OP}}

용어 "위치 벡터"는 주로 미분 기하학(differential geometry), 역학(mechanics) 및 때때로 벡터 미적분학(vector calculus)의 분야에서 사용됩니다.

자주 이것은 이-차원(two-dimensional) 또는 삼-차원 공간(three-dimensional space)에서 사용되지만, 임의의 차원(dimension)의 유클리드 공간(Euclidean space) 및 아핀 공간(affine space)으로 쉽게 일반화될 수 있습니다.^[2]

Relative position

점 P에 관한 점 Q의 상대 위치(relative position)는 두 개의 절대 위치 벡터 (각각 원점에 관한 것)를 뺀 결과인 유클리드 벡터입니다:

\Delta \mathbf {r} =\mathbf {s} -\mathbf {r} ={\overrightarrow {PQ}}

여기서 $\mathbf {s} ={\overrightarrow {OQ}}$ .

두 점 사이의 상대 방향(relative direction)은 단위 벡터(unit vector)로 정규화된 상대 위치입니다:

\Delta \mathbf {\hat {r}} =\Delta \mathbf {r} /\Delta {r}

여기서 분모는 두 점 사이의 거리, $\Delta r=\|\Delta \mathbf {r} \|$ 입니다.

Definition

Three dimensions

삼-차원(three dimensions)에서, 삼-차원 좌표의 임의의 집합 및 대응하는 기저 벡터는 공간에서 점의 위치를 정의하기 위해 사용될 수 있습니다—수작업에 대해 가장-간단한 어떤 것이든지 사용될 수 있습니다.

공통적으로, 우리는 친숙한 데카르트 좌표 시스템(Cartesian coordinate system) 또는 때때로 구형 극좌표(spherical polar coordinates), 또는 원통형 좌표(cylindrical coordinates)를 사용합니다:

{\begin{aligned}\mathbf {r} (t)&\equiv \mathbf {r} (x,y,z)\equiv x(t)\mathbf {\hat {e}} _{x}+y(t)\mathbf {\hat {e}} _{y}+z(t)\mathbf {\hat {e}} _{z}\\&\equiv \mathbf {r} (r,\theta ,\phi )\equiv r(t)\mathbf {\hat {e}} _{r}{\big (}\theta (t),\phi (t){\big )}\\&\equiv \mathbf {r} (r,\theta ,z)\equiv r(t)\mathbf {\hat {e}} _{r}{\big (}\theta (t){\big )}+z(t)\mathbf {\hat {e}} _{z},\\\end{aligned}}

여기서 t는 직교 또는 원통 대칭으로 인한 매개-변수(parameter)입니다. 이들 다른 좌표 및 해당 기저 벡터는 같은 위치 벡터를 나타냅니다. 보다 일반적인 곡선 좌표(curvilinear coordinates)가 대신 사용될 수 있고 연속체 역학(continuum mechanics) 및 일반 상대성(general relativity)과 같은 문맥에 있습니다 (후자 경우에서 우리는 추가적인 시간 좌표가 필요합니다).

n dimensions

선형 대수(Linear algebra)는 n-차원 위치 벡터를 추상화를 허용합니다. 위치 벡터는 기저(basis) 벡터의 선형 조합으로 표현될 수 있습니다:^[3]^[4]

\mathbf {r} =\sum _{i=1}^{n}x_{i}\mathbf {e} _{i}=x_{1}\mathbf {e} _{1}+x_{2}\mathbf {e} _{2}+\dotsb +x_{n}\mathbf {e} _{n}.

모든 위치 벡터의 집합(set)은 위치 공간(position space) (그의 원소가 위치 벡터인 벡터 공간(vector space))을 형성하는데, 왜냐하면 위치는 공간에서 또 다른 위치 벡터를 얻기 위해 더해지고 (벡터 덧셈(vector addition)) 길이에서 스케일될 (스칼라 곱셈(scalar multiplication)) 수 있기 때문입니다. "공간"의 개념은 직관적인데, 왜냐하면 각 x_i (i = 1, 2, …, n)는 임의의 값을 가질 수 있으며, 값 모음은 공간에서 점을 정의합니다.

위치 공간의 차원(dimension)은 n입니다 (역시 dim(R) = n으로 표시됩니다). 기저 벡터 e_i에 관한 벡터 r의 좌표(coordinates)는 x_i입니다. 좌표의 벡터는 좌표 벡터(coordinate vector) 또는 n-튜플(tuple) (x₁, x₂, …, x_n)을 형성합니다.

각 좌표 x_i는 다수의 매개변수(parameter) t로 매개변수화(parameterized)될 수 있습니다. 하나의 매개-변수 x_i(t)는 곡선화된 1D 경로를 설명하며, 두 개의 매개-변수 x_i(t₁, t₂)는 곡선화된 2D 표면을 설명하며, 세 개의 x_i(t₁, t₂, t₃)는 공간의 곡선화된 3D 부피를 설명하며, 등등을 설명합니다.

기저 집합 B = {e₁, e₂, …, e_n}의 선형 스팬(linear span)은 span(B) = R로 표시되는 위치 공간 R과 같습니다.

Applications

Differential geometry

위치 벡터 필드는 연속 및 미분-가능 공간 곡선을 설명하기 위해 사용되며, 이 경우에서 독립 매개-변수는 시간일 필요는 없지만, (예를 들어) 곡선의 호 길이일 수 있습니다.

Mechanics

임의의 운동 방정식(equation of motion)에서, 위치 벡터 r(t)는 보통 가장 추구하는 양인데 왜냐하면 이 함수는 입자 (즉, 점 질량(point mass)) – 어떤 시간 t에서 주어진 좌표 시스템(coordinate system)에 관한 그것의 위치 – 의 운동을 정의합니다.

위치의 관점에서 운동을 정의하기 위해, 각 좌표는 시간에 의해 매개-변수화(parametrized)될 수 있습니다; 시간의 각 연속적인 값은 좌표에 의해 주어진 연속적인 공간 위치의 수열에 해당하므로, 많은 연속적인 위치의 연속체 극한은 입자 자취의 경로입니다.

일-차원의 경우에서, 위치는 오직 하나의 성분을 가지므로, 그것은 스칼라 좌표로 효과적으로 퇴화됩니다. 말하자면, x 방향, 또는 방사형 r 방향에서 벡터일 수 있습니다. 동등한 표기법은 다음을 포함합니다:

\mathbf {x} \equiv x\equiv x(t),\quad r\equiv r(t),\quad s\equiv s(t).

Derivatives of position

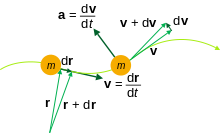
Kinematic quantities of a classical particle: mass m, position r, velocity v, acceleration a

시간 t의 함수인 위치 벡터 r에 대해, 시간 도함수(time derivative)는 t에 관해 계산될 수 있습니다. 이들 도함수는 운동학(kinematics), 제어 이론(control theory), 공학(engineering) 및 다른 과학 연구에서 공통적인 유용성을 가집니다.

속도(velocity): $\mathbf {v} ={\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}},$

여기서 dr는 무한소적으로(infinitesimally) 작은 변위(displacement)입니다.

가속도(acceleration): $\mathbf {a} ={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf {r} }{\mathrm {d} t^{2}}}.$

가가속도(Jerk): $\mathbf {j} ={\frac {\mathrm {d} \mathbf {a} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf {v} }{\mathrm {d} t^{2}}}={\frac {\mathrm {d} ^{3}\mathbf {r} }{\mathrm {d} t^{3}}}.$

위치의 일차, 이차 및 삼차 도함수에 대해 이들 이름은 기본 운동학에서 공통적으로 사용됩니다.^[5] 확장에 의해, 고차 도함수는 유사한 방식으로 계산될 수 있습니다. 이들 고차 도함수의 연구는 원래의 변위 함수의 근사를 향상시킬 수 있습니다. 그러한 고차 항은 변위 함수를 무한 수열의 합(a sum of an infinite sequence)으로 정확하게 나타내기 위해 필요하며, 공학 및 물리학에서 여러 분석적 기술을 활성화합니다.

Notes

^ The term displacement is mainly used in mechanics, while translation is used in geometry.
^ Keller, F. J, Gettys, W. E. et al. (1993), p 28–29
^ Riley, K. F.; Hobson, M. P.; Bence, S. J. (2010). Mathematical methods for physics and engineering. Cambridge University Press. ISBN 978-0-521-86153-3.
^ Lipschutz, S.; Lipson, M. (2009). Linear Algebra. McGraw Hill. ISBN 978-0-07-154352-1.
^ Stewart, James (2001). "§2.8. The Derivative As A Function". Calculus (2nd ed.). Brooks/Cole. ISBN 0-534-37718-1.

References

Keller, F. J, Gettys, W. E. et al. (1993). "Physics: Classical and modern" 2nd ed. McGraw Hill Publishing.

External links

Media related to Position (geometry) at Wikimedia Commons

[1] The term displacement is mainly used in mechanics, while translation is used in geometry.

[phys_keller-2] Keller, F. J, Gettys, W. E. et al. (1993), p 28–29

[3] Riley, K. F.; Hobson, M. P.; Bence, S. J. (2010). Mathematical methods for physics and engineering. Cambridge University Press. ISBN 978-0-521-86153-3.

[4] Lipschutz, S.; Lipson, M. (2009). Linear Algebra. McGraw Hill. ISBN 978-0-07-154352-1.

[stewart-5] Stewart, James (2001). "§2.8. The Derivative As A Function". Calculus (2nd ed.). Brooks/Cole. ISBN 0-534-37718-1.

[1]

[2]

[3]

[4]

[5]