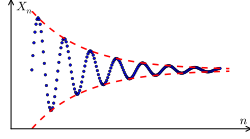
Cauchy sequence

(a) The plot of a Cauchy sequence

(x_{n}),

shown in blue, as

x_{n}

versus

n.

If the space containing the sequence is complete, then the sequence has a limit.

(b) A sequence that is not Cauchy. The elements of the sequence do not get arbitrarily close to each other as the sequence progresses.

수학(mathematics)에서, 코시 수열(Cauchy sequence) (French pronunciation: [koʃi]; English: /ˈkoʊʃiː/ KOH-shee)은, 오귀스탱-루이 코시(Augustin-Louis Cauchy)의 이름을 따서 지어졌으며, 수열이 진행함에 따라 그것의 원소(elements)가 임의적으로 서로 가까워지는 수열(sequence)입니다.^[1] 보다 정확하게, 임의의 작은 양의 거리가 주어지면, 수열의 유한한 숫자의 원소를 제외하고는 모두 원소는 서로로부터 해당 주어진 거리보다 작습니다.

그것은 각 항에 대해 앞의 항에 임의적으로 가까워지게 되기 위한 충분은 아닙니다. 예를 들어, 자연수의 제곱근의 수열에서: $a_{n}={\sqrt {n}},$

연속 항이 서로 임의적으로 가까워지게 됩니다: $a_{n+1}-a_{n}={\sqrt {n+1}}-{\sqrt {n}}={\frac {1}{{\sqrt {n+1}}+{\sqrt {n}}}}<{\frac {1}{2{\sqrt {n}}}}.$

어쨌든, 인덱스 $n$ 의 값이 증가함에 따라, 항 $a_{n}$ 은 임의적으로 커집니다. 따라서, 임의의 인덱스 $n$ 과 거리 $d$ 에 대해, $a_{m}-a_{n}>d$ 를 만족하는 충분하게 큰 인덱스 $m$ 이 존재합니다 (실제로, 임의의 $m>\left({\sqrt {n}}+d\right)^{2}$ 에 충분합니다.) 결과로써, 아무리 멀리 가더라도, 수열의 남아있는 부분은 결코 서로 가까워지지 않습니다; 따라서 그 수열은 코시가 아닙니다.

코시 수열의 유용성은 완비 메트릭 공간(complete metric space) (모든 그러한 수열이 극한에 수렴하는 것으로 알려진 곳)에서, 수렴(convergence)에 대해 기준이 오직 수열 자체의 항에 의존하고, 항뿐만 아니라 극한 값을 사용하는 수렴의 정의와 반대라는 사실에 있습니다. 이것은 반복 과정(iterative process)이 반복으로 구성되고, 따라서 종료와 같은 논리적 조건을 충족하는 코시 수열을 생성하기 위해 상대적으로 쉽게 표시될 수 있는 이론적 및 적용된 둘 다의 알고리듬(algorithm)에서 종종 이용됩니다.

보다 추상적인 균등 공간(uniform spaces)에서 코시 수열의 일반화는 코시 필터(Cauchy filter) 및 코시 네트(Cauchy net)의 형식으로 존재합니다.

In real numbers

실수의 다음 수열은 $x_{1},x_{2},x_{3},\ldots$

만약 모든 각 양의(positive) 실수 $\varepsilon$ 에 대해, 모든 자연수(natural numbers) $m,n>N$ 에 대해 다음을 만족하는 양의 정수(integer) N이 있으면 코시 수열이라고 불립니다: $|x_{m}-x_{n}|<\varepsilon ,$

여기서 수직 막대는 절댓값(absolute value)을 나타냅니다. 비슷한 방법으로, 우리는 유리수 또는 복소수의 코시 수열을 정의할 수 있습니다. 코시는 $x_{m}-x_{n}$ 를 무한 m, n의 모든 각 쌍에 대해 무한소(infinitesimal)가 되도록 요구함으로써 그러한 조건을 공식화했습니다.

임의의 실수 r에 대해, r의 잘린 십진 전개의 수열은 코시 수열을 형성합니다. 예를 들어, $r=\pi$ 일 때, 이 수열은 (3, 3.1, 3.14, 3.141, ...)입니다. m번째와 n번째 항은 m < n일 때 많아야 $10^{1-m}$ 만큼 다르고, m이 커질수록 이것은 임의의 고정된 양수 $\varepsilon$ 보다 작아지게 됩니다.

Modulus of Cauchy convergence

만약 $(x_{1},x_{2},x_{3},...)$ 가 집합 $X$ 에서 수열이면, 그 수열에 대해 코시 수열의 모듈러스는 모든 자연수(natural number) $k$ 와 자연수 $m,n>\alpha (k)$ 에 대해 $|x_{m}-x_{n}|<1/k$ 를 만족하는 자연수의 집합에서 자체로의 함수(function) $\alpha$ 입니다.

코시 수열의 모듈러스를 갖는 임의의 수열은 코시 수열입니다. 코시 수열에 대해 모율러스의 존재는 자연수의 바른-순서화 속성(well-ordering property)에서 따릅니다 ( $\alpha (k)$ 를 코시 수열의 정의에서 가장 작은 가능한 $N$ 으로 놓고, $r$ 을 $1/k$ 로 취합니다). 모듈러스의 존재는 역시 선택의 공리의 약한 형식인 종속 선택(dependent choice)의 원리에서 따르고, 그것은 역시 AC₀₀라고 불리는 훨씬 더 약한 조건에서 따릅니다. 정규 코시 수열은 주어진 코시 수렴의 모듈러서 (보통 $\alpha (k)=k$ 또는 $\alpha (k)=2^{k}$ )를 갖는 수열입니다. 코시 수렴의 모듈러스를 갖는 임의의 코시 수열은 정규 코시 수열과 동등합니다; 이것은 임의의 형식의 선택의 공리를 사용없이 입증될 수 있습니다.

코시 수렴의 모듈러스는 임의의 형식의 선택을 사용하기를 원하지 않는 건설적인 수학자에 의해 사용됩니다. 코시 수렴의 모듈러스를 사용하는 것은 건설적 해석에서 정의와 정리 둘 다를 단순화할 수 있습니다. 정규 코시 수열은 에렛 비숍(Errett Bishop)에 의해 그의 Foundations of Constructive Analysis에서 사용되었고, 더글러스 브리지(Douglas Bridges)에 의해 비-구성적 교과서 (ISBN 978-0-387-98239-7)에서 사용되었습니다.

In a metric space

코시 수열의 정의는 오직 메트릭 개념을 포함되므로, 그것을 임의의 매트릭 공간 X로 일반화하는 것이 간단합니다. 그렇게 하려면, 절댓값 $\left|x_{m}-x_{n}\right|$ 은 $x_{m}$ 와 $x_{n}.$ 사이의 거리 $d\left(x_{m},x_{n}\right)$ 로 대체됩니다 (여기서 d는 메트릭(metric)을 나타냅니다).

공식적으로, 주어진 메트릭 공간(metric space) $(X,d)$ 이 주어지면 다음 수열은 $x_{1},x_{2},x_{3},\ldots$

만약 모든 각 양의 실수(real number) $\varepsilon >0$ 에 대해, 모든 양의 정수 $m,n>N$ 에 대해 다음 거리를 만족하는 양의 정수(integer) $N$ 이 있으면 코시입니다: $d\left(x_{m},x_{n}\right)<\varepsilon .$

대략적으로 말하면, 수열의 항은 수열이 X에서 극한(limit)을 가져야 함을 암시하는 방법에서 점점 더 가까워지고 됩니다. 그럼에도 불구하고, 그러한 극한이 X 내에 항상 존재하는 것은 아닙니다: 모든 각 코시 수열이 공간에서 수렴하는 공간의 속성은 완비성(completeness)이라고 불리고, 아래에 자세히 설명되어 있습니다.

Completeness

모든 각 코시 수열은 X의 원소로 수렴하는 매트릭 공간 (X, d)는 완비(complete)라고 불립니다.

Examples

실수(real number)는 보통의 절댓값에 의해 유도된 메트릭 아래에서 완비이고, 실수의 표준 구성 중 하나는 유리수(rational number)의 코시 수열을 포함합니다. 이 구성에서, 특정 꼬리 행위를 갖는 유리수의 코시 수열의 각 동치 클래스–즉, 서로 임의적으로 가까워지는 수열의 각 클래스는 실수입니다.

다소 다른 유형의 예제는 이산 미터법(discrete metric)을 가지는 메트릭 공간 X에 의해 제공됩니다 (여기서 임의의 둘의 구별되는 점은 서로 거리 1에 있습니다). X의 원소의 임의의 코시 수열은 일부 고정된 점 이상으로 일정해야 하고, 결국 반복되는 항으로 수렴합니다.

Non-example: rational numbers

유리수(rational number) $\mathbb {Q}$ 는 (보통의 거리에 대해) 완비가 아닙니다:
( $\mathbb {R}$ 에서) 무리수(irrational number)에 수렴하는 유리수의 수열이 있습니다; 이것들은 $\mathbb {Q}$ 에서 극한을 가지지 않는 코시 수열입니다. 사실, 만약 실수 x가 무리수이면, 수열(x_n)은, 그것의 n-번째 항이 x의 십진 전개의 n 십진 자리까지 잘려지며, 무리수 극한 x를 갖는 유리수의 코시 수열을 제공합니다. 무리수는 확실히 $\mathbb {R}$ 에서 존재하며, 예를 들어:

$x_{0}=1,x_{n+1}={\frac {x_{n}+{\frac {2}{x_{n}}}}{2}}$ 에 의해 정의된 수열은 유리수 (1, 3/2, 17/12,...)로 구성되며, 이것은 정의로부터 분명합니다; 어쨌든 그것은 이의 무리수(irrational) 제곱근으로 수렴하며, 제곱근을 계산하는 바빌로니아 방법을 참조하십시오.
연속적인 피보나치 숫자(Fibonacci number)의 비율의 수열 $x_{n}=F_{n}/F_{n-1}$ 은, 만약 그것이 수렴한다면, $\phi ^{2}=\phi +1$ 을 만족시키는 극한 $\phi$ 로 수렴하고, 유리수는 이 속성을 가지지 않습니다. 만약 우리가 이것을 실수의 수열로 고려하면, 어쨌든, 그것은 실수 $\varphi =(1+{\sqrt {5}})/2,$ 무리수인 황금 비율(Golden ratio)로 수렴합니다.
지수, 사인과 코사인 함수, exp(x), sin(x), cos(x)의 값은 $x\neq 0$ 의 임의의 유리수 값에 대해 무리수로 알려져 있지만, 각각은 예를 들어 매클로린 급수(Maclaurin series)를 사용하여 유리수 코시 수열의 극한으로 정의될 수 있습니다.

Non-example: open interval

$\mathbb {R}$ 에서 보통의 거리를 갖는 실수의 집합에서 열린 구간 $X=(0,2)$ 은 완비 공간이 아닙니다: 그 안에 수열 $x_{n}=1/n$ 이 있으며, 이것은 코시입니다 ( 임의적인 작은 거리 경계 $d>0$ 에 대해 $n>1/d$ 의 모든 항 $x_{n}$ 은 $(0,d)$ 구간에 맞습니다), 어쨌든 $X$ 에서 수렴하지 않습니다 – 그것의 '극한', 숫자 0은 공간 $X$ 에 속하지 않습니다.

Other properties

(말하자면, 극한 s를 갖는) 모든 각 수렴하는 수열은 코시 수열인데, 왜냐하면, 임의의 실수 $\varepsilon >0$ 이 주어졌을 때, 어떤 고정점을 넘어서면, 수열의 모든 각 항은 s의 거리 $\varepsilon /2$ 내에 있으므로, 수열의 임의의 두 항은 서로의 거리 $\varepsilon$ 내에 있기 때문입니다.
임의의 메트릭 공간에서, 코시 수열 $x_{n}$ 은 경계진(bounded) 것입니다 (왜냐하면 일부 N에 대해, N-번째 앞으로부터 수열의 모든 항은 서로의 거리 1 내에 있고, 만약 M이 $x_{N}$ 과 N-번째까지 임의의 항 사이의 가장 큰 거리이면, 수열의 항은 $x_{N}$ 에서 $M+1$ 보다 더 큰 거리를 가지기 때문입니다).
임의의 메트릭 공간에서, 극한 s를 갖는 수렴하는 부분수열을 가지는 코시 수열은 (같은 극한을 갖는) 자체로 수렴하는데, 왜냐하면, 임의의 실수 r > 0이 주어졌을 때, 원래 수열에서 어떤 고정점을 넘어서면, 부분수열의 모든 각 항은 s의 거리 r/2 내에 있고, 원래 수열의 임의의 두 항은 서로 거리 r/2 내에 있으므로, 원래 수열의 모든 각 항은 s의 거리 r 내에 있기 때문입니다.

볼차노–바이어슈트라스 정리(Bolzano–Weierstrass theorem)와 함께, 이들 마지막 두 속성은 볼차노–바이어슈트라스 정리와 하이네–보렐 정리(Heine–Borel theorem) 둘 다와 밀접하게 관련된 실수의 완비성의 하나의 표준 증명을 산출합니다. 실수의 모든 각 코시 수열은 경계진 것이며, 따라서 볼차노–바이어슈트라스에 의해 수렴 부분수열을 가지며, 따라서 그 자체로 수렴합니다. 실수의 완비성의 이 증명은 암시적으로 최소 위쪽 경계 공리(least upper bound axiom)를 사용합니다. 실수를 유리수의 완비(completion)로 구성하는, 위에서 언급된, 대안적 접근은 실수의 완비성을 동어반복으로 만듭니다.

코시 수열로 동작할 수 있고 완비성을 사용할 수 있다는 이점의 표준 설명 중 하나는 실수의 (또는, 더 일반적으로, 임의의 완비 노름 선형 공간(normed linear space), 또는 바나흐 공간(Banach space)의 원소) 무한 급수(infinite series)의 합계의 고려에 의해 제공됩니다. 그러한 급수 ${\textstyle \sum _{n=1}^{\infty }x_{n}}$ 가 수렴으로 고려되는 것과 부분 합(partial sum) $(s_{m})$ 의 수열이 수렴하는 것은 필요충분 조건이며, 여기서 ${\textstyle s_{m}=\sum _{n=1}^{m}x_{n}}$ 입니다. 부분 합의 수열이 코시인지 여부를 결정하는 것은 일상적인 문제인데, 왜냐하면 양의 정수 $p>q$ 에 대해 다음이기 때문입니다: $s_{p}-s_{q}=\sum _{n=q+1}^{p}x_{n}.$

만약 $f:M\to N$ 가 메트릭 공간 M과 N 사이의 균등하게 연속(uniformly continuous) 맵이고 (x_n)이 M에서 코시 수열이면, $(f(x_{n}))$ 은 N에서 코시 수열입니다. 만약 $(x_{n})$ 와 $(y_{n})$ 가 유리수, 실수 또는 복소수에서 둘의 코시 수열이면, 합 $(x_{n}+y_{n})$ 과 곱 $(x_{n}y_{n})$ 은 역시 코시 수열입니다.

Generalizations

In topological vector spaces

역시 토폴로지적 벡터 공간(topological vector space) $X$ 에 대해 코시 수열의 개념이 있습니다: 0에 대한 $X$ 에 대해 지역적 기저(local base) $B$ 를 선택합니다; 그런-다음 ( $x_{k}$ )는 만약 각 구성원 $V\in B$ 에 대해, $n,m>N$ 일 때마다 $x_{n}-x_{m}$ 가 $V$ 의 원소임을 만족하는 일부 숫자 $N$ 이 있으면 코시 수열입니다. 만약 $X$ 의 토폴로지가 평행이동-불면 메트릭(translation-invariant metric) $d$ 과 호환되면, 두 정의는 일치합니다.

In topological groups

코시 수열의 토폴로지적 벡터 공간 정의는 오직 연속 "뺄셈" 연산이 있음을 요구하기 때문에, 그것은 단지 토폴로지적 그룹(topological group)의 문맥에서 다음과 같이 기술될 수 있습니다: 토폴로지적 공간 $G$ 에서 수열 $(x_{k})$ 는 만약 $G$ 에서 항등원(identity)의 모든 각 열린 이웃 $U$ 에 대해 $m,n>N$ 일 때마다 그것이 $x_{n}x_{m}^{-1}\in U$ 임을 따름을 만족하는 일부 숫자 $N$ 이 존재하면 코시 수열입니다. 위에서 처럼, $G$ 에 있는 항등원의 임의의 지역적 기저에 있는 이웃에 대해 이것을 확인하는 것으로 충분합니다.

메트릭 공간의 완비성의 구성에서와 같이, 우리는 게다가 $(x_{k})$ 와 $(y_{k})$ 가 만약 $G$ 에서 항등원의 모든 각 열린 이웃(neighbourhood) $U$ 에 대해 $m,n>N$ 일 때마다 그것은 $x_{n}y_{m}^{-1}\in U$ 임을 따름을 만족하는 일부 숫자 $N$ 이 존재하면 동등한 것인 $G$ 에서 코시 수열 위에 이항 관계를 정의할 수 있습니다. 이 관계는 동치 관계(equivalence relation)입니다: 그것은 수열이 코시 수열이기 때문에 반사적입니다. 그것은 대칭적인데 왜냐하면 역의 연속성에 의해 항등원의 또 다른 열린 이웃인 $y_{n}x_{m}^{-1}=(x_{m}y_{n}^{-1})^{-1}\in U^{-1}$ 이기 때문입니다. 그것은 전이적(transitive)인데 왜냐하면 $x_{n}z_{l}^{-1}=x_{n}y_{m}^{-1}y_{m}z_{l}^{-1}\in U'U''$ 이기 때문이며 여기서 $U'$ 와 $U''$ 는 $U'U''\subseteq U$ 를 만족하는 항등원의 열린 이웃입니다; 그러한 쌍은 그룹 연산의 연속성에 의해 존재합니다.

In groups

역시 그룹(group) $G$ 에서 코시 수열의 개념이 있습니다: $H=(H_{r})$ 를 유한 인덱스(index)의 $G$ 의 정규 부분그룹(normal subgroup)의 감소하는 수열로 놓습니다. 그런-다음 $G$ 에서 수열 $(x_{n})$ 은 ( $H$ 에 관한) 코시로 말해지는 것과 임의의 $r$ 에 대해, 모든 $m,n>N$ 에 대해 $x_{n}x_{m}^{-1}\in H_{r}$ 를 만족하는 $N$ 이 있는 것은 필요충분 조건입니다.

기술적으로, 이것은 $G$ 위에 특정 토폴로지의 선택에 대해, 즉, $H$ 가 지역적 기저라는 것에 대해 토폴로지적 그룹 코시 수열과 같은 것입니다.

그러한 코시 수열의 집합 $C$ 는 (성분별 곱에 대해) 그룹을 형성하고, 널 수열 ( $\forall r,\exists N,\forall n>N,x_{n}\in H_{r}$ 을 만족하는 수열)의 집합 $C_{0}$ 은 $C$ 의 정규 부분그룹입니다. 인수 그룹(factor group) $C/C_{0}$ 는 $H$ 에 관한 $G$ 의 완비라고 불립니다.

우리는 그런-다음 이 완비가 수열 $(G/H_{r})$ 의 역 극한(inverse limit)과 동형적임을 보일 수 있습니다.

숫자 이론(number theory)과 대수적 기하학(algebraic geometry)에 익숙한 이 구성의 예제는 소수(prime) $p$ 에 관한 정수의 $p$ -진수 완비의 구성입니다. 이 경우에서, $G$ 는 덧셈 아래에서 정수이고, $H_{r}$ 은 $p_{r}$ 의 정수 배수로 구성된 덧셈 부분그룹입니다.

만약 $H$ 가 공끝(cofinal) 수열이면 (즉, 유한 인덱스의 임의의 정규 부분그룹이 일부 $H_{r}$ 를 포함하며), 이 완비는 $(G/H)_{H}$ 의 역 극한과 동형적이라는 의미에서 정식(canonical)이며, 여기서 $H$ 는 유한 인덱스(index)의 모든 정규 부분그룹에 걸쳐 변합니다. 자세한 내용에 대해 랭(Lang)의 "대수학"에서 I.10장을 참조하십시오.

In a hyperreal continuum

실수 수열 $\langle u_{n}:n\in \mathbb {N} \rangle$ 은 자연스러운 초실수(hyperreal) 확장을 가지며, 보통의 자연수 n에 추가하여 인덱스 n의 초자연수(hypernatural) 값 H에 대해 정의됩니다. 그 수열이 코시인 것과 모든 각 무한 H와 K에 대해, 값 $u_{H}$ 와 $u_{K}$ 가 무한하게 근접, 또는 적합한(adequal), 즉 다음인 것은 필요충분 조건입니다:

\mathrm {st} (u_{H}-u_{K})=0

여기서 "st"는 표준 부분 함수(standard part function)입니다.

Cauchy completion of categories

Krause (2020)는 카테고리(category)의 코시 완비의 개념을 도입했습니다. $\mathbb {Q}$ 에 적용되면 (그것의 대상(objects)이 유리수인 카테고리, 및 x에서 y로의 사상(morphism)이 있는 것과 $x\leq y$ 인 것은 필요충분 조건이면), 이 코시 완비는 $\mathbb {R} \cup \left\{\infty \right\}$ 를 산출합니다 (다시 그것의 자연스러운 순서화를 사용하여 카테고리로 해석됩니다).

References

^ Lang, Serge (1993), Algebra (Third ed.), Reading, Mass.: Addison-Wesley Pub. Co., ISBN 978-0-201-55540-0, Zbl 0848.13001

External links

"Fundamental sequence", Encyclopedia of Mathematics, EMS Press, 2001 [1994]

[1] Lang, Serge (1993), Algebra (Third ed.), Reading, Mass.: Addison-Wesley Pub. Co., ISBN 978-0-201-55540-0, Zbl 0848.13001

[1]