Homomorphism

대수학(algebra)에서, 준동형(homomorphism)은 동일한 유형의 두 개의 대수적 구조 (예를 들어, 두 개의 그룹(group), 두 개의 링(ring), 또는 두 개의 벡터 공간(vector space)) 사이의 구조-보존하는(structure-preserving) 맵(map)입니다. 단어 homomorphism은 고대 그리스 언어: ὁμός (homos)는 "같은"을 의미하고 μορφή (morphe)는 "형태"또는 "모양"을 의미하는 것으로부터 유래합니다. 어쨌든, 그 단어는 "비슷한"을 의미하는 독일어 ähnlich에서 "같은"을 의미하는 ὁμός로 (잘못)번역으로 기인해서 분명히 수학에 도입되었습니다.^[1] "준동형"이라는 용어는 독일 수학자 펠릭스 클라인(Felix Klein) (1849–1925)에 기인했을 때 1892년 초에 나타났습니다.^[2]

벡터 공간의 준동형은 역시 선형 맵(linear map)이라고 불리고, 그것들의 연구는 선형 대수(linear algebra)의 주제입니다.

준동형의 개념은, 사상(morphism)의 이름 아래에서, 놓여있는 집합을 가지지 않거나, 대수적이 아닌 많은 다른 구조로 일반화되어 왔습니다. 이 일반화는 카테고리 이론(category theory)의 출발점입니다.

준동형은 동형(isomorphism), 자기-사상(endomorphism), 자기-동형(automorphism), 등일 수도 있습니다 (아래를 참조하십시오). 그것들 각각은 사상의 임의의 클래스로 일반화될 수 있는 방법에서 정의될 수 있습니다.

Definition

준동형은 구조의 연산(operations)을 보존하는 같은 유형 (즉, 동일한 이름)의 두 대수적 구조(algebraic structures) 사이의 맵입니다. 이것은 같은 구조를 갖춘 두 집합 $A$ , $B$ 사이의 맵 $f:A\to B$ 를 의미하며, 만약 $\cdot$ 가 구조의 연산 (여기서, 단순화를 위해, 이항 연산(binary operation)이라고 가정)이면, $A$ 원소의 모든 쌍 $x$ , $y$ 에 대해, 다음을 만족합니다:^{[note 1]}

f(x\cdot y)=f(x)\cdot f(y)

우리는 $f$ 가 연산을 보존하거나 연산과 호환된다고 종종 말합니다.

공식적으로, 맵 $f:A\to B$ 는 만약 $A$ 에서 모든 원소 $a_{1},...,a_{k}$ 에 대해 다음이면 $A$ 와 $B$ 둘 다 이에 정의되는 애리티(arity) $k$ 의 연산 $\mu$ 를 보존합니다:

f(\mu _{A}(a_{1},\ldots ,a_{k}))=\mu _{B}(f(a_{1}),\ldots ,f(a_{k}))

준동형에 의해 보존되어야 하는 연산은 0-항 연산(0-ary operations), 즉 상수를 포함합니다. 특히, 항등 원소(identity element)가 구조의 유형에 의해 요구되면, 첫 번째 구조의 항등 원소는 두 번째 구조의 해당 항등 원소에 매핑되어야 합니다.

예를 들어:

반-그룹 준동형(semigroup homomorphism)은 반그룹 연산을 보존하는 반-그룹(semigroups) 사이의 맵입니다.
모노이드 준동형(monoid homomorphism)은 모노이드 연산을 보존하고 첫 번째 모노이드(monoids)의 항등 원소를 두 번째 모노이드의 항등 원소에 매핑하는 모노이드 사이의 맵입니다 (항등 요소는 0-항 연산(0-ary operation)입니다).
그룹 준동형(group homomorphism)은 그룹 연산을 보존하는 그룹(groups) 사이의 맵입니다. 이것은 그룹 준동형이 첫 번째 그룹의 항등 원소를 두 번째 그룹의 항등 원소에 매핑하고, 첫 번째 그룹의 원소의 역(inverse)을 이 원소의 이미지의 역에 매핑한다는 것을 의미합니다. 따라서 그룹 사이의 반그룹 준동형은 필연적으로 그룹 준동형입니다.
링 준동형(ring homomorphism)은 링 덧셈, 링 곱셈, 및 곱셈 항등원(multiplicative identity)을 보존하는 링(rings) 사이의 맵입니다. 곱셈 항등원을 보존할지 여부는 사용 중인 링(ring)의 정의에 따라 다릅니다. 만약 곱셈 항등성이 보존되지 않으면, 렁(rng) 준동형을 가집니다.
선형 맵(linear map)은 벡터 공간(vector spaces)의 준동형입니다; 즉, 아벨 그룹 구조와 스칼라 곱셈(scalar multiplication)을 보존하는 벡터 공간 사이의 그룹 동형입니다.
모듈(modules) 사이의 선형 맵이라고도 불리는 모듈 준동형(module homomorphism)이 유사하게 정의됩니다.
대수 준동형(algebra homomorphism)은 대수(algebra) 연산을 보존하는 맵입니다.

대수적 구조는 하나보다 많은 연산을 가질 수 있고, 준동형이 각 연산을 보존하기 위해 요구됩니다. 따라서 일부 연산만 보존하는 맵은 구조의 준동형이 아니라, 보존된 연산만을 고려하여 얻은 부분-구조의 준동형일 뿐입니다. 예를 들어, 항등 원소가 아닌 모노이드 연산을 유지하는 모노이드 사이의 맵은 모노이드 준동형이 아니라 반그룹 준동형일 뿐입니다.

연산에 대해 표기법은 준동형의 소스와 타킷에서 같을 필요는 없습니다. 예를 들어, 실수(real numbers)는 덧셈에 대해 그룹을 형성하고, 양의 실수는 곱셈에 대해 그룹을 형성합니다. 다음 지수 함수(exponential function)는

x\mapsto e^{x}

다음을 만족시킵니다:

e^{x+y}=e^{x}e^{y},

그리고 따라서 이들 두 그룹 사이의 준동형입니다. 그것은 심지어 동형인데 (아래를 참조), 왜냐하면 그것의 역 함수(inverse function), 자연 로그(natural logarithm)는 다음을 만족시킵니다:

\ln(xy)=\ln(x)+\ln(y),

그리고 역시 그룹 준동형입니다.

Examples

실수(real numbers)는 덧셈과 곱셈 둘 다를 가지는 링(ring)입니다. 모든 2×2 행렬(matrices)의 집합은 행렬 덧셈(matrix addition)과 행렬 곱셈(matrix multiplication) 아래에서 링이기도 합니다. 만약 우리가 다음과 같이 이들 링 사이에 함수를 정의하면:

f(r)={\begin{pmatrix}r&0\\0&r\end{pmatrix}}

여기서 $r$ 은 실수이며, $f$ 는 링의 준동형인데, 왜냐하면 $f$ 는 다음 덧셈을 보존하고 $f(r+s)={\begin{pmatrix}r+s&0\\0&r+s\end{pmatrix}}={\begin{pmatrix}r&0\\0&r\end{pmatrix}}+{\begin{pmatrix}s&0\\0&s\end{pmatrix}}=f(r)+f(s)$

그리고 역시 곱셈을 보존하기 때문입니다:

f(rs)={\begin{pmatrix}rs&0\\0&rs\end{pmatrix}}={\begin{pmatrix}r&0\\0&r\end{pmatrix}}{\begin{pmatrix}s&0\\0&s\end{pmatrix}}=f(r)\,f(s).

또 다른 예를 들어, 비-영 복소수(complex numbers)는 비-영 실수와 마찬가지로 곱셈 연산 아래에서 그룹(group)을 형성합니다. (영은 두 그룹에서 제외되어야 하는데, 왜냐하면 그룹의 원소에 필요한 곱셈 역원(multiplicative inverse)이 없기 때문입니다.) 다음과 같이 비-영 복소수에서 비-영 실수로의 함수 $f$ 를 정의합니다:

f(z)=|z|.

즉, $f$ 는 복소수 $z$ 의 절댓값(absolute value) (또는 모듈러스)입니다. 그런-다음 $f$ 가 그룹의 준동형인데, 왜냐하면 그것이 곱셈을 보존하기 때문입니다:

f(z_{1}z_{2})=|z_{1}z_{2}|=|z_{1}||z_{2}|=f(z_{1})f(z_{2}).

$f$ 는 (복소수에서 실수로의) 링의 준동형으로 확장될 수 없음을 주목해야 하는데, 왜냐하면 그것은 덧셈을 보존하지 않기 때문입니다:

|z_{1}+z_{2}|\neq |z_{1}|+|z_{2}|.

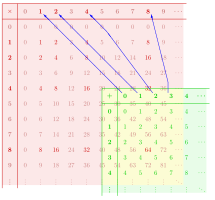
또 다른 예로서, 다이어그램은 모노이드 $(\mathbb {N} ,+,0)$ 에서 모노이드 $(\mathbb {N} ,\times ,1)$ 로의 모노이드(monoid) 준동형 $f$ 를 보여줍니다. 해당 연산의 다른 이름으로 인해, $f$ 에 의해 만족되는 구조 보존 속성은 $f(x+y)=f(x)\times f(y)$ 와 $f(0)=1$ 이 됩니다.

필드 $F$ 에 걸쳐 합성 대수(composition algebra) $A$ 는 노름(norm)이라고 불리는 이차 형식(quadratic form), $N:A\to F$ 이며, 이는 $A$ 의 곱셈 그룹(multiplicative group)에서 $F$ 의 곱셈 그룹으로의 그룹 준동형입니다.

Special homomorphisms

여러 종류의 준동형은 특정 이름을 가지며, 일반 사상(morphisms)에도 정의됩니다.

Isomorphism

같은 유형의 대수적 구조(algebraic structures) 사이의 동형(isomorphism)은 공통적으로 전단사(bijective) 준동형으로 정의됩니다.^[3]^: 134 ^[4]^: 28

카테고리 이론(category theory)의 보다 일반적인 맥락에서, 동형은 역시 사상(morphism)인 역(inverse)을 가지는 사상으로 정의됩니다. 대수적 구조의 특정 경우에서, 두 정의는 동등하지만, 그것들이 놓여있는 집합을 가지는 비-대수적 구조에 대해 다를 수 있습니다.

보다 정확하게, 만약 다음이

f:A\to B

(준)동형이면, 그것이 다음을 만족하는

f\circ g=\operatorname {Id} _{B}\qquad {\text{and}}\qquad g\circ f=\operatorname {Id} _{A}

다음 준동형이 존재하면 역을 가집니다:

g:B\to A.

만약 $A$ 와 $B$ 가 놓여있는 집합을 가지고, $f:A\to B$ 가 역 $g$ 를 가지면, $f$ 는 전단사입니다. 사실, $f$ 는 단사(injective)인데, 왜냐하면 $f(x)=f(y)$ 가 $x=g(f(x))=g(f(y))=y$ 를 의미하기 때문이고, $f$ 는 전사(surjective)인데, 왜냐하면, $B$ 에서 임의의 $x$ 에 대해, $x=f(g(x))$ 를 가지고, $x$ 는 $A$ 의 원소의 이미지이기 때문입니다.

반대로, 만약 $f:A\to B$ 가 대수적 구조 사이의 전단사 준동형이면, $g:B\to A$ 를 $g(y)$ 가 $f(x)=y$ 를 만족하는 $A$ 의 고유한 원소 $x$ 임을 만족하는 맵이라고 놓습니다. $f\circ g=\operatorname {Id} _{B}$ 와 $g\circ f=\operatorname {Id} _{A}$ 를 가지고, $g$ 가 준동형임을 보여주는 것만 남아 있습니다. 만약 $*$ 가 $B$ 의 원소의 모든 쌍 $x$ , $y$ 에 대해, 구조의 이항 연산이면, 다음을 가집니다:

g(x*_{B}y)=g(f(g(x))*_{B}f(g(y)))=g(f(g(x)*_{A}g(y)))=g(x)*_{A}g(y),

그리고 $g$ 는 따라서 $*$ 와 호환됩니다. 그 증명은 임의의 애리티(arity)에 대해 유사하므로, $g$ 가 준동형임을 나타냅니다.

이 증명은 비-대수적 구조에는 작동하지 않습니다. 예를 들어, 토폴로지적 공간(topological spaces)에 대해, 사상은 연속 맵이고, 전단사 연속 맵(continuous map)의 역은 반드시 연속적이지는 않습니다. 준동형(homeomorphism) 또는 쌍-연속 맵(bicontinuous map)이라고 불리는 토폴로지적 공간의 동형은 따라서 전단사 연속 맵이며, 그것의 역도 연속입니다.

Endomorphism

자기-사상(endomorphism)은 그것의 도메인(domain)이 코도메인(codomain)과 같은 준동형, 또는, 더 일반적으로 그것의 근원이 대상과 같은 사상(morphism)입니다.^[3]^: 135

대수적 구조, 또는 카테고리(category)의 대상의 자기사상은 합성 아래에서 모노이드(monoid)를 형성합니다.

벡터 공간(vector space) 또는 모듈(module)의 자기-사상은 링(ring)을 형성합니다. 벡터 공간 또는 유한-차원(dimension)의 자유 모듈(free module)에 대해, 기저(basis)의 선택은 자기-사상의 링과 같은 차원의 정사각 행렬(square matrices)의 링 사이에 링 동형(ring isomorphism)을 유도합니다.

Automorphism

자기동형(automorphism)은 역시 동형인 자기-사상입니다.^[3]^: 135

대수적 구조 또는 카테고리 대상의 자기동형은 구조의 자기동형 그룹(automorphism group)이라고 불리는 합성 아래 그룹(group)을 형성합니다.

이름을 받아 왔던 많은 그룹은 일부 대수적 구조의 자기동형 그룹입니다. 예를 들어, 일반 선형 그룹(general linear group) $\operatorname {GL} _{n}(k)$ 는 필드 $k$ 에 걸쳐 차원 $n$ 의 벡터 공간(vector space)의 자기동형 그룹입니다.

필드의 자기동형 그룹은 에바리스트 갈루아(Évariste Galois)에 의해 다항식(polynomials)의 근(roots)을 연구하기 위해 도입되었고, 갈루아 이론(Galois theory)의 기초입니다.

Monomorphism

대수적 구조에 대해, 단사-사상(monomorphisms)은 공통적으로 단사(injective) 준동형으로 정의됩니다.^[3]^: 134 ^[4]^: 29

카테고리 이론(category theory)의 보다 일반적인 맥락에서, 단사-사상은 왼쪽 취소-가능(left cancelable)인 사상(morphism)으로 정의됩니다.^[5] 이것은 (준)동형 $f:A\to B$ 가, 만약 임의의 다른 대상 $C$ 에서 $A$ 로의 사상의 임의의 쌍 $g$ , $h$ 에 대해, $f\circ g=f\circ h$ 가 $g=h$ 를 의미하면 단사-사상임을 의미합니다.

단사-사상(monomorphism)의 이들 두 정의는 모든 공통적인 대수적 구조에 대해 동등합니다. 보다 정확하게는, 그것들은 모든 각 준동형이 단사-사상인 필드에 대해 동등하고, 보편적 대수(universal algebra)의 다양성(varieties), 즉 연산과 공리 (항등)가 임의의 제한 없이 정의되는 대수적 구조에 대해 동등합니다 (필드가 다양성을 형성하지 않는데, 왜냐하면 곱셈 역(multiplicative inverse)은 단항 연산(unary operation)이나 곱셈의 속성으로 정의되고, 두 경우에서, 비-영 원소에 대해서만 정의되기 때문입니다).

특히, 단사-사상의 두 가지 정의는 집합(sets), 마그마(magmas), 반그룹(semigroups), 모노이드(monoids), 그룹(groups), 링(rings), 필드(fields), 벡터 공간(vector spaces), 및 모듈(modules)에 대해 동등합니다.

분할 단사-사상(split monomorphism)은 왼쪽 역(left inverse)을 가지는 동형이고 따라서 그것은 자체로 해당 다른 준동형의 오른쪽 역입니다. 즉, 준동형 $f\colon A\to B$ 은 $g\circ f=\operatorname {Id} _{A}$ 를 만족하는 준동형 $g\colon B\to A$ 가 존재하면 분할 단사-사상입니다. 분할 단사-사상은 단사-사상(monomorphism)의 두 가지 의미에 대해 항상 단사-사상입니다. 집합과 벡터 공간에 대해, 모든 각 단사-사상은 분할 단사-사상이지만, 이 속성은 대부분의 공통적인 대수적 구조에는 유지되지 않습니다.

Proof of the equivalence of the two definitions of monomorphisms

단사 준동형은 왼쪽 취소-가능입니다: 만약 $f\circ g=f\circ h$ 이면, $g$ 와 $h$ 의 공통 근원, $C$ 에서 모든 각 $x$ 에 대해 $f(g(x))=f(h(x))$ 를 가집니다. 만약 $f$ 가 단사이면, $g(x)=h(x)$ 이고, 따라서 $g=h$ 입니다. 이 증명은 대수적 구조뿐만 아니라, 그것의 대상이 집합이고 화살표가 이들 집합 사이의 맵인 임의의 카테고리(category)에 대해 작동합니다. 예를 들어, 단사 연속 맵은 토폴로지적 공간(topological space)의 카테고리에서 단사-사상입니다.

반대로, 왼쪽 취소-가능 준동형이 단사임을 입증함을 위해, $x$ 위에 자유 대상을 고려하는 것이 유용합니다. 대수적 구조의 다양성(variety)이 주어지면, $x$ 위에 자유 대상은 이 다양성 위에 대수적 구조 $L$ 과 다음 보편 속성을 만족시키는 $L$ 의 원소 $x$ 를 구성하는 한 쌍입니다: 다양성의 모든 각 구조 $S$ , 및 $S$ 의 모든 각 원소 $s$ 에 대해, $f(x)=s$ 를 만족하는 고유한 준동형 $f:L\to S$ 가 있습니다. 예를 들어, 집합에 대해, $x$ 위에 자유 대상은 간단히 $\{x\}$ 입니다; 반-그룹에 대해, $x$ 위에 자유 대상은 $\{x,x^{2},\ldots ,x^{n},\ldots \}$ 인데, 왜냐하면 반그룹은 양의 정수의 덧셈 반-그룹에 동형적이기 때문입니다; 모노이드에 대해, $x$ 위에 자유 대상은 $\{1,x,x^{2},\ldots ,x^{n},\ldots \}$ 인데, 왜냐하면 모노이드는 비-음의 정수의 덧셈 모노이드에 동형적이기 때문입니다; 그룹에 대해, $x$ 위에 자유 대상은 무한 순환 그룹 $\{\ldots ,x^{-n},\ldots ,x^{-1},1,x,x^{2},\ldots ,x^{n},\ldots \}$ 인데, 그룹은 정수의 덧셈 그룹에 동형적이기 때문입니다; 링에 대해, $x$ 위의 자유 대상은 다항식 링 $\mathbb {Z} [x]$ 입니다; 벡터 공간 또는 모듈에 대해, $x$ 위에 자유 대상은 $x$ 를 기저로 가지는 벡터 공간 또는 모듈입니다.

만약 $x$ 에 걸쳐 자유 대상이 존재하면, 모든 각 왼쪽 취소-가능 준동형은 단사입니다: $f\colon A\to B$ 를 왼쪽 취소-가능 준동형으로 놓고, $a$ 와 $b$ 를 $f(a)=f(b)$ 를 만족하는 $A$ 의 두 원소로 놓습니다. 자유 대상 $F$ 의 정의에 의해, $g(x)=a$ 와 $h(x)=b$ 를 만족하는 $F$ 에서 $A$ 로의 준동형 $g$ 와 $h$ 가 존재합니다. $f(g(x))=f(h(x))$ 이기 때문에, 보편 속성의 정의에서 고유성에 의해 $f\circ g=f\circ h$ 를 가집니다. $f$ 는 왼쪽 취소-가능이기 때문에, $g=h$ 를 가지고, 따라서 $a=b$ 입니다. 그러므로, $f$ 는 단사입니다.

다양성에 대해 $x$ 위에 자유 대상의 존재 (역시 Free object § Existence를 참조): $x$ 에 걸쳐 자유 대상을 건축에 대해, $x$ 와 구조의 연산으로 구축된 잘-형성된 공식의 집합 $W$ 를 생각해 보십시오. 두 개의 그러한 공식은 만약 우리가 공리 (구조의 항등원)을 적용함으로써 하나에서 나머지 다른 하나로 보낼 수 있으면 동등하다고 말합니다. 이것은, 만약 항등원이 조건의 대상이 아니면, 즉 다양성과 작동하면, 동치 관계를 정의합니다. 그런-다음 다양성의 연산은 이 관계에 대해 $W$ 의 동치 클래스의 집합 위에 잘 정의됩니다. 결과 대상이 $x$ 위에 자유 대상임을 보이는 것은 쉽습니다.

Epimorphism

대수학(algebra)에서, 전사-사상(epimorphisms)은 종종 전사(surjective) 준동형으로 정의됩니다.^[3]^: 134^[4]^: 43 다른 한편으로, 카테고리 이론(category theory)에서, 전사-사상(epimorphisms)은 오른쪽 취소-가능 사상(morphisms)으로 정의됩니다.^[5] 이것은 (준)동형 $f:A\to B$ 가, 만약 $B$ 에서 임의의 다른 대상 $C$ 로의 사상의 임의의 쌍 $g$ , $h$ 에 대해, 상등 $g\circ f=h\circ f$ 가 $g=h$ 임을 의미하면 단사-사상임을 의미합니다.

전사 준동형은 항상 오른쪽 취소-가능이지만, 그 전환은 대수적 구조에 대해 항상 참은 아닙니다. 어쨌든, 전사-사상(epimorphism)의 두 가지 정의는 집합(sets), 벡터 공간(vector spaces), 아벨 그룹(abelian groups), 모듈(modules) (증명에 대해 아래 참조), 및 그룹(groups)에 대해 동등합니다.^[6] 모든 수학, 특히 선형 대수(linear algebra)와 호몰로지 대수(homological algebra)에서 이들 구조의 중요성은 두 개의 비-동등한 정의의 공존을 설명할 수 있습니다.

비-전사 전사-사상이 존재하는 대수적 구조는 반그룹(semigroups)과 링(rings)을 포함합니다. 가장 기본적인 예는 유리수(rational numbers)에 정수(integers)의 포함이며, 이는 링과 곱셈 반그룹의 준동형입니다. 두 구조 모두에서 그것은 단사-사상과 비-전사 전사-사상이지만, 동형은 아닙니다.^[5]^[7]

이 예제의 광범위한 일반화는 곱셈 집합에 의한 링의 지역화(localization of a ring)입니다. 모든 각 지역화는, 일반적으로, 전사가 아닌 링 전사-사상입니다. 지역화는 교환 대수(commutative algebra)와 대수적 기하학(algebraic geometry)에서 기본이기 때문에, 이것은 이들 영역에서 전사-사상을 오른쪽 취소-가능 준동형으로 정의하는 것이 일반적으로 선호되는 이유를 설명할 수 있습니다.

분할 전사-사상(split epimorphism)은 오른쪽 역(right inverse)을 가지는 준동형이고 따라서 그것은 해당 다른 준동형의 자체 왼쪽 역입니다. 즉, 준동형 $f\colon A\to B$ 는 만약 $f\circ g=\operatorname {Id} _{B}$ 를 만족하는 준동형 $g\colon B\to A$ 가 존재하면 분할 전사-사상입니다. 분할 전사-사상은 전사-사상(epimorphism)의 두 가지 의미 모두에서 항상 전사-사상입니다. 집합과 벡터 공간에 대해, 모든 각 전사-사상은 분할 전사-사상이지만, 이 속성은 대부분의 공통적인 대수적 구조에는 유지되지는 않습니다.

요약해서, 다음을 가집니다:

{\text{split epimorphism}}\implies {\text{epimorphism (surjective)}}\implies {\text{epimorphism (right cancelable)}};

마지막 함축은 집합, 벡터 공간, 모듈, 및 아벨 그룹에 대한 동등성입니다; 첫 번째 함축은 집합과 벡터 공간에 대해 동등성입니다.

Equivalence of the two definitions of epimorphism

$f\colon A\to B$ 를 준동형으로 놓습니다. 우리는 그것이 전사가 아니면, 오른쪽 취소-가능이 아님을 입증하기를 원합니다.

집합의 경우에서, $b$ 를 $f(A)$ 에 속하지 않는 $B$ 의 원소라고 놓고, $g$ 가 항등 함수이고, $h(b)$ 가 $B$ 의 임의의 다른 원소임을 제외하고 모든 각 $x\in B$ 에 대해 $h(x)=x$ 임을 만족하는 $g,h\colon B\to B$ 를 정의합니다.

벡터 공간, 아벨 그룹과 모듈에서, 그 증명은 공커널의 존재와 영 맵이 준동형이라는 사실에 의존합니다: $C$ 를 $f$ 의 공커널이라고 놓고, $g\colon B\to C$ 를 $g(f(A))=0$ 를 만족하는 정식의 맵이라고 놓습니다. $h\colon B\to C$ 를 영 맵이라고 놓습니다. 만약 $f$ 가 전사가 아니면, $C\neq 0$ 이고, 따라서 $g\neq h$ 입니다 (하나는 영 맵이지만, 다른 하나는 그렇지 않습니다). 따라서 $f$ 는 취소-가능이 아닌데, 왜냐하면 $g\circ f=h\circ f$ 이기 때문입니다 (둘 다는 $A$ 에서 $C$ 로의 영 맵입니다).

Kernel

임의의 준동형 $f:X\to Y$ 는 $a\sim b$ 에 의한 $X$ 위에 동치 관계(equivalence relation)로 정의되는 것과 $f(a)=f(b)$ 인 것은 필요충분 조건입니다. 관계 $\sim$ 는 $f$ 의 커널(kernel)이라고 불립니다. 그것은 $X$ 위에 합동 관계(congruence relation)입니다. 몫 집합(quotient set) $X/{\sim }$ 은 그때에 $X$ 의 각 연산 $\ast$ 에 대해 $[x]\ast [y]=[x\ast y]$ 에 의한 몫의 연산을 정의함으로써, 자연스러운 방법에서, $X$ 와 같은 유형의 구조를 가질 수 있습니다. 그 경우에 동형 $f$ 아래의 $Y$ 에서 $X$ 의 이미지는 반드시 $X/\!\sim$ 와 동형(isomorphic)입니다; 이 사실은 동형 정리(isomorphism theorems) 중 하나입니다.

대수 구조가 어떤 연산에 대한 그룹(group)일 때, 이 연산의 항등 원소(identity element)의 동치 클래스(equivalence class) $K$ 는 동치 관계를 특성화하기에 충분합니다. 이 경우에서, 동치 관계에 의한 몫은 $X/K$ (보통 " $X$ 모드 $K$ "로 읽음)로 표시됩니다. 이 경우에도, $f$ 의 커널(kernel)이라고 불리는 것은 $\sim$ 가 아니라 $K$ 입니다. 주어진 유형의 대수적 구조의 준동형의 커널은 자연적으로 어떤 구조를 갖추고 있습니다. 이 커널의 구조 유형은 아벨 그룹(abelian groups), 벡터 공간(vector spaces), 및 모듈(modules)의 경우에서, 고려되는 구조와 같지만, 그룹 준동형(group homomorphisms)의 커널에 대해 정규 부분그룹(normal subgroup)과 링 준동형(ring homomorphisms)의 커널에 대해 아이디얼(ideals) (비-교환 링의 경우에서, 커널은 양-측 아이디얼(two-sided ideals)임)과 같은 다른 경우에 특정 이름을 받아 왔습니다.

Relational structures

모델 이론(model theory)에서, 대수적 구조의 개념은 연산과 관계 둘 다를 포함하는 구조로 일반화됩니다. L을 함수 기호와 관계 기호로 구성된 서명이라고 놓고, A, B를 두 개의 L-구조라고 놓습니다. 그런-다음 A에서 B로의 준동형(homomorphism)은 다음을 만족하는 A의 도메인에서 B의 도메인으로 매핑 h입니다:

L에서 각 n-항 함수 기호 F에 대해 h(F^A(a₁,…,a_n)) = F^B(h(a₁),…,h(a_n)),
L에서 각 n-항 관계 기호 R에 대해 R^A(a₁,…,a_n) implies R^B(h(a₁),…,h(a_n)).

단지 하나의 이항 관계를 갖는 특별한 경우에서, 우리는 그래프 준동형(graph homomorphism)의 개념을 얻습니다.^[8]

Formal language theory

준동형은 역시 형식 언어(formal languages)의 연구에서 사용되고^[9] 종종 간략하게 사상(morphisms)이라고 참조됩니다.^[10] 알파벳 $\Sigma _{1}$ 와 $\Sigma _{2}$ 가 주어지면, 모든 $u,v\in \Sigma _{1}$ 에 대해 $h(uv)=h(u)h(v)$ 를 만족하는 함수 $h\colon \Sigma _{1}^{*}\to \Sigma _{2}^{*}$ 는 $\Sigma _{1}^{*}$ 위에 준동형(homomorphism)이라고 불립니다.^{[note 2]} 만약 $h$ 가 $\Sigma _{1}^{*}$ 위의 준동형이고 $\varepsilon$ 가 빈 문자열을 나타내면, $h$ 는 $\Sigma _{1}^{*}$ 에서 모든 $x\neq \varepsilon$ 에 대해 $h(x)\neq \varepsilon$ 일 때 $\varepsilon$ -없는 준동형( $\varepsilon$ -free homomorphism)이라고 불립니다.

모든 $a\in \Sigma _{1}$ 에 대해 $|h(a)|=k$ 를 만족시키는 $\Sigma _{1}^{*}$ 위에 준동형 $h\colon \Sigma _{1}^{*}\to \Sigma _{2}^{*}$ 는 $k$ -균등 준동형( $k$ -uniform homomorphism)이라고 불립니다.^[11] 만약 모든 $a\in \Sigma _{1}$ 에 대해 $|h(a)|=1$ 이면 (즉, $h$ 가 1-균등이면), $h$ 는 역시 코딩(coding) 또는 투영(projection)이라고 불립니다.

알파벳 $\Sigma$ 에서 형성된 단어의 집합 $\Sigma ^{*}$ 은 $\Sigma$ 에 의해 생성된 자유 모노이드(free monoid)로 생각될 수 있습니다. 여기서 모노이드 연산은 연쇄(concatenation)이고 항등 원소는 빈 단어입니다. 이러한 관점에서, 언어 준동형은 정확히 모노이드 준동형입니다.^{[note 3]}

Notes

^ As it is often the case, but not always, the same symbol for the operation of both $A$ and $B$ was used here.
^ The ∗ denotes the Kleene star operation, while Σ^∗ denotes the set of words formed from the alphabet Σ, including the empty word. Juxtaposition of terms denotes concatenation. For example, h(u) h(v) denotes the concatenation of h(u) with h(v).
^ We are assured that a language homomorphism h maps the empty word ε to the empty word. Since h(ε) = h(εε) = h(ε)h(ε), the number w of characters in h(ε) equals the number 2w of characters in h(ε)h(ε). Hence w = 0 and h(ε) has null length.

Citations

^ Fricke, Robert (1897–1912). Vorlesungen über die Theorie der automorphen Functionen. B.G. Teubner. OCLC 29857037.
^
See:
- Ritter, Ernst (1892). "Die eindeutigen automorphen Formen vom Geschlecht Null, eine Revision und Erweiterung der Poincaré'schen Sätze" [The unique automorphic forms of genus zero, a revision and extension of Poincaré's theorem]. Mathematische Annalen (in German). 41: 1–82. doi:10.1007/BF01443449. S2CID 121524108. From footnote on p. 22: "Ich will nach einem Vorschlage von Hrn. Prof. Klein statt der umständlichen und nicht immer ausreichenden Bezeichnungen: "holoedrisch, bezw. hemiedrisch u.s.w. isomorph" die Benennung "isomorph" auf den Fall des holoedrischen Isomorphismus zweier Gruppen einschränken, sonst aber von "Homomorphismus" sprechen, … " (Following a suggestion of Prof. Klein, instead of the cumbersome and not always satisfactory designations "holohedric, or hemihedric, etc. isomorphic", I will limit the denomination "isomorphic" to the case of a holohedric isomorphism of two groups; otherwise, however, [I will] speak of a "homomorphism", … )
- Fricke, Robert (1892). "Ueber den arithmetischen Charakter der zu den Verzweigungen (2,3,7) und (2,4,7) gehörenden Dreiecksfunctionen" [On the arithmetic character of the triangle functions belonging to the branch points (2,3,7) and (2,4,7)]. Mathematische Annalen (in German). 41: 443–468. doi:10.1007/BF01443421. S2CID 120022176. From p. 466: "Hierdurch ist, wie man sofort überblickt, eine homomorphe*) Beziehung der Gruppe Γ₍₆₃₎ auf die Gruppe der mod. n incongruenten Substitutionen mit rationalen ganzen Coefficienten der Determinante 1 begründet." (Thus, as one immediately sees, a homomorphic relation of the group Γ₍₆₃₎ is based on the group of modulo n incongruent substitutions with rational whole coefficients of the determinant 1.) From footnote on p. 466: "*) Im Anschluss an einen von Hrn. Klein bei seinen neueren Vorlesungen eingeführten Brauch schreibe ich an Stelle der bisherigen Bezeichnung "meroedrischer Isomorphismus" die sinngemässere "Homomorphismus"." (Following a usage that has been introduced by Mr. Klein during his more recent lectures, I write in place of the earlier designation "merohedral isomorphism" the more logical "homomorphism".)
^ ^a ^b ^c ^d ^e Birkhoff, Garrett (1967) [1940], Lattice theory, American Mathematical Society Colloquium Publications, vol. 25 (3rd ed.), Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-1025-5, MR 0598630
^ ^a ^b ^c Stanley N. Burris; H.P. Sankappanavar (2012). A Course in Universal Algebra (PDF). ISBN 978-0-9880552-0-9.
^ ^a ^b ^c Mac Lane, Saunders (1971). Categories for the Working Mathematician. Graduate Texts in Mathematics. Vol. 5. Springer-Verlag. Exercise 4 in section I.5. ISBN 0-387-90036-5. Zbl 0232.18001.
^ Linderholm, C. E. (1970). A group epimorphism is surjective. The American Mathematical Monthly, 77(2), 176-177.
^ Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Șerban (2001). Hopf Algebra: An Introduction. Pure and Applied Mathematics. Vol. 235. New York, NY: Marcel Dekker. p. 363. ISBN 0824704819. Zbl 0962.16026.
^ For a detailed discussion of relational homomorphisms and isomorphisms see Section 17.3, in Gunther Schmidt, 2010. Relational Mathematics. Cambridge University Press, ISBN 978-0-521-76268-7
^ Seymour Ginsburg, Algebraic and automata theoretic properties of formal languages, North-Holland, 1975, ISBN 0-7204-2506-9,
^ T. Harju, J. Karhumӓki, Morphisms in Handbook of Formal Languages, Volume I, edited by G. Rozenberg, A. Salomaa, Springer, 1997, ISBN 3-540-61486-9.
^ Krieger (2006) p. 287

References

Krieger, Dalia (2006). "On critical exponents in fixed points of non-erasing morphisms". Developments in Language Theory: Proceedings 10th International Conference, DLT 2006, Santa Barbara, CA, USA, June 26–29, 2006. Oscar H. Ibarra, Zhe Dang. Springer-Verlag. pp. 280–291. ISBN 3-540-35428-X.
Stanley N. Burris; H.P. Sankappanavar (2012). A Course in Universal Algebra (PDF). ISBN 978-0-9880552-0-9.
Mac Lane, Saunders (1971), Categories for the Working Mathematician, Graduate Texts in Mathematics, vol. 5, Springer-Verlag, ISBN 0-387-90036-5, Zbl 0232.18001
Fraleigh, John B.; Katz, Victor J. (2003), A First Course in Abstract Algebra, Addison-Wesley, ISBN 978-1-292-02496-7

[3] As it is often the case, but not always, the same symbol for the operation of both $A$ and $B$ was used here.

[12] The ∗ denotes the Kleene star operation, while Σ^∗ denotes the set of words formed from the alphabet Σ, including the empty word. Juxtaposition of terms denotes concatenation. For example, h(u) h(v) denotes the concatenation of h(u) with h(v).

[14] We are assured that a language homomorphism h maps the empty word ε to the empty word. Since h(ε) = h(εε) = h(ε)h(ε), the number w of characters in h(ε) equals the number 2w of characters in h(ε)h(ε). Hence w = 0 and h(ε) has null length.

[1] Fricke, Robert (1897–1912). Vorlesungen über die Theorie der automorphen Functionen. B.G. Teubner. OCLC 29857037.

[2] See:
Ritter, Ernst (1892). "Die eindeutigen automorphen Formen vom Geschlecht Null, eine Revision und Erweiterung der Poincaré'schen Sätze" [The unique automorphic forms of genus zero, a revision and extension of Poincaré's theorem]. Mathematische Annalen (in German). 41: 1–82. doi:10.1007/BF01443449. S2CID 121524108. From footnote on p. 22: "Ich will nach einem Vorschlage von Hrn. Prof. Klein statt der umständlichen und nicht immer ausreichenden Bezeichnungen: "holoedrisch, bezw. hemiedrisch u.s.w. isomorph" die Benennung "isomorph" auf den Fall des holoedrischen Isomorphismus zweier Gruppen einschränken, sonst aber von "Homomorphismus" sprechen, … " (Following a suggestion of Prof. Klein, instead of the cumbersome and not always satisfactory designations "holohedric, or hemihedric, etc. isomorphic", I will limit the denomination "isomorphic" to the case of a holohedric isomorphism of two groups; otherwise, however, [I will] speak of a "homomorphism", … )

Fricke, Robert (1892). "Ueber den arithmetischen Charakter der zu den Verzweigungen (2,3,7) und (2,4,7) gehörenden Dreiecksfunctionen" [On the arithmetic character of the triangle functions belonging to the branch points (2,3,7) and (2,4,7)]. Mathematische Annalen (in German). 41: 443–468. doi:10.1007/BF01443421. S2CID 120022176. From p. 466: "Hierdurch ist, wie man sofort überblickt, eine homomorphe*) Beziehung der Gruppe Γ₍₆₃₎ auf die Gruppe der mod. n incongruenten Substitutionen mit rationalen ganzen Coefficienten der Determinante 1 begründet." (Thus, as one immediately sees, a homomorphic relation of the group Γ₍₆₃₎ is based on the group of modulo n incongruent substitutions with rational whole coefficients of the determinant 1.) From footnote on p. 466: "*) Im Anschluss an einen von Hrn. Klein bei seinen neueren Vorlesungen eingeführten Brauch schreibe ich an Stelle der bisherigen Bezeichnung "meroedrischer Isomorphismus" die sinngemässere "Homomorphismus"." (Following a usage that has been introduced by Mr. Klein during his more recent lectures, I write in place of the earlier designation "merohedral isomorphism" the more logical "homomorphism".)

[6] Ritter, Ernst (1892). "Die eindeutigen automorphen Formen vom Geschlecht Null, eine Revision und Erweiterung der Poincaré'schen Sätze" [The unique automorphic forms of genus zero, a revision and extension of Poincaré's theorem]. Mathematische Annalen (in German). 41: 1–82. doi:10.1007/BF01443449. S2CID 121524108. From footnote on p. 22: "Ich will nach einem Vorschlage von Hrn. Prof. Klein statt der umständlichen und nicht immer ausreichenden Bezeichnungen: "holoedrisch, bezw. hemiedrisch u.s.w. isomorph" die Benennung "isomorph" auf den Fall des holoedrischen Isomorphismus zweier Gruppen einschränken, sonst aber von "Homomorphismus" sprechen, … " (Following a suggestion of Prof. Klein, instead of the cumbersome and not always satisfactory designations "holohedric, or hemihedric, etc. isomorphic", I will limit the denomination "isomorphic" to the case of a holohedric isomorphism of two groups; otherwise, however, [I will] speak of a "homomorphism", … )

[7] Fricke, Robert (1892). "Ueber den arithmetischen Charakter der zu den Verzweigungen (2,3,7) und (2,4,7) gehörenden Dreiecksfunctionen" [On the arithmetic character of the triangle functions belonging to the branch points (2,3,7) and (2,4,7)]. Mathematische Annalen (in German). 41: 443–468. doi:10.1007/BF01443421. S2CID 120022176. From p. 466: "Hierdurch ist, wie man sofort überblickt, eine homomorphe*) Beziehung der Gruppe Γ₍₆₃₎ auf die Gruppe der mod. n incongruenten Substitutionen mit rationalen ganzen Coefficienten der Determinante 1 begründet." (Thus, as one immediately sees, a homomorphic relation of the group Γ₍₆₃₎ is based on the group of modulo n incongruent substitutions with rational whole coefficients of the determinant 1.) From footnote on p. 466: "*) Im Anschluss an einen von Hrn. Klein bei seinen neueren Vorlesungen eingeführten Brauch schreibe ich an Stelle der bisherigen Bezeichnung "meroedrischer Isomorphismus" die sinngemässere "Homomorphismus"." (Following a usage that has been introduced by Mr. Klein during his more recent lectures, I write in place of the earlier designation "merohedral isomorphism" the more logical "homomorphism".)

[Birkhoff.1967-4] Birkhoff, Garrett (1967) [1940], Lattice theory, American Mathematical Society Colloquium Publications, vol. 25 (3rd ed.), Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-1025-5, MR 0598630

[Burris.Sankappanavar.2012-5] Stanley N. Burris; H.P. Sankappanavar (2012). A Course in Universal Algebra (PDF). ISBN 978-0-9880552-0-9.

[workmath-6] Mac Lane, Saunders (1971). Categories for the Working Mathematician. Graduate Texts in Mathematics. Vol. 5. Springer-Verlag. Exercise 4 in section I.5. ISBN 0-387-90036-5. Zbl 0232.18001.

[7] Linderholm, C. E. (1970). A group epimorphism is surjective. The American Mathematical Monthly, 77(2), 176-177.

[8] Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Șerban (2001). Hopf Algebra: An Introduction. Pure and Applied Mathematics. Vol. 235. New York, NY: Marcel Dekker. p. 363. ISBN 0824704819. Zbl 0962.16026.

[9] For a detailed discussion of relational homomorphisms and isomorphisms see Section 17.3, in Gunther Schmidt, 2010. Relational Mathematics. Cambridge University Press, ISBN 978-0-521-76268-7

[10] Seymour Ginsburg, Algebraic and automata theoretic properties of formal languages, North-Holland, 1975, ISBN 0-7204-2506-9,

[11] T. Harju, J. Karhumӓki, Morphisms in Handbook of Formal Languages, Volume I, edited by G. Rozenberg, A. Salomaa, Springer, 1997, ISBN 3-540-61486-9.

[13] Krieger (2006) p. 287

[1]

[2]

[note 1]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[note 2]

[11]

[note 3]