Set theory

집합 이론(set theory)은 비공식적으로 대상의 모음으로 설명될 수 있는 집합(sets)을 연구하는 수학적 논리(mathematical logic)의 한 가지입니다. 비록 대상의 임의의 종류는 집합으로 수집될 수 있지만, 수학(mathematics)의 가지로 집합 이론은 대부분 수학(mathematics) 전체와 관련된 대상에 관련 있습니다.

집합 이론의 현대 연구는 1870년대 게오르크 칸토어(Georg Cantor)와 리하르트 데데킨트(Richard Dedekind)에 의해 시작되었습니다. 특히, 게오르크 칸토어는 공통적으로 집합 이론의 설립자로 고려됩니다. 이 초기 단계 동안 조사된 비-형식화된 시스템은 소박한 집합 이론(naive set theory)이라는 이름으로 진행됩니다. 소박한 집합 이론(naive set theory( 내에 (러셀의 역설(Russell's paradox), 칸토어의 역설(Cantor's paradox), 및 부랄리-포르티 역설(Burali-Forti paradox)과 같은) 역설(paradoxes)의 발견된 후, 다양한 공리적 시스템(axiomatic systems)이 20세기 초반에 제안되었으며, 그 중 체르멜로–프렝켈 집합 이론(Zermelo–Fraenkel set theory) (선택의 공리(axiom of choice) 포함 또는 제외) 여전히 가장 잘 알려져 있고 가장 많이 연구되고 있습니다.

집합 이론은 공통적으로 전체 수학, 특히 선택의 공리를 갖는 체르멜로–프렝켈 집합 이론의 형식에서 토대 시스템으로 사용됩니다.^[1] 그것의 토대 역할 외에도, 집합 이론은 역시 무한대(infinity)의 수학적 이론을 개발하기 위한 프레임워크를 제공하고, 컴퓨터 과학(computer science) (예를 들어, 관계 대수(relational algebra)의 이론), 철학(philosophy), 및 형식적 의미론(formal semantics)에서 다양한 응용을 가집니다. 그것의 토대적인 매력은, 그것의 역설(paradoxes), 무한대의 개념과 그것의 다중 응용에 대해 함축과 함께, 집합 이론을 논리학자(logician)와 수학의 철학자들(philosophers of mathematics)에 대해 주요 관심 영역으로 만들어 왔습니다. 집합 이론에 대한 현대 연구는 실수(real number) 직선의 구조에서 큰 세는-숫자(large cardinal)의 일관성(consistency) 연구에 이르기까지 광범위한 주제를 다룹니다.

History

수학적 주제는 전형적으로 많은 연구자 사이의 상호 작용을 통해 나타나고 진화합니다. 집합 이론은, 어쨌든, 1874년 게오르크 칸토어(Georg Cantor)에 의한 "On a Property of the Collection of All Real Algebraic Numbers"에 의해 설립되었습니다.^[2]^[3]

기원전 5세기부터, 서양에서 그리스 수학자 엘레아의 제논(Zeno of Elea)과 동양에서 초기 인도 수학자(Indian mathematicians)를 시작으로, 수학자들은 무한대(infinity)의 개념과 씨름해 왔습니다. 특히 주목할 만한 것은 19세기 전반부에서 버나드 볼차노(Bernard Bolzano)의 연구입니다.^[4] 무한대의 현대적 이해는 1870–1874년에 시작되었고, 실수 해석학(real analysis)에서 칸토어의 연구에서 동기를 받았습니다.^[5] 칸토어와 리하르트 데데킨트(Richard Dedekind) 사이의 1872년 만남은 칸토어의 생각에 영향을 주었고, 칸토어의 1874년 논문에서 절정에 달했습니다.

칸토어의 연구는 처음에 그 당시의 수학자들을 양극화시켰습니다. 카를 바이어슈트라스(Karl Weierstrass)와 데데킨트는 칸토어를 지지했지만, 현재 수학적 구성주의(mathematical constructivism)의 창시자로 여겨지는 레오폴트 크로네커(Leopold Kronecker)는 지지하지 않았습니다. 칸토어 집합 이론은 결국 집합 사이의 일-대-일 대응(one-to-one correspondence), 정수보다 실수(real number)가 더 많다는 그의 증명, 거듭제곱 집합(power set) 연산을 초래하는 "무한대" ("칸토어의 역설(Cantor's Paradise)")와 같은 칸토어 개념의 유용성으로 인해 널리 퍼졌습니다. 전원 설정 작업으로 인해 발생합니다. 집합 이론의 이러한 유용성은 아르투어 쇤플리스(Arthur Schoenflies)에 의한 1898년에 클라인의 백과사전(Klein's encyclopedia)에 기고된 "Mengenlehre"라는 기사로 이어졌습니다.

집합 이론에서 다음 흥분의 물결은 1900년경에 찾아왔으며, 당시 칸토어 집합 이론의 일부 해석이 이율배반(antinomies) 또는 역설(paradoxes)이라고 불리는 몇 가지 모순을 야기한다는 사실이 발견되었을 때였습니다. 버트런드 러셀(Bertrand Russell)과 에른스트 체르멜로(Ernst Zermelo)는 지금 러셀의 역설(Russell's paradox)이라고 불리는 가장 단순하고 가장 잘 알려진 역설을 독립적으로 발견했습니다: "자신의 구성원이 아닌 모든 집합의 집합"을 생각해 보십시오, 이것은 모순으로 이어지는데 왜냐하면 그것은 자체의 구성원이어야 하고 차제의 구성원이 아니기 때문입니다. 1899년에, 칸토어는 "모든 집합의 집합의 세는-숫자(cardinal number)는 무엇입니까?"라는 질문을 스스로 제기하고, 관련된 역설을 얻었습니다. 러셀은 그의 1903년 자신의 The Principles of Mathematics에서 유럽 대륙 수학의 검토에서 자신의 역설을 주제로 사용했습니다. 러셀은 집합이라는 용어 대신 클래스라는 용어를 사용했으며, 이후에 더 기술적으로 사용해 왔습니다.

1906년에, 용어 집합은 캠브리지 대학 출판부(Cambridge University Press)에 의해 발행된 남편과 아내 윌리엄 헨리 영(William Henry Young)과 그레이스 치즘 영(Grace Chisholm Young)에 의한 저서 Theory of Sets of Points에 등장했습니다.^[6]

집합 이론의 기세는 역설에 대한 논쟁이 그것의 포기로 이어지지 않을 정도였습니다. 1908년에 체르멜로의 연구와 1922년에 아브라함 프렝켈(Abraham Fraenkel)과 토랄프 스콜렘(Thoralf Skolem)의 연구는 ZFC 공리의 집합을 초래했으며, 이것은 집합 이론에 대해 가장 공통적으로 사용되는 공리의 집합이 되었습니다. 앙리 르베그(Henri Lebesgue)의 연구와 같은 해석가(analysts)의 연구는 집합 이론의 위대한 수학적 유용성을 보여주었으며, 이것은 이후 현대 수학의 옷장에 짜 넣어졌습니다. 집합 이론은 토대 시스템으로 공통적으로 사용되지만, 대수적 기하학(algebraic geometry)과 대수적 토폴로지(algebraic topology)와 같은 일부 영역에서 카테고리 이론(category theory)이 선호되는 토대로 생각됩니다.

Basic concepts and notation

집합 이론은 객체 $o$ 와 집합 $A$ 사이의 기본적인 이항 관계(binary relation)로 시작합니다. 만약 $o$ 가 $A$ 의 구성원(member) (또는 원소)이면, 표기법 $o \in A$ 가 사용됩니다. 집합은 쉼표로 구분된 원소를 나열하거나, 중괄호 { } 안에 그것의 원소의 속성을 부여함으로써 설명됩니다.^[7] 집합은 대상이기 때문에, 구성원 관계는 집합과도 관련될 수 있습니다.

두 집합 사이의 파생된 이항 관계는 집합 포함(set inclusion)이라고도 하는 부분집합 관계입니다. 만약 집합 $A$ 의 모든 구성원이 역시 집합 $B$ 의 구성원이면, $A$ 는 $B$ 의 부분집합(subset)이며, $A \subseteq B$ 로 표시됩니다. 예를 들어, ${1, 2}$ 는 ${1, 2, 3}$ 의 부분집합이고, ${2}$ 도 마찬가지이지만 ${1, 4}$ 는 그렇지 않습니다. 이 정의에 의해 암시된 것처럼, 집합은 자신의 부분집합입니다. 이 가능성이 부적절하거나 거부되는 것이 타당한 경우에 대해, 용어 적절한 부분집합(proper subset)이 정의됩니다. $A$ 가 $B$ 의 적절한 부분집합이라고 불리는 것과 $A$ 가 $B$ 의 부분집합이지만 $A$ 가 $B$ 와 같지 않은 것은 필요충분 조건입니다. 역시, 1, 2, 및 3은 집합 ${1, 2, 3}$ 의 구성원 (원소)이지만, 그것의 부분집합은 아닙니다; 그리고 차례로, ${1}$ 과 같은 부분집합은 집합 ${1, 2, 3}$ 의 구성원이 아닙니다.

산술(arithmetic)이 숫자(number)에 대한 이항 연산(binary operation)을 특징으로 하는 것처럼, 집합 이론은 집합에 대한 이항 연산을 특징으로 합니다.^[8] 다음은 그들 중의 일부 목록입니다:

집합 $A$ 와 $B$ 의 합집합(Union)은 $A \cup B$ 로 표시되며, $A$ , 또는 $B$ 또는 둘 다의 구성원인 모든 대상의 집합입니다.^[9] 예를 들어, ${1, 2, 3}$ 와 ${2, 3, 4}$ 의 합집합은 집합 ${1, 2, 3, 4}$ 입니다.
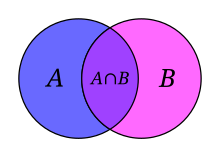
집합 $A$ 와 $B$ 의 교집합(Intersection)은, $A \cap B$ 로 나타내며, $A$ 와 $B$ 둘 다의 구성원인 모든 대상의 집합입니다. 예를 들어, ${1, 2, 3}$ 와 ${2, 3, 4}$ 의 교집합은 집합 ${2, 3}$ 입니다.
$U$ 와 $A$ 의 집합 차이(Set difference)는, $U \ A$ 로 표시되며, $A$ 의 구성원이 아닌 $U$ 의 모든 구성원의 집합입니다. 집합 차이 ${1, 2, 3} \ {2, 3, 4}$ 는 ${1}$ 이지만, 반대로, 집합 차이 ${2, 3, 4} \ {1, 2, 3}$ 는 ${4}$ 입니다. $A$ 가 $U$ 의 부분집합일 때, 집합 차이 $U \ A$ 는 역시 $U$ 안의 $A$ 의 여집합(complement)이라고 불립니다. 이 경우에서, 만약 $U$ 의 선택이 문맥에서 분명하면, 표기법 $A c$ 가 때때로 $U \ A$ 대신에 사용되며, 특히 만약 $U$ 가 벤 다이어그램(Venn diagram)의 연구에서 처럼 우주 집합(universal set)이면 그렇습니다.
집합 $A$ 와 $B$ 의 대칭 차이(Symmetric difference)는, $A △ B$ 또는 $A ⊖ B$ 로 표시되며, $A$ 와 $B$ 중 정확하게 하나의 구성원인 모든 대상의 집합입니다 (원소는 그 집합 중 하나에 있지만, 둘 다에 있지는 않습니다). 예를 들어, 집합 ${1, 2, 3}$ 와 ${2, 3, 4}$ 에 대해, 대칭 차이 집합은 ${1, 4}$ 입니다. 그것은 합집합과 교집합의 집합 차이, $(A ∪ B) \ (A ∩ B)$ 또는 $(A \ B) ∪ (B \ A)$ 입니다.
$A$ 와 $B$ 의 데카르트 곱(Cartesian product)은, $A \times B$ 로 표시되며, 그것의 구성원이 모든 가능한 순서화된 쌍(ordered pair) $(a, b)$ 인 집합이며, 여기서 $a$ 는 $A$ 의 구성원이고 $b$ 는 $B$ 의 구성원입니다. 예를 들어, {1, 2}와 {red, white}의 데카르트 곱은 {(1, red), (1, white), (2, red), (2, white)}입니다.
집합 $A$ 의 거듭제곱 집합(Power set)은, ${\mathcal {P}}(A)$ 로 표시되며, 그것의 구성원이 $A$ 의 모든 가능한 부분집합인 집합입니다. 예를 들어, ${1, 2}$ 의 거듭제곱 집합은 ${ {}, {1}, {2}, {1, 2} }$ 입니다.

중심적으로 중요한 몇 가지 기본 집합은 자연수(natural number) 집합, 실수(real number) 집합, 및 원소를 포함하지 않는 고유한 집합인 빈 집합(empty set)입니다. 빈 집합은 역시 때때로 널 집합이라고 불리지만,^[10] 이 이름은 모호하고 여러 해석으로 이어질 수 있습니다.

Some ontology

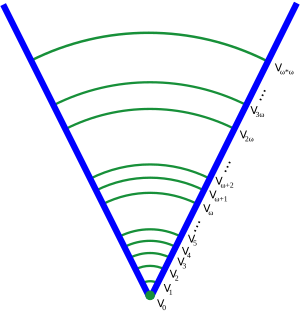
집합은 만약 그것의 모든 구성원이 집합이고, 그것의 구성원의 모든 구성원이 집합이고, 이런 식으로 계속되면 순수(pure)입니다. 예를 들어, 오직 빈 집합을 포함하는 집합 ${{}}$ 은 비-빈 순수 집합입니다. 현대 집합 이론에서, 순수 집합의 폰 노이만 우주(von Neumann universe)에 주의를 제한하는 것이 공통적이고, 공리적 집합 이론(axiomatic set theory)의 많은 시스템은 오직 순수 집합을 공리화하도록 설계되었습니다. 이 제한에는 많은 기술적 이점이 있고, 일반성이 거의 손실되지 않는데, 왜냐하면 본질적으로 모든 수학적 개념은 순수 집합에 의해 모델링될 수 있기 때문입니다. 폰 노이만 우주에서 집합은 해당 구성원, 구성원의 구성원, 등이 중첩된 깊이에 따라 누적 계층구조(cumulative hierarchy)로 구성됩니다. 이 계층구조에서 각 집합은 그것의 랭크(rank)로 알려진 순서-숫자(ordinal number) $\alpha$ 에 (초월유한 재귀(transfinite recursion)에 의해) 할당됩니다. 순수 집합 $X$ 의 랭크는 그것의 원소 중 임의의 것의 랭크보다 엄격하게 큰 최소 순서-숫자로 정의됩니다. 예를 들어, 빈 집합은 랭크 0이 할당되고, 반면에 오직 빈 집합을 포함하는 집합 ${{}}$ 은 랭크 1이 할당됩니다. 각 순서-숫자 $\alpha$ 에 대해, 집합 $V_{\alpha }$ 는 $\alpha$ 보다 작은 랭크를 갖는 모든 순수 집합으로 구성되도록 정의됩니다. 전체 폰 노이만 우주는 $V$ 로 표시됩니다.

Formalized set theory

기본 집합 이론은 비공식적이고 직관적으로 연구될 수 있고, 따라서 초등학교에서 벤 다이어그램(Venn diagram)을 사용하여 가르칠 수 있습니다. 직관적인 접근 방식은 집합이 임의의 특정 정의하는 조건을 만족시키는 모든 대상의 클래스에서 형성될 수 있다고 암묵적으로 가정합니다. 이 가정은 역설을 일으키며, 가장 단순하고 가장 잘 알려진 것은 러셀의 역설(Russell's paradox)과 부랄리-포르티 역설(Burali-Forti paradox)입니다. 공리적 집합 이론은 원래 그러한 역설의 집합 이론을 제거하기 위해 고안되었습니다.^{[note 1]}

공리적 집합 이론의 가장 널리 연구된 시스템은 모든 집합이 누적 계층구조(cumulative hierarchy)를 형성함을 의미합니다. 그러한 시스템은 그것의 존재론(ontology)이 다음을 구성하는 두 가지 풍미에서 옵니다:

집단 단독. 이것은 가장 공통적인 공리적 집합 이론, 선택의 공리(axiom of choice) (ZFC)를 갖는 체르멜로–프랭켈 집합 이론(Zermelo–Fraenkel set theory)을 포함합니다. ZFC의 파편은 다음을 포함합니다:
- 체르멜로 집합 이론(Zermelo set theory), 이것은 대체의 공리 스키마(axiom schema of replacement)를 분리(separation)의 것으로 대체합니다;
- 일반 집합 이론(General set theory), 페아노 공리(Peano axioms)와 유한 집합(finite set)에 대해 충분한 체르멜로 집합 이론(Zermelo set theory)의 작은 파편;
- 크립키–플레이텍 집합 이론(Kripke–Platek set theory), 이것은 무한대, 거듭제곱집합(powerset), 및 선택(choice)의 공리를 생략하고, 분리(separation)와 대체(replacement)의 공리 개요를 약화시킵니다.
집합과 적절한 클래스. 이것들은 집합 단독에 대한 정리에 대해 ZFC와 같은 강도를 가지는 폰 노이만-베르나이스-괴델 집합 이론(Von Neumann–Bernays–Gödel set theory)과 ZFC보다 둘 다 강력한 모스-켈리 집합 이론(Morse–Kelley set theory)과 타르스키–그로텐디크 집합 이론(Tarski–Grothendieck set theory)을 포함합니다.

위의 시스템은 원시-원소(urelement), 집합의 구성원이 될 수 있지만 자체로 집합이 아니고 임의의 구성원을 가지지 않는 대상을 허용하도록 수정될 수 있습니다.

NFU (원시-원소 허용함) 및 NF (원시-원소 없음)의 새로운 토대(New Foundations) 시스템은 누적 계층구조를 기반으로 하지 않습니다. NF와 NFU는 "모든 것의 집합"을 포함하며, 그것과 상대적으로 모든 각 집합은 여집합을 가집니다. 이들 시스템에서, 원시-원소는 중요한데, 왜냐하면 NFU가 아니라 NF가 선택의 공리(axiom of choice)가 유지되지 않는 집합을 생성하기 때문입니다. NF의 존재론은 전통적인 누적 계층 구조를 반영하지 않고 바른-토대됨(well-foundedness)을 위반하지만, 토머스 포스터(Thomas Forster)는 그것은 집합의 반복적 개념(iterative conception of set)을 반영한다고 주장했습니다.^[11]

CST, CZF, 및 IZF와 같은 구성적 집합 이론(constructive set theory)의 시스템은 그것들의 집합 공리를 고전적 논리(classical logic) 대신 직관적(intuitionistic)에서 삽입합니다. 그래도 다른 시스템은 고전적 논리를 수용하지만 비표준 구성원 관계를 특징으로 합니다. 이것들은 구성원 관계를 구현하는 원자 공식(atomic formula)의 값이 단순히 참 또는 거짓이 아닌 거친 집합 이론(rough set theory)과 퍼지 집합 이론(fuzzy set theory)을 포함합니다. ZFC의 부울-값 모델(Boolean-valued model)은 관련된 주제입니다.

내부 집합 이론(internal set theory)이라고 불리는 ZFC의 강화는 1977년 에드워드 넬슨(Edward Nelson)에 의해 제안되었습니다.

Applications

많은 수학적 개념은 오직 집합 이론적 개념을 사용하여 정확하게 정의될 수 있습니다. 예를 들어, 그래프(graph), 매니폴드(manifolds), 링(rings), 벡터 공간(vector space), 및 관계 대수(relational algebra)와 같은 다양한 수학적 구조는 모두 다양한 (공리적) 속성을 만족시키는 집합으로 정의될 수 있습니다. 동치(Equivalence)와 순서 관계(order relation)는 수학에서 도처에 존재하고, 수학적 관계(relations)의 이론은 집합 이론에서 설명될 수 있습니다.

집합 이론은 역시 많은 수학에서 유망한 기초적 시스템입니다. Principia Mathematica의 첫 번째 볼륨이 출판된 이후로, 대부분의 (또는 심지어 모든) 수학적 정리는 일-차(first) 또는 이-차 논리(second-order logic)를 사용하여 많은 정의가 증가된 집합 이론에 대해 적절하게 설계된 공리의 집합를 사용하여 파생될 수 있다고 주장되어 왔습니다. 예를 들어, 자연수(natural)와 실수(real number)의 속성은 집합 이론 내에서 파생될 수 있는데, 왜냐하면 각 숫자 시스템은 그것의 필드가 일부 무한 집합(infinite set)인 적절한 동치 관계(equivalence relation) 아래의 동치 클래스(equivalence class)의 집합으로 식별될 수 있기 때문입니다.

수학적 해석학, 토폴리지, 추상 대수학, 및 이산 수학의 기초로서의 집합 이론은 마찬가지로 논쟁의 여지가 없습니다; 수학자들은 (원칙적으로) 이들 영역에서 정리가 관련된 정의와 집합 이론의 공리에서 파생될 수 있다는 점을 인정합니다. 어쨌든, 집합 이론에서 복잡한 수학적 정리의 완전한 파생이 공식적으로 검증된 경우는 거의 없는데, 왜냐하면 그러한 형식적 파생은 종종 수학자들이 공통적으로 제시하는 자연 언어 증명보다 훨씬 더 길기 때문입니다. 하나의 검증 프로젝트, Metamath는 ZFC 집합 이론, 일-차 논리(first-order logic), 및 명제 논리(propositional logic)에서 시작하는 12,000개 이상의 정리의 인간-작성, 컴퓨터-검증된 파생을 포함합니다.

Areas of study

집합 이론은 수학에서 주요 연구 분야이며, 많은 관련된 하위분야를 가집니다.

Combinatorial set theory

조합론적 집합 이론은 유한 조합론(combinatorics)을 무한 집합으로의 확장과 관련됩니다. 이것은 세는-숫자 산술(cardinal arithmetic)의 연구와 에르되시–라도 정리(Erdős–Rado theorem)와 같은 램지의 정리(Ramsey's theorem)의 확장의 연구를 포함합니다.

Descriptive set theory

설명적 집합 이론은 실수 직선(real line)의 부분집합과, 보다 일반적으로, 폴란드 공간(Polish space)의 부분집합의 연구입니다. 그것은 보렐 계층(Borel hierarchy)의 점클래스(pointclass) 연구로 시작하고 투영 계층(projective hierarchy)과 워지 계층(Wadge hierarchy)과 같은 더 복잡한 계층의 연구로 확장됩니다. 보렐 집합(Borel set)의 많은 속성은 ZFC에서 설정될 수 있지만, 이들 속성이 더 복잡한 집합에 대해 유지된다는 것을 증명하려면 결정성과 큰 세는-숫자와 관련된 추가적인 공리를 요구합니다.

효과적인 설명적 집합 이론(effective descriptive set theory)의 분야는 집합 이론과 재귀 이론(recursion theory) 사이에 있습니다. 그것은 라이트페이스 점클래스(lightface pointclass)의 연구를 포함하고, 초산술적 이론(hyperarithmetical theory)과 밀접한 관련이 있습니다. 많은 경우에서, 고전적인 설명적 집합 이론의 결과는 효과적인 버전을 가집니다; 일부 경우에서, 새로운 결과는 먼저 효과적인 버전을 입증하고 그런-다음 그것을 더 광범위하게 적용할 수 있도록 확장 ("상대화")함으로써 얻어질 수 있습니다.

최근 연구의 영역은 보렐 동치 관계(Borel equivalence relation)와 보다 복잡한 정의-가능한 동치 관계(equivalence relation)에 관한 것입니다. 이것은 수학의 많은 분야에서 불변(invariants)의 연구에 중요한 응용을 가집니다.

Fuzzy set theory

칸토어(Cantor)에 의해 정의되고 체르멜로와 프랭켈에 의해 공리화된 집합 이론에서, 대상은 집합의 구성원이거나 구성원이 아닙니다. 퍼지 집합 이론(fuzzy set theory)에서 이 조건은 로트피 알리아스커 자데이(Lotfi A. Zadeh)에 의해 완화되었으므로 대상은 집합에서 구성원의 정도, 0과 1 사이의 숫자를 가집니다. 예를 들어, "키가 큰 사람"의 집합에서 한 사람의 구성원의 정도는 단순한 예 또는 아니오 대답보다 유연하고 0.75와 같은 실수가 될 수 있습니다.

Inner model theory

체르멜로–프래켈 집합 이론 (ZF)의 내부 모델(inner model)은 모든 순서-숫자를 포함하고 ZF의 모든 공리를 만족시키는 전이 클래스(class)입니다. 정식의 예제는 괴델에 의해 개발된 구성-가능 우주(constructible universe) L입니다. 내부 모델의 연구가 흥미로운 이유 중 하나는 일관성 결과를 입증하기 위해 사용될 수 있기 때문입니다. 예를 들어, ZF의 모델 V가 연속체 가설(continuum hypothesis) 또는 선택의 공리(axiom of choice)를 만족시키는지 여부에 관계없이, 원래 모델 내부에 구성된 내부 모델 L은 일반화된 연속체 가설과 선택의 공리 둘 다를 만족함을 보여줄 수 있습니다. 따라서 ZF가 일관적이라는 가정 (적어도 하나의 모델을 가짐)은 이들 두 가지 원칙과 함께 ZF는 일관적임을 의미합니다.

내부 모델의 연구는, 특히 선택의 공리와 모순되는 결정성의 공리와 같은 공리를 고려할 때, 결정성(determinacy)과 큰 세는-숫자(large cardinal)의 연구에서 공통적입니다. 심지어 집합 이론의 고정된 모형이 선택의 공리를 만족하더라도, 내부 모델에 대해 선택의 공리를 만족시키지 못할 가능성이 있습니다. 예를 들어, 충분하게 큰 세는-숫자의 존재는 결정성의 공리를 만족시키는 (및 따라서 선택의 공리를 만족시키지 않는) 내부 모델이 있음을 의미합니다.^[12]

Large cardinals

큰 세는-숫자는 여분의 속성을 갖는 세는-숫자입니다. 많은 그러한 속성은 비-접근가능 세는-숫자(inaccessible cardinal), 측정-가능 세는-숫자(measurable cardinal), 등을 포함하여 연구됩니다. 이들 속성은 전형적으로 세는-숫자가 매우 커야 함을 의미하며, 체르멜로–프랭켈 집합 이론(Zermelo–Fraenkel set theory)에서 입증할 수 없는 지정된 속성을 갖는 세는-숫자가 존재합니다.

Determinacy

결정성은 적절한 가정 아래에서, 완전한 정보의 특정 2인용 게임이 한 플레이어가 승리 전략을 가지고 있어야 한다는 의미에서 처음부터 결정된다는 사실을 참조합니다. 이들 전략의 존재는 설명적 집합 이론에서 중요한 결과를 가지는데, 왜냐하면 게임의 더 넓은 클래스가 결정된다는 가정은 종종 더 넓은 클래스의 집합이 토폴로지적 속성을 가질 것임을 암시하기 때문입니다. 결정성의 공리(axiom of determinacy) (AD)는 중요한 연구의 대상입니다; 비록 선택의 공리와 호환되지 않을지라도, AD는 실수 직선의 모든 부분집합이 (특히, 측정-가능이고 완전한 집합 속성과 함께) 잘 행동함을 의미합니다. AD는 워지 정도(Wadge degree)가 우아한 구조를 가짐을 입증하기 위해 사용될 수 있습니다.

Forcing

폴 코언(Paul Cohen)은 연속체 가설(continuum hypothesis)이 실패하는 ZFC 모델, 또는 선택의 공리(axiom of choice)가 실패하는 ZF 모델을 탐색하는 동안 강제화(forcing)의 방법을 발명했습니다. 강제화는 구성과 원래 모델에 의해 결정된 (즉, "강제된") 속성을 갖는 더 큰 모델을 생성하기 위해 집합 이론의 일부 주어진 모델에 추가적인 집합을 인접합니다. 예를 들어, 코언의 구성은 원래 모델의 세는-숫자의 임의의 변경없이 자연수(natural number)의 추가적인 부분집합에 인접합니다. 강제화는 유한한 방법에 의해 상대적 일관성(relative consistency)을 입증하는 두 가지 방법 중 하나이며, 나머지 하는의 방법은 부울-값 모델(Boolean-valued model)입니다.

Cardinal invariants

세는-숫자 불변은 세는-숫자에 의해 측정된 실수 직선의 속성입니다. 예를 들어, 잘-연구된 불변은 그것의 합집합이 전체 실수 직선인 실수의 마른 집합(meagre set)의 모음의 가장 작은 카디널리티입니다. 이것들은 집합 이론의 임의의 두 동형적 모델이 각 불변에 대해 같은 세는-숫자를 제공해야 한다는 점에서 불변입니다. 많은 세는-숫자 불변이 연구되어 왔고, 이것들 사이의 관계는 종종 복잡하고 집합 이론의 공리와 관련이 있습니다.

Set-theoretic topology

집합-이론적 토폴로지는 본질적으로 집합-이론적이거나 그것들의 해에 대해 집합 이론의 고급 방법을 요구하는 일반 토폴로지(general topology)의 문제를 연구합니다. 많은 이들 정리는 ZFC와 독립적이며, 그것들의 증명에 대해 더 강력한 공리를 요구합니다. 유명한 문제는 표준 무어 공간 질문(normal Moore space question), 일반 토폴로지에서 집중 연구의 주제였던 질문입니다. 통상 무어 우주 질문에 대한 답은 결국 ZFC와 독립적인 것으로 입증되었습니다.

Objections to set theory

집합 이론의 시작부터, 일부 수학자들은 수학에 대해 기초(foundation for mathematics)로 그것을 반대해 왔습니다. 집합 이론에 대한 가장 공통적인 반대는, 집합 이론의 처음 몇 년에 표명된 크로네커(Kronecker)의 반대로, 수학이 계산과 느슨하게 관련되어 있다는 구성주의자(constructivist) 관점에서 시작합니다. 만약 이 견해가 인정된다면, 무한 집합의 처리는, 소박한 집합 이론과 공리적 집합 이론에서 둘 다에서, 원칙적으로도 계산할 수 없는 방법과 대상을 수학에 도입합니다. 수학에 대해 대체 기초로서의 구성주의의 실현 가능성은 에렛 비숍(Errett Bishop)의 영향력 있는 책 Foundations of Constructive Analysis에 의해 크게 높아졌습니다.^[13]

앙리 푸앵카레(Henri Poincaré)에 의해 제기된 다른 반대는 사양(specification)과 대체(replacement)의 공리 스킴뿐만 아니라, 거듭제곱 집합의 공리(axiom of power set)를 사용하여 집합을 정의하는 것이 수학적 대상의 정의에 예측성(impredicativity), 순환성(circularity)의 한 유형을 도입한다는 것입니다. 공통적으로 인정된 체르멜로–프랭켈 이론의 범위보다는 적지만, 예측적으로 기반된 수학의 범위는 구성적 수학의 범위보다 훨씬 커서, 솔로몬 페퍼맨(Solomon Feferman)은 "과학적으로 적용-가능한 모든 분석은 [예측적인 방법을 사용하여] 개발될 수 있다"라고 말함으로써 강조합니다.^[14]

루트비히 비트겐슈타인(Ludwig Wittgenstein)은 집합 이론을 수학적 플라톤주의(mathematical platonism)의 그것의 언외의 의미에 대해 철학적으로 비난했습니다.^[15] 그는 "집합 이론은 틀렸다"고 썼는데, 왜냐하면 그것은 허구적 상징주의의 "넌센스"를 기반으로 하기 때문이고, "해로운 관용구"를 가지는데, 왜냐하면 "모든 숫자"에 대해 말하는 것은 무의미하기 때문이라고 썼습니다.^[16] 비트겐슈타인은 수학을 알고리듬적 인간의 연역과 동일시했습니다;^[17] 수학을 위한 안전한 토대에 대한 필요성은, 그에게, 무의미하게 보였습니다.^[18] 더욱이, 인간의 노력은 필연적으로 유한하기 때문에, 비트겐슈타인의 철학은 급진적 구성주의(constructivism)와 유한주의(finitism)에 대한 존재론적 헌신을 요구했습니다. 메타-수학적 명제는 – 이것은, 비트겐슈타인에 대해, 무한 도메인과 따라서 거의 모든 현대 집합 이론에 걸쳐 수량화하는 임의의 명제를 포함했습니다 – 수학이 아닙니다.^[19] 현대 철학자는 Remarks on the Foundations of Mathematics에서 엄청난 실수를 한 후 비트겐슈타인의 견해를 거의 채택하지 않습니다: 비트겐슈타인은 초록만 읽은 후 괴델의 불완전성 정리(Gödel's incompleteness theorems)를 반박하려고 시도했습니다. 평론가 카이즐(Kreisel), 베르나이스(Bernays), 더밋(Dummett), 및 굿스타인(Goodstein) 모두가 지적했듯이, 그의 비평 중 상당수는 논문 전체에 적용되지 않았습니다. 오직 최근에야 크리스핀 라이트(Crispin Wright)와 같은 철학자들이 비트겐슈타인의 주장을 재건하기 시작했습니다.^[20]

카테고리 이론가들(Category theorists)은 전통적인 공리적 집합 이론의 대안으로 토포스 이론(topos theory)을 제안해 왔습니다. 토포스 이론은 구성주의(constructivism), 유한 집합 이론, 및 계산-가능(computable) 집합 이론과 같은 해당 이론에 대한 다양한 대안을 해석할 수 있습니다.^[21]^[22] 토포스는 역시 ZF로부터 선택의 독립성을 강제화하고 논의하기 위한 자연스러운 설정을 제공할 뿐만 아니라, 점없는 토폴로지(pointless topology) 및 스톤 공간(Stone space)을 위한 프레임워크를 제공합니다.^[23]

연구의 활성 영역은 단일-결합 기초(univalent foundations)이고 이와 관련된 호모토피 유형 이론(homotopy type theory)입니다. 호모토피 유형 이론 내에서, 집합은 고차 귀납적 유형(higher inductive type)의 귀납적 및 재귀적 속성에서 발생하는 집합의 보편적 속성(universal properties)을 갖는 호모토피 0-유형으로 고려될 수 있습니다. 선택의 공리(axiom of choice)와 제외된 중간의 법칙(law of the excluded middle)과 같은 원칙은 집합 이론에서 고전적 공식화에 상응하는 방식으로 공식화되거나 아마도 유형 이론에 고유한 구별되는 방법의 스펙트럼으로 공식화될 수 있습니다. 이들 원칙 중 일부는 다른 원칙의 결과로 입증될 수 있습니다. 이들 공리적 원리의 다양한 형식화는 다양한 수학적 결과를 도출하기 위해 요구된 형식화의 상세한 분석을 허용합니다.^[24]^[25]

Set theory in mathematical education

집합 일론이 현대 수학의 토대로 인기를 얻으면서, 수학 교육(mathematics education) 초기에 소박한 집합 이론(naive set theory)의 기초를 도입하자는 아이디어에 대해 지원을 받아 왔습니다.

1960년대 미국에서, 다른 추상적인 개념 중에서, 기본 집합 이론을 초등학교(primary school) 학생에게 가르치는 것을 목표로 한 New Math 실험이 있었지만, 많은 비판을 받았습니다. 유럽 학교에서 수학 강의 계획서는 이러한 추세를 따랐고, 현재 모든 학년에서 다양한 수준에 그 주제를 포함하고 있습니다. 벤 다이어그램(Venn diagram)은 초등 학교 학생들에게 기본적인 집합-이론적 관계를 설명하기 위해 널리 사용됩니다 (존 벤(John Venn)은 원래 용어 논리(term logic)에서 추론(inference)의 타당성(validity)을 평가하기 위한 절차의 일부로 그것을 고안했지만).

집합 이론은 학생들에게 논리 연산자(logical operators) (NOT, AND, OR), 및 집합의 의미론적 또는 규칙 설명 (기술적으로 내부적 정의(intensional definition)^[26])을 소개하기 위해 사용되며 (예를 들어, "문자 A로 시작하는 월"), 이것은 컴퓨터 프로그램(computer programming)을 배울 때 유용할 수 있는데, 왜냐하면 부울 논리(boolean logic)가 다양한 프로그래밍 언어(programming language)에서 사용되기 때문입니다. 마찬가지로, 집합(set) 및 중복집합(multiset)과 목록(list)과 같은 다른 모음-계열 대상은 컴퓨터 과학(computer science)과 프로그래밍(programming)에서 공통적인 데이터유형(datatype)입니다.

그 외에도, 집합(set)은 다른 유형의 숫자 ( $N$ , $Z$ , $R$ , ...)에 대해 이야기할 때와 수학 함수(mathematical function)를 한 집합 (도메인(domain))에서 또 다른 집합 (치역(range))으로의 관계로 정의할 때 수학 교육에서 공통적으로 참조됩니다.

Notes

^ In his 1925 paper ""An Axiomatization of Set Theory", John von Neumann observed that "set theory in its first, "naive" version, due to Cantor, led to contradictions. These are the well-known antinomies of the set of all sets that do not contain themselves (Russell), of the set of all transfinite ordinal numbers (Burali-Forti), and the set of all finitely definable real numbers (Richard)." He goes on to observe that two "tendencies" were attempting to "rehabilitate" set theory. Of the first effort, exemplified by Bertrand Russell, Julius König, Hermann Weyl and L. E. J. Brouwer, von Neumann called the "overall effect of their activity . . . devastating". With regards to the axiomatic method employed by second group composed of Zermelo, Fraenkel and Schoenflies, von Neumann worried that "We see only that the known modes of inference leading to the antinomies fail, but who knows where there are not others?" and he set to the task, "in the spirit of the second group", to "produce, by means of a finite number of purely formal operations . . . all the sets that we want to see formed" but not allow for the antinomies. (All quotes from von Neumann 1925 reprinted in van Heijenoort, Jean (1967, third printing 1976), From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931, Harvard University Press, Cambridge MA, ISBN 0-674-32449-8 (pbk). A synopsis of the history, written by van Heijenoort, can be found in the comments that precede von Neumann's 1925 paper.

References

^ Kunen 1980, p. xi: "Set theory is the foundation of mathematics. All mathematical concepts are defined in terms of the primitive notions of set and membership. In axiomatic set theory we formulate a few simple axioms about these primitive notions in an attempt to capture the basic "obviously true" set-theoretic principles. From such axioms, all known mathematics may be derived."
^ Cantor, Georg (1874), "Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen", Journal für die reine und angewandte Mathematik (in German), 1874 (77): 258–262, doi:10.1515/crll.1874.77.258, S2CID 199545885
^ Johnson, Philip (1972), A History of Set Theory, Prindle, Weber & Schmidt, ISBN 0-87150-154-6
^ Bolzano, Bernard (1975), Berg, Jan (ed.), Einleitung zur Größenlehre und erste Begriffe der allgemeinen Größenlehre, Bernard-Bolzano-Gesamtausgabe, edited by Eduard Winter et al., vol. II, A, 7, Stuttgart, Bad Cannstatt: Friedrich Frommann Verlag, p. 152, ISBN 3-7728-0466-7
^ Dauben, Joseph (1979), Georg Cantor: His Mathematics and Philosophy of the Infinite, Harvard University Press, pp. 30–54, ISBN 0-674-34871-0.
^ Young, William; Young, Grace Chisholm (1906), Theory of Sets of Points, Cambridge University Press
^ "Introduction to Sets". www.mathsisfun.com. Retrieved 2020-08-20.
^ Kolmogorov, A.N.; Fomin, S.V. (1970), Introductory Real Analysis (Rev. English ed.), New York: Dover Publications, pp. 2–3, ISBN 0486612260, OCLC 1527264
^ "set theory | Basics, Examples, & Formulas". Encyclopedia Britannica. Retrieved 2020-08-20.
^ Bagaria, Joan (2020), "Set Theory", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Spring 2020 ed.), Metaphysics Research Lab, Stanford University, retrieved 2020-08-20
^ Forster, T. E. (2008). "The iterative conception of set" (PDF). The Review of Symbolic Logic. 1: 97–110.
^ Jech, Thomas (2003), Set Theory, Springer Monographs in Mathematics (Third Millennium ed.), Berlin, New York: Springer-Verlag, p. 642, ISBN 978-3-540-44085-7, Zbl 1007.03002
^ Bishop, Errett (1967), Foundations of Constructive Analysis, New York: Academic Press, ISBN 4-87187-714-0
^ Feferman, Solomon (1998), In the Light of Logic, New York: Oxford University Press, pp. 280–283, 293–294, ISBN 0-195-08030-0
^ Rodych, Victor (Jan 31, 2018). "Wittgenstein's Philosophy of Mathematics". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy (Spring 2018 ed.).
^ Wittgenstein, Ludwig (1975), Philosophical Remarks, §129, §174, Oxford: Basil Blackwell, ISBN 0-631-19130-5
^ Rodych 2018, §2.1: "When we prove a theorem or decide a proposition, we operate in a purely formal, syntactical manner. In doing mathematics, we do not discover pre-existing truths that were 'already there without one knowing' (PG 481)—we invent mathematics, bit-by-little-bit." Note, however, that Wittgenstein does not identify such deduction with philosophical logic; c.f. Rodych §1, paras. 7-12.
^ Rodych 2018, §3.4: "Given that mathematics is a 'motley of techniques of proof' (RFM III, §46), it does not require a foundation (RFM VII, §16) and it cannot be given a self-evident foundation (PR §160; WVC 34 & 62; RFM IV, §3). Since set theory was invented to provide mathematics with a foundation, it is, minimally, unnecessary."
^ Rodych 2018, §2.2: "An expression quantifying over an infinite domain is never a meaningful proposition, not even when we have proved, for instance, that a particular number $n$ has a particular property."
^ Rodych 2018, §3.6.
^ Ferro, Alfredo; Omodeo, Eugenio G.; Schwartz, Jacob T. (September 1980), "Decision Procedures for Elementary Sublanguages of Set Theory. I. Multi-Level Syllogistic and Some Extensions", Communications on Pure and Applied Mathematics, 33 (5): 599–608, doi:10.1002/cpa.3160330503
^ Cantone, Domenico; Ferro, Alfredo; Omodeo, Eugenio G. (1989), Computable Set Theory, International Series of Monographs on Computer Science, Oxford Science Publications, Oxford, UK: Clarendon Press, pp. xii, 347, ISBN 0-198-53807-3
^ Mac Lane, Saunders; Moerdijk, leke (1992), Sheaves in Geometry and Logic: A First Introduction to Topos Theory, Springer-Verlag, ISBN 978-0-387-97710-2
^ homotopy type theory in nLab
^ Homotopy Type Theory: Univalent Foundations of Mathematics. The Univalent Foundations Program. Institute for Advanced Study.
^ Frank Ruda (6 October 2011). Hegel's Rabble: An Investigation into Hegel's Philosophy of Right. Bloomsbury Publishing. p. 151. ISBN 978-1-4411-7413-0.

External links

Daniel Cunningham, Set Theory article in the Internet Encyclopedia of Philosophy.
Jose Ferreiros, The Early Development of Set Theory article in the [Stanford Encyclopedia of Philosophy].
Foreman, Matthew, Akihiro Kanamori, eds. Handbook of Set Theory. 3 vols., 2010. Each chapter surveys some aspect of contemporary research in set theory. Does not cover established elementary set theory, on which see Devlin (1993).
"Axiomatic set theory", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
"Set theory", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Schoenflies, Arthur (1898). Mengenlehre in Klein's encyclopedia.
Online books, and library resources in your library and in other libraries about set theory
Rudin, Walter B. (April 6, 1990). "Set Theory: An Offspring of Analysis". Marden Lecture in Mathematics. University of Wisconsin-Milwaukee. Archived from the original on 2021-10-31 – via YouTube.

[11] In his 1925 paper ""An Axiomatization of Set Theory", John von Neumann observed that "set theory in its first, "naive" version, due to Cantor, led to contradictions. These are the well-known antinomies of the set of all sets that do not contain themselves (Russell), of the set of all transfinite ordinal numbers (Burali-Forti), and the set of all finitely definable real numbers (Richard)." He goes on to observe that two "tendencies" were attempting to "rehabilitate" set theory. Of the first effort, exemplified by Bertrand Russell, Julius König, Hermann Weyl and L. E. J. Brouwer, von Neumann called the "overall effect of their activity . . . devastating". With regards to the axiomatic method employed by second group composed of Zermelo, Fraenkel and Schoenflies, von Neumann worried that "We see only that the known modes of inference leading to the antinomies fail, but who knows where there are not others?" and he set to the task, "in the spirit of the second group", to "produce, by means of a finite number of purely formal operations . . . all the sets that we want to see formed" but not allow for the antinomies. (All quotes from von Neumann 1925 reprinted in van Heijenoort, Jean (1967, third printing 1976), From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931, Harvard University Press, Cambridge MA, ISBN 0-674-32449-8 (pbk). A synopsis of the history, written by van Heijenoort, can be found in the comments that precede von Neumann's 1925 paper.

[FOOTNOTEKunen1980[httpsarchiveorgdetailssettheoryintrodu0000kunepagen13mode2up_xi]-1] Kunen 1980, p. xi: "Set theory is the foundation of mathematics. All mathematical concepts are defined in terms of the primitive notions of set and membership. In axiomatic set theory we formulate a few simple axioms about these primitive notions in an attempt to capture the basic "obviously true" set-theoretic principles. From such axioms, all known mathematics may be derived."

[cantor1874-2] Cantor, Georg (1874), "Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen", Journal für die reine und angewandte Mathematik (in German), 1874 (77): 258–262, doi:10.1515/crll.1874.77.258, S2CID 199545885

[3] Johnson, Philip (1972), A History of Set Theory, Prindle, Weber & Schmidt, ISBN 0-87150-154-6

[4] Bolzano, Bernard (1975), Berg, Jan (ed.), Einleitung zur Größenlehre und erste Begriffe der allgemeinen Größenlehre, Bernard-Bolzano-Gesamtausgabe, edited by Eduard Winter et al., vol. II, A, 7, Stuttgart, Bad Cannstatt: Friedrich Frommann Verlag, p. 152, ISBN 3-7728-0466-7

[5] Dauben, Joseph (1979), Georg Cantor: His Mathematics and Philosophy of the Infinite, Harvard University Press, pp. 30–54, ISBN 0-674-34871-0.

[6] Young, William; Young, Grace Chisholm (1906), Theory of Sets of Points, Cambridge University Press

[7] "Introduction to Sets". www.mathsisfun.com. Retrieved 2020-08-20.

[8] Kolmogorov, A.N.; Fomin, S.V. (1970), Introductory Real Analysis (Rev. English ed.), New York: Dover Publications, pp. 2–3, ISBN 0486612260, OCLC 1527264

[9] "set theory | Basics, Examples, & Formulas". Encyclopedia Britannica. Retrieved 2020-08-20.

[10] Bagaria, Joan (2020), "Set Theory", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Spring 2020 ed.), Metaphysics Research Lab, Stanford University, retrieved 2020-08-20

[12] Forster, T. E. (2008). "The iterative conception of set" (PDF). The Review of Symbolic Logic. 1: 97–110.

[13] Jech, Thomas (2003), Set Theory, Springer Monographs in Mathematics (Third Millennium ed.), Berlin, New York: Springer-Verlag, p. 642, ISBN 978-3-540-44085-7, Zbl 1007.03002

[14] Bishop, Errett (1967), Foundations of Constructive Analysis, New York: Academic Press, ISBN 4-87187-714-0

[15] Feferman, Solomon (1998), In the Light of Logic, New York: Oxford University Press, pp. 280–283, 293–294, ISBN 0-195-08030-0

[16] Rodych, Victor (Jan 31, 2018). "Wittgenstein's Philosophy of Mathematics". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy (Spring 2018 ed.).

[17] Wittgenstein, Ludwig (1975), Philosophical Remarks, §129, §174, Oxford: Basil Blackwell, ISBN 0-631-19130-5

[FOOTNOTERodych2018[httpsplatostanfordeduentrieswittgenstein-mathematicsWittInteConsForm_§2.1]-18] Rodych 2018, §2.1: "When we prove a theorem or decide a proposition, we operate in a purely formal, syntactical manner. In doing mathematics, we do not discover pre-existing truths that were 'already there without one knowing' (PG 481)—we invent mathematics, bit-by-little-bit." Note, however, that Wittgenstein does not identify such deduction with philosophical logic; c.f. Rodych §1, paras. 7-12.

[FOOTNOTERodych2018[httpsplatostanfordeduentrieswittgenstein-mathematicsWittLateCritSetTheoNonEnumVsNonDenu_§3.4]-19] Rodych 2018, §3.4: "Given that mathematics is a 'motley of techniques of proof' (RFM III, §46), it does not require a foundation (RFM VII, §16) and it cannot be given a self-evident foundation (PR §160; WVC 34 & 62; RFM IV, §3). Since set theory was invented to provide mathematics with a foundation, it is, minimally, unnecessary."

[FOOTNOTERodych2018[httpsplatostanfordeduentrieswittgenstein-mathematicsWittInteFini_§2.2]-20] Rodych 2018, §2.2: "An expression quantifying over an infinite domain is never a meaningful proposition, not even when we have proved, for instance, that a particular number $n$ has a particular property."

[FOOTNOTERodych2018[httpsplatostanfordeduentrieswittgenstein-mathematicsWittGodeUndeMathProp_§3.6]-21] Rodych 2018, §3.6.

[22] Ferro, Alfredo; Omodeo, Eugenio G.; Schwartz, Jacob T. (September 1980), "Decision Procedures for Elementary Sublanguages of Set Theory. I. Multi-Level Syllogistic and Some Extensions", Communications on Pure and Applied Mathematics, 33 (5): 599–608, doi:10.1002/cpa.3160330503

[23] Cantone, Domenico; Ferro, Alfredo; Omodeo, Eugenio G. (1989), Computable Set Theory, International Series of Monographs on Computer Science, Oxford Science Publications, Oxford, UK: Clarendon Press, pp. xii, 347, ISBN 0-198-53807-3

[24] Mac Lane, Saunders; Moerdijk, leke (1992), Sheaves in Geometry and Logic: A First Introduction to Topos Theory, Springer-Verlag, ISBN 978-0-387-97710-2

[25] topy type theory in nLab

[26] Homotopy Type Theory: Univalent Foundations of Mathematics. The Univalent Foundations Program. Institute for Advanced Study.

[Ruda2011-27] Frank Ruda (6 October 2011). Hegel's Rabble: An Investigation into Hegel's Philosophy of Right. Bloomsbury Publishing. p. 151. ISBN 978-1-4411-7413-0.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[note 1]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]