Addition

Original article: wikipedia:Addition

For other uses, see Addition (disambiguation).

"Add" redirects here. For other uses, see ADD (disambiguation).

3 + 2 = 5, 교과서에 자주 등장하는 사과

덧셈(Addition) (보통 더하기 기호(plus symbol) +를 의미함)은 산술(Arithmetic)의 네 가지 기본 연산(operations) 중에 하나이며, 다른 세 개는 뺄셈(subtraction), 곱셈(multiplication) 및 나눗셈(division)입니다. 두 자연수(whole numbers)의 덧셈은 결합된 그들 값의 총량 또는 합(sum)을 초래합니다. 인접한 그림에서 예제는 3개의 사과와 2개의 사과가 합해져서, 총 5개의 사과가 만드는 것을 보여줍니다. 이 관찰은 수학적 표현(mathematical expression) "3 + 2 = 5"와 동등합니다 (즉 "3 더하기 2 는 5와 같습니다(equal)").

항목을 세는 것 외에도, 덧셈은 역시, 정수(integer), 실수(real number) 및 복소수(complex number)와 같은, 대신 숫자(number)라고 불리는 추상화를 사용하여, 구체적인 대상을 참조하는 것없이 정의되고 실행될 수 있습니다. 덧셈은 수학의 한 가지, 산술(arithmetic)에 속합니다. 수학의 또 다른 분야, 대수학(algebra)에서, 덧셈은 벡터(vectors), 행렬(matrices), 부분공간(subspaces) 및 부분-그룹(subgroups)과 같은 추상적 대상에 역시 수행될 수 있습니다.

덧셈은 여러 중요한 속성을 가집니다. 연산의 순서가 문제가 되지 않는 것을 의미하는 교환적(commutative)이고, 둘 이상의 숫자를 더할 때, 덧셈이 수행되어진 순서가 문제가 되지 않은 것을 의미하는 결합적(associative)입니다 (합계(summation)를 참조하십시오). 반복되는 1의 덧셈은 세는 것(counting)과 같습니다; 0의 덧셈은 숫자를 변경하지 않습니다. 덧셈은 역시 뺄셈(subtraction)과 곱셈(multiplication)과 같은 관련된 연산과 관련되는 예측-가능한 규칙을 따릅니다.

덧셈을 수행하는 것은 가장 간단한 수치적 임무 중 하나입니다. 매우 작은 숫자의 덧셈은 유아가 접근할 수 있습니다; 가장 기본적인 과제, 1 + 1은 5개월이 지난 영아, 및 심지어 다른 동물 종의 일부 구성원에 의해 수행될 수 있습니다. 초등 교육(primary education)에서, 학생들은 십진(decimal) 시스템에서 숫자를 더하는 법을 배우며, 단일 자릿수로 시작하고 점차 더 어려운 문제를 해결합니다. 기계 보조 장치는 고대 주판(abacus)에서 현대 컴퓨터(computer)에 이르기까지 다양하며, 여기서 덧셈의 가장 효율적인 구현 방법에 대한 연구가 현재까지 계속 진행되고 있습니다.

Notation and terminology

더하기 부호

덧셈은 항 사이에 더하기 부호(plus sign) "+"를 사용하여 쓰입니다; 즉, 중위 표기법(infix notation)에서 표시됩니다. 그 결과는 등호 기호(equals sign)와 함께 표시됩니다. 예를 들어,

$1+1=2$ ("one plus one equals two")

$2+2=4$ ("two plus two equals four")

$1+2=3$ ("one plus two equals three")

$5+4+2=11$ (see "associativity" below)

$3+3+3+3=12$ (see "multiplication" below)

Columnar addition – 더하려는 숫자들을 열에 쓰고, 합계는 밑줄 아래에 숫자로 씁니다.

비록 덧셈 기호가 나타나지 않을지라도, 역시 덧셈으로 "이해"되는 상황이 있습니다:

• 분수(fraction)에 의해 즉시 뒤따른 자연수는, 혼합 수(mixed number)로 불리는, 그 둘의 합을 나타냅니다. 예를 들어,
        3½ = 3 + ½ = 3.5.
  이 표기법은 혼동을 일으킬 수 있는데, 왜냐하면 대부분의 다른 문맥에서, 병치(juxtaposition)는 대신 곱셈(multiplication)을 나타내기 때문입니다.

관련된 숫자의 급수(series)의 합은 대문자 시그마 표기법(capital sigma notation)을 통해 표현될 수 있으며, 이것은 간결하게 반복(iteration)을 나타냅니다. 예를 들어,

$\sum _{k=1}^{5}k^{2}=1^{2}+2^{2}+3^{2}+4^{2}+5^{2}=55.$

일반적인 덧셈에서 더해지는 숫자 또는 대상은, 항(terms), 더해지는 수(addends) 또는 합해지는 수(summands)로 총칭해서 참조됩니다; 이 용어는 여러 항의 합계에서 마찬가지입니다. 이것은 곱해지게(multiplied) 되는, 인수(factors)와 확실하게 구별됩니다. 일부 저자는 첫 번째 더해지는 수(addend)를 augend라고 부릅니다. 사실, 르네상스(Renaissance)시대 동안, 많은 저자들은 첫 번째 더해지는 수를 "더해지는 수(addend)"라고 고려하지 않았습니다. 오늘날, 덧셈의 교환 속성(commutative property)에 기인하여, "augend"는 거의 사용되지 않았고, 용어 둘 다는 일반적으로 더해지는 수(addend)라고 불렸습니다.

위의 모든 용어는 라틴어(Latin)에서 유래됩니다. "Addition"와 "add"는 라틴어 동사(verb) addere로부터 유래된 영어(English) 단어이며, 이것은 차례로 Proto-Indo-European root *deh₃-로부터 ad "to"와 dare "to give"의 합성(compound)입니다; 따라서 add는 것은 give to는 것입니다. 동명사적(gerundive) 접미사(suffix) -nd를 사용하면 "addend", "thing to be added"를 초래합니다. 마찬가지로 augere "to increase"로부터, 우리는 "augend", "thing to be increased"를 얻습니다.

Redrawn illustration from The Art of Nombryng, one of the first English arithmetic texts, in the 15th century.

"Sum" 및 "summand"는 라틴어 명사(noun) summa "the highest, the top"과 관련된 동사 summare으로부터 유래됩니다. 이것은 두 양수의 합은 그 둘보다 크기 때문에 뿐만 아니라, 고대 그리스인(ancient Greeks)과 로마인(Romans)에 대해 위로 향해 더하는 것이 공통적이기 때문에 적절하며, 합이 말 그대로 더해지는 수보다 커지게 되도록 아래로 향해 더해지는 현대적인 연습과는 대조적입니다. Addere와 summare는, 비트루비우스(Vitruvius)와 프론티누스(Frontinus)와 같은 초기 로마 작가가 아니라면, 적어도 보에티우스(Boethius)로 되돌아갑니다; 보에티우스는 역시 덧셈 연산에 여러 다른 용어를 사용했습니다. 후기 중세 영어(Middle English) 용어 "adden"과 "adding"은 초서(Chaucer)에 의해 대중화되었습니다.

더하기 기호(plus sign) "+" (유니 코드(Unicode):U+002B; 아스키(ASCII): +)는 라틴어 단어 et의 약어로, "and"를 의미합니다. 그것은 적어도 1489년으로 거슬러 올라가는 수학적 연구에서 나타납니다.

Interpretations

덧셈은 많은 물리적 과정을 모델링하기 위해 사용됩니다. 비록 자연수(natural number)를 더하는 간단한 경우에도, 많은 가능한 해석과 훨씬 더 많은 시각적 표현이 있습니다.

Combining sets

아마도 덧셈의 가장 기본적인 해석은 결합하는 집합에 놓입니다:

• 둘 이상의 서로소 모음이 단일 모음으로 결합될 때, 단일 모음에서 대상의 숫자는 원래 모음에서 대상의 숫자의 합입니다.

이 해석은 애매 모호한 위험없이 시각화하기 쉽습니다. 그것은 역시 고등 수학에서 유용합니다 (그것이 염감을 주는 엄격한 정의에 대해, 아래에 있는 § Natural numbers를 참조하십시오). 어쨌든, 우리가 덧셈의 이 버전을 분수 또는 음수를 포함하는 것으로 확장해야 하는 방법은 분명하지 않습니다.

한 가지 가능한 해결 방법은 파이, 또는 더 나은, 분할된 막대와 같이, 쉽게 나뉠 수 있는 대상의 모음을 고려하는 것입니다. 분할의 모음을 단지 결합하는 대신에, 막대가 끝에서-끝까지 합쳐질 수 있이며, 이것은 덧셈의 또 다른 개념을 묘사하는 것으로: 막대가 아니라 막대의 길이를 더하는 것으로 묘사됩니다.

Extending a length

A number-line visualization of the algebraic addition 2 + 4 = 6. A translation by 2 followed by a translation by 4 is the same as a translation by 6.

A number-line visualization of the unary addition 2 + 4 = 6. A translation by 4 is equivalent to four translations by 1.

덧셈의 두 번째 해석은 초기 길이를 주어진 길이만큼 늘리는 것에서 옵니다:

• 원래 길이가 주어진 양만큼 확장될 때, 최종 길이는 원래 길이와 확장의 길이의 합입니다.

합계 a + b는 a와 b를 결합하는 이항 연산(binary operation)으로 해석될 수 있으며, 대수적 의미에서, 또는 그것은 a에 b만큼 더 많은 단위의 덧셈으로 해석될 수 있습니다. 후자의 해석 아래에서, 합 a + b의 부분은 비대칭 역할을 하고, 연산 a + b는 a에 단항 연산(unary operation) +b를 적용한 것으로 보입니다. a와 b 둘 다를 더해지는 수로 부르는 대신에, 이 경우에서 a를 augend를 부르는 것이 더 적절한데, 왜냐하면 a는 수동적인 역할을 하기 때문입니다. 단항 보기는 뺄셈(subtraction)을 논의할 때 역시 유용한데, 왜냐하면 각 단항 덧셈 연산은 역 단항 뺄셈 연산을 가지기 때문이고, 그 반대도 마찬가지입니다.

Properties

Commutativity

4 + 2 = 2 + 4 with blocks

덧셈은 교환적(commutative)이며, 우리가 합에서 항의 순서를 바꿀 수 있지만, 여전히 같은 결과를 얻음을 의미합니다. 기호적으로, 만약 a와 b가 임의의 두 숫자이면, 다음입니다:

a + b = b + a.

덧셈이 교환적이라는 사실은 "덧셈의 교환 법칙" 또는 "덧셈의 교환 속성"으로 알려져 있습니다. 일부 다른 이항 연산(binary operation)은, 곱셈과 같이, 교환적이지만, 많은 다른 것이, 뺄셈과 나눗셈과 같이 그렇지 않습니다.

Associativity

2 + (1 + 3) = (2 + 1) + 3 with segmented rods

덧셈은 결합적(associative)이며, 이것은 세 개 이상의 숫자가 함께 더해질 때, 연산의 순서(order of operations)는 문제가 되지 않음을 의미합니다.

예제로써, 표현 a + b + c는 (a + b) + c 또는 a + (b + c)를 의미하도록 정의해야 할까요? 주어진 해당 덧셈은 결합적이며, 정의의 선택은 관련이 없습니다. 임의의 세 숫자 a, b, 및 c에 대해, (a + b) + c = a + (b + c)인 것은 참입니다. 예를 들어, (1 + 2) + 3 = 3 + 3 = 6 = 1 + 5 = 1 + (2 + 3)입니다.

덧셈이 다른 연산과 함께 사용될 때, 연산의 순서(order of operations)는 중요하게 됩니다. 연산의 표준 순서에서, 덧셈은 지수(exponentiation), n 제곱근(nth root), 곱셈 및 나눗셈보다 낮은 우선 순위이지만, 뺄셈과 같은 우선 순위가 주어집니다.

Identity element

5 + 0 = 5 with bags of dots

임의의 숫자에 영(zero)을 더할 때, 그 양은 변하지 않습니다; 영은 덧셈에 대해 항등 원소(identity element)이며, 역시 덧셈의 항등원(additive identity)이라고 알려져 있습니다. 기호로는, 임의의 a에 대해,

a + 0 = 0 + a = a.

이 법칙은 628 년에 브라마굽타(Brahmagupta)의 Brahmasphutasiddhanta에서 처음 발견되었지만, 그는 a가 음수, 양수, 또는 0 자체의 여부에 따라, 그것을 세 개의 분리된 법칙으로 썼었고, 그는 대수적 기호가 아닌 단어를 사용했습니다. 나중에 인도의 수학자들(Indian mathematicians)은 그 개념을 새롭게 정립했습니다; 830년 경에, 마하비러(Mahavira)는, 단항 명제 0 + a = a에 해당하는, "영은 그것에 무엇이 더해진 것과 같게 됩니다"라고 썼습니다. 12세기에, 바스카라(Bhaskara)는, 단항 명제 a + 0 = a에 해당하는, "영의 덧셈 또는 뺄셈에서, 그 양, 양수 또는 음수는 같게 유지됩니다"라고 썼습니다.

Successor

정수의 문맥 내에서, 일(one)의 덧셈은 역시 특별한 역할을 합니다: 임의의 정수 a에 대해, 정수 (a + 1)은 a보다 더 큰 최소 정수이며, 역시 a의 다음수(successor)로 알려져 있습니다. 예를 들어, 3은 2의 다음수이고, 7은 6의 다음수입니다. 이런 연속 때문에, a + b의 값은 a의 b번째 다음수로 보일 수 있으며, 반복된 연속 덧셈을 만듭니다. 예를 들어, 6 + 2는 8인데, 왜냐하면 8은 7의 다음수이며, 이것은 6의 다음수이기 때문이며, 8을 6의 2번째 다음수로 만듭니다.

Units

단위(units)와 함께 물리량을 수치적으로 더하기 위해, 그것들은 반드시 공통 단위로 표현되어야 합니다. 예를 들어, 150 밀리리터에 50 밀리리터를 더하는 것은 200 밀리리터를 제공합니다. 어쨌든, 만약 5 피트의 측정이 2 인치만큼 확장되면, 그 합은 60 인치인데, 왜냐하면 62 인치는 5 피트와 동의어이기 때문입니다. 다른 한편으로, 3 미터와 4 제곱미터를 더하는 것은 보통 의미가 없는데, 왜냐하면 그들 단위들은 비교할 수 없기 때문입니다; 이러한 종류의 고려 사항은 차원 해석(dimensional analysis)에서 기본적입니다.

Performing addition

Innate ability

1980년대부터 시작된 수학적 개발에 관한 연구는 습관화(habituation) 현상을 이용했습니다: 유아(infant)들은 예기치 않은 상황에서 더 오래 봅니다. 1992년에 카렌 윈(Karen Wynn)에 의한 스크린 뒤에서 조작된 미키 마우스(Mickey Mouse) 인형을 포함하는 실험에서 5개월된 유아는 1 + 1이 2가 될 것으로 예상하고, 그들은 물리적인 상황이 1 + 1이 1 또는 3임을 암시하는 것으로 보일 때 상대적으로 놀랐습니다. 이 발견은 이후 다른 방법론을 사용하는 다양한 실험실에 의해 확인되었습니다. 1992년의, 18개월에서 35개월 사이의 나이가 많은 유아(toddler)를 대상으로 한 실험은, 상자에서 탁구(ping-pong) 공을 그들에게 회수하는 것을 허용함으로써 모터 제어의 개발을 개척했습니다; 가장 어린 사람은 작은 숫자에 대해 잘 응답했지만, 좀 더 개월 수가 많은 아이는 5까지 합을 계산할 수 있었습니다.

심지어 일부 비인간 동물조차도 덧셈에 대한 제한된 능력을 보여주었으며, 특히 영장류(primate)가 그렇습니다. 1995년에 윈(Wynn)의 1992년 결과를 모방한 실험에서 (인형 대신에 가지(eggplant)를 사용함), 히말라야 원숭이(rhesus macaque)와 면화 타마린(cottontop tamarin) 원숭이는 인간 유아와 비슷하게 행동했습니다. 보다 극적으로, 아라비아 숫자(Arabic numerals) 0에서 4의 의미를 배운 후에, 한 침팬지(chimpanzee)는 더 이상의 훈련없이 두 숫자의 합계를 계산할 수 있었습니다. 보다 최근에는, 아시아 코끼리(Asian elephant)가 기본 산술을 수행할 수 있는 능력을 시연했습니다.

Childhood learning

전형적으로, 어린이들은 먼저 셈(counting)을 숙달합니다. 두 개의 항목과 세 개의 항목이 결합되어야 하는 문제가 주어질 때, 어린이들은 물리적 사물로 상황을 모델링하고, 종종 손가락이나 그림을 이용하고, 그런-다음 전체를 셉니다. 그들은 경험을 쌓아감으로써, "세는-것"의 전략을 배우거나 발견합니다: 이 더하기 삼이 뭐냐는 질문을 하면, 어린이들은 이를 지나 세 번을 셉니다, "삼, 사, 오"를 말하고 (보통 손가락을 접으며), 오에 이릅니다. 이 전략은 거의 보편적으로 보입니다; 어린이들은 동료나 선생님으로부터 쉽게 이것을 습득할 수 있습니다. 대부분 그것을 독립적으로 발견합니다. 더 많은 경험을 통해, 어린이들은 더 큰 수에서 셈으로써 덤셈의 교환성을 개척함으로써 더 빨리 더하는 것을 배우게 되며, 이 경우에서 삼으로 시작하여 "사, 오"로 셉니다. 결국 어린이들은, 경험이나 기계적 암기의 기억을 통해, 특정 덧셈 사실("숫자 연결(number bond)")을 회상하기 시작합니다. 한번 몇 가지 사실들이 기억에 남겨지면, 어린이들은 알려진 사실로부터 알려지지 않은 것을 도출하기 시작합니다. 예를 들어, 육 더하기 칠이 뭐냐는 질문을 받은 어린이는 6 + 6 = 12라는 것을 알고 그런-다음 6 + 7이 하나 더 많은 것, 또는 13이라는 것을 알 수 있습니다. 그러한 파생된 사실은 매우 빨리 발견될 수 있고 대부분의 초등 학생들은 유창하게 더하기 위해 암기된 사실과 파생된 사실의 혼합에 의존합니다.

다른 나라들은 다른 연령대에서 자연수와 산술을 소개하며, 많은 나라들이 유치원에서 덧셈을 가르칩니다. 어쨌든, 전 세계에 걸쳐, 초등학교 1학년이 끝날 때까지는 덧셈 수업이 진행됩니다.

Table

어린이들은 종종 암기를 하기 위해 1에서 10까지의 숫자 쌍의 덧셈 테이블을 증정 받습니다. 이것을 알면, 우리는 임의의 덧셈을 수행할 수 있습니다.

+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9	10
2	2	3	4	5	6	7	8	9	10	11
3	3	4	5	6	7	8	9	10	11	12
4	4	5	6	7	8	9	10	11	12	13
5	5	6	7	8	9	10	11	12	13	14
6	6	7	8	9	10	11	12	13	14	15
7	7	8	9	10	11	12	13	14	15	16
8	8	9	10	11	12	13	14	15	16	17
9	9	10	11	12	13	14	15	16	17	18

Decimal system

십진(decimal) 시스템에서 덧셈에 대한 전제-조건은 100 단일-자릿수 "덧셈 사실"을 유창하게 회상하거나 유도하는 것입니다. 우리는 암기(rote)에 의해 모든 사실을 외울(memorize) 수는 있지만, 패턴-기반 전략은 더 깨달음을 얻고, 대부분의 사람들에게, 더 효율적입니다:

• 교환 속성: 위에서 언급된, 패턴 a + b = b + a을 사용하는 것은 100에서 55로의 "덧셈 사실"의 숫자를 줄입니다.
• 하나 또는 둘 더: 1 또는 2를 더하는 것은 기본적인 임무이고, 세는 것을 통해 또는, 궁극적으로는 직관(intuition)을 통해 수행될 수 있습니다.
• 영: 영은 덧셈의 항등원이기 때문에, 영을 더하는 것은 자명합니다. 그럼에도 불구하고, 산술의 가르침에서, 일부 학생은 항상 더해지는 숫자를 증하가는 과정으로 덧셈을 도입합니다; 단어 문제(word problems)는 영의 "제외"를 합리화하는 데 도움이 될 수 있습니다.
• 두 배: 한 숫자를 자신에게 더하는 것은 둘만큼 세는 것과 곱셈(multiplication)과 관련됩니다. 두 배 사실은 많은 관련 사실의 중추를 형성하고, 학생들은 그것들을 상대적으로 이해하기 쉬운 것을 발견합니다.
• 거의-두 배: 6 + 7 = 13와 같은 합은 두 배 사실 6 + 6 = 12에 하나 더 더함으로써, 또는 7 + 7 = 14에 일을 뺌으로써 유도됩니다.
• 오와 십: 형식 5 + x 및 10 + x의 합은 보통 쉽게 기억되고 다른 사실을 유도하는 것에 사용될 수 있습니다. 예를 들어, 6 + 7 = 13는 5 + 7 = 12에 하나 더 더함으로써 유도될 수 있습니다.
• 십 만들기: 고급 전략은 10을 8 또는 9를 포함하는 합에 대한 중간과정으로 사용합니다; 예를 들어, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14.

학생들이 나이가 들면서, 그들은 더 많은 사실을 기억하고, 다른 사실을 빠르고 유창하게 유도하는 법을 배웁니다. 많은 학생들이 모든 사실을 기억하지는 못하지만, 여전히 임의의 기본적인 사실을 빠르게 찾을 수 있습니다.

Carry

Main article: Carry (arithmetic)

여러-자릿수 숫자를 더하는 것에 대한 표준 알고리듬은 더해지는 숫자를 수직으로 정렬하고 오른쪽 열부터 시작하여 열을 더하는 것입니다. 만약 열이 9를 초과하면, 여분의 자릿수가 다음 열로 "올림(carried)"됩니다. 예를 들어, 덧셈 27 + 59

  ¹
  27
+ 59
————
  86

7 + 9 = 16, 그리고 자릿수 1이 올림입니다. 대안적인 전략은 왼쪽의 최고 유효 자릿수부터 더하기 시작합니다; 이 경로는 올림을 다소 다루기 힘들게 만들지만, 합의 대략적인 평가를 구하는 것이 더 빠릅니다. 많은 대안적인 방법이 있습니다.

Decimal fractions

십진 분수(Decimal fractions)는 위의 과정의 간단히 수정에 의해 더해질 수 있습니다. 우리는 같은 위치에서 십진 점을 갖도록 서로 위에 두 개의 집진 분수를 정렬합니다. 만약 필요하면, 우리는 더 긴 십진수와 같은 길이를 만들기 위해 더 짧은 십진수에 후행 0을 더할 수 있습니다. 마지막으로, 우리는, 정확히 십진 점이 합해지는 숫자에서 위치되었던, 그것이 답에서 위치되는 것을 제외하고, 위에서 처럼 같은 덧셈 과정을 수행합니다.

예제로써, 45.1 + 4.34는 다음처럼 해결될 수 있습니다:

   4 5 . 1 0
+  0 4 . 3 4
————————————
   4 9 . 4 4

Scientific notation

Main article: Scientific notation § Basic operations

과학적 표기법(scientific notation)에서, 숫자는 형식 $x=a\times 10^{b}$에서 쓰이고, 여기서 $a$는 유효숫자이고 $10^{b}$는 지수 부분입니다. 덧셈은 두 유효숫자가 단순히 더해질 수 있도록, 과학적 표기법에서 같은 지수 부분을 사용하여 표현되는 것을 요구합니다.

예를 들어:

$2.34\times 10^{-5}+5.67\times 10^{-6}=2.34\times 10^{-5}+0.567\times 10^{-5}=2.907\times 10^{-5}$

Non-decimal

Main article: Binary addition

다른 밑수에서 덧셈은 십진 덧셈과 매우 유사합니다. 예를 들어, 우리는 이진에서 덧셈을 고려할 수 있습니다. 두 개의 단일-자릿수 이진수를 더하는 것은 올림의 형식을 사용하여 비교적 간단합니다:

0 + 0 → 0

0 + 1 → 1

1 + 0 → 1

1 + 1 → 0, 올림 1 (왜냐하면 1 + 1 = 2 = 0 + (1 × 2¹))

두 "1" 자릿수를 더하는 것은 자릿수 "0"을 생성하지만, 1은 반드시 다음 열에 더해져야 합니다. 이것은 특정 단일-자릿수 숫자가 함께 더해질 때 십진수에서 일어나는 것과 유사합니다; 만약 그 결과가 밑수 (10)의 값보다 같거나 초과하면, 왼쪽의 자릿수가 증가됩니다:

5 + 5 → 0, carry 1 (since 5 + 5 = 10 = 0 + (1 × 10¹))

7 + 9 → 6, carry 1 (since 7 + 9 = 16 = 6 + (1 × 10¹))

이것은 올림(carrying)으로 알려져 있습니다. 덧셈의 결과가 자릿수의 값을 초과할 때, 그 절차는 밑수로 나눈 초과 량 (즉, 10/10)을 왼쪽으로 "올리는 것"이고, 그것을 다음 위치 값에 더하는 것입니다. 이것은 다음 위치가 밑수와 같은 인수만큼 더 높은 가중치를 갖기 때문에 정확합니다. 올림은 이진에서 같은 방법으로 작동합니다:

  1 1 1 1 1    (올려진 자릿수)
    0 1 1 0 1
+   1 0 1 1 1
—————————————
  1 0 0 1 0 0 = 36

이 예제에서, 두 숫자 시스템은 함께 더해질 것입니다: 01101₂ (13₁₀) 및 10111₂ (23₁₀). 꼭대기 행은 사용된 올림 비트를 보입니다. 맨 오른쪽 열에서 시작하여, 1 + 1 = 10₂입니다. 1은 왼쪽에 올려지고, 0은 맨 오른쪽 열의 맨 아래에 쓰입니다. 오른쪽에서 두 번째 열이 더합니다: 다시 1 + 0 + 1 = 10₂입니다; 1이 올려지고, 0이 맨 아래에 쓰입니다. 세 번째 열: 1 + 1 + 1 = 11₂입니다. 이번에는, 1이 올려지고, 1이 맨 아래 행에 쓰입니다. 이렇게 진행하면 이것은 최종 답 100100₂ (36₁₀)을 제공합니다.

Computers

Addition with an op-amp. See Summing amplifier for details.

아날로그 컴퓨터(Analog computer)는 물리량으로 직접 작동하므로, 그것들의 덧셈 메커니즘은 덧셈의 형식에 따라 다릅니다. 기계적 덧셈장치는 두 개의 피합수를 슬라이딩 블록의 위치로 나타낼 수 있으며, 이 경우에서 그것들은 평균화(averaging) 레버(lever)로 더해질 수 있습니다. 만약 피합수가 두 샤프트(shafts)의 회전 속력이면, 그것들은 차동(differential)으로 더해질 수 있습니다. 수압 덧셈장치는 피스톤(piston)의 어셈블리에 대한 힘의 균형을 조정하기 위해 뉴턴의 두 번째 법칙(Newton's second law)을 활용함으로써 두 챔버의 압력(pressure)을 더할 수 있습니다. 일반적인-목적 아날로그 컴퓨터에 대해 가장 공통적인 상황은 (접지(ground)를 기준으로) 두 전압(voltage)을 더하는 것입니다; 이것은 대략 저항(resistor) 네트워크(network)와 함께 수행될 수 있지만, 더 나은 설계는 연산 증폭기(operational amplifier)를 활용합니다.

덧셈은 역시 디지털 컴퓨터(digital computers)의 작동에 기본적이며, 여기서 덧셈의 효율성은, 특히 올림(carry) 메커니즘에서, 전체 성능에 중요한 제한입니다.

Part of Charles Babbage's Difference Engine including the addition and carry mechanisms

주판(abacus)은, 역시 셈 프레임이라고 불리며, 쓰는 현대 숫자 시스템을 채택하기 수세기 전에 사용했었된 계산 도구이며, 아시아(Asia), 아프리카(Africa) 및 기타 지역에서 상인, 무역업자 및 점원에 의해 여전히 널리 사용되고 있습니다; 그것은 수메르(Sumer)에서 사용되었을 때, 적어도 기원전 2700–2300년으로 거슬러 올라갑니다.

블레즈 파스칼(Blaise Pascal)은 1642년에 기계식 계산기를 발명했습니다; 그것은 최초의 연산의 덧셈하는 기계(adding machine)였습니다. 그것은 중력-보조 올림 메커니즘을 사용했습니다. 그것은 17세기에서 유일하게 연산의 기계식 계산기였었고 최초의 자동, 디지털 컴퓨터였습니다. 파스칼의 계산기(Pascal's calculator)는 그것의 올림 메커니즘에 의해 제한되었으며, 이것은 그 바퀴를 오직 한 방향으로 회전하도록 강제해서 더할 수 있었습니다. 빼기 위해, 연산자는 파스칼의 계산기의 여(Pascal's calculator's complement)를 사용해야 했으며, 이것은 덧셈만큼 많은 단계를 요구했습니다. 조반니 뽈레니(Giovanni Poleni)는 파스칼에 뒤이어, 1709년에 두 번째 기능적인 기계식 계산기를 만들었으며, 나무로 만든 계산하는 시계는, 일단 설정하면, 자동으로 두 숫자를 곱할 수 있습니다.

"Full adder" logic circuit that adds two binary digits, A and B, along with a carry input C_in, producing the sum bit, S, and a carry output, C_out.

덧셈장치(Adders)는, 보통 이진 산술(binary arithmetic)을 사용하여, 전자 디지털 컴퓨터에서 정수 덧셈을 실행합니다. 가장 간단한 아키텍처는 표준 여러-자릿수 알고리듬을 따르는 물결 올림 덧셈장치입니다. 약간의 개선은, 다시 인간의 직관을 따르는, 올림 건너뜀(carry skip) 디자인입니다; 우리는 999 + 1을 계산할 때 모든 올림을 수행하지 않지만, 우리는 9들의 그룹을 우회하고 답으로 건너뜁니다.

실제에서, 계산적 덧셈은 아래 유사코드에 표시된 것처럼 비트시프트 연산을 갖는 논리곱에서 XOR 및 AND 비트 논리 연산을 통해 달성될 수 있습니다. XOR 및 AND 게이트 둘 다는 완전한 덧셈장치(full adder) 회로의 구현을 허용하는 디지털 논리에서 구현하는 것이 쉬우며 이것은 차례로 더 복잡한 논리 연산으로 결합될 수 있습니다. 현대 디지털 컴퓨터에서, 정수 덧셈은 전형적으로 가장 빠른 산술 명령어이지만, 여전히 그것은 성능에 가장 큰 영향을 미치는데, 왜냐하면 그것은 메모리(memory) 접근 동안 주소(address) 생성과 분기(branching) 동안 명령어(instructions) 가져오기와 같은 기본 임무뿐만 아니라 모든 부동-점(floating-point) 연산의 기초가 되기 때문입니다. 속도를 높이기 위해, 현대적인 디자인은 자릿수를 병렬(parallel)로 계산합니다; 이들 계획은 올림 선택, 올림 예측(carry lookahead), 및 링(Ling) 유사-올림과 같은 이름으로 사용됩니다. 많은 구현은, 사실, 이들 마지막 세 가지 디자인의 잡종입니다. 종이에서 덧셈과 달리, 컴퓨터에서 덧셈은 종종 피함수를 변경합니다. 고대 주판(abacus)과 덧셈하는 보드에서, 두 피합수는 모두 파괴되며, 오직 합을 남깁니다. 수학적 사고에 대한 주판의 영향은 초기 라틴어(Latin) 교과서는 종종 "숫자에 숫자"를 더하는 과정에서, 두 숫자가 모두 사라진다고 주장할 정도로 충분히 강력했습니다. 현대에서, 마이크로프로세서(microprocessor)의 ADD 명령어는 종종 첫 번째 피합수를 합으로 대체하지만 두 번째 피합수는 보존합니다. 높은-수준 프로그래밍 언어에서, a + b를 평가하는 것은 a 또는 b를 변경하지 않습니다; 만약 목적지가 a를 합으로 대체하는 것이면, 이것은 전형적으로 문장 a = a + b으로 명시적으로 요청되어야 합니다. C 또는 C++와 같은 일부 언어는 이것을 a += b로 축약되는 것을 허용합니다.

// Iterative Algorithm
int add(int x, int y){
    int carry = 0;
    while (y != 0){      
       carry = AND(x, y);   // Logical AND
       x     = XOR(x, y);   // Logical XOR
       y     = carry << 1;  // left bitshift carry by one
   }
   return x; 
}
// Recursive Algorithm
int add(int x, int y){
   return x if (y == 0) else add(XOR(x, y) , AND(x, y) << 1);
}

컴퓨터에서, 만약 덧셈의 결과가 저장하기에 너무 크면, 산술 오버플로(arithmetic overflow)가 발생하며, 오답을 결과로 초래합니다. 예상치 못한 산술 오버플로는 프로그램 오류(program errors)의 공통적인 원인입니다. 그러한 오버플로 버그는 발견하고 진단하는 것이 어려울 수 있는데 왜냐하면 그것들은 검증 테스트에서 사용하기 어려운 오직 매우 큰 입력 데이터 집합에 대해 나타날 수 있기 때문입니다. 년도 2000 문제(Year 2000 problem)는 수년간 2-자릿수 형식을 사용에 기인하여 오버플로 오류가 발생한 일련의 버그였습니다.

Addition of numbers

덧셈의 보통 속성을 입증하기 위해, 우리는 먼저 질문에서 그 문맥에 대한 덧셈을 정의해야 합니다. 덧셈은 먼저 자연수(natural number)에서 정의됩니다. 집합 이론(set theory)에서, 덧셈은 그런-다음 자연수를 포함하는 더 큰 집합: 정수(integer), 유리수(rational number), 및 실수(real number)로 점진적으로 확장됩니다. (수학 교육(mathematics education)에서, 양의 분수는 음수가 고려되기 전에 더합니다; 이것은 역시 역사적인 경로입니다.)

Natural numbers

Further information: Natural number

두 자연수 a와 b의 합을 정의하기 위한 두 가지 인기있는 방법이 있습니다. 만약 우리가 자연수를 유한 집합의 카디널리티(cardinalities)로 정의하면, (집합의 카디널리티는 집합에서 원소의 개수입니다), 그것은 다음처럼 그들의 합를 정의하는 것이 적절합니다:

• N(S)를 집합 S의 카디널리티로 놓습니다. N(A) = a 및 N(B) = b를 갖는, 두 서로소 집합 A와 B를 취하십시오. 그런-다음 a + b는 $N(A\cup B)$로 정의됩니다.

여기서, A ∪ B는 A와 B의 합집합(union0입니다. 이 정의의 대안적인 버전은 A와 B를 가 겹칠 수 있는 가능성을 허용하고 그런-다음 그들의 서로소 합집합(disjoint union), 공통 원소를 분리하고 따라서 두 번 세는 것을 허용하는 메커니즘을 취합니다.

다른 인기있는 정의는 재귀적입니다:

• n⁺를 n의 다음수(successor), 즉, 자연수에서 n을 뒤따르는 숫자로 놓습니다. 따라서 0⁺=1, 1⁺=2입니다. a + 0 = a를 정의하십시오. 일반적인 합을 재귀적으로 a + (b⁺) = (a + b)⁺로 정의하십시오. 그러므로 1 + 1 = 1 + 0⁺ = (1 + 0)⁺ = 1⁺ = 2입니다.

다시 한번, 문헌에서 이 정의에 대한 약간의 변형이 있습니다. 말 그대로, 위의 정의는 부분적으로 순서화된 집합(partially ordered set) N²에 대한 재귀 정리(recursion theorem)의 적용입니다. 다른 한편으로, 일부 출처는 자연수 집합에 오직 적용되는 제한된 재귀 정리를 사용하는 것을 선호합니다. 우리는 그런-다음 a를 일시적으로 "고정된" 것으로 고려하고, b에 대한 재귀를 함수 "a +"를 정의하기 위해 적용하고, 모든 a에 대해 함께 이들 단항 연산을 완전한 이항 연산을 형성하기 위해 붙여 넣습니다.

덧셈의 이 재귀 공식화는 데데킨트에 의해 빠르면 1854년에 개발되었었고, 그는 그것을 그 후 수십년 동안 확장했을 것입니다. 그는 수학적 귀납법(mathematical induction)을 통해, 다른 것들 중에서, 결합적 및 교환적 속성을 입증했습니다.

Integers

Further information: Integer

정수의 가장 간단한 개념은 그것이 절댓값(absolute value) (이것이 자연수입니다) 및 부호(sign) (일반적으로 양(positive) 또는 음(negative))로 구성된다는 것입니다. 정수 영은 양도 아니고 음도 아닌 특별한 세 번째 경우입니다. 덧셈의 해당하는 정의는 다음과 같은 경우에 따라 진행되어야 합니다:

• 정수 n에 대해, |n|을 그것의 절댓값으로 놓습니다. a와 b를 정수로 놓습니다. 만약 a 또는 b가 영이면, 그것을 항등원으로 처리합니다. 만약 a와 b가 둘 다 음수이면, a + b = −(|a| + |b|)를 정의합니다. 만약 a와 b가 다른 부호를 가지면, a + b를 그것의 절댓값이 더 큰 항의 부호와 함께, |a|와 |b| 사이의 차이로 정의합니다. 한 예제로써, −6 + 4 = −2입니다; 왜냐하면 −6과 4는 다른 부호를 가지기 때문이며, 그들의 절댓값은 빼지게 되고 음의 항의 절댓값이 더 크므로, 그 답은 음수입니다.

비록 이 정의가 구체적인 문제에 유용할 수 있지만, 고려해야 할 경우의 숫자가 불필요하게 증명을 복잡하게 합니다. 따라서 다음 방법이 정수를 정의하는 데 공통적으로 사용됩니다. 그것은 모든 각 정수가 두 개의 자연 정수의 차이이고 두 그러한 차이, a – b와 c – d가 같은 것과 a + d = b + c인 것은 필요충분 조건이라는 말을 기반으로 합니다. 따라서, 우리는 동치 관계(equivalence relation) 아래에서 자연수의 순서 쌍(ordered pair)의 동치 클래스(equivalence class)로 정수를 공식적으로 정의할 수 있습니다:

(a, b) ~ (c, d) if and only if a + d = b + c.

(a, b)의 동치 클래스는 a ≥ b이면 (a – b, 0), 또는 그렇지 않으면 (0, b – a)를 포함합니다. 만약 n이 자연수이면, 우리는 +n를 (n, 0)의 동치 클래스를, –n에 의해 (0, n)의 동치 클래스를 나타낼 수 있습니다. 이것은 동치 클래스 +n를 갖는 자연수 n을 식별하는 것을 허용합니다.

순서 쌍의 덧셈은 성분-별로 행해집니다:

$(a,b)+(c,d)=(a+c,b+d).$

간단한 계산은 결과의 동치 클래스가 피합수의 동치 클래스에 오직 의존한다는 것이고, 따라서 이것은 등가 클래스, 즉 정수의 덧셈을 정의한다는 것을 보여줍니다. 또 다른 간단한 계산은 이 덧셈이 위의 경우 정의와 같음을 보여줍니다.

정수를 자연수 쌍의 동치 클래스로 정의하는 이 방법은 취소 속성(cancellation property)을 갖는 임의의 교환 반그룹(semigroup)을 그룹(group)에 삽입하기 위해 사용될 수 있습니다. 여기서, 반-그룹은 자연수로 구성되고 그룹은 정수의 덧셈 그룹입니다. 유리수는 곱셈과 함께 비-영 정수를 반그룹으로 취함으로써 유사하게 구성됩니다.

이 구성은 그로텐디크 그룹(Grothendieck group)의 이름 아래에서 임의의 교환 반그룹의 경우로 일반화되어 왔습니다. 취소 속성없이 반그룹에서 그룹으로의 반그룹 준동형(semigroup homomorphism)은 비-단사적일 수 있습니다. 원래, 그로텐디크 그룹이 였었던, 보다 구체적으로, 이 구성의 결과가, 반그룹 연산으로 직접 합(direct sum)을 갖는, 아벨 카테고리(abelian category)의 대상의 동형 아래에서 동치 클래스에 적용되었습니다.

Rational numbers (fractions)

유리수(rational number)의 덧셈은 최소 공통 분모(least common denominator)를 사용하여 계산될 수 있지만, 개념적으로 더 간단한 정의는 오직 정수 덧셈과 곱셈을 포함합니다:

• ${\frac {a}{b}}+{\frac {c}{d}}={\frac {ad+bc}{bd}}$을 정의합니다.

예제로써, 합 ${\frac {3}{4}}+{\frac {1}{8}}={\frac {3\times 8+4\times 1}{4\times 8}}={\frac {24+4}{32}}={\frac {28}{32}}={\frac {7}{8}}$.

분수의 덧셈은 분모(denominator)가 같을 때 훨씬 더 간단합니다; 이 경우에서, 우리는 같은 분모를 남겨둔 채 분자를 단순히 더할 수 있습니다: ${\frac {a}{c}}+{\frac {b}{c}}={\frac {a+b}{c}}$, 따라서 ${\frac {1}{4}}+{\frac {2}{4}}={\frac {1+2}{4}}={\frac {3}{4}}$.

유리수 덧셈의 교환성과 결합성은 정수 산술의 법칙의 쉬운 결과입니다. 보다 엄격하고 일반적인 논의에 대해, 분수의 필드(field of fractions)를 참조하십시오.

Real numbers

Adding π²/6 and e using Dedekind cuts of rationals.

Further information: Construction of the real numbers

실수의 집합의 공통적인 구성은 유리수의 집합의 데데킨트 완비입니다. 실수는 유리수의 데데킨트 자름(Dedekind cut)으로 정의됩니다: 아래쪽으로 닫혀 있고 가장 큰 원소를 가지지 않는 유리수의 비-빈 집합(non-empty set)입니다. 실수 a와 b의 합은 원소별로 정의됩니다:

• $a+b=\{q+r\mid q\in a,r\in b\}$를 정의합니다.

이 정의는 1872년에 리하르트 데데킨트(Richard Dedekind)에 의해, 약간 수정된 형식으로, 처음 출판되었습니다. 실수 덧셈의 교환성 및 결합성은 즉각적입니다; 실수 0을 음의 합리수의 집합으로 정의하면, 그것은 덧셈의 항등원으로 쉽게 보일 수 있습니다. 아마도 덧셈과 관련된 이 구성에서 가장 까다로운 부분은 덧셈 역의 정의입니다.

Adding π²/6 and e using Cauchy sequences of rationals.

안타깝게도, 데데킨트 자름의 곱셈을 처리하는 것은 부호화된 정수의 덧셈과 유사한 시간이-많이-걸리는 경우-별 과정입니다. 또 다른 접근은 유리수의 메트릭 완성입니다. 실수는 본질적으로 유리수의 코시 수열(Cauchy sequence)의 극한: lim a_n으로 정의됩니다. 덧셈은 항별로 정의됩니다:

• $\lim _{n}a_{n}+\lim _{n}b_{n}=\lim _{n}(a_{n}+b_{n})$를 정의합니다.

이 정의는, 비록 그의 공식화가 약간 달랐지만, 역시 1872년에, 게오르크 칸토어(Georg Cantor)에 의해 처음 출판되었습니다. 우리는 이 연산이 잘 정의되어 있으며, 공동-코시 수열을 처리한다는 것을 입증해야 합니다. 일단 이 임무가 행재지면, 실수 덧셈의 모든 속성은 유리수의 속성을 즉시 따릅니다. 게다가, 곱셈을 포함한 다른 산술 연산은 간단하고, 유사한 정의를 가집니다.

Complex numbers

Addition of two complex numbers can be done geometrically by constructing a parallelogram.

복소수는 피함수의 실수 부분과 허수 부분을 더함으로써 더합니다. 즉 말하자면:

$(a+bi)+(c+di)=(a+c)+(b+d)i.$

복소 평면에서 복소수의 시각화를 사용하여, 덧셈은 다음 기하학적 해석을 가집니다: 복소 평면의 점으로 해석되는, 두 복소수 A와 B의 합은 그들 꼭짓점의 셋이 O, A 및 B인 평행사변형(parallelogram)을 구축함으로써 얻어진 점 X입니다. 동등하게, X는 꼭짓점 O, A, B, 및 X, B, A를 갖는 삼각형(triangle)이 합동(congruent)임을 만족하는 점입니다.

Generalizations

실수에 대한 덧셈 연산의 일반화로 보일 수 있는 많은 이항 연산이 있습니다. 추상 대수학(abstract algebra)의 분야는 그러한 일반화된 연산과 중심적으로 관련이 있고, 그것들은 집합 이론(set theory)과 카테고리 이론(category theory)에서 역시 나타납니다.

Abstract algebra

Vectors

Main article: Vector addition

선형 대수(linear algebra)에서, 벡터 공간(vector space)은 임의의 두 벡터(vectors)를 더하는 것을 허용하고 스케일링 벡터를 허용하는 대수적 구조입니다. 친숙한 벡터 공간은 실수의 모든 실수 쌍의 집합입니다; 순서쌍 (a, b)는 유클리드 평면에서 원점으로부터 그 평면에서 점 (a, b)로의 벡터로 해석됩니다. 두 벡터의 합은 개별적인 좌표를 더함으로써 얻습니다:

$(a,b)+(c,d)=(a+c,b+d).$

이 덧셈 연산은 고전 역학(classical mechanics)의 핵심이며, 이것에서 벡터는 힘(force)으로 해석됩니다.

Matrices

Main article: Matrix addition

행렬 덧셈은 같은 차원의 두 행렬에 대해 정의됩니다. 두 ("m by n"으로 발음하는) m × n 행렬 A와 B의 합은, A + B로 표시되며, 해당하는 원소를 더함으로써 계산된 다시 m × n 행렬입니다:

${\begin{aligned}\mathbf {A} +\mathbf {B} &={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{bmatrix}}+{\begin{bmatrix}b_{11}&b_{12}&\cdots &b_{1n}\\b_{21}&b_{22}&\cdots &b_{2n}\\\vdots &\vdots &\ddots &\vdots \\b_{m1}&b_{m2}&\cdots &b_{mn}\\\end{bmatrix}}\\&={\begin{bmatrix}a_{11}+b_{11}&a_{12}+b_{12}&\cdots &a_{1n}+b_{1n}\\a_{21}+b_{21}&a_{22}+b_{22}&\cdots &a_{2n}+b_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}+b_{m1}&a_{m2}+b_{m2}&\cdots &a_{mn}+b_{mn}\\\end{bmatrix}}\\\end{aligned}}$

예를 들어:

${\begin{bmatrix}1&3\\1&0\\1&2\end{bmatrix}}+{\begin{bmatrix}0&0\\7&5\\2&1\end{bmatrix}}={\begin{bmatrix}1+0&3+0\\1+7&0+5\\1+2&2+1\end{bmatrix}}={\begin{bmatrix}1&3\\8&5\\3&3\end{bmatrix}}$

Modular arithmetic

Main article: Modular arithmetic

모듈로 산술(modular arithmetic)에서, 정수 모듈로 12의 집합은 12 원소를 가집니다; 그것은 음악 집합 이론(musical set theory)의 핵심인 정수로부터 덧셈 연산을 상속합니다. 정수 모듈로 2의 집합은 단지 두 원소를 가집니다; 그것을 상속하는 덧셈 연산은 부울 논리(Boolean logic)에서 "배타적 또는(exclusive or)" 함수로 알려져 있습니다. 기하학(geometry)에서, 두 각도 측정(angle measures)의 합은 그들의 합을 실수 모듈로 2π로 종종 취합니다. 이것은 원(circle)에 대한 덧셈 연산에 해당하며, 이것은 차례로 많은-차원 토러스(torus)에 대한 덧셈 연산으로 일반화됩니다.

General theory

추상 대수학의 일반적인 이론은 "덧셈" 연산을 집합에 대한 임의의 결합적(associative) 및 교환적(commutative) 연산이 되도록 허용합니다. 그러한 덧셈 연산을 갖는 기본 대수적 구조(algebraic structure)는 교환적 모노이드(commutative monoid)와 아벨 그룹(abelian group)을 포함합니다.

Set theory and category theory

자연수의 덧셈에 대한 광범위한 일반화는 집합 이론에서 순서-숫자(ordinal number)와 세는-숫자(cardinal number)의 덧셈입니다. 이것들은 초월유한(transfinite)에 자연수의 덧셈의 두 가지 다른 일반화를 제공합니다. 대부분의 덧셈 연산과 달리, 순서-숫자의 덧셈은 교환적이 아닙니다. 세는-숫자의 덧셈은, 어쨌든, 서로소 합집합(disjoint union) 연산과 밀접하게 관련된 교환적 연산입니다.

카테고리 이론(category theory)에서, 서로소 합집합은 공동-곱(coproduct) 연산의 특정 경우로 보이고, 일반적인 공동-곱은 아마도 덧셈의 모든 일반화 중에서 가장 추상적입니다. 직접 합(direct sum) 및 쐐기 합(wedge sum)과 같은 일부 공동-곱은 덧셈과의 연결을 일깨우기 위해 이름이 지어졌습니다.

Related operations

뺄셈, 곱셈 및 나눗셈과 함께, 덧셈은 기본 연산 중 하나로 여겨지고 기본 산술(elementary arithmetic)에서 사용됩니다.

Arithmetic

뺄셈(Subtraction)은 일종의 덧셈–즉 덧셈 역(additive inverse)의 덧셈으로 생각될 수 있습니다. 뺄셈은 자체로 덧셈에 대한 역의 일종이며, 그것에서 x를 더하는 것과 x를 빼는 것은 역 함수(inverse function)입니다.

덧셈 연산을 갖는 집합이 주어지면, 우리는 해당 집합에 대한 대응하는 뺄셈 연산을 항상 정의할 수는 없습니다; 자연수의 집합은 간단한 예제입니다. 다른 한편으로, 뺄셈 연산은 덧셈 연산, 덧셈 역 연산, 및 덧셈 항등원을 고유하게 결정합니다; 이런 이유로, 덧셈 그룹은 뺄셈 아래에서 닫혀 있는 집합으로 설명될 수 있습니다.

곱셈(Multiplication)은 반복된 덧셈(repeated addition)으로 생각될 수 있습니다. 만약 단일 항 x가 합에서 n-번 나타나면, 그 합은 n과 x의 곱입니다. 만약 n이 자연수(natural number)가 아니면, 그 곱은 여전히 의미가 있을 수 있습니다; 예를 들어, −1에 의한 곱셉은 숫자의 덧셈의 역(additive inverse)을 산출합니다.

A circular slide rule

실수와 복소수에서, 덧셈과 곱셈은 지수 함수(exponential function)에 의해 교체될 수 있습니다:

$e^{a+b}=e^{a}e^{b}.$

이 항등식은 로그(logarithm)의 테이블(table)을 찾고 손으로 덧셈을 계산함으로써 곱셈을 수행하는 것을 허용합니다; 그것은 역시 미끄럼 자(slide rule)에서 곱셈을 활성화합니다. 그 공식은 리 그룹(Lie group)의 광범위한 문맥에서 여전히 좋은 일-차 근사이며, 여기에서 그것은 관련된 리 대수(Lie algebra)에서 벡터의 덧셈을 갖는 무한소 그룹 원소의 곱셈과 관련됩니다.

덧셈보다 곱셈의 훨씬 더 많은 일반화가 있습니다. 일반적으로, 곱셈 연산은 항상 덧셈에 걸쳐 분배(distribute)됩니다; 이 요구 사항은 링(ring)의 정의에서 공식화됩니다. 정수와 같은, 일부 문맥에서, 덧셈에 걸쳐 분배성 및 곱셈의 항등원의 존재는 곱셈 연산을 고유하게 결정하기에 충분합니다. 분배 속성은 역시 덧셈에 대한 정보를 제공합니다; 두 가지 방법에서 곱 (1 + 1)(a + b)을 전개함으로써, 우리는 덧셈이 교환적이 되도록 강제됨을 결론을 내릴 수 있습니다. 이러한 이유로, 링 덧셈은 일반적으로 교환적입니다.

나눗셈(Division)은 덧셈과 가장-작은-정도로 관련된 산술 연산입니다. a/b = a(b⁻¹)이므로, 나눗셈은 덧셈에 걸쳐 오른쪽 분배적입니다: (a + b) / c = a/c + b/c. 어쨌든, 나눗셈은 덧셈에 걸쳐 왼쪽 분배적이 아닙니다; 1 / (2 + 2)는 1/2 + 1/2과 같지 않습니다.

Ordering

Log-log plot of x + 1 and max (x, 1) from x = 0.001 to 1000

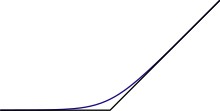
최대 연산 "max (a, b)"는 덧셈과 유사한 이항 연산입니다. 실제로, 만약 두 비-음 숫자 a와 b가 다른 크기의 정도(orders of magnitude)의 것이면, 그 합은 대략적으로 최댓값과 같습니다. 이 근사는 수학의 응용, 예를 들어 테일러 급수(Taylor series)를 자르는 것에서 매우 유용합니다. 어쨌든, 본질적으로 "max"는 역-가능이 아니기 때문에, 수치적 해석(numerical analysis)에서 끊임없는 어려움을 제공합니다. 만약 b가 a보다 훨씬 더 크면, (a + b) − b의 복잡하지 않은 계산은 받아들이기 어려운 반올림 오류(round-off error)가 누적될 수 있으며, 아마도 심지어 영을 반환할 수 있습니다. 역시 유효숫자의 손실(Loss of significance)을 참조하십시오.

근사는 무한 극한의 일종으로 정확하게 됩니다; 만약 a 또는 b가 무한 세는-숫자(cardinal number)이면, 세는-숫자 합은 둘 중 더 큰 것과 정확히 같습니다. 그에 따라서, 무한 세는-숫자에 대해 뺄셈 연산은 없습니다.

최대화는 덧셈과 마찬가지로 교환적이고 결합적입니다. 게다가, 덧셈은 실수의 순서화를 유지하므로, 곱셈이 덧셈에 걸쳐 분배되는 것과 같은 방법으로 덧셈은 "max"에 걸쳐 분배됩니다:

$a+\max(b,c)=\max(a+b,a+c).$

이들 이유로, 비유 기하학(tropical geometry)에서, 우리는 덧셈을 갖는 곱셈을 최대화를 갖는 덧셈으로 대체합니다. 이 문맥에서, 덧셈은 "비유적 곱셈"이라고 불리고, 최대화는 "비유적 덧셈"이라고 불리고, 비유적 "덧셈의 항등원"은 음의 무한대(negative infinity)입니다. 일부 저자는 최소화를 갖는 덧셈을 대체하는 것을 선호합니다; 덧셈의 항등원은 양의 무한대입니다.

이들 관측을 함께 묶으면, 비유적 덧셈은 근사적으로 로그(logarithm)를 통한 규칙적인 덧셈과 관련됩니다:

$\log(a+b)\approx \max(\log a,\log b),$

이것은 로그의 밑수가 증가할수록 더 정확하게 됩니다. 근사는 양자 역학(quantum mechanics)에서 플랑크의 상수(Planck's constant)와 유사하게 이름-지은, 상수 h를 추출하고, h가 영으로 경향일 때 "고전적 극한(classical limit)"을 취함으로써 정확하게 만들어질 수 있습니다:

$\max(a,b)=\lim _{h\to 0}h\log(e^{a/h}+e^{b/h}).$

이 의미에서, 최대 연산은 덧셈의 역-양자화(dequantized) 버전입니다.

Other ways to add

증분은, 역시 다음수(successor) 연산으로 알려져 있으며, 한 숫자에 1의 덧셈입니다.

합계(Summation)는, 보통 단지 둘 이상의, 임의적은 많은 숫자의 덧셈을 설명합니다. 그것은 그 자체인 단일 숫자의 합과 영(zero)인 빈 합(empty sum)의 아이디어를 포함합니다. 무한 합은 급수(series)로 알려진 섬세한 절차입니다.

유한 집합을 세는 것(Counting)은 그 집합에 걸쳐 1을 더하는 것과 동등합니다.

적분(Integration)은 연속체(continuum)에 걸쳐, 또는 보다 정확하고 일반적으로, 미분-가능 매니폴드(differentiable manifold)에 걸쳐 일종의 "합계"입니다. 영-차원 매니폴드에 걸쳐 적분은 합으로 줄어듭니다.

선형 조합(Linear combination)은 곱셈과 합계를 결합합니다; 이것들은 각 항이 배수, 보통 실수(real) 또는 복소수(complex)를 가지는 합입니다. 선형 조합은 복잡하지 않은 덧셈이 게임 이론(game theory)에서 전략(strategies)의 혼합(mixing) 또는 양자 역학(quantum mechanics)에서 상태(states)의 중첩(superposition)과 같이 일부 정규화 규칙을 위반하는 곳에서 특히 유용합니다.

합성곱(Convolution)은 분포 함수(distribution functions)에 의해 정의된 두 독립적인 확률 변수(random variable)를 더하는 것에 사용됩니다. 그것의 보통 정의는 적분, 뺄셈, 및 곱셈을 결합합니다. 일반적으로, 합성곱은 일종의 도메인-측 덧셈으로 유용합니다; 대조적으로, 벡터 덧셈은 일종의 치역-측 덧셈입니다.

See also

• Mental arithmetic
• Parallel addition (mathematics)
• Verbal arithmetic (also known as cryptarithms), puzzles involving addition

Further reading

• Baroody, Arthur; Tiilikainen, Sirpa (2003). The Development of Arithmetic Concepts and Skills. Two perspectives on addition development. Routledge. p. 75. ISBN 0-8058-3155-X.
• Davison, David M.; Landau, Marsha S.; McCracken, Leah; Thompson, Linda (1999). Mathematics: Explorations & Applications (TE ed.). Prentice Hall. ISBN 978-0-13-435817-8.
• Bunt, Lucas N.H.; Jones, Phillip S.; Bedient, Jack D. (1976). The Historical roots of Elementary Mathematics. Prentice-Hall. ISBN 978-0-13-389015-0.
• Poonen, Bjorn (2010). "Addition". Girls' Angle Bulletin. 3 (3–5). ISSN 2151-5743.
• Weaver, J. Fred (1982). "Addition and Subtraction: A Cognitive Perspective". Addition and Subtraction: A Cognitive Perspective. Interpretations of Number Operations and Symbolic Representations of Addition and Subtraction. Taylor & Francis. p. 60. ISBN 0-89859-171-6.