Trigonometric functions

수학(mathematics)에서, 삼각 함수(trigonometric functions) (원형 함수(circular functions), 각도 함수(angle functions) 또는 직각 함수(goniometric functions)로 역시 불림^[1]^[2])는 직각 삼각형(right-angled triangle)의 각도를 두 변 길이의 비율과 관련시키는 실수 함수(real function)입니다. 그것들은 항법(navigation), 고체 역학(solid mechanics), 천체 역학(celestial mechanics), 측지학(geodesy)과 같은 기하학(geometry), 및 많은 다른 분야와 관련된 모든 과학에서 널리 사용됩니다. 그것들은 가장 간단한 주기 함수(periodic function) 중 하나이고, 그와 같이 푸리에 해석(Fourier analysis)을 통해, 주기적인 현상을 연구하는 것에 대해 널리 사용됩니다.

가장 널리 사용되는 삼각 함수는 사인(sine), 코사인(cosine), 및 탄젠트(tangent)입니다. 그들의 역수(reciprocal)는 각각 코시컨트(cosecant), 시컨트(secant), 및 코탄젠트(cotangent)이며, 이것은 현대 수학에서는 덜 사용됩니다.

직각 삼각형과 관련된, 삼각 함수의 가장-오래된 정의는 오직 예리한 각도(acute angle)에서 그들을 정의합니다. 이들 정의를 함수(domain)의 도메인이 전체 투영적으로 확장된 실수 직선(projectively extended real line)인 함수로 확장하는 것에 대해, 우리는 표준 단위 원(unit circle) (반지름(radius) 1 단위를 갖는 원)을 사용하여 기하학적 정의를 사용할 수 있습니다. 현대의 정의는 삼각 함수를 무한 급수(infinite series) 또는 미분 방정식(differential equation)의 해로 표현합니다. 이는 사인과 코사인 함수의 도메인을 전체의 복소 평면(complex plane)으로 확장하고, 다른 삼각 함수의 도메인을 일부 고립된 점이 제거된 것으로부터 복소 평면으로 확장하는 것을 허용합니다.

Right-angled triangle definitions

Plot of the six trigonometric functions and the unit circle for an angle of 0.7 radians

이 섹션에서, 같은 대문자는 삼각형의 꼭짓점과 해당 각도의 측정값을 나타냅니다; 같은 소문자는 삼각형의 변과 그의 길이를 나타냅니다.

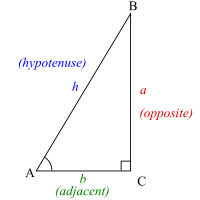
직각 삼각형(right-angled triangle)의 예리한 각도(acute angle) $A$ = $θ$ 가 주어지면, 빗변(hypotenuse) $h$ 는 두 예각을 연결하는 변입니다. $A$ 에 인접한(adjacent) 변 $b$ 는 $θ$ 를 직각에 연결하는 삼각형의 변입니다. 세 번째 변 $a$ 는 $θ$ 에 반대(opposite) 변으로 말합니다.

만약 각도 $θ$ 가 주어지면, 직각 삼각형의 모든 변은 스케일링 인수까지(up to) 잘 정의됩니다. 이것은 임의의 두 변 길이의 비율은 오직 $θ$ 에 의존함을 의미합니다. 이들 여섯 비율은 따라서 $θ$ 의 여섯 함수를 정의하며, 이것은 삼각 함수입니다. 보다 정확하게, 여섯 삼각 함수는 다음입니다:^[3]

사인: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sin \theta= \frac a h = \frac \mathrm{opposite}\mathrm{hypotenuse}}
코사인: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cos \theta= \frac b h = \frac \mathrm{adjacent}\mathrm{hypotenuse}}
탄젠트: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \tan \theta= \frac a b = \frac \mathrm{opposite}\mathrm{adjacent}}
코시컨트: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \csc \theta= \frac h a = \frac \mathrm{hypotenuse}\mathrm{opposite}}
시컨트: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sec \theta= \frac h b = \frac \mathrm{hypotenuse}\mathrm{adjacent}}
코탄젠트: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cot \theta= \frac b a = \frac \mathrm{adjacent}\mathrm{opposite}}

직각 삼각형에서, 두 개의 예리한 각도의 합은 직각, 즉 90° 또는 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\textstyle \frac \pi 2} 라디안(radian)입니다.

삼각 하수 사이의 관계의 요약^[4]
함수	약어	설명	관계(Relationship)
함수	약어	설명	라디안(radian)에서	각도(degree)에서
사인	sin	opposite/hypotenuse	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sin \theta = \cos\left(\frac{\pi}{2} - \theta \right) = \frac{1}{\csc \theta}}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sin x = \cos\left(90^\circ - x \right) = \frac{1}{\csc x}}
코사인	cos	adjacent/hypotenuse	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cos \theta = \sin\left(\frac{\pi}{2} - \theta \right) = \frac{1}{\sec \theta}\,}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cos x = \sin\left(90^\circ - x \right) = \frac{1}{\sec x}\,}
탄젠트	tan (or tg)	opposite/adjacent	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \tan \theta = \frac{\sin \theta}{\cos \theta} = \cot\left(\frac{\pi}{2} - \theta \right) = \frac{1}{\cot \theta} }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \tan x = \frac{\sin x}{\cos x} = \cot\left(90^\circ - x \right) = \frac{1}{\cot x} }
코탄젠트	cot (or cotan or cotg or ctg or ctn)	adjacent/opposite	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cot \theta = \frac{\cos \theta}{\sin \theta} = \tan\left(\frac{\pi}{2} - \theta \right) = \frac{1}{\tan \theta} }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cot x = \frac{\cos x}{\sin x} = \tan\left(90^\circ - x \right) = \frac{1}{\tan x} }
시컨트	sec	hypotenuse/adjacent	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sec \theta = \csc\left(\frac{\pi}{2} - \theta \right) = \frac{1}{\cos \theta} }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sec x = \csc\left(90^\circ - x \right) = \frac{1}{\cos x} }
코시컨트	csc (or cosec)	hypotenuse/opposite	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \csc \theta = \sec\left(\frac{\pi}{2} - \theta \right) = \frac{1}{\sin \theta} }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \csc x = \sec\left(90^\circ - x \right) = \frac{1}{\sin x} }

Radians versus degrees

기하학적 응용에서, 삼각 함수의 인수는 일반적으로 각도(angle)의 측정입니다. 이 목적에 대해, 임의의 각의 단위(angular unit)가 편리하고, 각도는 가장 공통적으로 각도(degrees)로 측정됩니다.

미적분학(calculus)에서 삼각 함수를 사용할 때, 그들 인수는 일반적으로 각도가 아니라, 오히려 실수(real number)입니다. 이 경우에서, 원의 중심을 꼭짓점으로 하는 각도로 경계를-짓는 단위 원(unit circle)의 호(arc)의 길이로 삼각 함수의 인수를 표현하는 것이 더 적합합니다. 그러므로, 우리는 각의 단위로 라디안(radian)을 사용합니다: 일 라디안은 단위 원에서 길이 1의 호를 경계-짓는 각도입니다. 완전한 한 바퀴(turn)는, 따라서, $2 π$ 라디안의 각도입니다.

라디안의 가장-큰 장점은 많은 공식이 그것을 사용할 때 훨씬 더 간단해진다는 것인데, 전형적으로 도함수(derivative)와 적분(integral)과 관련된 모든 공식이 그렇습니다.

이것이, 따라서, 각의 단위가 명시적으로 지정되지 않았을 때, 삼각 함수의 인수는 항상 라디안으로 표시됩니다라는, 일반적인 관례입니다.

Unit-circle definitions

여섯 삼각 함수는 단위 원(unit circle)과 관련된 유클리드 평면(Euclidean plane) 위의 점의 좌표 값(coordinate values)으로 정의될 수 있으며, 단위 원은 이 좌표 시스템의 원점 $O$ 를 중심으로 한 반지름 일의 원(circle)입니다. 직각 삼각형 정의(right-angled triangle definitions)는 $0$ 과 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\textstyle \frac{\pi}{2}} 라디안(radian) $(90°)$ 사이의 각도에 대해 삼각 함수의 정의를 허용하지만, 단위 원 정의는 삼각 함수의 도메인(domain)을 모든 양과 음의 실수로 확장하는 것을 허용합니다.

x-축의 양의 절반의 방향으로부터 반직선(ray)을 각도 $θ$ (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \theta > 0} 에 대해 반-시계-방향(counterclockwise) 및 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \theta < 0} 에 대해 시계-방향)로 회전하면 단위 원과 이 반직선의 교차 점: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \mathrm{A} = (x_\mathrm{A},y_\mathrm{A})} (그림을 참조하십시오), 및, 만약 필요하다면, 반직선을 하나의 직선으로 확장함으로써, 직선 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \text{“}x=1\text{”}:\;\mathrm{B} = (x_\mathrm{B},y_\mathrm{B})} 의 교점, 및 직선 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \text{“}y=1\text{”}:\;\mathrm{C} = (x_\mathrm{C},y_\mathrm{C})} 의 교점을 산출합니다. 이 반직선에 수직인, 점 $A$ 에서 단위 원에 대한 접선은 점 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \mathrm{D} = (0,y_\mathrm{D})} 및 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \mathrm{E} = (x_\mathrm{E},0)} 에서 y- 및 x-축과 교차합니다. 이들 점의 좌표 값은 다음 방법에서 $θ$ 의 임의의 실수 값에 대해 삼각 함수의 모든 존재하는 값을 제공합니다.

삼각 함수 $cos$ 및 $sin$ 은 점 $A$ 의 x- 및 y-좌표 값으로, 각각, 정의됩니다. 즉,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cos \theta = x_\mathrm{A} \quad} 및 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \quad \sin \theta = y_\mathrm{A}.} ^[6]

범위 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle 0 \le \theta \le \pi/2} 에서 이 정의는 빗변(hypotenuse)으로 단위 반지름 $OA$ 를 가지는 직각 삼각형을 취함으로써 직각 삼각형 정의와 일치하고, 단위 원 위의 모든 점 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \mathrm{P} = (x,y)} 에 대해 방정식 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle x^2+y^2=1} 이 유지되므로, 코사인 및 사인의 이 정의는 다음 피타고라스 항등식을 역시 만족시킵니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cos^2\theta+\sin^2\theta=1.}

다른 삼각 함수는 다음으로 단위 원을 따라 찾아질 수 있습니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \tan \theta = y_\mathrm{B} \quad} 및 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \quad\cot \theta = x_\mathrm{C},}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \csc \theta\ = y_\mathrm{D} \quad} 및 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \quad\sec \theta = x_\mathrm{E}.}

피타고라스 항등식 및 기하학적 증명 방법을 적용함으로써, 이들 정의는 사인과 코사인의 관점에서 탄젠트, 코탄젠트, 시컨트 및 코시컨트의 정의를 일치시키는 것을 쉽게 알 수 있습니다. 즉,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \tan \theta =\frac{\sin \theta}{\cos\theta},\quad \cot\theta=\frac{\cos\theta}{\sin\theta},\quad \sec\theta=\frac{1}{\cos\theta},\quad \csc\theta=\frac{1}{\sin\theta}.}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \pm2\pi} 의 각도의 회전은 모양의 위치 또는 크기를 변경하지 않기 때문에, 점 $A$ , $B$ , $C$ , $D$ , 및 $E$ 는 그의 차이가 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle 2\pi} 의 정수배인 두 각도에 대해 같습니다. 따라서 삼각 함수는 주기 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle 2\pi} 를 갖는 주기 함수(periodic function)입니다. 즉, 상등

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sin\theta = \sin\left(\theta + 2 k \pi \right)\quad} 및 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \quad \cos\theta = \cos\left(\theta + 2 k \pi \right)}

은 임의의 각도 $θ$ 와 임의의 정수(integer) $k$ 에 대해 유지됩니다. 같은 것은 네 다른 삼각 함수에 대해 참입니다. 네 사분면에서 함수 사인, 코사인, 코시컨트, 및 시컨트의 부호와 단조성을 관찰하면, $2 π$ 가 그들이 주기적인 것에 대해 가장-작은 값, 즉, $2 π$ 는 이들 함수의 기본 주기(fundamental period)임을 보입니다. 어쨌든, 이미 각도 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \pi} 에 의해 회전 후에 $B$ 와 $C$ 는 탄젠트 함수 및 코탄젠트 함수는 $π$ 의 기본 주기를 가지도록, 그들의 원래 위치로 돌아갑니다. 즉, 상등

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \tan\theta = \tan(\theta + k\pi) \quad} 및 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \quad \cot\theta = \cot(\theta + k\pi)}

은 임의의 각도 $θ$ 와 임의의 정수 $k$ 에 대해 유지됩니다.

Algebraic values

가장 중요한 각도에 대해 대수적 표현(algebraic expression)은 다음입니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sin 0 = \sin 0^\circ \quad= \frac{\sqrt0}2 = 0} (직진 각도)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sin \frac\pi6 = \sin 30^\circ = \frac{\sqrt1}2 = \frac{1}{2}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sin \frac\pi4 = \sin 45^\circ = \frac{\sqrt{2}}{2} = \frac{\sqrt2}2}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sin \frac\pi3 = \sin 60^\circ = \frac{\sqrt{3}}{2} = \frac{\sqrt3}2}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sin \frac\pi2 = \sin 90^\circ = \frac{\sqrt4}2 = 1} (직각)

2의 분모를 갖는, 분자를 연속적인 비-음의 정수의 제곱근으로 쓰면, 값을 기억하기 쉬운 방법을 제공합니다.^[7]

그러한 간단한 표현은 일반적으로 직진 각도의 유리 배수인 다른 각도에 대해 존재하지 않습니다. 각도에서 측정된 3의 배수인 각도에 대해, 사인과 코사인은 제곱근(square root)의 관점에서 표현될 수 있습니다. 실수 제곱근에서 표현된 삼각 상수를 참조하십시오. 사인 및 코사인의 이들 값은 따라서 직선자와 컴퍼스(ruler and compass)에 의해 구성될 수 있습니다.

각도의 정수의 각도에 대해, 사인 및 코사인은 비-실수 복소수(complex number)의 제곱근(square root) 및 세제근(cube root)의 관점에서 표현될 수 있습니다. 갈루아 이론(Galois theory)은, 만약 각도가 3°의 배수가 아니면, 비-실수 세제곱은 불가피함을 입증하는 것을 허용합니다.

각도에서 측정된, 유리수(rational number)인 각도에 대해, 사인 및 코사인은 대수적 숫자(algebraic number)이며, 이것은 $n$ 번째 근의 관점에서 표현될 수 있습니다. 이것은 원분 다항식(cyclotomic polynomial)의 갈루아 그룹(Galois group)이 주기적(cyclic)이라는 사실에서 비롯됩니다.

각도에서 측정된 유리수가 아닌 각도에 대해, 각도 또는 사인과 코사인 둘 다 중에 하나는 초월적 숫자(transcendental number)입니다. 이것이 베이커의 정리(Baker's theorem)의 따름정리이며, 1966년에 입증되었습니다.

Simple algebraic values

다음 테이블은 삼각 함수의 가장-간단한 대수 값을 요약한 것입니다.^[8] 기호 $\infty$ 는 투영적으로 확장된 실수 직선(projectively extended real line) 위에 무한대에서 점(point at infinity)을 표현합니다; 그것은 부호가 없는데, 왜냐하면, 그것이 테이블에서 나타날 때, 인수가 테이블에서 값에 경향이 있을 때, 해당하는 삼각 함수는 한 변에서 $+\infty$ 로 경향이 있고, 나머지 다른 변에서 $-\infty$ 로 경향이 있기 때문입니다.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{array}{|c|ccccccccc|} \hline \begin{matrix}\text{Radian}\\ \text{Degree}\end{matrix} & \begin{matrix}0\\ 0^\circ\end{matrix} & \begin{matrix}\frac{\pi}{12}\\ 15^\circ\end{matrix} & \begin{matrix}\frac{\pi}{8}\\ 22.5^\circ\end{matrix} & \begin{matrix}\frac{\pi}{6}\\ 30^\circ\end{matrix} & \begin{matrix}\frac{\pi}{4}\\ 45^\circ\end{matrix} & \begin{matrix}\frac{\pi}{3}\\ 60^\circ\end{matrix} & \begin{matrix}\frac{3\pi}{8}\\ 67.5^\circ\end{matrix} & \begin{matrix}\frac{5\pi}{12}\\ 75^\circ\end{matrix} & \begin{matrix}\frac{\pi}{2}\\ 90^\circ\end{matrix} \\ \hline \sin & 0 & \frac{ \sqrt{6} - \sqrt{2} } {4} & \frac{ \sqrt{2 - \sqrt{2}} } {2} & \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{2} & \frac{ \sqrt{2 + \sqrt{2}} } {2} & \frac{ \sqrt{6} + \sqrt{2} } {4} & 1 \\ \cos & 1 & \frac{\sqrt{6}+\sqrt{2}}{4} & \frac{ \sqrt{2 + \sqrt{2}} } {2} & \frac{\sqrt{3}}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} & \frac{ \sqrt{2 - \sqrt{2}} } {2} & \frac{ \sqrt{6} - \sqrt{2}} {4} & 0 \\ \tan & 0 & 2-\sqrt{3} & \sqrt{2} - 1 & \frac{\sqrt{3}}{3} & 1 & \sqrt{3} & \sqrt{2} + 1 & 2+\sqrt{3} & \infty \\ \cot & \infty & 2+\sqrt{3} & \sqrt{2} + 1 & \sqrt{3} & 1 & \frac{\sqrt{3}}{3} & \sqrt{2} - 1 & 2-\sqrt{3} & 0 \\ \sec & 1 & \sqrt{6} - \sqrt{2} & \sqrt{2} \sqrt{ 2 - \sqrt{2} } & \frac{2\sqrt{3}}{3} & \sqrt{2} & 2 & \sqrt{2} \sqrt{ 2 + \sqrt{2} } & \sqrt{6}+\sqrt{2} & \infty \\ \csc & \infty & \sqrt{6}+\sqrt{2} & \sqrt{2} \sqrt{ 2 + \sqrt{2} } & 2 & \sqrt{2} & \frac{2\sqrt{3}}{3} & \sqrt{2} \sqrt{ 2 - \sqrt{2} } & \sqrt{6} - \sqrt{2} & 1 \\\hline \end{array} }

In calculus

The sine function (blue) is closely approximated by its Taylor polynomial of degree 7 (pink) for a full cycle centered on the origin.

삼각 함수는 미분-가능(differentiable)입니다. 이것은 위의 기하학적 정의로부터 즉시 분명하지는 않습니다. 게다가, 수학에서 현대 경향은 그 반대라기 보다는 미적분학(calculus)에서 기하학(geometry)을 만드는 것입니다. 그러므로, 초급 수준을 제외하고, 삼각 함수는 미적분법의 방법을 사용하여 정의됩니다.

미적분학 내부의 삼각 함수를 정의하기 위해, 거듭제곱 급수(power series) 또는 미분 방정식(differential equation)을 사용하는 두 가지 동등한 가능성이 있습니다. 이들 정의는 동등한데, 왜냐하면 그 중 하나에서 시작하여, 다른 하나를 속성으로 쉽게 검색할 수 있기 때문입니다. 어쨌든 미분 방정식을 통한 정의는 약간 더 자연스러운데, 왜냐하면, 예를 들어, 거듭제곱 급수의 계수의 선택은 상당히 임의적인 것으로 보일 수 있고, 피타고라스의 항등식(Pythagorean identity)은 미분 방정식에서 추론하는 것이 훨씬 더 쉽기 때문입니다.

Definition by differential equations

사인과 코사인은 다음 방정식을 만족하는 고유한 미분-가능 함수(differentiable function)입니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align} \frac{d}{dx}\sin x&= \cos x,\\ \frac{d}{dx}\cos x&= -\sin x,\\ \sin 0&=0,\\ \cos 0&=1. \end{align} }

이들 방정식을 미분화하면, 우리는 사인과 코사인 둘 다가 다음 미분 방정식(differential equation)의 해임을 알 수 있습니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle y''+y=0.}

코사인에 의한 사인의 몫으로 탄젠트의 정의에 몫 규칙(quotient rule)을 적용하면, 우리는 탄젠트 함수가 다음임을 입증함을 알 수 있습니다.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \frac{d}{dx}\tan x = 1+\tan^2 x.}

Power series expansion

불확정 계수를 갖는 거듭제곱 급수(power series)에 미분 방정식을 적용하면, 우리는 사인과 코사인 함수의 테일러 급수(Taylor series)의 계수에 대한 재귀 관계(recurrence relation)를 추론할 수 있습니다. 이들 재귀 관계는 해결하기 쉽고, 다음 급수 전개를 제공합니다:^[9]

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align} \sin x & = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \\[8pt] & = \sum_{n=0}^\infty \frac{(-1)^n x^{2n+1}}{(2n+1)!} \\[8pt] \cos x & = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots \\[8pt] & = \sum_{n=0}^\infty \frac{(-1)^n x^{2n}}{(2n)!}. \end{align} }

이들 급수의 수렴의 반지름(radius of convergence)은 무한입니다. 그러므로, 사인과 코사인은 전해석 함수(entire function) ("사인" 및 "코사인"이라고도 불림)로 확장될 수 있으며, 이것은 전체 복소 평면(complex plane) 위에 정의되고 정칙(holomorphic)인 (정의에 의해) 복소-값 함수(complex-valued function)입니다.

전해석 함수의 분수로 정의됨으로써, 나머지 삼각 함수는 유리형 함수(meromorphic function), 즉 극점(poles)으로 불리는 일부 고립된 점을 제외하고, 전체 복소 평면에서 정칙인 함수로 확장될 수 있습니다. 여기서, 극점은 탄젠트와 시컨트에 대해 형식 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\textstyle (2k+1)\frac \pi 2} , 또는 코탄젠트와 코시컨트에 대해 형식 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle k\pi} 의 숫자이며, 여기서 $k$ 는 임의의 정수입니다.

재귀 관계는 다른 삼각 함수의 테일러 급수(Taylor series)의 계수에 대해 역시 계산될 수 있습니다. 이들 급수는 유한 수렴의 반지름(radius of convergence)을 가집니다. 그들의 계수는 조합적(combinatorial) 해석을 가집니다: 그들은 유한 집합의 교대하는 순열(alternating permutation)을 열거합니다.^[10]

보다 정확하게, 다음을 정의합니다:

U n

,

n

번째 위/아래 숫자,

B n

,

n

번째 베르누이 숫자, 및

E n

는

n

번째 오일러 숫자,

우리는 다음 급수 전개를 가집니다:^[11]

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align} \tan x & {} = \sum_{n=0}^\infty \frac{U_{2n+1} x^{2n+1}}{(2n+1)!} \\ & {} = \sum_{n=1}^\infty \frac{(-1)^{n-1} 2^{2n} \left(2^{2n}-1\right) B_{2n} x^{2n-1}}{(2n)!} \\ & {} = x + \frac{1}{3}x^3 + \frac{2}{15}x^5 + \frac{17}{315}x^7 + \cdots, \qquad \text{for } |x| < \frac{\pi}{2}. \end{align} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align} \csc x & {} = \sum_{n=0}^\infty \frac{(-1)^{n+1} 2 \left(2^{2n-1}-1\right) B_{2n} x^{2n-1}}{(2n)!} \\ & {} = x^{-1} + \frac{1}{6}x + \frac{7}{360}x^3 + \frac{31}{15120}x^5 + \cdots, \qquad \text{for } 0 < |x| < \pi. \end{align} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align} \sec x & {} = \sum_{n=0}^\infty \frac{U_{2n} x^{2n}}{(2n)!} = \sum_{n=0}^\infty \frac{(-1)^n E_{2n} x^{2n}}{(2n)!} \\ & {} = 1 + \frac{1}{2}x^2 + \frac{5}{24}x^4 + \frac{61}{720}x^6 + \cdots, \qquad \text{for } |x| < \frac{\pi}{2}. \end{align} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align} \cot x & {} = \sum_{n=0}^\infty \frac{(-1)^n 2^{2n} B_{2n} x^{2n-1}}{(2n)!} \\ & {} = x^{-1} - \frac{1}{3}x - \frac{1}{45}x^3 - \frac{2}{945}x^5 - \cdots, \qquad \text{for } 0 < |x| < \pi. \end{align} }

코탄젠트 함수와 역수 함수(reciprocal function)의 극점(pole)이 일치하는 것을 만족하는, 방금 변환된 역수 함수가 합해지는 부분 분수 전개(partial fraction expansion)로 급수 표현이 있습니다:^[12]

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \pi \cot \pi x = \lim_{N\to\infty}\sum_{n=-N}^N \frac{1}{x+n}. }

이 항등식은 헤르글로츠(Herglotz) 속임수로 입증될 수 있습니다.^[13] $n$ 번째 항과 $(- n)$ 번째 항을 결합하면 다음 절대적으로 수렴하는(absolutely convergent) 급수로 이어집니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \pi \cot \pi x = \frac{1}{x} + 2x\sum_{n=1}^\infty \frac{1}{x^2-n^2}\ , \quad \frac{\pi}{\sin \pi x} = \frac{1}{x} + 2x\sum_{n=1}^\infty \frac{(-1)^n}{x^2-n^2}. }

Infinite product expansion

사인에 대해 다음 무한 곱이 복소수 해석학에서 매우 중요합니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sin z=z\displaystyle\prod_{n=1}^\infty \left(1-\frac{z^2}{n^2 \pi^2}\right), \quad z\in\mathbb C.}

이 확장의 증명에 대해, 사인(Sine)을 참조하십시오. 이것으로부터, 그것은 다음임으로 추론될 수 있습니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cos z=\displaystyle\prod_{n=1}^\infty \left(1-\frac{z^2}{\left(n-\frac12\right)^2 \pi^2}\right), \quad z\in\mathbb C.}

Relationship to exponential function (Euler's formula)

오일러의 공식(Euler's formula)은 사인과 코사인을 지수 함수(exponential function)와 관련시킵니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle e^{ix} = \cos x + i\sin x. }

이 공식은 공통적으로 $x$ 의 실수 값에 대해 고려되지만, 그것은 모든 복소수 값에 대해 참을 유지합니다.

증명: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle f_1(x)=\cos x + i\sin x} 및 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle f_2(x)=e^{ix}} 으로 놓습니다. 우리는 $j = 1, 2$ 에 대해 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\textstyle \frac{d}{dx}f_j(x)= if_j(x)} 을 가집니다. 몫 규칙(quotient rule)은 따라서 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\textstyle \frac{d}{dx}\left(\frac{f_1(x)}{f_2(x)}\right)=0} 임을 의미합니다. 그러므로, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\textstyle \frac{f_1(x)}{f_2(x)}} 는 상수 함수이며, 이것은 1과 같은데, 왜냐하면 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle f_1(0)=f_2(0)=1} 이기 때문입니다. 이것은 공식을 입증합니다.

우리는 다음을 가집니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align} e^{ix} &= \cos x + i\sin x\\[5pt] e^{-ix} &= \cos x - i\sin x. \end{align}}

사인과 코사인에서 이 선형 시스템(linear system)을 풀면, 우리는 지수 함수의 관점에서 그들을 표현할 수 있습니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align}\sin x &= \frac{e^{i x} - e^{-i x}}{2i}\\[5pt] \cos x &= \frac{e^{i x} + e^{-i x}}{2}. \end{align}}

$x$ 가 실수일 때, 이것은 다음으로 다시-쓸 수 있을 것입니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cos x = \operatorname{Re}\left(e^{i x}\right), \qquad \sin x = \operatorname{Im}\left(e^{i x}\right).}

대부분 삼각 항등식(trigonometric identities)은 위의 공식에서 사용함으로써 복소 지수 함수의 관점에서 삼각 함수를 표현하고, 그런-다음 결과를 단순화하는 것에 대해 항등식 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle e^{a+b}=e^ae^b} 을 사용함으로써 입증될 수 있습니다.

Definitions using functional equations

우리는 다양한 함수의 방정식(functional equation)을 사용하여 삼각 함수를 역시 정의할 수 있습니다.

예를 들어,^[14] 사인과 코사인은 다음 공식과 조건을 여기서 다음 차이 공식

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cos(x- y) = \cos x\cos y + \sin x\sin y\,}

및 다음 더해지는 조건

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle 0 < x\cos x < \sin x < x\quad\text{ for }\quad 0 < x < 1}

을 만족시키는 연속 함수(continuous function)의 고유한 쌍을 형성합니다.

In the complex plane

복소수(complex number) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle z=x+iy} 의 사인 및 코사인은 다음으로 실수 사인, 코사인, 및 쌍곡선 함수(hyperbolic function)로 표현될 수 있습니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align}\sin z &= \sin x \cosh y + i \cos x \sinh y\\[5pt] \cos z &= \cos x \cosh y - i \sin x \sinh y\end{align}}

도메인 색칠(domain coloring)의 이점을 취함으로써, 복소-값 함수로 삼각 함수를 그래프로 나타낼 수 있습니다. 복소 함수에 고유한 다양한 특색은 그래프에서 보일 수 있습니다; 예를 들어, 사인과 코사인 함수는 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle z} 의 허수 부분이 커짐에 따라 무-경계진 것으로 보일 수 있고 (왜냐하면 흰색이 무한대를 나타내기 때문입니다), 함수가 간단한 영 또는 극(zeros or poles)을 포함한다는 사실은 색조는 각 영 또는 극 주위에서 정확히 한번 순환한다는 사실로부터 명백합니다. 이들 그래프를 해당하는 쌍곡 함수의 그래프와 비교하면 둘 사이의 관계가 강조됩니다.

**Trigonometric functions in the complex plane**

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sin z\, }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cos z\, }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \tan z\, }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cot z\, }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sec z\, }	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \csc z\, }

Basic identities

많은 항등식(identities)은 삼각 함수와 서로 관련됩니다. 이 섹션은 가장 기본적인 것들을 포함합니다; 더 많은 항등식에 대해, 삼각 항등식의 목록(List of trigonometric identities)을 참조하십시오. 이들 동일성은 단위-원 정의 또는 직각 삼각형 정의로부터 기하학적으로 입증될 수 있습니다 (하지만, 후자 정의에 대해, 구간 $[0, π /2]$ 에 있지 않은 각도에 대해 주의를 기울여야 합니다. 삼각 항등식의 증명(Proofs of trigonometric identities)을 참조하십시오). 오직 미적분(calculus)의 도구를 사용하는 비-기하학적 증명에 대해, 우리는 오일러의 항등식의 위의 증명의 그것과 유사한 방법에서, 미분 방정식을 직접 사용할 수 있습니다. 우리는 복소 지수의 관점에서 모든 삼각 함수를 표현하고 지수 함수의 속성을 사용하는 것에 대해 오일러의 항등식을 역시 사용할 수 있습니다.

Parity

코사인과 시컨트는 짝수 함수(even function)입니다; 나머지 다른 삼각 함수는 홀수 함수(odd function)입니다. 즉:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align} \sin(-x) &=-\sin x\\ \cos(-x) &=\cos x\\ \tan(-x) &=-\tan x\\ \cot(-x) &=-\cot x\\ \csc(-x) &=-\csc x\\ \sec(-x) &=\sec x. \end{align}}

Periods

모든 삼각 함수는 주기 $2 π$ 의 주기 함수(periodic function)입니다. 탄젠트와 코탄젠트를 제외하고, 이것은 가장-작은 주기이며, 탄젠트와 코탄젠트는 가장-작은 주기로 $π$ 를 가집니다. 이것은, 모든 각 정수 $k$ 에 대해, 우리가 다음을 가짐을 의미합니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align} \sin (x+2k\pi) &=\sin x\\ \cos (x+2k\pi) &=\cos x\\ \tan (x+k\pi) &=\tan x\\ \cot (x+k\pi) &=\cot x\\ \csc (x+2k\pi) &=\csc x\\ \sec (x+2k\pi) &=\sec x. \end{align}}

Pythagorean identity

피타고라스의 항등식(Pythagorean identity)은 삼각 함수의 관점에서 피타고라스 정리(Pythagorean theorem)의 표현입니다. 그것은 다음입니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \sin^2 x + \cos^2 x = 1 . }

Sum and difference formulas

합과 차이 공식은 각도 자체의 사인, 코사인, 및 탄젠트의 관점에서 두 각도의 합 또는 차이의 사인, 코사인, 및 탄젠트로 확장함을 허용합니다. 이것들은 프톨레마이오스(Ptolemy)의 시대로 확인되는 논증을 이용하여, 기하학적으로 도출될 수 있습니다. 우리는 오일러의 공식(Euler's formula)을 사용하여 대수적으로 그들을 역시 생성할 수 있습니다.

합: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align} \sin\left(x+y\right)&=\sin x \cos y + \cos x \sin y,\\ \cos\left(x+y\right)&=\cos x \cos y - \sin x \sin y,\\ \tan(x + y) &= \frac{\tan x + \tan y}{1 - \tan x\tan y}. \end{align}}
차이: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align} \sin\left(x-y\right)&=\sin x \cos y - \cos x \sin y, \\ \cos\left(x-y\right)&=\cos x \cos y + \sin x \sin y,\\ \tan(x - y) &= \frac{\tan x - \tan y}{1 + \tan x\tan y}. \end{align}}

두 각도가 같을 때, 합 공식은 배-각 공식(double-angle formulae)으로 알려진 더 간단한 방정식으로 줄어듭니다.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align} \sin 2x &= 2 \sin x \cos x = \frac{2\tan x}{1+\tan^2 x}, \\ \cos 2x &= \cos^2 x - \sin^2 x = 2 \cos^2 x - 1 = 1 - 2 \sin^2 x = \frac{1-\tan^2 x}{1+\tan^2 x},\\ \tan 2x &= \frac{2\tan x}{1-\tan^2 x}. \end{align}}

이들 항등식은 곱-을-합 항등식(product-to-sum identities)을 도출하기 위해 사용될 수 있습니다.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \theta=2x} 및 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle t=\tan x} 을 설정함으로써, 이것은 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \theta} 의 모든 삼각 함수를 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\textstyle t=\tan \frac{\theta}{2}} 의 유리 분수(rational fraction)로 표현함을 허용합니다.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{align} \sin \theta &= \frac{2t}{1+t^2}, \\ \cos \theta &= \frac{1-t^2}{1+t^2},\\ \tan \theta &= \frac{2t}{1-t^2}. \end{align}}

다음과 함께

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle d\theta = \frac{2}{1+t^2} \, dt,}

이것은 탄젠트 반-각 치환(tangent half-angle substitution)이며, 삼각 함수의 적분(integral) 및 역도함수(antiderivative)의 계산을 유리 분수의 그것으로 줄임을 허용합니다.

Derivatives and antiderivatives

삼각 함수의 도함수(derivative)는 몫 규칙을 적용함으로써 사인 및 코사인의 그것으로부터 비롯됩니다. 다음 테이블에서 역도함수(antiderivative)에 대해 주어진 값은 그들을 미분함으로써 검증될 수 있습니다. 숫자 $C$ 는 적분화의 상수(constant of integration)입니다.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{array}{|c|c|c|}\hline f(x) & f'(x) & \int f(x)\,dx \\ \hline \sin x & \cos x & -\cos x + C \\ \cos x & -\sin x & \sin x + C \\ \tan x & \sec^2 x = 1+\tan^2 x & -\ln \left( |\cos x|\right ) + C \\ \cot x & -\csc^2 x = -(1+\cot^2 x) & \ln \left (|\sin x|\right ) + C \\ \sec x & \sec x\tan x & \ln \left (|\sec x + \tan x|\right ) + C \\ \csc x & -\csc x \cot x & -\ln \left (|\csc x + \cot x|\right ) + C \\ \hline \end{array} }

Inverse functions

삼각 함수는 주기적이고, 따라서 단사적(injective)이지 않으므로, 엄밀히 말하자면, 그들은 역함수(inverse function)를 가지지 않습니다. 어쨌든, 삼각 함수가 단조적(monotonic)인 각 구간 위에, 우리는 역함수를 정의할 수 있고, 이것은 역 삼각 함수를 다중-값 함수(multivalued function)로 정의합니다. 진정한 역함수를 정의하기 위해, 우리는 함수가 단조적인 구간으로 도메인을 제한해야 하고, 따라서 이 구간에서 함수에 의한 이미지로 전단사(bijective)입니다. 주요 값(principal value)의 집합으로 불리는, 이 간격에 대한 공통 선택은 다음 표에서 제공됩니다. 보통처럼, 역 삼각 함수는 함수의 이름 또는 축약어 앞에 접두사 "arc"와 함께 표시됩니다.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \begin{array}{|c|c|c|c|} \hline \text{Function} & \text{Definition} & \text{Domain} &\text{Set of principal values} \\ \hline y = \arcsin x & \sin y = x & -1 \le x \le 1 & -\frac{\pi}{2} \le y \le \frac{\pi}{2} \\ y = \arccos x & \cos y = x & -1 \le x \le 1 & 0 \le y \le \pi \\ y = \arctan x & \tan y = x & -\infty \le x \le \infty & -\frac{\pi}{2} < y < \frac{\pi}{2} \\ y = \arccot x & \cot y = x & -\infty \le x \le \infty & 0 < y < \pi \\ y = \arcsec x & \sec y = x & x<-1 \text{ or } x>1 & 0 \le y \le \pi,\; y \ne \frac{\pi}{2} \\ y = \arccsc x & \csc y = x & x<-1 \text{ or } x>1 & -\frac{\pi}{2} \le y \le \frac{\pi}{2},\; y \ne 0 \\\hline \end{array} }

표기법 sin^−1, cos^−1, 등등은 종종 arcsin 및 arccos 등등에 사용됩니다. 이 표기법이 사용될 때, 역함수는 곱셈의 역수와 혼동될 수 있습니다. "arc" 접두사를 갖는 표기법은, 비록 아크시컨트에 대해 "arcsec"이 "arcsecond"와 혼동될지라도, 그러한 혼동을 피합니다.

사인 및 코사인과 마찬가지로, 역 삼각 함수는 무한 급수의 관점에서 역시 표현될 수 있습니다. 그들은 복소 로그(complex logarithm)의 관점에서 역시 표현될 수 있습니다. 자세한 것에 대해 역 삼각 함수(Inverse trigonometric functions)를 참조하십시오.

Applications

Angles and sides of a triangle

이 섹션에서, $A, B, C$ 는 삼각형의 세 (내부) 각도를 나타내고, $a, b, c$ 는 각각의 반대 가장자리의 길이를 나타냅니다. 그것들은 다양한 공식에 의해 관련되며, 이것은 그들이 포함한 삼각 함수에 의해 이름-지어집니다.

Law of sines

사인의 법칙(law of sines)은 변 $a$ , $b$ , 및 $c$ 와 그들 변에 반대되는 각 $A$ , $B$ 및 $C$ 를 가진 임의의 삼각형에 대해 다음임을 말합니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c} = \frac{2\Delta}{abc},}

여기서 $Δ$ 는 삼각형의 넓이입니다. 또는, 동등하게,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R,}

여기서 $R$ 은 삼각형의 외접-반지름(circumradius)입니다.

그것은 삼각형을 두 개의 직각 삼각형으로 나누고 위의 사인의 정의를 사용함으로써 입증될 수 있습니다. 사인의 법칙은, 만약 두 각도와 한 변이 알려져 있으면, 삼각형에서 알 수 없는 한 변의 길이를 계산하는 것에 유용합니다. 이것은 삼각분할(triangulation), 두 각도와 접근-가능한 둘러싸인 거리를 측정함으로써 미지수 거리를 결정하는 기법에서 발생하는 공통 상황입니다.

Law of cosines

(코사인 공식 또는 코사인 규칙으로 역시 알려진) 코사인의 법칙(law of cosines)은 피타고라스 정리(Pythagorean theorem)의 확장입니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle c^2=a^2+b^2-2ab\cos C, \, }

또는 동등하게,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cos C=\frac{a^2+b^2-c^2}{2ab}.}

이 공식에서, $C$ 에서 각도는 변 $c$ 의 반대에 있습니다. 이 정리는 삼각형을 두 직각 삼각형으로 나누고 피타고라스 정리(Pythagorean theorem)를 사용함으로써 입증될 수 있습니다.

코사인의 법칙은, 만약 두 변과 그들 사이의 각도가 알려져 있으면, 삼각형의 한 변을 결정하기 위해 사용될 수 있습니다. 그것은, 만약 모든 변의 길이가 알려져 있으면, 각도의 코사인 (및 결과적으로 각도 자체)을 찾기 위해 역시 사용될 수 있습니다.

Law of tangents

다음 모두는 탄젠트의 법칙을 형성합니다:^[15]

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \frac{\tan \frac{A-B}{2 }}{\tan \frac{A+B}{2 } } = \frac{a-b}{a+b}\,; \qquad \frac{\tan \frac{A-C}{2 }}{\tan \frac{A+C}{2 } } = \frac{a-c}{a+c}\,; \qquad \frac{\tan \frac{B-C}{2 }}{\tan \frac{B+C}{2 } } = \frac{b-c}{b+c}.}

단어에서 공식의 표현은 번거로울 수 있지만, 길이와 해당하는 반대 각도에 대해, 합과 차이의 패턴은 정리에서 분명합니다.

Law of cotangents

만약 다음

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \zeta = \sqrt{\frac{1}{s} (s-a)(s-b)(s-c)} ~} (삼각형에 대해 내접된 원의 반지름)

및

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle s = \frac{a+b+c}{2 } ~} (삼각형에 대해 반-둘레),

이면 다음 모두는 코탄젠트의 법칙을 형성합니다:^[15]

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \cot{ \frac{A}{2 }} = \frac{s-a}{\zeta } ~; \qquad \cot{ \frac{B}{2 }} = \frac{s-b}{\zeta } ~; \qquad \cot{ \frac{C}{2 }} = \frac{s-c}{\zeta } ~.}

그것은 다음임을 따릅니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle \frac{\cot \dfrac{A}{2}}{s-a} = \frac{\cot \dfrac{B}{2}}{s-b} = \frac{\cot \dfrac{C}{2}}{s-c} = \frac{1}{\zeta} ~.}

다시 말해 정리는 다음입니다: 반-각의 코탄젠트는 반-둘레에서 말해진 각에 반대 변을 뺀 것과 삼각형에 대해 내접-반지름에 대한 비율과 같습니다.

Periodic functions

삼각 함수는 물리에서 역시 중요합니다. 사인 및 코사인 함수는, 예를 들어, 단순 조화 운동(simple harmonic motion)을 설명하는 것에 사용되며, 이것은 스프링에 부착된 질량의 움직임 및, 작은 각도에 대해 끈에 의해 매달려 있는 질량의 스윙 운동과 같은 많은 자연 현상을 모델링합니다. 사인 및 코사인 함수는 균등 원형 운동(uniform circular motion)의 일-차원 투영입니다.

삼각 함수는 일반적인 주기 함수(periodic function)의 연구에서 유용한 것으로 역시 입증되었습니다. 주기적 함수의 특징적인 파동 패턴은 음파 또는 광파(wave)와 같은 반복하는 현상을 모델링하는 것에 유용합니다.^[16]

약간 일반적인 조건 아래에서, 주기 함수 $f (x)$ 는 푸리에 급수(Fourier series)에서 사인 파 또는 코사인 파의 합으로 표현될 수 있습니다.^[17] 사인 또는 코사인 기본 함수(basis functions)를 $φ k$ 로 나타내면, 주기 함수 $f (t)$ 의 확장은 다음 형식을 취합니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle f(t) = \sum _{k=1}^\infty c_k \varphi_k(t). }

예를 들어, 정사각 파(square wave)는 다음 푸리에 급수(Fourier series)로 쓸 수 있습니다:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:7231/localhost/v1/":): {\displaystyle f_\text{square}(t) = \frac{4}{\pi} \sum_{k=1}^\infty {\sin \big( (2k-1)t \big) \over 2k-1}.}

오른쪽 위에서 네모진 파의 애니메이션에서, 단지 몇 개의 항이 꽤 좋은 근사를 이미 생성함을 볼 수 있습니다. 톱니 파(sawtooth wave)의 확장에서 여러 항의 중첩이 아래에 표시됩니다.

History

삼각법의 초기 연구는 고대로 거슬러 올라갈 수 있지만, 그들이 오늘날 사용되는 것과 같은 삼각 함수는 중세 시대에 개발되었습니다. 현(chord) 함수는 니케아(Nicaea)의 히파르쿠스(Hipparchus) (기원전 180–125) 및 로마 이집트(Roman Egypt)의 프톨레마이오스(Ptolemy) (기원후 90–165)에 의해 발견되었습니다. 사인 및 벌사인(versine) (1 − 코사인)의 함수는, 산스크리트어에서 아랍어로 번역되고 그런-다음 아랍어에서 라틴어로 번역을 통해, 굽타 시대(Gupta period) 인도 천문학(Indian astronomy) (Aryabhatiya, Surya Siddhanta)에서 사용된 jyā 및 koti-jyā 함수로 거슬러 올라갈 수 있습니다.^[18] (아리아바타의 사인 테이블(Aryabhata's sine table)을 참조하십시오.)

현재 사용에서 모든 여섯 삼각 함수는, 삼각형을 푸는 것(solving triangles)에서 사용되는 사인의 법칙(law of sines)과 같이, 9세기까지 이슬람 수학(Islamic mathematics)에서 알려져 있었습니다.^[19] 사인의 예외와 함께 (이것은 인도 수학에서 채택되었습니다), 다른 다섯 현대 삼각 함수는 코사인, 탄젠트, 코탄젠트, 시컨트 및 코시컨트를 포함한 아랍어 수학자에 의해 발견되었습니다.^[19] 알-콰리즈미(Al-Khwārizmī) (c. 780–850)는 사인, 코사인 및 탄젠트의 테이블을 생성했습니다. 830년경, 해바쉬 알-하시 알-마래쥐(Habash al-Hasib al-Marwazi)는 코탄젠트를 발견하고, 탄젠트와 코탄젠트 테이블을 생성했습니다.^[20]^[21] 무하미드 이븐 자비르 알-하라니 알-바타니(Muhammad ibn Jābir al-Harrānī al-Battānī) (853—929)는 시컨트와 코시컨트의 역수 함수를 발견했고, 1°에서 90°까지 각 각도에 대해 코시컨트의 첫 번째 테이블을 만들었습니다.^[21] 삼각 함수는 나중에 오마르 카야얌(Omar Khayyám), 바스카라 II(Bhāskara II), 나시르 알-딘 알-투시(Nasīr al-Dīn al-Tūsī), 잠쉬드 알-캐시(Jamshīd al-Kāshī) (14세기), 울루그 베그(Ulugh Beg) (14세기), 레기오몬타누스(Regiomontanus) (1464), 레티쿠스(Rheticus), 레티쿠스의 학생 발렌티누스 오토(Valentinus Otho)를 포함한 수학자에 의해 연구되었습니다.

산가마그라마의 마드하바(Madhava of Sangamagrama) (c. 1400)는 무한 급수(infinite series)의 관점에서 삼각 함수의 해석학(analysis)에서 초기 연구를 했습니다.^[22] (마드하바 급수(Madhava series) 및 마드하바의 사인 테이블(Madhava's sine table)을 참조하십시오.)

용어 tangent 및 secant는 그의 책 Geometria rotundi (1583)에서 덴마크(Danish) 수학자 토마스 핀키(Thomas Fincke)에 의해 처음으로 도입되었습니다.^[23]

16세기 프랑스 수학자 알버트 지라드(Albert Girard)는 그의 책 Trigonométrie에서 축약어 sin, cos, 및 tan의 첫 번째 출판된 사용을 만들었습니다.^[24]

1682년에 출판된 논문에서, 라이프니츠(Leibniz)는 $sin x$ 가 $x$ 의 대수적 함수(algebraic function)가 아님을 입증했습니다.^[25]

레온하르트 오일러(Leonhard Euler)의 Introductio in analysin infinitorum (1748)는 유럽에서 삼각 함수의 해석적 처리를 설정하고, 역시 이것을 무한 급수로 정의하고 "오일러의 공식(Euler's formula)"을 제시한 것뿐만 아니라, 근-현대 약어 (sin., cos., tang., cot., sec., 및 cosec.)에 대해 대체로 공헌했습니다.^[18]

몇 개의 함수는 역사적으로 공통이었지만, 현재는 드물게 사용하며, 현(chord), 벌사인(versine) (이것은 가장-초기의 테이블에 나타났습니다^[18]), 코벌사인(coversine), 헤벌사인(haversine)^[26], 엑시컨트(exsecant) 및 엑코시컨트(excosecant)가 있습니다. 삼각 항등식의 목록(list of trigonometric identities)은 이들 함수 사이의 관계를 보입니다.

$crd(θ) = 2 sin(θ / 2)$
$versin(θ) = 1 - cos(θ) = 2 sin 2 (θ / 2)$
$coversin(θ) = 1 - sin(θ) = versin(π / 2 - θ)$
$haversin(θ) = 1 / 2 versin(θ) = sin 2 (θ / 2)$
$exsec(θ) = sec(θ) - 1$
$excsc(θ) = exsec(π / 2 - θ) = csc(θ) - 1$

Etymology

단어 사인은 "굽음; 만"을 의미하는 라틴어(Latin) sinus에서 유래하고,^[27] 보다 구체적으로 "토가(toga)의 위쪽 부분의 매달린 겹", "의류의 가슴", 이것은 알-바타니(Al-Battani)와 알-콰리즈미(al-Khwārizmī)에 의해 중세 라틴어(Medieval Latin)로 번역된 12 세기 연구에서 "호주머니" 또는 "겹"을 의미하는 아랍어 단어 jaib로 해석된 것이었던 번역으로 선택되었습니다.^[28] 그 선택은 아랍어로 쓰인 형식 j-y-b (جيب)의 잘못-읽은-것에 기초한 것이며, 그 자체는 산스크리트 jīvā에서 음역(transliteration)으로 비롯되며, 이것은 그의 동의어 jyā (사인에 대해 표준 산스크리트어 용어)와 함께 "시위(bowstring)"로 번역되며, 고대 그리스어(Ancient Greek) χορδή "끈(string)"으로부터 차례로 채택됩니다.^[29]

단어 tangent는 "접촉하는"을 의미하는 라틴어 tangens에서 유래하는데, 왜냐하면 직선이 단위 반지름의 원에 접촉하기 때문이며, 반면에 secant는 라틴어 secans—"자름(cutting)"—에서 유래하는데, 왜냐하면 직선은 원을 원을 자르기 때문입니다.^[30]

("코사인", "코탄젠트", "코시컨트"에서) 접두사 "코-(co-)"는 에드문 군터(Edmund Gunter)의 Canon triangulorum (1620)에서 찾을 수 있으며, 이것은 코사인을 sinus complementi (보완 각도(complementary angle)의 사인)에 대해 약어로 정의하고, 비슷하게 cotangens를 정의하기 위해 나아갑니다.^[31]^[32]

Notes

^ Klein, Christian Felix (1924) [1902]. Elementarmathematik vom höheren Standpunkt aus: Arithmetik, Algebra, Analysis (in German). Vol. 1 (3rd ed.). Berlin: J. Springer.
^ Klein, Christian Felix (2004) [1932]. Elementary Mathematics from an Advanced Standpoint: Arithmetic, Algebra, Analysis. Translated by Hedrick, E. R.; Noble, C. A. (Translation of 3rd German ed.). Dover Publications, Inc. / The Macmillan Company. ISBN 978-0-48643480-3. Archived from the original on 2018-02-15. Retrieved 2017-08-13.
^ Protter & Morrey (1970, pp. APP-2, APP-3)
^ Protter & Morrey (1970, p. APP-7)
^ Heng, Cheng and Talbert, "Additional Mathematics" Archived 2015-03-20 at the Wayback Machine, page 228
^ Bityutskov, V.I. (2011-02-07). "Trigonometric Functions". Encyclopedia of Mathematics. Archived from the original on 2017-12-29. Retrieved 2017-12-29.
^ Larson, Ron (2013). Trigonometry (9th ed.). Cengage Learning. p. 153. ISBN 978-1-285-60718-4. Archived from the original on 2018-02-15. Extract of page 153 Archived 2018-02-15 at the Wayback Machine
^ Abramowitz, Milton and Irene A. Stegun, p.74
^ See Ahlfors, pages 43–44.
^ Stanley, Enumerative Combinatorics, Vol I., page 149
^ Abramowitz; Weisstein.
^ Aigner, Martin; Ziegler, Günter M. (2000). Proofs from THE BOOK (Second ed.). Springer-Verlag. p. 149. ISBN 978-3-642-00855-9. Archived from the original on 2014-03-08.
^ Remmert, Reinhold (1991). Theory of complex functions. Springer. p. 327. ISBN 978-0-387-97195-7. Archived from the original on 2015-03-20. Extract of page 327 Archived 2015-03-20 at the Wayback Machine
^ Kannappan, Palaniappan (2009). Functional Equations and Inequalities with Applications. Springer. ISBN 978-0387894911.
^ ^a ^b The Universal Encyclopaedia of Mathematics, Pan Reference Books, 1976, page 529-530. English version George Allen and Unwin, 1964. Translated from the German version Meyers Rechenduden, 1960.
^ Farlow, Stanley J. (1993). Partial differential equations for scientists and engineers (Reprint of Wiley 1982 ed.). Courier Dover Publications. p. 82. ISBN 978-0-486-67620-3. Archived from the original on 2015-03-20.
^ See for example, Folland, Gerald B. (2009). "Convergence and completeness". Fourier Analysis and its Applications (Reprint of Wadsworth & Brooks/Cole 1992 ed.). American Mathematical Society. pp. 77ff. ISBN 978-0-8218-4790-9. Archived from the original on 2015-03-19.
^ ^a ^b ^c Boyer, Carl B. (1991). A History of Mathematics (Second ed.). John Wiley & Sons, Inc. ISBN 0-471-54397-7, p. 210.
^ ^a ^b Gingerich, Owen (1986). "Islamic Astronomy". Scientific American. Vol. 254. p. 74. Archived from the original on 2013-10-19. Retrieved 2010-07-13.
^ Jacques Sesiano, "Islamic mathematics", p. 157, in Selin, Helaine; D'Ambrosio, Ubiratan, eds. (2000). Mathematics Across Cultures: The History of Non-western Mathematics. Springer Science+Business Media. ISBN 978-1-4020-0260-1.
^ ^a ^b "trigonometry". Encyclopedia Britannica.
^ O'Connor, J. J.; Robertson, E. F. "Madhava of Sangamagrama". School of Mathematics and Statistics University of St Andrews, Scotland. Archived from the original on 2006-05-14. Retrieved 2007-09-08.
^ "Fincke biography". Archived from the original on 2017-01-07. Retrieved 2017-03-15.
^ O'Connor, John J.; Robertson, Edmund F., "Trigonometric functions", MacTutor History of Mathematics archive, University of St Andrews.
^ Bourbaki, Nicolás (1994). Elements of the History of Mathematics. Springer.
^ Nielsen (1966, pp. xxiii–xxiv)
^ The anglicized form is first recorded in 1593 in Thomas Fale's Horologiographia, the Art of Dialling.
^
Various sources credit the first use of sinus to either
- Plato Tiburtinus's 1116 translation of the Astronomy of Al-Battani
- Gerard of Cremona's translation of the Algebra of al-Khwārizmī
- Robert of Chester's 1145 translation of the tables of al-Khwārizmī
See Merlet, A Note on the History of the Trigonometric Functions in Ceccarelli (ed.), International Symposium on History of Machines and Mechanisms, Springer, 2004
See Maor (1998), chapter 3, for an earlier etymology crediting Gerard.
See Katx, Victor (July 2008). A history of mathematics (3rd ed.). Boston: Pearson. p. 210 (sidebar). ISBN 978-0321387004.
^ See Plofker, Mathematics in India, Princeton University Press, 2009, p. 257
See "Clark University". Archived from the original on 2008-06-15.
See Maor (1998), chapter 3, regarding the etymology.
^ Oxford English Dictionary
^ Gunter, Edmund (1620). Canon triangulorum.
^ Roegel, Denis, ed. (2010-12-06). "A reconstruction of Gunter's Canon triangulorum (1620)" (Research report). HAL. inria-00543938. Archived from the original on 2017-07-28. Retrieved 2017-07-28.

References

Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
Lars Ahlfors, Complex Analysis: an introduction to the theory of analytic functions of one complex variable, second edition, McGraw-Hill Book Company, New York, 1966.
Boyer, Carl B., A History of Mathematics, John Wiley & Sons, Inc., 2nd edition. (1991). ISBN 0-471-54397-7.
Gal, Shmuel and Bachelis, Boris. An accurate elementary mathematical library for the IEEE floating point standard, ACM Transactions on Mathematical Software (1991).
Joseph, George G., The Crest of the Peacock: Non-European Roots of Mathematics, 2nd ed. Penguin Books, London. (2000). ISBN 0-691-00659-8.
Kantabutra, Vitit, "On hardware for computing exponential and trigonometric functions," IEEE Trans. Computers 45 (3), 328–339 (1996).
Maor, Eli, Trigonometric Delights, Princeton Univ. Press. (1998). Reprint edition (February 25, 2002): ISBN 0-691-09541-8.
Needham, Tristan, "Preface"" to Visual Complex Analysis. Oxford University Press, (1999). ISBN 0-19-853446-9.
Nielsen, Kaj L. (1966), Logarithmic and Trigonometric Tables to Five Places (2nd ed.), New York, USA: Barnes & Noble, LCCN 61-9103
O'Connor, J. J., and E. F. Robertson, "Trigonometric functions", MacTutor History of Mathematics archive. (1996).
O'Connor, J. J., and E. F. Robertson, "Madhava of Sangamagramma", MacTutor History of Mathematics archive. (2000).
Pearce, Ian G., "Madhava of Sangamagramma", MacTutor History of Mathematics archive. (2002).
Protter, Murray H.; Morrey, Charles B., Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, LCCN 76087042{{citation}}: CS1 maint: multiple names: authors list (link)
Weisstein, Eric W., "Tangent" from MathWorld, accessed 21 January 2006.

External links

"Trigonometric functions", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Visionlearning Module on Wave Mathematics
GonioLab Visualization of the unit circle, trigonometric and hyperbolic functions
q-Sine Article about the q-analog of sin at MathWorld
q-Cosine Article about the q-analog of cos at MathWorld

[Klein_1924-1] Klein, Christian Felix (1924) [1902]. Elementarmathematik vom höheren Standpunkt aus: Arithmetik, Algebra, Analysis (in German). Vol. 1 (3rd ed.). Berlin: J. Springer.

[Klein_2004-2] Klein, Christian Felix (2004) [1932]. Elementary Mathematics from an Advanced Standpoint: Arithmetic, Algebra, Analysis. Translated by Hedrick, E. R.; Noble, C. A. (Translation of 3rd German ed.). Dover Publications, Inc. / The Macmillan Company. ISBN 978-0-48643480-3. Archived from the original on 2018-02-15. Retrieved 2017-08-13.

[3] Protter & Morrey (1970, pp. APP-2, APP-3)

[4] Protter & Morrey (1970, p. APP-7)

[Heng-5] Heng, Cheng and Talbert, "Additional Mathematics" Archived 2015-03-20 at the Wayback Machine, page 228

[6] Bityutskov, V.I. (2011-02-07). "Trigonometric Functions". Encyclopedia of Mathematics. Archived from the original on 2017-12-29. Retrieved 2017-12-29.

[Larson_2013-7] Larson, Ron (2013). Trigonometry (9th ed.). Cengage Learning. p. 153. ISBN 978-1-285-60718-4. Archived from the original on 2018-02-15. Extract of page 153 Archived 2018-02-15 at the Wayback Machine

[Abramowitz_and_Stegun-8] Abramowitz, Milton and Irene A. Stegun, p.74

[9] See Ahlfors, pages 43–44.

[10] Stanley, Enumerative Combinatorics, Vol I., page 149

[11] Abramowitz; Weisstein.

[Aigner_2000-12] Aigner, Martin; Ziegler, Günter M. (2000). Proofs from THE BOOK (Second ed.). Springer-Verlag. p. 149. ISBN 978-3-642-00855-9. Archived from the original on 2014-03-08.

[Remmert_1991-13] Remmert, Reinhold (1991). Theory of complex functions. Springer. p. 327. ISBN 978-0-387-97195-7. Archived from the original on 2015-03-20. Extract of page 327 Archived 2015-03-20 at the Wayback Machine

[Kannappan_2009-14] Kannappan, Palaniappan (2009). Functional Equations and Inequalities with Applications. Springer. ISBN 978-0387894911.

[Allen_1976-15] The Universal Encyclopaedia of Mathematics, Pan Reference Books, 1976, page 529-530. English version George Allen and Unwin, 1964. Translated from the German version Meyers Rechenduden, 1960.

[Farlow_1993-16] Farlow, Stanley J. (1993). Partial differential equations for scientists and engineers (Reprint of Wiley 1982 ed.). Courier Dover Publications. p. 82. ISBN 978-0-486-67620-3. Archived from the original on 2015-03-20.

[Folland_1992-17] See for example, Folland, Gerald B. (2009). "Convergence and completeness". Fourier Analysis and its Applications (Reprint of Wadsworth & Brooks/Cole 1992 ed.). American Mathematical Society. pp. 77ff. ISBN 978-0-8218-4790-9. Archived from the original on 2015-03-19.

[Boyer_1991-18] Boyer, Carl B. (1991). A History of Mathematics (Second ed.). John Wiley & Sons, Inc. ISBN 0-471-54397-7, p. 210.

[Gingerich_1986-19] Gingerich, Owen (1986). "Islamic Astronomy". Scientific American. Vol. 254. p. 74. Archived from the original on 2013-10-19. Retrieved 2010-07-13.

[Sesiano-20] Jacques Sesiano, "Islamic mathematics", p. 157, in Selin, Helaine; D'Ambrosio, Ubiratan, eds. (2000). Mathematics Across Cultures: The History of Non-western Mathematics. Springer Science+Business Media. ISBN 978-1-4020-0260-1.

[Britannica-21] "trigonometry". Encyclopedia Britannica.

[mact-biog-22] O'Connor, J. J.; Robertson, E. F. "Madhava of Sangamagrama". School of Mathematics and Statistics University of St Andrews, Scotland. Archived from the original on 2006-05-14. Retrieved 2007-09-08.

[Fincke-23] "Fincke biography". Archived from the original on 2017-01-07. Retrieved 2017-03-15.

[MacTutor-24] O'Connor, John J.; Robertson, Edmund F., "Trigonometric functions", MacTutor History of Mathematics archive, University of St Andrews.

[Bourbaki_1994-25] Bourbaki, Nicolás (1994). Elements of the History of Mathematics. Springer.

[26] Nielsen (1966, pp. xxiii–xxiv)

[27] The anglicized form is first recorded in 1593 in Thomas Fale's Horologiographia, the Art of Dialling.

[28] Various sources credit the first use of sinus to either
Plato Tiburtinus's 1116 translation of the Astronomy of Al-Battani

Gerard of Cremona's translation of the Algebra of al-Khwārizmī

Robert of Chester's 1145 translation of the tables of al-Khwārizmī
See Merlet, A Note on the History of the Trigonometric Functions in Ceccarelli (ed.), International Symposium on History of Machines and Mechanisms, Springer, 2004
See Maor (1998), chapter 3, for an earlier etymology crediting Gerard.
See Katx, Victor (July 2008). A history of mathematics (3rd ed.). Boston: Pearson. p. 210 (sidebar). ISBN 978-0321387004.

[29] Plato Tiburtinus's 1116 translation of the Astronomy of Al-Battani

[30] Gerard of Cremona's translation of the Algebra of al-Khwārizmī

[31] Robert of Chester's 1145 translation of the tables of al-Khwārizmī

[Plofker_2009-29] See Plofker, Mathematics in India, Princeton University Press, 2009, p. 257
See "Clark University". Archived from the original on 2008-06-15.
See Maor (1998), chapter 3, regarding the etymology.

[30] Oxford English Dictionary

[Gunter_1620-31] Gunter, Edmund (1620). Canon triangulorum.

[Roegel_2010-32] Roegel, Denis, ed. (2010-12-06). "A reconstruction of Gunter's Canon triangulorum (1620)" (Research report). HAL. inria-00543938. Archived from the original on 2017-07-28. Retrieved 2017-07-28.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]