Function of a real variable

수학적 해석학(mathematical analysis)에서, 그리고 기하학(geometry), 응용 수학(applied mathematics), 공학(engineering) 및 자연 과학(natural science)의 응용에서, 실수 변수의 함수(real variable of function)는, 그의 도메인(domain)이 실수(real number)인 $ℝ$ , 또는 양의 길이의 구간(interval)을 포함하는 $ℝ$ 의 부분 집합(subset)인, 함수(function)입니다. 고려되고 연구된 대부분의 실수 함수는 일부 구간에서 미분 가능(differentiable)입니다. 가장 널리 고려된 그런 함수는, 실수 변수의 실수-값 함수인, 즉, 그의 도메인(codomain)이 실수의 집합인 실수 변수의 함수인, 실수 함수(real functions)입니다.

그럼에도 불구하고, 실수 변수의 함수의 코도메인은 임의의 집합일 수 있습니다. 어쨌든, 그것은 종종 실제 위에 $ℝ$ -벡터 공간의 구조를 갖는 것으로 종종 가정됩니다. 즉, 코도메인은 유클리드 공간, 좌표 벡터, 주어진 크기의 실수의 행렬(matrices)의 집합, 또는 복소수 또는 사원수:쿼터니언과 같은, $ℝ$ -대수(algebra)일 수 있습니다. 코도메인의 구조 $ℝ$ -벡터 공간은 함수에 $ℝ$ -벡터 공간의 구조를 유도합니다. 만약 코도메인이 $ℝ$ -대수의 구조를 가지면, 같은 것이 함수에 대해서 참입니다.

실수 변수의 함수의 이미지(image)는 코도메인 내의 곡선(curve)입니다. 이런 맥락에서, 곡선을 정의하는 함수는 곡선의 매개 변수적 방정식(parametric equation)이라고 불립니다.

실수 변수의 함수의 코도메인이 유한-차원 벡터 공간(finite-dimensional vector space)이면, 함수는 실수 함수의 수열로써 보일 수 있습니다. 이것은 응용에서 종종 사용됩니다.

Real function

실수 함수는 $\mathbb {R}$ 의 부분집합에서 $\mathbb {R}$ 로의 함수(function)이며, 여기서 $\mathbb {R}$ 은 보통의 실수(real number) 집합을 나타냅니다. 즉, 실수 함수의 도메인(domain)은 부분집합 $\mathbb {R}$ 의 부분집합이고, 그것의 코도메인(codomain)은 $\mathbb {R}$ 입니다. 그것은 일반적으로 도메인은 양수 길이의 구간(interval)을 포함한다고 가정됩니다.

Basic examples

많은 공통적으로 사용되는 실수 함수에 대해, 도메인은 실수의 전체 집합이고, 함수는 도메인의 모든 각 점에서 연속(continuous)이고 미분-가능(differentiable)입니다. 우리는 이들 함수가 정의되고, 모든 곳에서 연속이고 미분 가능하다고 말합니다. 이것은 다음의 경우입니다:

상수 함수(constant function)와 선형 함수(linear functions)를 포함한 모든 다항 함수(polynomial function)
사인(Sine)과 코사인(cosine) 함수
지수 함수(Exponential function)

일부 함수는 모든 곳에서 정의되지만, 일부 점에서 연속이 아닙니다. 예를 들어,

헤비사이드 계단 함수(Heaviside step function)는 모든 곳에서 정의되지만, 영에서 연속이 아닙니다.

일부 함수는 모든 곳에서 정의되고 연속이지만, 모든 곳에서 미분-가능은 아닙니다.

절댓값(absolute value)은 모든 곳에서 연속이지만, 영을 제외한 모든 곳에서 미분-갸능입니다.
세제곱근(cubic root)은 모든 곳에서 정의되고 연속이고, 영을 제외한 모든 곳에서 미분-가능입니다.

많은 공통 함수가 모든 곳에서 정의되지는 않지만, 그것들이 정의된 모든 곳에서 연속이고 미분-가능입니다. 예를 들어:

유리 함수(rational function)는 두 다항 함수의 몫이고, 분모의 영들(zeros)에서 정의되지 않습니다.
탄젠트 함수(tangent function)는 ${\frac {\pi }{2}}+k\pi$ 에 대해 정의되지 않으며, 여기서 $k$ 는 임의의 정수입니다.
로그 함수(logarithm function)는 오직 변수의 양의 값에 대해 정의됩니다.

일부 함수는 그것들의 전체 도메인에서 연속이고, 일부 점에서 미분-가능이 아닙니다. 이것은 다음의 경우입니다:

제곱근(square root)은 오직 변수의 비-음의 값에 대해 정의되고, 영에서 미분-가능이 아닙니다 (그것은 변수의 모든 양의 값에 대해 미분-가능입니다).

General definition

실수 변수의 실수-값 함수는 공통적으로 변수(variable) x로 표시되는 실수(real number)를 입력으로 취하여, 또 다른 실수, 공통적으로 f(x)로 표시되는 함수의 값을 생성하는 함수(function)입니다. 단순화를 위해, 이 기사에서 실수 변수의 실수-값 함수는 단순히 함수라고 합니다. 임의의 모호성을 피하기 위해, 발생할 수 있는 다른 유형의 함수는 명시적으로 지정될 것입니다.

일부 함수는 변수의 모든 실수 값에 대해 정의되지만 (우리는 그것들이 모든 곳에 정의된다고 말합니다), 일부 다른 함수는 오직 변수 값이 함수의 도메인(domain), ℝ의 부분집합 X에서 취해지면 정의되며, 이것은 항상 양수 길이의 구간(interval)을 포함하는 것으로 가정됩니다. 다시 말해서, 실수 변수의 실수-값 함수는 그것의 도메인 X가 양의 길이의 구간을 포함하는 ℝ의 부분집합을 만족하는 다음 함수입니다:

f:X\to \mathbb {R}

.

한 변수에서 간단한 함수의 예제는 다음일 수 있습니다:

f:X\to \mathbb {R}

X=\{x\in \mathbb {R} \,:\,x\geq 0\}

f(x)={\sqrt {x}}

이것은 x의 제곱근(square root)입니다.

Image

함수의 이미지(image) $f(x)$ 는 변수 $x$ 가 $f$ 의 전체 도메인에서 실행될 때 $f$ 의 모든 값의 집합입니다. 연결된 도메인을 갖는 연속 (정의에 대해 아래를 참조) 실수-값 함수에 대해, 이미지는 구간(interval) 또는 단일 값입니다. 후자에 대해, 함수는 [[constant function|상수 함수(constant function)입니다.

주어진 실수 y의 이전-이미지(preimage)는 방정식(equation) y = f(x)의 해집합입니다.

Domain

여러 실수 변수의 함수의 도메인(domain)은 때때로 명시적으로 정의되는 ℝ의 부분집합입니다. 사실, 만약 우리가 함수 f의 도메인 X를 부분집합 Y ⊂ X로 제한하면, 우리는 공식적으로 다른 함수, f를 Y로의 제한을 얻게 되며, 이것은 f_|Y로 표시됩니다. 실제로, f와 f_|Y를 식별하고 아래첨자 _|Y를 생략하는 것은 종종 해롭지 않습니다.

반대로, 예를 들어 연속성(continuity) 또는 해석적 연속(analytic continuation)에 의해 주어진 함수의 도메인을 자연스럽게 확장하는 것이 때때로 가능합니다. 이것은 실제 변수의 함수의 도메인을 명시적으로 정의하는 것은 가치가 없다는 것을 의미합니다.

Algebraic structure

산술 연산은 다음과 같은 방식에서 함수에 적용될 수 있습니다:

모든 각 실수 r에 대해, 상수 함수(constant function) $(x)\mapsto r$ 는 모든 곳에서 정의됩니다.
모든 각 실수 r과 모든 각 함수 f에 대해, 함수 $rf:(x)\mapsto rf(x)$ 는 f와 같은 도메인을 가집니다 (또는 r = 0이면 모든 곳에서 정의됩니다).
만약 f와 g가 X∩Y가 ℝ의 열린 부분집합을 포함함을 만족하는 각각 도메인 X와 Y의 두 함수이면, $f+g:(x)\mapsto f(x)+g(x)$ 와 $f\,g:(x)\mapsto f(x)\,g(x)$ 는 X∩Y를 포함하는 도메인을 가지는 함수입니다.

모든 곳에서 정의되는 n 개의 변수의 함수와 주어진 점의 일부 이웃(neighbourhood)에 정의된 n 개의 변수의 함수는 둘 다 실수 (ℝ-대수)에 걸쳐 교환 대수(commutative algebras)를 형성합니다.

우리는 유사하게 $1/f:(x)\mapsto 1/f(x)$ 를 정의할 수 있으며, 이것은 오직 ℝ의 열린 부분집합을 포함하는 f(x) ≠ 0을 만족하는 f의 도메인에 있는 점 (x)의 집합이면 함수입니다. 이 제약 조건은 위의 두 대수가 필드(fields)가 아님을 의미합니다.

Continuity and limit

19세기 후반까지, 오직 연속 함수(continuous function)가 수학자들에 의해 고려되었습니다. 그 당시, 토폴로지적 공간(topological space)의 형식적 정의와 토폴로지적 공간 사이의 연속 맵(continuous map)보다 훨씬 오래 전에 연속성의 개념은 하나 또는 여러 실수 변수의 함수에 대해 정교화되었습니다. 실수 변수의 연속 함수는 수학에서 어디에나 있으므로, 토폴로지적 공간 사이의 연속 맵의 일반적인 개념을 참조없이 이 개념을 정의할 가치가 있습니다.

연속성을 정의하기 위해, 2개의 실수 변수에 대해 정의된 함수인 ℝ의 거리 함수(distance function)를 고려하는 것이 유용합니다:

d(x,y)=|x-y|

만약, 모든 각 양의 실수 $ε$ 에 대해, $d(x,a)<\varphi$ 를 만족하는 모든 $x$ 에 대해 $|f(x)-f(a)|<\varepsilon$ 를 만족하는 양의 실수 $φ$ 가 존재하면, 함수 f는 그것의 도메인에 대한 내부(interior)인 점 $a$ 에서 연속입니다. 다시 말해서, $φ$ 는 $f(a)$ 를 중심으로 하는 길이 $2 ε$ 의 구간에 포함된 $a$ 를 중심으로 반지름 $φ$ 의 구간의 f만큼 이미지를 갖도록 충분히 작게 선택될 수 있습니다. 함수는 그것의 도메인의 모든 각 점에서 연속이면 연속입니다.

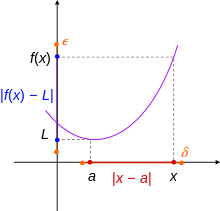
실수 변수의 실수-값 함수의 극한(limit)은 다음과 같습니다.^[1] a를 함수 f의 도메인 X의 토폴로지적 클로저(topological closure)의 한 점으로 놓습니다. 그 함수는, f가 x가 a로 가는 경향일 때 극한 L을 가지며, 다음과 같이 표시되는데,

L=\lim _{x\to a}f(x),

다음 조건이 만족된다는 가정 아래에 있습니다: 모든 각 양의 실수 ε > 0에 대해, 다음을 만족하는

d(x,a)<\delta

도메인에서 모든 x에 대해 다음을 만족하는

|f(x)-L|<\varepsilon

양의 실수 δ > 0가 있습니다.

만약 극한이 존재하면, 그것은 고유합니다. 만약 a가 도메인의 내부이면, 극한이 존재하는 것과 그 함수가 a에서 연속인 것은 필요충분 조건입니다. 이 경우에서, 우리는 다음을 가집니다:

f(a)=\lim _{x\to a}f(x).

a가 f의 도메인의 경계(boundary)에 있고, 만약 f가 a에서 극한을 가지면, 후자 공식은 f의 도메인을 a로 "연속성에 의해 확장"하는 것을 허용합니다.

Calculus

우리는 실수 변수 각각에 대해 여러 함수를 수집할 수 있습니다: 말하자면 다음을

y_{1}=f_{1}(x)\,,\quad y_{2}=f_{2}(x)\,,\ldots ,y_{n}=f_{n}(x)

x에 의한 매개변수화된 벡터로 수집할 수 있습니다:

\mathbf {y} =(y_{1},y_{2},\ldots ,y_{n})=[f_{1}(x),f_{2}(x),\ldots ,f_{n}(x)]

벡터 y의 도함수는 i = 1, 2, ..., n에 대해 f_i(x)의 벡터 도함수입니다:

{\frac {d\mathbf {y} }{dx}}=\left({\frac {dy_{1}}{dx}},{\frac {dy_{2}}{dx}},\ldots ,{\frac {dy_{n}}{dx}}\right)

우리는 역시 변수 x에 관해 적분함으로써, 위치 벡터(position vector) r = r(x)를 갖는, x로 매개변수화된 공간 곡선(space curve)을 따라 곡선 적분(line integral)을 수행할 수 있습니다:

\int _{a}^{b}\mathbf {y} (x)\cdot d\mathbf {r} =\int _{a}^{b}\mathbf {y} (x)\cdot {\frac {d\mathbf {r} (x)}{dx}}dx

여기서 ·은 점 곱(dot product)이고, x = a와 x = b는 곡선의 시작과 끝점입니다.

Theorems

적분과 미분의 정의와 함께, 핵심 정리는 미적분의 기본 정리(fundamental theorem of calculus), 부분에 의한 적분화(integration by parts), 및 테일러의 정리(Taylor's theorem)를 포함하여 공식화될 수 있습니다. 적분과 미분의 혼합 평가는 적분 기호 아래에서 미분(differentiation under the integral sign) 정리를 사용함으로써 수행될 수 있습니다.

Implicit functions

실수 변수의 실수-값 암시적 함수는 "y = f(x)" 형식으로 쓰이지 않습니다. 대신, 매핑은 공간 ℝ²에서 ℝ에서 영 원소(zero element) (단지 보통의 영 0)로의 것입니다: 다음 둘은

\phi :\mathbb {R} ^{2}\to \{0\}

및

\phi (x,y)=0

변수에서 방정식입니다. 암시적 함수는 함수를 표현하기 위한 보다 일반적인 방법인데, 왜냐하면 만약 다음이면

y=f(x)

우리는 항상 다음을 정의할 수 있습니다:

\phi (x,y)=y-f(x)=0

그러나 그 역은 항상 가능하지 않으며, 즉, 모든 암시적 함수가 이 방정식의 형식을 가지지는 않습니다.

One-dimensional space curves in ℝⁿ

Formulation

다음이 되도록, 모두의 공통 변수 t에 대해 함수 r₁ = r₁(t), r₂ = r₂(t), ..., r_n = r_n(t)가 주어지면:

{\begin{aligned}r_{1}:\mathbb {R} \rightarrow \mathbb {R} &\quad r_{2}:\mathbb {R} \rightarrow \mathbb {R} &\cdots &\quad r_{n}:\mathbb {R} \rightarrow \mathbb {R} \\r_{1}=r_{1}(t)&\quad r_{2}=r_{2}(t)&\cdots &\quad r_{n}=r_{n}(t)\\\end{aligned}}

또는 함께 취해져서:

\mathbf {r} :\mathbb {R} \rightarrow \mathbb {R} ^{n}\,,\quad \mathbf {r} =\mathbf {r} (t)

매개변수화된 다음 n-튜플은

\mathbf {r} (t)=[r_{1}(t),r_{2}(t),\ldots ,r_{n}(t)]

일-차원 공간 곡선(space curve)을 묘사합니다.

Tangent line to curve

어떤 상수 t = c에 대해, 점 r(t = c) = a = (a₁, a₂, ..., a_n)에서, 해당 점에서 곡선에 대한 일-차원 접선의 방정식은 t에 관한 r₁(t), r₂(t), ..., r_n(t), 및 r의 보통의 도함수(ordinary derivative)의 항에서 주어집니다:

{\frac {r_{1}(t)-a_{1}}{dr_{1}(t)/dt}}={\frac {r_{2}(t)-a_{2}}{dr_{2}(t)/dt}}=\cdots ={\frac {r_{n}(t)-a_{n}}{dr_{n}(t)/dt}}

Normal plane to curve

r = a에서 접선에 수직인 n-차원 초평면의 방정식은 다음과 같습니다:

(p_{1}-a_{1}){\frac {dr_{1}(t)}{dt}}+(p_{2}-a_{2}){\frac {dr_{2}(t)}{dt}}+\cdots +(p_{n}-a_{n}){\frac {dr_{n}(t)}{dt}}=0

또는 점 곱(dot product)의 관점에서 다음과 같습니다:

(\mathbf {p} -\mathbf {a} )\cdot {\frac {d\mathbf {r} (t)}{dt}}=0

여기서 p = (p₁, p₂, ..., p_n)는 공간 곡선 위에 있지 않고 평면 안에 있는 점들입니다.

Relation to kinematics

Kinematic quantities of a classical particle: mass m, position r, velocity v, acceleration a.

dr(t)/dt의 물리적 및 기하학적 해석은 경로 r(t)를 따라 이동하는 점-모양 입자(particle)의 "속도(velocity)"이며, r을 시간 t에 의한 매개변수화된 공간 위치 벡터(position vector) 좌표로 취급하고, 운동의 순간 방향에서 모든 t에 대해 공간 곡선에 접하는 벡터입니다. t = c에서, 공간 곡선은 접선 벡터 dr(t)/dt|_{t = c}를 가지고, t = c에서 공간 곡선에 수직인 초평면은 역시 t = c에서 접선에 수직입니다. 이 평면 (p − a)의 임의의 벡터는 dr(t)/dt|_{t = c}에 수직이어야 합니다.

유사하게, d²r(t)/dt²는 입자의 "가속도(acceleration)"이고, 곡률의 반지름(radius of curvature)을 따라 향하는 곡선에 수직인 벡터입니다.

Matrix valued functions

행렬(matrix)은 역시 단일 변수의 함수일 수 있습니다. 예를 들어, 2d에서 회전 행렬(rotation matrix)은:

R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}

원점에 대한 회전 각도의 행렬 값 함수입니다. 유사하게, 특수 상대성(special relativity)에서, 순수 부스트에 대한 로렌츠 변환(Lorentz transformation) 행렬 (회전 없음)은:

\Lambda (\beta )={\begin{bmatrix}{\frac {1}{\sqrt {1-\beta ^{2}}}}&-{\frac {\beta }{\sqrt {1-\beta ^{2}}}}&0&0\\-{\frac {\beta }{\sqrt {1-\beta ^{2}}}}&{\frac {1}{\sqrt {1-\beta ^{2}}}}&0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}

부스트 매개변수 β = v/c의 함수이며, 이것에서 v는 기준 프레임 (연속 변수) 사이의 상대 속도(relative velocity)이고, c는 빛의 속도(speed of light), 상수입니다.

Banach and Hilbert spaces and quantum mechanics

이전 섹션을 일반화하면, 실수 변수의 함수 출력은 역시 바나흐 공간 또는 힐베르트 공간에 있을 수 있습니다. 이들 공간에서, 나눗셈, 곱셈과 극한이 모두 정의되므로, 도함수와 적분과 같은 개념이 여전히 적용됩니다. 이것은 ket 또는 연산자(operator)의 도함수를 취하는 양자 역학에서 특히 자주 발생합니다. 이것은, 예를 들어, 일반적인 시간-종속 슈뢰딩거 방정식(Schrödinger equation)에서 발생합니다.

i\hbar {\frac {\partial }{\partial t}}\Psi ={\hat {H}}\Psi

여기서 우리는 여러 다른 힐베르트 공간의 원소가 될 수 있는 파동 함수의 도함수를 취합니다.

Complex-valued function of a real variable

실수 변수의 복소-값 함수는 실수-값 함수의 정의에서 실수에 대한 코도메인의 제한을 완화하고, 복소수(complex) 값을 허용함으로써 정의될 수 있습니다.

만약 $f (x)$ 가 그러한 복소-값 함수이면, 그것은 다음으로 분해될 수 있습니다:

f (x)

=

g (x)

+

ih (x)

,

여기서 $g$ 와 $h$ 는 실수-값 함수입니다. 다시 말해서, 복소-값 함수의 연구는 실수-값 함수의 쌍의 연구로 쉽게 축소됩니다.

Cardinality of sets of functions of a real variable

실수 변수의 실수-값 함수 집합의 카디널리티(cardinality), $\mathbb {R} ^{\mathbb {R} }=\{f:\mathbb {R} \to \mathbb {R} \}$ 은 연속체(continuum) (즉, 모든 실수의 집합)의 카디널리티보다 엄격하게 더 큰 $\beth _{2}=2^{\mathfrak {c}}$ 입니다. 이 사실은 세는 산술로 쉽게 확인될 수 있습니다:

$\mathrm {card} (\mathbb {R} ^{\mathbb {R} })=\mathrm {card} (\mathbb {R} )^{\mathrm {card} (\mathbb {R} )}={\mathfrak {c}}^{\mathfrak {c}}=(2^{\aleph _{0}})^{\mathfrak {c}}=2^{\aleph _{0}\cdot {\mathfrak {c}}}=2^{\mathfrak {c}}.$

게다가, 만약 $X$ 가 $2\leq \mathrm {card} (X)\leq {\mathfrak {c}}$ 를 만족하는 집합이면, 집합 $X^{\mathbb {R} }=\{f:\mathbb {R} \to X\}$ 의 카디널리티는 역시 $2^{\mathfrak {c}}$ 인데, 왜냐하면 다음이기 때문입니다:

$2^{\mathfrak {c}}=\mathrm {card} (2^{\mathbb {R} })\leq \mathrm {card} (X^{\mathbb {R} })\leq \mathrm {card} (\mathbb {R} ^{\mathbb {R} })=2^{\mathfrak {c}}.$

어쨌든, 연속 함수(continuous function)의 집합 $C^{0}(\mathbb {R} )=\{f:\mathbb {R} \to \mathbb {R} :f\ \mathrm {continuous} \}$ 은 엄격하게 더 작은 카디널리티, 연속체의 카디널리티, ${\mathfrak {c}}$ 를 가집니다. 이것은 연속 함수가 그것의 도메인의 조밀한 부분집합에 대한 값에 의해 완전하게 결정된다는 사실에서 비롯됩니다.^[2] 따라서, 실수에 대한 연속 실수-값 함수의 집합의 카디널리티는 유리 변수의 실수-값 함수의 집합의 카디널리티보다 더 크지 않습니다. 세는 산술에 의해:

$\mathrm {card} (C^{0}(\mathbb {R} ))\leq \mathrm {card} (\mathbb {R} ^{\mathbb {Q} })=(2^{\aleph _{0}})^{\aleph _{0}}=2^{\aleph _{0}\cdot \aleph _{0}}=2^{\aleph _{0}}={\mathfrak {c}}.$

다른 한편으로, $\mathbb {R}$ 와 $C^{0}(\mathbb {R} )$ 의 부분집합을 형성하는 상수 함수 $\{f:\mathbb {R} \to \mathbb {R} :f(x)\equiv x_{0}\}$ 의 집합 사이에 분명한 전단사가 존재하기 때문에, $\mathrm {card} (C^{0}(\mathbb {R} ))\geq {\mathfrak {c}}$ 는 역시 유지되어야 합니다. 따라서, $\mathrm {card} (C^{0}(\mathbb {R} ))={\mathfrak {c}}$ 입니다.

References

^ R. Courant. Differential and Integral Calculus. Vol. 2. Wiley Classics Library. pp. 46–47. ISBN 0-471-60840-8.
^ Rudin, W. (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. pp. 98–99. ISBN 0-07-054235X.

F. Ayres, E. Mendelson (2009). Calculus. Schaum's outline series (5th ed.). McGraw Hill. ISBN 978-0-07-150861-2.
R. Wrede, M. R. Spiegel (2010). Advanced calculus. Schaum's outline series (3rd ed.). McGraw Hill. ISBN 978-0-07-162366-7.
N. Bourbaki (2004). Functions of a Real Variable: Elementary Theory. Springer. ISBN 354-065-340-6.

External links

[1] R. Courant. Differential and Integral Calculus. Vol. 2. Wiley Classics Library. pp. 46–47. ISBN 0-471-60840-8.

[2] Rudin, W. (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. pp. 98–99. ISBN 0-07-054235X.

[1]

[2]

Function
$x \mapsto f (x)$
History of the function concept
Examples of domains and codomains
$X$ → $\mathbb {B}$ , $\mathbb {B}$ → $X$ , $\mathbb {B} ^{n}$ → $X$ $X$ → $\mathbb {Z}$ , $\mathbb {Z}$ → $X$ $X$ → $\mathbb {R}$ , $\mathbb {R}$ → $X$ , $\mathbb {R} ^{n}$ → $X$ $X$ → $\mathbb {C}$ , $\mathbb {C}$ → $X$ , $\mathbb {C} ^{n}$ → $X$
Classes/properties
Constant Identity Linear Polynomial Rational Algebraic Analytic Smooth Continuous Measurable Injective Surjective Bijective
Constructions
Restriction Composition λ Inverse
Generalizations
Binary relation Partial Multivalued Implicit Space
v t e