Projection (mathematics)

수학(mathematics)에서, 투영(projection)은 집합 (또는 다른 수학적 구조)을 부분집합 (또는 부분-구조)으로 거듭상등 매핑(mapping)입니다. 이 경우에서, 거듭상등은 두 번 투영하는 것이 한 번 투영하는 것과 같다는 것을 의미합니다. 거듭상등 속성이 손실된 경우에도 투영의 부분공간에 대한 제한(restriction)은 역시 투영(projection)이라고 불립니다. 투영의 일상적인 예제는 평면 (종이) 위로의 그림자를 드리우는 것입니다: 점의 투영은 종이에 그것의 그림자이고, 종이 위에 점의 투영 (그림자)은 점 자체 (거듭상등)입니다. 삼-차원 구의 그림자는 닫힌 디스크입니다. 원래, 투영의 개념은 그림자 예제와 같이 삼-차원 유클리드 공간(Euclidean space)을 그것 안의 평면 위로의 투영하는 것을 나타내기 위해 유클리드 기하학(Euclidean geometry)에 도입되었습니다. 이러한 종류의 두 가지 주요 투영은 다음과 같습니다:

한 점에서 평면 위로의 투영 또는 중심 투영: 만약 C가 투영의 중심이라고 불리는 한 점이면, C와 다른 점 P에서 C를 포함하지 않는 평면 위로의 투영은 평면과 직선 CP와 교차입니다. 직선 CP가 그 평면에 평행함을 만족하는 점 P는 투영에 의한 어떤 이미지를 가지지 않지만, 종종 그것들이 평면의 무한대에서 점으로 투영한다고 말합니다 (이 용어의 형식화에 대해 투영 기하학을 참조하십시오). 점 C 자체의 투영은 정의되지 않습니다.
방향 D로의 평행한 평면 위로에 투영, 또는 평행 투영: 점 P의 이미지는 P를 통과하는 D에 평행한 직선의 평면과 교차합니다. 임의의 차원으로 일반화된, 정확한 정의에 대해 Affine space § Projection을 참조하십시오.

수학에서 투영의 개념은 매우 오래된 것이고, 실제 물체가 땅에 드리우는 그림자 현상에 뿌리를 두고 있을 가능성이 큽니다. 이 기본적인 아이디어는 처음에는 기하학적 맥락에서, 나중에는 다른 수학 분야에서 세련되고 추상화되었습니다. 시간이 지남에 따라 개념의 다른 버전이 개발되었지만, 오늘날에는 충분히 추상적인 설정에서, 이들 변형을 통합할 수 있습니다.

지도-제작(cartography)에서, 지도 투영법(map projection)은 지구 표면의 일부를 평면에 그린 지도로, 항상 그런 것은 아니지만 일부 경우에서 위의 의미에서 투영의 제한입니다. 3D 투영은 원근법(perspective) 이론의 기초이기도 합니다.

두 종류의 투영을 통합하고 투영 중심과 다른 임의의 점의 중심 투영에 의해 이미지를 정의할 필요성이 투영 기하학(projective geometry)의 기원에 있습니다. 어쨌든, 투영 변환(projective transformation)은 투영 공간(projective space)의 전단사(bijection)이며, 이 기사의 투영과 공유되지 않는 속성입니다.

Definition

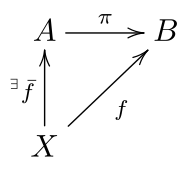
The commutativity of this diagram is the universality of the projection π, for any map f and set X.

일반적으로, 도메인과 코도메인이 같은 집합 (또는 수학적 구조)인 매핑은 만약 그 매핑이 거듭상등(idempotent)이면 투영이며, 이는 투영이 자체와의 합성(composition)과 같음을 의미합니다. 투영은 오른쪽 역(right inverse)을 가지는 매핑을 참조할 수도 있습니다. 두 개념은 다음과 같이 밀접하게 관련되어 있습니다. p를 집합 A에서 자체로의 거듭상등 매핑 (따라서 p ∘ p = p)이라고 놓고 B = p(A)를 p의 이미지라고 놓습니다. 만약 우리가 A에서 B 위로의 매핑으로 보이는 맵 p를 π로 표시하고 B를 A로의 (p = i ∘ π가 되도록) 단사를 i로 표시하면, 우리는 (π는 오른쪽 역을 가지도록) π ∘ i = Id_B를 가집니다. 반대로, 만약 π가 오른쪽 역을 가지면, π ∘ i = Id_B는 i ∘ π가 거듭상등임을 의미합니다.

Applications

투영의 원래 개념은 다음과 같은 기하학과 관련된 다양한 수학적 상황으로 확장되거나 일반화되어 왔지만, 항상 그런 것은 아닙니다, 예를 들어:

집합 이론(set theory):
- 데카르트 곱 X₁ × ⋯ × X_j × ⋯ × X_n의 원소 x = (x₁, ..., x_j, ..., x_n)을 값 proj_j(x) = x_j으로 취하는 j^번째 투영 맵으로 대표되는 연산, proj_j로 작성됨.^[1] 이 맵은 항상 전사적(surjective)이고, 각 공간 X_k가 토폴로지(topology)를 가질 때, 이 맵은 역시 연속적(continuous)이고 열린 것입니다.^[2]
- 주어진 동치 관계(equivalence relation) 아래에서 원소를 해당 동치 클래스(equivalence class)로 가져오는 매핑은 정식의 투영(canonical projection)이라고 알려져 있습니다.^[3]
- 평가 맵은 고정된 x에 대해 함수 f를 값 f(x)로 보냅니다. 함수 Y^X의 공간은 데카르트 곱 ${\textstyle \prod _{i\in X}Y}$ 으로 식별될 수 있고, 평가 맵은 데카르트 곱으로부터 투영 맵입니다.
관계형 데이터베이스(relational databases)와 질의 언어(query languages)에 대해, 투영(projection)은 $\Pi _{a_{1},\ldots ,a_{n}}(R)$ 으로 작성된 단항 연산(unary operation)이며, 여기서 $a_{1},\ldots ,a_{n}$ 은 속성 이름의 집합입니다. 그러한 투영의 결과는 R에서 모든 튜플(tuples)이 집합 $\{a_{1},\ldots ,a_{n}\}$ 으로 제한될 때 얻어지는 집합(set)으로 정의됩니다.^[4]^[5]^[6] R은 데이터베이스-관계(database-relation)입니다.
구형 기하학(spherical geometry)에서, 평면 위로의 구의 투영은 프톨레마이오스(Ptolemy, ~150)에 의해 그의 Planisphaerium에서 사용되었습니다.^[7] 그 방법은 입체 투영(stereographic projection)이라고 불리고 구에 접하는 평면과 접선 지점과 지름적으로 반대에 있는 극점 C를 사용합니다. C 이외의 구 위에 있는 임의의 점 P는 P에 대해 투영된 점에서 평면과 교차하는 직선 CP를 결정합니다.^[8] 대응은 무한대에서 점(point at infinity)이 C에 해당하도록 포함될 때 구를 평면에 대한 한-점 컴팩트화(one-point compactification)로 만들며, 그렇지 않으면 평면 위에 투영을 가지지 않습니다. 공통적인 예제는 컴팩트화가 리만 구(Riemann sphere)에 해당하는 복소 평면(complex plane)입니다. 대안적으로, 반구(hemisphere)는 자주 그노모닉 투영(gnomonic projection)을 사용하여 평면 위로 투영됩니다.
선형 대수(linear algebra)에서, 두 번 적용되면 변하지 않고 유지하는 선형 변환(linear transformation): p(u) = p(p(u)). 다시 말해서, 거듭상등(idempotent) 연산자입니다. 예를 들어, 삼-차원에서 점 (x, y, z)를 점 (x, y, 0)으로 취하는 매핑은 투영입니다. 이러한 유형의 투영은 자연스럽게 매핑의 도메인에 대해 임의의 차원의 숫자 n과 코도메인에 대해 k ≤ n으로 일반화됩니다. Orthogonal projection, Projection (linear algebra)을 참조하십시오. 직교 투영의 경우에서, 공간은 분해를 곱으로 인정하고, 투영 연산자는 마찬가지로 해당 의미에서 투영입니다.^[9]^[10]
미분 토폴로지(differential topology)에서, 임의의 섬유 다발(fiber bundle)은 그것의 정의의 일부로 투영 맵을 포함합니다. 지역적으로 적어도 이 맵은 곱 토폴로지의 의미에서 투명 맵처럼 보이고 따라서 열린 것이고 전사적입니다.
토폴로지(topology)에서, 수축(retraction)은 그것의 이미지 위에 항등 맵(identity map)으로 제한하는 연속 맵(continuous map) r: X → X입니다.^[11] 이것은 유사한 거듭상등 조건 r² = r을 만족시키고 투영 맵의 일반화로 고려될 수 있습니다. 수축의 이미지는 원래 공간의 수축이라고 불립니다. 항등으로의 호모토피적(homotopic)인 수축은 변형 수축(deformation retraction)으로 알려져 있습니다. 이 용어는 역시 카테고리 이론에서 임의의 분할 전사-사상(split epimorphism)을 참조하기 위해 사용됩니다. [인용 필요]
한 벡터를 또 다른 벡터 위로의 스칼라 투영(scalar projection).
카테고리 이론(category theory)에서, 집합의 데카르트 곱에 대한 위의 개념은 임의적인 카테고리(categories)로 일반화될 수 있습니다. 일부 대상의 곱은 각 인수로의 정식의 투영(canonical projection) 사상을 가집니다. 이 투영은 다양한 카테고리에서 많은 형식을 띨 것입니다. 집합의 데카르트 곱, 토폴로지 공간의 곱 토폴로지 (항상 전사적이고 열린 것임), 또는 그룹의 직접 곱, 등으로부터의 투영. 비록 이들 사상이 종종 전사-사상(epimorphisms)이고 심지어 전사적이지만, 그것들이 반드시 그럴 필요는 없습니다.^[12]