Normal distribution

Original article: w:Normal distribution

This article is about the univariate normal distribution. For normally distributed vectors, see Multivariate normal distribution.

"Bell curve" redirects here. For other uses, see Bell curve (disambiguation).

Normal distribution

Probability density function The red curve is the standard normal distribution
Cumulative distribution function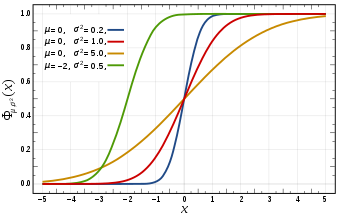
Notation	${\mathcal {N}}(\mu ,\sigma ^{2})$
Parameters	$\mu \in \mathbb {R}$ = mean (location) $\sigma ^{2}>0$ = variance (squared scale)
Support	$x\in \mathbb {R}$
PDF	${\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}$
CDF	${\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]$
Quantile	$\mu +\sigma {\sqrt {2}}\operatorname {erf} ^{-1}(2p-1)$
Mean	$\mu$
Median	$\mu$
Mode	$\mu$
Variance	$\sigma ^{2}$
MAD	$\sigma {\sqrt {2/\pi }}$
Skewness	$0$
Ex. kurtosis	$0$
Entropy	${\frac {1}{2}}\log(2\pi e\sigma ^{2})$
MGF	$\exp(\mu t+\sigma ^{2}t^{2}/2)$
CF	$\exp(i\mu t-\sigma ^{2}t^{2}/2)$
Fisher information	${\mathcal {I}}(\mu ,\sigma )={\begin{pmatrix}1/\sigma ^{2}&0\\0&2/\sigma ^{2}\end{pmatrix}}$ ${\mathcal {I}}(\mu ,\sigma ^{2})={\begin{pmatrix}1/\sigma ^{2}&0\\0&1/(2\sigma ^{4})\end{pmatrix}}$
Kullback-Leibler divergence	$D_{\text{KL}}({\mathcal {N}}_{0}\parallel {\mathcal {N}}_{1})={1 \over 2}\left\{\left({\frac {\sigma _{0}}{\sigma _{1}}}\right)^{2}+{\frac {(\mu _{1}-\mu _{0})^{2}}{\sigma _{1}^{2}}}-1+2\ln {\sigma _{1} \over \sigma _{0}}\right\}$

확률 이론(probability theory)에서, 정규(normal) (또는 가우시안(Gaussian) 또는 가우스(Gauss) 또는 라플라스-가우스(Laplace-Gauss)) 분포(distribution)는 연속-값 확률 변수에 대해 연속 확률 분포(continuous probability distribution)의 유형입니다. 그의 확률 밀도 함수의 일반적인 형식은 다음입니다:

$f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}$

매개-변수 $\mu$는 분포의 평균(mean) 또는 기대(expectation) (및 역시 그의 중앙값(median)과 최빈값(mode))입니다; 그리고 $\sigma$는 표준 편차(standard deviation)입니다. 분포의 분산(variance)은 $\sigma ^{2}$입니다. 가우시안 분포를 갖는 확률 변수(random variable)는 정규적으로 분포되었다(normally distributed)고 말해지고 정규 편차(normal deviate)라고 불립니다.

정균 분포는 통계학(statistics)에서 중요하고 그의 분포가 알려지지 않는 실수-값 확률 변수를 나타내기 위해 자연(natural) 및 사회 과학(social science)에서 종종 사용됩니다. 그들의 중요성은 중심 극한 정리(central limit theorem)에 부분적으로 기인합니다. 일부 조건 아래에서, 유한 평균(mean)과 분산(variance)을 갖는 확률 변수(random variable)의 많은 표본 (관측)의 평균은 그의 분포가 표본의 숫자가 증가함에 따라 정규 분포로 수렴하는(converges) 자체로 확률 변수임을 말합니다. 그러므로, (측정 오류(measurement error)와 같은) 많은 독립적인 과정의 합으로 예상되는 물리적 양은 종종 거의 정규인 분포를 가집니다.

게다가, 가우시안 분포는 해석적 연구에서 유용한 일부 고유한 속성을 가집니다. 예를 들어, 정규 이탈의 고정된 모음의 임의의 선형 조합은 정규 이탈입니다. (불확실성의 전파(propagation of uncertainty)와 최소 제곱(least squares 매개-변수 적합과 같은) 많은 결과와 방법은, 관련 변수가 정규적으로 분포될 때, 명시적 형식에서 해석적으로 유도될 수 있습니다.

정규 분포는 때때로 비공식적으로 종 곡선(bell curve)으로 불립니다. 어쨌든, 많은 다른 분포는 (코시(Cauchy), 스튜던트의 t(Student's t), 및 로지스틱(logistic) 분포와 같은) 종-모양입니다.

Definitions

Standard normal distribution

정규 분포의 가장 간단한 경우는 표준 정규 분포로 알려져 있습니다. 이것은 $\mu =0$ 및 $\sigma =1$일 때 특수한 경우이고, 그것은 다음 확률 밀도 함수(probability density function)로 묘사됩니다:

$\varphi (x)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}}$

이 확장에서 인수 $1/{\sqrt {2\pi }}$는 곡선 $\varphi (x)$ 아래의 전체 넓이가 일과 같음을 보장합니다. 지수에서 인수 $1/2$는 분포가 단위 분산을 가지고 (즉, 분산은 일과 같습니다), 따라서 역시 단위 표준 편차임을 보장합니다. 이 함수는 $x=0$ 주위로 대칭이며, 여기서 그것의 최댓값 $1/{\sqrt {2\pi }}$에 도달하고 $x=+1$ 및 $x=-1$에서 변곡점(inflection point)을 가집니다.

저자는 정규 분포가 "표준" 정규 분포로 불려야 하는 것이 다릅니다. 카를 프리드리히 가우스(Carl Friedrich Gauss)는 표준 정규를 분산 $\sigma ^{2}=1/2$을 가지는 것으로 정의했으며, 즉,

$\varphi (x)={\frac {e^{-x^{2}}}{\sqrt {\pi }}}$

스티글러(Stigler)는 더 나아가, 표준 편차를 분산 $\sigma ^{2}=1/(2\pi )$을 갖는 것으로 정의합니다:

$\varphi (x)=e^{-\pi x^{2}}$

General normal distribution

모든 각 정규 분포는 그의 도메인이 인수 $\sigma$ (표준 편차)만큼 확장되어지고 그런-다음 $\mu$ (평균 값)에 의해 평행-이동되는 표준 정규 분포의 버전입니다.

$f(x\mid \mu ,\sigma ^{2})={\frac {1}{\sigma }}\varphi \left({\frac {x-\mu }{\sigma }}\right)$

확률 밀도는 적분이 여전히 1이 되도록 $1/\sigma$에 의해 스케일되어야 합니다.

만약 $Z$이 표준 정규 편차(standard normal deviate)이면, $X=\sigma Z+\mu$는 기댓값 $\mu$와 표준 편차 $\sigma$를 갖는 정규 분포를 가질 것입니다. 반대로, 만약 $X$가 매개-변수 $\mu$와 $\sigma ^{2}$를 갖는 정규 이탈이면, $Z=(X-\mu )/\sigma$는 표준 정규 분포를 가질 것입니다. 이 변이는 $X$의 표준화된 형식으로 불립니다.

Notation

영 평균과 단위 분산을 갖는 표준 가우시안 분포 (표준 정규 분포)의 확률 밀도는 그리스 문자 $\phi$ (phi)로 종종 표시됩니다. 그리스 문자 phi, $\varphi$의 대안적인 형식은 역시 꽤 자주 사용됩니다.

정규 분포는 $N(\mu ,\sigma ^{2})$ 또는 ${\mathcal {N}}(\mu ,\sigma ^{2})$로 종종 참조됩니다. 따라서 확률 변수 $X$가 평균 $\mu$와 분산 $\sigma ^{2}$를 갖는 정규적으로 분포되면, 우리는 다음을 쓸 수 있습니다:

$X\sim {\mathcal {N}}(\mu ,\sigma ^{2}).$

Alternative parameterizations

일부 저자는 편차 $\sigma$ 또는 분산 $\sigma ^{2}$ 대신에 분포의 너비를 정의하는 매개-변수로 정밀도(precision) $\tau$를 사용하는 것을 주장합니다. 정밀도는 통상적으로 분산의 역수, $1/\sigma ^{2}$로 정의됩니다. 분포에 대한 공식은 그런-다음 다음이 됩니다:

$f(x)={\sqrt {\frac {\tau }{2\pi }}}e^{-\tau (x-\mu )^{2}/2}.$

이 선택은 $\sigma$가 영에 매우 가깝고 다변수 정규 분포(multivariate normal distribution)를 갖는 변수의 베이즈 추론(Bayesian inference)에서 처럼 일부 문맥에서 공식을 단순화할 때 수치적 계산에 이점을 가진다고 주장됩니다.

역시 표준 편차의 역수 $\tau ^{\prime }=1/\sigma$는 정밀도로 정의될 수 있고 정규 분포의 표현은 다음이 됩니다:

$f(x)={\frac {\tau ^{\prime }}{\sqrt {2\pi }}}e^{-(\tau ^{\prime })^{2}(x-\mu )^{2}/2}.$

스티글러에 따르면, 이 공식화는 훨씬 더 간단하고 쉽게-기억되는 공식, 및 분포의 분위-숫자(quantile)에 대해 간단한 근사 공식이기 때문에 이점이 있습니다.

정규 분포는 자연스러운 매개-변수(natural parameter) $\textstyle \theta _{1}={\frac {\mu }{\sigma ^{2}}}$와 $\textstyle \theta _{2}={\frac {-1}{2\sigma ^{2}}}$, 및 자연스러운 통계량 x와 x²을 갖는 지수 가족(exponential family)을 형성합니다. 이중, 정규 분포에 대해 기대 매개-변수는 η₁ = μ와 η₂ = μ² + σ²입니다.

Cumulative distribution function

표준 정규 분포의 누적 분포 함수(cumulative distribution function, 줄여서 CDF)는, 보통 대문자 그리스 문자 $\Phi$ (phi)로 표시되면, 다음 적분입니다:

$\Phi (x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{-t^{2}/2}\,dt$

관련된 오차 함수(error function) $\operatorname {erf} (x)$는 범위 $[-x,x]$ 안에 떨어지는 평균 0과 분산 1/2의 정규 분포를 갖는 확률 변수의 확률을 제공합니다; 즉,

$\operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,dt$

이들 적분은 기본 함수의 관점에서 절대 표현되지 않고, 종종 특수 함수(special function)라고 말합니다. 어쨌든, 많은 수치적 근사가 알려져 있습니다; 아래(below)를 참조하십시오.

두 함수는 밀접하게 관련되며, 즉,

$\Phi (x)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]$

밀도 $f$, 평균 $\mu$ 및 분산 $\sigma$을 가즌 일반 정규 분포에 대해, 누적 분포 함수는 다음입니다:

$F(x)=\Phi \left({\frac {x-\mu }{\sigma }}\right)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]$

표준 정규 CDF의 여, $Q(x)=1-\Phi (x)$는, 특별히 공학 텍스트에서, 종종 Q-함수(Q-function)로 불립니다. 그것은 표준 정규 확률 변수 $X$의 값이 $x$를 초과: $P(X>x)$일 확률을 제공합니다. $Q$-함수의 다른 정의는, 그것의 모두는 $\Phi$의 간단한 변환이며, 때때로 역시 사용됩니다.

표준 정규 CDF $\Phi$의 그래프(graph)는 점 (0,1/2) 주위로 2-겹 회전 대칭(rotational symmetry): 즉, $\Phi (-x)=1-\Phi (x)$을 가집니다. 그것의 역도함수(antiderivative) (부정 적분)는 다음입니다:

$\int \Phi (x)\,dx=x\Phi (x)+\varphi (x)+C.$

표준 정규 분포의 CDF는 부분에 의한 적분화(Integration by parts)를 사용하여 급수(series)로 확장될 수 있습니다:

$\Phi (x)={\frac {1}{2}}+{\frac {1}{\sqrt {2\pi }}}\cdot e^{-x^{2}/2}\left[x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{3\cdot 5}}+\cdots +{\frac {x^{2n+1}}{(2n+1)!!}}+\cdots \right]$

여기서 $!!$는 두-배 팩토리얼(double factorial)을 나타냅니다.

큰 x에 대해 CDF의 점근 전개(asymptotic expansion)는 부분에 의한 적분화를 사용하여 역시 유도될 수 있습니다; Error function#Asymptotic expansion를 참조하십시오.

Standard deviation and coverage

Further information: Interval estimation and Coverage probability

For the normal distribution, the values less than one standard deviation away from the mean account for 68.27% of the set; while two standard deviations from the mean account for 95.45%; and three standard deviations account for 99.73%.

정규 분포에서 도출된 값의 약 68%는 평균에서 일 표준 편차 σ 이내에 있습니다; 값의 약 95%는 이 표준 편차 이내에 놓입니다; 그리고 약 99.7%가 삼 표준 편차 이내에 있습니다. 이 사실은 68-95-99.7 (경험적) 규칙 또는 3-시그마 규칙으로 알려져 있습니다.

보다 정확하게, 정규 이탈이 $\mu -n\sigma$와 $\mu +n\sigma$ 사이의 범위에 놓일 확률은 다음에 의해 제공됩니다:

$F(\mu +n\sigma )-F(\mu -n\sigma )=\Phi (n)-\Phi (-n)=\operatorname {erf} \left({\frac {n}{\sqrt {2}}}\right).$

12 유효 숫자로, $n=1,2,\ldots ,6$에 대해 값은 다음입니다:

$n$	$p=F(\mu +n\sigma )-F(\mu -n\sigma )$	${\text{i.e. }}1-p$	${\text{or }}1{\text{ in }}p$	OEIS
1	0.682689492137	0.317310507863	3 .15148718753	OEIS: A178647
2	0.954499736104	0.045500263896	21 .9778945080	OEIS: A110894
3	0.997300203937	0.002699796063	370 .398347345	OEIS: A270712
4	0.999936657516	0.000063342484	15787 .1927673
5	0.999999426697	0.000000573303	1744277 .89362
6	0.999999998027	0.000000001973	506797345 .897

Quantile function

Further information: Quantile function § Normal distribution

분포의 분위-숫자 함수(quantile function)는 누적 분포 함수의 역입니다. 표준 정규 분포의 분위-숫자 함수는 프로빗 함수(probit function)로 불리고, 역 오차 함수(error function)의 관점에서 표현될 수 있습니다:

$\Phi ^{-1}(p)={\sqrt {2}}\operatorname {erf} ^{-1}(2p-1),\quad p\in (0,1).$

평균 $\mu$와 분산 $\sigma ^{2}$을 갖는 정규 확률 변수에 대해, 분위-숫자 함수는 다음입니다:

$F^{-1}(p)=\mu +\sigma \Phi ^{-1}(p)=\mu +\sigma {\sqrt {2}}\operatorname {erf} ^{-1}(2p-1),\quad p\in (0,1).$

표준 정규 분포의 분위-숫자(quantile) $\Phi ^{-1}(p)$은 $z_{p}$로 공통적으로 표시됩니다. 이들 값은 가설 테스트(hypothesis testing), 신뢰 구간(confidence interval)과 Q-Q 그림(Q-Q plot)의 구성에서 사용됩니다. 정규 확률 변수 $X$는 확률 $1-p$를 갖는 $\mu +z_{p}\sigma$를 초과할 것이고, 확률 $2(1-p)$를 갖는 구간 $\mu \pm z_{p}\sigma$ 밖에 놓일 것입니다. 특히, 분위-숫자 $z_{0.975}$는 1.96입니다; 그러므로 정규 확률 변수는 경우의 오직 5%에서 구간 $\mu \pm 1.96\sigma$ 밖에 놓일 것입니다.

다음 테이블은 $X$가 지정된 확률 $p$를 갖는 범위 $\mu \pm z_{p}\sigma$ 안에 놓일 것을 만족하는 분위-숫자 $z_{p}$을 제공합니다. 이들 값은 표본 평균(sample averages) 및 정규 (또는 점근적으로 정규) 분포를 갖는 다른 통계적 추정기(estimator)에 대해 허용 구간(tolerance interval)을 결정하기 위해 유용합니다. 참고 : 다음 테이블은 위에서 정의된 것처럼 ${\sqrt {2}}\operatorname {erf} ^{-1}(p)=\Phi ^{-1}\left({\frac {p+1}{2}}\right)$이고, $\Phi ^{-1}(p)$은 아님을 보여줍니다.

$p$	$z_{p}$		$p$	$z_{p}$
0.80	1.281551565545		0.999	3.290526731492
0.90	1.644853626951		0.9999	3.890591886413
0.95	1.959963984540		0.99999	4.417173413469
0.98	2.326347874041		0.999999	4.891638475699
0.99	2.575829303549		0.9999999	5.326723886384
0.995	2.807033768344		0.99999999	5.730728868236
0.998	3.090232306168		0.999999999	6.109410204869

작은 $p$에 대해, 분위-숫자 함수는 유용한 점근적 전개를 가집니다:

$\Phi ^{-1}(p)=-{\sqrt {\ln {\frac {1}{p^{2}}}-\ln \ln {\frac {1}{p^{2}}}-\ln(2\pi )}}+{\mathcal {o}}(1).$

Properties

정규 분포는 처음 둘 이외 (즉, 평균 및 분산(variance)이 아닌)의 누적(cumulant)은 영인 유일한 분포입니다. 그것은 역시 지정된 평균과 분산에 대해 최대 엔트로피(maximum entropy)를 갖는 연속 분포입니다. 기어리는, 평균과 분산이 유한하다고 가정할 때, 정규 분포는 독립 추첨의 집합에서 계산된 평균과 분산이 서로 독립인 유일한 분포라는 것을 보였습니다.

정규 분포는 타원형 분포(elliptical distribution)의 부분-클래스입니다. 정규 분포는 그의 평균에 대해 대칭(symmetric)이고, 전체 실수 직선에 걸쳐 비-영입니다. 따라서 사람의 몸무게(weight) 또는 주식(share)의 가격과 같은 본질적으로 양수 또는 강하게 왜곡된 변수에 대해 적합한 모델이 아닐 수 있습니다. 그러한 변수는 로그-정규 분포(log-normal distribution) 또는 파레토 분포(Pareto distribution)와 같은 다른 분포에 의해 더 잘 묘사될 수 있을 것입니다.

정규 분포의 값은, 값 $x$가 평균에서 적지 않은 표준 편차(standard deviation) 이상 떨어져 있을 때 실제로 영입니다 (예를 들어, 삼 표준 편차의 확산이 전체는 아니지만 전체 분포의 0.27%를 제외하고 덮습니다). 그러므로, 우리가 이상값(outlier)–평균에서 멀어짐에 따라 많은 표준 편차에 놓이는 값–의 상당 부분을 기대할 때 적절한 모델이 아닐 수 있고 정규적으로 분포된 변수에 대해 최적인 최소 제곱 및 다른 통계적 추론(statistical inference) 방법이 그러한 데이터에 적용될 때 종종 매우 신뢰할 수 없게 됩니다. 그들의 경우에서, 보다 두꺼운-꼬리(heavy-tailed) 분포가 가정되어야 하고 적절한 건장한 통계적 추론(robust statistical inference) 방법을 적용되어야 합니다.

가우시안 분포는 평균 또는 분산이 유한한지 여부에 관계없이 독립, 동일하게 분포된(independent, identically distributed) 분포의 합의 유인자인 안정 분포(stable distribution)의 가족에 속합니다. 극한하는 경우인 가우시안을 제외하고, 모든 안정 분포는 두꺼운 꼬리와 무한 분산을 가집니다. 그것은 안정적이고 해석적으로 표현될 수 있는 확률 밀도 함수를 갖는 몇 개의 분포 중 하나이며, 다른 것은 코시 분포(Cauchy distribution)와 리비 분포(Lévy distribution)입니다.

Symmetries and derivatives

밀도 $f(x)$ (평균 $\mu$ 및 표준 편차 $\sigma >0$)를 갖는 정규 분포는 다음 속성을 가집니다:

• 그것은 점 $x=\mu$ 주위로 대칭이며, 이것은 동시에 분포의 최빈값(mode), 중앙값(median) 및 평균(mean)입니다.
• 그것은 단일-봉우리(unimodal)입니다: 그것의 첫 번째 도함수(derivative)는 $x<\mu$에 대해 양수, $x>\mu$에 대해 음수 및 $x=\mu$에서 오직 영입니다.
• 곡선 아래 및 $x$-축에 걸친 넓이는 단위입니다 (즉, 일과 같습니다).
• 그것의 밀도는 두 변곡점(inflection point)을 가지며 (여기서 $f$의 두 번째 도함수는 영이고 부호를 바꿉니다), 평균으로부터 일 표준 편차, 즉 $x=\mu -\sigma$ 및 $x=\mu +\sigma$에 위치합니다.
• 그것의 밀도는 로그-오목(log-concave)입니다.
• 그것의 밀도는 무한하게 미분-가능(differentiable), 사실 차수 2의 초-매끄러움(supersmooth)입니다.

게다가, 표준 정규 분포 (즉, $\mu =0$ 및 $\sigma =1$)의 밀도 $\varphi$는 역시 다음 속성을 가집니다:

• 그것의 첫 번째 도함수는 $\varphi ^{\prime }(x)=-x\varphi (x)$입니다.
• 그것의 두 번째 도함수는 $\varphi ^{\prime \prime }(x)=(x^{2}-1)\varphi (x)$입니다.
• 보다 일반적으로, 그것의 n번째 도함수는 $\varphi ^{(n)}(x)=(-1)^{n}\operatorname {He} _{n}(x)\varphi (x),$이며 여기서 $\operatorname {He} _{n}(x)$는 n번째 (확률론의) 에르미트 다항식(Hermite polynomial)입니다.
• 알려진 $\mu$와 $\sigma$를 갖는 정규적으로 분포된 변수 $X$가 특정 집합 안에 있을 확률은 분수 $Z=(X-\mu )/\sigma$가 표준 정규 분포를 가진다는 사실을 사용함으로써 계산될 수 있습니다.

Moments

See also: List of integrals of Gaussian functions

변수 $X$의 일반 및 절대 모멘트(moments)는 각각 $X^{p}$ 및 $|X|^{p}$의 기댓값입니다. 만약 $X$의 기댓값 $\mu$가 영이면, 이들 매개-변수는 중심 모멘트로 불립니다. 보통 우리가 정수 순서 $\ p$를 갖는 모멘트에 오직 관심이 있습니다.

만약 $X$가 정규 분포이면, 이들 모멘트는 존재하고 그의 실수 부분이 −1보다 더 큰 임의의 $p$에 대해 유한입니다. 임의의 비-음의 정수 $p$에 대해, 보통 중심 모멘트는 다음입니다:

$\operatorname {E} \left[(X-\mu )^{p}\right]={\begin{cases}0&{\text{if }}p{\text{ is odd,}}\\\sigma ^{p}(p-1)!!&{\text{if }}p{\text{ is even.}}\end{cases}}$

여기서 $n!!$는 두-배 팩토리얼(double factorial), 즉, $n$과 같은 패리티를 가지는 $n$에서 1까지 모든 숫자의 곱을 나타냅니다.

중심 절대 모멘트는 모든 짝수 차수에 대해 보통 모멘트와 일치하지만, 홀수 차수에 대해 비-영입니다. 임의의 비-음의 정수 $p$에 대해,

${\begin{aligned}\operatorname {E} \left[|X-\mu |^{p}\right]&=\sigma ^{p}(p-1)!!\cdot {\begin{cases}{\sqrt {\frac {2}{\pi }}}&{\text{if }}p{\text{ is odd}}\\1&{\text{if }}p{\text{ is even}}\end{cases}}\\&=\sigma ^{p}\cdot {\frac {2^{p/2}\Gamma \left({\frac {p+1}{2}}\right)}{\sqrt {\pi }}}.\end{aligned}}$

마지막 공식은 임의의 비-정수 $p>-1$에 대해 역시 유효합니다. 평균 $\mu \neq 0$일 때, 보통 및 절대 모멘트는 합류 초기하 함수(confluent hypergeometric function) ${}_{1}F_{1}$ 및 $U$의 관점에서 표현될 수 있습니다.

${\begin{aligned}\operatorname {E} \left[X^{p}\right]&=\sigma ^{p}\cdot (-i{\sqrt {2}})^{p}U\left(-{\frac {p}{2}},{\frac {1}{2}},-{\frac {1}{2}}\left({\frac {\mu }{\sigma }}\right)^{2}\right),\\\operatorname {E} \left[|X|^{p}\right]&=\sigma ^{p}\cdot 2^{p/2}{\frac {\Gamma \left({\frac {1+p}{2}}\right)}{\sqrt {\pi }}}{}_{1}F_{1}\left(-{\frac {p}{2}},{\frac {1}{2}},-{\frac {1}{2}}\left({\frac {\mu }{\sigma }}\right)^{2}\right).\end{aligned}}$

이들 표현은 심지어 $p$가 정수가 아니더라도 유효하게 남습니다. 역시 일반화된 에르미트 다항식(generalized Hermite polynomials)을 참조하십시오.

Order	Non-central moment	Central moment
1	$\mu$	$0$
2	$\mu ^{2}+\sigma ^{2}$	$\sigma ^{2}$
3	$\mu ^{3}+3\mu \sigma ^{2}$	$0$
4	$\mu ^{4}+6\mu ^{2}\sigma ^{2}+3\sigma ^{4}$	$3\sigma ^{4}$
5	$\mu ^{5}+10\mu ^{3}\sigma ^{2}+15\mu \sigma ^{4}$	$0$
6	$\mu ^{6}+15\mu ^{4}\sigma ^{2}+45\mu ^{2}\sigma ^{4}+15\sigma ^{6}$	$15\sigma ^{6}$
7	$\mu ^{7}+21\mu ^{5}\sigma ^{2}+105\mu ^{3}\sigma ^{4}+105\mu \sigma ^{6}$	$0$
8	$\mu ^{8}+28\mu ^{6}\sigma ^{2}+210\mu ^{4}\sigma ^{4}+420\mu ^{2}\sigma ^{6}+105\sigma ^{8}$	$105\sigma ^{8}$

$X$가 구간 $[a,b]$ 안에 놓이는 사건에 조건화된 $X$의 기대는 다음에 의해 제공됩니다:

$\operatorname {E} \left[X\mid a<X<b\right]=\mu -\sigma ^{2}{\frac {f(b)-f(a)}{F(b)-F(a)}}$

여기서 $f$와 $F$는 각각 $X$의 밀도 및 누적 분포 함수입니다. $b=\infty$에 대해, 이것은 역 밀스 비율(inverse Mills ratio)로 알려져 있습니다. 위의, $X$의 밀도 $f$는 역 밀스 비율에서 처럼 표준 정규 밀도 대신에 사용되므로, 여기서 우리는 $\sigma$ 대신에 $\sigma ^{2}$를 가짐을 주목하십시오.

Fourier transform and characteristic function

평균 $\mu$와 표준 편차 $\sigma$를 갖는 정규 밀도 $f$의 푸리에 변환(Fourier transform)은 다음입니다:

${\hat {f}}(t)=\int _{-\infty }^{\infty }f(x)e^{-itx}\,dx=e^{-i\mu t}e^{-{\frac {1}{2}}(\sigma t)^{2}}$

여기서 $i$는 허수 단위(imaginary unit)입니다. 만약 평균 $\mu =0$이면, 첫 번째 인수는 1이고, 푸리에 변환은, 상수 인수와는 별개로, 평균 0과 표준 편차 $1/\sigma$을 갖는 주파수 도메인(frequency domain)에 대한 정규 밀도입니다. 특히, 표준 정규 분포 $\varphi$는 푸리에 변한의 고유-함수(eigenfunction)입니다.

확률 이론에서, 실수-값 확률 변수 $X$의 확률 분포의 푸리에 변환은 해당 변수의 특성 함수(characteristic function)와 밀접하게 연결되며, 이것은 $e^{itX}$의 기댓값(expected value), (푸리에 변환의 주파수(frequency) 매개-변수) 실수 변수 $t$의 함수로 정의됩니다. 이 정의는 복소-값 변수 $t$로 해석적으로 확장될 수 있습니다. 둘 사이의 관계는 다음입니다:

$\varphi _{X}(t)={\hat {f}}(-t)$

Moment and cumulant generating functions

확률 변수 $X$의 모멘트 생성 함수(moment generating function)는 실수 매개-변수 $t$의 함수로 $e^{tX}$의 기댓값입니다. 밀도 $f$, 평균 $\mu$ 및 편차 $\sigma$를 갖는 정규 분포에 대해, 모멘트 생성 함수는 존재하고 다음과 같습니다:

$M(t)=\operatorname {E} [e^{tX}]={\hat {f}}(it)=e^{\mu t}e^{{\tfrac {1}{2}}\sigma ^{2}t^{2}}$

누적 생성 함수(cumulant generating function)는 모멘트 생성 함수의 로그입니다. 즉,

$g(t)=\ln M(t)=\mu t+{\tfrac {1}{2}}\sigma ^{2}t^{2}$

이것은 $t$에서 이차 다항식이므로, 오직 첫 번째 두 누적(cumulant)이 비-영, 즉 평균 $\mu$과 분산 $\sigma ^{2}$입니다.

Stein operator and class

스타인의 방법 내에서 확률 변수 $X\sim {\mathcal {N}}(\mu ,\sigma ^{2})$의 클래스는 ${\mathcal {A}}f(x)=\sigma ^{2}f'(x)-(x-\mu )f(x)$ 및 $\mathbb {E} [|f'(X)|]<\infty$를 만족하는 모든 절대적으로 연속 함수 $f:\mathbb {R} \to \mathbb {R}$의 클래스 ${\mathcal {F}}$입니다.

Zero-variance limit

극한(limit)에서 $\sigma$이 영으로 경향일 때, 확률 밀도 $f(x)$는 결국 임의의 $x\neq \mu$에서 영으로 경향이지만, 만약 $x=\mu$이면 한도없이 점점 성장하며, 반면에 그것의 적분은 여전히 1과 같습니다. 그러므로, 정규 분포는 $\sigma =0$일 때, 보통의 함수(function)로 정의되지 않습니다.

어쨌든, 우리는 일반화된 함수(generalized function); 특히, 평균에 의해 이동된 디랙의 "델타 함수" $\delta$, 즉, $f(x)=\delta (x-\mu )$으로 영 분산을 갖는 정규 분포를 정의할 수 있습니다. 그것의 CDF는 그런-다음 평균 $\mu$에 의해 이동된 헤비사이드 계단 함수(Heaviside step function)입니다, 즉,

$F(x)={\begin{cases}0&{\text{if }}x<\mu \\1&{\text{if }}x\geq \mu \end{cases}}$

Maximum entropy

지정된 평균 $\mu$ 및 분산 $\sigma ^{2}$를 갖는 실수에 걸쳐 모든 확률 분포 중 정규 분포 $N(\mu ,\sigma ^{2})$는 최대 엔트로피(maximum entropy)를 가진 하나입니다. 만약 $X$가 확률 밀도(probability density) $f(x)$를 갖는 연속 확률 변수(continuous random variable)이면, $X$의 엔트로피는 다음으로 정의됩니다:

$H(X)=-\int _{-\infty }^{\infty }f(x)\log f(x)\,dx$

여기서 $f(x)\log f(x)$는 $f(x)=0$일 때마다 영인 것으로 이해됩니다. 이 함수형은, 변화의 계산법(variational calculus)을 사용함으로써 분포가 적절하게 정규화되고 지정된 분산을 가지는 구속-조건에 따라, 최대화될 수 있습니다. 두 라그랑주 곱셈수(Lagrange multipliers)를 갖는 함수는 정의됩니다:

$L=\int _{-\infty }^{\infty }f(x)\ln(f(x))\,dx-\lambda _{0}\left(1-\int _{-\infty }^{\infty }f(x)\,dx\right)-\lambda \left(\sigma ^{2}-\int _{-\infty }^{\infty }f(x)(x-\mu )^{2}\,dx\right)$

여기서 $f(x)$는, 지금은, 평균 $\mu$ 및 표준 편차 $\sigma$를 갖는 일부 밀도 함수로 여겨집니다.

최대 엔트로피에서, $f(x)$에 대한 작은 변화 $\delta f(x)$는 $L$에 대한 변화 $\delta L$을 생성할 것이며 이것은 0과 같습니다:

$0=\delta L=\int _{-\infty }^{\infty }\delta f(x)\left(\ln(f(x))+1+\lambda _{0}+\lambda (x-\mu )^{2}\right)\,dx$

이 방법은 임의의 작은 $\delta f(x)$에 대해 반드시 유지되며, 괄호 안의 항은 반드시 영이 되고, $f(x)$에 대해 풀면 다음을 산출합니다:

$f(x)=e^{-\lambda _{0}-1-\lambda (x-\mu )^{2}}$

$\lambda _{0}$ 및 $\lambda$에 대해 풀기 위해 구속 방정식을 사용하면 정규 분포의 밀도를 산출합니다:

$f(x,\mu ,\sigma )={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}$

정규 분포의 엔트리피는 다음과 같습니다:

$H(x)={\tfrac {1}{2}}(1+\log(2\sigma ^{2}\pi ))$

Operations on normal deviates

정규 분포의 가족은 선형 변환 아래에 닫혀 있습니다: 만약 $X$가 평균 $\mu$ 및 표준 편차 $\sigma$와 함께 정규적으로 분포되면, 임의의 실수 $a$와 $b$에 대해, 변수 $Y=aX+b$는 평균 $a\mu +b$ 및 표준 편차 $|a|\sigma$와 함께 역시 정규적으로 분포됩니다.

역시 만약 $X_{1}$와 $X_{2}$가 평균 $\mu _{1}$, $\mu _{2}$ 및 표준 편차 $\sigma _{1}$, $\sigma _{2}$를 갖는 두 독립(independent) 정규 확률 변수이면, 그들의 합 $X_{1}+X_{2}$은 평균 mean $\mu _{1}+\mu _{2}$ 및 분산 $\sigma _{1}^{2}+\sigma _{2}^{2}$와 함께 역시 정규적으로 분포될 것입니다.^[proof]

특히, 만약 $X$와 $Y$가 영 평균과 분산 $\sigma ^{2}$을 갖는 독립 정규 이탈이면, $X+Y$와 $X-Y$는 영 평균과 분산 $2\sigma ^{2}$와 함께 역시 독립이고 정규적으로 분포됩니다. 이것은 극화 항등식(polarization identity)의 특별한 경우입니다.

역시, 만약 $X_{1}$, $X_{2}$가 평균 $\mu$ 및 편차 $\sigma$를 갖는 독립 정규 이탈이고, $a$, $b$가 임의의 실수이면, 변수

$X_{3}={\frac {aX_{1}+bX_{2}-(a+b)\mu }{\sqrt {a^{2}+b^{2}}}}+\mu$

는 평균 $\mu$ 및 편차 $\sigma$와 함께 역시 정규적으로 분포됩니다. 그것은 정규 분포가 (지수 $\alpha =2$와 함께) 안정(stable)인 것을 따릅니다.

보다 일반적으로, 독립 정규 이탈의 임의의 선형 조합(linear combination)은 정규 이탈입니다.

Infinite divisibility and Cramér's theorem

임의의 양의 정수 ${\text{n}}$에 대해, 평균 $\mu$ 및 분산 $\sigma ^{2}$을 갖는 정규 분포는 평균 ${\frac {\mu }{n}}$ 및 분산 ${\frac {\sigma ^{2}}{n}}$을 갖는 각각이, ${\text{n}}$ 독립 정규 이탈의 합의 분포입니다. 이 속성은 무한 나눔가능성(infinite divisibility)으로 불립니다.

반대로, 만약 $X_{1}$와 $X_{2}$가 독립 확률 변수이고 그들의 합 $X_{1}+X_{2}$이 정규 분포를 가지면, $X_{1}$과 $X_{2}$ 둘 다가 반드시 정규 이탈이어야 합니다.

이 결과는 크라메르의 분해 정리(Cramér’s decomposition theorem)로 알려져 있고, 두 분포의 합성곱(convolution)이 정규인 것과 둘 다가 정규인 것은 필요충분 조건임을 말하는 것과 동등합니다. 크라메르의 정리는 독립 비-가우시안 변수의 선형 조합이, 비록 그것이 밀접하게 임의적으로 접근할 수 있을지라도, 정확하게 정규 분포를 절대 가질 수 없음을 의미합니다.

Bernstein's theorem

베른슈타인의 정리는 만약 $X$와 $Y$가 독립이고 $X+Y$와 $X-Y$가 역시 독립이면, X와 Y 둘 다는 반드시 필연적으로 정규 분포를 가짐을 말합니다.

보다 일반적으로, 만약 $X_{1},\ldots ,X_{n}$이 독립 확률 변수이면, 두 구별되는 선형 조합 $\sum {a_{k}X_{k}}$와 $\sum {b_{k}X_{k}}$이 독립일 것인 것과 모든 $X_{k}$가 정규이고$\sum {a_{k}b_{k}\sigma _{k}^{2}=0}$인 것과 필요충분 조건이며, 여기서 $\sigma _{k}^{2}$는 $X_{k}$의 분산을 나타냅니다.

Other properties

1. 만약 확률 변수 $X$의 특성 함수 $\phi _{X}$가 형식 $\phi _{X}(t)=\exp ^{Q(t)}$이며, 여기서 $Q(t)$가 다항식(polynomial)이면, (유제프 마르친키에비치(Józef Marcinkiewicz)의 이름을 따서 지은) 마르친키에비치 정리는 $Q$가 많아야 이차 다항식이고, 따라서 $X$는 정규 확률 변수임을 주장합니다. 이 결과의 결론은 정규 분포는 비-영 누적(cumulant)의 (둘) 유한 숫자를 갖는 유일한 분포라는 것입니다.
2. 만약 $X$와 $Y$가 결합적으로 정규(jointly normal)이고 비-상관(uncorrelated)이면, 그들은 독립(independent)입니다. $X$ and $Y$가 결합적으로 정규이어야 하는 요구-조건은 본질적입니다; 그것없이 속성은 유지되지 않습니다.^[proof] 비-정규 확률 변수에 대해, 비-상관성은 독립을 의미하지 않습니다.
3. 또 다른 $X_{2}\sim N(\mu _{2},\sigma _{2}^{2})$에서 하나의 정규 분포 $X_{1}\sim N(\mu _{1},\sigma _{1}^{2})$의 쿨백–라이블러 발산(Kullback–Leibler divergence)은 다음에 의해 제공됩니다:

   $D_{\mathrm {KL} }(X_{1}\,\|\,X_{2})={\frac {(\mu _{1}-\mu _{2})^{2}}{2\sigma _{2}^{2}}}+{\frac {1}{2}}\left({\frac {\sigma _{1}^{2}}{\sigma _{2}^{2}}}-1-\ln {\frac {\sigma _{1}^{2}}{\sigma _{2}^{2}}}\right)$

   같은 분포 사이의 헬링거 거리(Hellinger distance)는 다음과 같습니다:

   $H^{2}(X_{1},X_{2})=1-{\sqrt {\frac {2\sigma _{1}\sigma _{2}}{\sigma _{1}^{2}+\sigma _{2}^{2}}}}e^{-{\frac {1}{4}}{\frac {(\mu _{1}-\mu _{2})^{2}}{\sigma _{1}^{2}+\sigma _{2}^{2}}}}$

4. 정규 분포에 대해 피셔 정보 행렬(Fisher information matrix)은 대각 행렬이고 다음 형식을 취합니다:
   ${\mathcal {I}}={\begin{pmatrix}{\frac {1}{\sigma ^{2}}}&0\\0&{\frac {1}{2\sigma ^{4}}}\end{pmatrix}}$
5. 정규 분포의 평균의 켤레 이전(conjugate prior)은 또 다른 정규 분포입니다. 구체적으로 특별히, 만약 $x_{1},\ldots ,x_{n}$이 iid $\sim N(\mu ,\sigma ^{2})$이고 이전은 $\mu \sim N(\mu _{0},\sigma _{0}^{2})$이면, $\mu$의 추정기에 대해 이후 분포는 다음일 것입니다:
   $\mu \mid x_{1},\ldots ,x_{n}\sim {\mathcal {N}}\left({\frac {{\frac {\sigma ^{2}}{n}}\mu _{0}+\sigma _{0}^{2}{\bar {x}}}{{\frac {\sigma ^{2}}{n}}+\sigma _{0}^{2}}},\left({\frac {n}{\sigma ^{2}}}+{\frac {1}{\sigma _{0}^{2}}}\right)^{-1}\right)$
6. 정규 분포의 가족은 지수 가족(exponential family) (EF)을 형성할 뿐만 아니라, 사실 이차 분산 함수(variance function) (NEF-QVF)를 갖는 자연스러운 지수 가족(natural exponential family) (NEF)를 형성합니다. 정규 분포의 많은 속성이 일반적으로 NEF-QVF 분포, NEF 분포, 또는 EF 분포의 속성으로 일반화됩니다. NEF-QVF 분포는 6 가족을 이루며, 푸아송, 감마, 이항, 및 음의 이항 분포를 포함하지만, 확률과 통계에서 연구된 공통 가족의 많은 것은 NEF 또는 EF입니다.
7. 정보 기하(information geometry)에서, 정규 분포의 가족은 상수 곡률(constant curvature) $-1$을 갖는 통계적 매니폴드(statistical manifold)를 형성합니다. 같은 가족은 (±1)-연결 ∇$^{(e)}$ 및 ∇$^{(m)}$에 관한 평탄(flat)입니다.

Related distributions

Central limit theorem

As the number of discrete events increases, the function begins to resemble a normal distribution

Comparison of probability density functions, $p(k)$ for the sum of $n$ fair 6-sided dice to show their convergence to a normal distribution with increasing $na$, in accordance to the central limit theorem. In the bottom-right graph, smoothed profiles of the previous graphs are rescaled, superimposed and compared with a normal distribution (black curve).

Main article: Central limit theorem

중심 극한 정리는 특정 (꽤 공통) 조건 아래에서, 많은 확률 변수의 합이 근사적으로 정규 분포를 가질 것이라고 말합니다. 보다 구체적으로, 여기서 $X_{1},\ldots ,X_{n}$가 같은 임의의 분포, 영 평균, 및 분산 $\sigma ^{2}$ 및 $Z$가 ${\sqrt {n}}$에 의해 스케일된 그들의 평균을 갖는 독립이고 동일하게 분포된(independent and identically distributed) 확률 변수입니다:

$Z={\sqrt {n}}\left({\frac {1}{n}}\sum _{i=1}^{n}X_{i}\right)$

그런-다음, $n$이 증가할 때, $Z$의 확률 분포는 영 평균과 분산 $\sigma ^{2}$를 갖는 정규 분포로 경향일 것입니다.

그 정리는 만약 특정 구속-조건이 의존의 정도와 분포의 모멘트에 올려지면 독립이 아니고/아니거나 동일하게 분포되지 않은 변수 $(X_{i})$로 확장될 수 있습니다.

실제에서 발생하는 많은 테스트 통계량(test statistic), 점수(scores), 및 추정기(estimator)는 특정 확률 변수의 합을 포함하고, 훨씬 더 많은 추정기는 영향 함수(influence functions)의 사용을 통해 확률 변수의 합으로 표시될 수 있습니다. 중심 극한 정리는 그들의 통계적 매개-변수가 점근적으로 정규 분포를 가질 것임을 의미합니다.

중심 극한 정리는 특정 분포가 정규 분포에 의해 근사될 수 있음을 역시 의미합니다. 예를 들어:

• 이항 분포(binomial distribution) $B(n,p)$는 큰 $n$에 대해 및 0 또는 1과 너무 가까지 않는 $p$에 대해 평균 $np$와 분산 $np(1-p)$을 갖는 근사적으로 정규(approximately normal)입니다.
• 매개-변수 $\lambda$를 갖는 푸아송 분포(Poisson distribution)는 $\lambda$의 큰 값에 대해 평균 $\lambda$와 분산 $\lambda$를 갖는 근사적으로 정규입니다.
• 카이-제곱된 분포(chi-squared distribution) $\chi ^{2}(k)$는 큰 $k$에 대해 평균 $k$와 분산 $2k$를 갖는 근사적으로 정규입니다.
• 스튜던트의 t-분포(Student's t-distribution) $t(\nu )$는 $\nu$가 클 때 평균 0과 분산 1을 갖는 근사적으로 정규입니다.

이들 근사가 충분히 정확한지 여부는 그들이 필요되는 것에 대해 목적, 및 정규 분포에 대한 수렴의 율에 따라 다릅니다. 전형적으로 그러한 근사가 분포의 꼬리에서 덜 정확한 경우입니다.

중심 극한 정리에서 근사 오차에 대해 일반적인 위쪽 경계는 베리–에센 정리(Berry–Esseen theorem)에 의해 제공되며, 근사의 개선은 에지워스 확장(Edgeworth expansion)에 의해 제공됩니다.

Operations on a single random variable

만약 X가 평균 μ와 분산 σ²을 갖는 정규적으로 분포되면,

• X의 지수는 로그-정규적으로(log-normally): e^X ~ ln(N (μ, σ²))으로 분포됩니다.
• X의 절댓값은 겹화 정규 분포(folded normal distribution): |X| ~ N_f (μ, σ²)을 가집니다. 만약 μ = 0이면, 이것은 반-정규 분포(half-normal distribution)로 알려져 있습니다.
• 정규화된 잔여의 절댓값, |X − μ|/σ은 일 자유도를 갖는 차이 분포(chi distribution): |X − μ|/σ ~ $\chi _{1}$를 가집니다.
• X/σ의 제곱은 일 자유도를 갖는 비-중심 카이-제곱된 분포(noncentral chi-squared distribution): X²/σ² ~ $\chi _{1}^{2}$(μ²/σ²)를 가집니다. 만약 μ = 0이면, 분포는 간단히 chi-squared(카이-제곱된)으로 불립니다.
• 구간 [a, b]로 제한된 변수 X의 분포는 잘린 정규 분포(truncated normal distribution)로 불립니다.
• (X − μ)⁻²는 위치 0과 스케일 σ⁻²을 갖는 리비 분포(Lévy distribution)를 가집니다.

Combination of two independent random variables

만약 $X_{1}$와 $X_{2}$는 평균 0과 분산 1을 갖는 두 독립 표준 정규 확률 변수이면,

• 그들의 합과 차는 평균 영과 분산 이를 갖는 정규적으로 분포됩니다: $X_{1}\pm X_{2}\sim N(0,2)$.
• 그들의 곱 $Z=X_{1}X_{2}$는 밀도 함수 $f_{Z}(z)=\pi ^{-1}K_{0}(|z|)$를 갖는 "곱-정규" 분포를 따르며 여기서 $K_{0}$는 두 번째 종류의 수정된 베셀 함수(modified Bessel function of the second kind)입니다. 이 분포는 영 주위에 대칭, $z=0$에서 비경계진 것이고, 특성 함수(characteristic function) $\phi _{Z}(t)=(1+t^{2})^{-1/2}$를 가집니다.
• 그들의 비율은 표준 코시 분포(Cauchy distribution): $X_{1}/X_{2}\sim \operatorname {Cauchy} (0,1)$를 따릅니다.
• 그들의 유클리드 노름 ${\sqrt {X_{1}^{2}+X_{2}^{2}}}$은 레일리 분포(Rayleigh Distribution)를 따릅니다.

Combination of two or more independent random variables

• 만약 $X_{1},X_{2},\ldots ,X_{n}$가 독립 표준 정규 확률 변수이면, 그들의 제곱의 합은 ${\text{n}}$ 자유도를 갖는 카이-제곱된 분포(chi-squared distribution)를 가집니다:

$X_{1}^{2}+\cdots +X_{n}^{2}\sim \chi _{n}^{2}.$

• 만약 $X_{1},X_{2},\ldots ,X_{n}$가 평균 $\mu$와 분산 $\sigma ^{2}$을 갖는 독립 정규적으로 분포된 확률 변수이면, 그들의 표본 평균(sample mean)은 표본 표준 편차(standard deviation)으로부터 독립이며, 이것은 바수의 정리(Basu's theorem) 또는 카크랜의 정리(Cochran's theorem)를 사용하여 시연될 수 있습니다. 이들 두 양의 비율은 ${\text{n}}-1$ 자유도를 갖는 스튜던트의 t-분포(Student's t-distribution)를 가질 것입니다:

$t={\frac {{\overline {X}}-\mu }{S/{\sqrt {n}}}}={\frac {{\frac {1}{n}}(X_{1}+\cdots +X_{n})-\mu }{\sqrt {{\frac {1}{n(n-1)}}\left[(X_{1}-{\overline {X}})^{2}+\cdots +(X_{n}-{\overline {X}})^{2}\right]}}}\sim t_{n-1}.$

• 만약 $X_{1},X_{2},\ldots ,X_{n}$, $Y_{1},Y_{2},\ldots ,Y_{m}$이 독립 표준 정규 확률 변수이면, 제곱의 정규화된 합의 비율이 (n, m) 자유도를 갖는 F-분포(F-distribution)를 가질 것입니다:

$F={\frac {\left(X_{1}^{2}+X_{2}^{2}+\cdots +X_{n}^{2}\right)/n}{\left(Y_{1}^{2}+Y_{2}^{2}+\cdots +Y_{m}^{2}\right)/m}}\sim F_{n,m}.$

Operations on the density function

분할 정규 분포(split normal distribution)는 다른 정규 분포의 밀도 함수의 스케일링된 섹션을 결합하고 밀도를 다시 스케일링하여 하나에 통합하는 관점에서 가장 직접적으로 정의됩니다. 잘린 정규 분포(truncated normal distribution)는 단일 밀도 함수의 섹션을 다시-스케일링으로부터 생성됩니다.

Extensions

확률 이론에서 가장 중요한 분포 중 하나, 정규 분포 개념은 일변수 (즉 일-차원) 경우 (Case 1)의 표준 프레임워크를 훨씬 넘어서 확장되어 왔습니다. 모든 이들 확장은 정규 또는 가우시안 법칙으로 역시 불리우므로, 이름에서 특정한 모호성이 존재합니다.

• 다변수 정규 분포(multivariate normal distribution)는 k-차원 유클리드 공간(Euclidean space)에서 가우시안 법칙을 묘사합니다. 벡터 X ∈ R^k는 만약 그의 성분의 임의의 선형 조합 ∑^k
  _j=1a_j X_j이 (일변수) 정규 분포를 가지면 다변수-정규적으로 분포됩니다. X의 분산은 k×k 대칭 양의-한정하는 행렬 V입니다. 다변수 정규 분포는 타원형 분포(elliptical distribution)의 특별한 경우입니다. 마찬가지로, k = 2 경우에서 그의 등-밀도 궤적은 타원(ellipse)이고 임의의 k의 경우에서 타원면체(ellipsoid)입니다.
• 정류된 가우시안 분포(Rectified Gaussian distribution): 모든 음의 원소를 0으로 재설정하는 정규 분포의 정류된 버전
• 복소 정규 분포(complex normal distribution)는 복소 정규 벡터를 다룹니다. 복소 벡터 X ∈ C^k는 마약 실수와 허수 성분 둘 다가 2k-자원 다변수 정규 분포를 결합적으로 소유하면 정규로 말합니다. X의 분산-공분산 구조는 두 행렬: 분산 행렬 Γ, 및 관계 행렬 C에 의해 묘사됩니다.
• 행렬 정규 분포(matrix normal distribution)는 정규적으로 분포된 행렬의 경우를 묘사합니다.
• 가우시안 과정(Gaussian process)은 정규적으로 분포된 확률 과정(stochastic process)입니다. 이들은 일부 무한-차원 힐베르트 공간(Hilbert space) H의 원소로 보일 수 있고, 따라서 경우 k = ∞에 대해 다변수 정규 벡터의 아날로그입니다. 확률 원소 h ∈ H는 만약 임의의 상수 a ∈ H에 대해 스케일 곱(scalar product) (a, h)가 (일변수) 정규 분포를 가지면 정규라고 말합니다. 그러한 가우시안 확률 원소의 분산 구조는 선형 공분산 operator K: H → H의 관점에서 묘사될 수 있습니다. 여러 가우시안 과정은 자체 이름을 가질 정도로 충분히 대중화되었습니다:
  • 브라운 운동(Brownian motion),
  • 브라운 다리(Brownian bridge),
  • 오언스타인–율린벡 과정(Ornstein–Uhlenbeck process).
• 가우시안 q-분포(Gaussian q-distribution)는 정규 분포의 "q-아날로그(q-analogue)"를 나타내는 추상적인 수학적 구조입니다.
• q-가우시안(q-Gaussian)은, 그것이 트살리스 엔트로피(Tsallis entropy)를 최대화하고, 트살리스 분포(Tsallis distribution)의 한 유형이라는 의미에서, 가우시안 분포의 아날로그입니다. 이 분포는 위의 가우시안 q-분포(Gaussian q-distribution)와 다름에 주목하십시오.

확률 변수 X가 만약 그것이 다음 분포를 가지면 두-조각 정규 분포를 가집니다:

$f_{X}(x)=N(\mu ,\sigma _{1}^{2}){\text{ if }}x\leq \mu$

$f_{X}(x)=N(\mu ,\sigma _{2}^{2}){\text{ if }}x\geq \mu$

여기서 μ는 평균이고 σ₁과 σ₂는 각각 평균의 왼쪽과 오른쪽에 대한 분포의 표준 편차입니다.

이 분포의 평균, 분산 및 세 번째 중심 모멘트는 결정되어 왔습니다:

$\operatorname {E} (X)=\mu +{\sqrt {\frac {2}{\pi }}}(\sigma _{2}-\sigma _{1})$

$\operatorname {V} (X)=\left(1-{\frac {2}{\pi }}\right)(\sigma _{2}-\sigma _{1})^{2}+\sigma _{1}\sigma _{2}$

$\operatorname {T} (X)={\sqrt {\frac {2}{\pi }}}(\sigma _{2}-\sigma _{1})\left[\left({\frac {4}{\pi }}-1\right)(\sigma _{2}-\sigma _{1})^{2}+\sigma _{1}\sigma _{2}\right]$

여기서 E(X), V(X) 및 T(X)는 각각 평균, 분산, 및 세 번째 중심 모멘트입니다.

가우시안 법칙의 주요 실제적인 사용의 하나는 실제에서 부딪히는 많은 다른 확률 변수의 경험적 분포를 모델하는 것입니다. 그러한 경우에서 가능한 확장은 분포의 더 풍분한 가족이 될 것이며, 둘 보다 많은 매개-변수를 가지고 따라서 보다 정확하게 경험적 분포에 맞추는 것이 가능합니다. 그러한 확장의 예제는 다음입니다:

• 피어슨 분포(Pearson distribution) — 정규 법칙을 다른 기울어짐과 뾰족 값을 포함하도록 확장하는 확률 분포의 넷-매개변수 가족.
• 일반화된 정규 분포(generalized normal distribution)는, 역시 지수 거듭제곱 분포로 알려져 있음, 더 두꺼운 또는 더 얇은 점근적 행동을 갖는 분포를 허용합니다.

Statistical Inference

Estimation of parameters

See also: Maximum likelihood § Continuous distribution, continuous parameter space

우리가 정규 분포의 매개-변수를 알지 못하지만, 대신에 그들을 추정(estimate)하기를 원하는 경우가 종종 있습니다. 즉, 정규 $N(\mu ,\sigma ^{2})$ 모집단으로부터 표본 $(x_{1},\ldots ,x_{n})$을 가지면, 우리는 매개-변수 $\mu$와 $\sigma ^{2}$의 근사적인 값을 배우기를 원할 것입니다. 이 문제에 대한 표준 접근은 최대 가능성(maximum likelihood) 방법이며, 이것은 로그-가능성 함수를 최대화를 요구합니다:

$\ln {\mathcal {L}}(\mu ,\sigma ^{2})=\sum _{i=1}^{n}\ln f(x_{i}\mid \mu ,\sigma ^{2})=-{\frac {n}{2}}\ln(2\pi )-{\frac {n}{2}}\ln \sigma ^{2}-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}.$

$\mu$와 $\sigma ^{2}$에 관해 도함수를 취하고 첫 번째 차수 조건의 결과 시스템을 풀면 최대 가능성 추정을 산출합니다:

${\hat {\mu }}={\overline {x}}\equiv {\frac {1}{n}}\sum _{i=1}^{n}x_{i},\qquad {\hat {\sigma }}^{2}={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}.$

Sample mean

See also: Standard error of the mean

추정기 $\textstyle {\hat {\mu }}$는 표본 평균(sample mean)으로 불리는데, 왜냐하면 그것은 모든 관측의 산술 평균이기 때문입니다. 통계량 $\textstyle {\overline {x}}$은 $\mu$에 대해 완전(complete) 및 충분(sufficient)이고, 따라서 레만–셰페 정리(Lehmann–Scheffé theorem)에 의해, $\textstyle {\hat {\mu }}$는 균등하게 최소 분산 불-편향(uniformly minimum variance unbiased) (UMVU) 추정기입니다. 유한 표본에서 그것은 정규적으로 분포됩니다:

${\hat {\mu }}\sim {\mathcal {N}}(\mu ,\sigma ^{2}/n).$

이 추정기의 분산은 역 피셔 정보 행렬(Fisher information matrix) $\textstyle {\mathcal {I}}^{-1}$의 μμ-원소와 같습니다. 이것은 추정기가 유한-표본 효율적(finite-sample efficient)임을 의미합니다. 실제로 중요한 것은 $\textstyle {\hat {\mu }}$의 표준 오류(standard error)가 $\textstyle 1/{\sqrt {n}}$에 비례한다는 것입니다. 즉, 만약 우리가 표준 오차를 10의 인수로 줄이려면, 우리는 표본에서 점의 숫자를 100의 인수로 늘려야 합니다. 이 사실은 몬테-카를로 시뮬레이션(Monte Carlo simulation)에서 여론 조사의 표본의 크기와 시행의 횟수를 결정하는 데 널리 사용됩니다.

점근적 이론(asymptotic theory)의 관점에서, $\textstyle {\hat {\mu }}$은 일관적입니다. 즉 그것은 $n\rightarrow \infty$일 때 $\mu$로 확률에서 수렴(converges in probability)합니다. 그 추정기는 역시 점근적으로 정규(asymptotically normal)이며, 이것은 유한 표본에서 정규라는 사실의 간단한 따름정리입니다:

${\sqrt {n}}({\hat {\mu }}-\mu )\,\xrightarrow {d} \,{\mathcal {N}}(0,\sigma ^{2}).$

Sample variance

See also: Standard deviation § Estimation, and Variance § Estimation

추정기 $\textstyle {\hat {\sigma }}^{2}$는 표본 분산(sample variance)으로 불리는데, 왜냐하면 그것은 표본 ($(x_{1},\ldots ,x_{n})$)의 분산이기 때문입니다. 실제에서, 또 다른 추정기는 $\textstyle {\hat {\sigma }}^{2}$ 대신에 자주 사용됩니다. 이 다른 추정기는 $s^{2}$으로 표시되고, 역시 표본 분산으로 불리며 이것은 용어에서 특정 모호성을 나타냅니다; 그것의 제곱근 $s$는 표본 표준 편차로 불립니다. 추정기 $s^{2}$는 분모에서 n 대신에 (n − 1)을 가짐으로써 $\textstyle {\hat {\sigma }}^{2}$와 다릅니다 (소위 베젤의 보정(Bessel's correction)입니다):

$s^{2}={\frac {n}{n-1}}{\hat {\sigma }}^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}.$

$s^{2}$과 $\textstyle {\hat {\sigma }}^{2}$ 사이의 차이는 큰 n'에 대해 무시할 정도로 작게 됩니다. 유한 표본에서 어쨌든, $s^{2}$의 사용에 숨겨진 동기는 그것이 놓여-있는 매개-변수 $\sigma ^{2}$의 불-편향 추정기(unbiased estimator)이지만, $\textstyle {\hat {\sigma }}^{2}$은 편향된 것입니다. 역시, 레만–셰페 정리(Lehmann–Scheffé theorem)에 의해 추정기 $s^{2}$은 균등한 최소 분산 불-편향 (UMVU)이며 이것은 모든 불-편향인 것 중에서 "최고의" 추정기입니다. 어쨌든 편향된 추정기 $\textstyle {\hat {\sigma }}^{2}$가 평균 제곱된 오차(mean squared error) (MSE) 기준의 관점에서 $s^{2}$보다 "더 나은" 것으로 표시될 수 있습니다. 유한 표본에서 $s^{2}$와 $\textstyle {\hat {\sigma }}^{2}$ 둘 다는 (n − 1) 자유도를 가진 카이-제곱된 분포(chi-squared distribution)를 가집니다.

$s^{2}\sim {\frac {\sigma ^{2}}{n-1}}\cdot \chi _{n-1}^{2},\qquad {\hat {\sigma }}^{2}\sim {\frac {\sigma ^{2}}{n}}\cdot \chi _{n-1}^{2}.$

이들 표현의 첫 번째는 $s^{2}$의 분산이 $2\sigma ^{4}/(n-1)$과 같으며, 이것은 역 피셔 정보 행렬 $\textstyle {\mathcal {I}}^{-1}$의 σσ-원소보다 약간 더 큼을 보입니다. 따라서, $s^{2}$은 $\sigma ^{2}$보다 효율적인 추정기가 아니고, 게다가, $s^{2}$이 UMVU이므로, 우리는 $\sigma ^{2}$에 대해 유한-표본 효율적인 추정기가 존재하지 않는다는 결론을 내릴 수 있습니다.

점근적 이론을 적용하면, 추정기 $s^{2}$와 $\textstyle {\hat {\sigma }}^{2}$ 둘 다는 일관적입니다. 즉, 그들은 표본 크기 $n\rightarrow \infty$일 때 확률에서 $\sigma ^{2}$로 수렴합니다. 두 추정기는 역시 둘 다 점근적으로 정규입니다:

${\sqrt {n}}({\hat {\sigma }}^{2}-\sigma ^{2})\simeq {\sqrt {n}}(s^{2}-\sigma ^{2})\,\xrightarrow {d} \,{\mathcal {N}}(0,2\sigma ^{4}).$

특히, 추정기 둘 다는 $\sigma ^{2}$에 대해 점근적으로 효율적입니다.

Confidence intervals

See also: Studentization

카크랜의 정리(Cochran's theorem)에 의해, 정규 분포에 대해 표본 평균 $\textstyle {\hat {\mu }}$과 표본 분산 s²가 독립(independent)이며, 이것은 결합 분포(joint distribution)를 고려하는 것에서 이득이 없음을 의미합니다. 반대 이론이 역시 있습니다: 만약 표본에서 표본 평균과 표본 분산이 독립이면, 표본은 정규 분포에서 나온 것이어야 합니다. $\textstyle {\hat {\mu }}$와 s 사이의 독립은 소위 t-통계량을 구성하기 위해 사용될 수 있습니다:

$t={\frac {{\hat {\mu }}-\mu }{s/{\sqrt {n}}}}={\frac {{\overline {x}}-\mu }{\sqrt {{\frac {1}{n(n-1)}}\sum (x_{i}-{\overline {x}})^{2}}}}\sim t_{n-1}$

이 양 t는 (n − 1) 자유도를 갖는 스튜던트의 t-분포(Student's t-distribution)를 가지고, 그것은 보조 통계량(ancillary statistic) (매개-변수의 값의 독립)입니다. 이 t-통계의 분포를 역화하면 μ에 대해 신뢰 구간(confidence interval)을 구성하는 것을 허용할 것입니다; 비슷하게, 통계량 s²의 χ² 분포를 역화하면, σ²에 대해 신뢰 구간을 제공할 것입니다:

$\mu \in \left[{\hat {\mu }}-t_{n-1,1-\alpha /2}{\frac {1}{\sqrt {n}}}s,{\hat {\mu }}+t_{n-1,1-\alpha /2}{\frac {1}{\sqrt {n}}}s\right]\approx \left[{\hat {\mu }}-|z_{\alpha /2}|{\frac {1}{\sqrt {n}}}s,{\hat {\mu }}+|z_{\alpha /2}|{\frac {1}{\sqrt {n}}}s\right],$

$\sigma ^{2}\in \left[{\frac {(n-1)s^{2}}{\chi _{n-1,1-\alpha /2}^{2}}},{\frac {(n-1)s^{2}}{\chi _{n-1,\alpha /2}^{2}}}\right]\approx \left[s^{2}-|z_{\alpha /2}|{\frac {\sqrt {2}}{\sqrt {n}}}s^{2},s^{2}+|z_{\alpha /2}|{\frac {\sqrt {2}}{\sqrt {n}}}s^{2}\right],$

여기서 t_k,p와 χ 2
k,p 는 각각 t- 및 χ²-분포의 p번째 분위-숫자(quantile)입니다. 이들 신뢰 구간은 신뢰 수준(confidence level) 1 − α의 것이며, 참값 μ와 σ²이 확률 (또는 유의 수준(significance level)) α를 갖는 이들 구간의 밖에 떨어지는 것을 의미합니다. 실제에서 사람들은 보통 α = 5%를 취하며, 95% 신뢰 구간을 초래합니다. 위에서 보인 근사 공식은 $\textstyle {\hat {\mu }}$와 s²의 점근 분포에서 유도됩니다. 근사 공식은 n의 큰 값에 대해 유효하게 되고, 수동 계산에 대해 보다 편리한데 왜냐하면 표준 정규 분위-숫자 z_α/2는 n에 의존하지 않기 때문입니다. 특히 α = 5%의 가장 인기있는 값은 |z_0.025| = 1.96를 낳습니다.

Normality tests

Main article: Normality tests

정규성 테스트는 주어진 데이터 집합 {x₁, ..., x_n}이 정규 분포에서 나올 가능성을 평가합니다. 전형적으로 무 가설(null hypothesis) H₀는 관측이 지정되지 않은 평균 μ와 분산 σ²를 갖는 정규적으로 분포되는 것과 비교하여, 대안적인 H_a는 분포가 임의의 것입니다. 많은 테스트 (40개 이상)가 이 문제에 대해 고안되어 왔으며, 그 중에 보다 두드러진 것은 아래에 요약됩니다:

• "시각적" 테스트는 보다 직관적으로 호소력이 있지만 동시에 주관적인데, 왜냐하면 그들은 무 가설을 수용 또는 거부하는 것에 비공식적 인간의 판단에 의존하기 때문입니다.
  • Q-Q 그림(Q-Q plot)은 표준 정규 분포에서 해당하는 분위-숫자의 기댓값에 대항하는 데이터 집합에서 정렬된 값의 그림입니다. 즉, 그것은 그려지는 점 p_k가 p_k = (k − α)/(n + 1 − 2α)과 같고 α는 0과 1 사이의 임의의 값이 될 수 있는 저장 상수인, 형식 (Φ⁻¹(p_k), x_(k))의 점의 그림입니다. 만약 무 가설이 참이면, 그려진 점은 근사적으로 직선 위에 놓여야 합니다.
  • P-P 그림(P-P plot)는 Q-Q 그림과 유사하지만, 훨씬 덜 자주 사용됩니다. 이 방법은 점 (Φ(z_(k)), p_k)를 그리는 것으로 구성되며, 여기서 $\textstyle z_{(k)}=(x_{(k)}-{\hat {\mu }})/{\hat {\sigma }}$입니다. 정규 분포 데이터에 대해, 이 그림은 (0, 0)과 (1, 1) 사이의 45° 직선 위에 놓여야 합니다.
  • 샤피로-윌크 테스트(Shapiro-Wilk test)는 Q-Q 그림에서 직선이 σ의 기울기를 가지는 사실을 사용합니다. 테스트는 해당 기울기의 최소 제곱 추정과 표본 분산을 비교하고, 마약 이들 두 양이 크게 다르면, 무 가설을 배척합니다.
  • 정규 확률 그림(normal probability plot) (랭킷(rankit) 그림)
• 모멘트 테스트:
  • 다그스티노 K-제곱된 테스트(D'Agostino's K-squared test)
  • 하르케–베라 테스트(Jarque–Bera test)
• 경험적 분포 함수 테스트:
  • 릴리펄스 테스트(Lilliefors test) (콜모고로프–스미르노프 테스트(Kolmogorov–Smirnov test)의 적응)
  • 앤더슨–달링 테스트(Anderson–Darling test)

Bayesian analysis of the normal distribution

정규적으로 분포된 데이터의 베이즈 해석은 고려될 수 있는 많은 다른 가능성에 의해 복잡하게 됩니다:

• 평균, 또는 분산 중 하나, 또는 둘 다 아닌 것이 고정된 양으로 고려될 수 있습니다.
• 분산이 미지수일 때, 해석은 분산의 관점, 또는 정밀도(precision), 즉, 분산의 역수의 관점에서 직접 행해질 수 있습니다. 정밀도의 관점에서 공식을 표현하는 이유는 대부분 경우의 해석은 단순화되는 것입니다.
• 일변수 및 다변수(multivariate) 경우 둘 다는 고려되어야 합니다.
• 켤레(conjugate) 또는 부적절한(improper) 이전 분포(prior distribution) 중 하나는 미지수 변수에 배치될 수 있습니다.
• 추가적인 경우의 집합은 베이즈 선형 회귀(Bayesian linear regression)에서 발생하며, 여기서 기본 모델에서 데이터는 정규적으로 분포된 것으로 가정되고, 정규 이전은 회귀 계수(regression coefficient)로 배치됩니다. 결과 해석은 독립 동일하게 분포된(independent identically distributed) 데이터의 기본 경우와 비슷하지만 보다 복잡합니다.

비-선형 회귀 경우에 대해 공식은 켤레 이전(conjugate prior) 기상에서 요약됩니다.

Sum of two quadratics

Scalar form

다음 보조 공식은 이후(posterior) 업데이트 방정식을 단순화하는 데 유용하며, 그렇지 않으면 상당히 지루합니다.

$a(x-y)^{2}+b(x-z)^{2}=(a+b)\left(x-{\frac {ay+bz}{a+b}}\right)^{2}+{\frac {ab}{a+b}}(y-z)^{2}$

이 방정식은 제곱을 전개하고,x에서 항을 그룹화하고, 제곱식을 완성(completing the square)함으로써 x에서 두 이차의 합을 다시-씁니다. 일부 항에 첨부된 복소 상수 인수에 대한 다음을 주목하십시오:

1. 인수 ${\frac {ay+bz}{a+b}}$는 y와 z의 가중된 평균(weighted average)의 형식을 가집니다.
2. ${\frac {ab}{a+b}}={\frac {1}{{\frac {1}{a}}+{\frac {1}{b}}}}=(a^{-1}+b^{-1})^{-1}.$

이것은 이 인수가 양 a와 b의 역수(reciprocals)를 직접 더한 상황에서 비롯된 것으로 생각될 수 있으며, a와 b를 결합하기 위해, 역수를 취하고, 더하고, 원래 단위로 돌아오기 위해 결과를 다시 역수 취하는 것이 요구됨을 보여줍니다. 이것은 정확히 조화 평균(harmonic mean)에 의해 수행되는 연산의 일종이므로, ${\frac {ab}{a+b}}$가 a와 b의 조화 평균(harmonic mean)의 절반이라는 것은 놀라운 일이 아닙니다.

Vector form

비슷한 공식은 두 벡터 이차의 합에 대해 쓸 수 있습니다: 만약 x, y, z가 길이 k의 벡터이고, A와 B가 크기 $k\times k$의 대칭(symmetric), 역-가능한 행렬(invertible matrices)이면,

${\begin{aligned}&(\mathbf {y} -\mathbf {x} )'\mathbf {A} (\mathbf {y} -\mathbf {x} )+(\mathbf {x} -\mathbf {z} )'\mathbf {B} (\mathbf {x} -\mathbf {z} )\\={}&(\mathbf {x} -\mathbf {c} )'(\mathbf {A} +\mathbf {B} )(\mathbf {x} -\mathbf {c} )+(\mathbf {y} -\mathbf {z} )'(\mathbf {A} ^{-1}+\mathbf {B} ^{-1})^{-1}(\mathbf {y} -\mathbf {z} )\end{aligned}}$

여기서

$\mathbf {c} =(\mathbf {A} +\mathbf {B} )^{-1}(\mathbf {A} \mathbf {y} +\mathbf {B} \mathbf {z} )$

형식 x′ A x가 이차 형식(quadratic form)으로 불리고 스칼라(scalar)임을 주목하십시오:

$\mathbf {x} '\mathbf {A} \mathbf {x} =\sum _{i,j}a_{ij}x_{i}x_{j}$

달리 말해서, 그것은 각각에 대해 별도의 계수를 갖는 x에서 원소의 쌍의 곱의 모든 가능한 조합을 요약합니다. 게다가, $x_{i}x_{j}=x_{j}x_{i}$이므로, 오직 합 $a_{ij}+a_{ji}$은 A의 임의의 대각선-이외의 원소에 중요하고, A가 대칭(symmetric)이라고 가정하는 것에서 일반성을 잃지 않습니다. 게다가, 만약 A가 대칭이면, 형식 $\mathbf {x} '\mathbf {A} \mathbf {y} =\mathbf {y} '\mathbf {A} \mathbf {x}$입니다.

Sum of differences from the mean

또 다른 유용한 공식은 다음과 같습니다:

$\sum _{i=1}^{n}(x_{i}-\mu )^{2}=\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}$

여기서 ${\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}$입니다.

With known variance

크기 n의 i.i.d. 정규적으로 분포된 데이터 점 X의 집합에 대해 여기서 각 개별 점 x는 알려진 분산(variance) σ²을 갖는 $x\sim {\mathcal {N}}(\mu ,\sigma ^{2})$을 따르며, 켤레 이전(conjugate prior) 분포는 역시 정규적으로 분포됩니다.

이것은 정밀도(precision), 즉, τ = 1/σ²을 사용하는 것으로 분산을 다시-씀으로써 보다 쉽게 보일 수 있습니다. 그런-다음 만약 $x\sim {\mathcal {N}}(\mu ,1/\tau )$ 및 $\mu \sim {\mathcal {N}}(\mu _{0},1/\tau _{0})$이면, 우리는 다음처럼 진행합니다.

먼저, 가능도 함수(likelihood function)는 다음입니다 (평균으로부터 차이의 합에 대해 위의 공식을 사용합니다):

${\begin{aligned}p(\mathbf {X} \mid \mu ,\tau )&=\prod _{i=1}^{n}{\sqrt {\frac {\tau }{2\pi }}}\exp \left(-{\frac {1}{2}}\tau (x_{i}-\mu )^{2}\right)\\&=\left({\frac {\tau }{2\pi }}\right)^{n/2}\exp \left(-{\frac {1}{2}}\tau \sum _{i=1}^{n}(x_{i}-\mu )^{2}\right)\\&=\left({\frac {\tau }{2\pi }}\right)^{n/2}\exp \left[-{\frac {1}{2}}\tau \left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)\right].\end{aligned}}$

그런-다음, 우리는 다음처럼 진행합니다:

${\begin{aligned}p(\mu \mid \mathbf {X} )&\propto p(\mathbf {X} \mid \mu )p(\mu )\\&=\left({\frac {\tau }{2\pi }}\right)^{n/2}\exp \left[-{\frac {1}{2}}\tau \left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)\right]{\sqrt {\frac {\tau _{0}}{2\pi }}}\exp \left(-{\frac {1}{2}}\tau _{0}(\mu -\mu _{0})^{2}\right)\\&\propto \exp \left(-{\frac {1}{2}}\left(\tau \left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)+\tau _{0}(\mu -\mu _{0})^{2}\right)\right)\\&\propto \exp \left(-{\frac {1}{2}}\left(n\tau ({\bar {x}}-\mu )^{2}+\tau _{0}(\mu -\mu _{0})^{2}\right)\right)\\&=\exp \left(-{\frac {1}{2}}(n\tau +\tau _{0})\left(\mu -{\dfrac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}\right)^{2}+{\frac {n\tau \tau _{0}}{n\tau +\tau _{0}}}({\bar {x}}-\mu _{0})^{2}\right)\\&\propto \exp \left(-{\frac {1}{2}}(n\tau +\tau _{0})\left(\mu -{\dfrac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}\right)^{2}\right)\end{aligned}}$

위의 유도에서, 우리는 두 이차의 합에 대해 위의 공식을 사용하고 μ를 포함하지 않는 모든 상수 인수를 제거합니다. 그 결과는 평균 ${\frac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}$ 및 정밀도 $n\tau +\tau _{0}$를 갖는 정규 분포의 커널(kernel)이며, 즉,

$p(\mu \mid \mathbf {X} )\sim {\mathcal {N}}\left({\frac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}},{\frac {1}{n\tau +\tau _{0}}}\right)$

이것은 이전 매개-변수의 관점에서 이후 매개-변수에 대해 베이즈 업데이트 방정식의 집합으로 쓸 수 있습니다:

${\begin{aligned}\tau _{0}'&=\tau _{0}+n\tau \\\mu _{0}'&={\frac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}\\{\bar {x}}&={\frac {1}{n}}\sum _{i=1}^{n}x_{i}\end{aligned}}$

즉, n 데이터 점을 nτ의 전체 정밀도 (또는 동등하게, n/σ²의 전체 분산)와 값의 평균 ${\bar {x}}$와 결합하기 위해, 간단히 데이터의 전체 정밀도를 이전 전체 정밀도에 더함으로써 새로운 전체 정밀도를 도출하고, 정밀도-가중된 평균, 즉, 데이터 평균의 가중된 평균(weighted average) 및 이전 평균, 결합된 전체 정밀도에 의해 가중된 각각을 통해 새로운 평균을 형성합니다. 이것은 만약 정밀도가 관측의 확실성을 나타내는 것으로 생각되면 논리적 의미를 만듭니다: 이후 평균의 분포에서, 입력 성분의 각각은 그의 확실성에 의해 가중되고, 이 분포의 확실성은 개별 확실성의 합입니다. (이것의 직관에 대해, 표현 "전체가 그것의 부분의 합보다 크다 (또는 크지 않다)"를 비교하십시오. 게다가, 이후의 지식은 이전과 가능도의 지식의 조합에서 나온다는 점을 고려하므로, 우리는 그것의 성분 중 하나의 것보다 그것의 보다 확실한 것임에 의미가 있습니다.)

위의 공식은 정밀도의 관점에서 정규 분포에 대해 켤례 이전(conjugate prior)의 베이즈 해석(Bayesian analysis)을 행하는 것이 더 편리한 이유를 보여줍니다. 이후 정밀도는 단순히 이전과 가능도 정밀도의 합이고, 이후 평균은 위에서 묘사된 것처럼 정밀도-가중된 평균을 통해 계산됩니다. 같은 공식은 모든 정밀도를 역화함으로써 분산의 관점에서 쓸 수 있으며, 보더 심술궂은 수식을 생성합니다:

${\begin{aligned}{\sigma _{0}^{2}}'&={\frac {1}{{\frac {n}{\sigma ^{2}}}+{\frac {1}{\sigma _{0}^{2}}}}}\\\mu _{0}'&={\frac {{\frac {n{\bar {x}}}{\sigma ^{2}}}+{\frac {\mu _{0}}{\sigma _{0}^{2}}}}{{\frac {n}{\sigma ^{2}}}+{\frac {1}{\sigma _{0}^{2}}}}}\\{\bar {x}}&={\frac {1}{n}}\sum _{i=1}^{n}x_{i}\end{aligned}}$

With known mean

크기 n의 i.i.d. 정규적으로 분포된 데이터 점 X의 집합에 대해 여기서 각 개별 점 x는 알려진 평균 μ를 갖는 $x\sim {\mathcal {N}}(\mu ,\sigma ^{2})$를 따르며, 분산(variance)의 켤레 이전(conjugate prior)은 역 감마 분산(inverse gamma distribution) 또는 스케일된 역 카이-제곱된 분포(scaled inverse chi-squared distribution)를 가집니다. 그 둘은 다른 매개-변수화(parameterization)를 가지는 것을 제외하고 동등합니다. 비록 역 감마가 보도 공통적으로 사용될지라도, 우리는 편리의 목적에 대해 스케일된 역 카이-제곱된 것을 사용합니다. σ²에 대해 이전은 다음과 같습니다:

$p(\sigma ^{2}\mid \nu _{0},\sigma _{0}^{2})={\frac {(\sigma _{0}^{2}{\frac {\nu _{0}}{2}})^{\nu _{0}/2}}{\Gamma \left({\frac {\nu _{0}}{2}}\right)}}~{\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}\propto {\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}$

분산의 관점에서 쓰인, 위에서 처럼 가능도 함수(likelihood function)는 다음입니다:

${\begin{aligned}p(\mathbf {X} \mid \mu ,\sigma ^{2})&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}\right]\\&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {S}{2\sigma ^{2}}}\right]\end{aligned}}$

여기서

$S=\sum _{i=1}^{n}(x_{i}-\mu )^{2}.$

그런-다음:

${\begin{aligned}p(\sigma ^{2}\mid \mathbf {X} )&\propto p(\mathbf {X} \mid \sigma ^{2})p(\sigma ^{2})\\&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {S}{2\sigma ^{2}}}\right]{\frac {(\sigma _{0}^{2}{\frac {\nu _{0}}{2}})^{\frac {\nu _{0}}{2}}}{\Gamma \left({\frac {\nu _{0}}{2}}\right)}}~{\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}\\&\propto \left({\frac {1}{\sigma ^{2}}}\right)^{n/2}{\frac {1}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}\exp \left[-{\frac {S}{2\sigma ^{2}}}+{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]\\&={\frac {1}{(\sigma ^{2})^{1+{\frac {\nu _{0}+n}{2}}}}}\exp \left[-{\frac {\nu _{0}\sigma _{0}^{2}+S}{2\sigma ^{2}}}\right]\end{aligned}}$

위의 것은 역시 스케일된 역 카이-제곱된 분포이며 여기서

${\begin{aligned}\nu _{0}'&=\nu _{0}+n\\\nu _{0}'{\sigma _{0}^{2}}'&=\nu _{0}\sigma _{0}^{2}+\sum _{i=1}^{n}(x_{i}-\mu )^{2}\end{aligned}}$

또는 동등하게

${\begin{aligned}\nu _{0}'&=\nu _{0}+n\\{\sigma _{0}^{2}}'&={\frac {\nu _{0}\sigma _{0}^{2}+\sum _{i=1}^{n}(x_{i}-\mu )^{2}}{\nu _{0}+n}}\end{aligned}}$

역 감마 분포(inverse gamma distribution)의 관점에서 다시-매개변수화하면, 그 결과는 다음입니다:

${\begin{aligned}\alpha '&=\alpha +{\frac {n}{2}}\\\beta '&=\beta +{\frac {\sum _{i=1}^{n}(x_{i}-\mu )^{2}}{2}}\end{aligned}}$

With unknown mean and unknown variance

크기 n의 i.i.d. 정규적으로 분포된 데이터 점 X의 집합에 대해 여기서 각 개별 점 x가 미지수 평균 μ와 미지수 분산(variance) σ²을 갖는 $x\sim {\mathcal {N}}(\mu ,\sigma ^{2})$을 따르며, 조합된 (다변수) 켤레 이전(conjugate prior)은 평균과 분산에 걸쳐 배치되며, 정규-역-감마 분포(normal-inverse-gamma distribution)를 구성합니다. 논리적으로, 이것은 다음에서 기원합니다:

1. 미지수 평균이지만 알려진 분산을 갖는 경우의 해석으로부터, 우리는 업데이트 방정석이 데이터 점의 평균과 데이터 점의 전체 분산을 구성하는 데이터로부터 계산된, 차례로 알려진 분산을 데이터 점의 숫자로 나눈 것으로부터 계산된 충분 통계량(sufficient statistic)을 포함함을 압니다.
2. 미지수 분산과 알려진 평균을 갖는 경우의 해석으로부터, 우리는 업데이트 방정식이 데이터 점의 숫자와 제곱된 편차의 합(sum of squared deviations)을 구성하는 데이터에 걸쳐 충분 통계량을 포함함을 압니다.
3. 이후 업데이트 값은 추가 데이터가 처리될 때 이전 분포로 사용됨을 명심하십시오. 따라서, 우리가 같은 의미론을 가능한 한 많이 염두에 두고 방금 설명한 충분 통계량의 관점에서 이전을 논리적으로 생각해야 합니다.
4. 평균과 분산 둘 다가 미지수인 경우를 처리하기 위해, 우리는 평균 평균, 전체 분산, 분산 이전을 계산하기 위해 사용된 데이터 점의 숫자, 및 제곱된 편차의 합의 고정된 추정과 함께, 평균과 분산에 걸쳐 독립 이전을 배치할 수 있습니다. 어쨌든 실제에서, 평균의 전체 분산은 미지수 분산에 의존하고, 분산 이전에 들어가는 제곱된 편차의 합은 미지수 평균에 의존함을 주목하십시오. 실제에서, 후자의 의존성은 상대적으로 중요하지 않습니다; 실제 평균을 이동하면 생성된 점이 같은 양만큼 이동하고, 평균에서 제곱된 편차는 같은 것으로 남을 것입니다. 이것은 어쨌든 평균의 전체 분산을 갖는 경우는 아닙니다: 미지수 분산이 증가함에 따라, 평균의 전체 분산이 비례적으로 증가할 것이고, 우리는 이 의존성을 포착하고 싶을 것입니다.
5. 이것은 우리가, 이전과 결합된 유사-관측(pseudo-observation)의 평균을 지정하는 초-매개변수, 및 유사-관측의 숫자를 지정하는 또 다른 매개-변수와 함께, 미지수 분산에 대한 평균의 조건부 이전을 생성하는 것을 제안합니다. 이 숫자는 분산 위에 스케일링 매개-변수로 사용되며, 실제 분산 매개-변수에 관련된 평균의 전부의 분산을 제어하는 것을 가능하게 만듭니다. 분산에 대한 이전은 두 초-매개변수를 역시 가지며, 하나는 이전과 결합된 유사-관측의 제곱된 편차의 합을 지정하는 것, 및 다른 하나는 유사-관측의 숫자를 다시 한번 지정합니다. 이전의 각각은 유사-관측의 숫자를 지정하는 초-매개변수를 가지고, 각 경우에서 이것은 해당 이전의 상대 분산을 제어함을 주목하십시오. 이것들은 두 이전의 분산 (일명 신뢰도)가 개별적으로 제어될 수 있도록 두 개별 초-매개변수로 제공됩니다.
6. 이것은 정규-역-감마 분포(normal-inverse-gamma distribution)로 즉시 이어지며, 이것은 사용된 켤레 이전(conjugate prior) (분산에 걸쳐 역 감마 분포(inverse gamma distribution), 및 분산 위에 조건부, 평균에 걸쳐 정규 분포) 및 바로 정의된 같은 네 매개-변수를 갖는 바로 정의된 두 분포의 곱입니다.

이전들은 다음과 같이 정규적으로 분포됩니다:

${\begin{aligned}p(\mu \mid \sigma ^{2};\mu _{0},n_{0})&\sim {\mathcal {N}}(\mu _{0},\sigma ^{2}/n_{0})\\p(\sigma ^{2};\nu _{0},\sigma _{0}^{2})&\sim I\chi ^{2}(\nu _{0},\sigma _{0}^{2})=IG(\nu _{0}/2,\nu _{0}\sigma _{0}^{2}/2)\end{aligned}}$

업데이트 방정식은 유도될 수 있고, 다음처럼 보입니다:

${\begin{aligned}{\bar {x}}&={\frac {1}{n}}\sum _{i=1}^{n}x_{i}\\\mu _{0}'&={\frac {n_{0}\mu _{0}+n{\bar {x}}}{n_{0}+n}}\\n_{0}'&=n_{0}+n\\\nu _{0}'&=\nu _{0}+n\\\nu _{0}'{\sigma _{0}^{2}}'&=\nu _{0}\sigma _{0}^{2}+\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+{\frac {n_{0}n}{n_{0}+n}}(\mu _{0}-{\bar {x}})^{2}\end{aligned}}$

각각의 유사-관측의 숫자는 그들에 실제 관측의 숫자를 더합니다. 새로운 평균 초-매개변수는 다시 한번 가중된 평균이며, 이번에는 관측의 상대적 숫자에 의해 가중됩니다. 마지막으로, $\nu _{0}'{\sigma _{0}^{2}}'$에 대해 업데이트는 알려진 평균을 갖는 경우에 유사하지만, 이 경우에서 제곱된 편차의 합은 참 평균이 아닌 관측된 데이터 평균과 관련되어 취해지고, 결과적으로, 새로운 "상호-작용 항"이 이전과 데이터 평균 사이의 편차로부터 발생하는 추가적인 오차 원천을 처리하기 위해 더해질 필요가 있습니다.

[증명]

이전 분포는 다음입니다:

${\begin{aligned}p(\mu \mid \sigma ^{2};\mu _{0},n_{0})&\sim {\mathcal {N}}(\mu _{0},\sigma ^{2}/n_{0})={\frac {1}{\sqrt {2\pi {\frac {\sigma ^{2}}{n_{0}}}}}}\exp \left(-{\frac {n_{0}}{2\sigma ^{2}}}(\mu -\mu _{0})^{2}\right)\\&\propto (\sigma ^{2})^{-1/2}\exp \left(-{\frac {n_{0}}{2\sigma ^{2}}}(\mu -\mu _{0})^{2}\right)\\p(\sigma ^{2};\nu _{0},\sigma _{0}^{2})&\sim I\chi ^{2}(\nu _{0},\sigma _{0}^{2})=IG(\nu _{0}/2,\nu _{0}\sigma _{0}^{2}/2)\\&={\frac {(\sigma _{0}^{2}\nu _{0}/2)^{\nu _{0}/2}}{\Gamma (\nu _{0}/2)}}~{\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+\nu _{0}/2}}}\\&\propto {(\sigma ^{2})^{-(1+\nu _{0}/2)}}\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right].\end{aligned}}$

그러므로, 결합 이전은 다음입니다:

${\begin{aligned}p(\mu ,\sigma ^{2};\mu _{0},n_{0},\nu _{0},\sigma _{0}^{2})&=p(\mu \mid \sigma ^{2};\mu _{0},n_{0})\,p(\sigma ^{2};\nu _{0},\sigma _{0}^{2})\\&\propto (\sigma ^{2})^{-(\nu _{0}+3)/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+n_{0}(\mu -\mu _{0})^{2}\right)\right].\end{aligned}}$

알려진 분산을 갖는 위의 섹션으로부터 가능도 함수(likelihood function)는 다음입니다:

${\begin{aligned}p(\mathbf {X} \mid \mu ,\sigma ^{2})&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\sum _{i=1}^{n}(x_{i}-\mu )^{2}\right)\right]\end{aligned}}$

정밀도가 아닌 분산의 관점에서 그것을 쓰면, 우리는 다음을 얻습니다:

${\begin{aligned}p(\mathbf {X} \mid \mu ,\sigma ^{2})&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)\right]\\&\propto {\sigma ^{2}}^{-n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(S+n({\bar {x}}-\mu )^{2}\right)\right]\end{aligned}}$

여기서 $S=\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}.$

그러므로, 이후는 다음입니다 (초-매개변수를 조건하는 인수로 버립니다):

${\begin{aligned}p(\mu ,\sigma ^{2}\mid \mathbf {X} )&\propto p(\mu ,\sigma ^{2})\,p(\mathbf {X} \mid \mu ,\sigma ^{2})\\&\propto (\sigma ^{2})^{-(\nu _{0}+3)/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+n_{0}(\mu -\mu _{0})^{2}\right)\right]{\sigma ^{2}}^{-n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(S+n({\bar {x}}-\mu )^{2}\right)\right]\\&=(\sigma ^{2})^{-(\nu _{0}+n+3)/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+S+n_{0}(\mu -\mu _{0})^{2}+n({\bar {x}}-\mu )^{2}\right)\right]\\&=(\sigma ^{2})^{-(\nu _{0}+n+3)/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+S+{\frac {n_{0}n}{n_{0}+n}}(\mu _{0}-{\bar {x}})^{2}+(n_{0}+n)\left(\mu -{\frac {n_{0}\mu _{0}+n{\bar {x}}}{n_{0}+n}}\right)^{2}\right)\right]\\&\propto (\sigma ^{2})^{-1/2}\exp \left[-{\frac {n_{0}+n}{2\sigma ^{2}}}\left(\mu -{\frac {n_{0}\mu _{0}+n{\bar {x}}}{n_{0}+n}}\right)^{2}\right]\\&\quad \times (\sigma ^{2})^{-(\nu _{0}/2+n/2+1)}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+S+{\frac {n_{0}n}{n_{0}+n}}(\mu _{0}-{\bar {x}})^{2}\right)\right]\\&={\mathcal {N}}_{\mu \mid \sigma ^{2}}\left({\frac {n_{0}\mu _{0}+n{\bar {x}}}{n_{0}+n}},{\frac {\sigma ^{2}}{n_{0}+n}}\right)\cdot {\rm {IG}}_{\sigma ^{2}}\left({\frac {1}{2}}(\nu _{0}+n),{\frac {1}{2}}\left(\nu _{0}\sigma _{0}^{2}+S+{\frac {n_{0}n}{n_{0}+n}}(\mu _{0}-{\bar {x}})^{2}\right)\right).\end{aligned}}$

달리 말해서, 이후 분포는, 위의 업데이트 방정식과 같은 매개-변수를 갖는, p(μ | σ²)에 걸쳐 정규 분포의 곱 곱하기 p(σ²)에 걸쳐 역 감마 함수의 형식을 가집니다.

Occurrence and applications

실제 문제에서 정규 분포의 발생은 네가지 카테고리로 느슨하게 분류될 수 있습니다:

1. 정확히 정규 분포;
2. 근사적으로 정규 법칙, 예를 들어 그러한 근사가 중심 극한 정리(central limit theorem)에 의해 정당화될 때; 및
3. 정규 모델링된 분포 – 정규 분포는 주어진 평균과 분산에 대해 최대 엔트로피(maximum entropy)를 갖는 분포입니다.
4. 회귀 문제 – 정규 분포가 체계적인 효과가 충분히 잘 모델링된 후에 발견됩니다.

Exact normality

The ground state of a quantum harmonic oscillator has the Gaussian distribution.

특정 양은 물리학(physics)에서, 제임스 클러크 맥스웰(James Clerk Maxwell)에 의해 처음 시연된 것처럼, 정규적으로 분포됩니다. 그러한 양의 예제는 다음입니다:

• 양자 조화 진동자(quantum harmonic oscillator)에서 접지 상태의 확률 밀도 함수.
• 확산(diffusion)을 겪는 입자의 위치. 만약 처음에는 입자가 특정 지점에 위치되면 (즉, 그것의 확률 분포는 드랙 델타 함수(dirac delta function)입니다), 시간 t 이후에 그 위치는 분산 t를 갖는 정규 분포로 설명되며, 이것은 확산 방정식(diffusion equation) ${\frac {\partial }{\partial t}}f(x,t)={\frac {1}{2}}{\frac {\partial ^{2}}{\partial x^{2}}}f(x,t)$을 만족시킵니다. 만약 초기 위치가 특정 밀도 함수 $g(x)$에 의해 주어지면, 시간 t에서 밀도는 g와 정규 PDF의 합성곱(convolution)입니다.

Approximate normality

근사적으로 정규 분포는, 중심 극한 정리(central limit theorem)에 의해 설명되는 것처럼, 많은 상황에서 발생합니다. 결과가 덧셈적이고 독립적으로 작용하는 많은 작은 효과에 의해 생성될 때, 그것의 분포는 정규에 가까워질 것입니다. 정규 분포는 만약 효과가 (덧셈적 대신에) 곱셈적으로 작용하거나, 만약 나머지 효과보다 상당히 큰 크기를 가지는 단일 외부 영향이 있으면 유효하지 않을 것입니다.

• 세는 문제에서, 다음과 같은, 여기서 중심 극한 정리가 이산-대-연속체 근사를 포함하고 여기서 무한하게 나눌-수-있는(infinitely divisible) 및 분해-가능한(decomposable) 분포가 포함됩니다,
  • 이항 확률 변수(Binomial random variables), 이진 응답 변수와 결합됩니다;
  • 푸아송 확률 변수(Poisson random variables), 드문 사건과 결합됩니다;
• 열복사(Thermal radiation)는 매우 짧은 시간 규모의 보스–아인슈타인(Bose–Einstein) 분포를 가지고, 더 긴 시간-규모의 정규 분포는 중심 극한 정리에 기인합니다.

Assumed normality

Histogram of sepal widths for Iris versicolor from Fisher's Iris flower data set, with superimposed best-fitting normal distribution.

나는 매우 비정상적인 현상일 때 정규 곡선 – 오차의 라플라스 곡선 – 의 발생을 오직 인식할 수 있습니다. 특정 분포에서 대략적으로 근사됩니다; 이 이유에 대해, 및 그것의 아름다운 단순함을 고려하여, 우리는, 아마도, 특히 이론적 조사에서, 그것을 첫 번째 근사로 사용할 수 있습니다.

— Pearson (1901)

해당 가정을 경험적으로 테스트하기 위한 통계적 방법이 있으며, 위의 정규성 테스트(Normality tests) 섹션을 참조하십시오.

• 생물학(biology)에서, 다양한 변수의 로그는 정규 분포를 갖는 경향입니다. 즉, 그들은, 다음을 포함하는 예제와 함께, (남성/여성 소집단에서 분리한 후에) 로그-정규 분포(log-normal distribution)를 갖는 경향입니다.
  • 살아있는 조직 (길이, 키, 피부 면적, 체중)의 크기의 측정;
  • 성장의 방향에서, 생물학적 표본의 둔한 부속기 (머리카락, 발톱, 손톱, 치아)의 길이; 추측하건대 나무 껍질의 두께는 역시 이 카테고리 아래에 떨어집니다;
  • 성인의 혈압과 같은, 특정 생리적 측정.
• 금융, 특히 블랙–숄즈 모델(Black–Scholes model)에서, 환율, 가격 지수, 및 주식 시장 지수의 로그에서 변화가 정규를 가정됩니다 (이들 변수는 단순한 이자가 아닌 복리(compound interest)처럼 행동하고, 따라서 곱셈적입니다). 벤누아 맨델브랏(Benoit Mandelbrot)와 같은 일부 수학자들은 두꺼운 꼬리(heavy tails)를 가진 로그-리비 분포(log-Levy distributions)가, 특히 주식 시장 붕괴(stock market crash)에 대한 해석에 대해, 보다 적절한 모델이 될 것이라고 주장해 왔습니다. 재무 모델에서 발생하는 정규 분포의 가정의 사용은 그의 연구에서 나심 니컬러스 탈레브(Nassim Nicholas Taleb)에 의해 역시 비판되어 왔습니다.
• 물리적 실험에서 측정 오류(Measurement errors)는 종종 정규 분포로 모델링됩니다. 정규 분포의 이 사용은 우리가 측정 오차가 정규적으로 분포된 것을 가정한다는 것을 의미하지는 않으며, 차라리 정규 분포를 사용하면 오차의 평균 및 분산에 대한 주어진 지식만으로 가능한 가장 보수적 예측을 생성합니다.
• 표준화된 테스팅(standardized testing)에서, 결과는 (IQ 테스트(IQ test)에서 처럼) 질문의 숫자와 난이도를 선택 또는 그들을 정규 분포에 맞춤으로써 원시 테스트 점수를 "출력" 점수로 변환함으로써 정규 분포를 가지는 것으로 만들어질 수 있습니다. 예를 들어, SAT의 전통적인 200–800의 범위는 500이 평균이고 100의 표준 편차를 갖는 정규 분포를 기반으로 합니다.

Fitted cumulative normal distribution to October rainfalls, see distribution fitting

• 많은 점수는 백분위수 순위(percentile rank) ("퍼센타일" 또는 "분위-숫자"), 정규 곡선 동등(normal curve equivalent), 스태나인(stanine), z-점수(z-scores), 및 T-점수를 포함하여 정규 분포에서 파생됩니다. 추가적으로, 일부 행동 통계적 절차는 점수가 정규적으로 분포됨을 가정합니다; 예를 들어, t-테스트(t-tests) 및 ANOVAs입니다. 종 곡선 등급(Bell curve grading)은 점수의 정규 분포를 기준으로 상대 등급을 할당합니다.
• 수문학(hydrology)에서, 장기간 강 배출 또는 강우의 분포, 예를 들어 월별 및 연간 총계는 종종 중심 극한 정리(central limit theorem)에 따라 실질적으로 정규인 것으로 생각됩니다. CumFreq로 만든, 파란색 그림은 이항 분포(binomial distribution)를 기반으로 90% 신뢰 벨트(confidence belt)를 나타내는 순위-매겨진 10월 강우량에 정규 분포를 맞추는 예를 보여줍니다. 강우량 데이터는 누적 빈도 분석(cumulative frequency analysis)의 일부로 위치를 그림(plotting position)으로써 표시됩니다.

Produced normality

회귀 분석(regression analysis)에서, 잔여(residuals)에서 정규성이 부족은 가정된 모델이 데이터에서 경향을 설명하는 데 부적절하고 증강될 필요가 있음을 단순히 나타냅니다; 다시 말해서, 잔여에서 정규성은 적절하게 구성된 모델이 주어지면 항상 달성될 수 있습니다.

Computational methods

Generating values from normal distribution

The bean machine, a device invented by Francis Galton, can be called the first generator of normal random variables. This machine consists of a vertical board with interleaved rows of pins. Small balls are dropped from the top and then bounce randomly left or right as they hit the pins. The balls are collected into bins at the bottom and settle down into a pattern resembling the Gaussian curve.

컴퓨터 모의실험에서, 특히 몬테-카를로 방법(Monte-Carlo method)의 응용에서, 정규적으로 분포되는 값을 생성하는 것이 종종 바람직합니다. 아래 나열된 알고리듬은 모두 표준 정규 이탈을 생성하는데, 왜냐하면 N(μ, σ²
)는 X = μ + σZ로 생성될 수 있기 때문이여, 여기서 Z는 표준 정규입니다. 모든 이들 알고리듬은 균등(uniform) 확률 변이를 생성할 수 있는 확률 숫자 생성기(random number generator) U의 가용성에 의존합니다.

• 가장 간단한 방법은 확률 적분 변환(probability integral transform) 속성을 기반으로 합니다: 만약 U가 (0,1) 위에 균등하게 분포되면, Φ⁻¹(U)는 표준 정규 분포를 가질 것입니다. 이 방법의 단점은 분석적으로 수행될 수 없는 프로빗 함수(probit function) Φ⁻¹의 계산에 의존한다는 것입니다. 일부 근사적인 방법은 Hart (1968)와 erf 기사에 설명됩니다. 윌치라는 이 함수를 십진점 이하 16자리까지 계산할 수 있는 빠른 알고리듬을 제공했으며, 이것은 정규 분포의 확률 변이를 계산하기 위해 R에 의해 사용됩니다.
• 중심 극한 정리(central limit theorem)에 의존하는 근사적인 접근을 프로그램하기 위한 쉬운 것은 다음과 같습니다: 12 균등 U(0,1) 변이를 생성하고, 그들을 모두 합하고, 6을 뺍니다 – 결과 확률 변수는 근사적으로 표준 정규 분포를 가질 것입니다. 실제에서, 분포는 어윈–홀(Irwin–Hall)일 것이며, 이것은 정규 분포에 대한 12-섹션 11차 다항식 근사입니다. 이 확률 변이는 (−6, 6)의 극한적인 범위를 가질 것입니다.
• 박스–밀러 방법(Box–Muller method)은 (0,1) 위에 균등하게(uniformly) 분포된 두 독립 확률 변수 U와 V를 사용합니다. 그런-다음 두 확률 변수 X와 Y

$X={\sqrt {-2\ln U}}\,\cos(2\pi V),\qquad Y={\sqrt {-2\ln U}}\,\sin(2\pi V).$

는 둘 다 표준 정규 분포를 가지고, 독립(independent)일 것입니다. 이 공식화는 이변수 정규(bivariate normal) 확률 변수 (X, Y)에 대해 제곱된 노름 X² + Y²이 이 자유도를 갖는 카이-제곱된 분포(chi-squared distribution)를 가질 것이기 때문에 발생하며, 이것은 이들 방정식에서 양 −2ln(U)에 해당하는 쉽게 생성된 지수 확률 변수(exponential random variable)입니다; 그리고 각도는 확률 변수 V에 의해 선택된, 원 주위에 균등하게 분포됩니다.

• 마르살리아 극 방법(Marsaglia polar method)은 사인 코사인 함수의 계산을 요구하지 않는 박스–밀러 방법의 수정입니다. 이 방법에서, U와 V는 균등 (−1,1) 분포에서 그어지고, 그런-다음 S = U² + V²는 계산됩니다. 만약 S가 1보다 크거나 같으면, 그 방법은 시작하고, 그렇지 않으면 두 방정식

$X=U{\sqrt {\frac {-2\ln S}{S}}},\qquad Y=V{\sqrt {\frac {-2\ln S}{S}}}$

이 반환됩니다. 다시, X와 Y가 독립, 표준 정규 확률 변수입니다.

• 비율 방법은 배제 방법입니다. 알고리듬은 다음과 같이 진행합니다:
  • 두 독립 균등 이탈 U와 V를 생성합니다;
  • X = √8/e (V − 0.5)/U를 계산합니다;
  • 선택적: 만약 X² ≤ 5 − 4e^1/4U이면 X를 받아들이고 알고리듬을 종료합니다;
  • 선택적: 만약 X² ≥ 4e^−1.35/U + 1.4이면 X를 받지 않고 단계 1에서 시작합니다;
  • 만약 X² ≤ −4 lnU이면 X를 받아들이고, 그렇지 않으면 알고리듬을 시작합니다.

두 선택적 단계는 대부분 경우에서 피해야 하는 마지막 단계에서 알고리듬의 평가를 허용합니다. 이들 단계는 로그를 거의 평가하지 않도록 크게 개선될 것입니다.

• 지구랫 알고리듬(ziggurat algorithm)은 박스–밀러 변환보다 더 빠르고 여전히 정확합니다. 모든 경우의 약 97%에서 그것이 오직 두 확률 변수, 하나의 확률 정수 및 하나의 확률 균등, 하나의 곱셈 및 if-테스트를 사용합니다. 경우의 오직 3%에서, 여기서 그들의 둘의 조합이 "지구랫의 핵심" (알고리듬을 사용하여 배제 표본화의 한 종류) 밖에 떨어지며, 지수를 수행하고 보다 균등 확률 숫자가 사용되어야 합니다.
• 정수 산술은 표준 정규 분포에서 표본에 사용될 수 있습니다. 이 방법은 그것이 이상적인 근사의 조건을 만족시킨다는 의미에서 정확합니다; 즉, 표준 정규 분포에서 실수를 표본화하고 이것을 가장-가까운 표현-가능한 부동 소수점 숫자로 반올림하는 것과 동등합니다.
• 빠른 아다마르 변환(Hadamard transform)과 정규 분포 사이의 연결에 대한 일부 조사도 있는데, 왜냐하면 변환은 단지 덧셈과 뺄셈을 사용하고 중심 극한 정리에 의해 거의 임의의 분포로부터 확률 숫자가 정규 분포로 변환될 것이기 때문입니다. 이와 관련하여 일련의 아다마르 변환은 임의의 데이터 집합을 정규적으로 분포된 데이터로 돌리기 위해 확률 순열과 결합될 수 있습니다.

Numerical approximations for the normal CDF

표준 정규 CDF는 과학 및 통계적 컴퓨팅에 널리 사용됩니다.

값 Φ(x)는 수치적 적분화(numerical integration), 테일러 급수(Taylor series), 점근적 급수(asymptotic series) 및 연속된 분수(continued fractions)와 같은 다양한 방법에 의해 매우 정확하게 근사될 수 있습니다. 다른 근삿값이 원하는 정확도 수준에 따라 사용됩니다.

• Zelen & Severo (1964)는 x > 0에 대해 절대 오차 |ε(x)| < 7.5·10⁻⁸를 갖는 Φ(x)에 대해 근사를 제공합니다 (알고리듬 26.2.17):

  $\Phi (x)=1-\varphi (x)\left(b_{1}t+b_{2}t^{2}+b_{3}t^{3}+b_{4}t^{4}+b_{5}t^{5}\right)+\varepsilon (x),\qquad t={\frac {1}{1+b_{0}x}},$

  여기서 ϕ(x)는 표준 정규 PDF이고, b₀ = 0.2316419, b₁ = 0.319381530, b₂ = −0.356563782, b₃ = 1.781477937, b₄ = −1.821255978, b₅ = 1.330274429입니다.
• Hart (1968)는 erfc() 함수에 대해 – 지수없이 또는 지수와 함께, 유리 함수를 수단으로 – 수십 가지 근사를 목록화합니다. 그의 알고리듬은 24 자릿수의 최대 절대 정밀도를 갖는 복잡도 및 결과 정밀도의 정도에서 변합니다. West (2009)에 의한 알고리듬은 Hart의 알고리듬 5666과 16-자릿수 정밀도를 갖는 빠른 계산 알고리듬을 제공하기 위해 꼬리에서 연속된 분수(continued fraction) 근사를 결합합니다.
• Cody (1969)는 Hart68 해가 erf에 적합하지 않다고 생각한 후 유리 체비쇼프 근사(Rational Chebyshev Approximation)을 통해 최대 상대 오차 경계를 갖는 erf 및 erfc 둘 다에 대한 해를 제공합니다.
• Marsaglia (2004)는 임의의 정밀도를 갖는 Φ(x)를 계산하는 것에 대해 테일러 급수 전개

  $\Phi (x)={\frac {1}{2}}+\varphi (x)\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{3\cdot 5}}+{\frac {x^{7}}{3\cdot 5\cdot 7}}+{\frac {x^{9}}{3\cdot 5\cdot 7\cdot 9}}+\cdots \right)$

  에 기초한 간단한 알고리듬을 제안했습니다. 이 알고리듬의 단점은 비교적적으로 느린 게산 시간입니다 (예를 들어, x = 10일 때 16 자릿수의 정밀도를 갖는 함수를 계산하기 위해 300 반복 이상을 취합니다).
• GNU Scientific Library는 Hart의 알고리듬과 체비쇼프 다항식(Chebyshev polynomial)의 근사를 사용하여 표준 정규 CDF의 값을 계산합니다.

Shore (1982)는 신뢰성 공학 및 재고 분석과 같은 공학 및 운영 연구의 확률론적 최적화 모델에 통합될 수 있는 간단한 근사를 도입했습니다. p=Φ(z)를 나타내면, 분위-숫자 함수에 대해 가장-간단한 근사는 다음입니다:

$z=\Phi ^{-1}(p)=5.5556\left[1-\left({\frac {1-p}{p}}\right)^{0.1186}\right],\qquad p\geq 1/2$

이 근사는 z에 대해 최대 절대 오차 0.026 (0.5 ≤ p ≤ 0.9999에 대해, 0 ≤ z ≤ 3.719에 해당하는)을 제공합니다. p < 1/2에 대해 p를 1 − p로 바꾸고 부호를 변경하십시오. 다소 덜 정확한 또 다른 근사는 단일-매개변수 근사입니다:

$z=-0.4115\left\{{\frac {1-p}{p}}+\log \left[{\frac {1-p}{p}}\right]-1\right\},\qquad p\geq 1/2$

후자는 다음에 의해 정의된 정규 분포의 손실 적분에 대해 간단한 근사를 도출하기 위해 사용되어 왔습니다:

${\begin{aligned}L(z)&=\int _{z}^{\infty }(u-z)\varphi (u)\,du=\int _{z}^{\infty }[1-\Phi (u)]\,du\\[5pt]L(z)&\approx {\begin{cases}0.4115\left({\dfrac {p}{1-p}}\right)-z,&p<1/2,\\\\0.4115\left({\dfrac {1-p}{p}}\right),&p\geq 1/2.\end{cases}}\\[5pt]{\text{or, equivalently,}}\\L(z)&\approx {\begin{cases}0.4115\left\{1-\log \left[{\frac {p}{1-p}}\right]\right\},&p<1/2,\\\\0.4115{\dfrac {1-p}{p}},&p\geq 1/2.\end{cases}}\end{aligned}}$

이 근사는 오른쪽 끝-꼬리에 대해 특히 정확합니다 (z≥1.4에 대해 10⁻³의 최대 오차). 반응 모델링 방법론(Response Modeling Methodology) (RMM, Shore, 2011, 2012)을 기반으로 한 CDF에 대해 매우 정확한 근사는 Shore (2005)에 나와 있습니다.

더 많은 근사는 Error function#Approximation with elementary functions에서 찾을 수 있습니다. 특히, CDF $\Phi$ 및 마찬가지로 분위-숫자 함수 $\Phi ^{-1}$에 대해 전체 도메인 위에 작은 상대 오차는 2008년에 세르게이 비니츠기(Sergei Winitzki)에 의해 명시적으로 역-가능한 공식을 통해 달성됩니다.

History

Development

일부 저자들은 드 무아브르(de Moivre)에게 정규 분포의 발견에 대한 공로를 인정했는데, 그는 1738년에 그의 "The Doctrine of Chances" 2판에서 (a + b)ⁿ의 이항 전개(binomial expansion)에서 계수의 연구를 발표했습니다. 드 무아브르는 이 전개에서 중간 항이 $2/{\sqrt {2\pi n}}$의 근사 크기를 가지고, "만약 m 또는 ½n이 무한하게 큰 양이면, 한 항이 구간 ℓ에 의해 중간에서 거리인 비율의 로그는 $-{\frac {2\ell \ell }{n}}$입니다." 비록 이 정리가 정규 확률 법칙에 대한 첫 번째 모호한 표현으로 해석될지라도, 스티글러(Stigler)는 드 무아브르 자신이 그의 결과를 이항 계수에 대한 근사 규칙 이상의 어떤 것으로 해석하지 않았고, 특히 드 무아브르는 확률 밀도 함수의 개념이 결여되어 있다고 지적합니다.

Carl Friedrich Gauss discovered the normal distribution in 1809 as a way to rationalize the method of least squares.

1809년에 가우스(Gauss)는 그의 연구논문 "Theoria motus corporum coelestium in sectionibus conicis solem ambientium"을 출판했고 여기서 다른 것들 사이에서 그는 최소 제곱의 방법(method of least squares), 최대 가능도의 방법(method of maximum likelihood), 정규 분포와 같은 중요한 통계적 개념을 도입했습니다. 가우스는 M, M′, M′′, ...을 어떤 미지수 양 V의 측정을 표시하기 위해 사용했고, 해당 양의 "가장 가능성이 높은" 추정: 관측된 실험적인 결과를 얻는 것의 확률 φ(M − V) · φ(M′ − V) · φ(M′′ − V) · ...을 최대화하는 하나를 찾았습니다. 그의 표기법에서 φΔ는 크기 Δ의 측정 오차의 확률 법칙입니다. 함수 φ가 무엇인지 모르는 가우스는 그의 방법이 잘 알려진 답: 측정된 값의 산술 평균으로 줄여야 함을 필요로 합니다. 이들 원칙에서 시작하여, 가우스는 위치 매개-변수의 추정으로 산술 평균의 선택을 합리화하는 유일한 법칙은 오차의 정규 법칙임을 시연합니다:

$\varphi {\mathit {\Delta }}={\frac {h}{\surd \pi }}\,e^{-\mathrm {hh} \Delta \Delta },$

여기서 h는 "관측의 정밀도의 측정"입니다. 이 정규 법칙을 실험에서 오류에 대한 일반적인 모델로 사용하여, 가우스는 현재 비-선형 가중된 최소 제곱 (NWLS) 방법으로 알려진 것을 공식화합니다.

Marquis de Laplace proved the central limit theorem in 1810, consolidating the importance of the normal distribution in statistics.

비록 가우스가 정규 분포 법칙을 제안한 것은 처음이었지만, 라플라스(Laplace)는 상당한 기여를 했습니다. 비록 그의 해결책이 라플라시안 분포(Laplacian distribution)를 가져왔음에도 불구하고, 1774년에 여러 관측 값을 집계하는 문제를 처음 제기한 것은 라플라스였습니다. 1782년에 적분 ∫ e^−t2 dt = √π의 값을 먼저 계산하여, 정규 분포에 대한 정규화 상수를 제공한 것은 라플라스였습니다. 마지막으로, 1810년에 라플라스는 기본 중심 극한 이론(central limit theorem)을 증명하고 아카데미에 제시했으며, 이것은 정규 분포의 이론적 중요성을 강조했습니다.

1809년에 미국 수학자 아드리안(Adrain)은 가우스와 동시에 및 독립적으로, 정규 확률 법칙의 두 가지 파생물을 발표했다는 점에 주목할 필요가 있습니다. 그의 연구는 1871년에 아비(Abbe)에 의해 "재발견"될 때까지 과학계에 의해 거의 눈에 띄지 않았습니다.

19세기 중반에서 맥스웰(Maxwell)은 정규 분포가 단지 편리한 수학적 도구일뿐만 아니라, 자연 현상에서 역시 발생할 수 있음을 시연했습니다: "x와 x + dx 사이에 놓이는, 특정 방향으로 분해되는 속도를 가진 입자의 숫자는 다음입니다":

$\operatorname {N} {\frac {1}{\alpha \;{\sqrt {\pi }}}}\;e^{-{\frac {x^{2}}{\alpha ^{2}}}}\,dx$

Naming

그것의 도입 이래로, 정규 분포는 오차의 법칙, 오차의 공간의 법칙, 라플라스의 두 번째 법칙, 가우시안 법칙, 등 많은 다른 이름으로 알려져 왔습니다. 가우스 자신은 "보통"이 아닌 직교라는 기술적 의미를 가지는 정규와 함께 "정규 방정식"을 참조하여 그 용어를 분명히 만들었습니다. 어쨌든, 19세기 말에 일부 저자들은 이름 정규 분포를 사용하기 시작했으며, 여기서 단어 "정규"는 형용사로 사용되었습니다 – 이 용어는 이제 이 분포가 전형적이고 공통적인 것으로 보인다는 사실의 반영한 것으로 여겨집니다 – 따라서 "정규"입니다. 퍼스 (그들의 저자 중 한 명)는 한 번 "정규"를 다음과 같이 정의했습니다: "... '정규'는 실제로 발생하는 것의 평균 (또는 평균의 임의의 다른 종류)이 아니라, 특정 환경 아래에서, 장기적으로, 발생할 수 있는 것입니다." 20세기 초, 피어슨(Pearson)은 이 분포에 대해 명칭으로 용어 정규를 대중화했습니다.

Many years ago I called the Laplace–Gaussian curve the normal curve, which name, while it avoids an international question of priority, has the disadvantage of leading people to believe that all other distributions of frequency are in one sense or another 'abnormal'.

— Pearson (1920)

역시, 현대 표기법에서 처럼, 표준 편차 σ의 관점에서 분포를 처음 쓴 사람은 피어슨이었습니다. 그 후 곧 1915년에, 피셔(Fisher)는 정규 분포에 대해 공식에 위치 매개-변수를 더했고, 요즘 쓰는 방법으로 표현했습니다:

$df={\frac {1}{\sqrt {2\sigma ^{2}\pi }}}e^{-(x-m)^{2}/(2\sigma ^{2})}\,dx$

영 평균 및 단위 분산을 갖는 정규 분포를 나타내는, 용어 "표준 정규"는 1950년대 경에 일반적으로 사용되었으며, P.G. Hoel (1947) "Introduction to mathematical statistics" 및 A.M. Mood (1950) "Introduction to the theory of statistics"에 의해 인기있는 교과서에 나타났습니다.

그 이름이 사용될 때, "가우시안 분포"는 카를 프레드리히 가우스(Carl Friedrich Gauss)의 이름을 따서 지어졌으며, 그는 1809년에 위에서 설명된 최소 제곱의 방법(method of least squares)을 합리화하는 방법으로 분포를 도입했습니다. 영어 사용자들 사이에서, "정규 분포"와 "가우시안 분포" 둘 다는 공통적으로 사용되며, 다른 용어는 다른 공동체에 의해 선호됩니다.

See also

• Wrapped normal distribution — the Normal distribution applied to a circular domain
• Bates distribution — similar to the Irwin–Hall distribution, but rescaled back into the 0 to 1 range
• Behrens–Fisher problem — the long-standing problem of testing whether two normal samples with different variances have same means;
• Bhattacharyya distance – method used to separate mixtures of normal distributions
• Erdős–Kac theorem—on the occurrence of the normal distribution in number theory
• Gaussian blur—convolution, which uses the normal distribution as a kernel
• Normally distributed and uncorrelated does not imply independent
• Reciprocal normal distribution
• Ratio normal distribution
• Standard normal table
• Sub-Gaussian distribution
• Sum of normally distributed random variables
• Tweedie distribution — The normal distribution is a member of the family of Tweedie exponential dispersion models
• Z-test— using the normal distribution
• Stein's lemma

External links

• "Normal distribution", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Normal distribution calculator, More powerful calculator