Venn diagram

Original article: w:Venn diagram

Venn diagram showing the uppercase glyphs shared by the Greek, Latin, and Cyrillic alphabets

벤 다이어그램은 1880년대 존 벤(John Venn)에 의해 대중화된 집합(sets) 사이의 논리적 관계를 보여주는 널리 사용되는 다이어그램(diagram) 스타일입니다. 그 다이어그램은 기본 집합 이론(set theory)을 가르치고, 확률(probability), 논리(logic), 통계(statistics), 언어학(linguistics), 및 컴퓨터 과학(computer science)에서 간단한 집합 관계를 묘사하기 위해 사용됩니다. 벤 다이어그램은 평면에 그려진 단순한 닫힌 곡선을 집합을 나타내기 위해 사용합니다. 매우 자주, 이들 곡선은 원 또는 타원입니다.

유사한 아이디어가 벤 이전에 제안되어 왔습니다. 예를 들어, 1712년 Christian Weise (Nucleus Logicoe Wiesianoe)와 1768년 레온하르트 오일러 (Letters to a German Princess)는 유사한 아이디어를 내놓았습니다. 그 아이디어는 1881년 벤에 의해 Symbolic Logic, Chapter V "Diagrammatic Representation"에서 대중화되었습니다.

Details

벤 다이어그램은 역시 집합 다이어그램 또는 논리 다이어그램이라고 불립니다. 그것은 서로 다른 집합의 유한 모음 사이의 모든 가능한 논리적 관계를 보여주는 다이어그램입니다. 이들 다이어그램은 원소(element)를 평면에서 점으로 묘사하고, 집합을 닫힌 곡선 내부의 영역으로 묘사합니다. 벤 다이어그램은 여러 개의 겹치는 닫힌 곡선, 보통 원으로 구성되며, 각각은 하나의 집합을 나타냅니다. S라고 이름-지정된 곡선 내부의 점은 집합 S의 원소를 나타내고, 반면에 경계 외부의 점은 집합 S에 있지 않은 원소를 나타냅니다. 이것은 직관적인 시각화에 적합합니다; 예를 들어, S ∩ T로 표시되고 "S와 T의 교집합"으로 읽히는 집합 S와 T 둘 다의 구성원인 모든 원소의 집합은 S와 T 영역의 겹친 영역으로 시각적으로 표시됩니다.

벤 다이어그램에서, 곡선은 모든 각 가능한 방법으로 겹쳐지며, 집합 사이의 모든 가능한 관계를 보여줍니다. 그것들은 따라서 모든 관계를 반드시 표시하지는 않는 오일러 다이어그램(Euler diagram)의 특수한 경우입니다. 벤 다이어그램은 약 1880년에 존 벤에 의해 고안되었습니다. 그것들은 기본 집합 이론을 가르치기 위해 사용되고, 마찬가지로 확률, 논리, 통계, 언어학, 및 컴퓨터 과학에서 간단한 집합 관계를 묘사하기 위해 사용됩니다.

각 모양의 넓이가 그것이 포함하는 원소의 숫자에 비례하는 벤 다이어그램은 넓이-비례적 (또는 스케일된) 벤 다이어그램이라고 불립니다.

벤 다이어그램은 추론의 가지 클래스의 논리(logic of class)에서 많이 사용됩니다.

Example

Sets A (creatures with two legs) and B (creatures that fly)

이 예제는 여기에서 색깔있는 원으로 표시된 두 집합 A와 B를 포함합니다. 주황색 원, 집합 A는 두 발 달린 모든 유형의 생물을 나타냅니다. 파란색 원, 집합 B는 날 수 있는 생물을 나타냅니다. 각각의 개별 유형의 생물은 다이어그램의 어딘가에 있는 점으로 상상될 수 있습니다. 날 수 있고 두 다리를 가진 생물–예를 들어, 앵무새–은 두 집합에 모두 있으므로 파란색과 주황색 원이 겹치는 영역에서 점에 해당합니다. 이 겹치는 영역은 집합 A (두발 달린 생물)와 집합 B(나는 생물)의 구성원인 오직 그들의 원소 (이 예제에서, 생물)를 포함합니다.

사람과 펭귄은 두 발이 있고, 따라서 주황색 원 안에 있지만, 그것들은 날 수 없기 때문에, 파란색 원과 겹치지 않는 주황색 원의 왼쪽 부분에 나타납니다. 모기는 날 수 있지만, 두 다리가 아닌 여섯을 가지므로, 모기에 대해 점은 주황색 원과 겹치지 않는 파란색 원 부분에 있습니다. 두 다리가 없고 날 수도 없는 생물 (예를 들어, 고래와 거미)은 모두 두 원 밖의 점으로 표시됩니다.

집합 A와 B의 조합된 영역은 A ∪ B로 표시되는 A와 B의 합집합(union)이라고 불립니다. 이 경우에서 합집합은 두 다리가 있거나 날 수 있는 (또는 둘 다) 모든 생물을 포함합니다.

A와 B 둘 다에 포함된 두 집합이 겹치는 영역은 A ∩ B로 표시되는 A와 B의 교집합(intersection)입니다. 이 예제에서, 주황색 원과 파란색 원 둘 다에 있는 생물을 나타내는 점이 있기 때문에, 두 집합의 교집합은 빈 것이 아닙니다.

History

Stained-glass window with Venn diagram in Gonville and Caius College, Cambridge

벤 다이어그램은 1880년 존 벤(John Venn)에 의한 Philosophical Magazine and Journal of Science에서 다이어그램에 의해 제안(proposition)을 표현하는 다른 방법에 대한 "On Diagrammatic and Mechanical Representation of Propositions and Reasonings"라는 제목의 논문에서 소개되었습니다. 프랭크 러스키(Frank Ruskey)와 Mark Weston에 따르면, 형식적 논리(formal logic)에서 이들 유형의 다이어그램의 사용은 "추적하기 쉬운 역사가 아니지만, 실제로 벤과 대중적으로 관련된 그 다이어그램이 훨씬 더 일찍 시작되었다는 것은 확실합니다. 그것들은 벤과 올바르게 연관되어 있는데, 어쨌든, 왜냐하면 그가 그것들의 사용법을 종합적으로 조사하고 공식화했고, 처음으로 일반화했기 때문입니다."

벤 자신은 "벤 다이어그램"이라는 용어를 사용하지 않았고 그의 발명을 "오일러 서클(Eulerian Circle)"이라고 참조했습니다. 예를 들어, 그의 1880년 논문의 첫 문장에서, 벤은 다음과 같이 썼습니다. "다이어그램적 표시의 개요는 지난 세기 정도 동안 논리적 논문에 너무도 친숙하게 도입되어 심지어 논리학에 대한 전문적인 연구를 하지 않은 독자라도 그러한 장치의 일반적인 본성과 목적을 알고 있다고 생각할 수 있습니다. 이들 개요 중 단 하나가, 즉, 공통적으로 '오일러 원'이라고 불리며, 임의의 일반적인 수용을 만나게 되었습니다..." 루이스 캐럴(Lewis Carroll) (Charles L. Dodgson)은 그의 책 Symbolic Logic (1896년에 출판된 4판)의 "Appendix, Addressed to Teachers"에서 "Venn's Method of Diagrams"와 "Euler's Method of Diagrams"를 포함합니다. "벤 다이어그램"이라는 용어는 나중에 1918년 크라렌스 어빙 루이스(Clarence Irving Lewis)에 의한 그의 책 A Survey of Symbolic Logic에서 사용되었습니다.

벤 다이어그램은 18세기에 레온하르트 오일러에 의해 발명된 오일러 다이어그램과 매우 유사합니다. 마가렛 배런(Margaret Baron)은 라이프니츠(Leibniz) (1646–1716)가 17세기 오일러 이전에 유사한 다이어그램을 생성했지만, 그것의 대부분은 출판되지 않았다고 언급했습니다. 그녀는 역시 13세기에 라몬 유이(Ramon Llull)에 의한 훨씬 더 이른 오일러-계열 다이어그램을 관찰합니다.

20세기에서, 벤다이어그램이 더욱 발전되었습니다. 데이비드 윌슨 헨더슨(David Wilson Henderson)은 1963년에 n-겹 회전적 대칭(rotational symmetry)을 갖는 n-벤 다이어그램의 존재가 n이 소수(prime number)였음을 암시한다는 것을 보였습니다. 그는 역시 n이 5 또는 7일 때 그러한 대칭적 벤다이어그램이 존재함을 보였습니다. 2002년에, 피터 햄버거(Peter Hamburger)는 n = 11에 대해 대칭적 벤 다이어그램을 찾았고 2003년에, Griggs, Killian, 및 Savage는 모든 다른 소수에 대해 대칭적 벤 다이어그램이 존재함을 보였습니다. 이들 조합된 결과는 회전적으로 대칭적 벤 다이어그램이 존재하는 것과 n이 소수인 것은 필요충분 조건임을 보입니다.

벤 다이어그램과 오일러 다이어그램은 1960년대 새로운 수학(new math) 운동의 일부로, 집합 이론에서 교육의 일부로 통합되었습니다. 그 이후로, 그것들은 역시 읽기와 같은 다른 분야의 커리큘럼에 채택되어 왔습니다.

Overview

See also: Set (mathematics) § Basic operations

• 
  Intersection of two sets $~A\cap B$
• 
  Union of two sets $~A\cup B$
• 
  Symmetric difference of two sets $A~\triangle ~B$
• 
  Relative complement of A (left) in B (right) $A^{c}\cap B~=~B\setminus A$
• 
  Absolute complement of A in U $A^{c}~=~U\setminus A$

벤 다이어그램은 평면에 그려진 간단한 닫힌 곡선 모음으로 구성됩니다. 루이스(Lewis)에 따르면, "이들 다이어그램의 원리는 클래스 [또는 집합]가 서로 그러한 관계에서 영역에 의해 표현되어 이들 클래스의 모든 가능한 논리적 관계가 같은 다이어그램에 표시될 수 있다는 것입니다. 즉, 그 다이어그램은 처음에 클래스의 가능한 임의의 관계에 대해 자리를 남겼고, 그런-다음 실제 또는 주어진 관계는 어떤 특정 영역이 널 또는 널-아님임을 표시함으로써 지정될 수 있습니다."

벤 다이어그램은 통상적으로 겹치는 원(circle)으로 구성됩니다. 원의 내부는 집합의 원소를 상징적으로 나타내고, 반면에 외부는 집합의 구성원이 아닌 원소를 나타냅니다. 예를 들어, 두-집합 벤 다이어그램에서, 하나의 원은 모든 나무로 된 물체의 그룹을 나타내고, 반면에 나머지 다른 원은 모든 테이블의 집합을 나타낼 수 있습니다. 겹치는 영역, 또는 교집합은 그때에 모든 나무로 된 테이블의 집합을 나타냅니다. 벤 자신의 상위 집합 다이어그램에 의해 아래에 보인 것처럼 원 이외의 모양이 사용될 수 있습니다. 벤 다이어그램은 일반적으로 집합의 상대 또는 절대 크기 (카디널리티(cardinality))에 대한 정보가 포함하지 않습니다. 즉, 그것들은 일반적으로 스케일에 맞게 그려지지 않은 개요의(schematic) 다이어그램입니다.

벤 다이어그램은 오일러 다이어그램과 유사합니다. 어쨌든, n 구성 요소 집합에 대해 벤 다이어그램은 각 구성 요소 집합에 포함 또는 제외의 일부 조합에 해당하는 모든 2ⁿ 가상적인 가능한 영역을 포함해야 합니다. 오일러 다이어그램은 주어진 문맥에서 오직 실제로 가능한 영역을 포함합니다. 벤 다이어그램에서. 음영-처리된 영역은 빈 영역을 나타낼 수 있지만, 오일러 다이어그램에서, 대응하는 영역이 다이어그램에서 누락됩니다. 예를 들어, 만약 하나의 집합이 유제품을 나타내고 또 다른 집합이 치즈를 나타내면, 벤 다이어그램은 유제품이 아닌 치즈에 대해 영역을 포함합니다. 그 문맥에서 치즈가 어떤 유형의 유제품을 의미한다고 가정하면. 오일러 다이어그램은 유제품 영역 내에 전적으로 포함된 치즈 영역을 가집니다–(비-존재) 비-유제품 치즈에 대해 영역은 없습니다. 이것은 구분선의 숫자가 증가함에 따라, 오일러 다이어그램이 전형적으로 동등한 벤 다이어그램보다 시각적으로 덜 복잡하다는 것을 의미합니다. 특히 비-빈 교집합의 숫자가 작으면 더욱 그렇습니다.

오일러 다이어그램과 벤 다이어그램 사이의 차이점은 다음 예제에서 보일 수 있습니다. 세 집합을 취하십시오:

• $A=\{1,\,2,\,5\}$
• $B=\{1,\,6\}$
• $C=\{4,\,7\}$

이들 집합의 오일러와 벤 다이어그램은 다음과 같습니다:

• 
  Euler diagram
• 
  Venn diagram

Extensions to higher numbers of sets

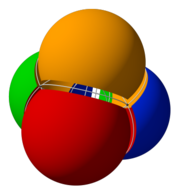
벤 다이어그램은 전형적으로 둘 또는 셋의 집합을 나타내지만, 더 높은 수를 허용하는 형식이 있습니다. 아래 그림에서, 넷의 교차하는 구는 심플렉스(simplex)의 대칭을 가지고 시각적으로 표현될 수 있는 최고차 벤 다이어그램을 형성합니다. 16 교집합이 테서랙트(tesseract) (또는 각각 16 셀의 셀들)의 꼭짓점에 해당합니다.

더 높은 집합의 숫자에 대해, 다이어그램에서 일부 대칭 손실이 불가피합니다. 벤은 더 높은 집합의 숫자를 나타내는 "대칭적 그림...그 자체로 우아한"을 찾기 위해 열심이었고, 그는 타원(ellipse)을 사용하여 우아한 넷의-집합 다이어그램을 고안했습니다 (아래를 참조). 그는 역시 집합을 구분하는 각각의 연속적인 곡선이 셋의-원 다이어그램으로 시작하여 이전 곡선과 교차하는 임의의 집합의 숫자에 대해 벤 다이어그램에 대한 구성을 제공했습니다.

• 
  Venn's construction for four sets
• 
  Venn's construction for five sets
• 
  Venn's construction for six sets
• 
  Venn's four-set diagram using ellipses
• 
  Non-example: This Euler diagram is not a Venn diagram for four sets as it has only 13 regions (excluding the outside); there is no region where only the yellow and blue, or only the red and green circles meet.
• 
  Five-set Venn diagram using congruent ellipses in a five-fold rotationally symmetrical arrangement devised by Branko Grünbaum. Labels have been simplified for greater readability; for example, A denotes A ∩ B^c ∩ C^c ∩ D^c ∩ E^c, while BCE denotes A^c ∩ B ∩ C ∩ D^c ∩ E.
• 
  Six-set Venn diagram made of only triangles (interactive version)

Edwards–Venn diagrams

• 
  Three sets
• 
  Four sets
• 
  Five sets
• 
  Six sets

앤서니 윌리엄 페어뱅크 에드워즈(Anthony William Fairbank Edwards)는 구의 표면을 분할함으로써 더 높은 집합의 숫자에 대해 일련의 벤 다이어그램을 구성했으며, 이것은 에드워즈-벤 다이어그램으로 알려지게 되었습니다. 예를 들어, 셋의 집합은 구의 셋의 반구를 직각에서 취함으로써 쉽게 표현될 수 있습니다 (x = 0, y = 0, 및 z = 0). 네 번째 집합은 적도를 중심으로 위아래로 휘어지는 테니스 공의 이음새와 유사한 곡선을 취함으로써 표현에 더해질 수 있고, 이런 식으로 계속됩니다. 결과 집합은 그런-다음 여기에 표시된 것처럼 톱니 숫자가 증가하는 톱니바퀴 다이어그램을 제공하기 위해 평면에 다시 투영될 수 있습니다. 이들 다이어그램은 벤을 기리기 위해 스테인드-글라스 창을 디자인하는 동안 고안되었습니다.

Other diagrams

에드워즈–벤 다이어그램은 측면의 숫자를 증가하는 교차 다각형을 기반으로 했던 브랭코 그린바움(Branko Grünbaum)에 의해 고안된 다이어그램과 토폴로지적으로 동등(topologically equivalent)입니다. 그것들은 역시 초-입방체(hypercube)의 이-차원 표현입니다.

헨리 존 스티븐 스미스(Henry John Stephen Smith)는 다음 일련의 방정식을 갖는 사인(sine) 곡선을 사용하여 유사한 n-집합 다이어그램을 고안했습니다:

$y_{i}={\frac {\sin \left(2^{i}x\right)}{2^{i}}}{\text{ where }}0\leq i\leq n-2{\text{ and }}i\in \mathbb {N} .$

찰스 럿위지 도지슨(Charles Lutwidge Dodgson) (역시 루이스 캐롤이라고 알려져 있음)은 캐롤의 정사각형(Carroll's square)으로 알려진 다섯의-집합 다이어그램을 고안했습니다. Joaquin과 Boyles는, 다른 한편으로, 특정 문제 사례를 설명하기 위해, 표준 벤 다이어그램에 대해 보충적인 규칙을 제안했습니다. 예를 들어, 단수형 명제를 나타내는 문제와 관련하여, 그들은 벤다이어그램 원을 어떤 것의 하나의 집합의 표현으로 고려할 것을 제안하고, 일-차 논리(first-order logic)와 집합 이론을 카테고리적 명제를 집합에 대한 명제로 취급할 것을 제안합니다. 추가적으로, 그들은 단수형 명제를 집합 구성원(set membership)에 대한 명제로 취급할 것을 제안합니다. 따라서, 예를 들어, 이 재구성된 벤 다이어그램에서 "a is F"라는 명제를 나타내기 위해, 소문자 "a"가 집합 F를 나타내는 원 안에 배치될 수 있습니다.

Related concepts

Venn diagram as a truth table

벤 다이어그램은 그것의 각 영역이 진리 테이블(truth table)의 하나의 행에 해당한다는 의미에서 제안 $x\in A$, $x\in B$, 등에 대해 진리 테이블에 해당합니다. 이 유형은 역시 존스턴(Johnston) 다이어그램으로 알려져 있습니다. 집합을 나타내는 또 다른 방법은 John F. Randolph의 R-다이어그램(R-diagram)을 사용하는 것입니다.

See also

• Existential graph (by Charles Sanders Peirce)
• Logical connectives
• Information diagram
• Marquand diagram (and as further derivation Veitch chart and Karnaugh map)
• Spherical octahedron – A stereographic projection of a regular octahedron makes a three-set Venn diagram, as three orthogonal great circles, each dividing space into two halves.
• Three circles model
• Triquetra
• Vesica piscis

Further reading

• Mahmoodian, Ebadollah S.; Rezaie, M.; Vatan, F. (March 1987). "Generalization of Venn Diagram" (PDF). Eighteenth Annual Iranian Mathematics Conference. Tehran and Isfahan, Iran. Archived from the original (PDF) on 1 May 2017. Retrieved 2017-05-01.
• Edwards, Anthony William Fairbank (1989-01-07). "Venn diagrams for many sets". New Scientist. 121 (1646): 51–56.
• Watkinson, John (1990). "4.10. Hamming distance". Coding for Digital Recording. Stoneham, MA, USA: Focal Press. pp. 94–99, foldout in backsleeve. ISBN 978-0-240-51293-8. (NB. The book comes with a 3-page foldout of a seven-bit cylindrical Venn diagram.)
• Stewart, Ian (June 2003) [1992]. "Chapter 4. Cogwheels of the Mind". Another Fine Math You've Got Me Into (reprint of 1st ed.). Mineola, New York, USA: Dover Publications, Inc. (W. H. Freeman). pp. 51–64. ISBN 978-0-486-43181-9.
• Glassner, Andrew (2004). "Venn and Now". Morphs, Mallards, and Montages: Computer-Aided Imagination. Wellesley, MA, USA: A. K. Peters. pp. 161–184. ISBN 978-1568812311.
• Mamakani, Khalegh; Ruskey, Frank (2012-07-27). "A New Rose: The First Simple Symmetric 11-Venn Diagram". p. 6452. arXiv:1207.6452. Bibcode:2012arXiv1207.6452M. Archived from the original on 2017-05-01. Retrieved 2017-05-01.

External links

• "Venn diagram", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Lewis Carroll's Logic Game – Venn vs. Euler at Cut-the-knot
• Six sets Venn diagrams made from triangles
• Interactive seven sets Venn diagram
• VBVenn a free open source program for calculating and graphing quantitative two-circle Venn diagrams