Analytic geometry

Original article: w:Analytic geometry

This article is about co-ordinate geometry. For the study of analytic varieties, see Algebraic geometry § Analytic geometry.

고전 수학에서, 해석 기하학(analytic geometry)은, 역시 좌표 기하학(coordinate geometry) 또는 데카르트 기하학(Cartesian geometry)으로 알려져 있으며, 좌표 시스템(coordinate system)을 사용하는 기하학(geometry)의 연구입니다. 이것은 합성 기하학(synthetic geometry)과 대조됩니다.

해석 기하학은 물리학(physics)과 공학(engineering)에서, 그리고 역시 항공(aviation), 로켓(rocket), 우주 과학(space science)과 우주-비행(spaceflight)에서 사용됩니다. 그것은 대수적(algebraic), 미분(differential), 이산(discrete) 및 계산 기하학(computational geometry)을 포함하여, 가장 현대적인 기하학의 분야에서 토대입니다.

보통 데카르트 좌표 시스템(Cartesian coordinate system)은 평면(plane), 직선(straight line), 및 정사각형(square)에 대해, 종종 이차원에서 및 때때로 삼차원에서 방정식(equation)을 조작하기 위해 적용됩니다. 기하학적으로, 우리는 유클리드 평면(Euclidean plane) (이 차원(two dimensions))과 유클리드 공간(Euclidean space) (삼 차원(three dimensions))을 연구합니다. 교과서에서 가르친 것처럼, 해석 기하학은 더 간단하게 설명될 수 있습니다: 그것은 기하학적 모양을 수치적 방법에서 정의하고 표현하고 모양의 수치적 정의와 표현으로부터 수치적 정보를 추출하는 것과 관련됩니다. 실수(real numbers)의 대수를 사용할 수 있다는 것은 기하학의 선형 연속체에 대한 결과를 산출하기 위해 칸토어–데데킨트 공리(Cantor–Dedekind axiom)에 의존합니다.

History

Ancient Greece

그리스(Greek) 수학자 메나이크모스(Menaechmus)는 좌표의 사용과 매우 유사점을 가졌었던 방법을 사용함으로써 문제를 해결하고 정리를 증명했었고 그것이 때때로 그가 해석 기하학을 도입한 것으로 주장되어 왔습니다.

페르가의 아폴로니우스(Apollonius of Perga)는, On Determinate Section에서, 직선 위에 다른 점과 비율이 일치하는 점을 찾는 문제와 함께; 일차원의 해석적 기하학이라고 불릴 수 있는 방식으로 문제를 다루었습니다. 아폴로니우스는 Conics에서 해석적 기하학과 매우 유사한 방법을 더 나아가서 개발하여 그의 연구는 때때로 약 1800년에서 데카르트(Descartes)의 연구를 예상한 것으로 생각될 지경입니다. 기준선, 지름 및 접선의 그의 응용은 좌표 프레임의 우리의 현대 사용과 본질적으로 다르지 않으며, 여기서 접하는 점에서 지름을 따라 측정된 거리는 앱시서이고, 접선에 평행하고 축과 직선 사이에서 가로챈 선분은 올디닛입니다. 그는 수사학적 곡선의 방정식과 동등한 앱시서와 해당하는 올디닛 사이의 관계를 더욱 발전시켰습니다. 어쨌든, 비록 아폴로니우스가 해석 기하학을 개발하는 것에 가까워을지라도, 그는 그렇게 다루지는 않았는데 왜냐하면 그는 음의 크기를 고려하지 않았고 모든 각 경우에서 좌표 시스템이 주어진 곡선 선험(a priori) 대신에 이후(a posteriori)에 겹쳐졌기 때문입니다. 즉, 방정식은 곡선에 의해 결정되었지만, 곡선은 방정식에 의해 결정되지 않았습니다. 좌표, 변수, 및 방정식은 특정 기하학적 상황에 적용되는 보조 개념이었습니다.

Persia

11-세기 페르시아(Persian)의 수학자 오마르 카야얌(Omar Khayyám)은 기하학과 대수학 사이의 강한 관계를 보았고, 그의 일반적인 삼차 방정식(cubic equation)의 기하학적 해와 함께 수치적 대수와 기하학적 대수 사이의 간격을 좁히는 데 도움을 주었을 때 올바른 방향으로 움직이고 있었지만, 결정적인 단계는 나중에 데카르트와 함께 나왔습니다. 오마르 카야얌은 대수적 기하학(algebraic geometry)의 토대를 확인한 공로를 인정받았고, 그의 책 Treatise on Demonstrations of Problems of Algebra (1070)은, 대수학의 원리를 세웠으며, 결국 유럽으로 전달된 페르시아 수학의 몸통의 일부입니다. 대수 방정식에 대한 그의 철저한 기하학적 접근때문에, 카야얌은 해석적 기하학의 발명에서 데카르트의 선구자로 여길 수 있습니다.

Western Europe

해석적 기하학은, 비록 데카르트가 때때로 단독으로 인정받을지라도, 르네 데카르트(René Descartes)와 피에르 드 페르마(Pierre de Fermat)에 의해 독립적으로 발명되었습니다. 데카르트 기하학(Cartesian geometry), 해석적 기하학에 대해 사용되는 대안적인 용어는 데카르트의 이름을 따서 지어졌습니다.

데카르트는 La Geometrie (Geometry)라는 제목의 수필, 1637년에 그의 Discourse on the Method for Rightly Directing One's Reason and Searching for Truth in the Sciences와 함께 출판된 세 개의 따르는 수필 (부록) 중 하나에서 그 방법으로 상당한 진전을 이루었으며, 공통적으로 Discourse on Method으로 참조됩니다. La Geometrie는, 그의 모국어 프랑스(French) 말과 그것의 철학적 원칙으로 쓰였으며, 유럽에서 미적분학(calculus)에 대해 토대를 제공했습니다. 초기에는 그 연구는, 부분적으로, 논쟁과 복잡한 방정식에서 많은 격차로 인해 잘 받아들여지지 않았습니다. 오직 라틴어로 번역되고 1649년에 반 스카우테(van Schooten)의 주석 (및 그에 따른 추가적인 연구)이 추가된 후 데카르트의 걸작은 정당한 인정을 받았습니다.

피에르 드 페르마는 역시 해석적 기하학의 개발을 개척했습니다. 비록 그의 생애에 출판되지는 않았을지라도, Ad locos planos et solidos isagoge (평면 및 고체 위치에 대한 도입)의 원고 형식은 데카르트 Discourse의 출판되기 직전, 1637년에 파리에서 유통되었습니다. 명확하게 쓰이고 호평을 받은, Introduction은 역시 해석적 기하학에 대해 토대를 마련했습니다. 페르마와 데카르트의 취급 사이의 핵심 차이점은 관점의 문제입니다: 페르마는 항상 대수적 방정식으로 시작했고 그런-다음 그것을 만족시키는 기하학적 곡선을 설명했지만, 데카르트는 기하학적 곡선으로 시작하고 그것들의 방정식을 곡선의 여러 속성 중 하나로 생성했습니다. 이 접근법의 결과로, 데카르트는 더 복잡한 방정식을 다루어야 했었고 그는 더 높은 차수의 다항 방정식을 다루는 방법을 개발해야 했습니다. 공간 곡선과 표면의 시스템적인 연구에서 좌표 방법을 처음 적용한 사람은 레온하르트 오일러(Leonhard Euler)였습니다.

Main article: Coordinate systems

Illustration of a Cartesian coordinate plane. Four points are marked and labeled with their coordinates: (2,3) in green, (−3,1) in red, (−1.5,−2.5) in blue, and the origin (0,0) in purple.

해석 기하학에서, 평면(plane)은 좌표 시스템에 의해 제공되며, 그것에 의해 모든 각 점(point)은 한 쌍의 실수(real number) 좌표를 가집니다. 유사하게, 유클리드 공간(Euclidean space)은 모든 각 점이 세 좌표를 가지는 좌표를 제공합니다. 좌표 값은 초기 원점의 선택에 의존합니다. 사용되는 다양한 좌표 시스템이 있지만, 가장 공통적인 것은 다음과 같습니다:

Cartesian coordinates (in a plane or space)

Main article: Cartesian coordinate system

사용하기 위한 가장 공통적인 좌표 시스템은 데카르트 좌표 시스템(Cartesian coordinate system)이며, 여기서 각 점은 그것의 수평 위치를 나타내는 x-좌표와 그것의 수직 위치를 나타내는 y-좌표를 가집니다. 이것들은 전형적으로 순서화된 쌍(ordered pair) (x, y)으로 쓰입니다. 이 시스템은 역시 삼-차원 기하학에서 사용될 수 있으며, 여기서 유클리드 공간(Euclidean space)에서 모든 각 점은 좌표 (x, y, z)의 순서화된 세-쌍(ordered triple)에 의해 표시됩니다.

Polar coordinates (in a plane)

Main article: Polar coordinates

극 좌표(polar coordinates)에서, 평면의 모든 각 점은 원점으로부터의 그것의 거리 r과 통상적으로 양의 x-축으로부터 반시계방향으로 측정된 각도(angle) θ에 의해 표시됩니다. 이 표기법을 사용하여, 점은 전형적으로 순서화된 쌍 (r, θ)으로 쓰입니다. 우리는 공식: $x=r\,\cos \theta ,\,y=r\,\sin \theta ;\,r={\sqrt {x^{2}+y^{2}}},\,\theta =\arctan(y/x)$을 사용함으로써 이-차원 데카르트 좌표와 극 좌표 사이를 앞뒤로 변환할 수 있습니다. 이 시스템은 원통형(cylindrical) 또는 구형(spherical) 좌표의 사용을 통해 삼-차원 공간으로 일반화될 수 있습니다.

Cylindrical coordinates (in a space)

Main article: Cylindrical coordinates

원통형 좌표(cylindrical coordinates)에서, 공간의 모든 각 점은 그것의 높이 z, z-축으로부터 그것의 반지름(radius) r과 수평 축에 관해 xy-평면에 대한 투영을 만드는 각도(angle) θ에 의해 표시됩니다.

Spherical coordinates (in a space)

Main article: Spherical coordinates

구형 좌표(spherical coordinates)에서, 공간에서 모든 각 점은 원점으로부터 그것의 거리 ρ, 수평 축에 관한 그것의 xy-평면에 대한 투영으로 만드는 각도 θ, 및 그것이 z-축에 관해 만드는 각도 φ에 의해 표시됩니다. 각도의 이름은 물리학에서 종종 순서가 뒤바뀝니다.

Equations and curves

Main articles: Solution set and Locus (mathematics)

해석적 기하학에서, 좌표를 포함하는 임의의 방정식(equation)은 평면의 부분집합(subset), 즉 방정식에 대해 해 집합(solution set), 또는 자취(locus)를 지정합니다. 예를 들어, 방정식 y = x는 그것의 x-좌표와 y-좌표가 같은 평면 위의 모든 점의 집합에 해당합니다. 이들 점은 직선을 형성하고, y = x는 이 직선에 대해 방정식이라고 말합니다. 일반적으로, x와 y를 포함하는 선형 방정식은 직선을 지정, 이차 방정식(quadratic equation)은 원뿔 단면(conic section)을 지정하고, 더 복잡한 방정식은 더 복잡한 그림을 설명합니다.

보통, 단일 방정식은 평면 위에 곡선(curve)에 해당합니다. 이것은 항상 그런 경우는 아닙니다: 자명한 방정식 x = x는 전체 평면을 지정하고, 방정식 x² + y² = 0은 오직 단일 점 (0, 0)을 지정합니다. 삼-차원에서, 단일 방정식은 보통 표면(surface)을 제공하고, 곡선은 두 표면의 교차(intersection)로 (아래 참조), 또는 매개변수 방정식(parametric equation)의 시스템으로 지정되어야 합니다. 방정식 x² + y² = r²은 반지름 r을 갖는 원점 (0, 0)에 중심을 둔 임의의 원에 대해 방정식입니다.

Lines and planes

Main articles: Line (geometry) and Plane (geometry)

데카르트 평면(Cartesian plane)에서, 또는 보다 일반적으로, 아핀 좌표(affine coordinates)에서 직선은 선형 방정식에 의해 대수적으로 설명될 수 있습니다. 이-차원에서, 비-수직 직선에 대해 방정식은 종종 기울기-절편 형식(slope-intercept form)으로 주어집니다:

$y=mx+b\,$

여기서:

m은 직선의 기울기(slope) 또는 그래디언트(gradient)입니다.

b는 직선의 y-절편(y-intercept)입니다.

x는 함수 y = f(x)의 독립 변수(independent variable)입니다.

이-차원 공간에서 직선이 그것들의 방정식에 대해 점-경사 형식을 사용하여 설명되는 방법과 유사한 방식으로, 삼-차원 공간에서 평면은 평면에서 점과 그것의 "경사"를 나타내기 위해 그것에 직교하는 벡터 (법선 벡터(normal vector))를 사용하여 자연스러운 설명을 가집니다.

구체적으로 특별히, $\mathbf {r} _{0}$를 어떤 점 $P_{0}=(x_{0},y_{0},z_{0})$의 위치 벡터로 놓고, $\mathbf {n} =(a,b,c)$를 비-영 벡터로 놓습니다. 이 점과 벡터에 의해 결정된 평면은, $P_{0}$로부터 $P$로 그려진 벡터가 $\mathbf {n}$에 수직임을 만족하는 위치 벡터 $\mathbf {r}$과 함께, 그들 점 $P$로 구성됩니다. 두 벡터가 수직인 것과 그들의 점 곱이 영인 것은 필요충분 조검임을 상기하면, 원했던 평면은 다음을 만족하는 모든 점 $\mathbf {r}$의 집합으로 설명될 수 있습니다:

$\mathbf {n} \cdot (\mathbf {r} -\mathbf {r} _{0})=0.$

(점은 여기서 점 곱(dot product)을 의미하고, 스칼라 곱셈이 아닙니다.) 전개된 것은 다음이 됩니다:

$a(x-x_{0})+b(y-y_{0})+c(z-z_{0})=0,$

이것은 평면의 방정식의 점-법선 형식입니다. 이것은 단지 선형 방정식(linear equation)입니다:

$ax+by+cz+d=0,{\text{ where }}d=-(ax_{0}+by_{0}+cz_{0}).$

반대로, 만약 a, b, c 및 d가 상수이고 a, b, 및 c가 모든 영이 아니면, 다음 방정식의 그래프는

$ax+by+cz+d=0,$

법선으로 벡터 $\mathbf {n} =(a,b,c)$을 가지는 평면임을 쉽게 표시됩니다. 평면에 대해 이 친숙한 방정식은 평면의 방정식의 일반적인 형식이라고 불립니다.

삼-차원에서, 직선은 단일 선형 방정식으로 설명될 수 없으므로, 그것들은 자주 매개변수의 방정식(parametric equation)에 의해 설명됩니다:

$x=x_{0}+at\,$

$y=y_{0}+bt\,$

$z=z_{0}+ct\,$

여기서:

x, y, 및 z는 모두 실수에 걸쳐 변화하는 독립 변수 t의 함수입니다.

(x₀, y₀, z₀)는 직선 위의 임의의 점입니다.

a, b, 및 c는 벡터(vector) (a, b, c)가 직선에 평행한 것을 만족하는 직선의 기울기와 관련됩니다.

Conic sections

Main article: Conic section

데카르트 좌표 시스템(Cartesian coordinate system)에서, 두 변수에서 이차 방정식(quadratic equation)의 그래프(graph)는 항상 원뿔 단면입니다 – 비록 그것이 퇴화될 수 있을지라도, 그리고 모든 원뿔 단면이 이 방법에서 발생합니다. 그 방정식은 다음 형식이 될 것입니다:

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0{\text{ with }}A,B,C{\text{ not all zero.}}\,$

모든 여섯 상수를 모두 스케일링하면 같은 영의 자취를 산출하기 때문에, 우리는 원뿔 곡선을 오-차원 투영 공간(projective space) $\mathbf {P} ^{5}$에서 점으로 고려할 수 있습니다.

이 방정식에 의해 묘사된 원뿔 단면은 다음 판별식(discriminant)을 사용하여 분류될 수 있습니다:

$B^{2}-4AC.\,$

만약 원뿔형이 비-퇴화이면,

• 만약 $B^{2}-4AC<0$이면, 방정식은 타원(ellipse)을 나타냅니다;
  • 만약 $A=C$이고 $B=0$이면, 방정식은 원(circle)을 나타내며, 이것은 타원의 특별한 경우입니다;
• 만약 $B^{2}-4AC=0$이면, 방정식은 포물선(parabola)을 나타냅니다;
• 만약 $B^{2}-4AC>0$이면, 방정식은 쌍곡선(hyperbola)을 나타냅니다;
  • 만약 우리가 역시 $A+C=0$를 가지면, 방정식은 직교 쌍곡선(rectangular hyperbola)을 나타냅니다.

Quadric surfaces

Main article: Quadric surface

이차-초곡면(quadric, 또는 quadric surface)은 삼-차원 공간에서 이차 다항식(quadratic polynomial)의 영들(zeros)의 자취(locus)로 정의된 이-차원 표면(surface)입니다. 좌표 x₁, x₂,x₃에서, 일반적인 이차-초곡면은 다음 대수적 방정식(algebraic equation)에 의해 정의됩니다:

$\sum _{i,j=1}^{3}x_{i}Q_{ij}x_{j}+\sum _{i=1}^{3}P_{i}x_{i}+R=0.$

이차 초곡면은 (구(sphere)를 포함하는) 타원면체(ellipsoid), 포물면체(paraboloid), 쌍곡면체(hyperboloid), 원기둥(cylinder), 원뿔(cones), 및 평면(planes)을 포함합니다.

Distance and angle

Main articles: Distance and Angle

The distance formula on the plane follows from the Pythagorean theorem.

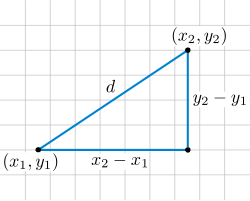
해석 기하학에서, 거리(distance)와 각도(angle) 측정과 같은 기하학적 개념은 공식(formula)을 사용하여 정의됩니다. 이들 정의는 놓여있는 유클리드 기하학(Euclidean geometry)과 일치하도록 설계되었습니다. 예를 들어, 평면 위에 데카르트 좌표(Cartesian coordinates)를 사용하여, 두 점 (x₁, y₁)과 (x₂, y₂) 사이의 거리는 다음 공식에 의해 정의됩니다:

$d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}},\!$

이것은 피타고라스 정리(Pythagorean theorem)의 버전으로 보일 수 있습니다. 비슷하게, 직선이 수평선과 이르는 각도는 다음 공식에 의해 정의될 수 있습니다:

$\theta =\arctan(m),$

여기서 m은 직선의 기울기(slope)입니다.

삼-차원에서, 거리는 피타고라스 정리의 일반화에 의해 주어집니다:

$d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}},\!$,

반면에 두 벡서 사이의 각도는 점 곱(dot product)에 의해 주어집니다. 두 유클리드 벡터 A와 B의 점 곱은 다음에 의해 정의됩니다:

$\mathbf {A} \cdot \mathbf {B} {\stackrel {\mathrm {def} }{=}}\|\mathbf {A} \|\,\|\mathbf {B} \|\cos \theta ,$

여기서 θ는 A and B 사이의 각도(angle)입니다.

Transformations

a) y = f(x) = |x|       b) y = f(x+3)       c) y = f(x)-3       d) y = 1/2 f(x)

변환은 부모 함수를 유사한 특성을 가진 새 함수로 전환하기 위해 그것에 적용됩니다.

$R(x,y)$의 그래프는 다음과 같이 표준 변환에 의해 변경됩니다:

• $x$를 $x-h$로 변경하는 것은 그래프를 오른쪽으로 $h$ 단위만큼 이동합니다.
• $y$를 $x-k$로 변경하는 것은 그래프를 위로 $k$ 단위만큼 이동합니다.
• $x$를 $x/b$로 변경하는 것은 그래프를 수평적으로 $b$의 인수만큼 펼칩니다. ($x$를 확장되는 것으로 생각)
• $y$를 $y/a$로 변경하는 것은 수직으로 그래프를 펼칩니다.
• $x$를 $x\cos A+y\sin A$로 변경하고 $y$를 $-x\sin A+y\cos A$로 변경하는 것은 그래프를 각도 $A$만큼 회전합니다.

초등 해석 기하학에서 전형적으로 연구되지 않는 다른 표준 변환이 있는데 왜냐하면 그 변환은 보통 고려되지 않는 방법으로 대상의 모양을 변경하기 때문입니다. 기울임(Skewing)은 보통 고려되지 않는 변형의 한 예제입니다. 자세한 정보에 대해, 아핀 변환(affine transformations)에 대한 기사를 참조하십시오.

예를 들어, 부모 함수 $y=1/x$는 수평 및 수직 점근선을 가지고, 첫 번째 및 세 번째 사분면을 차지하고, 그것의 모든 변환된 형식은 하나의 수평과 수직 점근선을 가지고, 첫 번째와 세 번째 또는 두 번째와 네 번째 사분면을 차지합니다. 일반적으로, 만약 $y=f(x)$이면, 그것은 $y=af(b(x-k))+h$로 변환될 수 있습니다. 새로운 변환된 함수에서, $a$는 만약 그것이 1보다 크면 함수를 수직적으로 펼쳐거나 만약 그것이 1보다 작으면 함수를 수직적으로 압축하는 인수이고, 음의 $a$ 값에 대해, 함수는 $x$-축에서 반사됩니다. $b$ 값은 만약 1보다 크면 수평적으로 함수의 그래프를 압축하고 만약 1보다 작으면 수평적으로 함수를 펼치고, $a$와 마찬가지로, 그것이 음수일 때 $y$-축에서 함수를 반사합니다. $k$와 $h$ 값은 평행이동, $h$, 수직, 및 $k$ 수평을 도입합니다. 양의 $h$와 $k$ 값은 함수가 그것의 축의 양의 끝으로 평행이동됨을 의미하고 음수는 음의 끝을 향한 평행이동을 의미합니다.

변환은 방정식이 함수를 나타내는지 여부에 관계없이 임의의 기하학적 방정식에 적용될 수 있습니다. 변환은 개별적인 트랜잭션으로 또는 조합에서 처리될 수 있습니다.

$R(x,y)$가 $xy$ 평면에서 관계임을 가정합니다. 예를 들어, 다음은 단위 원을 묘사하는 관계입니다:

$x^{2}+y^{2}-1=0$.

Finding intersections of geometric objects

Main article: Intersection (geometry)

관계 $P(x,y)$와 $Q(x,y)$에 의해 표현된 두 기하학적 대상 P와 Q에 대해, 교차는 양쪽 변에 있는 모든 점 $(x,y)$의 집합입니다.

예를 들어, $P$는 반지름 1과 중심 $(0,0)$을 갖는 원: $P=\{(x,y)|x^{2}+y^{2}=1\}$일 수 있고 $Q$는 반지름 1과 중심 $(1,0)$을 갖는 원: $Q=\{(x,y)|(x-1)^{2}+y^{2}=1\}$일 수 있습니다. 이들 두 원의 교차는 양쪽 방정식을 참으로 만드는 점의 집합입니다. 점 $(0,0)$은 양쪽 방정식을 참으로 만듭니까? $(x,y)$에 대해 $(0,0)$을 사용하면, $Q$에 대해 방정식은 $(0-1)^{2}+0^{2}=1$ 또는 $(-1)^{2}=1$이 되며 이것은 참이므로, $(0,0)$는 관계 $Q$ 안에 있습니다. 다른 한편으로, 여전히 $(x,y)$에 대해 $(0,0)$을 사용하면, $P$에 대해 방정식은 $0^{2}+0^{2}=1$ 또는 $0=1$이 되며 이것은 거짓입니다. $(0,0)$은 $P$ 안에 있지 않으므로 그것은 교차점이 아닙니다.

$P$와 $Q$의 교차점은 연립 방정식을 풂으로써 구할 수 있습니다:

$x^{2}+y^{2}=1$

$(x-1)^{2}+y^{2}=1.$

교차를 찾는 전통적인 방법은 치환과 제거를 포함합니다.

치환: 첫 번째 방정식을 $x$에 관한 $y$에 대해 풀고 그런-다음 $y$에 대한 표현을 두 번째 방정식에 치환하십시오:

$x^{2}+y^{2}=1$

$y^{2}=1-x^{2}$.

우리는 그런-다음 $y^{2}$에 대한 이 값을 나머지 다른 방정식에 치환하고 $x$에 대해 풀기 위해 진행하십시오:

$(x-1)^{2}+(1-x^{2})=1$

$x^{2}-2x+1+1-x^{2}=1$

$-2x=-1$

$x=1/2.$

다음으로, 우리는 $x$의 이 값을 원래 방정식의 하나에 대입하고 $y$에 대해 푸십시오:

$(1/2)^{2}+y^{2}=1$

$y^{2}=3/4$

$y={\frac {\pm {\sqrt {3}}}{2}}.$

따라서 우리의 교차는 두 점을 가집니다:

$\left(1/2,{\frac {+{\sqrt {3}}}{2}}\right)\;\;\mathrm {and} \;\;\left(1/2,{\frac {-{\sqrt {3}}}{2}}\right).$

제거: 변수 중 하나가 제거되도록 한 방정식의 배수를 다른 방정식에 더하거나 빼십시오. 우리의 현재 예제에서, 만약 우리가 두 번째 방정식에서 첫 번째 방정식을 빼면 우리는 $(x-1)^{2}-x^{2}=0$를 얻습니다. 첫 번째 방정식에서 $y^{2}$은 $y$ 항을 남기지 않도록 두 번째 방정식에서 $y^{2}$에서 빼집니다. 변수 $y$가 제거되었습니다. 우리는 그런-다음 치환 방법에서 처럼 같은 방법으로 $x$에 대해 남아있는 방정식을 풉니다:

$x^{2}-2x+1+1-x^{2}=1$

$-2x=-1$

$x=1/2.$

우리는 그런-다음 이 $x$의 값을 원래 방정식 중 하나에 대입하고 $y$에 대해 풉니다:

$(1/2)^{2}+y^{2}=1$

$y^{2}=3/4$

$y={\frac {\pm {\sqrt {3}}}{2}}.$

따라서 우리의 교차는 두 점을 가집낟:

$\left(1/2,{\frac {+{\sqrt {3}}}{2}}\right)\;\;\mathrm {and} \;\;\left(1/2,{\frac {-{\sqrt {3}}}{2}}\right).$

원뿔 단면에 대해, 교차점에 최대 4개의 점이 있을 수 있습니다.

Finding intercepts

Main articles: x-intercept and y-intercept

널리 연구되고 있는 교차의 유형 중 하나는 기하학적 대상과 $x$ 및 $y$ 좌표 축의 교차입니다.

기하학적 대상과 $y$-축의 교차는 대상의 $y$-절편이라고 불립니다. 기하학적 대상과 $x$-축의 교차는 대상의 $x$-절편이라고 불립니다.

직선 $y=mx+b$에 대해, 매개변수 $b$는 직선이 $y$ 축을 교차하는 점을 지정합니다. 문맥에 따라, $b$ 또는 점 $(0,b)$가 $y$-절편이라고 불립니다.

Tangents and normals

Tangent lines and planes

Main article: Tangent

기하학(geometry)에서, 주어진 점(point)에서 평면 곡선(curve)에 접하는 직선(tangent line) (또는 단순히 접선(tangent))은 해당 점에서 곡선에 "간신히 접촉하는" 직선(straight line)입니다. 비공식적으로, 곡선에서 무한히 가까운(infinitely close) 한 쌍의 점을 통과하는 직선입니다. 보다 정확하게, 직선이 만약 그것이 곡선 위의 점 (c, f(c))를 통과하고 기울기 f'(c)를 가지면 점 x = c에서 곡선 y = f(x)의 접선이라고 말해지며, 여기서 f'는 f의 도함수(derivative)입니다. 비슷한 정의는 n-차원 유클리드 공간(Euclidean space)에서 공간 곡선(space curve)과 곡선에 적용됩니다.

접하는 직선과 곡선이 만나는 점을 통과할 때, 접하는 점(point of tangency)이라고 불림, 접선은 곡선과 "같은 방향으로 진행"하고, 따라서 해당 점에서 곡선에 가장 가까운 직선 근사입니다.

비슷하게, 주어진 점에서 표면에 접하는 평면(tangent plane)은 해당 점에서 표면(surface)에 "간신히 접촉하는" 평면(plane)입니다. 접하는 것의 개념은 미분 기하학(differential geometry)에서 가장 기본 개념 중 하나이고 광범위하게 일반화되어 왔습니다; 접하는 공간(Tangent space)을 참조하십시오.

Normal line and vector

Main article: Normal (geometry)

기하학(geometry)에서, 법선(normal)은 주어진 대상에 수직(perpendicular)인 직선 또는 벡터와 같은 대상입니다. 예를 들어, 이-차원 경우에서, 주어진 점에서 곡선에 대한 법선(normal line)은 그 점에서 곡선에 대한 접선(tangent line)에 수직인 직선입니다.

삼-차원 경우에서, 점 P에서 표면(surface)에 대한 표면 법선(surface normal), 또는 단순히 법선(normal)은 P에서 해당 표면에 대한 접하는 평면(tangent plane)에 수직(perpendicular)인 벡터(vector)입니다. 단어 "normal"은 역시 형용사로 사용됩니다: 평면(plane)에 수직(normal)인 직선(line), 힘(force)의 법선(normal) 성분, 법선 벡터(normal vector) 등. 정규성 개념은 직교성으로 일반화됩니다. 법선성(normality)의 개념은 직교성(orthogonality)으로 일반화됩니다.

See also

• Cross product
• Rotation of axes
• Translation of axes
• Vector space

References

Books

• Boyer, Carl B. (2004) [1956], History of Analytic Geometry, Dover Publications, ISBN 978-0486438320
• Cajori, Florian (1999), A History of Mathematics, AMS, ISBN 978-0821821022
• John Casey (1885) Analytic Geometry of the Point, Line, Circle, and Conic Sections, link from Internet Archive.
• Katz, Victor J. (1998), A History of Mathematics: An Introduction (2nd Ed.), Reading: Addison Wesley Longman, ISBN 0-321-01618-1
• Struik, D. J. (1969), A Source Book in Mathematics, 1200-1800, Harvard University Press, ISBN 978-0674823556

Articles

• Bissell, C. C., Cartesian geometry: The Dutch contribution
• Boyer, Carl B. (1944), "Analytic Geometry: The Discovery of Fermat and Descartes", Mathematics Teacher, 37 (3): 99–105
• Boyer, Carl B., Johann Hudde and space coordinates
• Coolidge, J. L. (1948), "The Beginnings of Analytic Geometry in Three Dimensions", American Mathematical Monthly, 55 (2): 76–86, doi:10.2307/2305740, JSTOR 2305740
• Pecl, J., Newton and analytic geometry

External links

• Coordinate Geometry topics with interactive animations