Monoid

추상 대수학(abstract algebra), 수학(mathematics)의 한 가지에서, 모노이드(monoid)는 결합적(associative) 이항 연산(binary operation)과 항등 원소(identity element)를 갖춘 집합입니다. 예를 들어, 덧셈을 갖는 비-음의 정수(integers)는 모노이드를 형성하며, 항등 원소는 0입니다.

모노이드는 항등원을 갖는 반-그룹(semigroup)입니다. 그러한 대수적 구조(algebraic structure)는 수학의 여러 가지에서 발생합니다.

집합에서 자체로의 함수는 함수 합성에 관한 모노이드를 형성합니다. 보다 일반적으로, 카테고리 이론(category theory)에서, 대상(object)에서 자체로의 사상은 모노이드를 형성하고, 반대로, 모노이드는 단일 대상을 갖는 카테고리로 볼 수 있습니다.

컴퓨터 과학(computer science)과 컴퓨터 프로그래밍(computer programming)에서, 주어진 문자(characters)의 집합에서 구축된 문자열(strings)의 집합은 자유 모노이드(free monoid)입니다. 전이 모노이드(transition monoid)와 구문 모노이드(syntactic monoid)는 유한-상태 기계(finite-state machine)를 설명하는 데 사용됩니다. 트레이스 모노이드(trace monoid)와 히스토리 모노이드(history monoid)는 프로세스 계산(process calculi)와 컨커런트 컴퓨팅(concurrent computing)을 위한 토대를 제공합니다.

이론적 컴퓨터 과학(theoretical computer science)에서, 모노이드의 연구는 오토마타 이론(automata theory) (크론–로즈 이론(Krohn–Rhodes theory))과 형식적 언어 이론(formal language theory) (별 높이 문제(star height problem))에 대해 기본입니다.

주제의 역사와 모노이드의 일부 다른 일반적인 속성에 대해 반그룹(semigroup)을 참조하십시오.

Definition

이항 연산(binary operation) $S \times S \to S$ 를 갖춘 집합(set) S는, 이항 연산은 •로 표시할 것이며, 만약 그것이 다음 두 가지 공리를 만족시키면 모노이드입니다:

결합성(Associativity): S에서 모든 a, b 및 c에 대해, 방정식 $(a • b) • c = a • (b • c)$ 이 유지됩니다.
항등 원소(Identity element): S에서 모든 각 원소 a에 대해, 방정식 $e • a = a$ 와 $a • e = a$ 가 유지됨을 만족하는 원소 e가 S에 존재합니다.

다시 말해, 모노이드는 항등 원소(identity element)를 갖는 반그룹(semigroup)입니다. 그것은 역시 결합성과 항등원을 갖는 마그마(magma)로 생각될 수 있습니다. 모노이드의 항등 원소는 고유합니다.^[1] 이러한 이유로, 항등원은 상수(constant), 즉, 0-항 (또는 영-항) 연산으로 고려됩니다. 모노이드는 따라서 세-쌍 (S, • , e)의 사양에 의해 특징짓습니다.

문맥에 따라, 이항 연산에 대해 기호는 그 연산이 병치에 의해 표시되도록 생략될 수 있습니다; 예를 들어, 모노이드 공리는 $(ab) c = a (bc)$ 와 $ea = ae = a$ 로 쓸 수 있습니다. 이 표기법은 숫자가 곱해지는 것을 의미하지 않습니다.

각 원소가 역원(inverse)을 가지는 모노이드는 그룹(group)입니다.

Monoid structures

Submonoids

모노이드의 부분-모노이드(submonoid) $(M, •)$ 는 모노이드 연산 아래에서 닫혀 있고 M의 항등 원소 e를 포함하는 M의 부분집합(subset) N입니다.^[2]^[3] 기호적으로, N은 만약 $x, y \in N$ 와 $e \in N$ 일 때마다 $N \subseteq M$ , $x • y \in N$ 이면 M의 부분모노이드입니다. 이 경우에서, N은 M에서 상속된 이항 연산 아래에서 모노이드입니다.

다른 한편으로, 만약 N이 모노이드 연산 아래에서 닫혀 있는 모노이드의 부분집합이고, 이 상속된 연산에 대해 모노이드이면, N은 항상 부분모노이드가 아닌데, 왜냐하면 항등 원소가 다를 수 있기 때문입니다. 예를 들어, 한원소 집합(singleton set) ${0}$ 은 곱셈 아래에서 닫혀 있고, 비-음의 정수(nonnegative integers)의 (곱셈) 모노이드의 부분모노이드가 아닙니다.

Generators

M의 부분집합 S는 만약 S를 포함하는 M의 가장 작은 부분모노이드가 M이면 M을 생성한다고 말합니다. 만약 M을 생성하는 유한 집합이 있으면, M은 유한하게 생성된 모노이드(finitely generated monoid)라고 말합니다.

Commutative monoid

그 연산이 교환적(commutative)인 모노이드는 교환 모노이드(commutative monoid, 또는, 덜 공통적으로, 아벨 모노이드(abelian monoid))라고 불립니다. 교환 모노이드는 종종 덧셈적으로 씁니다. 임의의 교환 모노이드는 만약 $x + z = y$ 임을 만족하는 z가 존재하면 $x \leq y$ 에 의해 표시되며 그것의 대수적 준순서화(preordering) $\leq$ 를 부여됩니다.^[4] 교환 모노이드 M의 순서-단위(order-unit)는 M의 임의의 원소 x에 대해, $x \leq v$ 임을 만족하는 u에 의해 생성된 집합에 v가 존재함을 만족하는 M의 원소 u입니다. 이것은 종종 부분적으로 순서화된(partially ordered) 아벨 그룹(abelian group) G의 경우의 양수 원뿔(positive cone)이며, 이 경우에서 우리는 u가 G의 순서-단위라고 말합니다.

Partially commutative monoid

연산이 일부 원소에 대해 교환적이지만, 전체 원소에 대해 그렇지 않은 모노이드는 트레이스 모노이드입니다; 트레이스 모노이드는 공통적으로 컨커런트 계산(concurrent computation)의 이론에서 발생합니다.

Examples

16 개의 가능한 이항 부울 연산자(binary Boolean operators) 중 4 개는 교환적이고 결합적인 양쪽-변 항등원을 가지고 있습니다. 이들 네 가지 각각은 집합 {False, True}를 교환 모노이드로 만듭니다. 표준 정의 아래에서, AND와 XNOR는 항등원 True를 가지고 반면에 XOR와 OR은 항등원 False를 가집니다. AND와 OR에서 모노이드는 역시 거듭상등(idempotent)이고 반면에 XOR와 XNOR에서 모노이드는 그렇지 않습니다.
자연수의 집합 $\mathbb {N} =\{0,1,2,\ldots \}$ 은 덧셈 (항등 원소 0) 또는 곱셈 (항등 원소 1) 아래에서 교환 모노이드입니다. 덧셈 아래에서 $N$ 의 부분모노이드는 수치 모노이드(numerical monoid)라고 불립니다.
양의 정수의 집합 $\mathbb {N} \setminus \{0\}$ 은 곱셈 (항등 원소 1) 아래에서 교환 모노이드입니다.
집합 $A$ 가 주어지면, $A$ 의 부분집합의 집합은 교집합 (항등 원소는 $A$ 자체임) 아래에서 교환 모노이드입니다.
집합 $A$ 가 주어지면, $A$ 의 부분집합의 집합은 합집합 (항등 원소는 빈 집합(empty set)임) 아래에서 교환 모노이드입니다.
이전 예제를 일반화하면, 모든 각 경계진 반격자(semilattice)는 거듭상등(idempotent) 교환 모노이드입니다.
- 특히, 임의의 경계진 격자(lattice)는 만남(meet)- 및 접합(join)- 모노이드 구조를 모두 부여될 수 있습니다. 항등 원소는 각각 격자의 꼭대기와 그것의 바닥입니다. 격자이기 때문에, 헤이팅 대수(Heyting algebras)와 부울 대수(Boolean algebras)는 이들 모노이드 구조로 부여됩니다.
이항 연산 • 아래에서 닫혀 있는 모든 각 한원소 집합(singleton set) ${x}$ 는 자명한 (한-원소) 모노이드를 형성하며, 이는 역시 자명한 그룹(trivial group)이라고 불립니다.
모든 각 그룹은 모노이드이고 모든 각 아벨 그룹(abelian group)은 교환 모노이드입니다.
임의의 반그룹(semigroup) S는 단순히 S에 있지 않은 원소 e에 인접하고 모든 s ∈ S에 대해 e • s = s = s • e를 정의함으로써 모노이드로 바뀔 수 있습니다. 임의의 반그룹을 모노이드로의 변환은 반그룹의 카테고리와 모노이드의 카테고리 사이의 자유 함수자(free functor)에 의해 수행됩니다.^[5]
- 따라서, 거듭상등 모노이드 (때때로 find-first로 알려져 있음)는 항등 원소 e를 집합 S에 걸쳐 왼쪽 영 반그룹(left zero semigroup)에 인접함으로써 형성될 수 있습니다. 반대 모노이드 (때때로 find-last로 불림)는 S에 걸쳐 오른쪽 영 반그룹(right zero semigroup)에서 형성됩니다.
  - 항등원 $e$ 를 두 원소 ${lt, gt}$ 를 갖는 왼쪽-영 반그룹에 인접하십시오. 그런-다음 결과 거듭상등 모노이드 ${lt, e, gt}$ 는 e를 나타내는 상등과 함께 그 원소의 순서에 의해 주어진 수열의 사전식 순서(lexicographical order)를 모델링합니다.
연산으로 덧셈 또는 곱셈을 갖는 임의의 링(ring)의 놓여있는 집합. (정의에 의해, 링은 곱셈 항등원 1을 가집니다.
- 연산으로 덧셈 또는 곱셈을 갖는 정수, 유리수, 실수, 또는 복소수.^[6]
- 연산으로 행렬 덧셈 또는 행렬 곱셈을 갖는 주어진 링에 걸쳐 모든 $n$ x $n$ 행렬의 집합.
일부 고정된 알파벳 $Σ$ 에 걸쳐 모든 유한 문자열(strings)의 집합은 연산으로 문자열 연쇄(string concatenation)를 갖는 모노이드를 형성합니다. 빈 문자열(empty string)은 항등 원소로 역할을 합니다. 이 모노이드는 $Σ *$ 로 표시되고 $Σ$ 에 걸쳐 자유 모노이드(free monoid)라고 불립니다. 그것은 만약 $Σ$ 가 적어도 두 개의 원소를 가지면 교환적이지 않습니다.
임의의 모노이드 $M$ 이 주어지면, 반대 모노이드(opposite monoid) $M op$ 는 $M$ 과 같은 운반(carrier) 집합과 항등 원소를 가지고, 그것의 연산은 $x • op y = y • x$ 에 의해 정의됩니다. 임의의 교환 모노이드는 그 자체의 반대 모노이드입니다.
모노이드 구조 (또는, 일반적으로, 임의의 유한 숫자의 모노이드 $M 1, ..., M k$ )가 부여된 두 집합 $M$ 과 $N$ 이 주어지면, 그것들의 데카르트 곱(Cartesian product) $M \times N$ 은 역시 모노이드입니다 (각각, $M 1 \times \dots \times M k$ ). 결합 연산과 항등 원소는 쌍-별로 정의됩니다.^[7]
모노이드 $M$ 을 고정하십시오. 주어진 집합에서 $M$ 으로의 모든 함수의 집합은 역시 모노이드입니다. 항등 원소는 임의의 값을 $M$ 의 항등원에 매핑하는 상수 함수(constant function)입니다; 결합 연산은 점-별(pointwise)로 정의됩니다.
연산 $•$ 과 항등 원소 $e$ 를 갖는 모노이드를 고정하고 $M$ 의 모든 부분집합(subsets)으로 구성되는 그것의 거듭제곱 집합(power set) $P (M)$ 을 생각해 보십시오. 그러한 부분집합에 대해 이항 연산은 $S • T = {s • t : s \in S, t \in T}$ 에 의해 정의될 수 있습니다. 이것은 $P (M)$ 을 항등 원소 ${e}$ 를 갖는 모노이드로 바꿉니다. 같은 방법에서, 그룹 $G$ 의 거듭제곱 집합은 그룹 부분집합의 곱(product of group subsets) 아래에서 모노이드입니다.
$S$ 를 집합으로 놓습니다. 모든 집합 $S \to S$ 의 집합은 함수 합성(function composition) 아래에서 모노이드를 형성합니다. 항등원은 바로 항등 함수(identity function)입니다. 그것은 역시 $S$ 의 완전 변환 모노이드(full transformation monoid)라고 불립니다. 만약 $S$ 가 $n$ 원소를 갖는 유한한 것이면, $S$ 위에 함수의 모노이드는 $n n$ 원소를 갖는 유한한 것입니다.
이전 예제를 일반화하면, $C$ 를 카테고리라고 놓고 $X$ 를 $C$ 의 대상이라고 놓습니다. $X$ 의 모든 자기-사상(endomorphisms)의 집합은, $End C (X)$ 로 표시되며, 사상(morphisms)의 합성 아래에서 모노이드를 형성합니다. 카테고리 이론과 모노이드 사이의 관계에 대한 자세한 내용에 대해 아래를 참조하십시오.
연결된 합(connected sum)을 갖는 컴팩트 표면(compact surfaces)의 위상-동형(homeomorphism) 클래스(classes)의 집합. 그것의 단위 원소는 보통의 2-구의 클래스입니다. 더욱이, 만약 $a$ 가 토러스(torus)의 클래스를 표시하고, b가 투영 평면의 클래스를 표시하면, 모노이드의 모든 각 원소 c는 형식 $c = na + mb$ 의 고유한 표현을 가지며 여기서 $n$ 은 양의 정수이고 $m = 0, 1$ , 또는 $2$ 입니다. 우리는 $3 b = a + b$ 를 가집니다.
$\langle f\rangle$ 를 차수 $n$ 의 순환 모노이드, 즉, $\langle f\rangle =\left\{f^{0},f^{1},\dots ,f^{n-1}\right\}$ 라고 놓습니다. 그런-다음 일부 $0\leq k<n$ 에 대해 $f^{n}=f^{k}$ 입니다. 실제로, 각각의 그러한 $k$ 는 차수 $n$ 의 구별되는 모노이드를 제공하고, 모든 각 순환 모노이드는 이들 중 하나에 동형적입니다.
더욱이, $f$ 는 다음에 의해 주어진 점 $\{0,1,2,\dots ,n-1\}$ 위에 함수로 고려될 수 있습니다: ${\begin{bmatrix}0&1&2&\cdots &n-2&n-1\\1&2&3&\cdots &n-1&k\end{bmatrix}}$ 또는, 동등하게 $f(i):={\begin{cases}i+1,&{\text{if }}0\leq i<n-1\\k,&{\text{if }}i=n-1.\end{cases}}$ $\langle f\rangle$ 에서 원소의 곱셈은 is 그때에 함수 합성에 의해 주어집니다.
$k=0$ 일 때 함수 $f$ 는 $\{0,1,2,\dots ,n-1\}$ 의 순열이고, 차수 $n$ 의 고유한 순환 그룹(cyclic group)을 제공합니다.

Properties

모노이드 공리는 항등 원소 $e$ 가 고유하다는 것을 암시합니다: 만약 $e$ 와 $f$ 가 모노이드의 항등 원소이면, $e = ef = f$ 입니다.

Products and powers

각각의 비-음의 정수 $n$ 에 대해, 우리는 모노이드의 $n$ 원소의 임의의 수열 $(a_{1},\ldots ,a_{n})$ 의 곱 $p_{n}=\textstyle \prod _{i=1}^{n}a_{i}$ 을 재귀적으로 정의할 수 있습니다: $p 0 = e$ 라고 놓고 $1 \leq m \leq n$ 에 대해 $p m = p m -1 • a m$ 라고 놓습니다.

특별한 경우로, 우리는 모노이드의 원소 $x$ 의 비-음의 정수 거듭제곱을 정의할 수 있습니다: $x 0 = 1$ 와 $n \geq 1$ 에 대해 $x n = x n -1 • x$ . 그런-다음 모든 $m, n \geq 0$ 에 대해 $x m + n = x m • x n$ .

Invertible elements

원소 $x$ 는 만약 $x • y = e$ 와 $y • x = e$ 임을 만족하는 원소 $y$ 가 존재하면 역-가능(invertible)이라고 불립니다. 원소 $y$ 는 $x$ 의 역이라고 불립니다. 역은, 만약 그것들이 존재하면, 고유합니다: 만약 $y$ 와 $z$ 가 $x$ 의 역이면, 결합성에 의해 $y = ey = (zx) y = z (xy) = ze = z$ 입니다.^[8]

만약 $x$ 가 역-가능이면, 말하자면 역 $y$ 를 가지면, 우리는 각 $n \geq 1$ 에 대해 $x - n = y n$ 를 설정함으로써 $x$ 의 음의 거듭제곱을 정의할 수 있습니다; 이것은 방정식 $x m + n = x m • x n$ 을 모든 $m, n \in Z$ 에 대해 유지되도록 만듭니다.

모노이드에서 모든 역-가능 원소의 집합은, 연산 •와 함께, 그룹(group)을 형성합니다.

Grothendieck group

모든 각 모노이드가 그룹 안에 있는 것은 아닙니다. 예를 들어, 두 개의 원소 $a$ 와 $b$ 가 심지어 $b$ 가 항등 원소가 아니더라도 $a • b = a$ 가 유지됨을 만족하게 존재하는 모노이드를 가지는 것이 완벽하게 가능합니다. 그러한 모노이드는 그룹에 삽입될 수 없는데, 왜냐하면 그룹에서 양쪽 변에 $a$ 의 역을 곱하면 $b = e$ 임을 얻을 수 있으며, 이는 사실이 아니기 때문입니다.

모노이드 $(M, •)$ 는 만약 $M$ 에서 모든 $a$ , $b$ , 및 $c$ 에 대해, 상등 $a • b = a • c$ 가 $b = c$ 를 의미하고, 상등 $b • a = c • a$ 는 $b = c$ 를 의미하면 취소 속성(cancellation property)을 가집니다 (또는 취소-가능입니다).

취소 속성을 갖는 교환 모노이드는 항상 그로텐디크 그룹 구성(Grothendieck group construction)을 통해 그룹에 삽입될 수 있습니다. 그것이 정수의 덧셈 그룹 (연산 +을 갖는 그룹)이 자연수의 덧셈 모노이드 (연산 +와 취소 속성을 갖는 교환 모노이드)에서 구성되는 방법입니다. 어쨌든, 비-교환 취소 모노이드는 그룹에 삽입될 필요가 없습니다.

만약 모노이드가 취소 속성을 가지고 유한한 것이면, 그것은 사실상 그룹입니다.^[9]

모노이드의 오른쪽- 및 왼쪽-취소 원소는 차례로 부분모노이드를 형성합니다 (즉, 연산 아래에서 닫혀 있고 분명히 항등원을 포함합니다). 이것은 임의의 교환 모노이드의 취소 원소가 그룹으로 확장될 수 있음을 의미합니다.

모노이드에서 취소 속성은 그로텐디크 구성을 수행하는 데 필요하지 않습니다 – 교환성은 충분 조건입니다. 어쨌든, 만약 교환 모노이드가 취소 속성을 가지지 않으면, 모노이드를 그로텐디크 그룹으로의 준동형은 단사가 아닙니다. 보다 정확하게, 만약 $a • b = a • c$ 이면, $b$ 와 $c$ 는 심지어 $b \neq c$ 이더라도 그로텐디크 그룹에서 같은 이미지를 가집니다. 특히, 만약 모노이드가 흡수 원소(absorbing element)를 가지면, 그로텐디크 그룹은 자명한 그룹(trivial group)입니다.

Types of monoids

역 모노이드(inverse monoid)는 M에서 모든 각 a에 대해, $a = a • a -1 • a$ 와 $a -1 = a -1 • a • a -1$ 임을 만족하는 고유한 a⁻¹가 M에 존재하는 모노이드입니다. 만약 역 모노이드가 취소적이면, 그것은 그룹입니다.

반대 방향에서, 영합자유 모노이드(zerosumfree monoid)는 $a + b = 0$ 이 $a = 0$ 이고 $b = 0$ 임을 의미하는 덧셈적으로 작성된 모노이드입니다;^[10] 동등하게, 영 이외의 어떤 원소도 덧셈 역원을 가지지 않습니다.

Acts and operator monoids

M을 •에 의해 표시된 이항 연산과 e에 의해 표시된 항등 원소를 갖는 모노이드라고 놓습니다. 그런-다음 (왼쪽) M-작용 (또는 M에 걸쳐 왼쪽 작용)은 다음으로 모노이드 구조와 호환되는 연산 $\cdot : M \times X \to X$ 과 함께 집합 X입니다:

X에서 모든 x에 대해: $e \cdot x = x$ ;
M에서 모든 a, b와 X에서 x에 대해: $a \cdot (b \cdot x) = (a • b) \cdot x$ .

이것은 (왼쪽) 그룹 동작(group action)의 모노이드 이론에서 아날로그입니다. 오른쪽 M-작용은 역시 유사한 방법으로 정의됩니다. 작용을 갖는 모노이드는 역시 연산자 모노이드(operator monoid)라고 알려져 있습니다. 중요한 예제는 반-오토마타(semiautomata)의 전이 시스템(transition systems)을 포함합니다. 변환 반그룹(transformation semigroup)은 항등 변환에 인접함으로써 연산자 모노이드로 만들 수 있습니다.

Monoid homomorphisms

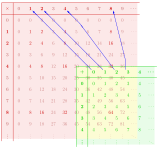
두 개의 모노이드 $(M, *)$ 과 $(N, •)$ 사이의 준동형(homomorphism)은 다음임을 만족하는 함수 $f : M \to N$ 입니다:

M에서 모든 x, y에 대해 $f (x * y) = f (x) • f (y)$
$f (e M) = e N$ ,

여기서 e_M과 e_N은 각각 M과 N의 항등원입니다. 모노이드 준동형은 때때로 간단히 모노이드 사상(monoid morphisms)이라고 불립니다.

모노이드 사이의 모든 각 반그룹 준동형(semigroup homomorphism)이 모노이드 준동형은 아닌데, 왜냐하면 그것은 심지어 항등원이 준동형의 이미지의 항등원이더라도 항등원을 대상 모노이드의 항등원에 매핑하지 않을 수 있기 때문입니다.^[11] 예를 들어, 곱셈을 갖춘 잔여 클래스(residue classes) 모듈로 $n$ 의 집합, $M_{n}$ 을 생각해 보십시오. 특히, $1$ 의 클래스는 항등원입니다. $f(k)=3k$ 에 의해 주어진 함수 $f\colon M_{3}\to M_{6}$ 은 $M_{6}$ 에서 $3k\cdot 3l=9kl=3kl$ 으로 반그룹 준동형입니다. 어쨌든, $f(1)=3\neq 1$ 이므로, 모노이드 준동형은 첫 번째 모노이드의 항등원을 두 번째 모노이드의 항등원으로 매핑하는 모노이드 사이의 반그룹 준동형이고 후자의 조건은 생략될 수 없습니다.

대조적으로, 그룹 사이의 반그룹 준동형은 항상 그룹 준동형(group homomorphism)인데, 왜냐하면 그것은 항등원을 반드시 보존하기 때문입니다 (왜냐하면, 그룹에서, 항등원은 $x \cdot x = x$ 임을 만족하는 유일한 원소이기 때문입니다).

전단사(bijective) 모노이드 준동형은 모노이드 동형(isomorphism)이라고 불립니다. 두 모노이드는 만약 그것들 사이에 모노이드 동형이 있으면 동형적이라고 말합니다.

Equational presentation

모노이드는 그룹이 그룹 표시(group presentation)를 수단으로 지정될 수 있는 것과 매우 유사한 방법으로 표시(presentation)를 제공할 수 있습니다. 우리는 생성기 Σ의 집합과 자유 모노이드(free monoid) Σ^∗ 위에 관계의 집합을 지정함으로써 이를 수행합니다. 우리는 Σ^∗ 위에 (유한) 이항 관계(binary relations)를 모노이드 합동으로 확장하고, 그런-다음 위와 같이 몫 모노이드를 구성함으로써 이를 수행합니다.

이진 관계 $R \subset Σ * \times Σ *$ 가 주어지면, 우리는 그것의 대칭 클로저를 $R \cup R -1$ 로 정의합니다. 이것은 $x ~ E y$ 를 정의함으로써 대칭 관계 $E \subset Σ * \times Σ *$ 로 확장될 수 있는 것과 $(u, v) \in R \cup R -1$ 를 갖는 일부 문자열 $u, v, s, t \in Σ *$ 에 대해 $x = sut$ 와 $y = svt$ 인 것은 필요충분 조건입니다. 마지막으로, 우리는 E의 반사적 및 전이적 클로저를 취하며, 이는 모노이드 합동입니다.

전형적인 상황에서, 관계 R은 $R=\{u_{1}=v_{1},\cdots ,u_{n}=v_{n}\}$ 이 되도록 단순히 방정식의 집합으로 주어집니다. 따라서, 예를 들어, 다음은

\langle p,q\,\vert \;pq=1\rangle

쌍-순환 모노이드(bicyclic monoid)에 대해 방정식 표시이고, 다음은

\langle a,b\,\vert \;aba=baa,bba=bab\rangle

차수 2의 플래틱 모노이드(plactic monoid)입니다 (그것은 무한 차수를 가집니다). 이 플래틱 모노이드의 원소는 그 관계가 ba가 a와 b 모두와 교환함을 보일 때, 정수 i, j, k에 대해 $a^{i}b^{j}(ba)^{k}$ 로 쓸 수 있습니다.

Relation to category theory

Group-like structures
	Totality^α	Associativity	Identity	Inverse	Commutativity
Semigroupoid	Unneeded	Required	Unneeded	Unneeded	Unneeded
Small category	Unneeded	Required	Required	Unneeded	Unneeded
Groupoid	Unneeded	Required	Required	Required	Unneeded
Magma	Required	Unneeded	Unneeded	Unneeded	Unneeded
Quasigroup	Required	Unneeded	Unneeded	Required	Unneeded
Unital magma	Required	Unneeded	Required	Unneeded	Unneeded
Semigroup	Required	Required	Unneeded	Unneeded	Unneeded
Loop	Required	Unneeded	Required	Required	Unneeded
Monoid	Required	Required	Required	Unneeded	Unneeded
Group	Required	Required	Required	Required	Unneeded
Commutative monoid	Required	Required	Required	Unneeded	Required
Abelian group	Required	Required	Required	Required	Required
^α The closure axiom, used by many sources and defined differently, is equivalent.

모노이드는 카테고리(categories)의 특수 클래스로 볼 수 있습니다. 사실, 모노이드 연산의 요구된 공리는 소스와 타켓이 주어진 대상인 모든 사상의 집합으로 제한될 때 정확히 사상 합성의 요구된 공리입니다.^[12] 즉,

모노이드는 본질적으로 단일 대상을 갖는 카테고리와 같은 것입니다.

보다 정확하게, 모노이드 $(M, •)$ 가 주어지면, 우리는 단 하나의 대상과 그 사상이 M의 원소인 작은 카테고리를 구성할 수 있습니다. 사상의 합성은 모노이드 연산 •에 의해 제공됩니다.

마찬가지로, 모노이드 준동형은 단일 대상 카테고리 사이의 함수자(functors)일 뿐입니다.^[12] 따라서 이 구성은 (작은) 모노이드 Mon의 카테고리와 (작은) 카테고리 Cat의 카테고리의 전체 부분-카테고리 사이에 동등성(equivalence)을 제공합니다. 마찬가지로, 그룹의 카테고리는 Cat의 또 다른 전체 부분-카테고리와 동등합니다.

이런 의미에서, 카테고리 이론은 모노이드의 개념의 확장으로 생각될 수 있습니다. 모노이드에 대한 많은 정의와 정리는 둘 이상의 대상을 갖는 작은 카테고리로 일반화될 수 있습니다. 예를 들어, 하나의 대상을 갖는 카테고리의 몫은 몫 모노이드일 뿐입니다.

모노이드는, 다른 대수적 구조와 마찬가지로, 자체 카테고리, Mon을 형성하며, 그것의 대상은 모노이드이고 그것의 사상은 모노이드 준동형입니다.^[12]

카테고리에서 모노이드가 무엇인지에 대한 추상적 정의인 모노이드 대상(monoid object)의 개념도 있습니다. Set에서 모노이드 대상은 단지 모노이드일 뿐입니다.

Monoids in computer science

컴퓨터 과학에서, 많은 추상 데이터 유형(abstract data types)은 모노이드 구조가 부여될 수 있습니다. 공통적인 패턴에서, 모노이드의 원소의 수열(sequence)은 최종 값을 생성하기 위해 "접힘(folded)" 또는 "누적"됩니다. 예를 들어, 많은 반복 알고리듬은 각 반복에서 일종의 "실행하는 전체"를 업데이트해야 합니다; 이 패턴은 모노이드 연산에 의해 우아하게 표현될 수 있습니다. 대안적으로, 모노이드 연산의 결합성은 여러 코어 또는 프로세서를 효율적으로 활용하기 위해 접두 합(prefix sum) 또는 유사한 알고리듬을 사용함으로써 연산이 병렬화(parallelized)되는 것을 보장합니다.

항등 원소 $\varepsilon$ 와 결합 연산 $\bullet$ 을 갖는 유형 M의 값의 수열이 주어지면, 접는(fold) 연산은 다음과 같이 정의됩니다:

\mathrm {fold} :M^{*}\rightarrow M=\ell \mapsto {\begin{cases}\varepsilon &{\mbox{if }}\ell =\mathrm {nil} \\m\bullet \mathrm {fold} \,\ell '&{\mbox{if }}\ell =\mathrm {cons} \,m\,\ell '\end{cases}}

게다가, 임의의 데이터 구조(data structure)는 그 원소의 직렬화가 지정된 유사한 방법으로 '접힐' 수 있습니다. 예를 들어, "접힘"의 결과 이진 트리(binary tree)는 이전-순서 대. 이후-순서 트리 순회(tree traversal)에 따라 다를 수 있습니다.

MapReduce

컴퓨터 과학에서 모노이드의 응용은 소위 MapReduce 프로그래밍 모델입니다 (Encoding Map-Reduce As A Monoid With Left Folding를 참조하십시오). 컴퓨팅에서 MapReduce는 둘 또는 셋의 연산으로 구성됩니다. 데이터셋이 주어지면, "맵(Map)"은 임의적인 데이터를 특정 모노이드의 원소에 매핑하는 것으로 구성됩니다. "감소(Reduce)"는 결국에는 하나의 원소만 생성하도록 이들 원소를 접는 것으로 구성됩니다.

예를 들어, 만약 우리가 중복집합(multiset)을 가지면, 프로그램에서 그것은 원소에서 그것들의 숫자로의 맵으로 표시됩니다. 이 경우에서 원소는 키라고 불립니다. 구별되는 키의 숫자가 너무 클 수 있고, 이 경우에서, 중복집합(multiset)이 조각납니다. 감소를 적절하게 마무리하기 위해, "혼합(Shuffling)" 단계는 노드 사이에 데이터를 다시 그룹화합니다. 만약 이 단계가 필요하지 않으면, 전체 Map/Reduce는 매핑과 감소로 구성됩니다; 두 연산 모두 병렬화-가능하며, 전자는 원소-별 본성으로 인해, 후자는 모노이드의 결합성으로 인한 것입니다.

Complete monoids

완전한 모노이드(complete monoid)는 다음임을 만족하는 임의의 인덱스 집합(index set) $I$ 에 대해 무한-항(infinitary) 합 연산 $\Sigma _{I}$ 를 장착한 교환 모노이드입니다:^[13]^[14]^[15]^[16]

\sum _{i\in \emptyset }{m_{i}}=0;\quad \sum _{i\in \{j\}}{m_{i}}=m_{j};\quad \sum _{i\in \{j,k\}}{m_{i}}=m_{j}+m_{k}\quad {\text{ for }}j\neq k

그리고

\sum _{j\in J}{\sum _{i\in I_{j}}{m_{i}}}=\sum _{i\in I}m_{i}\quad {\text{ if }}\bigcup _{j\in J}I_{j}=I{\text{ and }}I_{j}\cap I_{j'}=\emptyset \quad {\text{ for }}j\neq j'

.

순서화된 교환 모노이드(ordered commutative monoid)는 모든 각 $a \in M$ 에 대해 $a \geq 0$ 이고, $a \leq b$ 는 모든 $a, b, c \in M$ 에 대해 $a + c \leq b + c$ 를 의미함을 만족하는 부분 순서화(partial ordering) $\leq$ 를 갖는 교환 모노이드 $M$ 입니다.

연속 모노이드(continuous monoid)는 모든 방향화된 부분집합이 최소 위쪽 경계(least upper bound)를 가지고, 이들 최소 위쪽 경계가 모노이드 연산과 호환되는 순서화된 교환 모노이드 $(M, \leq)$ 입니다: 모든 각 $a \in M$ 와 $M$ 의 방향화된 부분집합 $S$ 에 대해,

a+\sup S=\sup(a+S)

만약 $(M,\leq)$ 가 연속 모노이드이면, 인덱스 집합 $I$ 및 원소의 모음 $(a i) i \in I$ 에 대해, 다음임을 정의할 수 있습니다:

\sum _{I}a_{i}=\sup _{{\text{finite }}E\subset I}\;\sum _{E}a_{i},

그리고 이 무한-항 합 연산과 함께 $M$ 은 완전한 모노이드입니다.^[16]

Notes

^ If both e₁ and e₂ satisfy the above equations, then e₁ = e₁ • e₂ = e₂.
^ Jacobson 2009.
^ Some authors omit the requirement that a submonoid must contain the identity element from its definition, requiring only that it have an identity element, which can be distinct from that of M.
^ Gondran, Michel; Minoux, Michel (2008). Graphs, Dioids and Semirings: New Models and Algorithms. Operations Research/Computer Science Interfaces Series. Vol. 41. Dordrecht: Springer-Verlag. p. 13. ISBN 978-0-387-75450-5. Zbl 1201.16038.
^ Rhodes, John; Steinberg, Benjamin (2009), The q-theory of Finite Semigroups: A New Approach, Springer Monographs in Mathematics, vol. 71, Springer, p. 22, ISBN 9780387097817.
^ Jacobson 2009, p. 29, examples 1, 2, 4 & 5.
^ Jacobson 2009, p. 35.
^ Jacobson, I.5. p. 22
^ Proof: Fix an element $x$ in the monoid. Since the monoid is finite, $x n = x m$ for some $m > n > 0$ . But then, by cancellation we have that $x m - n = e$ where $e$ is the identity. Therefore, $x • x m - n - 1 = e$ , so $x$ has an inverse.
^ Wehrung, Friedrich (1996). "Tensor products of structures with interpolation". Pacific Journal of Mathematics. 176 (1): 267–285. doi:10.2140/pjm.1996.176.267. S2CID 56410568. Zbl 0865.06010.
^ $f (x)* f (e M) = f (x * e M) = f (x)$ for each $x$ in $M$ , when $f$ is a semigroup homomorphism and $e M$ is the identity of its domain monoid $M$ .
^ ^a ^b ^c Awodey, Steve (2006). Category Theory. Oxford Logic Guides. Vol. 49. Oxford University Press. p. 10. ISBN 0-19-856861-4. Zbl 1100.18001.
^ Droste, M., & Kuich, W. (2009). Semirings and Formal Power Series. Handbook of Weighted Automata, 3–28. doi:10.1007/978-3-642-01492-5_1, pp. 7–10
^ Hebisch, Udo (1992). "Eine algebraische Theorie unendlicher Summen mit Anwendungen auf Halbgruppen und Halbringe". Bayreuther Mathematische Schriften (in German). 40: 21–152. Zbl 0747.08005.
^ Kuich, Werner (1990). "ω-continuous semirings, algebraic systems and pushdown automata". In Paterson, Michael S. (ed.). Automata, Languages and Programming: 17th International Colloquium, Warwick University, England, July 16-20, 1990, Proceedings. Lecture Notes in Computer Science. Vol. 443. Springer-Verlag. pp. 103–110. ISBN 3-540-52826-1.
^ ^a ^b Kuich, Werner (2011). "Algebraic systems and pushdown automata". In Kuich, Werner (ed.). Algebraic foundations in computer science. Essays dedicated to Symeon Bozapalidis on the occasion of his retirement. Lecture Notes in Computer Science. Vol. 7020. Berlin: Springer-Verlag. pp. 228–256. ISBN 978-3-642-24896-2. Zbl 1251.68135.

References

Howie, John M. (1995), Fundamentals of Semigroup Theory, London Mathematical Society Monographs. New Series, vol. 12, Oxford: Clarendon Press, ISBN 0-19-851194-9, Zbl 0835.20077
Jacobson, Nathan (1951), Lectures in Abstract Algebra, vol. I, D. Van Nostrand Company, ISBN 0-387-90122-1
Jacobson, Nathan (2009), Basic algebra, vol. 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1
Kilp, Mati; Knauer, Ulrich; Mikhalev, Alexander V. (2000), Monoids, acts and categories. With applications to wreath products and graphs. A handbook for students and researchers, de Gruyter Expositions in Mathematics, vol. 29, Berlin: Walter de Gruyter, ISBN 3-11-015248-7, Zbl 0945.20036
Lothaire, M. (1997), Combinatorics on words, Encyclopedia of Mathematics and Its Applications, vol. 17, Perrin, D.; Reutenauer, C.; Berstel, J.; Pin, J. E.; Pirillo, G.; Foata, D.; Sakarovitch, J.; Simon, I.; Schützenberger, M. P.; Choffrut, C.; Cori, R.; Lyndon, Roger; Rota, Gian-Carlo. Foreword by Roger Lyndon (2nd ed.), Cambridge University Press, doi:10.1017/CBO9780511566097, ISBN 0-521-59924-5, MR 1475463, Zbl 0874.20040

External links

"Monoid", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Weisstein, Eric W. "Monoid". MathWorld.
Monoid at PlanetMath.org.

[1] If both e₁ and e₂ satisfy the above equations, then e₁ = e₁ • e₂ = e₂.

[FOOTNOTEJacobson2009-2] Jacobson 2009.

[3] Some authors omit the requirement that a submonoid must contain the identity element from its definition, requiring only that it have an identity element, which can be distinct from that of M.

[4] Gondran, Michel; Minoux, Michel (2008). Graphs, Dioids and Semirings: New Models and Algorithms. Operations Research/Computer Science Interfaces Series. Vol. 41. Dordrecht: Springer-Verlag. p. 13. ISBN 978-0-387-75450-5. Zbl 1201.16038.

[5] Rhodes, John; Steinberg, Benjamin (2009), The q-theory of Finite Semigroups: A New Approach, Springer Monographs in Mathematics, vol. 71, Springer, p. 22, ISBN 9780387097817.

[FOOTNOTEJacobson200929,_examples_1,_2,_4_&_5-6] Jacobson 2009, p. 29, examples 1, 2, 4 & 5.

[FOOTNOTEJacobson200935-7] Jacobson 2009, p. 35.

[8] Jacobson, I.5. p. 22

[9] Proof: Fix an element $x$ in the monoid. Since the monoid is finite, $x n = x m$ for some $m > n > 0$ . But then, by cancellation we have that $x m - n = e$ where $e$ is the identity. Therefore, $x • x m - n - 1 = e$ , so $x$ has an inverse.

[10] Wehrung, Friedrich (1996). "Tensor products of structures with interpolation". Pacific Journal of Mathematics. 176 (1): 267–285. doi:10.2140/pjm.1996.176.267. S2CID 56410568. Zbl 0865.06010.

[11] $f (x)* f (e M) = f (x * e M) = f (x)$ for each $x$ in $M$ , when $f$ is a semigroup homomorphism and $e M$ is the identity of its domain monoid $M$ .

[Awo10-12] Awodey, Steve (2006). Category Theory. Oxford Logic Guides. Vol. 49. Oxford University Press. p. 10. ISBN 0-19-856861-4. Zbl 1100.18001.

[droste-13] Droste, M., & Kuich, W. (2009). Semirings and Formal Power Series. Handbook of Weighted Automata, 3–28. doi:10.1007/978-3-642-01492-5_1, pp. 7–10

[14] Hebisch, Udo (1992). "Eine algebraische Theorie unendlicher Summen mit Anwendungen auf Halbgruppen und Halbringe". Bayreuther Mathematische Schriften (in German). 40: 21–152. Zbl 0747.08005.

[15] Kuich, Werner (1990). "ω-continuous semirings, algebraic systems and pushdown automata". In Paterson, Michael S. (ed.). Automata, Languages and Programming: 17th International Colloquium, Warwick University, England, July 16-20, 1990, Proceedings. Lecture Notes in Computer Science. Vol. 443. Springer-Verlag. pp. 103–110. ISBN 3-540-52826-1.

[Kuich11-16] Kuich, Werner (2011). "Algebraic systems and pushdown automata". In Kuich, Werner (ed.). Algebraic foundations in computer science. Essays dedicated to Symeon Bozapalidis on the occasion of his retirement. Lecture Notes in Computer Science. Vol. 7020. Berlin: Springer-Verlag. pp. 228–256. ISBN 978-3-642-24896-2. Zbl 1251.68135.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

α

[12]

[13]

[14]

[15]

[16]