Polyhedron

Original article: w:Polyhedron

For other uses, see Polyhedron (disambiguation).

"Polyhedra" redirects here. For the relational database system, see Polyhedra DBMS.

Examples of polyhedra

Regular tetrahedron Platonic solid	Small stellated dodecahedron Kepler–Poinsot solid
Icosidodecahedron Archimedean solid	Great cubicuboctahedron Uniform star-polyhedron
Rhombic triacontahedron Catalan solid	A toroidal polyhedron

기하학(geometry)에서, 다면체 (polyhedron, 복수형 polyhedra 또는 polyhedrons; 그리스어 πολύ (poly-) '많은', 및 εδρον (-hedron) '밑면, 자리'에서 유래)는 평평한 다각형(polygon) 면(faces), 직선 가장자리(edges)와 날카로운 모서리 또는 꼭짓점(vertices)을 갖는 삼-차원(three-dimensional) 모양입니다.

볼록 다면체(convex polyhedron)는 모두 같은 평면에 있지는 않은 유한하게 많은 점의 볼록 껍질(convex hull)입니다. 정육면체(Cube)와 피라미드(pyramids)는 볼록 다면체의 예제입니다.

다면체는 임의의 차원의 수에서 보다 일반적인 폴리토프(polytope)의 3-차원 예제입니다.

Definition

A skeletal polyhedron (specifically, a rhombicuboctahedron) drawn by Leonardo da Vinci to illustrate a book by Luca Pacioli

볼록 다면체(Convex polyhedra)는 몇 가지 동등한 표준 정의와 함께 잘-정의됩니다. 어쨌든, 볼록할 필요가 없는 다면체의 형식적 수학적 정의는 문제가 있어 왔습니다. "다면체"의 많은 정의가 특정 문맥에서 주어져 왔으며, 일부는 다른 것보다 더 엄격하고, 이들 중 무엇을 선택해야 하는지에 대한 보편적인 동의는 없습니다. 이들 정의 중 일부는 종종 다면체로 세어져 왔던 모양 (예를 들어, 자체-교차하는 다면체(self-crossing polyhedra))을 제외하거나 종종 유효한 다면체로 고려되지 않는 모양 (예를 들어, 그것의 경계가 매니폴드(manifold)가 아닌 입체)을 포함합니다. 브랭코 그란보움(Branko Grünbaum)이 관찰한 바와 같이,

"다면체 이론의 원죄는 유클리드로 거슬러 올라가고, 케플러, 푸앵소, 코시와 기타 많은 사람들을 통해 ... 각 단계에서 ... 저자는 다면체가 무엇인지 정의하는 데 실패했습니다."

그럼에도 불구하고, 다면체는 꼭짓점(vertices) (모서리 점), 가장자리(edges) (특정 꼭짓점의 쌍을 연결하는 선분), 면(faces) (이-차원 다각형(polygon))에 의해 설명될 수 있는 입체 또는 표면이고, 때때로 특정한 삼-차원 내부 부피(volume)를 갖는다고 말할 수 있는 일반적인 합의가 있습니다. 우리는 정의가 다면체를 입체로 기술하는지 여부, 정의가 다면체를 표면으로 기술하는지 여부, 또는 정의가 그것들을 투사 기하학(incidence geometry)을 기반으로 더 추상적으로 기술하는지 여부에 따라 이들 다양한 정의를 구별할 수 있습니다.

• 다면체의 공통적이고 다소 소박한 정의는 그것의 경계가 유한하게 많은 평면으로 덮혀질 수 있는 입체 또는 유한하게 많은 볼록 다면체의 합집합으로 형성된 입체라는 것입니다. 이 정의의 자연스러운 개선은 입체를 경계지고, 연결된 매부를 가지고, 역시 연결된 경계를 가지는 것을 요구합니다. 그러한 다면체의 면은 그것을 덮는 각 평면 내 경계 부분의 연결된 구성 요소(connected components)로 정의될 수 있고, 모서리와 꼭짓점은 면이 만나는 선분과 점으로 정의될 수 있습니다. 어쨌든, 이러한 방법으로 정의된 다면체는 그것의 면이 단순 다각형(simple polygon)을 형성하지 않을 수 있고, 그것의 가장자리 중 일부가 둘보다 많은 면에 속할 수 있는 자체-교차하는 별 다면체를 포함하지 않습니다.
• 입체가 아닌 경계하는 면의 아이디어에 기반한 정의도 공통적입니다. 예를 들어, O'Rourke (1993)는 임의의 두 다각형의 교집합이 공유된 꼭짓점 또는 가장자리 또는 빈 집합(empty set)이 되도록 그리고 그것들의 합집합이 매니폴드(manifold)가 되도록 공간에서 정렬된 볼록 다각형(convex polygon) (그것들의 면)의 합집합으로 다각형을 정의합니다. 만약 그러한 표면의 평면 부분이 자체로 볼록 다각형이 아니면, O'Rourke는 그것을 그것들 사이의 평평한 이면각을 갖는 더 작은 볼록 다각형으로 세분할 것을 요구합니다. 다소 더 일반적으로, Grünbaum은 각 꼭짓점이 적어도 세 개의 가장자리에 입사하고 각각의 두 면이 공유된 꼭짓점과 각 가장자리에서 오직 교차하는 삽입된 매니폴드를 형성하는 단순 다각형의 집합으로 어캅틱 다면체(acoptic polyhedron)를 정의합니다. Cromwell의 Polyhedra는 비슷한 정의를 제공하지만 꼭짓점당 적어도 셋의 가장자리의 제한이 없습니다. 다시 말하지만, 이러한 유형의 정의는 자기-교차하는 다면체를 포함하지 않습니다. 유사한 개념이 토폴로지적 매니폴드의 세분화를 그것의 쌍별 교차점이 점 (꼭짓점), 토폴로지적 호 (가장자리), 또는 빈 집합이 되어야 하는 토폴로지적 디스크(topological disks) (면)로의 다양체의 토폴로지적 정의의 기초를 형성합니다. 어쨌든, 어캅틱 다면체로 실현될 수 없는 토폴로지적 다면체 (심지어 모든 면이 삼각형이더라도)가 존재합니다.
• 한 가지 현대적인 접근 방식은 추상 다면체(abstract polyhedra)의 이론을 기반으로 합니다. 이것들은 그것의 원소가 다면체의 꼭짓점, 가장자리, 및 면인 부분적으로 순서화된 집합(partially ordered set)으로 정의될 수 있습니다. 꼭짓점 또는 가장자리가 가장자리 또는 면의 일부일 때 꼭짓점 또는 가장자리 원소는 가장자리 또는 면 원소 (이 부분 순서로)보다 작습니다. 추가적으로, 우리는 이 부분 순서의 특별한 바닥 원소 (빈 집합을 나타냄)와 전체 다면체를 나타내는 최상위 요소를 포함할 수 있습니다. 만약 3단계 떨어진 원소들 사이 (즉, 각 면과 바닥 원소 사이, 및 최상위 원소와 각 꼭짓점 사이)의 부분 순서의 섹션이 다각형의 추상 표현과 같은 구조를 가지면, 이들 부분적으로 순서화된 집합은 토폴로지적 다면체와 정확히 동일하게 같은 정보를 전달합니다. 어쨌든, 이들 요구 사항은 종종 두 수준으로 떨어져 있는 원소 사이의 섹션이 선분의 추상 표현과 같은 구조를 가짐을 오직 대신 요구하기 위해 완화됩니다. (이것은 각 가장자리가 둘의 꼭짓점을 포함하고 둘의 면에 속함을 의미하고, 한 면 위의 각 꼭짓점은 해당 면의 두 가장자리에 속함을 의미합니다.) 다른 방식으로 정의된 기하학적 다면체는 이러한 방법으로 추상적으로 설명될 수 있지만, 기하학적 다면체의 정의의 기초로 추상 다면체를 사용할 수도 있습니다. 추상 다면체의 실현(realization)은 일반적으로 각 면의 점이 공통 평면에 있음을 만족하는 추상 다면체의 꼭짓점에서 기하학적 점으로의 매핑으로 취합니다. 기하학적 다면체는 그런-다음 추상 다면체의 구현으로 정의될 수 있습니다. 면 평면성의 요구 사항을 생략하거나, 대칭의 추가 요구 사항을 부과하거나, 꼭짓점을 더 높은 차원 공간에 매핑하는 구현도 고려되어 왔습니다. 입체-기반과 표면-기반 정의와 달리, 이것은 별 다면체에 완벽하게 작동합니다. 어쨌든, 추가 제한없이, 이 정의는 퇴화(degenerate)하거나 부정확한 다면체를 허용하고 (예를 들어, 모든 꼭짓점을 단일 점으로 매핑함으로써) 이들 퇴화를 피하기 위해 실현을 제한하는 방법의 문제는 해결되지 않았습니다.

이들 모든 정의에서, 다면체는 전형적으로 임의의 차원의 숫자에서 보다 일반적인 폴리토프(polytope)의 삼-차원 예제로 이해됩니다. 예를 들어, 다각형은 이-차원 몸체를 가지고 면이 없지만, 4-폴리토프(4-polytope)는 4차원 몸체와 삼-차원 "셀"의 추가적인 집합을 가집니다. 어쨌든, 고-차원 기하학에 대한 일부 문헌은 "다면체"라는 용어를 삼-차원 폴리토프가 아니라, 어떤 면에서 폴리토프와 다른 모양과 같은 다른 것을 의미하기 위해 사용합니다. 예를 들어, 일부 출처는 볼록 다면체를 유한하게 많은 절반-공간(half-spaces)의 교차로 정의하고, 폴리토프를 경계진 다면체로 정의합니다. 이 기사의 나머지 부분에서는 오직 삼-차원 다면체를 고려합니다.

Characteristics

Number of faces

다면체는 분류될 수 있고 종종 면의 개수에 따라 이름-지정됩니다. 이름짓는 체계는 고전 그리스어를 기반으로 하고, 면을 세는 접두사에 "밑변" 또는 "자리"를 의미하고 면을 참조하는 접미사 "면체(hedron)"을 결합합니다. 예를 들어 사면체(tetrahedron)는 4개의 면을 갖는 다면체이고, 오면체(pentahedron)는 5개의 면을 갖는 다면체이고, 육면체(hexahedron)는 6개의 면을 갖는 다면체입니다. 그리스 숫자-표시 접두사의 전체 목록에 대해, 그리스 세는-숫자에 대해 열에서 Numeral prefix § Table of number prefixes in English을 참조하십시오. 사면체, 육면체, 팔면체, 십이면체, 및 이십면체의 이름은 때때로 플라톤의 고체(Platonic solid)를 참조하기 위해 추가적인 자격증명없이 사용되고, 때때로 보다 일반적으로 임의의 대칭의 가정없이 주어진 변의 숫자를 갖는 다면체를 참조하기 위해 사용됩니다.

Topological classification

Main article: Toroidal polyhedron

The tetrahemihexahedron, a non-orientable self-intersecting polyhedron with four triangular faces (red) and three square faces (yellow). As with a Möbius strip or Klein bottle, a continuous path along the surface of this polyhedron can reach the point on the opposite side of the surface from its starting point, making it impossible to separate the surface into an inside and an outside.

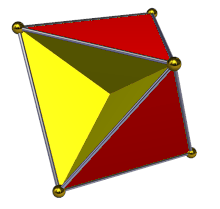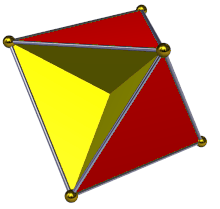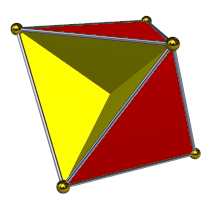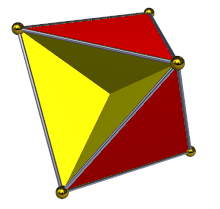
일부 다면체는 그것들의 표면에 두 개의 구별되는 면을 가집니다. 예를 들어, 볼록 다면체(convex polyhedron) 종이 모델의 내부와 외부는 각각 다른 색상을 지정될 수 있습니다 (비록 내부 색상이 보기에서 숨겨질지라도). 이들 다면체는 방향가능(orientable)입니다. 같은 것은 자체-교차없이 비-볼록 다면체에 대해 참입니다. 일부 비-볼록 자체-교차하는 다면체는 같은 방법에서 색칠될 수 있지만 양쪽 색상이 다른 위치에서 외부에 나타나도록 영역이 "뒤집어지게" 된 영역을 가집니다; 이것들은 여전히 방향-가능인 것으로 여겨집니다. 어쨌든, 사면반육면체(tetrahemihexahedron)와 같은 단순-다각형 면을 갖는 다른 자체-교차하는 다면체에 대해, 인접한 면이 일관된 색상을 갖도록 두 개의 다른 색상을 갖는 각 면의 두 개의 측면을 색칠하는 것이 가능하지 않습니다. 이 경우에서, 그 다면체는 비-방향가능이라고 말합니다. 자체-교차하는 면을 갖는 다면체에 대해, 인접한 면에 대해 일관되게 색칠되도록 한다는 것이 무엇을 의미하는지 명확하지 않을 수 있지만, 이들 다면체에 대해 꼭짓점, 가장자리, 및 면 사이에 같은 발생을 갖는 토폴로지적 세포 복합체(cell complex)를 고려함으로써 방향-가능 또는 비-방향가능이 무엇인지 결정하는 것이 여전히 가능합니다.

다면체 표면 사이의 더 미묘한 구별은 다면체의 꼭짓점 $V$, 가장자리 $E$, 및 면 $F$의 개수를 다음 공식에 의해 정의되는 단일 숫자 $\chi$와 결합하는 그것들의 오일러 특성(Euler characteristic)에 의해 제공됩니다:

$\chi =V-E+F.\$

같은 공식은 역시 다른 종류의 토폴로지적 표면의 오일러 특성에 사용됩니다. 그것은 단일 표면이 하나보다 많은 방법에서 꼭짓점, 가장자리, 및 면으로 세분화될 때 오일러 특성이 이들 세분화에 대해 같을 것임을 의미하는 불변입니다. 볼록 다면체, 또는 보다 일반적으로 표면 토폴로지적 구를 갖는 임의의 단순 연결된 다면체에 대해, 그것은 항상 2와 같습니다. 보다 복잡한 모양에 대해, 오일러 특성은 표면에서 트로이드(toroid) 구멍, 핸들 또는 교차-캡(cross-cap)의 수와 관련이 있고 2보다 작을 것입니다. 홀수 오일러 특성을 갖는 모든 다면체는 비-방향가능입니다. 짝수 오일러 특성을 갖는 주어진 그림은 방향-가능일 수도 있고 그렇지 않을 수도 있습니다. 예를 들어, 구멍이 하나인 트로이드(toroid)와 클라인 병(Klein bottle)은 둘 다 $\chi =0$을 가지며, 첫 번째는 방향-가능이고 다른 하나는 그렇지 않습니다.

다면체를 정의하는 (전부는 아니지만) 많은 방법에서, 다면체의 표면은 매니폴드(manifold)이어야 함을 요구됩니다. 이것은 모든 가장자리가 정확하게 두 면의 경계의 일부이고 (공유된 가장자리를 따라서만 만나는 두 정육면체의 합집합과 같은 모양을 허용하지 않음) 모든 각 꼭짓점은 가장자리와 면의 단일 교대하는 주기에 발생함을 (단일 꼭짓점만을 공유하는 두 정육면체의 합집합과 같은 모양을 허용하지 않음) 의미합니다. 이들 방법에서 정의된 다면체에 대해, 매니폴드의 분류(classification of manifolds)는 표면의 토폴로지적 유형이 그것의 오일러 특성과 방향가능성의 조합에 의해 완전하게 결정됨을 의미합니다. 예를 들어, 표면이 방향가능 매니폴드이고 오일러 특성이 2인 모든 각 다면체는 토폴로지적 구여야 합니다.

트로이드 다면체(toroidal polyhedron)는 오일러 특성(Euler characteristic)이 0보다 작거나 같은, 또는 그것들의 속(genus)이 1 이상인 다면체입니다. 토폴로지적으로, 그러한 다면체의 표면은 중간을 관통하는 하나 이상의 구멍을 가지는 토러스(torus) 표면입니다.

Duality

Main article: Dual polyhedron

The octahedron is dual to the cube

모든 각 볼록 다면체에 대해, 다음을 가지는 이중 다면체가 존재합니다:

• 원래의 꼭짓점 자리에 면을 가지고 그 반대도 마찬가지입니다. 그리고
• 같은 숫자의 가장자리를 가집니다.

볼록 다면체의 이중은 극 역화(polar reciprocation)의 과정에 의해 구할 수 있습니다. 이중 다면체는 쌍으로 존재하고, 이중의 이중은 다시 원래의 다면체입니다. 일부 다면체는 자기-이중이며, 다면체의 이중이 원래 다면체와 합동임을 의미합니다.

추상 다면체는 역시 그것의 이중 또는 반대 순서를 얻기 위해 다면체를 정의하는 부분 순서(partial order)를 반전함으로써 얻어진 이중을 가지고 있습니다. 이갓들은 초기 다면체와 같은 오일러 특성과 방향가능성을 갖습니다. 어쨌든, 이러한 형식의 이중성은 이중 다면체의 형태를 기술하는 것이 아니라, 그것의 조합 구조만을 기술합니다. 비-볼록 기하 다면체의 일부 정의에 대해, 그것의 추상 이중이 같은 정의 아래에서 기하 다면체로 구현될 수 없는 다면체가 존재합니다.

Vertex figures

Main article: Vertex figure

모든 각 꼭짓점에 대해, 우리는 꼭짓점 주변에 다면체의 지역적 구조를 설명하는 꼭짓점 그림(vertex figure)을 정의할 수 있습니다. 정확한 정의는 다양하지만, 꼭짓점 그림은 다면체를 통한 슬라이스가 모서리를 잘리는 노출된 다각형으로 생각될 수 있습니다.

Surface area and distances

다면체의 표면 넓이(surface area)는 면의 면적이 잘 정의된 다면체의 정의를 위해 그것의 면의 넓이의 합입니다. 다면체의 표면 위의 두 점 사이의 측지선(geodesic) 거리는 표면 내에 남아 있는 두 점을 연결하는 가장 짧은 곡선의 길이를 측정합니다. 알렉산드로프의 고유성 정리(Alexandrov's uniqueness theorem)에 의해, 모든 각 볼록 다면체는 그것의 표면 위의 측지선 거리의 메트릭 공간(metric space)에 의해 고유하게 결정됩니다. 어쨌든, 비-볼록 다면체는 서로 같은 표면 거리를 가질 수 있거나, 특정 볼록 다면체와 같은 표면 거리를 가질 수 있습니다.

Volume

다면체는 그것들이 얼마나 많은 공간을 차지하는지를 측정하는 부피(volume)라고 하는 관련된 수량을 가지고 있습니다. 단순 고체의 가족은 그것들의 부피에 대해 간단한 공식을 가질 수 있습니다; 예를 들어, 각뿔, 각기둥, 및 평행육면체(parallelepiped)의 부피는 그것들의 가장자리 길이 또는 다른 좌표의 관점에서 쉽게 표현될 수 있습니다. (이들 공식의 많은 것을 포함하는 목록에 대해 부피 공식을 참조하십시오.)

더 복잡한 다면체의 부피는 간단한 공식을 가지지 않을 수 있습니다. 그러한 다면체의 부피는 다면체를 더 작은 조각으로 (예를 들어, 삼각분할(triangulation)에 의해) 세분화함으로써 계산될 수 있습니다. 예를 들어, 정규 다면체의 부피(volume of a regular polyhedron)는 합동 각뿔로 나눔으로써 계산될 수 있으며, 각 각뿔(pyramids)은 다면체의 면을 밑변으로 가지고 다면체의 중심을 꼭대기로 가집니다.

일반적으로, 다면 입체의 부피는 다음에 의해 주어지는 발산 정리(divergence theorem)로부터 유도될 수 있습니다: $${\frac {1}{3}}\left|\sum _{F}(Q_{F}\cdot N_{F})\operatorname {area} (F)\right|,$$

여기서 합은 다면체의 면 F 위에 있고, Q_F는 면 F의 임의의 점이고, N_F는 고체 외부를 가리키는 F에 수직인 단위 벡터(unit vector)이고, 곱셈 점은 점 곱(dot product)입니다. 더 높은 차원에서, 부피 계산은 부분적으로 오직 그것의 꼭짓점에 의해 지정된 볼록 다면체의 면을 나열하는 어려움때문에 어려울 수 있고, 이들 경우에서 부피를 결정하기 위한 특수한 알고리듬(algorithm)이 있습니다.

Dehn invariant

Main article: Dehn invariant

이-차원에서, 볼야이–게르빈 정리(Bolyai–Gerwien theorem)는 임의의 다각형은 그것을 유한하게 많은 다각형 조각으로 자르고 재배열함으로써 같은 넓이의 임의의 다른 다각형으로 변환될 수 있다고 주장합니다. 다면체에 대해 유사한 질문은 힐베르트의 세 번째 문제(Hilbert's third problem)의 주제였습니다. 막스 덴(Max Dehn)은 2-차원 경우에서와 달리 더 작은 다면체로 자르고 서로 재조립될 수 없는 같은 부피의 다면체가 존재한다는 것을 보여줌으로써 이 문제를 해결했습니다. 이것을 입증하기 위해 덴은 다면체와 관련된 또 다른 값, 덴 불변량(Dehn invariant)을 발견했으며, 두 다면체는 같은 부피와 같은 덴 불변량을 가질 때만 서로 해부될 수 있습니다. 그것은 나중에 사이들러(Sydler)에 의해 이것이 해부에 대한 유일한 장애물이라는 것이 입증되었습니다: 같은 부피와 덴 불변량을 갖는 모든 각 두 개의 유클리드 다면체는 잘리고 서로 재조립될 수 있습니다. 덴 불변량은 숫자가 아니라, 다면체의 가장자리의 길이와 이면각(dihedral angle)으로 결정되는 무한-차원 벡터 공간에서 벡터(vector)입니다.

힐베르트의 또 다른 문제, 힐베르트의 18번째 문제(Hilbert's 18th problem)는 타일 공간(tile space)에 관한 (여러 것들 중에서) 다면체에 관한 것입니다. 모든 각 그러한 다면체는 덴 불변 영을 가져야 합니다. 덴 불변량은 역시 강한 벨로우즈 정리에 의해 유연한 다면체(flexible polyhedra)와 연결되어 왔으며, 그 정리는 임의의 유연한 다면체의 덴 불변량이 그것이 구부러질 때 불변으로 유지된다는 것을 나타냅니다.

Convex polyhedra

Convex polyhedron blocks on display at the Universum museum in Mexico City

삼-차원 고체는 만약 그것이 그것의 두 점을 연결하는 모든 각 선분을 포함하면 볼록 집합(convex set)입니다. 볼록 다면체(convex polyhedron)는 고체로 볼록 집합을 형성하는 다면체입니다. 볼록 다면체는 유한하게 많은 절반-공간(half-spaces)의 경계진(bounded) 교차로, 또는 유한하게 많은 점의 볼록 껍질(convex hull)로 정의될 수도 있습니다.

볼록 다면체의 중요한 클래스는 높게 대칭적인 플라톤 고체(Platonic solid), 아르키메데스 고체(Archimedean solids)와 그것들의 이중 카탈랑 고체(Catalan solid), 및 정규-면 존슨 고체(Johnson solid)를 포함합니다.

Symmetries

Some polyhedra rotating around a symmetrical axis (at Matemateca IME-USP)

가장 많이 연구된 다면체의 대부분은 고도로 대칭적(symmetrical)이며, 즉, 그것들의 모양은 공간의 일부 반사 또는 회전에 의해 변경되지 않습니다. 그러한 각각의 대칭은 주어진 꼭짓점, 면, 또는 가장자리의 위치를 변경할 수 있지만, (면, 가장자리와 마찬가지로) 모든 꼭짓점의 집합은 변경되지 않습니다. 다면체의 대칭의 모음은 그것의 대칭 그룹(symmetry group)이라고 불립니다.

대칭에 의해 서로 중첩될 수 있는 모든 요소는 대칭 궤도(symmetry orbit)를 형성한다고 말합니다. 예를 들어, 정육면체의 모든 면은 한 궤도에 놓이지만, 모든 가장자리는 또 다른 궤도에 놓입니다. 만약 주어진 차원의 모든 요소, 말하자면 모든 면이 같은 궤도에 놓이면, 그 그림은 해당 궤도에서 전이적이라고 말합니다. 예를 들어, 정육면체는 면-전이적이지만, 잘린 정육면체에는 두 개의 면의 대칭 궤도를 가집니다.

같은 추상 구조가 다소 대칭적인 기하학적 다면체를 지원할 수 있습니다. 그러나 이십십이면체(icosidodecahedron)와 같이 다면체 이름이 주어지면, 달리 명시되지 않은 한 가장 대칭적인 기하학이 거의 항상 암시됩니다.

고도로 대칭적인 다면체에는 여러 유형이 있으며, 면, 가장지리, 또는 꼭짓점과 같은 요소의 종류가 단일 대칭 궤도에 속하는 것으로 분류됩니다:

• 정규(Regular): 꼭짓점-전이, 가장자리-전이 및 면-전이. (이것은 모든 각 면이 같은 정규 다각형(regular polygon)임을 의미합니다; 그것은 역시 모든 각 꼭짓점이 정규임을 의미합니다.)
• 준-정규(Quasi-regular): 꼭짓점-전이 및 가장지리-전이 (및 따라서 정규 면을 가짐)이지만 면-전이는 아닙니다. 준-정규 이중(quasi-regular dual)은 면-전이 및 가장자리-전이 (및 따라서 모든 각 꼭짓점은 정규적임)이지만 꼭짓점-전이는 아닙니다.
• 반-정규(Semi-regular): 꼭짓점-전이이지만 가장자리-전이가 아니고, 모든 각 면이 정규 다각형입니다. (이것은 저자에 따라 용어의 여러 정의 중 하나입니다. 일부 정의는 준-정규 클래스와 겹칩니다.) 이들 다면체는 반-정규 각기둥(prisms) 및 역각기둥(antiprism)을 포함합니다. 반-정규 이중(semi-regular dual)은 면-전이이지만 꼭짓점-전이가 아니고, 모든 각 꼭짓점은 정규입니다.
• 균등(Uniform): 꼭짓점-전이 및 모든 각 면이 정규 다각형, 즉, 그것은 정규, 준-정규 또는 반-정규입니다. 균등 이중은 면-전이이고 정규 꼭짓점을 가지지만, 반드시 꼭짓점-전이인 것은 아닙니다.
• 등각(Isogonal): 꼭짓점-전이.
• 등변(Isotoxal): 가장자리-전이.
• 등면(Isohedral): 면-전이.
• 노블(Noble): 면-전이 및 꼭짓점-전이 (그러나 반드시 가장자리-전이인 것은 아닙니다). 정규 다면체는 역시 노블입니다; 그것들은 유일한 노블 균등 다면체입니다. 노블 다면체의 이중은 그 자체로 노블입니다.

일부 다면체 클래스에는 단일 주요 대칭축만 가집니다. 이것들은 각뿔(pyramids), 쌍-각뿔(bipyramid), 트래프조히드론(trapezohedra), 큐폴라(cupolae)와 마찬가지로 반-정규 각기둥과 역각기둥을 포함합니다.

Regular polyhedra

Main articles: Platonic solid and Kepler–Poinsot polyhedron

정규 다면체는 가장 고도로 대칭적입니다. 모두 9개의 정규 다면체: 5개의 볼록 다면체와 4개의 별 다면체가 있습니다.

다섯 개의 볼록 다면체의 예제는 고대부터 알려져 있었고 플라톤의 고체(Platonic solids)라고 불립니다. 이것들은 삼각형 각뿔 또는 사면체(tetrahedron), 정육면체(cube), 팔면체(octahedron), 십이면체(dodecahedron) 및 이십면체(icosahedron)입니다:

네 개의 정규 별다면체도 있으며, 발견자들의 이름을 따서 케플러–푸앵소 다면체(Kepler–Poinsot polyhedra)로 알려져 있습니다.

정규 다면체의 이중은 역시 정규입니다.

Uniform polyhedra and their duals

Main article: Uniform polyhedron

균등 다면체는 꼭짓점-전이(vertex-transitive)이고 모든 각 면은 정규 다각형(regular polygon)입니다. 그것들은 정규(regular), 준-정규(quasi-regular), 또는 반-정규(semi-regular)로 세분될 수 있고, 볼록 또는 별 모양일 수 있습니다.

균등 다면체의 이중은 부정규 면을 가지지만 면-전이(face-transitive)이고 모든 각 꼭짓점 도형(vertex figure)은 정규 다각형입니다. 균등 다면체는 그것의 이중과 같은 대칭 궤도를 가지며, 면과 꼭짓점이 단순히 교환합니다. 볼록 아르키메데스 다면체의 이중은 때때로 카탈랑 고체(Catalan solid)라고 불립니다.

균등 다면체와 그것들의 이중은 전통적으로 그것들의 대칭의 정도와 그것들이 볼록(convex)인지 그렇지 않은지 여부에 따라 분류됩니다.

	볼록 균등	볼록 균등 이중	별 균등	별 균등 이중
정규	Platonic solids		Kepler–Poinsot polyhedra
준정규	Archimedean solids	Catalan solids	Uniform star polyhedron
반정규
	Prisms	Bipyramids	Star prisms	Star bipyramids
	Antiprisms	Trapezohedra	Star antiprisms	Star trapezohedra

Isohedra

Main article: Isohedron

등면체(isohedron)는 그것의 면에 전이적으로 작용하는 대칭을 갖는 다면체입니다. 그것들의 토폴로지는 면 구성(face configuration)에 의해 표현될 수 있습니다. 모든 5개의 플라톤 고체(Platonic solids)와 13개의 카탈랑 고체(Catalan solid)는 등면체이고, 마찬가지로 트래프조히드론(trapezohedra)과 쌍-각뿔(bipyramid)의 무한 가족입니다. 일부 등면체는 오목 및 자체-교차하는 형식을 포함한 기하학적 변형을 허용합니다.

Symmetry groups

Full icosahedral symmetry divides the sphere into 120 triangular domains.

삼-차원에서 많은 대칭 또는 점 그룹은 결합된 대칭을 가지는 다면체의 이름을 따서 지어졌습니다. 이것들은 다음을 포함합니다:

• T – 카이럴(chiral) 사면체 대칭(tetrahedral symmetry); 정규 사면체(tetrahedron)에 대해 회전 그룹; 순서 12.
• T_d – 완전(full) 사면체 대칭(tetrahedral symmetry); 정규 사면체(tetrahedron)에 대해 대칭 그룹; 순서 24.
• T_h – pyritohedral symmetry; pyritohedron의 대칭; 순서 24.
• O – 카이럴 팔면체 대칭; 정육면체(cube)와 팔면체의 회전 그룹; 순서 24.
• O_h – 완전 팔면체 대칭; 정육면체(cube)와 팔면체의 대칭 그룹; 순서 48.
• I – 카이럴 이십면체 대칭; 이십면체와 십이면체의 회전 그룹; 순서 60.
• I_h – 완전 이십면체 대칭; 이십면체와 십이면체의 대칭 그룹; 순서 120.
• C_nv – n-겹 각뿔 대칭
• D_nh – n-겹 각기둥 대칭
• D_nv – n-겹 역각기둥 대칭.

카이럴(chiral) 대칭을 갖는 그것들은 반사 대칭을 가지지 않고 따라서 서로의 반사인 두 개의 거울상(enantiomorphous) 형식을 가집니다. 예제는 스넙 육팔면체(snub cuboctahedron)와 스넙 이십십이면체(snub icosidodecahedron)를 포함합니다.

Other important families of polyhedra

Polyhedra with regular faces

정규이고 균등한 다면체 외에도, 정규 면을 갖지만 더 낮은 전체적인 대칭을 갖는 일부 다른 클래스가 있습니다.

Equal regular faces

모든 각 면이 같은 종류의 정규 다각형인 볼록 다면체는 세 가지 가족에서 찾을 수 있습니다:

• 삼각형: 이러한 다면체를 삼각면체(deltahedra)라고 합니다. 여덟 개의 볼록 삼각면체가 있습니다: 셋의 플라톤 고체와 다섯의 비-균등 예제가 있습니다.
• 정사각형: 정육면체는 유일한 볼록 예제입니다. 다른 예제 (정사각면체(polycubes))는 정육면체를 함께 결합함으로써 얻어질 수 있지만, 공통-평면(coplanar)은 피해져야 하기 때문에 주의해야 합니다.
• 오각형: 정규 십이면체는 유일한 볼록 예제입니다.

6개 이상의 합동 정규 면을 갖는 다면체는 모두 비-볼록입니다.

같은 정규 면을 갖는 볼록 다면체의 총 개수는 10개입니다: 5개의 플라톤 고체와 5개의 비-균등 삼각면체입니다. 무한하게 많은 비-볼록 예제가 있습니다. 무한 비스듬한 다면체(infinite skew polyhedra)라고 하는 무한 스펀지-같은 예제가 이들 가족 중 일부에 존재합니다.

Johnson solids

Main article: Johnson solid

노먼 존슨(Norman Johnson)은 볼록 비-균등 다면체가 모두 같을 필요는 없지만 정규 면을 갖는 것을 찾았습니다. 1966년에, 그는 그러한 92개의 그러한 다면체의 목록을 발표하고, 그것들 이름과 번호를 부여하고, 다른 다면체는 없다고 추측했습니다. 빅터 잘갈러(Victor Zalgaller)는 1969년에 이들 존슨 고체(Johnson solid)의 목록이 완전하다는 것을 증명했습니다.

Pyramids

Main article: Pyramid (geometry)

각뿔은 4-면 이집트 피라미드(Egyptian pyramid)와 같이 모든 다면체 중에서 가장 유서 깊고 유명한 일부를 포함합니다.

Stellations and facettings

Main articles: Stellation and Faceting

다면체의 별모양은 그것들이 새로운 다면체를 형성하기 위해 만나도록 (평면 내에서) 면을 확장하는 과정입니다.

그것은 임의의 새로운 꼭짓점을 생성없이 다면체의 일부를 제거하는 과정인 패싯 과정과 정확한 역과정입니다.

아래 그림은 정규 팔면체, 정규 십이면체, 및 정규 이십면체의 일부 별모양을 보여줍니다.

Zonohedra

Main article: Zonohedron

조노다면체(zonohedron)는 모든 각 면이 180° 회전 아래에서 대칭인 다각형(polygon)인 볼록 다면체입니다. 조노다면체는 역시 선분의 민코프스키 합(Minkowski sum)으로 특징지어질 수 있고, 몇 가지 중요한 공간-채우는 다면체를 포함합니다.

Space-filling polyhedra

Main article: Honeycomb (geometry)

공간-채우는 다면체는 공간을 채우기 위해 자신의 복사본으로 포장합니다. 그러한 밀착-포장 또는 공간-채우기는 종종 공간의 테셀레이션 또는 벌집이라고 합니다. 공간-채우는 다면체는 영과 같은 덴 불변량(Dehn invarian)t을 가져야 합니다. 일부 벌집은 하나보다 많은 종류의 다면체를 포함합니다.

Lattice polyhedra

Main article: Ehrhart polynomial

모든 꼭짓점이 정수 좌표를 가지는 볼록 다면체는 격자 다면체(lattice polyhedron) 또는 정수 다면체(integral polyhedron)라고 불립니다. 격자 다면체의 이어하르트 다항식은 스케일 인수의 함수로 다면체의 스케일링된 사본 내에 놓이는 정수(integer) 좌표를 갖는 점이 몇 개 있는지 셉니다. 이들 다항식의 연구는 조합론(combinatorics)과 교환 대수(commutative algebra)의 교차점에 있습니다.

Flexible polyhedra

Main article: Flexible polyhedron

일부 다면체에 대해 그것들의 가장자리의 각도를 변화시킴으로써 그것들의 면의 모양을 같게 유지하면서 전체 모양을 변경하는 것이 가능합니다. 이것을 할 수 있는 다면체를 유연한 다면체라고 불립니다. 코시의 강성 정리(Cauchy's rigidity theorem)에 의해, 유연한 다면체는 비-볼록이어야 합니다. 유연한 다면체의 부피는 그것이 구부러질 때 일정하게 유지되어야 합니다; 이 결과는 벨로스(bellows) 정리로 알려져 있습니다.

Compounds

Main article: Polyhedral compound

다면체 혼합은 공통 중심을 공유하는 둘 이상의 다면체로 구성됩니다. 대칭 혼합은 종종 다른 잘-알려진 다면체와 같은 꼭짓점을 공유하고 종종 별모양에 의해 형성될 수도 있습니다. 일부는 위닝어 다면체 모델의 목록에 나열되어 있습니다.

Orthogonal polyhedra

Some orthogonal polyhedra made of Soma cube pieces, themselves polycubes

직교 다면체는 그것들의 모든 면이 직각(right angle)으로 만나고, 그것들의 모든 가장자리가 데카르트 좌표 시스템의 축에 평행한 다면체입니다. (예슨의 이십면체(Jessen's icosahedron)는 이들 두 조건 중 하나만 만족시키는 다면체의 예제를 제공합니다.) 직육면체(rectangular cuboid)를 제외하고, 직교 다면체는 비-볼록입니다. 그것들은 2D 직교 다각형의 3D 아날라고이며, 역시 직선 다각형(rectilinear polygon)으로도 알려져 있습니다. 직교 다면체는 계산적 기하학(computational geometry)에 사용되며, 여기서 구속된 구조는, 예를 들어, 다면체의 표면을 다각형 그물(polygonal net)로 펼치는 것과 같은 임의적인 다면체에 대해 해결되지 않은 문제로의 진보를 가능하게 해 왔습니다.

폴리큐브(Polycube)는 동일한 정육면체로 분해될 수 있는 직교 다면체의 특별한 경우이고, 평면 폴리오미노(polyomino)의 삼-차원 아날로그입니다.

Embedded regular maps with planar faces

정규 맵은 플래그 전이 추상 2-매니폴드이고 그것들은 이미 19세기에 연구되어 왔습니다. 그것들 중 일부는 클라인의 사차를 나타내는 것과 같은 삼-차원 다면체 삽입을 가지고 있습니다.

Generalisations of polyhedra

'다면체(polyhderon)'라는 이름은 전통적인 다면체(polyhedra)와 유사한 구조적 속성을 가지는 다양한 대상에 사용되게 되었습니다.

Apeirohedra

고전적인 다면체 표면에는 가장자리를 따라 쌍으로 접합된 유한한 숫자의 면을 가집니다. 에이피로히드라(apeirohedra)는 무한하게 많은 면을 갖는 관련된 대상의 클래스를 형성합니다. 에이피로히드라의 예제는 다음을 포함합니다:

• 평면의 타일링 테셀레이션(tessellations), 그리고
• 무한 경사 다면체(infinite skew polyhedra)라고 하는 스폰지-같은 구조.

Complex polyhedra

Main article: Complex polytope

복소 다면체라고 하는 대상이 있으며, 이것에 대해 놓여있는 공간은 실수 유클리드 공간이 아닌 복소(complex) 힐베르트 공간(Hilbert space)입니다. 정확한 정의는 그것의 대칭 그룹이 복소 반사 그룹(complex reflection groups)인 정규 복소 다면체에 대해서만 존재합니다. 복소 다면체는 수학적으로 실수 다면체보다 구성(configurations)과 더 밀접하게 관련되어 있습니다.

Curved polyhedra

일부 연구 분야는 다면체에게 곡선 면과 곡선 가장자리를 가지는 것을 허용합니다. 곡선 면은 양의 넓이를 갖는 대각선(digonal) 패싯을 존재하는 것을 허용합니다.

Spherical polyhedra

Main article: Spherical polyhedron

구의 표면이 유한하게 많은 큰 호(great arcs) (동등하게, 구의 중심을 통과하는 평면)에 의해 나뉠 때, 그 결과는 구형 다면체라고 합니다. 어느 정도의 대칭성을 갖는 많은 볼록 폴리토프 (예를 들어, 모든 플라톤 고체)는 구형 다면체를 생성하기 위해 동심 구의 표면에 투영될 수 있습니다. 어쨌든, 역 과정이 항상 가능한 것은 아닙니다; 일부 구형 다면체 (예를 들어, 호소헤드라(hosohedra))는 평면한-면 유사체를 가지지 않습니다.

Curved spacefilling polyhedra

만약 면이 볼록뿐만 아니라 오목도 허용되면, 인접한 면이 틈없이 함께 만나도록 만들어질 수 있습니다. 이들 구부러진 다면체 중 일부는 공간을 채우기 위해 함께 포장될 수 있습니다. 두 가지 중요한 유형은 다음과 같습니다:

• Bubbles in froths and foams, such as Weaire-Phelan bubbles.
• 건축에서 사용되는 양식.

Ideal polyhedra

Main article: Ideal polyhedron

볼록 다면체는 유클리드 공간에서와 같은 방법으로 삼-차원 쌍곡선 공간(hyperbolic space)에서 유한 점 집합의 볼록 껍질(convex hulls)로 정의될 수 있습니다. 어쨌든, 쌍곡선 공간에서, 아이디얼 점(ideal points)과 그 공간 내에 있는 점들을 고려하는 것도 가능합니다. 아이디얼 다면체는 유한한 아이디얼 점의 집합의 볼록 껍질입니다. 그것의 면은 아이디얼 다각형(ideal polyhedron)이지만, 그것의 가장자리는 선분이 아닌 전체 쌍곡형 곡선으로 정의되고, 그것의 꼭짓점 (그것의 아이디얼 점이 볼록 껍질인 점)은 쌍곡선 공간 내에 놓이지 않습니다.

Skeletons and polyhedra as graphs

면 구조를 잊음으로써, 임의의 다면체는 대응하는 꼭짓점과 가장자리를 갖는 그것의 뼈대(skeleton)라고 하는 그래프(graph)를 야기합니다. 그러한 도형은 오랜 역사를 가지고 있습니다: 레오나르도 다 빈치(Leonardo da Vinci)는 파치올리(Pacioli)의 책 Divina Proportione을 위해 그린 정규 고체의 프레임 모델을 고안했었고, 유사한 와이어-프레임(wire-frame) 다면체는 마우리츠 코르넬리스 에셔(M.C. Escher)의 인쇄물, Stars에 나타납니다. 이 접근 방식의 한 가지 두드러진 것은 볼록 다면체의 뼈대의 순수하게 그래프-이론적인 특성을 제공하는 슈타이니츠의 정리(Steinitz's theorem)입니다: 그것은 모든 각 볼록 다면체의 뼈대가 3-연결 평면 그래프(3-connected planar graph)이고, 모든 각 3-연결 평면 그래프는 일부 볼록 다면체의 뼈대라고 말합니다.

추상 다면체의 초기 아이디어는 브랭코 그륀바움(Branko Grünbaum)의 "구멍-면 다면체(hollow-faced polyhedra)"의 연구에서 개발되었습니다. 그륀바움은 면을 주기적으로 순서화된 꼭짓점의 집합으로 정의했고, 그것들에게 평면뿐만 아니라 꼬인(skew) 것을 허용했습니다.

그래프 관점은 그래프 용어(graph terminology)와 속성을 다면체에 적용하는 것을 허용합니다. 예를 들어, 사면체와 차사르 다면체(Császár polyhedron)는 그것의 뼈대가 완전 그래프(complete graphs) (K₄)인 유일한 알려진 다면체이고, 다면체에 대한 다양한 대칭 제한이 대칭 그래프(symmetric graphs)인 뼈대를 야기합니다.

Alternative usages

20세기 후반부터, 다양한 수학적 구조가 전통적인 다면체에도 존재하는 속성을 가지는 것으로 밝혀져 왔습니다. 삼-차원 폴리토프를 설명하기 위해 "다면체"라는 용어를 제한하는 대신, 관련되어 있지만 구별되는 다양한 종류의 구조를 설명하기 위해 채택되어 왔습니다.

Higher-dimensional polyhedra

다면체는 평평한 면을 가지는 임의의 차원 n의 실수(real) 아핀(affine) (또는 유클리드(Euclidean)) 공간의 점의 집합으로 정의되어 왔습니다. 그것은 대안적으로 유한하게 많은 절반-공간(half-spaces)의 교차로 정의될 수 있습니다. 전통적인 다면체와 달리, 그것은 경계진 또는 무경계진 것일 수 있습니다. 이러한 의미에서, 폴리토프(polytope)는 경계진 다면체입니다.

해석적으로, 그러한 볼록 다면체는 선형 부등식의 시스템에 대한 해 집합으로 표현됩니다. 이러한 방법으로 다면체를 정의하는 것은 선형 프로그래밍(linear programming)에서 문제에 대한 기하학적 관점을 제공합니다. 많은 전통적인 다면체 형태는 이러한 의미에서 다면체입니다. 다른 예제는 다음을 포함합니다:

• 평면의 사분면. 예를 들어, 수평 축 위와 수직 축의 오른쪽의 모든 점으로 구성된 데카르트 평면의 영역: { ( x, y ) : x ≥ 0, y ≥ 0 } . 그 변은 두 개의 양의 축이고, 그렇지 않으면 그것은 무경계진 것입니다.
• 유클리드 3-공간에서 팔분-공간, { ( x, y, z ) : x ≥ 0, y ≥ 0, z ≥ 0 } .
• 무한대 확장의 각기둥. 예를 들어, 3-공간에서 이중으로 무한 정사각 각기둥은 z-축을 따라 휩쓸린 xy-평면에서 정사각형으로 구성됩니다: { ( x, y, z ) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 } .
• 보로노이 테셀레이션(Voronoi tessellation)에서 각 셀(cell)은 볼록 다면체입니다. 집합 S의 보로노이 테셀레이션에서, 점 c ∈ S에 해당하는 셀 A는 c가 S의 볼록 껍질(convex hull) 내부(interior)에 놓일 때 경계지고 (따라서 전통적인 다면체), 그렇지 않으면 (c가 S의 볼록 껍질의 경계(boundary) 위에 놓일 때) A는 무경계진 것입니다.

Topological polyhedra

토폴로지적 폴리토프는 볼록 폴리토프(convex polytopes)와 토폴로지적으로 동등하고 정규 방법에서 서로 부착되는 모양으로의 특정 분해와 함께 제공되는 토폴로지적 공간입니다.

그러한 그림은 그것의 각 영역이 심플렉스이면, 즉 n-차원 공간에서 각 영역이 n+1개의 꼭짓점을 가지면 단순한(simplicial) 것이라고 합니다. 단순한 폴리토프의 이중은 단순(simple)이라고 합니다. 유사하게, 폴리토프 (다면체)의 널리 연구된 클래스는 기본 빌딩 블록이 n-차원 정육면체일 때 정육면체 다면체의 클래스입니다.

Abstract polyhedra

Main article: Abstract polytope

추상 폴리토프(abstract polytope)는 그것의 부분 순서화가 특정 발생 규칙 (연결성)과 순위매김을 따르는 원소의 부분적으로 순서화된 집합(partially ordered set) (포셋)입니다. 집합의 원소는 폴리토프의 꼭짓점, 가장자리, 면 등에 해당합니다: 꼭짓점은 순위 0이고 가장자리는 순위 1, 등이며, 기하학적 원소의 차원성에 해당하는 부분적으로 순서화된 순위매김을 가집니다. 집합 이론에 의해 요구되는 빈 집합은 −1의 순위이고 때때로 널 폴리토프(null polytope)에 해당한다고 합니다. 추상 다면체는 다음 순위매김을 가지는 추상 다면체입니다:

• 순위 3: 때로는 몸체와 동일시되는 최대 요소.
• 순위 2: 다각형 면.
• 순위 1: 가장자리.
• 순위 0: 꼭짓점.
• 순위 −1: 때때로 null polytope 또는 nullitope와 동일시되는 빈 집합.

임의의 기하학적 다면체는 위에서 설명된 추상 포셋의 실수 공간에서의 "실현"이라고 합니다.

History

Ancient

Prehistory

다면체는 정육면체와 정육면체형과 같은 초기 건축 형태(architectural forms)로 나타났으며, 고대 이집트(Egypt)의 가장 초기의 4-면 피라미드도 석기 시대부터 시작되었습니다.

에트루리아인(Etruscans)은 몬테 로파(Monte Loffa)에서 동석(soapstone)으로 만들어진 에트루리아(Etruscan) 십이면체(dodecahedron)의 발견에 의해 입증된 바와 같이 정규 다면체의 적어도 일부의 그들의 인식에서 그리스인보다 앞서 있었습니다. 그것의 면은 다른 디자인으로 표시되어, 일부 학자에게 게임 주사위로 사용되어 왔을 수 있음을 시사합니다.

Greek civilisation

이들 모양의 가장 오래된 알려진 쓰인 기록은 고대 그리스(Greek) 작가로부터 나온 것이며, 그는 역시 처음으로 그들의 알려진 수학적 설명을 제공했습니다. 초기 그리스인들은 주로 볼록 정규 다면체(convex regular polyhedra)에 관심이 있었으며, 이것은 플라톤 고체(Platonic solids)로 알려지게 되었습니다. 피타고라스(Pythagoras)는 그 중 적어도 3개를 알고 있었고, 테아이테토스(Theaetetus) (기원전 417년경)는 5개 모두를 설명했습니다. 결국, 유클리드(Euclid)는 그의 원론(Elements)에서 그들의 구성을 설명했습니다. 나중에, 아르키메데스(Archimedes)는 그의 연구를 지금 그의 이름을 딴 볼록 균등 다면체(convex uniform polyhedra)로 확장했습니다. 그의 원래 연구는 소실되었고 그의 고체는 파푸스(Pappus)를 통해 우리에게 내려옵니다.

China

중국의 정육면체 게임 주사위는 기원전 600년으로 거슬러 올라갑니다.

기원후 236년까지, 유 휘는 정육면체를 그것의 특징적인 사면체 (직교도식) 및 관련 고체로 분해하는 방법을 설명했으며, 이들 고체의 조립품을 공학 발굴 중에 이동할 지구의 부피를 계산하는 기초로 사용했습니다.

Islamic civilisation

고전 시대가 끝난 후, 이슬람 문명의 학자들은 계속해서 그리스 지식을 발전시켰습니다 (중세 이슬람 수학을 참조하십시오).

9세기 학자 타비트 이븐 커라(Thabit ibn Qurra)는 잘린 각기둥과 같은 다면체의 부피를 계산하는 데 공식을 제공했습니다.

그런 다음 10세기에 아불 와파(Abu'l Wafa)는 볼록 정규 다면체와 준정규 구형 다면체를 설명했습니다.

Renaissance

이슬람 학자들에 의해 유지되고 강화된 그리스 사상의 다른 영역과 마찬가지로, 다면체에 대한 서구의 관심은 이탈리아 르네상스(Renaissance) 시대에 부활했습니다. 예술가들은 뼈대 다면체를 구성하여, 원근법(perspective)에 대한 조사의 일환으로 삶에서 그것들을 묘사했습니다. 그 기간의 상감 세공 패널에 몇 가지가 나타납니다. 피에로 델라 프란체스카(Piero della Francesca)는 다면체의 그러한 투시 관점의 직접적인 기하학 구성에 대한 최초의 쓰인 설명을 제공했습니다. 레오나르도 다 빈치(Leonardo da Vinci)는 여러 다면체의 뼈대 모델을 만들고 파치올리(Pacioli)의 책에 대한 삽화를 그렸습니다. 파치올리의 익명의 예술가와 학생의 그림은 물이 반쯤 채워진 유리 마름모면체(rhombicuboctahedron)를 묘사합니다.

르네상스가 이탈리아 전역으로 퍼짐에 따라, Wenzel Jamnitzer, Dürer와 같은 후기 예술가들도 상상력이 풍부한 에칭으로 다양한 종류의 다면체를 묘사했는데, 그 중 상당수는 참신했습니다.

Star polyhedra

거의 2,000년 동안, 볼록 고체로서의 다면체의 개념은 고대 그리스 수학자들에 의해 개발된 채로 남아 있었습니다.

르네상스(Renaissance) 시대에 별 형태가 발견되었습니다. 베니스의 산마르코 대성당(St. Mark's Basilica) 바닥에 있는 대리석 타르시아는 별모양 십이면체를 묘사하고 있습니다. Wenzel Jamnitzer와 같은 예술가들은 증가하는 복잡성의 새로운 별-같은 형태를 묘사하는 것을 좋아했습니다.

요하네스 케플러(Johannes Kepler) (1571–1630)는 별 다각형(star polygons), 전형적으로 오각형(pentagrams)을, 별 다면체를 만들기 위해 사용했습니다. 이들 그림들 중 일부는 케플러 시대 이전에 발견되었을 수 있지만, 그는 정규 다면체는 볼록이어야 한다는 제한을 제거하면 "정규"로 고려될 수 있다는 것들을 처음으로 인식했습니다. 나중에 루이 푸앵소(Louis Poinsot)는 별 꼭짓점 그림(vertex figures) (각 모서리 주위의 회로)도 사용할 수 있다는 것을 깨달았고 나머지 두 개의 정규 별 다면체를 발견했습니다. 코시는 푸앵소의 목록이 완전함을 증명했고, 코시는 (케플러의) 작은 별모양 십이면체(small stellated dodecahedron)와 큰 별모양 십이면체(great stellated dodecahedron), 및 (푸앵소의) 큰 이십면체(great icosahedron)와 큰 십이면체(great dodecahedron)와 같이 수용되는 영어 이름을 제공했습니다. 집합적으로 그것들은 케플러–푸앵소 다면체(Kepler–Poinsot polyhedra)라고 합니다.

케플러–푸앵소 다면체는 별모양화(stellation)라고 하는 과정에 의해 플라톤의 고체로부터 구성될 수 있습니다. 대부분의 별모양화는 정규가 아닙니다. 플라톤 고체의 별모양화에 대한 연구는 1938년에 H.S.M. Coxeter와 다른 사람들에 의해 지금은 유명한 논문 The 59 icosahedra와 함께 큰 추진력을 받았습니다.

별모양화에 대한 역화 과정은 패싯팅(facetting) (또는 faceting)이라고 합니다. 하나의 폴리토프의 모든 각 별모양화는 이중 폴리토프의 일부 패싯팅에 대한, 이중(dual) 또는 역화입니다. 정규 별 다면체는 플라톤 고체를 패싯팅에 의해 얻어질 수도 있습니다. Bridge (1974)는 십이면체의 더 단순한 패싯팅을 나열하고, "59"의 집합에서 누락되었던 이십면체의 별모양화를 발견하기 위해 그것들을 역화했습니다. 그 이후로 더 많은 것이 발견되어 왔고, 그 이야기는 아직 끝나지 않았습니다.

Euler's formula and topology

두 가지 다른 현대 수학적 발전은 다면체 이론에 심오한 영향을 미쳤습니다.

1750년 레온하르트 오일러(Leonhard Euler)는 다면체의 가장자리를 처음으로 고려하여, 꼭짓점, 가장자리, 및 면의 숫자와 관련된 다면체 공식을 발견했습니다. 이것은 때때로 "고무 종이 기하학(rubber sheet geometry)"이라고도 하는 토폴로지의 탄생을 의미했고, 앙리 푸앵카레(Henri Poincaré)는 19세기 말경에 그것의 핵심 아이디어를 개발했습니다. 이것은 다면체인지 아닌지에 대한 많은 오래된 문제를 해결하도록 허용했습니다.

Max Brückner는 자신의 책 "Vielecke und Vielflache: Theorie und Geschichte" (다각형과 다면체: 이론과 역사)에서 자신의 많은 발견을 포함하여 당시까지 다면체에 대한 연구를 요약했습니다. 1900년에 독일어로 출판되었지만, 그것은 거의 알려지지 않았습니다.

한편, 더 높은 차원의 발견은 더 일반적인 폴리토프의 삼-차원 예로서 다면체의 아이디어로 이어졌습니다.

Twentieth-century revival

20세기 초반까지, 수학자들은 전진했었고 기하학은 거의 연구되지 않았습니다. The Fifty-Nine Icosahedra에서 콕세터(Coxeter)의 분석은 그래프 이론(graph theory)과 조합론(combinatorics)의 현대적 아이디어를 다면체 연구에 도입하여, 기하학에 대한 관심의 부활을 알렸습니다.

콕세터 자신은 처음으로 별 균등 다면체를 열거하고, 평면의 타일링을 다면체로 취급하고, 정규 꼬인 다면체(regular skew polyhedra)를 발견하고, 1952년 Shephard에 의해 처음 발견된 복소 다면체(complex polyhedra) 이론을 개발하고, 기하학의 다른 많은 영역에 대한 근본 공헌을 만들었습니다.

20세기 후반에, Grünbaum은 두 가지 영역에서 중요한 연구를 출판했습니다. 하나는 볼록 폴리토프(convex polytopes)에 있었으며, 그는 수학자들이 "다면체"를 그 순간의 필요에 맞게 다른 방식으로, 때로는 양립할 수 없는 방식으로 정의하는 경향을 지적했습니다. 다른 하나는 예를 들어 많은 새로운 정규 다면체(regular polyhedra)를 발견하는 것과 같이 다면체의 수용된 정의를 확장하는 일련의 논문이었습니다. 20세기 말에, 이들 후자의 아이디어는 투사 복합체(incidence complexes)에 대한 다른 연구와 병합되어 추상 다면체 (추상 3-폴리토프)의 현대적 아이디어를 생성했으며, 특히 McMullen과 Schulte에 의해 제시되었습니다.

In nature

정규 다면체의 자연 발생에 대해, Regular polyhedron § Regular polyhedra in nature를 참조하십시오.

비-정규 다면체는 자연에서 결정체(crystals)로 나타납니다.

See also

• Defect
• Deltohedron
• Extension of a polyhedron
• Goldberg polyhedron
• List of books about polyhedra
• List of small polyhedra by vertex count
• Near-miss Johnson solid
• Polyhedron models
• Schlegel diagram
• Spidron
• Lists of shapes
• Stella (software)

External links

General theory

• Weisstein, Eric W. "Polyhedron". MathWorld.
• Polyhedra Pages
• Uniform Solution for Uniform Polyhedra by Dr. Zvi Har'El
• Symmetry, Crystals and Polyhedra

Lists and databases of polyhedra

• Virtual Reality Polyhedra – The Encyclopedia of Polyhedra.
• Electronic Geometry Models – Contains a peer reviewed selection of polyhedra with unusual properties.
• Polyhedron Models – Virtual polyhedra.
• Paper Models of Uniform (and other) Polyhedra
• Polyhedra Viewer – Web-based tool for visualizing the relationships between the convex, regular-faced polyhedra.

Free software

• A Plethora of Polyhedra – An interactive and free collection of polyhedra in Java. Features includes nets, planar sections, duals, truncations and stellations of more than 300 polyhedra.
• Hyperspace Star Polytope Slicer – Explorer java applet, includes a variety of 3d viewer options.
• openSCAD – Free cross-platform software for programmers. Polyhedra are just one of the things you can model. The openSCAD User Manual is also available.
• OpenVolumeMesh – An open source cross-platform C++ library for handling polyhedral meshes. Developed by the Aachen Computer Graphics Group, RWTH Aachen University.
• Polyhedronisme – Web-based tool for generating polyhedra models using Conway Polyhedron Notation. Models can be exported as 2D PNG images, or as 3D OBJ or VRML2 files. The 3D files can be opened in CAD software, or uploaded for 3D printing at services such as Shapeways.

Resources for making physical models

• Paper Models of Polyhedra Free nets of polyhedra.
• Simple instructions for building over 30 paper polyhedra
• Polyhedra plaited with paper strips – Polyhedra models constructed without use of glue.
• Adopt a Polyhedron - Interactive display, nets and 3D printer data for all combinatorial types of polyhedra with up to nine vertices.