Complex plane

수학(mathematics)에서, 복소 평면(complex plane)은 실수 축이라고 불리는 $x$ -축이 실수(real number)에 의해 형성되고, 허수 축이라고 불리는 $y$ -축이 허수(imaginary number)에 의해 형성됨을 만족하는 데카르트 좌표 시스템(Cartesian coordinate system)을 갖는 복소수(complex number)에 의해 형성된 평면(plane)입니다.

복소 평면은 복소수의 기하학적 해석을 허용합니다. 덧셈(addition) 아래에서, 그것들은 벡터(vector)처럼 더합니다. 두 복소수의 곱셈(multiplication)은 극 좌표(polar coordinates)에서 더 쉽게 표현될 수 있습니다—곱의 크기 또는 모듈러스(modulus)는 두 절댓값(absolute value), 또는 모듈러스의 곱이고, 곱의 각도(angle) 또는 편각(argument)은 두 각도, 또는 편각의 합입니다. 특히, 모듈러스 1의 복소수에 의한 곱셈은 회전으로 행동합니다.

복소 평면은 때때로 아르강 평면(Argand plane) 또는 가우스 평면(Gauss plane)으로 알려져 있습니다.

Notational conventions

Complex numbers

복소 해석학(complex analysis)에서, 복소수는 관습적으로 기호 z에 의해 표시되며, 이것은 실수 (x)와 허수 (y) 부분으로 분리될 수 있습니다:

$z=x+iy$

예를 들어: z = 4 + 5i, 여기서 x와 y는 실수이고, i는 허수 단위(imaginary unit)입니다. 이 관습적인 표기법에서, 복소수 z는 데카르트 평면(Cartesian plane)에서 점 (x, y)에 해당합니다.

데카르트 평면에서, 점 (x, y)는 역시 다음으로 극 좌표(polar coordinates)에서 표현될 수 있습니다:

$(x,y)=(r\cos \theta ,r\sin \theta )\qquad (r,\theta )=\left({\sqrt {x^{2}+y^{2}}},\quad \arctan {\frac {y}{x}}\right).$

데카르트 평면에서, 아크탄젠트(arctangent)는 (라디안(radian)에서) −π/2에서 π/2까지의 값을 취한다고 가정될 수 있고, 일부 주의는 x ≤ 0일 때 점 (x, y)에 대해 보다 완전한 아크탄젠트 함수를 정의하기 위해 취해져야 합니다.^{[note 1]} 복소 평면에서, 이들 극좌표는 다음 형식을 취합니다:

$z=x+iy=|z|\left(\cos \theta +i\sin \theta \right)=|z|e^{i\theta }$

여기서^{[note 2]} $|z|={\sqrt {x^{2}+y^{2}}};\quad \theta =\arg(z)={\frac {1}{i}}\ln {\frac {z}{|z|}}=-i\ln {\frac {z}{|z|}}.$

여기서 |z|는 복소수 z의 절댓값 또는 모듈러스입니다; θ, z의 편각은 보통 구간 $0 \leq θ < 2 π$ 에서 취합니다; 그리고 (|z|e^iθ에 대한) 마지막 상등은 오일러의 공식(Euler's formula)으로부터 취합니다. θ의 범위 위에 구속없이, z의 편각은 여러-값인데, 왜냐하면 복소 지수 함수(complex exponential function)는 주기 2π i를 갖는 주기적이기 때문입니다. 따라서, 만약 θ는 arg(z)의 하나의 값이면, 다른 값은 $arg(z) = θ + 2 nπ$ 에 의해 제공되며, 여기서 n은 임의의 비-영 정수입니다.^[2]

명시적으로 사용되는 경우는 드물지만, 복소수의 기하학적 관점은 차원 2의 그것의 유클리드 벡터 공간의 구조에 암시적으로 근거를 두며, 여기서 복소수 $w$ 와 $z$ 의 안의 곱(inner product)은 $\Re (w{\overline {z}})$ 에 의해 제공됩니다; 그때에 복소수 $z$ 에 대해, 그것의 절댓값 $| z |$ 은 그것의 유클리드 노름과 일치하고, 그것의 편각 $arg(z)$ 은 1에서 $z$ 까지 회전하는 각도와 일치합니다.

윤곽 적분화(contour integration)의 이론은 복소 해석학의 주요 부분을 이룹니다. 이 문맥에서, 닫힌 곡선 주위의 이동의 방향이 중요합니다 – 곡선이 가로질렀던 방향을 반전하면 적분의 값에 −1을 곱합니다. 관례에 의해, 양의 방향은 반-시계-방향입니다. 예를 들어, 단위 원(unit circle)은 우리가 점 z = 1에서 시작할 때, 양의 방향으로 이동하고, 그럼-다음 점 z = i을 통해 왼쪽 위로 이동하고, 그런-다음 −1을 통해 왼쪽 아래로 이동하고, −i를 통해 오른쪽 아래로 이동하고, 마지막으로 z = 1로 오른쪽 위로 이동하며, 여기가 우리가 시작했던 점입니다.

복소 해석학의 거의 모두가 복소 함수(complex functions)와 관련이 있습니다 – 즉, 복소 평면의 일부 부분집합을 복소 평면의 일부 다른 (아마도 겹치는, 심지어 동일한) 부분집합에 매핑하는 함수를 가집니다. 여기서 f(z)의 도메인(domain)을 z-평면에 놓여-있는 것으로 말하는 것이 관례적이지만, f(z)의 치역(range)을 w-평면에서 점의 집합으로 참조합니다. 기호에서, 우리는 다음을 씁니다:

$z=x+iy;\qquad f(z)=w=u+iv$

그리고 함수 f를 (좌표 (x, y)를 갖는) z-평면에서 (좌표 (u, v)를 갖는) w-평면으로의 변환으로 종종 생각합니다.

Complex plane notation

복소 평면은 $\mathbb {C}$ 로 표시됩니다.

Argand diagram

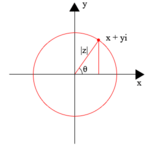
아르강 다이어그램은 x-축을 실수 축으로 사용하고 y-축을 허수 축으로 사용하여 복소수를 점 $z = x + iy$ 로 기하학적 그림(plot)으로 참조합니다.^[3] 그러한 그림은, 비록 그것들이 처음 노르웨이–덴마크 토지 측량사이자 수학자 캐스퍼 비슬(Caspar Wessel) (1745–1818)이 묘사했음에도 불구하고, 장-로베르 아르강(Jean-Robert Argand) (1768–1822)의 이름을 따서 지어졌습니다.^{[note 3]} 아르강 다이어그램은 복소 평면에서 함수의 영점과 극점(zeros and poles)의 위치를 그리기 위해 자주 사용됩니다.

Stereographic projections

복소 평면을 그것이 구의 표면을 차지하는 것처럼 생각하는 것이 유용할 수 있습니다. 단위 반지름의 구(sphere)가 주어지면, 그것의 중심을 복소 평면의 원점에 놓고, 구 위의 적도가 평면에서 단위 원과 일치하고, 북극이 평면 "위"에 있도록 방향을 지정합니다.

우리는 구의 표면에서 북극을 뺀 점과 복소 평면에서 점 사이에 다음과 같이 일-대-일 대응관계를 설립할 수 있습니다. 평면에서 한 점이 주어지면, 그것을 구 위의 북극과 연결하는 직선을 그립니다. 해당 직선은 정확하게 하나의 다른 점에서 구의 표면과 교차할 것입니다. 점 $z = 0$ 는 구의 남극 위로 투영될 것입니다. 단위 원의 내부는 구 내부에 놓이기 때문에, 해당 전체 영역 ( $| z | < 1$ )은 남반구 위로 매핑될 것입니다. 단위 원 자체 ( $| z | = 1$ )는 적도 위에 매핑될 것이고, 단위 원의 외부 ( $| z | > 1$ )는 북반구에서 북극을 뺀 북반구에 매핑될 것입니다. 분명히 이 절차는 되돌릴 수 있습니다 – 북극이 아닌 구의 표면 위의 임의의 점이 주어지면, 우리는 해당 점을 북극에 연결하고 정확하게 한 점에서 평면을 교차하는 직선을 그릴 수 있습니다.

이 입체 투영법에서 북극 자체는 복소 평면에서 임의의 점과도 결합되지 않습니다. 우리는 복소 평면에 점을 하나 – 소위 무한대에서 점 – 더 추가하고 그것을 구 위의 북극과 식별함으로써 일-대-일 대응을 완성합니다. 이 토폴로지적 공간, 복소 평면 더하기 무한대에서 점은 확장된 복소 평면(extended complex plane)으로 알려져 있습니다. 우리는 복소 해석학을 논의할 때 단일 "무한대에서 점"에 대해 이야기합니다. 실수 직선(real number line) 위에 무한대에서 둘의 점 (양수, 음수)가 있지만, 확장된 복소 평면에서 무한대에서 오직 하나 (북극)가 있습니다.^[5]

그것들이 구에서 평면 위로 투영될 때 위도와 경도 선에 어떤 일이 일어날지 잠시 상상해 보십시오. 위도 선은 모두 적도와 평행하므로, 그것들은 원점 $z = 0$ 을 중심으로 하는 완전한 원이 될 것입니다. 그리고 경도 선은 원점을 통과하는 직선이 될 것입니다 (그리고 "무한에서 점"을 통과하는데, 왜냐하면 그것들은 구 위의 북극과 남극을 모두 통과하기 때문입니다).

이것은 둘 이상의 값으로 구성된 평면 위로의 구의 투영의 유일하게 가능하지만 그럴듯한 입체적 상황은 아닙니다. 예를 들어, 구의 북극은 원에 접하는 평면에서 원점 $z = -1$ 의 꼭대기에 배치될 수 있습니다. 세부 사항은 별로 중요하지 않습니다. 평면 위로의 구의 입체적 투영은 하나의 "무한대에서 점"을 생성할 것이고, 구 위의 위도와 경도의 선을 각각 평면에서 원과 직선으로 매핑합니다.

Cutting the plane

복소 변수의 함수를 논의할 때 종종 복소 평면에서 절단(cut)을 생각하는 것이 편리합니다. 이 아이디어는 여러 다른 문맥에서 자연스럽게 발생합니다.

Multi-valued relationships and branch points

간단한 두-값 관계를 생각해 보십시오: $w=f(z)=\pm {\sqrt {z}}=z^{1/2}.$

우리가 이 관계를 단일-값 함수(function)로 취급하기 전에, 결과 값의 범위는 어떻게든 제한되어야 합니다. 비-음의 실수의 제곱근을 다룰 때 이것은 쉽게 수행됩니다. 예를 들어, 우리는 단지 $y 2 = x$ 을 만족하는 비-음의 실수 y가 되도록 다음을 정의할 수 있습니다: $y=g(x)={\sqrt {x}}=x^{1/2}$

이 아이디어는 이-차원 복합 평면에서 잘 작동하지 않습니다. 그 이유를 알아보기 위해, 점 z가 단위원 주위를 이동할 때 f(z) 값이 어떻게 변하는지 생각해 보십시오. 우리는 다음을 쓸 수 있습니다: $z=re^{i\theta }\quad {\text{and take}}\quad w=z^{1/2}={\sqrt {r}}\,e^{i\theta /2}\qquad (0\leq \theta \leq 2\pi ).$

분명하게, z가 원 주위를 모든 방법에서 이동할 때, w는 오직 원의 절반을 추적합니다. 따라서 복소 평면에서 한 번의 연속 운동은 양의 제곱근 e⁰ = 1를 음의 제곱근 $e iπ = -1$ 으로 변환했습니다.

이 문제는 점 z = 0가 단지 하나의 제곱근을 가지지만, 모든 각 다른 복소수 z ≠ 0는 정확하게 둘의 제곱근을 가지기 때문에 발생합니다. 실수 직선 위에서, 우리는 단일 점 x = 0에 "장벽"을 세움으로써 이 문제를 우회할 수 있습니다. 더 큰 장벽이 복소 평면에서 필요하여, 임의의 닫힌 윤곽을 가지 점(branch point) z = 0을 완전하게 둘러싸는 것으로부터 방지합니다. 이것은 공통적으로 가지 자름을 도입함으로써 수행됩니다; 이 경우에서 "절단"은 절단 평면에서 변수 z의 편각이 범위 0 ≤ arg(z) < 2π로 제한되도록 양의 실수 축을 따라 점 z = 0에서 무한대에서 점까지 확장될 수 있습니다.

우리는 이제 $w = z 1 ⁄ 2$ 의 완전한 설명을 제공할 수 있습니다. 그렇게 하기 위해, 우리는 그것들의 각각이 실수 축을 따라 절단된 둘의 z-평면 복사본을 필요로 합니다. 한 복사본에서, 우리는 1의 제곱근을 $e 0 = 1$ 으로 정의하고, 다른 복사본에서 우리는 1의 제곱근을 e^iπ = −1로 정의합니다. 우리는 이들 둘의 완전한 절단 평면 시트의 복사본을 호출합니다. 연속성 편각을 만듦으로써 우리는 (이제 단일-값) 함수 $w = z 1 ⁄ 2$ 가 첫 번째 시트를 w-평면의 위쪽 절반에 매핑한다는 것을 알 수 있으며, 여기서 $0 \leq arg(w) < π$ 이고, 반면에 두 번째 시트를 w-평면의 아래쪽 절반에 매핑합니다 (여기서 $π \leq arg(w) < 2 π$ ).^[6]

이 예제에서 가지 절단은 실수 축을 따라 놓일 필요가 없습니다. 그것은 심지어 직선일 필요도 없습니다. 원점 z = 0와 무한대에서 점을 연결하는 임의의 연속 곡선이 작동할 것입니다. 일부 경우에서, 가지 절단이 무한대에서 점을 통과할 필요조차 없습니다. 예를 들어, 다음 관계를 생각해 보십시오: $w=g(z)=\left(z^{2}-1\right)^{1/2}.$

여기서 다항식 z² − 1은 $z = \pm1$ 일 때 사라지므로, g는 분명하게 둘의 가지 점을 가집니다. 우리는 −1에서 1까지 실수 축을 따라 평면을 "절단"할 수 있고, g(z)가 단일-값 함수인 시트를 얻을 수 있습니다. 대안적으로, 그 절단이 z = 1에서 무한대에서 점을 통과하는 양의 실수 축을 따라 실행되고, 그런-다음 음의 실수 축을 다른 가지 점, z = −1까지 "위로" 계속할 수 있습니다.

이러한 상황은 위에서 설명된 입체적 투영법을 사용함으로써 가장 쉽게 시각화될 수 있습니다. 구에서 이들 절단 중 하나는 남반구를 세로로 통과하여, 적도의 한 점 (z = −1)과 적도의 또 다른 점 (z = 1)을 연결하고, 도중에 남극 (원점, z = 0)을 통과합니다. 절단의 두 번째 버전은 북반구를 세로로 통과하고 북극 (즉, 무한대에서 점)을 통과함으로써 같은 둘의 적도 점을 연결합니다.

Restricting the domain of meromorphic functions

유리형 함수(meromorphic function)는 정칙(holomorphic)이고 따라서 유한 점, 또는 셀-수-있는 무한(countably infinite), 점의 숫자를 제외하고 그것의 도메인에서 모든 곳에서 해석적(analytic)인 복소 함수입니다.^{[note 4]} 그러한 함수가 정의될 수 없는 점은 유리형 함수의 극점(pole)이라고 불립니다. 때때로 이들 모든 극점이 일직선으로 놓여 있습니다. 해당 경우에서 수학자들은 그 함수는 "절단 평면에서 정칙"이라고 말할 수 있습니다. 다음은 간단한 예입니다.

다음에 의해 정의된 감마 함수(gamma function)는 $\Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{n=1}^{\infty }\left[\left(1+{\frac {z}{n}}\right)^{-1}e^{z/n}\right]$

여기서 γ는 오일러–마스케로니 상수(Euler–Mascheroni constant)이고, 0, −1, −2, −3, ...에서 단순 극점을 가지는데 왜냐하면 무한 곱(infinite product)에서 정확하게 하나의 분모가 z가 영, 또는 음의 정수일 때 사라지기 때문입니다.^{[note 5]} 모든 그것의 극이 z = 0에서 무한대에서 점까지 음의 실수 축에 놓이기 때문에, 이 함수는 "절단 평면 위에 정칙, 음의 실수 축을 따라 0 (포함)에서 무한대에서 점까지 연장되는 절단"으로 설명될 수 있습니다.

대안적으로, Γ(z)는 "−π < arg(z) < π이고 점 z = 0을 제외하는 절단 평면에서 정칙"으로 설명될 수 있습니다.

이 절단은 그것이 실제로 절단 평면에서 음의 실수 축을 제외하기 때문에 우리가 이미 만난 가지 절단과 약간 다릅니다. 가지 절단은 한 쪽 (0 ≤ θ)의 절단 평면과 연결된 실수 축을 남겼지만, 다른 쪽 (θ < 2π)을 따라 절단 평면에서 그것을 절단했습니다.

물론, Γ(z)가 정칙인 도메인을 구성하기 위해 z = 0에서 −∞까지의 전체 선분을 실제로 제외할 필요는 없습니다. 우리가 정말로 해야 할 일은 셀-수-있는 무한 점 {0, −1, −2, −3, ...}의 집합에서 평면을 뚫는 것입니다. 그러나 구멍-뚫린 평면에서 닫힌 윤곽은 Γ(z)의 극 중 하나 이상을 둘러쌀 수 있으며, 잔여 정리(residue theorem)에 의해 반드시 0일 필요는 없는 윤곽 적분(contour integral)을 제공합니다. 복소 평면을 절단함으로써, 우리는 Γ(z)가 이 제한된 도메인에서 정칙임을 보장할 뿐만 아니라 절단 평면에 놓인 임의의 닫힌 곡선에 걸쳐 Γ의 윤곽 적분이 동일하게 영과 같도록 보장합니다.

Specifying convergence regions

많은 복소 함수는 무한 급수(infinite series), 또는 연속된 분수(continued fractions)로 정의됩니다. 이러한 무한하게 긴 표현의 해석에서 기본적인 고려 사항은 그것들이 유한 값으로 수렴하는 복소 평면의 부분을 식별하는 것입니다. 다음 예에서 볼 수 있듯이, 평면에서 절단은 이 과정을 용이하게 할 수 있습니다.

무한 급수에 의해 정의된 함수를 생각해 보십시오: $f(z)=\sum _{n=1}^{\infty }\left(z^{2}+n\right)^{-2}.$

모든 각 복소수 z에 대해 z² = (−z)²이기 때문에, f(z)는 z의 짝수 함수(even function)임이 분명하므로, 해석은 복소 평면의 절반으로 제한될 수 있습니다. 그리고 그 급수가 다음일 때 정의되지 않기 때문에, $z^{2}+n=0\quad \iff \quad z=\pm i{\sqrt {n}},$

전체 허수 축을 따라 평면을 자르고 z가 순수 허수일 때 f(z)를 검사하는 더 힘든 작업을 수행하기 전에 z의 실수 부분이 영이 아닌 이 급수의 수렴을 설정하는 것이 합리적입니다.^{[note 6]}

이 예제에서 절단은 무한 합이 정의되지 않은 점이 분리되고, 절단 평면이 적절하게 구멍-뚫린 평면으로 대체될 수 있기 때문에 단순한 편의입니다. 어떤 상황에서 그 절단이 필요하고, 단지 편리하기만 한 것이 아닙니다. 무한 주기 연속된 분수를 생각해 보십시오: $f(z)=1+{\cfrac {z}{1+{\cfrac {z}{1+{\cfrac {z}{1+{\cfrac {z}{\ddots }}}}}}}}.$

f(z)는 유한 값으로 수렴하는 것과 z가 $z < - 1 ⁄ 4$ 를 만족하는 음의 실수가 아닌 것은 필요충분 조건임을 보여줄 수 있습니다. 다시 말해, 이 연속된 분수에 대해 수렴 영역은 −1⁄4에서 무한대에서 점까지 음의 실수 축을 따라 절단이 진행되는 절단 평면입니다.^[8]

Gluing the cut plane back together

우리는 다음 관계가 $w=f(z)=\pm {\sqrt {z}}=z^{1/2}$

f의 도메인을 둘의 비-연결된 시트로 분리함으로써 단일-값 함수로 만들어질 수 있는 방법을 이미 보였습니다. $f (z) = z 1/2$ 가 그것의 이미지가 (점 $w = 0$ 를 제외한) 전체 w-평면인 정칙 함수로 정의될 수 있는 단일 리만 표면을 형성하기 위해 그것들 두 시트를 함께 다시 "접착"하는 것도 가능합니다. 작동 방법은 다음과 같습니다.

절단된 복합 평면의 두 복사본, $z = 0$ 에서 무한대에서 점까지 양의 실수 축을 따라 확장되는 절단부를 상상해 보십시오. 한 시트에 정의에 의해 $1 1/2 = e 0 = 1$ 가 되도록 $0 \leq arg(z) < 2 π$ 를 정의합니다. 두 번째 시트에서 다시 정의에 의해 $1 1/2 = e iπ = -1$ 가 되도록 $2 π \leq arg(z) < 4 π$ 를 정의합니다. 이제 두 번째 시트를 거꾸로 뒤집어서, 허수 축이 첫 번째 시트의 허수 축과 반대 방향을 가리키도록 하고, 두 실수 축이 같은 방향을 가리키도록 하고, (" $θ = 0$ "으로 이름-지정된 첫 번째 시트의 가장자리가 두 번째 시트에서 " $θ < 4 π$ "로 이름-지정된 가장자리에 연결되고, " $θ = 2 π$ "로 이름-지정된 두 번째 시트의 가장자리는 첫 번째 시트에서 " $θ < 2 π$ "로 이름-지정된 가장자리에 연결되도록) 두 시트를 함께 "접착"합니다. 결과는 $f (z) = z 1/2$ 가 단일-값이고 ( $z = 0$ 일 때를 제외한) 정칙인 리만 표면 도메인입니다.^[6]

f가 이 도메인에서 단일-값인 이유를 이해하기 위해, 첫 번째 시트에서 $z = 1$ 로 시작하는 단위 원 주위의 회로를 상상해 보십시오. $0 \leq θ < 2 π$ 일 때, 우리는 여전히 첫 번째 시트에 있습니다. $θ = 2 π$ 일 때, 우리는 두 번째 시트로 건너갔고, 시작점으로 되돌아가기 전에 가지 점 $z = 0$ 주위에 두 번째 완전한 회로를 만들어야 하며, 여기서 $θ = 4 π$ 는 $θ = 0$ 와 동등한데, 왜냐하면 우리가 두 시트를 함께 붙인 방법때문입니다. 다시 말해서, 변수 z가 가지 점을 두 번 완전히 회전할 때, w-평면에서 z의 이미지는 단지 하나의 완전한 원을 추적합니다.

형식적 미분화는 다음임을 보여줍니다: $f(z)=z^{1/2}\quad \Rightarrow \quad f'(z)={\tfrac {1}{2}}z^{-1/2}$

이것으로부터 우리는 f의 도함수가 존재하고 $z = 0$ 일 때를 제외하고 리만 표면 위의 모든 곳에서 유한하다는 결론을 내릴 수 있습니다. (즉, f는 $z = 0$ 일 때를 제외하고 정칙입니다).

위에서 논의된 함수 다음 함수에 대해 리만 표면을 어떻게 구성할 수 있습니까? $w=g(z)=\left(z^{2}-1\right)^{1/2},$

다시 한 번 우리는 z-평면의 두 복사본으로 시작하지만, 이번에는 각각이 $z = -1$ 에서 $z = 1$ 까지 확장하는 실수 선분을 따라 절단됩니다 – 이것들은 g(z)의 두 가지 점입니다. 우리는 이들 중 하나를 위에서 아래로 뒤집으므로, 둘의 허수 축이 반대 방향을 가리키도록 하고, 두 절단 시트의 해당 가장자리를 함께 붙입니다. 우리는 g가 $z = 1$ 에 중심을 둔 단위 반지름의 원 주위의 회로를 추적함으로써 이 표면 위에 단일-값 함수임을 확인할 수 있습니다. 첫 번째 시트의 $z = 2$ 점에서 시작하여 우리는 $z = 0$ 에서 절단을 만나기 전에 원을 반바퀴 회전합니다. 그 절단은 z가 가지 점 $z = 1$ 을 중심으로 완전히 한 바퀴 도는 것을 추적할 때, w는 단지 완전히 바퀴의 절반을 취하고, w의 반전되고 (왜냐하면 $e iπ = -1$ ), 우리의 경로는 우리를 표면의 두 번째 시트 위의 점 $z = 2$ 로 데려가도록 두 번째 시트로 밀어 넣습니다. 계속해서 또 다른 반바퀴를 더 돌리면 우리는 절단의 다른 변, $z = 0$ 을 만나고, 가지 점을 완전히 두 바퀴 도는 후 마침내 시작 점 (첫 번째 시트에서 $z = 2$ )에 도달합니다.

이 예제에서 $θ = arg(z)$ 에 이름-지정하는 자연스러운 방법은 첫 번째 시트에서 $- π < θ \leq π$ 를 설정하고 두 번째 시트에서 $π < θ \leq 3 π$ 로 설정하는 것입니다. 두 시트의 허수 축은 닫힌 윤곽이 한 시트에서 다른 시트로 이동할 때 반시계 방향의 양의 회전 감각이 유지되도록 반대 방향을 가리킵니다 (두 번째 시트는 거꾸로 있음을 기억하십시오). 두 시트가 모두 xy-평면에 평행한 삼-차원 공간에 삽입된 이 표면을 상상해 보십시오. 그런-다음 둘의 절단부가 함께 결합되는 표면에 수직 구멍이 있는 것처럼 보입니다. 만약 $z = -1$ 에서 실수 축 아래로 무한대에서 점까지 절단이 이루어지고, $z = 1$ 에서 절단이 자체와 만날 때까지 실수 축 위로 절단이 이루어지면 어떻게 될까요? 다시 리만 표면이 구성될 수 있지만, 이번에는 "구멍"이 수평입니다. 토폴로지적으로 말하자면, 이 리만 표면의 두 버전은 동등합니다 – 그것들은 지너스(genus) 일의 방향가능(orientable) 이-차원 표면입니다.

Use of the complex plane in control theory

제어 이론(control theory)에서, 복소 평면의 한 가지 용도는 's-평면'으로 알려져 있습니다. 그것은 시스템의 행위 (특성 방정식)을 그래픽으로 설명하는 방정식의 근을 시각화하기 위해 사용됩니다. 그 방정식은 통상적으로 라플라스 변환(Laplace transform)의 매개변수 's'에서 다항식으로 표현되고, 따라서 그 이름 's' 평면입니다. s-평면에서 점은 $s=\sigma +j\omega$ 형식을 취하며, 여기서 'j'는 보통의 'i' 대신에 허수 성분을 나타내기 위해 사용됩니다.

복소 평면의 또 다른 관련된 용도는 나이퀴스트 안정성 기준(Nyquist stability criterion)과 함께 사용하는 것입니다. 이것은 복소 평면에서 주파수 (또는 루프 전달 함수(transfer function))의 함수로 그것의 열린-루프 크기와 위상 응답의 나이퀴스트 플롯(Nyquist plot)을 검사함으로써 닫힌-루프 피드백 시스템의 안정성을 결정할 수 있도록 하는 기하학적 원리입니다.

'z-평면'은 s-평면의 이산 시간 버전으로, 여기서 z-변환(z-transform)이 라플라스 변환 대신 사용됩니다.

Quadratic spaces

복소 평면은 둘의 구별되는 이차 공간(quadratic space)과 결합됩니다. 복소 평면에서 점 $z = x + iy$ 에 대해, 제곱 함수(squaring function) z²와 노름된-제곱 $x^{2}+y^{2}$ 는 둘 다 이차 형식(quadratic form)입니다. 전자는 복소 평면 위에 메트릭(metric)을 설정에서 후자의 사용 여파로 자주 무시됩니다. 이차 공간으로 복소 평면의 이들 구별되는 면은 케일리–딕슨 프로세스(Cayley–Dickson process)를 갖는 필드에 걸쳐 대수(algebras over a field)의 구성에서 발생합니다. 해당 절차는 임의의 필드(field)에 적용될 수 있고, 필드 R과 C에 대해 다른 결과가 발생합니다: R이 도약 필드일 때, C는 이차 형식 $x^{2}+y^{2}$ 으로 구성하지, 이 프로세스는 역시 C와 z²로 시작할 수 있고, 해당 경우 R에서 파생된 것과 다른 대수를 생성합니다. 어떤 경우에도, 생성된 대수는 합성 대수(composition algebra)입니다; 이 경우에서, 복소 평면은 둘의 구별되는 합성 대수학에 대해 점 집합입니다.

Other meanings of "complex plane"

이 기사의 이전 섹션은 복소수의 기하학적 표시의 관점에서 복소 평면을 다룹니다. 비록 "복소 평면"이라는 용어의 사용법이 길고 수학적으로 풍부한 역사를 가지고 있지만, "복소 평면"으로 특징지을 수 있는 유일한 수학적 개념은 결코 아닙니다. 적어도 세 가지 추가 가능성이 있습니다.

이-차원 복소 벡터 공간, 그것의 좌표가 복소수인 이-차원 벡터 공간이라는 의미에서 "복소 평면". 역시 참조: Complex affine space § Two dimensions.
(1 + 1)-차원 민코프스키 공간(Minkowski space)은, 역시 분할-복소 평면(split-complex plane)으로 알려져 있으며, 대수적 분할-복소수(split-complex number)가 데카르트 평면에서 점 $(x, y)$ 와 쉽게 결합될 수 있는 둘의 실수 성분으로 분리될 수 있는 의미에서 "복소 평면"입니다.
실수에 걸쳐 이중 숫자(dual number)의 집합은 데카르트 평면의 점 $(x, y)$ 과 일-대-일 대응으로 배치될 수 있고, "복소 평면"의 또 다른 예제를 나타냅니다.

Terminology

용어 "복소 평면"은 역사적으로 받아 들여졌지만, 그 대상은 일-차원 복소 벡터 공간(complex vector space)이므로 "복소 직선"이라는 이름이 더 적절할 수 있습니다.

Notes

^ A detailed definition of the complex argument in terms of the complete arctangent can be found at the description of the atan2 function.
^ All the familiar properties of the complex exponential function, the trigonometric functions, and the complex logarithm can be deduced directly from the power series for $e^{z}$ . In particular, the principal value of $\log r$ , where $|r|=1$ , can be calculated without reference to any geometrical or trigonometric construction.^[1]
^ Wessel's memoir was presented to the Danish Academy in 1797; Argand's paper was published in 1806.^[4]
^ See also Proof that holomorphic functions are analytic.
^ The infinite product for Γ(z) is uniformly convergent on any bounded region where none of its denominators vanish; therefore it defines a meromorphic function on the complex plane.^[7]
^ When Re(z) > 0 this sum converges uniformly on any bounded domain by comparison with ζ(2), where ζ(s) is the Riemann zeta function.

References

^ See (Whittaker & Watson 1927), Appendix.
^ See (Whittaker & Watson 1927), p. 10.
^ Weisstein, Eric W. "Argand Diagram". mathworld.wolfram.com. Retrieved 19 April 2018.
^ See (Whittaker & Watson 1927), p. 9.
^ See (Flanigan 1983), p. 305.
^ ^a ^b See (Moretti 1964), pp. 113–119.
^ See (Whittaker & Watson 1927), pp. 235–236.
^ See (Wall 1948), p. 39.

Works Cited

Flanigan, Francis J. (1983). Complex Variables: Harmonic and Analytic Functions. Dover. ISBN 0-486-61388-7.
Moretti, Gino (1964). Functions of a Complex Variable. Prentice-Hall.
Wall, H. S. (1948). Analytic Theory of Continued Fractions. D. Van Nostrand Company. Reprinted (1973) by Chelsea Publishing Company ISBN 0-8284-0207-8.
Whittaker, E. T.; Watson, G. N. (1927). A Course in Modern Analysis (Fourth ed.). Cambridge University Press.

External links

Weisstein, Eric W. "Argand Diagram". MathWorld.
Jean-Robert Argand, "Essai sur une manière de représenter des quantités imaginaires dans les constructions géométriques", 1806, online and analyzed on BibNum [for English version, click 'à télécharger']

[1] A detailed definition of the complex argument in terms of the complete arctangent can be found at the description of the atan2 function.

[3] All the familiar properties of the complex exponential function, the trigonometric functions, and the complex logarithm can be deduced directly from the power series for $e^{z}$ . In particular, the principal value of $\log r$ , where $|r|=1$ , can be calculated without reference to any geometrical or trigonometric construction.^[1]

[7] Wessel's memoir was presented to the Danish Academy in 1797; Argand's paper was published in 1806.^[4]

[10] See also Proof that holomorphic functions are analytic.

[12] The infinite product for Γ(z) is uniformly convergent on any bounded region where none of its denominators vanish; therefore it defines a meromorphic function on the complex plane.^[7]

[13] When Re(z) > 0 this sum converges uniformly on any bounded domain by comparison with ζ(2), where ζ(s) is the Riemann zeta function.

[2] See (Whittaker & Watson 1927), Appendix.

[4] See (Whittaker & Watson 1927), p. 10.

[5] Weisstein, Eric W. "Argand Diagram". mathworld.wolfram.com. Retrieved 19 April 2018.

[6] See (Whittaker & Watson 1927), p. 9.

[8] See (Flanigan 1983), p. 305.

[Moretti-9] See (Moretti 1964), pp. 113–119.

[11] See (Whittaker & Watson 1927), pp. 235–236.

[14] See (Wall 1948), p. 39.

[note 1]

[note 2]

[2]

[3]

[note 3]

[5]

[6]

[note 4]

[note 5]

[note 6]

[8]

[1]

[4]

[7]