Conic section

Original article: w:Conic section

Types of conic sections:
1. Parabola
2. Circle and ellipse
3. Hyperbola

Table of conics, Cyclopaedia, 1728

수학에서 원뿔 단면(conic section:원뿔 곡선, 원추 곡선) (또는 원뿔형)은 원뿔(cone)의 표면(surface)과 평면(plane)의 교차점으로 얻어지는 곡선(curve)입니다. 원뿔 단면의 세 가지 유형은 타원(ellipse), 포물선(parabola) 및 쌍곡선(hyperbola)입니다; 원(circle)은, 비록 그것이 때때로 네 번째 유형으로 불릴지라도, 타원의 특수한 경우입니다. 고대 그리스 수학자들은 원뿔 단면을 연구했는데, 그들의 속성에 대해 페르가의 아폴로니우스(Apollonius of Perga)의 체계적인 연구와 함께 기원전 200년 경에 절정에 달했습니다.

유클리드 평면(Euclidean plane)에서 원뿔 단면은 다양한 구별되는 속성을 가지는데, 이 중 많은 것이 대안적인 정의로 사용될 수 있습니다. 그러한 속성 중 하나는, 초점(focus)이라고 불리는, 일부 특정 점까지의 거리와 방향선(directrix:준선)이라고 불리는 특정 직선에 대한 거리가 이심률(eccentricity)이라는 불리는 고정 비율로 있는, 그들 점들의 집합으로 비-원형 원뿔형을 정의합니다. 원뿔형의 유형은 이심률의 값에 의해 결정됩니다. 해석 기하학(analytic geometry)에서, 원뿔형은 차수 2의 평면 대수 곡선(plane algebraic curve); 즉, 좌표가 두 변수에서 이차 방정식(quadratic equation)을 만족시키는 점들의 집합으로 정의될 수 있습니다. 이 방정식은 행렬 형식으로 쓸 수 있고, 일부 기하학적 속성은 대수적 조건으로 연구될 수 있습니다.

유클리드 평면에서, 원뿔 단면의 세 유형은 꽤 다르게 보이지만, 많은 속성을 공유합니다. 무한대에서 직선을 포함하도록 유클리드 평면을 확장하여, 투영 평면(projective plane)을 얻음으로써, 명백한 차이는 사라집니다: 쌍곡선의 가지는 무한대에서 두 점이 만나고, 하나의 닫힌 곡선을 만듭니다; 그리고 포물선의 두 끝은 그것을 무한대에서 직선에 접하는 닫힌 곡선을 만들기 위해 만납니다. 게다가 실수 좌표를 복소수(complex) 좌표를 허용하도록 확장함으로써, 확장은 대수적으로 이 통일을 보기 위해 방법을 제공합니다.

Euclidean geometry

원뿔 단면은 수천 년 동안 연구되어 왔고 유클리드 기하학(Euclidean geometry)에서 흥미롭고 아름다운 풍부한 출처를 제공해 왔습니다.

Definition

The black boundaries of the colored regions are conic sections. Not shown is the other half of the hyperbola, which is on the unshown other half of the double cone.

원뿔형(conic)은 이중 원뿔(cone) (두 개의 내프(nappes)을 가진 원뿔)의 표면을 갖는, 절단 평면(cutting plane)이라고 불리는, 평면(plane)의 교차점으로 얻은 곡선입니다. 그것은 보통 원뿔은 쉬운 설명의 목적에 대해 수직 원형 원뿔이라고 가정하지만, 이것은 요구되지 않습니다; 어떤 원형 교차-단면을 갖는 임이의 이중 원뿔은 충분할 것입니다. 원뿔의 꼭짓점을 통과하는 평면은 점, 직선 또는 한 쌍의 교차 직선에서 원뿔과 교차할 것입니다. 이것을 퇴화 원뿔형(degenerate conics)이라고 불리고 일부 저자는 그것들을 전혀 원뿔형이라고 생각하지 않습니다. 달리 언급되지 않은 한, 이 기사에서 "원뿔형"은 비-퇴화 원뿔형을 참조할 것입니다.

원뿔형의 세 가지 유형: 타원(ellipse), 포물선(parabola) 및 쌍곡선(hyperbola)이 있습니다. 원(circle)은, 비록 역사적으로 역사적으로 알폴로니우스는 네 번째 유형으로 여겼을지라도, 타원의 특별한 종류입니다. 타원은 원뿔과 평면의 교차점이 닫힌 곡선(closed curve)일 때 발생합니다. 원은 절단 평면이 원뿔의 생성하는 원의 평면과 평행(parallel)일 때 얻습니다; 수직 원뿔에 대해, 이것은 절단 평면이 축에 수직임을 의미합니다. 만약 절단 평면이 원뿔의 정확하게 하나의 생성 직선과 평행이면, 원뿔형은 무경계이고 포물선이라고 불립니다. 남아있는 경우에서, 그림은 쌍곡선입니다: 평면은 원뿔의 양쪽 절반을 교차하여, 두 개의 구별되는 무경계의 곡선을 생성합니다.

Eccentricity, focus and directrix

Circle (e=0), ellipse (e=1/2), parabola (e=1) and hyperbola (e=2) with fixed focus F and directrix (e=∞).

대안적으로, 우리는 평면 기하학의 관점에서 순수하게 원뿔 단면을 정의할 수 있습니다: 그것은 (초점(focus)이라고 불리는) 고정 점 F까지의 거리가 P에서 (방향선(directrix)이라고 불리는) 고정된 직선 L까지의 거리의 (이심률(eccentricity) e이라고 불리는) 일정한 배수인 모든 점 P의 자취(locus)입니다. 0 < e < 1에 대해, 우리는 타원, e = 1에 대해 포물선, 및 e > 1에 대해 쌍곡선을 얻습니다.

원은 제한적인 경우이고 유클리드 평면에서 초점과 방향선에 의해 정의되지 않습니다. 원의 이심률은 영인 것으로 정의되고 초점은 원의 중심이지만, 방향선은 투영 평면 안의 무한대에서 직선으로 오직 취할 수 있습니다.

타원의 이심률은 타원이 원형에서 벗어나는 정도의 측정으로 보일 수 있습니다.

만약 원뿔의 표면과 그의 축 사이의 각도가 $\beta$이고 자르는 평면과 축 사이의 각도가 $\alpha$이면, 이심률은 ${\frac {\cos \alpha }{\cos \beta }}$입니다.

초점-방향선 속성으로 정의된 위의 곡선이 원뿔과 교차하는 평면에서 얻은 것과 같다는 증명은 당들랭 구(Dandelin spheres)의 사용으로 용이하게 됩니다.

Conic parameters

Conic parameters in the case of an ellipse

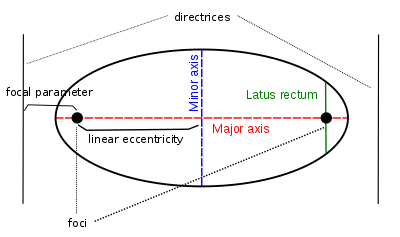
이심률 (e), 초점, 및 방향선 외에도 다양한 기하학적 특징과 길이가 원뿔 단면과 연관되어 있습니다.

주축(principal axis)는 타원 또는 쌍곡선의 초점을 연결하는 선이고, 그의 중간 점은 곡선의 중심(center)입니다. 포물선은 중심을 가지지 않습니다.

선형 이심률(linear eccentricity) (c)는 중심과 초점 사이의 거리입니다.

래투스 렉툼(latus rectum)은 초점을 통과하고 방향선과 평행한 현(chord)입니다; 그의 절반-길이는 반-래투스 렉툼 (ℓ)입니다.

초점 매개변수(focal parameter) (p)는 초점에서 해당 방향선까지의 거리입니다.

주요 축(major axis)은 두 꼭짓점 사이의 현입니다: 타원의 가장 긴 현, 쌍곡선의 가지 사이에서 가장 짧은 현입니다. 그의 절반-길이는 반-주요 축(semi-major axis) (a)입니다. 타원 또는 쌍곡선이 아래 방정식에서 처럼 표준 위치, x-축에 초점이 있고 원점에 중심이 있을 때, 원뿔형의 꼭짓점은 비-음의 a와 함께 좌표 (−a, 0) 및 (a, 0)를 가집니다.

보조 축(minor axis)은 타원의 가장 짧은 현이고, 그의 절반-길이는 반-보조 축 (b)이며, 아래의 표준 방정식에서 처럼 같은 값 b입니다. 유사하게, 쌍곡선에 대해 우리는 표준 방정식에서 매개변수 b를 반-보조 축이라고 역시 부릅니다.

다음 관계는 유지됩니다:

• $\ \ell =pe$
• $\ c=ae$
• $\ p+c={\frac {a}{e}}$

표준 위치에서 원뿔형에 대해, 이들 매개변수는 다음 값을 가지며, $a,b>0$를 취합니다.

원뿔 단면	방정식	이심률 (e)	선형 이심률 (c)	세미-랙투스 렉툼 (ℓ)	초점 매개변수 (p)
원(circle)	$x^{2}+y^{2}=a^{2}\,$	$0\,$	$0\,$	$a\,$	$\infty$
타원(ellipse)	${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$	${\sqrt {1-{\frac {b^{2}}{a^{2}}}}}$	${\sqrt {a^{2}-b^{2}}}$	${\frac {b^{2}}{a}}$	${\frac {b^{2}}{\sqrt {a^{2}-b^{2}}}}$
포물선(parabola)	$y^{2}=4ax\,$	$1\,$	N/A	$2a\,$	$2a\,$
쌍곡선(hyperbola)	${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$	${\sqrt {1+{\frac {b^{2}}{a^{2}}}}}$	${\sqrt {a^{2}+b^{2}}}$	${\frac {b^{2}}{a}}$	${\frac {b^{2}}{\sqrt {a^{2}+b^{2}}}}$

Standard forms in Cartesian coordinates

Standard forms of an ellipse

Standard forms of a parabola

Standard forms of a hyperbola

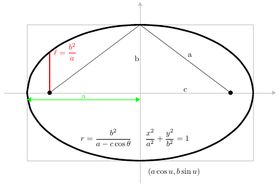
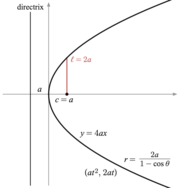
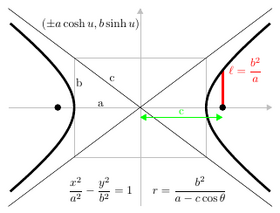
데카르트 좌표(Cartesian coordinates)를 도입한 후, 초점-방향선 속성은 원뿔 단면의 점으로 만족시키는 방정식을 생성하기 위해 사용될 수 있습니다. 좌표 변경 (축의 회전(rotation) 및 평행-이동(translation)))을 통해, 이들 방정식은 표준 형식(standard forms)로 넣어질 수 있습니다. 타원 및 쌍곡선에 대해 표준 형식는 주축으로 x-축 및 중심으로 원점 (0,0)을 가집니다. 꼭짓점은 (±a, 0)이고 초점은 (±c, 0)입니다. 타원에 대해 방정식 c² = a² − b², 쌍곡선에 대해 c² = a² + b²으로 b를 정의합니다. 원에 대해, c = 0이므로 a² = b²입니다. 포물선에 대해, 표준 형식은 점 (a, 0)에서 x-축 위에 초점을 가지고 방향선은 방정식 x = −a을 갖는 직선입니다. 표준 형식에서 포물선은 항상 원점을 통과합니다.

그의 점근선이 수직으로 만나는, 직각(rectangular) 또는 등변(equilateral) 쌍곡선에 대해, 점근선이 좌표-축이고 직선 x = y가 주축인 것에서 대안적인 표준 형식이 있습니다. 초점은 그런 다음 좌표 (c, c) 및 (−c, −c)를 가집니다.

• 원(Circle): x² + y² = a²
• 타원(Ellipse): x²/a² + y²/b² = 1
• 포물선(Parabola): y² = 4ax with a > 0
• 쌍곡선(Hyperbola): x²/a² − y²/b² = 1
• 직각 쌍곡선(Rectangular hyperbola): xy = c²/2

이들 형태 중 처음 네 개는 (원, 타원 및 쌍곡선에 대해) x-축과 y-축, 또는 (포물선에 대해) 오직 x-축에 대해 대칭입니다. 직각 쌍곡선은, 어쨌든, 직선 y = x 및 y = −x에 대해 대칭입니다.

이들 표준 형식은 다음과 같이 매개변수적(parametrically)으로 쓸 수 있습니다:

• 원(circle): (a cos θ, a sin θ),
• 타원(ellipse): (a cos θ, b sin θ),
• 포물선(parabola): (at², 2at),
• 쌍곡선(hyperbola): (a sec θ, b tan θ) or (±a cosh u, b sinh u),
• 직각 쌍곡선(Rectangular hyperbola): $(dt,{\frac {d}{t}})$ where $d={\frac {c}{\sqrt {2}}}.$

General Cartesian form

데카르트 좌표 시스템(Cartesian coordinate system)에서, 두 변수에서 이차 방정식(quadratic equation)의 그래프(graph)는 (비록 그것이 퇴화될 수 있을지라도) 항상 원뿔 단면이고, 모든 원뿔 단면은 이러한 방식으로 발생합니다. 가장 일반적인 방정식은 다음 형식입니다:

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0,$

여기서 모든 계수는 실수(real number)이고 A, B, C는 모두 영은 아닙니다.

Matrix notation

Main article: Matrix representation of conic sections

위의 방정식은 다음으로 행렬 표기법에서 쓸 수 있습니다:

$\left({\begin{matrix}x&y\end{matrix}}\right)\left({\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right)\left({\begin{matrix}x\\y\end{matrix}}\right)+\left({\begin{matrix}D&E\end{matrix}}\right)\left({\begin{matrix}x\\y\end{matrix}}\right)+F=0.$

일반적인 방정식은 다음으로 역시 쓸 수 있습니다:

$\left({\begin{matrix}x&y&1\end{matrix}}\right)\left({\begin{matrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{matrix}}\right)\left({\begin{matrix}x\\y\\1\end{matrix}}\right)=0.$

이 형식은 투영 기하학의 보다 일반적인 설정에서 사용되는 동차 형식의 특수화입니다 (아래를 참조하십시오).

Discriminant

이 방정식에 의해 묘사된 원뿔 단면은, 방정식의 판별식(discriminant)이라고 불리는, 값 $B^{2}-4AC$의 관점에서 분류될 수 있습니다: 따라서, 판벽식은 − 4Δ이며, 여기서 Δ는 행렬의 행렬식 $\left|{\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right|$입니다.

만약 원뿔형이 비-퇴화(non-degenerate)이면,

• 만약 B² − 4AC < 0이면, 방정식은 타원(ellipse)을 나타냅니다;
  • 만약 A = C 및 B = 0이면, 방정식은 원(circle)을 나타내며, 이것은 타원의 특별한 경우입니다;
• 만약 B² − 4AC = 0이면, 방정식은 포물선(parabola)을 나타냅니다;
• 만약 B² − 4AC > 0이면, 방정식은 쌍곡선(hyperbola)을 나타냅니다;
  • 만약 A + C = 0이면, 방정식은 직각 쌍곡선(rectangular hyperbola)을 나타냅니다.

여기서 사용된 표기법에서, A와 B는 다항식 계수이며, 일부 출처에서 A와 B로 반주요와 반보조를 나타내는 것과 대조적입니다.

Invariants

원뿔 단면의 이차 방정식의 판별식 (또는 동등하게 2×2 행렬의 행렬식(determinant) AC – B²/4) 및 양 A + C (2×2 행렬의 대각합(trace)은 좌표 축의 임의의 회전과 평행-이동 아래에서 불변인데, 왜냐하면 위의 3×3 행렬의 행렬식이기 때문입니다. 상수 항 F 및 합 D²+E²은 오직 회전 아래에서 불변입니다.

Eccentricity in terms of coefficients

원뿔 단면이 다음으로 대수적으로 쓰일 때

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0,\,$

이심률은 이차 방정식의 계수의 함수로 쓸 수 있습니다. 만약 4AC = B²이면, 원뿔형은 포물선이고 그것의 이심률은 1과 같습니다 (그것이 비-퇴화로 제공됩니다). 그렇지 않으면, 방정식이 비-퇴화 쌍곡선 또는 타원을 나타내는 것으로 가정하면, 이심률은 다음에 의해 제공됩니다:

$e={\sqrt {\frac {2{\sqrt {(A-C)^{2}+B^{2}}}}{\eta (A+C)+{\sqrt {(A-C)^{2}+B^{2}}}}}},$

여기서 만약 위의 3×3 행렬의 행렬식이 음수이면 η = 1이고 만약 행렬식이 양수이면 η = −1입니다.

그것은 이심률이 다음 방정식의 양수 해임을 역시 보일 수 있습니다:

$\Delta e^{4}+[(A+C)^{2}-4\Delta ]e^{2}-[(A+C)^{2}-4\Delta ]=0,$

여기서 다시 $\Delta =AC-{\frac {B^{2}}{4}}$입니다. 이것은 포물선 또는 타원의 경우에서 정확히 하나의 양의 해—이심률—를 가지고 있고, 반면에 쌍곡선의 경우에서 그것은 두 개의 양의 해를 가지는데, 그 중 하나는 이심률입니다.

Conversion to canonical form

See also: Ellipse § Canonical form

타원 또는 쌍곡선의 경우에서, 방정식

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0\,$

은 다음으로 변환된 변수 $x',y'$에서 정식의 형식으로 변환될 수 있습니다:

${\frac {x'^{2}}{-S/(\lambda _{1}^{2}\lambda _{2})}}+{\frac {y'^{2}}{-S/(\lambda _{1}\lambda _{2}^{2})}}=1,$

또는 동등하게

${\frac {x'^{2}}{-S/(\lambda _{1}\Delta )}}+{\frac {y'^{2}}{-S/(\lambda _{2}\Delta )}}=1,$

여기서 $\lambda _{1}$과 $\lambda _{2}$는 행렬 $\left({\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right)$의 고윳값(eigenvalue)입니다 — 즉, 다음 방정식의 해

$\lambda ^{2}-(A+C)\lambda +(AC-(B/2)^{2})=0$

— 및 $S$는 위의 3×3 행렬의 행렬식이고, $\Delta =\lambda _{1}\lambda _{2}$는 다시 2×2 행렬의 행렬식입니다. 타원의 경우에서, 두 반-축의 제곱은 정식의 형식에서 분모로 제공됩니다.

Polar coordinates

Development of the conic section as the eccentricity e increases

극-좌표(polar coordinates)에서, 원점에 하나의 초점을 가지고, 만약 있다면, x-축 위에 (타원에 대해) 음의 값 또는 (쌍곡선에 대해) 양의 값에 다른 것을 가진 원뿔 단면은 다음 방정식으로 제공됩니다:

$r={\frac {l}{1+e\cos \theta }},$

여기서 e는 이심률이고 l은 세미-랙투스 렉텀입니다.

위에서 처럼, e = 0에 대해, 그래프는 원, 0 < e < 1에 대해 타원, e = 1에 대해 포물선, 및 e > 1에 대해 쌍곡선입니다.

원뿔형의 방정식의 극 형식은 종종 동력학(dynamics)에서 사용됩니다; 예를 들어, 태양을 중심으로 회전하는 대상의 궤도를 결정합니다.

Properties

두 개의 (구별되는) 점이 하나의 직선을 결정하는 것처럼, 다섯 개의 점이 하나의 원뿔형을 결정(five points determine a conic)합니다. 공식적으로, 임의의 세 점이 같은-직선(collinear:공선) 위에 있지 않는 것을 의미하는, 일반적인 선형 위치(general linear position)에서 평면 안의 임의의 다섯 점이 주어지면, 그것들을 통과하는 유일한 원뿔형이 있으며, 이것은 비-퇴화일 것입니다; 이것은 유클리드 평면과 그의 확장, 실수 투영 평면 모두에서 참입니다. 실제로, 임의의 다섯 점이 주어지면, 그것을 통과하는 원뿔형이 있지만, 만약 점의 세 개가 같은-직선에 있으면 원뿔형은 퇴화될 것이고 (비-기약인데, 왜냐하면 그것은 직선을 포함하기 때문입니다), 유일하지 않을 수 있습니다; 추가 토론(further discussion)을 참조하십시오.

일반적인 선형 위치에서 평면 안의 네 점은 처음 세 점을 지나는 유일한 원뿔형을 결정하고 중심으로 네 번째 점을 가집니다. 따라서 중심을 아는 것은 곡선을 결정하는 목적에 대해 원뿔형 위의 두 점을 아는 것과 동등합니다.

게다가, 원뿔형은 그것을 지나는 일반적인 위치에서 k 점의 임의의 조합으로 결정되고 5 – k 직선은, 0≤k≤5에 대해, 원뿔에 접하는 직선입니다.

평면에서 임의의 점은 원뿔형의 영, 하나 또는 둘 접선(tangent line) 위에 있습니다. 단지 하나의 접선 위의 점은 원뿔형 위의 점입니다. 접선이 없는 점은 원뿔형의 내부 점(interior point) (또는 안의 점(inner point))이라고 말해지며, 반면에 두 접선 위의 점은 외부 점(exterior point) (또는 밖의 점(outer point))입니다.

모든 원뿔 단면은 다음으로 표현될 수 있는 반사 속성(reflection property)을 공유합니다: 비-퇴화 원뿔 단면의 모양에서 모든 거울은 하나의 초점에서 들어오는 또는 나가는 빛을 다른 초점을 향하도록 또는 멀어지도록 반사합니다. 포물선의 경우에서, 두 번째 초점은 무한히 멀리 떨어져 있는 것으로 생각될 필요가 있으므로, 두 번째 초점을 향하는 또는 들어오는 반직선은 평행합니다.

파스칼의 정리(Pascal's theorem)는 임의의 비-퇴화 원뿔형 위의 여섯 점의 집합으로 구성된 세 점의 같은-직선 성질(collinearity)과 관련이 있습니다. 그 정리는 두 직선으로 구성되는 퇴화 원뿔형에 대해 역시 유지되지만, 이 경우에서 그것은 파푸스의 정리(Pappus's theorem)로 알려져 있습니다.

비-퇴화 원뿔 단면은 항상 "매끄럽습니다(smooth)". 이것은, 매끄러운 표면이 층을 이루는 흐름(laminar flow:층류)을 보증하고 난류(turbulence)를 방지하기 위해 요구되는, 공기역학과 같은 많은 응용 분야에 대해 중요합니다.

History

Menaechmus and early works

원뿔 단면의 첫 번째 정의는 델리안(Delian) 문제 (정육면체 두 배(Duplicating the cube:입방체배적))에 대한 해결책의 일부로 메나이크모스(Menaechmus) (기원전 320년에 사망함)에 의해 제공되었다고 믿어집니다. 그의 연구는 살아남지 못했으며, 심지어 그가 이들 곡선에 사용했던 이름도 살아남지 못했고, 오직 제이의 계정을 통해서 알려졌습니다. 그 당시에 사용된 정의는 오늘날 공통으로 사용되는 정의와 다릅니다. 원뿔은 다리 중 하나를 중심으로 직각 삼각형을 회전시켜 구성되었으므로 빗변이 원뿔의 표면을 생성합니다 (그러한 직선은 생성선(generatrix)으로 불립니다). 원뿔의 세 가지 유형은 (직각 삼각형에서 회전되어지는 빗변과 다리에 의해 형성된 각도의 두 배함으로써 즉정되는) 꼭짓점 각도에 의해 결정되었습니다. 원뿔 단면은 그런 다음 이들 원뿔 중 하나를 생성선에 직각으로 그려진 평면과 교차시킴으로써 결정되었습니다. 원뿔형의 유형은 원뿔의 유형, 즉 원뿔의 꼭짓점에 형성된 각도에 의해 결정됩니다; 만약 각도가 예각이라면 원뿔형은 타원입니다; 만약 각도가 직각이면 원뿔형은 포물선입니다; 만약 각도가 둔각이면 원뿔형은 쌍곡선입니다 (그러나 곡선의 한 가지를 형성합니다).

유클리드(Euclid) (기원전 fl. 300년)는 원뿔형에 대한 네 권의 책을 썼다고 말했지만 이것도 마찬가지로 잃어버렸습니다. 아르키메데스(Archimedes) (기원전 c. 212년에 사망)는, Quadrature of the Parabola에서 포물선과 현에 의해 경계진 넓이를 결정하기 위해, 원뿔형을 연구한 것으로 알려져 있습니다. 그의 주요 관심사는 원뿔형과 관련된 넓이와 부피의 측정에 관한 것이었고, 이 연구의 일부는 원뿔형의 회전 고체에 대한 그의 책, On Conoids and Spheroids에 남아 있습니다.

Apollonius of Perga

Diagram from Apollonius' Conics, in a 9th-century Arabic translation

고대 그리스인에 의한 원뿔형의 연구에서 가장 큰 발전은 페르가의 아폴로니우스(Apollonius of Perga) (기원전 c. 190년에 사망)에 기인한 것으로, 그의 8-권 Conic Sections 또는 Conics은 기존 지식을 요약하고 크게 확장시켰습니다. 이들 곡선의 속성의 아폴로니우스의 연구는, 각도에 관계없이, 고정된 이중 원뿔을 절단하는 임의의 평면이 이전 정의에 따라 원뿔형을 생성하고, 오늘날 공통적으로 사용되는 정의로 이어질 수 있음을 보이는 것을 가능하게 했습니다. 이전 방법으로 구성될 수 없었던, 원은 이런 방식으로 역시 얻을 수 있습니다. 이것은 아폴로니우스가 원을, 더 이상 만들어지지 않은 하나의 구별, 네 번째 원뿔 단면으로 여겼는지 그 이유를 설명할 수 있습니다. 아폴로니우스는 이들 곡선에 대해 이름 타원, 포물선, 및 쌍곡선을 사용했으며, 그 지역에서 초기 피타고라스 연구로부터 용어를 빌렸습니다.

알렉산드리아의 파푸스(Pappus of Alexandria) (기원전 c. 350년에 사망함)는 원뿔형의 초점의 개념의 중요성에 대한 상세히 설명한 것, 및 (아폴로니우스의 알려진 작품에서 부족한 것이었던) 포물선의 경우를 포함한 방향선(directrix)의 관련된 개념을 세부적으로 묘사한 것으로 인정받았습니다.

Al-Kuhi

원뿔 단면을 그리는 도구는 이슬람 수학자 알-피(Al-Kuhi)에 의해 1000년경에 처음 묘사되었습니다.

Omar Khayyám

아폴로니우스의 연구는 아랍어로 번역되었고, 그의 연구의 대부분은 아랍어 버전을 통해 오직 살아남습니다. 페르시아인은 이론의 응용을 찾았고, 특히 페르시아 수학자이자 시인 오마르 카야얌(Omar Khayyám)은 원뿔 단면을 삼보다 크지 않은 차수의 대수 방정식을 풀기 위해 사용했습니다.

Europe

요하네스 케플러(Johannes Kepler)는, 극한 개념의 선구적 원리, "연속성의 원리(principle of continuity)"를 통해 원뿔형의 이론을 확장했습니다. 케플러는 1604년에 용어 초점을 최초로 사용했습니다.

지라르 데자그르(Girard Desargues)와 블레이즈 파스칼(Blaise Pascal)은 투영 기하학(projective geometry)의 최기 형식을 사용하여 원뿔형의 이론을 개발했고 이것은 이 새로운 분야의 연구에 대해 새로운 에너지를 제공하는 것에 도움이 되었습니다. 특히, 파스칼은 원뿔형의 많은 다른 성질이 추론될 수 있는 신비로운 육각형(hexagrammum mysticum)으로 알려진 정리를 발견했습니다.

르네 데카르트(René Descartes)와 피에르 페르마(Pierre Fermat) 둘 다는 그들이 새롭게 발견한 해석적 기하학(analytic geometry)을 원뿔형의 연구에 적용했습니다. 이것은 원뿔형의 기하학적 문제를 대수학에서 문제로 줄이는 효과를 가졌습니다. 어쨌든, 그것은 존 월리스(John Wallis)였는데, 그는 1655년 논문 Tractatus de sectionibus conicis에서 원뿔 단면을 이차 방정식의 예제로 처음 정의했습니다. 이전에 쓰여졌지만, 나중에 출판된, 한 데 비츠(Jan de Witt)의 Elementa Curvarum Linearum은 원뿔형의 케플러의 운동학적(kinematic) 구성을 시작하고 그런 다음 대수 방정식을 개발합니다. 페르마의 방법론과 데카르트의 표기법을 사용하는 이 연구는 이 주제에 대한 첫 번째 교과서로 묘사되었습니다. 데 비츠는 용어 방향선(directrix)를 도입했습니다.

Applications

For specific applications of each type of conic section, see Circle, Ellipse, Parabola, and Hyperbola.

The paraboloid shape of Archeocyathids produces conic sections on rock faces

원뿔 단면은 천문학(astronomy)에서 중요합니다: 보편적 중력의 뉴턴 법칙에 따라 상호-작용하는 두 개의 거대한 물체의 궤도(orbit)는 만약 그들의 공통 질량의 중심(center of mass)이 정지되어 있는 것으로 여겨지면 원뿔 단면입니다. 만약 그들이 함께 묶여 있으면, 그들 둘 다는 타원으로 추적될 것입니다; 만약 그들이 움직여 멀어지면, 그들 둘 다는 포물선 또는 쌍곡선을 따를 것입니다. 두-몸체 문제(two-body problem)를 참조하십시오.

원뿔 단면의 반사 속성은 탐조등, 무선-망원경 및 일부 광학 망원경의 설계에서 사용됩니다. 탐조등은 초점에 전구를 가진 반사기로 포물선 거울을 사용합니다; 비슷한 구성은 포물선 마이크로폰(parabolic microphone)에 대해 사용됩니다. 카나리아 제도에서, 라 팔마 위에 4.2 미터 허셜 광학 망원경(Herschel optical telescope)은 이차 쌍곡선 거울을 향해 빛을 반사하기 위해 일차 포물면 거울을 사용하며, 이차 거울은 그것을 일차 거울 뒤의 초점에 다시 반사됩니다.

In the real projective plane

원뿔 단면은 유클리드 평면에서 일부 매우 유사한 속성을 가지고 이것에 대해 이유는, 원뿔형이 더 큰 기하학의 관점으로부터 보일 때, 더 명확해집니다. 유클리드 평면은 실수 투영 평면(real projective plane)에 내장될 수 있고 원뿔형은 이 투영 기하학에서 대상으로 여길 수 있습니다. 이것을 하기 위한 한 가지 방법은 동차 좌표(homogeneous coordinates)를 도입하는 것 및 그의 좌표가 세 변수에서 기약 이차 방정식을 만족시키는 점 (또는 동등하게, 기약 이차 형식(quadratic form)의 영들)의 집합이 되도록 원뿔형을 정의하는 것입니다. 보다 기술적으로, (임의의 숫자의 변수에서) 이차 형식의 영들인 점의 집합은 이차 초곡면(quadric)이라고 불리고, 이-차원 투영 공간 (즉, 세 개의 변수를 가짐)에서 기약 이차 초곡면은 전통적으로 원뿔형이라고 불립니다.

유클리드 평면 R²는 평행선의 무한대에 직선(line at infinity) (및 그의 해당하는 무한대에 점(points at infinity))에 인접함으로써 실수 투영 평면에 내장되므로, 평행 클래스의 모든 직선은 이 직선에서 만납니다. 다른 한편으로, 실수 투영 평면으로 시작하면, 유클리드 평면은 일부 직선을 무한대에 직선으로 구별하고 그것과 모든 그의 점을 제거함으로써 얻습니다.

Intersection at infinity

임의의 나눗셈 링에 걸쳐, 그러나 특히 실수 또는 복소수에 걸쳐 투영 공간(projective space)에서, 모든 비-퇴화 원뿔형은 동일하고, 따라서 투영 기하학에서 우리는 유형을 지정하는 것없이 단순히 "하나의 원뿔형"이라고 말합니다. 즉, 임의의 비-퇴화 원뿔형을 임의의 다른 비-퇴화 원뿔에 매핑할 수 있는 투영 변환이 있습니다.

원뿔 단면의 세 가지 유형은 투영 공간의 직선을 무한대에 직선이 되도록 선택함으로써 얻어진 아핀 평면에서 다시 나타날 것입니다. 세 가지 유형은 그런 다음 무한대에 이 직선이 투영 공간에서 원뿔형과 어떻게 교차하는지에 따라 결정됩니다. 해당하는 아핀 공간에서, 우리는 만약 원뿔형이 무한대에 직선과 교차하지 않으면 타원, 만약 원뿔형이 축에 해당하는 하나의 이중 점(double point)에서 무한대에 직선과 교차하면 포물선, 만약 원뿔형이 점근선에 해당하는 두 점에서 무한대에 직선과 교차하면 쌍곡선을 얻습니다.

Homogeneous coordinates

동차 좌표(homogeneous coordinates)에서 원뿔 단면은 다음으로 표현될 수 있습니다:

$Ax^{2}+Bxy+Cy^{2}+Dxz+Eyz+Fz^{2}=0.$

또는 행렬(matrix) 표기법에서

$\left({\begin{matrix}x&y&z\end{matrix}}\right)\left({\begin{matrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{matrix}}\right)\left({\begin{matrix}x\\y\\z\end{matrix}}\right)=0.$

위의 3 × 3 행렬은 원뿔 단면의 행렬(the matrix of the conic section)이라고 불립니다.

일부 저자는 다음으로 일반적인 동차 방정식을 쓰는 것을 선호합니다:

$Ax^{2}+2Bxy+Cy^{2}+2Dxz+2Eyz+Fz^{2}=0,$

(또는 이것의 일부 변형) 그래서 원뿔 단면의 행렬은 다음과 같이 더 단순한 형태를 가집니다:

$M=\left({\begin{matrix}A&B&D\\B&C&E\\D&E&F\end{matrix}}\right),$

그러나 이 표기법은 이 기사에서 사용하지 않습니다.

만약 원뿔 단면의 행렬의 행렬식이 영이면, 원뿔 단면은 퇴화(degenerate)입니다.

모든 여섯 계수에 같은 비-영 스칼라를 곱하는 것은 영들의 같은 집합과 함께 방정식이 생성되므로, 우리는, 오-차원 투영 공간(projective space) $\mathbf {P} ^{5}$에서 점으로 (A, B, C, D, E, F)에 의해 표시되는, 원뿔형을 고려할 수 있습니다.

Projective definition of a circle

유클리드 기하학의 메트릭(Metrical) 개념 (길이 및 각도를 측정하는 것과 관련된 개념)은 실수 투영 평면으로 즉시 확장될 수 없습니다. 그들은 이 새로운 기하학에서 반드시 재정의 (및 일반화)되어야 합니다. 이것은 임의의 투영 평면(projective plane)에 대해 행해질 수 있지만, 확장된 유클리드 평면으로 실수 투영 평면을 얻기 위해, 일부 특정 선택이 만들어져야 합니다.

절대 직선(absolute line)으로 참조되어야 하는 투영 평면에서 임의의 직선을 고정하십시오. 절대 직선 위에 두 개의 구별되는 점을 선택하고 그들을 절대 점(absolute points)이라고 언급하십시오. 여러가지 메트릭 개념은 이들 선택을 참조하여 정의될 수 있습니다. 예를 들어, 점 A와 B를 포함하는 직선이 주어지면, 선분 AB의 중간점(midpoint)은 A와 B에 관한 절대 직선과 AB의 교차 점의 투영 조화 켤레(projective harmonic conjugate)인 점 C로 정의됩니다.

두 개의 절대 점을 포함하는 투영 평면에서 원뿔형은 원이라고 불립니다. 다섯 점이 원뿔형을 결정하므로, (퇴화될 수 있는) 원은 세 점에 의해 결정됩니다. 확장된 유클리드 평면을 얻기 위해, 절대 직선은 유클리드 평면의 무한대에 직선인 것을 선택되고 절대 점은 무한대에 원형 점(circular points at infinity)이라고 불리는 해당 직선 위의 두 개의 특수 점입니다. 실수 좌표를 가진 두 점을 포함하는 직선은 무한대에 원형 점을 통과하지 않으므로, 유클리드 평면에서 원은, 이 정의 아래에서, 같은-직선(collinear:공선)이 아닌 세 점에 의해 결정됩니다.

유클리드 평면에서 원은 초점-방향선 속성에 의해 절대 정의될 수 없음을 언급해 왔습니다. 어쨌든, 만약 우리가 방향선으로 무한대에 직선을 고려하면, 이심률을 e = 0이 되도록 취함으로써 원은 초점-방향선 속성을 가질 것이지만, 그것은 여전히 그 속성에 의해 정의되지 않습니다. 우리는 이 상황에서 이심률의 정의를 초점에서 원 위의 점 거리 (반지름의 길이)와 방향선에서 그 점의 거리 (이 거리는 무한대입니다)의 (극한 값으로 영을 제공하는) 비율로 올바르게 사용하기 위해 반드시 주의해야 합니다.

Steiner's projective conic definition

Main article: Steiner conic

Definition of the Steiner generation of a conic section

투영 평면에서 원뿔 단면을 정의하기 위한 합성적(synthetic) (좌표-없는) 접근법은 1867년 야코프 슈타이너(Jakob Steiner)에 의해 제공되었습니다.

• 두 점 $U,V$에서 직선의 두 개의 연필 $B(U),B(V)$ 및 $B(U)$를 $B(V)$위로의 투영(projective)이지만 원근(perspective)이 아닌 매핑 $\pi$가 주어졌습니다. 그런 다음 해당하는 직선의 교차 점은 비-퇴화 투영 원뿔 단면을 형성합니다.

연필 $B(U)$를 연필 $B(V)$ 위로의 원근(perspective) 매핑 $\pi$는 해당하는 직선이 관점 $\pi$의 축이라고 불리는 고정된 직선 $a$ 위에 교차하는 것을 만족하는 전단사(bijection) (1-1 대응)입니다.

투영 매핑은 관점 매핑의 유한한 수열입니다.

필드에 걸쳐 투영 평면 (파푸스 평면(pappian plane:파피언 평면)에서 투영 매핑은 세 직선의 이미지를 규정함으로써 고유하게 결정되므로, 원뿔 단면의 슈타이너 생성에 대해, 두 점 $U,V$외에 오직 3 직선의 이미지가 주어져야 합니다. 이들 5 항목 (2 점, 3 직선)은 원뿔 단면을 고유하게 결정합니다.

Line conics

투영 평면에서 이원성 원리(Principle of Duality)에 의해, 각 점의 이중은 직선이고, 점의 자취 (어떤 조건을 만족시키는 점들의 집합)의 이중은 직선의 봉투(envelope)라고 불립니다. 슈타이너의 원뿔형의 정의 (점들의 이 자취는 지금 점 원뿔형(point conic)으로 참조됩니다)를 두 개의 관련된 연필의 해당하는 반직선의 만남으로 사용하면, 다른 기저 (점들이 놓여 있는 직선들) 위에 두 개의 관련된 영역 (직선 위의 점들)의 해당하는 점의 결합으로 구성되는 해당하는 봉투를 쉽게 이중화하고 얻을 수 있습니다. 그러한 봉투는 직선 원뿔형(line conic) (또는 이중 원뿔형(dual conic))이라고 불립니다.

실수 투영 평면에서, 점 원뿔형은 모든 각 직선이 두 점 (그것은 일치할 수 있고, 또는 복소수일 수 있습니다)에서 그것을 만나는 속성을 가지고 이 속성을 가진 점의 임의의 집합은 점 원뿔형입니다. 그것은 이중으로, 직선 원뿔형은 모든 각 점을 통해 그의 직선들의 두 개를 가지고 이 속성을 가진 직선들의 임의의 봉투는 직선 원뿔형이라는 것을 따릅니다. 점 원뿔형의 모든 각 점에서 고유한 접선이 있고, 이중으로, 직선 원뿔형의 모든 각 직선 위에 접촉의 점(point of contact)으로 불리는 고유한 점이 있습니다. 중요한 정리는 점 원뿔형의 접선이 직선 원뿔형을 형성하고, 이중으로, 직선 원뿔형의 접촉의 점이 점 원뿔형을 형성한다고 말합니다.

Von Staudt's definition

Main article: Von Staudt conic

카를 게오르크 크리스티안 폰 슈타우트(Karl Georg Christian von Staudt)는 원뿔형을 절대 점을 가지는 극성(polarity)의 모든 절대 점에 의해 주어진 점으로 정의했습니다. 폰 슈타우트는 투영 기하학에서 모든 메트릭 개념을 제거하기 위한 시도의 일부로 Geometrie der Lage (1847)에서 이 정의를 도입했습니다.

투영 평면, P의 극성(polarity), π는 투사 관계(incidence relation)를 보존하는 P의 점과 직선 사이의 인볼류션(involutory) (즉, 차수 2의) 전단사(bijection)입니다. 따라서 극성은 직선 q를 가진 점 Q를 관련시키고, 다음의 제르곤(Gergonne), q는 Q의 극선(polar)이라고 불리고 Q는 q의 극점(pole)이라고 불립니다. 극성의 절대 점 (직선)은 그의 극선 (극점)과 발생하는 것입니다.

투영 평면에서 폰 슈타우트 원뿔형은 슈타이너 원뿔형(Steiner conic)과 동등합니다.

Constructions

원뿔형의 연속적인 호는 직선자와 컴퍼스와 함께 구성될 수 없습니다. 어쨌든, 호 위의 개별 점의 임의의 숫자에 대해 여러가지 직선자-와-컴퍼스 구성이 있습니다.

그것 중 하나는 파스칼 정리의 역을 기반으로 합니다. 즉, 만약 육각형의 대변들의 교차의 점들이 같은-직선 위에 있지 않으면, 여섯 꼭짓점은 원뿔형 위에 놓입니다. 구체적으로, 다섯 점, A, B, C, D, E 및 E를 통과하는 하나의 직선, 말자하면 EG가 주어지면, 이 직선 위에 있고 다섯 점에 의해 결정된 원뿔형 위에 있는 하나의 점 F는 구성될 수 있습니다. AB는 L에서 DE를 만나고, BC는 M에서 EG를 만나는 것으로 놓고, CD는 N에서 LM을 만나는 것으로 놓습니다. 그런 다음 AN은 요구된 점 F에서 EG를 만납니다. E를 통해 직선을 변화시킴으로써, 원하는 만큼 많이 원뿔형 위의 추가적인 점은 구성될 수 있습니다.

Parallelogram method for constructing an ellipse

슈타이너의 구성을 기반으로 하고 공학 응용에서 유용한, 또 다른 방법은 평행사변형 방법(parallelogram method)이며, 여기서 원뿔형은 수평 직선과 수직 직선 위에 일정한 간격으로 배치된 특정 점을 연결하는 것에 의해 한 점씩 구성됩니다. 구체적으로, 방정식 x²/a² + y²/b² = 1을 가진 타원을 구성하기 위해, 먼저 꼭짓점 A(a, 0), B(a, 2b), C(−a, 2b) 및 D(−a, 0)를 가진 직사각형 ABCD를 구성하십시오. 변 BC를 n 개의 같은 선분으로 나누고, 변 AB 위에 같은 선분을 형성하기 위해 (이들 선분의 길이는 BC 위의 선분의 길이의 b/a배가 될 것입니다), 대각선 AC에 관하여 평행 투영을 사용하십시오. 변 BC 위에 선분의 왼쪽 끝점에, B에서 시작하고 C를 향해서 가면서, A₁에서 A_n까지 라벨링을 하십시오. 변 AB 위에 선분의 위의 끝점에, A에서 시작하고 B를 향해서 가면서, D₁에서 D_n까지 라벨링을 하십시오.1 ≤ i ≤ n에 대해 교차점 AA_i ∩ DD_i는 A와 P(0, b) 사이의 타원의 점일 것입니다. 라벨링은 A를 통해 연필의 직선을 D를 통한 연필의 직선과 투영적이지만 원근적이 아닌 것으로 결합시킵니다. 원뿔형에 대한 추구는 이 구성에 의해 얻어지는데 왜냐하면 세 점 A, D 및 P와 두 접선 (A와 D에서 수직 직선)은 원뿔형을 고유하게 결정하기 때문입니다. 만약 또 다른 지름 (및 그의 켤레 지름)은 타원의 주요 축과 보조 축 대신에 사용되면, 직사각형이 아닌 평행사변형이, 방법이 이름이 제공하는, 구성에서 사용됩니다. 연필의 직선의 결합은 타원 위의 다른 점을 얻기 위해 확장될 수 있습니다. 쌍곡선과 포물선에 대해 구성은 비슷합니다.

또 다른 일반적인 방법은 극성 특성을 사용하여 원뿔형 (하나의 직선 원뿔형)의 접선 봉투를 구성하기 위해 극성 속성을 사용합니다.

In the complex projective plane

복소 평면 C²에서, 타원과 쌍곡선은 구별되지 않습니다: 우리는 쌍곡선을 허수 축 길이를 가진 타원으로 여길 수 있습니다. 예를 들어, 타원 $x^{2}+y^{2}=1$은 치환 $y=iw$, 기하학적으로 복소수 회전 아래에서, $x^{2}-w^{2}=1$를 산출하여, 쌍곡선이 됩니다. 따라서 2-방법 분류: 타원/쌍곡선과 포물선이 있습니다. 곡선을 복소수 투영 평면으로 확장하면, 이것은 (두 점근선에 해당하는) 2 구별되는 점 또는 (포물선의 축에 해당하는) 1 이중 점 중 하나에서 무한대에 직선(line at infinity)을 교차시키는 것에 해당합니다; 따라서 실수 쌍곡선은 복소수 타원/쌍곡선에 대해 보다 암시적인 실수 이미지인데, 왜냐하면 그것은 무한대에 직선을 가진 2 (실수) 교차를 역시 가지기 때문입니다.

복소수 투영 평면(complex projective plane) CP²에서 추가적인 통합이 발생합니다: 비-퇴화 원뿔형은 서로로부터 절대 구별될 수 없는데, 왜냐하면 임의의 것은 투영 선형 변환(projective linear transformation)에 의해 다른 것으로 취할 수 있기 때문입니다.

그것은 CP²에서 입증될 수 있는데, 두 원뿔 단면은 (만약 우리가 중복도(multiplicity)를 설명하면) 공통으로 네 점을 가지므로, 1과 4 사이의 교차(intersection) 점이 있습니다. 교차 가능성은 다음과 같습니다: 네 개의 구별되는 점, 두 특이점 및 하나의 이중 점, 두 개의 이중 점, 하나의 특이점과 중복도 3을 가진 하나의 점, 중복도 4를 가진 하나의 점. 만약 임의의 교차 점이 중복도 > 1이면, 두 곡선은 접한다(tangent)고 말합니다. 만약 적어도 3의 중복도의 교차점이 있으면, 두 곡선은 진동한다(osculating)고 말합니다. 만약 중복도 4를 가진 오직 하나의 교차 점이 있으면, 두 곡선은 초진동한다(superosculating)고 말합니다.

게다가, 각각의 직선(straight line)은 각 원뿔 단면을 두 번 교차합니다. 만약 교차 점이 두 배이면, 직선은 접선(tangent line)입니다. 무한대에 직선과 교차하면, 각 원뿔 단면은 무한대에 두 점을 가집니다. 만약 이들 점이 실수라면, 곡선은 쌍곡선(hyperbola)입니다; 만약 그것들이 허수 켤레라면, 그것은 타원(ellipse)입니다; 만약 오직 하나의 이중 점이 있으면, 그것은 포물선(parabola)입니다. 만약 무한대에 점이 순환 점(cyclic points) (1, i, 0) 및 (1, –i, 0)이면, 원뿔 단면은 원(circle)입니다. 만약 원뿔 단면의 계수가 실수이면, 무한대에 점은 실수 또는 복소수 켤레(complex conjugate) 중 하나입니다.

Degenerate cases

Further information: Degenerate conic

원뿔형의 퇴화 경우(degenerate case)로 고려해야 할 것은 사용되어진 정의와 원뿔 단면에 대해 기하학적 설정에 달려 있습니다. 원뿔형을 이-차원 비-퇴화 이차-초곡면으로 정의하는 일부 저자들이 있습니다. 이 용어와 함께, 퇴화 원뿔형 (오직 퇴화 이차-초곡면)은 없지만, 우리는 보다 전통적인 용어를 사용해야 하고 그 정의를 피해야 합니다.

유클리드 평면에서, 기하학적 정의를 사용하면, 퇴화 경우는 자르는 평면이 원뿔의 꼭대기(apex:꼭짓점)를 통과할 때 발생합니다. 퇴화 원뿔형은 다음 중 하나입니다: 평면이 오직 꼭대기에서 원뿔과 교차할 때, 하나의 점(point); 평면이 원뿔에 접할 때 (그것은 원뿔의 정화히 하나의 생성기를 포함합니다), 하나의 직선(straight line); 또는 한 쌍의 교차하는 직선 (원뿔의 두 생성기). 이들은 타원, 포물선, 및 쌍곡선의 극한적인 형태에 각각 해당합니다.

만약 유클리드 평면에서 원뿔형이 이차 방정식의 영들 (즉, 이차-초곡면)에 의해 정의되는 것이면, 퇴화 원뿔형은 다음과 같습니다: 빈 집합(empty set), 하나의 점 또는 평행, 한 점에서 교차하는, 또는 일치할 수 있는 한 쌍의 직선. 빈 집합 경우는 방정식 $x^{2}+1=0$와 같은 복소수 켤레(complex conjugate) 평행선의 쌍, 또는 방정식 $x^{2}+y^{2}+1=0$와 같은 허수 타원(imaginary ellipse)에 해당할 수 있습니다. 허수 타원은 퇴화성의 일반적인 정의를 만족시키지 못하고 따라서 통상적으로 퇴화된 것으로 여겨지지 않습니다. 두 직선 경우는 이차 표현이 두 개의 선형 인수로 인수화될 때 발생하며, 각각의 영들은 직선을 제공합니다. 인수가 같은 경우에서, 해당하는 직선은 일치하고 우리는 직선을 이중(double) 직선 (중복도(multiplicity) 2를 가진 직선)으로 그 직선을 참조하고 이것은 접하는 자르는 평면의 이전 경우입니다.

실수 투영 평면에서, 평행 직선은 무한대에 직선 위에 한 점에서 만나므로, 유클리드 평면의 평행 직선 경우는 교차하는 직선으로 보일 수 있습니다. 어쨌든, 교차의 점이 원뿔의 꼭대기이기 때문에, 원뿔 그 자체는 원기둥(cylinder), 즉 무한대에 꼭대기를 가진 것으로 불립니다. 이 경우에서 다른 단면은 원기둥 단면(cylindric sections)이라고 불립니다. 비-퇴화 원기둥 단면은 타원 (또는 원)입니다.

복소수 투영 평면의 원근으로부터 보일 때, 실수 이차-초곡면의 퇴화 경우 (즉, 이차 방정식은 실제 계수를 가집니다)는 모두, 아마도 일치할 수 있는, 한 쌍의 직선으로 여겨집니다. 빈 집합은 이중 직선으로 여겨지는 무한대에 직선일 수 있으며, 하나의 (실수) 점은 두 복소수 켤레 직선(complex conjugate line)의 교차 및 이전에 언급된 것처럼 다른 경우입니다.

행렬 표기법을 사용하여, 퇴화 경우를 비-퇴화 경우 (후자와 함께 빈 집합을 포함하는)와 구별하기 위해, β를 원뿔 단면의 3×3 행렬의 행렬식–즉, β = (AC − B²/4)F + BED − CD² − AE²/4로 놓습니다; 그리고 α = B² − 4AC를 판별식으로 놓습니다. 그런 다음 원뿔 단면이 비-퇴화인 것과 β ≠ 0인 것은 필요충분 조건입니다. 만약 β = 0이면, 우리는 α < 0일 때 하나의 점, α = 0일 때 두 평행 직선 (아마도 일치할 수 있는), 또는 α > 0일 때 두 교차하는 직선입니다.

Pencil of conics

(비-퇴화) 원뿔형은 평면에서 (세 같은-직선은 없는) 일반 위치에서 다섯 점(five points)에 의해 완전하게 결정되고 (다시 평면에서 및 세 같은-직선 없는) 네 점의 고정된 집합를 통과하는 원뿔형의 시스템은 원뿔형의 연필(pencil of conics)이라고 불립니다. 네 공통 점은 연필의 기저 점(base points)이라고 불립니다. 기저 점 이외의 임의의 점을 통해, 연필의 하나의 원뿔형을 통과합니다. 이 개념은 원의 연필(pencil of circles)을 일반화합니다.

대수적으로 닫힌 필드(algebraically closed field)에 걸쳐 정의된 투영 평면(projective plane)에서, 임의의 두 원뿔형은 (중복도와 함께 세어서) 네 점에서 만나고 그래서, 이들 네 점을 기반으로 원뿔형의 연필을 결정합니다. 게다가, 네 기저 점은 세 직선 쌍 (기저 점을 통한 퇴화 원뿔형(degenerate conic), 정확히 두 기저 점을 포함하는 쌍의 각 직선)을 결정하고 그래서 원뿔형의 각 연필은 최대 세 퇴화 원뿔형을 포함할 것입니다.

원뿔형의 연필은 다음 방법으로 대수적으로 표현될 수 있습니다. C₁ 및 C₂를 대수적으로 닫힌 필드 K에 걸쳐 정의된 투영 평면에서 두 구별되는 원뿔형으로 놓습니다. K의, 둘 다 영이 아닌, 원소의 모든 각 쌍 λ, μ에 대해, 표현

$\lambda C_{1}+\mu C_{2}$

은 C₁ 및 C₂에 의해 결정된 연필에서 원뿔형을 나타냅니다. 이 기호적 표현은 (같은 표기법을 사용하여 대상과 마찬가지로 대상을 정의하는 방정식을 나타내기 위해) 약간의 표기법의 남용을 구체적으로 만들 수 있습니다. 말하자면, C₁을 세-부분으로-구성된(ternary) 이차 형식(quadratic form)으로 생각하면, C₁ = 0은 "원뿔형 C₁"의 방정식입니다. 또 다른 구체적인 실현은 C₁을 그것을 나타내는 3x3 대칭 행렬(3×3 symmetric matrix)로 생각함으로써 얻어질 수 있습니다. 만약 C₁ 및 C₂가 그러한 구체적인 실현을 가지고 있으면, 위 연필의 모든 각 구성원은 마찬가지일 것입니다. 그 설정은 투영 평면에서 동차 좌표를 사용하므로, 두 구체적인 표현 (방정식 또는 행렬)은 만약 그들이 비-영 곱셈의 상수에 의해 다르면 같은 원뿔형을 제공합니다.

Intersecting two conics

두 변수에서 두 이차 방정식의 시스템에 대한 해는 두 일반적인 원뿔 단면의 교차의 점의 좌표로 보일 수 있습니다. 특히, 두 원뿔형은 없는 것, 둘 또는 네 가능한 일치하는 교차 점을 가질 수 없습니다. 이들 해를 찾는 효율적인 방법은 원뿔 단면의 동차 행렬 표현(homogeneous matrix representation of conic sections), 즉 여섯 매개변수에 의존하는 3x3 대칭 행렬(symmetric matrix)를 활용합니다.

교차 점을 찾는 절차는 이들 단계를 따릅니다, 여기서 원뿔형은 행렬로 표현됩니다:

• 두 원뿔형 $C_{1}$ 및 $C_{2}$가 주어지면, 선형 조합 $\lambda C_{1}+\mu C_{2}$에 의해 주어진 원뿔형의 연필을 생각하십시오.
• 연필의 퇴화 원뿔형에 해당하는 동차 매개변수 $(\lambda ,\mu )$을 식별하십시오. 이것은 $\det(\lambda C_{1}+\mu C_{2})=0$인 조건을 두고 $\lambda$와 $\mu$에 대해 해결함으로써 행해질 수 있습니다. 이들은 삼차 방정식의 해가 되는 것으로 밝혀졌습니다.
• 퇴화 원뿔형 $C_{0}$가 주어지면, 그것을 구성하는 두 개의, 아마도 일치할 수 있는, 직선을 식별하십시오.
• 각각의 식별된 직선을 두 원래의 원뿔형 중 하나와 교차시키십시오; 이 단계는 $C_{0}$의 이중 원뿔형 표현을 사용하여 효율적으로 행해질 수 있습니다.
• 교차의 점은 초기 방정식 시스템에 대한 해로 나타날 것입니다.

Generalizations

원뿔형은 다른 필드에 걸쳐 (즉, 다른 파푸스 기하학(pappian geometries)에서) 정의될 수 있습니다. 어쨌든, 그 필드가 특성(characteristic) 2를 가질 때 일부 주의를 기울여야 하는데, 왜냐하면 일부 공식은 사용될 수 없기 때문입니다. 예를 들어, 위에서(above) 사용된 행렬 표현은 2로 나누어야 합니다.

투영 평면에서 비-퇴화 원뿔형의 일반화는 달걀-모양(oval)입니다. 달걀-모양은 다음 속성을 가진 점 집합입니다, 이것은 원뿔형에 의해 보유됩니다: 1) 임의의 직선은 없음, 하나 또는 둘 점에서 달걀-모양과 교차합니다. 2) 달걀-모양의 임의의 점에서 고유한 접선이 존재합니다.

두 개보다 많은 초점이 있는 경우에 대한 원뿔형의 초점 속성을 일반화하는 것은 일반화된 원뿔형(generalized conic)이라고 불리는 집합을 생성합니다.

In other areas of mathematics

타원, 포물선, 및 쌍곡선으로의 분류는 수학에 널리 퍼져 있고, 필드를 매우 날카롭게 구별되는 부분-필드로 종종 나눕니다. 분류는 이차 형식 (두 변수에서 이것은 결합된 판별식(discriminant)에 해당합니다)의 존재로 인해 주로 발생하지만, 이심률에 역시 해당할 수 있습니다.

이차 형식 분류:

이차 형식(Quadratic form)들

실수에 걸쳐 이차 형식은 실베스터의 관성 법칙(Sylvester's law of inertia), 즉, 그들의 양의 인덱스, 영 인덱스, 및 음의 인덱스에 의해 분류됩니다: n 변수에서 이차 형식은 대각선 형식(diagonal form), $x_{1}^{2}+x_{2}^{2}+\cdots +x_{k}^{2}-x_{k+1}^{2}-\cdots -x_{k+\ell }^{2}$으로 변환될 수 있으며, 여기서 +1 계수의 숫자, k는 양의 인덱스, −1 계수의 숫자, ℓ은 음의 인덱스, 및 남아있는 변수는 영 인덱스 m이므로, $k+\ell +m=n$입니다. 두 변수에서, 비-영 이차 형식은 다음으로 분류됩니다:

• $x^{2}+y^{2}$ – 타원에 해당하는, 양수-한정(definite) (음수는 역시 포함됩니다),
• $x^{2}$ – 포물선에 해당하는, 퇴화, 및
• $x^{2}-y^{2}$ – 쌍곡선에 해당하는, 비-한정(indefinite:부정).

두 변수에서, 이차 형식은, 원뿔형과 유사하게, 판별식에 의해 분류되지만, 더 큰 차원에서 보다 유용한 분류는 한정(definite) (모든 양수 또는 모두 음수), 퇴화(degenerate) (일부 영들), 또는 비-한정(indefinite) (양수와 음수가 섞여있지만 영은 제외)입니다. 이 분류는 따르는 많은 것들의 기초가 됩니다.

곡률

표면(surface)의 가우스 곡률(Gaussian curvature)은 무한소 기하학을 설명하고, 각 지점에서 양수 – 타원 기하학(elliptic geometry), 영 – 유클리드 기하학(Euclidean geometry) (평지, 포물선), 또는 음수 – 쌍곡선 기하학(hyperbolic geometry)이 될 수 있습니다; 무한소적으로, 이차 표면은 $x^{2}+y^{2}$, $x^{2}$ (또는 0), 또는 $x^{2}-y^{2}$의 그래프처럼 보입니다. 실제로, 균일화 정리(uniformization theorem)에 의해, 모든 각 표면은 전체적으로 (모든 각 점에서) 양의 구부러진, 평지, 또는 음의 구부러진 것이 될 수 있습니다. 더 큰 차원에서, 리만 곡률 텐서(Riemann curvature tensor)는 보다 복잡한 대상이지만, 상수 단면의 곡률을 가진 매니폴드(manifolds with constant sectional curvature)는 흥미로운 연구의 대상이고, 단면의 곡률(sectional curvature)에서 토론한 것처럼, 놀랍도록 다른 속성을 가집니다.

이차 PDE들

이차(second order)의 부분 미분 방정식(Partial differential equation) (PDE)은 각 점에서 타원, 포물선, 또는 쌍곡선으로 분류되며, 그에 따라 그들의 이차 항은 타원, 포물선, 또는 쌍곡선 이차 형식에 해당합니다. PDF의 이들 다른 유형의 동작과 이론은 놀랍게도 다릅니다 – 대표적인 예제는 푸아송 방정식(Poisson equation)은 타원, 열 방정식(heat equation)은 포물선, 파동 방정식(wave equation)이 쌍곡선이라는 것입니다.

이심률 분류(Eccentricity classifications)는 다음을 포함합니다:

뫼비우스 변환(Möbius transformation)들

실수 뫼비우스 변환 (PSL₂(R) 또는 그의 2-폴드 덮개, SL₂(R)의 원소)은 타원, 포물선, 또는 쌍곡선으로 분류(classified)되며, 그에 따라 그들의 반-트레이스는 이심률에 의한 분류를 반사하는 $0\leq |\operatorname {tr} |/2<1$, $|\operatorname {tr} |/2=1$, 또는 $|\operatorname {tr} |/2>1$입니다.

분산-대-평균 비율(Variance-to-mean ratio)

분산-대-평균 비율은 이산 확률 분포(discrete probability distribution)의 여러-가지 중요한 가족을 분류합니다: 원형으로 상수 분포 (이심률 0), 타원형으로 이항 분포(binomial distribution), 포물선형으로 푸아송 분포(Poisson distribution), 및 쌍곡선형으로 음의 이항 분포(negative binomial distribution) 등이 있습니다. 이것은 일부 이산 확률 분포의 누적(cumulants of some discrete probability distributions)에서 정교화됩니다.

In this interactive SVG, move left and right over the SVG image to rotate the double cone

See also

• Circumconic and inconic
• Conic Sections Rebellion, protests by Yale university students
• Director circle
• Elliptic coordinate system
• Equidistant set
• Nine-point conic
• Parabolic coordinates
• Quadratic function

References

• Akopyan, A.V.; Zaslavsky, A.A. (2007). Geometry of Conics. American Mathematical Society. ISBN 978-0-8218-4323-9.
• Artzy, Rafael (2008) [1965], Linear Geometry, Dover, ISBN 978-0-486-46627-9
• Boyer, Carl B. (2004) [1956], History of Analytic Geometry, Dover, ISBN 978-0-486-43832-0
• Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1999), Geometry, Cambridge University Press, ISBN 978-0-521-59787-6
• Coxeter, H.S.M. (1964), Projective Geometry, Blaisdell, ISBN 9780387406237
• Coxeter, H.S.M. (1993), The Real Projective Plane, Springer Science & Business Media
• Downs, J.W. (2003) [1993], Practical Conic Sections: The geometric properties of ellipses, parabolas and hyperbolas, Dover, ISBN 0-486-42876-1
• Eves, Howard (1963), A Survey of Geometry (Volume One), Boston: Allyn and Bacon
• Hartmann, Erich, Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes (PDF), retrieved 20 September 2014 (PDF; 891 kB).
• Katz, Victor J. (1998), A History of Mathematics / An Introduction (2nd ed.), Addison Wesley Longman, ISBN 978-0-321-01618-8
• Kendig, Keith (2005), Conics, The Mathematical Association of America, ISBN 978-0-88385-335-1
• Faulkner, T. E. (1952), Projective Geometry (2nd ed.), Edinburgh: Oliver and Boyd
• Merserve, Bruce E. (1983) [1959], Fundamental Concepts of Geometry, Dover, ISBN 0-486-63415-9
• Protter, Murray H.; Morrey, Jr., Charles B. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, LCCN 76087042
• Samuel, Pierre (1988), Projective Geometry, Undergraduate Texts in Mathematics (Readings in Mathematics), New York: Springer-Verlag, ISBN 0-387-96752-4
• Thomas, George B.; Finney, Ross L. (1979), Calculus and Analytic Geometry (fifth ed.), Addison-Wesley, p. 434, ISBN 0-201-07540-7
• Wilson, W.A.; Tracey, J.I. (1925), Analytic Geometry (Revised ed.), D.C. Heath and Company

External links

• Conic section (Geometry) at Encyclopædia Britannica
• Can You Really Derive Conic Formulae from a Cone? archive 2007-07-15 Gary S. Stoudt (Indiana University of Pennsylvania
• Conic sections at Special plane curves.
• Weisstein, Eric W. "Conic Section". MathWorld.
• Occurrence of the conics. Conics in nature and elsewhere.
• See Conic Sections at cut-the-knot for a sharp proof that any finite conic section is an ellipse and Xah Lee for a similar treatment of other conics.
• Eight Point Conic at Dynamic Geometry Sketches
• Second-order implicit equation locus An interactive Java conics grapher; uses a general second-order implicit equation.