Mathematical constant

Original article: w:Mathematical constant

For broader coverage of this topic, see Constant (mathematics).

수학적 상수는 그것의 값이 모호하지 않은 정의에 의해 고정된 핵심 숫자(number)이며, 종종 기호 (예를 들어, 알파벳 문자(alphabet letter)) 또는 여러 수학적 문제(mathematical problem)에 걸쳐 그것을 사용하여 용이하게 하기 위해 수학자의 이름에 의해 참조됩니다. 상수는 수학(mathematics)의 많은 영역에서 발생하며, e와 π와 같은 상수는 기하학(geometry), 숫자 이론(number theory), 및 미적분(calculus)과 같은 다양한 문맥에서 발생합니다.

상수에 대해 "자연적으로" 발생하는 것이 무엇을 의미하는지, 및 상수를 "흥미롭게" 만드는 것이 무엇인지는, 궁극적으로 기호의 문제이며, 단지 일부 수학 상수는 내재적인 수학적 흥미보다는 역사적인 이유로 더 유명합니다. 보다 유명한 상수는 여러 연대에 걸쳐 연구되어 왔고 많은 십진 자리까지 계산됩니다.

모든 이름-지은 수학적 상수는 정의-가능 숫자(definable numbers)이고, 보통 역시 계산-가능 숫자(computable number)입니다 (카이틴의 상수(Chaitin's constant)는 중요한 예외입니다).

Basic mathematical constants

이것들은 많은 국가에서 대학-이전 교육 동안 만날 가능성이 있는 상수입니다.

Archimedes' constant π

Main article: Pi

The circumference of a circle with diameter 1 is π.

상수 π (파이)는 유클리드 기하학(Euclidean geometry)에서 자연스러운 정의(definition) (원의 둘레(circumference)와 지름(diameter) 사이의 비율)를 가지지만, 수학의 많은 곳에서 발견될 수 있습니다: 예를 들어, 복소 해석학(complex analysis)에서 가우스 적분(Gaussian integral), 숫자 이론(number theory)에서 단위원의 근(roots of unity), 및 확률(probability)에서 코시 분포(Cauchy distribution), 등에서 발견됩니다. 어쨌든, 그것의 편재성은 순수한 수학에 국한되지 않습니다. 그것은 물리학에서 많은 공식에 나타나고, 여러 물리적 상수(physical constant)는 π 또는 그 역수를 인수화해서 가장 자연스럽게 정의됩니다. 어쨌든, 그러한 모습이 어떤 의미에서든 근본적인 것인지 여부는 논쟁의 여지가 있습니다. 예를 들어, 교과서 수소 원자의 비-상대론적 기저 상태 파동 함수는 다음입니다:

$\psi (\mathbf {r} )={\frac {1}{(\pi a_{0}^{3})^{1/2}}}e^{-r/a_{0}},$

여기서 $a_{0}$는 보어 반지름입니다. 이 공식은 π를 포함하지만, 그것이 물리적 의미에서 근본적인지, 또는 그것이 단지 (반지름 $r$을 갖는 구의 표면 넓이에 대해) 표현 ${4\pi r^{2}}$에서 π를 반영하는 것인지 분명하지 않습니다.

게다가, 이 공식은 물리적 현실의 오직 근사적 설명을 제공하는데, 왜냐하면 그것은 전자기 필드(electromagnetic field) 자체의 스핀, 상대성, 및 양자 본성을 생략하기 때문입니다. 마찬가지로, SI 단위에서 쿨롱의 법칙(Coulomb's law)에 대한 공식에서 π의 출현은 단위의 해당 선택에 의존하고, 소위 자유 공간의 유전율(permittivity of free space)이 1901년에 조반니 조르지(Giovanni Giorgi)에 의해 전자기의 실행에 어떻게 도입되는 방법과 함께 관련된 역사적인 사고입니다. 일단 다양한 상수가 하나의 관계에서 선택되면, 다른 관계에서 π의 출현은 피할 수 없지만, 그 출현은 항상 위의 수소 원자 파동 함수의 예제에서와 같이 수학적 이유로 인한 것이지 물리적 이유는 아니라는 것이 진실입니다.

π의 숫자 값은 근사적으로 3.1415926536 (OEIS에서 수열 A000796)입니다. π의 점점 더 정확한 자릿수를 암기하는 것은 세계 기록의 추구입니다.

The imaginary unit i

Main article: Imaginary unit

i in the complex or Cartesian plane. Real numbers lie on the horizontal axis, and imaginary numbers lie on the vertical axis

허수 단위 또는 단위 허수 숫자는, i로 표시되며, 실수(real number) 시스템 ℝ을 복소수(complex number) 시스템 ℂ로 확장하고, 이것은 차례로 모든 각 다항식(polynomial) P(x)에 대해 적어도 하나의 근(root)을 제공하는 수학적(mathematical) 개념입니다 (대수적 닫힘(algebraic closure)과 대수학의 기본 정리(fundamental theorem of algebra)를 참조하십시오). 허수 단위의 핵심 속성은 i² = −1이라는 것입니다. 여기서, 용어 "허수(imaginary)"가 사용되는데 왜냐하면 음의 제곱(square)을 가지는 실수(real number)가 없기 때문입니다.

사실, 마치 모든 각 다른 모든 실수의 두 복소 제곱근이 있는 것처럼, −1의 두 복소 제곱근, 즉 i과 −i가 있습니다 (영zero)을 제외하며, 이것은 하나이 이중 제곱근을 가집니다).

i가 모호하거나 문제되는 문맥에서, j 또는 그리스어 ι가 때때로 사용됩니다 (see 대안 표기법(alternative notations)을 참조하십시오). 전기 공학(electrical engineering)과 제어 시스템 공학(control systems engineering)의 분야에서, 허수 단위는 종종 i 대신 j로 표시되는데, 왜냐하면 i는 이러한 분야에서 공통적으로 전류(electric current)를 나타내기 위해 사용되기 때문입니다.

Euler's number e

Main article: e (mathematical constant)

Exponential growth (green) describes many physical phenomena.

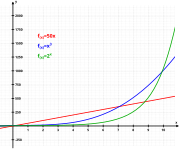
오일러의 숫자(Euler's number) e는, 역시 지수 성장(exponential growth) 상수라고 알려져 있으며, 수학의 많은 영역에서 나타나고, 그것의 가능한 정의 중 하나는 다음 식의 값입니다:

$e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$

예를 들어, 스위스(Swiss) 수학자 야콥 베르누이(Jacob Bernoulli)는 e가 복리(compound interest)에서 발생하는 것을 발견했습니다: $1에서 시작하고, 연속 복리를 갖는 연이율 R로 이자를 산출하는 계정은 일년 말에서 e^R 달러로 누적될 것입니다.

상수 e는 역시 확률 이론(probability theory)에서 응용을 가지며, 여기서 그것은 지수적 성장과 분명히 관련이 없는 방법에서 발생합니다. 예제로서, n에서 일 승리의 확률을 갖는 슬롯 머신은 n 번 플레이된다고 가정하면, 큰 n (예를 들어, 백만)에 대해, 어떤 것도 이기지 않을 확률(probability)은 n이 무한대 경향일 때 1/e 경향일 것입니다.

e의 또 다른 응용은, 프랑스(French)의 수학자 피에르 레몽 드 몽모르(Pierre Raymond de Montmort)와 함께 야곱 베르누이(Jacob Bernoulli)에 의해 부분적으로 발견되며, 교란(derangement)의 문제에 있으며, 역시 모자 확인 문제로 알려져 있습니다. 여기서, n 명의 손님이 파티에 초대되고, 문에서 각 손님은 집사와 함께 자신의 모자를 확인하고, 그런-다음 그것들을 레이블-붙인 상자에 넣습니다. 집사는 손님의 이름을 모르고, 따라서 그것들을 무작위로 선택된 상자에 넣어야 합니다. 드 몽모르(de Montmort)의 문제는 이것입니다: 모자가 올바른 상자에 들어가지 않을 확률은 얼마입니까? 그 답은 다음입니다:

$p_{n}=1-{\frac {1}{1!}}+{\frac {1}{2!}}-{\frac {1}{3!}}+\cdots +(-1)^{n}{\frac {1}{n!}}$

이것은, n이 무한대 경향일 때, 1/e로 접근합니다.

e의 숫자 값은 대략적으로 2.7182818284입니다 (OEIS에서 수열 A001113).

Pythagoras' constant √2

Main article: Square root of 2

The square root of 2 is equal to the length of the hypotenuse of a right-angled triangle with legs of length 1.

2의 제곱근(square root of 2)은, 종종 루트 2, 제곱근 2, 또는 피타고라스의 상수로 알려져 있고, √2로 쓰이며, 자체와 곱해질 때, 숫자 2를 제공하는 양의 대수적 숫자(algebraic number)입니다. 그것은 보다 정확하게 2의 주요 제곱근(principal square root of 2)라고 불리며, 같은 속성을 갖는 음수로부터 그것을 구별하기 위함입니다.

기하학적으로 2의 제곱근(square root)은 일 단위 길이의 변을 갖는 정사각형을 가로지르는 대각선의 길이입니다; 이것은 피타고라스 정리(Pythagorean theorem)를 따릅니다. 그것은 아마도 무리수(irrational)인 것으로 알려진 첫 번째 숫자였을 것입니다. 그것의 65 십진 자리(decimal places)에서 잘린 숫자 값은 다음입니다:

1.41421356237309504880168872420969807856967187537694807317667973799... (OEIS에서 수열 A002193).

The square root of 2.

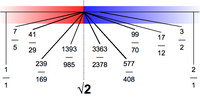
대안적으로, 이의 제곱근에 대해 빠른 근사 99/70 (≈ 1.41429)는 자주 사용됩니다. 오직 70의 분모(denominator)를 가짐에도 불구하고, 그것은 정확한 값과 1/10,000 미만 (근사적으로 7.2 × 10 ⁻⁵)만큼 다릅니다.

Theodorus' constant √3

Main article: Square root of 3

Constants in advanced mathematics

이것들은 고등 수학(higher mathematics)에서 자주 접하는 상수입니다.

The Feigenbaum constants α and δ

Main article: Feigenbaum constants

Bifurcation diagram of the logistic map.

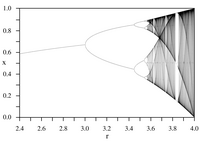
연속 맵의 반복은 동역학적 시스템(dynamical system)에 대해 모델의 가장 간단한 예제로 쓰입니다. 수학적 물리학자 미철 파이겐봄(Mitchell Feigenbaum)의 이름을 따서 지은, 둘의 파이겐봄 상수(Feigenbaum constants)는 그러한 반복 과정에 나타납니다: 그것들은 이차 최대 점과 분기 다이어그램(bifurcation diagram)을 갖는 로지스틱 맵(logistic map)의 수학적 불변입니다.

로지스틱 맵은 다항식(polynomial) 매핑이며, 매우 단순한 비-선형(non-linear) 동역학적 방정식에서 혼란스러운 행동이 어떻게 발생할 수 있는지의 원형 예제로 종종 인용됩니다. 그 맵은 호주 생물학자 로버트 메이(Robert May)에 의해 생산적인 1976년 논문에서, 피에르 프랑수아 베르훌스트(Pierre François Verhulst)에 의해 처음 생성된 로지스틱 방정식과 유사한 이산-시간 인구통계학의 모델로 부분에서 대중화되었습니다. 차이 방정식은 번식과 기아의 두 효과를 포착하기 위해 의도됩니다.

α의 숫자 값은 근사적으로 2.5029입니다. δ의 숫자 값은 근사적으로 4.6692입니다.

Apéry's constant ζ(3)

Main article: Apéry's constant

아페리 상수는 다음 급수(series)의 합입니다:

$\zeta (3)=1+{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}+{\frac {1}{4^{3}}}+\cdots$

아페리의 상수는 무리수(irrational number)이고 그것의 숫자 값은 근사적으로 1.2020569입니다.

리만 제타 함수(Riemann zeta function)의 특별한 값임에도 불구하고, 아페리 상수는 양자 전기역학(quantum electrodynamics)을 사용하여 계산된 전자(electron)의 자이로자기 비율(gyromagnetic ratio)의 이차와 삼차 항을 포함하여 여러 물리적 문제에서 자연스럽게 발생합니다.

The golden ratio φ

Main article: Golden ratio

Golden rectangles in a regular icosahedron

$F_{n}={\frac {\varphi ^{n}-(1-\varphi )^{n}}{\sqrt {5}}}$

An explicit formula for the nth Fibonacci number involving the golden ratio φ.

숫자 φ는, 역시 황금 비율(golden ratio)이라고 불리며, 기하학(geometry), 특히 오각 대칭(symmetry)을 가진 그림에서 자주 나타납니다. 실제로, 정규 오각형(pentagon)의 대각선(diagonal)의 길이는 φ 곱하기 변의 길이입니다. 정규 이십면체(icosahedron)의 꼭짓점은 셋의 서로 직교(orthogonal)하는 황금 사각형(golden rectangle)의 꼭짓점입니다. 역시, 그것은 재귀(recursion)에 의한 성장과 관련하여, 피보나치 수열(Fibonacci sequence)에 나타납니다. 케플러(Kepler)는 그것이 연속적인 피보나치 숫자의 비율의 극한임을 입증했습니다. 황금 비율은 임의의 무리수 중에서 가장 느리게 수렴을 가집니다. 그것은, 해당 이유로, 라그랑주의 근사 정리(Lagrange's approximation theorem)의 최악의 경우(worst cases) 중 하나이고 디오판토스 근사(Diophantine approximation)에 대한 후르비츠 부등식(Hurwitz inequality)의 극단적인 경우입니다. 이것이 황금 비율에 가까운 각도가 종종 잎차례(phyllotaxis) (식물의 성장)에 나타나는 이유일 수 있습니다. 그것은 근사적으로 1.6180339887498948482, 또는 더 정확하게 2⋅sin(54°) = $\scriptstyle {\frac {1+{\sqrt {5}}}{2}}$와 같습니다.

The Euler–Mascheroni constant γ

Main article: Euler–Mascheroni constant

The area between the two curves (red) tends to a limit.

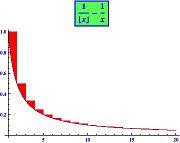
오일러–마스케로니 상수(Euler–Mascheroni constant)는 숫자 이론(number theory)에서 되풀이하는 상수입니다. 벨기에(Belgian)의 수학자 샤를 장 드 라 발레-푸생(Charles Jean de la Vallée-Poussin)은 1898년에 임의의 양의 정수 n을 취하고 n보다 작은 각 양의 정수 m으로 나눌 때, 몫 n/m이 다음 정수에 미치지 못하는 것에 의한 평균(average) 분수가, n이 무한대(infinity)로 가는 경향일 때, $\gamma$ (0.5가 아님) 경향이 있음을 입증했습니다. 오일러–마스케로니 상수는 역시 메르텐스의 세 번째 정리(Merten's third theorem)에 나타나고 감마 함수(gamma function), 제타 함수(zeta function) 및 많은 다른 적분(integral)과 급수(series)와 관련을 가집니다. 오일러–마스케로니 상수의 정의는 이산(discrete)과 연속(continuous) 사이의 밀접한 연결을 나타냅니다 (왼쪽의 곡선을 참조하십시오).

$\gamma$의 숫자 값은 근사적으로 0.57721입니다.

Conway's constant λ

Main article: Conway's constant

${\begin{matrix}1\\11\\21\\1211\\111221\\312211\\\vdots \end{matrix}}$

Conway's look-and-say sequence

콘웨이의 상수(Conway's constant)는 보고-말하기 수열(look-and-say sequence)과 유사한 모든 파생된 문자열(derived string)의 불변 성장률입니다 (하나의 자명한 수열은 제외합니다).

그것은 정수 계수를 갖는 차수 71의 다항식(polynomial)의 고유한 양의 실수 근으로 주어집니다.

λ의 값은 근사적으로 1.30357입니다.

Khinchin's constant K

Main article: Khinchin's constant

만약 실수 r이 단순 연속된 분수(simple continued fraction)로 쓰입니다:

$r=a_{0}+{\dfrac {1}{a_{1}+{\dfrac {1}{a_{2}+{\dfrac {1}{a_{3}+\cdots }}}}}},$

여기서 a_k는 모든 k에 대해 자연수(natural number)이며, 그런-다음, 러시아의 수학자 알렉산드르 케인체인(Aleksandr Khinchin)이 1934년에 증명했듯이, n이 기하 평균(geometric mean)의 무한대(infinity)로 경향일 때 극한(limit): (a₁a₂...a_n)^1/n이 존재하고 측정(measure) 0의 집합을 제외하고 하나의 상수, 케인체인의 상수(Khinchin's constant)입니다.

K의 숫자 값은 근사적으로 2.6854520010입니다.

The Glaisher–Kinkelin constant A

Main article: Glaisher–Kinkelin constant

글레이셔–킨켈린 상수(Glaisher–Kinkelin constant)는 다음 극한(limit)으로 정의됩니다:

$A=\lim _{n\rightarrow \infty }{\frac {\prod _{k=1}^{n}k^{k}}{n^{n^{2}/2+n/2+1/12}e^{-n^{2}/4}}}$

그것은 리만 제타 함수(Riemann zeta function)의 도함수에 대해 많은 표현에서 나타나는 중요한 상수입니다. 그것은 근사적으로 1.2824271291의 숫자 값을 가집니다.

Mathematical curiosities and unspecified constants

Simple representatives of sets of numbers

This Babylonian clay tablet gives an approximation of the square root of 2 in four sexagesimal figures: 1; 24, 51, 10, which is accurate to about six decimal figures.

$c=\sum _{j=1}^{\infty }10^{-j!}=0.\underbrace {\overbrace {110001} ^{3!{\text{ digits}}}000000000000000001} _{4!{\text{ digits}}}000\dots$

Liouville's constant is a simple example of a transcendental number.

2의 제곱근(square root of 2), 리우빌의 상수(Liouville's constant), 및 챔퍼나운 상수(Champernowne constant)와 같은 일부 상수는:

$C_{10}=0.{\color {blue}{1}}2{\color {blue}{3}}4{\color {blue}{5}}6{\color {blue}{7}}8{\color {blue}{9}}10{\color {blue}{11}}12{\color {blue}{13}}14{\color {blue}{15}}16\dots$

중요한 수학적 불변량은 아니지만 특수한 숫자 집합, 각각 무리수(irrational number), 초월적 숫자(transcendental number), 및 정규 숫자(normal number) (밑수 10)의 단순 대표라는 점에 관심이 있습니다. 무리수(irrational number)의 발견은 보통 2의 제곱근의 무리성을 기하학적으로 증명한 피타고라스학파(Pythagorean) 메타폰툼의 히파수스(Hippasus of Metapontum)로 공인됩니다. 프랑스 수학자 조제프 리우빌(Joseph Liouville)의 이름을 따서 지은 리우빌의 상수에 관해서는, 그것이 초월적인 것으로 입증된 최초의 숫자였습니다.

Chaitin's constant Ω

알고리듬 정보 이론(algorithmic information theory)의 컴퓨터 과학(computer science) 하위-분야에서, 카이틴의 상수(Chaitin's constant)는 무작위로 선택된 튜링 기계가 정지할 확률을 나타내는 실수로, 아르헨티나계 미국인 수학자이자 컴퓨터 과학자, 그레고리 카이틴(Gregory Chaitin)에 의해 구성되었습니다. 카르틴의 상수는, 비록 계산가능하지 않지만, 초월적(transcendental)이고 정규(normal)인 것으로 입증되어 왔습니다. 카르틴의 상수는, 튜링 기계에 사용되는 숫자 인코딩에 크게 의존하기 때문에 보편적이지 않습니다; 어쨌든, 그것의 흥미로운 속성은 인코딩과 무관합니다.

Unspecified constants

지정되지 않을 때, 상수는 유사한 대상, 공통적으로 함수의 클래스를 나타나며, 모두는 상수까지(up to) 같습니다–기술적으로 말하면, 이것은 '상수까지의 유사성'으로 보일 수 있습니다. 그러한 상수는 적분(integral)과 미분 방정식(differential equation)을 다룰 때 자주 나타납니다. 비록 지정되지는 않았지만, 그것들은 특정 값을 가지며, 종종 중요하지 않습니다.

Solutions with different constants of integration of $y'(x)=-2y+e^{-x}$.

In integrals

부정 적분(Indefinite integral)은 그것들의 해가 오직 상수까지 고유하기 때문에 부정이라고 합니다. 예를 들어, 실수의 필드(field)에 걸쳐 동작할 때

$\int \cos x\ dx=\sin x+C$

여기서 C는 적분 상수(constant of integration)이며, 고정된 실수입니다. 달리 말해서, C의 값이 무엇이든 x에 관해 sin x + C를 미분(differentiating)하면 항상 cos x를 산출합니다.

In differential equations

비슷한 방식으로, 상수는 초기 값(initial value) 또는 경계 조건(boundary condition)이 충분하지 않은 미분 방정식의 해에 나타납니다. 예를 들어, 보통의 미분 방정식(ordinary differential equation) y^' = y(x)은 해 Ce^x를 가지며 여기서 C는 임의의 상수입니다.

부분 미분 방정식(partial differential equation)을 다룰 때, 상수는 함수(functions), 일부 변수에 관한 상수일 수 있습니다 (그러나 반드시 모든 변수에는 아닙니다). 예를 들어, 다음 PDE는

${\frac {\partial f(x,y)}{\partial x}}=0$

해 f(x,y) = C(y)를 가지며, 여기서 C(y)는 변수(variable) y에서 임의의 함수입니다.

Notation

Representing constants

십진 표현(decimal representation) (또는 단지 처음 몇 자릿수)을 제공함으로써 상수의 숫자 값을 표현하는 것이 공통적입니다. 두 가지 이유로, 이 표현은 문제를 일으킬 수 있습니다. 첫째, 심지어 유리수는 모두 유한하거나 계속-반복되는 십진 확장을 가지고 있지만, 무리수는 이러한 방식으로 완전하게 설명할 수 없는 그런 표현을 갖지 없습니다. 역시, 숫자의 십진 전재가 반드시 고유한 것은 아닙니다. 예를 들어, 두 표현 0.999...와 1은 그것들이 같은 숫자를 나타낸다는 의미에서 동등합니다.

상수의 10진법 전개의 자릿수를 계산하는 것은 수세기 동안 공통적인 작업이었습니다. 예를 들어, 16세기 독일 수학자 Ludolph van Ceulen은 인생의 대부분을 파이의 처음 35 자릿수를 계산하는 데 보냈습니다. 컴퓨터와 슈퍼컴퓨터를 사용하여, π, e, 및 2의 제곱근을 포함한 일부 수학 상수는 천억 자릿수 이상으로 계산되어 왔습니다. 빠른 알고리듬(algorithm)이 개발되어 왔으며, 그 중 일부는 – 아페리 상수에서 처럼(Apéry's constant) – 예상 외로 빠릅니다.

$G=\left.{\begin{matrix}3\underbrace {\uparrow \ldots \uparrow } 3\\\underbrace {\vdots } \\3\uparrow \uparrow \uparrow \uparrow 3\end{matrix}}\right\}{\text{64 layers}}$

Graham's number defined using Knuth's up-arrow notation.

일부 상수는 보통의 종류와 너무 달라서 그것들을 합리적으로 나타내기 위해 새로운 표기법이 고안되어 왔습니다. 그레이엄의 숫자(Graham's number)는 커누스의 윗-화살표 표기법(Knuth's up-arrow notation)이 사용됨에 따라 이것을 설명합니다.

통계 해석학을 포함하여 다양한 연구를 수행하기 위해 연속된 분수(continued fraction)를 사용하여 그것들을 나타내는 것이 흥미로울 수 있습니다. 많은 수학 상수는 해석적 형식(analytic form)을 가지며. 즉, 계산에 쉽게 도움이 되는 잘-알려진 연산을 사용하여 구성될 수 있습니다. 모든 상수가 알려진 해석적 형식을 가지고 있는 것은 아닙니다; 그로스만의 상수 및 포이아스 상수(Foias' constant)가 예제입니다.

Symbolizing and naming of constants

상수를 문자로 기호화하는 것은 표기법(notation)을 더 간결하게 만드는 빈번한 수단입니다. 17세기에 르네 데카르트(René Descartes)와 18세기에 레온하르트 오일러(Leonhard Euler)에 의해 선동된, 공통적인 관례(convention)는 일반적으로 상수를 다룰 때, 라틴 알파벳 $a,b,c,\dots$ 또는 그리스 알파벳 $\alpha ,\beta ,\,\gamma ,\dots$의 시작 부분에서 소문자(lower case)를 사용하는 것입니다.

어쨌든, 더 중요한 상수에 대해, 기호가 더 복잡할 수 있고 여분의 문자, 별표(asterisk), 숫자, 렘니스케이트(lemniscate)를 가지거나, 히브리어(Hebrew), 키릴(Cyrillic), 또는 고딕(Gothic)과 같은 다른 알파벳을 사용합니다.

Erdős–Borwein constant $E_{B}$
Embree–Trefethen constant $\beta ^{*}$
Brun's constant for twin prime $B_{2}$
Champernowne constants $C_{b}$
cardinal number aleph naught $\aleph _{0}$

Examples of different kinds of notation for constants.

때때로, 상수를 나타내는 기호는 전체 단어입니다. 예를 들어, 미국 수학자 에드워드 캐스너(Edward Kasner)의 9세 조카는 googol과 googolplex라는 이름을 만들었습니다.

$\mathrm {googol} =10^{100}\,\ ,\ \mathrm {googolplex} =10^{\mathrm {googol} }=10^{10^{100}}$

다른 이름은 상수의 의미 (보편 포물선 상수(universal parabolic constant), 쌍둥이 소수 상수(twin prime constant), ...), 또는 특정 사람 (시에르핀스키 상수(Sierpiński's constant), 조지프슨 상수(Josephson constant), 등)과 관련이 있습니다.

The universal parabolic constant is the ratio, for any parabola, of the arc length of the parabolic segment (red) formed by the latus rectum (blue) to the focal parameter (green).

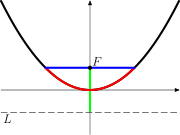
Table of selected mathematical constants

Main article: List of mathematical constants

Abbreviations used:

R – 유리수, I – 무리수 (대수적 또는 초월적일 수 있음), A – 대수적 숫자 (무리수), T – 초월적 숫자 (무리수)

Gen – 일반, NuT – 숫자 이론, ChT – 카오스 이론, Com – 조합론, Inf – 정보 이론, Ana – 수학 해석학

Symbol	Value	Name	Field	N	First described	Number of known decimal digits
0	= 0	Zero	Gen	R	by c. 500 BC	all
1	= 1	One, Unity	Gen	R		all
i	= √–1	Imaginary unit, unit imaginary number	Gen, Ana	A	by c. 1500	all
π	≈ 3.14159 26535 89793 23846 26433 83279 50288	Pi, Archimedes' constant or Ludolph's number	Gen, Ana	T	by c. 2600 BC	62,831,853,071,796
e	≈ 2.71828 18284 59045 23536 02874 71352 66249	e, Napier's constant, or Euler's number	Gen, Ana	T	1618	31,415,926,535,897
√2	≈ 1.41421 35623 73095 04880 16887 24209 69807	Pythagoras' constant, square root of 2	Gen	A	by c. 800 BC	10,000,000,000,000
√3	≈ 1.73205 08075 68877 29352 74463 41505 87236	Theodorus' constant, square root of 3	Gen	A	by c. 800 BC	2,199,023,255,552
√5	≈ 2.23606 79774 99789 69640 91736 68731 27623	square root of 5	Gen	A	by c. 800 BC	2,199,023,255,552
$\gamma$	≈ 0.57721 56649 01532 86060 65120 90082 40243	Euler–Mascheroni constant	Gen, NuT		1735	600,000,000,100
$\varphi$	≈ 1.61803 39887 49894 84820 45868 34365 63811	Golden ratio	Gen	A	by c. 200 BC	10,000,000,000,000
$\Lambda$	$0\leq \Lambda \leq 0.2$	de Bruijn–Newman constant	NuT, Ana		1950	none
M1	≈ 0.26149 72128 47642 78375 54268 38608 69585	Meissel–Mertens constant	NuT		1866 1874	8,010
$\beta$	≈ 0.28016 94990 23869 13303	Bernstein's constant	Ana
$\lambda$	≈ 0.30366 30028 98732 65859 74481 21901 55623	Gauss–Kuzmin–Wirsing constant	Com		1974	385
$\sigma$	≈ 0.35323 63718 54995 98454 35165 50432 68201	Hafner–Sarnak–McCurley constant	NuT		1993
L	≈ 0.5	Landau's constant	Ana			1
Ω	≈ 0.56714 32904 09783 87299 99686 62210 35554	Omega constant	Ana	T
$\lambda$, $\mu$	≈ 0.62432 99885 43550 87099 29363 83100 83724	Golomb–Dickman constant	Com, NuT		1930 1964
	≈ 0.64341 05462	Cahen's constant		T	1891	4000
C2	≈ 0.66016 18158 46869 57392 78121 10014 55577	Twin prime constant	NuT			5,020
	≈ 0.66274 34193 49181 58097 47420 97109 25290	Laplace limit
$\beta$*	≈ 0.70258	Embree–Trefethen constant	NuT
K	≈ 0.76422 36535 89220 66299 06987 31250 09232	Landau–Ramanujan constant	NuT			30,010
B4	≈ 0.87058 838	Brun's constant for prime quadruplets	NuT			8
K	≈ 0.91596 55941 77219 01505 46035 14932 38411	Catalan's constant	Com			1,000,000,001,337
B´L	= 1	Legendre's constant	NuT	R		all
K	≈ 1.13198 824	Viswanath's constant	NuT			8
$\zeta (3)$	≈ 1.20205 69031 59594 28539 97381 61511 44999	Apéry's constant		I	1979	1,200,000,000,100
$\lambda$	≈ 1.30357 72690 34296 39125 70991 12152 55189	Conway's constant	NuT	A
$\theta$	≈ 1.30637 78838 63080 69046 86144 92602 60571	Mills' constant	NuT		1947	6850
$\rho$	≈ 1.32471 79572 44746 02596 09088 54478 09734	Plastic constant	NuT	A	1928
$\mu$	≈ 1.45136 92348 83381 05028 39684 85892 02744	Ramanujan–Soldner constant	NuT	I		75,500
	≈ 1.45607 49485 82689 67139 95953 51116 54356	Backhouse's constant
	≈ 1.46707 80794	Porter's constant	NuT		1975
	≈ 1.53960 07178	Lieb's square ice constant	Com	A	1967
EB	≈ 1.60669 51524 15291 76378 33015 23190 92458	Erdős–Borwein constant	NuT	I
	≈ 1.70521 11401 05367 76428 85514 53434 50816	Niven's constant	NuT		1969
B2	≈ 1.90216 05831 04	Brun's constant for twin primes	NuT		1919	12
P2	≈ 2.29558 71493 92638 07403 42980 49189 49039	Universal parabolic constant	Gen	T
$\alpha$	≈ 2.50290 78750 95892 82228 39028 73218 21578	Feigenbaum constant	ChT
K	≈ 2.58498 17595 79253 21706 58935 87383 17116	Sierpiński's constant
	≈ 2.68545 20010 65306 44530 97148 35481 79569	Khinchin's constant	NuT		1934	7350
F	≈ 2.80777 02420 28519 36522 15011 86557 77293	Fransén–Robinson constant	Ana
	≈ 3.27582 29187 21811 15978 76818 82453 84386	Lévy's constant	NuT
$\psi$	≈ 3.35988 56662 43177 55317 20113 02918 92717	Reciprocal Fibonacci constant		I
$\delta$	≈ 4.66920 16091 02990 67185 32038 20466 20161	Feigenbaum constant	ChT		1975

See also

• Invariant (mathematics)
• List of mathematical symbols
• List of numbers
• Physical constant

External links

• Constants – from Wolfram MathWorld
• Inverse symbolic calculator (CECM, ISC) (tells you how a given number can be constructed from mathematical constants)
• On-Line Encyclopedia of Integer Sequences (OEIS)
• Simon Plouffe's inverter
• Steven Finch's page of mathematical constants (BROKEN LINK)
• Steven R. Finch, "Mathematical Constants," Encyclopedia of mathematics and its applications, Cambridge University Press (2003).
• Xavier Gourdon and Pascal Sebah's page of numbers, mathematical constants and algorithms