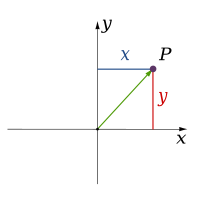Dimension
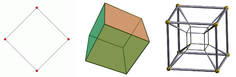

- Two points can be connected to create a line segment.
- Two parallel line segments can be connected to form a square.
- Two parallel squares can be connected to form a cube.
- Two parallel cubes can be connected to form a tesseract.
| Geometry |
|---|
 |
| Geometers |
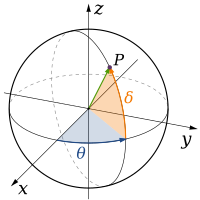
물리학(physics)과 수학(mathematics)에서, 수학적 공간(mathematical space) (또는 대상)의 차원(dimension)은 그 안에 임의의 점(point)을 지정하는 것에 필요한 좌표(coordinates)의 최소 숫자로 비공식적으로 정의됩니다.[1][2] 따라서, 직선(line)은 하나의 차원 (1D)을 가지는데 왜냐하면 오직 하나의 좌표가 그 위의 점 – 예를 들어, 수직선 위의 5에서 점을 지정하기 위해 필요하기 때문입니다. 원통(cylinder) 또는 구(sphere)의 경계(boundary)와 같은 표면(surface)은 그 위의 한 점을 지정하기 위해 두 좌표가 필요하기 때문에 이의 차원 (2D)을 가집니다 – 예를 들어, 위도(latitude)와 경도(longitude)는 둘 다 구의 표면 위의 점을 배치하기 위해 요구됩니다. 이-차원 유클리드 공간(two-dimensional Euclidean space)은 평면 위에 이-차원 공간입니다. 정육면체(cube), 원통, 또는 구의 내부는 이들 공간 내부의 한 점을 지정하기 위해 세 개의 좌표가 필요하기 때문에 삼-차원 (3D)입니다.
고전 역학에서, 공간과 시간은 서로 다른 카테고리이고 절대 공간과 시간을 참조합니다. 그 세계의 해당 개념은 사-차원 공간이지만 전자기학을 기술하는 것에 필요한 것으로 밝혀진 것은 아닙니다. 시공간의 사 차원 (4D)은 공간적, 시간적으로 절대적으로 정의되는 것이 아니라, 관측자(observer)의 움직임에 상대적으로 알려진 사건(event)으로 구성됩니다. 민코프스키 공간(Minkowski space)은 중력 없이 우주를 첫 번째로 근사화합니다; 일반 상대성의 준 리만 매니폴드(pseudo-Riemannian manifold)는 물질과 중력과의 시공간을 묘사합니다. 10 차원은 초월-끈 이론(superstring theory) (6D 초공간(hyperspace) + 4D)을 설명하기 위해 사용되며, 11 차원은 초월-중력(supergravity)과 M-이론(M-theory) (7D 초공간 + 4D)을 설명할 수 있고, 양자 역학의 상태-공간은 무한-차원의 함수 공간입니다.
차원의 개념은 물리적 대상에만 제한되지 않습니다. 고-차원 공간(High-dimensional spaces)은 수학과 과학에서 자주 발생합니다. 그것들은 매개-변수 공간 또는 라그랑주(Lagrangian)이나 해밀턴 역학(Hamiltonian mechanics)에서와 같은 구성 공간(configuration space)일 수 있습니다; 이것들은 우리가 사는 물리적 공간과는 독립적인, 추상 공간(space)입니다.
In mathematics
수학에서, 대상의 차원은, 대략적으로 말하면, 이 대상 위에서 움직이는 점의 자유도(degrees of freedom)의 숫자입니다. 다시 말해서, 차원은 대상 위에 있도록 구속되는 점의 위치를 정의하는 데 필요한 독립 매개-변수(parameters) 또는 좌표(coordinates)의 숫자입니다. 예를 들어, 점의 차원은 영입니다; 직선의 차원은 일인데, 왜냐하면 한 점은 한 방향 (또는 반대 방향)으로만 직선 위에서 이동할 수 있기 때문입니다; 평면(plane)의 차원은 2이고, 등입니다.
차원은 대상이 포함되어 있거나 삽입될 수 있는 공간의 차원과 독립이다는 의미에서 대상의 고유한 속성입니다. 예를 들어, 원(circle)과 같은 곡선(curve)은 일-차원인데, 왜냐하면 곡선 위에 한 점의 위치는 곡선을 따라 곡선의 고정된 점까지의 부호화된 거리에 의해 결정되기 때문입니다. 이것은 곡선이, 직선이 아닌 한, 2보다 낮은 차원의 유클리드 공간(Euclidean space)에 삽입될 수 없다는 사실과 무관합니다.
유클리드 n-공간 En 의 차원은 n입니다. 다른 유형의 공간으로 일반화하려고 할 때, "En 을 n-차원으로 만드는 것은 무엇입니까?"라는 질문에 직면하게 됩니다. 한 가지 대답은 En 에서 고정된 공을 반지름 ε의 작은 공으로 덮기 위해, ε−n 정도의 작은 공이 필요하다는 것입니다. 이 관찰은 민코프스키 차원(Minkowski dimension)과 더 정교한 변형, 하우스도르프 차원(Hausdorff dimension)의 정의로 이어지지만, 그 질문에 대한 다른 답변도 있습니다. 예를 들어, En 에서 공의 경계는 지역적으로 En-1 처럼 보이고 이것은 귀납적 차원(inductive dimension)의 개념으로 이어집니다. 이들 개념은 En에 동의하지만, 그것들은 보다 일반적인 공간에서 바라볼 때 다른 것으로 판명됩니다.
테서랙트(tesseract)는 사-차원 대상의 예입니다. 수학 외부에서 "차원"이라는 용어의 사용은 "테서랙트는 사-차원을 가집니다"와 같은 것이지만, 수학자들은 보통 이를 "테서랙트는 차원 4를 가집니다", 또는 "테서랙트의 차원은 4입니다" 또는 4D라고 표현합니다.
더 높은 차원의 개념은 르네 데카르트(René Descartes)로 거슬로 올라가지만, 고차원 기하학의 실질적인 발전은 Arthur Cayley, William Rowan Hamilton, Ludwig Schläfli, 및 Bernhard Riemann의 연구를 통해 19세기에만 시작되었습니다. 리만의 1854 Habilitationsschrift, Schläfli의 1852 Theorie der vielfachen Kontinuität, 및 Hamilton의 쿼터니언(quaternions) 발견과 1843년 John T. Graves의 옥토니언(octonions) 발견은 고차원 기하학의 시작을 표시했습니다.
이 섹션의 나머지 부분에서는 차원에 대한 보다 중요한 수학적 정의를 살펴봅니다.
Vector spaces
벡터 공간(vector space)의 차원은 공간에 대해 임의의 기저(basis) 벡터의 숫자, 즉 임의의 벡터를 지정하기 위해 필요한 좌표의 숫자입니다. 차원의 이러한 개념 (기저의 카디널리티(cardinality))은 종종 다른 차원 개념과 구별하기 위해 하멜 차원(Hamel dimension) 또는 대수적 차원(algebraic dimension)으로 참조됩니다.
비-자유(free) 경우에 대해, 이것은 모듈의 길이(length of a module)의 개념으로 일반화합니다.
Manifolds
모든 각 연결된(connected) 토폴로지적 매니폴드(manifold)의 고유하게 정의된 차원은 계산될 수 있습니다. 연결된 토폴로지적 매니폴드는 숫자 n이 매니폴드의 차원인 유클리드 n-공간과 지역적(locally)으로 위상-동형(homeomorphic)입니다.
연결된 미분-가능 매니폴드(differentiable manifolds)에 대해, 차원은 임의의 점에서 접 벡터 공간(tangent vector space)의 차원입니다.
기하학적 토폴로지(geometric topology)에서, 매니폴드의 이론은 차원 1과 2가 상대적으로 기본적인 방법에 의해 특징지어지며, 고-차원 경우 n > 4는 "작동"할 여분의 공간을 가짐으로써 단순화됩니다; 그리고 n = 3과 4의 경우는 어떤 의미에서는 가장 어렵습니다. 이러한 상황은 서로 다른 네 가지 증명 방법이 적용되는 푸앵카레 추측(Poincaré conjecture)의 다양한 사례에서 두드러지게 나타났습니다.
Complex dimension
매니폴드의 차원은 유클리드 공간이 정의되는 기본 필드에 따라 다릅니다. 해석학은 보통 실수에 걸쳐 매니폴드를 가정하지만, 때때로 복소 매니폴드와 대수적 다양체(algebraic varieties) 연구에서는 복소수에 대해 연구하는 것이 유용합니다. 복소수 (x + iy)는 실수 부분(real part) x와 허수 부분(imaginary part) y를 가지며, 이것에서 x와 y는 모두 실수입니다; 따라서 복소수 차원은 실수 차원의 절반입니다.
반대로, 대수적으로 제약이 없는 문맥에서, 단일 복소 좌표 시스템은 두 개의 실수 차원을 가지는 대상에 적용될 수 있습니다. 예를 들어, 보통의 이-차원 구형 표면(spherical surface)은, 복소 메트릭을 제공될 때, 일 복소 차원의 리만 구(Riemann sphere)가 됩니다.
Varieties
대수적 다양체(algebraic variety)의 차원은 다양한 동등한 방법에서 정의될 수 있습니다. 가장 직관적인 방법은 아마도 대수적 다양체의 임의의 정규 점에서 접 공간(tangent space)의 차원일 것입니다. 또 다른 직관적인 방법은 차원을 유한한 수의 점 (차원 영)으로 줄이는 다양체와의 교차점을 가지기 위해 필요한 초평면(hyperplanes)의 숫자로 정의하는 것입니다. 이 정의는 초평면이 다양체를 포함하지 않은 한 초평면과 다양체의 교차로 차원이 1 감소한다는 사실에 근거합니다.
대수적 집합(algebraic set)은 대수적 대양체의 유한한 합집합이며, 그 차원은 그것의 구성 요소 차원의 최댓값입니다. 그것은 주어진 대수적 집합의 부분-다양체에 대한 체인 의 최대 길이와 같습니다 (그러한 체인의 길이는 ""의 숫자입니다).
각 대양체는 대수적 스택(algebraic stack)으로 고려될 수 있고, 다양체로서의 차원은 스택으로서의 차원과 일치합니다. 어쨌든 다양체에 해당하지 않는 스택이 많이 있고, 이들 중 일부는 음의 차원을 가집니다. 특히, V가 차원 m의 다양체이고 G가 V에 작용하는 차원 n의 대수적 그룹(algebraic group)이면, 몫 스택(quotient stack) [V/G]은 차원 m − n을 가집니다.[3]
Krull dimension
교환 링(commutative ring)의 크룰 차원(Krull dimension)은 그 안에 있는 소수 아이디얼(prime ideals) 체인의 최대 길이이며, 길이 n의 체인은 포함과 관련된 소수 아이디얼 열 입니다. 그것은 다양체 위에 다항식 링의 부분-다양체와 소수 아이디얼 사이의 자연스러운 일치 때문에 대수적 다양체의 차원과 강하게 관련되어 있습니다.
필드에 걸쳐 대수(algebra over a field)에 대해, 벡터 공간(vector space)으로서의 차원이 유한인 것과 그것의 크룰 차원이 0인 것은 필요충분 조건입니다.
Topological spaces
임의의 정규 토폴로지적 공간(normal topological space) X에 대해, X의 르베그 덮는 차원(Lebesgue covering dimension)은 다음이 유지하는 가장 작은 정수 n으로 정의됩니다: 임의의 열린 덮개(open cover)는 어떤 점도 n + 1보다 많은 원소에 포함되지 않음을 만족하는 열린 정제를 가집니다 (두 번째 열린 덮개에서 각 원소는 첫 번째 덮개에서 원소의 부분집합입니다). 이 경우에서 dim X = n입니다. X 매니폴드에 대해, 이것은 위에서 언급한 차원과 일치합니다. 만약 그러한 정수 n이 존재하지 않으면, X의 차원은 무한대라고 말하고, dim X = ∞라고 씁니다. 더욱이, X가 차원 −1, 즉, dim X = −1인 것과 X가 빈 것임은 필요충분 조건입니다. 덮는 차원의 이러한 정의는 정의에서 "열린"이라는 용어를 "함수적으로 열린(functionally open)"이라는 용어로 단지 대체함으로써 일반 공간의 클래스에서 모든 티호노프 공간(Tychonoff space)으로 확장될 수 있습니다.
귀납적 차원(inductive dimension)은 다음과 같이 귀납적(inductively)으로 정의될 수 있다. 점의 이산 집합(discrete set) (예를 들어, 점의 유한 모음)을 0-차원으로 생각해 보십시오. 0-차원 대상을 어떤 방향으로 끎으로써, 1-차원 대상을 얻습니다. 1-차원 대상을 새로운 방향으로 끎으로써, 2-차원 대상을 얻습니다. 일반적으로 n-차원 대상을 새로운 방향으로 끎으로써 (n + 1)-차원 대상을 얻습니다. 토폴로지적 공간의 귀납적 차원은 작은 귀납적 차원 또는 큰 귀납적 차원을 참조할 수 있고, 메트릭 공간에 대해, (n + 1)-차원 공이 n-차원 경계(boundaries)를 갖는다는 유추를 기반으로 하며, 열린 집합의 경계의 차원에 기반한 귀납적 정의를 허용합니다. 게다가, 점의 이산 집합의 경계는 빈 집합이고, 따라서 빈 집합은 차원 −1을 가지는 것으로 취할 수 있습니다.[4]
유사하게, CW 복합체(CW complexes)의 클래스에 대해, 대상의 차원은 n-뼈대(n-skeleton)가 비-자명한 것에 대해 가장 큰 n입니다. 직관적으로, 이것은 다음과 같이 설명될 수 있습니다: 만약 원래 공간이 복잡한 표면으로 면에서 결합된 더-높은 차원의 삼각형(higher-dimensional triangles)의 모음으로 연속적으로 변형될(continuously deformed) 수 있다면, 대상의 차원은 해당 삼각형의 차원입니다.
Hausdorff dimension
하우스도르프 차원(Hausdorff dimension)은 구조적으로 복잡한 집합, 특히 프랙탈(fractals)을 연구하는 데 유용합니다. 하우스도르프 차원은 모든 메트릭 공간(metric spaces)에 대해 정의되고, 위에서 고려된 차원과 달리, 비-정수 실수 값을 가질 수도 있습니다.[5] 상자 차원(box dimension) 또는 민코프스키 차원(Minkowski dimension)은 같은 아이디어의 변형입니다. 일반적으로, 매우 불규칙한 집합에 대해 작동하고 비-정수 양의 실수 값을 얻는 프랙탈 차원(fractal dimensions)의 더 많은 정의가 있습니다.
Hilbert spaces
모든 각 힐베르트 공간(Hilbert space)은 직교-정규 기저(orthonormal basis)를 허용하고, 특정 공간에 대한 두 개의 그러한 기저는 같은 카디널리티를 가집니다. 이 카디널리티는 힐베르트 공간의 차원이라고 불립니다. 이 차원이 유한인 것과 공간의 하멜 차원(Hamel dimension)이 유한인 것은 필요충분 조건이고, 이 경우에서 두 차원이 일치합니다.
In physics
Spatial dimensions
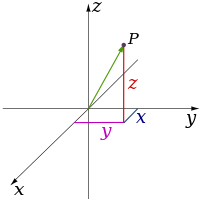
고전 물리학 이론은 세 가지 물리적 차원(physical dimensions)을 설명합니다: 공간(space)에서 특정 점에서, 우리가 이동할 수 있는 기본 방향은 위/아래, 왼쪽/오른쪽, 및 앞/뒤입니다. 임의의 다른 방향으로의 움직임은 단지 이들 세 가지로 표현될 수 있습니다. 아래로 이동하는 것은 음의 거리로 이동하는 것과 같습니다. 대각선으로 위쪽과 앞쪽으로 이동하는 것은 방향의 이름에서 의미하는 것과 같습니다; 즉, 위쪽과 앞쪽의 선형 조합(linear combination)으로 이동합니다. 가장 단순한 형식으로, 직선은 일 차원을 설명하고, 평면은 이 차원을 설명하고, 정육면체는 삼 차원을 설명합니다. (공간(Space)과 데카르트 좌표 시스템(Cartesian coordinate system)을 참조하십시오.)
Number of
dimensions |
Example co-ordinate systems | |||
|---|---|---|---|---|
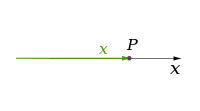
| 1 |
| |||
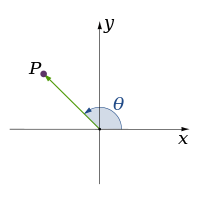
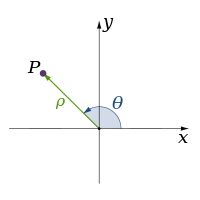
| 2 |
| |||
| 3 |
|
Time
시간적 차원(temporal dimension), 또는 시간 차원(time dimension)은 시간의 차원입니다. 시간은 이러한 이유로 종종 "네 번째 차원(fourth dimension)"으로 참조되지만, 그것이 공간적 차원을 의미하는 것은 아닙니다. 시간적 차원은 물리적 변화를 측정하는 한 가지 방법입니다. 차원 중 하나만 있다는 점과, 우리는 시간에서 자유롭게 움직일 수 없지만 주관적으로 한 방향으로 움직인다는 점에서 세 개의 공간적 차원과 다르게 지각됩니다.
현실을 모델링하기 위해 물리학에서 사용되는 방정식은 인간이 공통적으로 그것을 인식하는 것과 같은 방법에서 시간을 취급하지 않습니다. 고전 역학(classical mechanics)의 방정식은 시간에 관해 대칭이고, 양자 역학의 방정식은 시간과 다른 양 (예를 들어, 전하 및 패리티)이 모두 뒤집히면 전형적으로 대칭입니다. 이들 모델에서, 한 방향으로 흐르는 시간의 인식은 열역학 법칙(laws of thermodynamics)의 인위적 결과입니다 (우리는 시간을 엔트로피(entropy)를 증가하는 방향으로 흐르는 것으로 인식합니다).
시간을 차원으로 처리하는 것으로 가장 잘 알려진 것은 푸앵카레와 아인슈타인의 특수 상대성(special relativity) (및 일반 상대성(general relativity)으로 확장됨)으로, 이는 지각된 공간과 시간을 시공간(spacetime)으로 알려져 있는 사-차원 매니폴드(manifold)의 구성 요소로 취급하고, 특수한 경우에서, 민코프스키 공간(Minkowski space)으로 평평한 경우로 취급합니다. 시간은 그것이 모든 공간적 차원에서 작동할 때 다른 공간적 차원과 다릅니다. 시간은 첫 번째, 두 번째, 세 번째뿐만 아니라 네 번째 공간 차원과 같은 이론적 공간 차원에서도 작동합니다. 어쨌든, 무한히 작은 점은 변화가 없고 따라서 시간이 없기 때문에 기하학적 점(geometric point)으로 정의되는 절대 무한 특이성(singularity)의 단일 점에 시간이 존재하지 않습니다. 물체가 공간에서 위치(positions)를 이동할 때와 마찬가지로, 역시 시간에서 위치를 통해서도 이동합니다. 이런 의미에서, 임의의 물체를 움직이게 하는 힘(force)은 시간입니다.[6][7][8][9]
Additional dimensions
물리학에서, 공간의 삼 차원과 시간의 일 차원이 허용되는 표준입니다. 어쨌든, 여분의 차원/초공간을 도입함으로써 네 개의 기본 힘(fundamental forces)을 통합을 시도하는 이론이 있습니다. 가장 주목할만한, 초월-끈 이론은 10 개의 시공간 차원을 요구하고, 이전에 다섯 개의 구별되는 초월-끈 이론을 포함하는 잠정적으로 M-이론(M-theory)이라고 불리는 보다 근본적인 11-차원 이론에서 비롯됩니다. 초월-중력 이론(Supergravity theory)은 역시 11D 시공간 = 7D 초공간 + 4개의 공통 차원을 촉진합니다. 현재까지, 이들 여분의 차원의 존재를 뒷받침하는 직접적인 실험적 또는 관찰적 증거는 없습니다. 만약 초월-공간이 존재하면, 그것은 어떤 물리적 메커니즘에 의해 우리에게 숨겨져 있어야 합니다. 하나의 잘-연구된 가능성은 여분의 차원이 현재 실험에서 효과적으로 보이지 않을 정도로 작은 규모에서 "말려 있을" 수 있다는 것입니다. 여분의 차원의 크기와 다른 속성 위에 제한은 Large Hadron Collider에서 실험과 같은 입자 실험 의해 설정됩니다.[10]
1921년에, 칼루차–클라인 이론(Kaluza–Klein theory)은 공간의 여분의 차원을 포함하는 5D를 제안했습니다. 양자 필드 이론(quantum field theory)의 수준에서, 칼루차–클라인 이론은 작고, 조밀한 여분의 차원에서 전파되는 중력이 장거리에서 게이지 상호 작용과 동등하다는 인식을 기반으로 중력을 게이지 상호 작용과 통합합니다. 특히 여분의 차원의 기하학이 자명할 때, 그것은 전자기(electromagnetism)를 재현합니다. 어쨌든 충분하게 높은 에너지 또는 짧은 거리에서, 이 설정은 여전히 양자 중력(quantum gravity)을 기술하기 위해 직접적인 시도를 방해하는 것으로 유명한 같은 병리를 앓고 있습니다. 그러므로, 이들 모델은 끈 이론이 제공하고자 하는 종류의 UV 완성(UV completion)을 요구합니다. 특히, 초월-끈 이론은 칼라비–야우 매니폴드(Calabi–Yau manifold)를 형성하는 6개의 컴팩트한 차원 (6D 초공간)을 요구합니다. 따라서 칼루차–클라인 이론은 그 자체로 불완전한 설명으로, 또는 끈 이론 모델 구축의 부분집합으로 고려될 수 있습니다.
작고 말려 있는 여분의 차원 외에도, 우리의 보이는 우주와 결합된 문제가 (3 + 1)-차원 부분공간에 국한되어 있기 때문에 대신 명확하지 않은 여분의 차원이 있을 수 있습니다. 따라서 여분의 차원은 작고 컴팩트할 필요는 없지만 큰 여분의 차원(large extra dimensions)일 수 있습니다. D-브레인(D-branes)은 이러한 역할을 할 수 있는 끈 이론에 의해 예측된 다양한 차원의 동적 확장 물체입니다. 그것들은 게이지 상호 작용과 결합된 열린 끈 자극이 그것들의 끝점에 의해 브레인에 국한되는 반면, 중력 상호 작용을 매개하는 닫힌 끈은 전체 시공간, 또는 "벌크"로 자유롭게 전파되는 특성을 가지고 있습니다. 이것은 중력이 다른 힘보다 기하급수적으로 약한 이유와 관련이 있을 수 있는데, 왜냐하면 중력은 더 높은 차원의 부피로 전파될 때 스스로를 효과적으로 희석하기 때문입니다.
브레인 물리의 일부 측면은 우주론(cosmology)에 적용되어 왔습니다. 예를 들어, 브레인 가스 우주론은 토폴로지적 및 열역학적 고려 사항을 사용하여 공간의 삼 차원이 있는 이유를 설명하려고 시도합니다.[11][12] 이 아이디어에 따르면, 삼은 끈이 일반적으로 교차할 수 있는 공간 차원의 가장 큰 숫자이기 때문입니다. 만약 초기에 컴팩트 차원 주위에 많은 끈의 감김이 있으면, 이들 감김이 제거된 후에만 공간이 거시적 크기로 확장될 수 있습니다. 그러나 끈은 삼 차원에서 의미 있는 율로 소멸하기 위해 서로를 찾을 수 있을 뿐이므로, 이러한 종류의 초기 구성에서는 삼 차원 공간만 커질 수 있음을 따릅니다.
모든 필드가 그 안에서 똑같이 자유롭게 전파된다면 여분의 차원은 보편적(universal)이라고 합니다.
In computer graphics and spatial data
여러 유형의 디지털 시스템은 일러스트레이션 소프트웨어, 컴퓨터-지원 설계와 지리 정보 시스템을 포함하여 기하학적 모양의 저장, 분석, 및 시각화를 기반으로 합니다. 다른 벡터 시스템은 다양한 데이터 구조를 모양을 나타내기 위해 사용하지만, 거의 모든 것이 기본적으로 공간 차원에 해당하는 기하학적 원시(geometric primitives)의 집합을 기반으로 합니다:[13]
- 점(Point, 0-차원), 데카르트 좌표 시스템(Cartesian coordinate system)에서 단일 좌표.
- 직선(Line 또는 여러-직선(Polyline), 1-차원), 보통 연속 직선에서 표본화된 점의 순서화된 목록으로 표시되며, 따라서 소프트웨어는 직선 또는 곡선 선분으로 선의 중간 모양을 보간(interpolate)할 것으로 예상됩니다.
- 다각형(Polygon, 2-차원), 보통 끝점에서 닫히는 직선으로 표시되며, 이-차원 영역의 경계를 나타냅니다. 소프트웨어는 이 경계를 2-차원 공간을 내부와 외부로 분할하기 위해 사용할 것으로 예상됩니다.
- 표면(Surface, 3-차원), 연결된 다각형 면으로 구성된 다면체(polyhedron)와 같은 다양한 전략을 사용하여 표현됩니다. 소프트웨어는 이 표면을 삼-차원 공간을 내부와 외부로 분할하기 위해 사용할 것으로 예상됩니다.
자주 이들 시스템, 특히 GIS와 지도학(Cartography)에서, 실-세계 현상의 표시는 표시되는 현상과 다른 (보통 더 낮은) 차원을 가질 수 있습니다. 예를 들어, 도시 (이-차원 영역)는 점으로 표시될 수 있고, 도로 (물질의 삼-차원 부피)는 선으로 표시될 수 있습니다. 이러한 차원의 일반화(dimensional generalization)는 공간 인식에서 경향과 상관관계가 있습니다. 예를 들어, 두 도시 사이의 거리를 묻는 것은 도시의 개념적 모델을 점으로 가정하는 반면, 도로를 "위", "아래로" 또는 "따라" 이동과 관련된 방향을 제공하는 것은 일-차원 개념적 모델을 의미합니다. 이것은 데이터 효율성, 시각적 단순성 또는 인식 효율성을 목적으로 자주 수행되고, 표현과 표현된 사이의 구분이 이해되려면 허용되지만, 정보 사용자가 디지털 모양이 현실의 완벽한 표시라고 가정하면 혼동을 일으킬 수 있습니다 (즉, 도로가 실제로 선이라고 믿는 것입니다).
In literature
공상 과학 소설(Science fiction) 텍스트는 평행 또는 교대 우주 또는 기타 상상된 존재의 평면을 언급할 때 종종 "차원"의 개념을 언급합니다. 이 사용법은 평행/교대 우주/존재의 평면으로 여행하려면 표준 우주 이외의 방향/차원으로 여행해야 한다는 아이디어에서 파생됩니다. 사실상, 다른 우주/평면은 우리 우주에서 아주 작은 거리에 있지만, 그 거리는 표준 차원이 아닌 네 번째 (또는 더 높은) 공간 (또는 비-공간) 차원에 있습니다.
진정한 기하학적 차원에 관한 가장 예고된 공상 과학 소설 중 하나이고, 그러한 문제를 이제 막 조사하기 시작하는 사람들에게 종종 시작 점으로 권장되는 것은 Edwin A. Abbott의 1884년 소설 Flatland입니다. 아이작 아시모프(Isaac Asimov)는 Signet Classics 1984 판의 서문에서 Flatland를 "차원을 인식하는 방식으로 찾을 수 있는 최고의 입문서"라고 설명했습니다.
다른 차원에 대한 아이디어는 많은 초기 공상 과학 소설에 통합되었으며, 예를 들어 Miles J. Breuer의 The Appendix and the Spectacles (1928)과 Murray Leinster의 The Fifth-Dimension Catapult (1931); 및 1940년대까지 공상 과학 소설에 불규칙적으로 등장했습니다. 다른 차원과 관련된 고전적인 이야기에는 Robert A. Heinlein의 —And He Built a Crooked House (1941)가 포함되며, 이것에서 캘리포니아 건축가는 테서랙트의 삼-차원 투영을 기반으로 집을 설계합니다; Alan E. Nourse의 Tiger by the Tail과 The Universe Between (둘 다 1951); 및 Walter Tevis의 The Ifth of Oofth (1957)를 포함합니다. 또 다른 참고 자료는 Madeleine L'Engle의 소설 A Wrinkle In Time (1962)으로, 다섯 번째 차원을 "우주를 테서렉트(tesseracting)"하거나 공간을 빠르게 가로질러 이동하기 위해 공간을 "접는" 방법으로 사용합니다. 네 번째 차원과 다섯 번째 차원은 역시 William Sleator의 책 The Boy Who Reversed Himself 자신의 책의 핵심 구성 요소입니다.
In philosophy
1783년 임마누엘 칸트(Immanuel Kant)는 다음과 같이 썼습니다: "모든 곳에서 공간 (또 다른 공간의 자체 경계가 아닌)은 삼-차원을 가지고 일반적으로 공간은 더 많은 차원을 가질 수 없다는 것은 한 점에서 세 개보다 많은 직선이 직각으로 교차할 수 없다는 제안에 기반합니다. 이 제안은 개념으로부터는 전혀 보일 수 없고, 직관에 즉각적으로 의존하고 그것이 묵시적으로 (시연적으로) 확실하기 때문에 실제로는 순수 직관 선험(a priori)으로 의존합니다."[14]
"공간은 사-차원을 가진다"는 독일 철학자이자 실험 심리학자인 구스타프 페흐너가 "미제스 박사"라는 필명(pseudonym)으로 1846년에 출판한 단편 소설입니다. 이야기에서 주인공은 다른 그림자를 인지하고 소통할 수 있지만 이-차원 표면에 갇힌 그림자입니다. Fechner에 따르면, 이 "그림자-인간"은 삼 차원을 시간의 하나로 생각할 것입니다.[15] 그 이야기는 플라톤의 The Republic (기원전 380년경)에 나오는 "동굴의 비유(Allegory of the Cave)"와 매우 유사합니다.
Simon Newcomb은 1898년 "The Philosophy of Hyperspace"라는 제목의 Bulletin of the American Mathematical Society에 기고했습니다.[16] Linda Dalrymple Henderson은 20세기 초 예술의 4차원에 대한 1983년 논문에서 형이상학적 주제를 탐구하기 위해 더 높은 차원을 사용하는 글쓰기를 설명하는 데 사용되는 "초공간 철학"이라는 용어를 만들었습니다.[17] "초공간 철학자"의 예로는 1888년에 "tesseract"라는 단어를 사용한 최초의 작가인 Charles Howard Hinton; 및 러시아 esotericist P. D. Ouspensky가 있습니다.
More dimensions
| Geometry |
|---|
 |
| Geometers |
See also
Topics by dimension
- Zero
- One
- Two
- Three
- Four
- Higher dimensions
- in mathematics
- in physics
- Infinite
References
- ^ "Curious About Astronomy". Curious.astro.cornell.edu. Archived from the original on 2014-01-11. Retrieved 2014-03-03.
- ^ "MathWorld: Dimension". Mathworld.wolfram.com. 2014-02-27. Archived from the original on 2014-03-25. Retrieved 2014-03-03.
- ^ Fantechi, Barbara (2001), "Stacks for everybody" (PDF), European Congress of Mathematics Volume I, Progr. Math., vol. 201, Birkhäuser, pp. 349–359, archived (PDF) from the original on 2006-01-17
- ^ Hurewicz, Witold; Wallman, Henry (2015). Dimension Theory (PMS-4), Volume 4. Princeton University Press. p. 24. ISBN 978-1-4008-7566-5. Extract of page 24
- ^ Fractal Dimension Archived 2006-10-27 at the Wayback Machine, Boston University Department of Mathematics and Statistics
- ^ Rylov, Yuri A. (2007). "Non-Euclidean method of the generalized geometry construction and its application to space-time geometry". arXiv:math/0702552.
- ^ "Download Limit Exceeded". citeseerx.ist.psu.edu.
- ^ Lane, Paul M.; Lindquist, Jay D. (May 22, 2015). "Definitions for The Fourth Dimension: A Proposed Time Classification System1". In Bahn, Kenneth D. (ed.). Proceedings of the 1988 Academy of Marketing Science (AMS) Annual Conference. Developments in Marketing Science: Proceedings of the Academy of Marketing Science. Springer International Publishing. pp. 38–46. doi:10.1007/978-3-319-17046-6_8. ISBN 978-3-319-17045-9 – via Springer Link.
- ^ Wilson, Edwin B.; Lewis, Gilbert N. (1912). "The Space-Time Manifold of Relativity. The Non-Euclidean Geometry of Mechanics and Electromagnetics". Proceedings of the American Academy of Arts and Sciences. 48 (11): 389–507. doi:10.2307/20022840. JSTOR 20022840 – via JSTOR.
- ^ CMS Collaboration (2011). "Search for Microscopic Black Hole Signatures at the Large Hadron Collider". Phys. Lett. B. 697 (5): 434–453. arXiv:1012.3375. Bibcode:2011PhLB..697..434C. doi:10.1016/j.physletb.2011.02.032. S2CID 118488193. CMS-EXO-10-017, CERN-PH-EP-2010-073.
- ^ Brandenberger, R.; Vafa, C. (1989). "Superstrings in the early universe". Nuclear Physics B. 316 (2): 391–410. Bibcode:1989NuPhB.316..391B. doi:10.1016/0550-3213(89)90037-0.
- ^ Scott Watson, Brane Gas Cosmology Archived 2014-10-27 at the Wayback Machine (pdf).
- ^ Vector Data Models, Essentials of Geographic Information Systems, Saylor Academy, 2012
- ^ Prolegomena, § 12
- ^ Banchoff, Thomas F. (1990). "From Flatland to Hypergraphics: Interacting with Higher Dimensions". Interdisciplinary Science Reviews. 15 (4): 364. doi:10.1179/030801890789797239. Archived from the original on 2013-04-14.
- ^ Newcomb, Simon (1898). "The Philosophy of Hyperspace". Bulletin of the American Mathematical Society. 4 (5): 187. doi:10.1090/S0002-9904-1898-00478-0.
- ^ Kruger, Runette (2007). "Art in the Fourth Dimension: Giving Form to Form – The Abstract Paintings of Piet Mondrian" (PDF). Spaces of Utopia: An Electronic Journal (5): 11. Archived (PDF) from the original on 2011-09-29.
Further reading
- Murty, Katta G. (2014). "1. Systems of Simultaneous Linear Equations" (PDF). Computational and Algorithmic Linear Algebra and n-Dimensional Geometry. World Scientific Publishing. doi:10.1142/8261. ISBN 978-981-4366-62-5.
- Abbott, Edwin A. (1884). Flatland: A Romance of Many Dimensions. London: Seely & Co.
- —. Flatland: ... Project Gutenberg.
- —; Stewart, Ian (2008). The Annotated Flatland: A Romance of Many Dimensions. Basic Books. ISBN 978-0-7867-2183-2.
- Banchoff, Thomas F. (1996). Beyond the Third Dimension: Geometry, Computer Graphics, and Higher Dimensions. Scientific American Library. ISBN 978-0-7167-6015-3.
- Pickover, Clifford A. (2001). Surfing through Hyperspace: Understanding Higher Universes in Six Easy Lessons. Oxford University Press. ISBN 978-0-19-992381-6.
- Rucker, Rudy (2014) [1984]. The Fourth Dimension: Toward a Geometry of Higher Reality. Courier Corporation. ISBN 978-0-486-77978-2. Google preview
- Kaku, Michio (1994). Hyperspace, a Scientific Odyssey Through the 10th Dimension. Oxford University Press. ISBN 978-0-19-286189-4.
- Krauss, Lawrence M. (2005). Hiding in the Mirror. Viking Press. ISBN 978-0-670-03395-9.
External links
- Copeland, Ed (2009). "Extra Dimensions". Sixty Symbols. Brady Haran for the University of Nottingham.