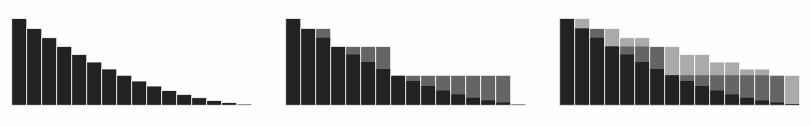Cauchy condensation test

수학(mathematics)에서, 코시 응집 테스트(Cauchy condensation test)는, 오귀스탱-루이 코시(Augustin-Louis Cauchy)의 이름을 따서 지어졌으며, 무한 급수(infinite series)에 대해 표준 수렴 테스트(convergence test)입니다. 비-음의 실수의 비-증가하는(non-increasing) 수열(sequence) $f(n)$ 에 대해, 급수 $\displaystyle \sum \limits _{n=1}^{\infty }f(n)$ 이 수렴하는 것과 "응집된" 급수 $\displaystyle \sum \limits _{n=0}^{\infty }2^{n}f(2^{n})$ 이 수렴하는 것은 필요충분 조건입니다. 게다가, 만약 그들이 수렴하면, 응집된 급수의 합은 많아야 원래의 합의 두 배만큼 커집니다.

Estimate

코시 응집 테스트는 더 강력한 추정으로부터 따릅니다:

\sum _{n=1}^{\infty }f(n)\leq \sum _{n=0}^{\infty }2^{n}f(2^{n})\leq \ 2\sum _{n=1}^{\infty }f(n),

이것은 확장된 실수(extended real numbers)의 부등식으로 이해되어야 합니다. 증명의 본질적인 요점은 조화 급수(harmonic series)의 발산의 오렘의(Oresme's) 증명을 패턴화된 것을 따릅니다.

첫 번째 부등식을 보기 위해, 원래 급수의 항은 길이가 2의 거듭제곱인 실행으로 재-괄호화되고 각 실행은 각 항을 해당 실행에서 가장-큰 항으로 대체함으로써 위로 경계집니다. 해당 항이 항상 첫 번째 항인데, 왜냐하면 항이 비-증가하는 것으로 가정되기 때문입니다.

{\begin{array}{rcccccccl}\displaystyle \sum \limits _{n=1}^{\infty }f(n)&=&f(1)&+&f(2)+f(3)&+&f(4)+f(5)+f(6)+f(7)&+&\cdots \\&=&f(1)&+&{\Big (}f(2)+f(3){\Big )}&+&{\Big (}f(4)+f(5)+f(6)+f(7){\Big )}&+&\cdots \\&\leq &f(1)&+&{\Big (}f(2)+f(2){\Big )}&+&{\Big (}f(4)+f(4)+f(4)+f(4){\Big )}&+&\cdots \\&=&f(1)&+&2f(2)&+&4f(4)&+&\cdots =\sum \limits _{n=0}^{\infty }2^{n}f(2^{n})\end{array}}

두 번째 부등식을 보기 위해, 이들 두 급수가 다시 2 길이의 거듭제곱의 실행으로 재-괄호화되지만, 아래에 보이는 것처럼 "오프셋"되므로, $\textstyle f(2^{n})$ 로 시작하는 $\textstyle 2\sum _{n=1}^{\infty }f(n)$ 의 실행은 $\textstyle f(2^{n})$ 으로 끝나는 $\textstyle \sum _{n=0}^{\infty }2^{n}f(2^{n})$ 의 실행의 끝에 일렬로 세우므로, 전자는 항상 후자의 "앞에" 정지합니다.

{\begin{array}{rcl}\sum \limits _{n=0}^{\infty }2^{n}f(2^{n})&=&f(1)+{\Big (}f(2)+f(2){\Big )}+{\Big (}f(4)+f(4)+f(4)+f(4){\Big )}+\cdots \\&=&{\Big (}f(1)+f(2){\Big )}+{\Big (}f(2)+f(4)+f(4)+f(4){\Big )}+\cdots \\&\leq &{\Big (}f(1)+f(1){\Big )}+{\Big (}f(2)+f(2)+f(3)+f(3){\Big )}+\cdots =2\sum \limits _{n=1}^{\infty }f(n)\end{array}}

Visualization of the above argument. Partial sums of the series $\textstyle \sum f(n)$ , $\sum 2^{n}f(2^{n})$ , and $2\sum f(n)$ are shown overlaid from left to right.

Integral comparison

"응집" 변환 $\textstyle f(n)\rightarrow 2^{n}f(2^{n})$ 은 $\textstyle f(x)\,\mathrm {d} x\rightarrow e^{x}f(e^{x})\,\mathrm {d} x$ 을 산출하는 적분 변수 치환 $\textstyle x\rightarrow e^{x}$ 을 소환합니다.

이 아이디어를 추구하여, 수렴에 대해 적분 테스트(integral test for convergence)는 단조 f의 경우에서 $\sum \limits _{n=1}^{\infty }f(n)$ 가 수렴하는 것과 $\displaystyle \int _{1}^{\infty }f(x)\,\mathrm {d} x$ 가 수렴하는 것은 필요충분 조건임을 우리에게 제공합니다. 치환 $\textstyle x\rightarrow 2^{x}$ 은 적분 $\displaystyle \log 2\,\int _{0}^{\infty }\!2^{x}f(2^{x})\,\mathrm {d} x$ 을 산출하고 또 다르 적분 테스트는 우리에게 응집된 급수 $\displaystyle \sum \limits _{n=0}^{\infty }2^{n}f(2^{n})$ 를 가져옵니다.

Examples

테스트는 n이 f에서 분모에서 처럼 나타나는 급수에 대해 유용할 수 있습니다. 이 종류의 가장 기본 예제에 대해, 조화 급수 $\textstyle \sum _{n=1}^{\infty }1/n$ 는 급수 $\textstyle \sum 1$ 로 변환되며, 이것은 분명히 발산합니다.

보다 복잡한 예제로, 다음을 취하십시오:

f(n):=n^{-a}(\log n)^{-b}(\log \log n)^{-c}

.

여기서 급수는 a > 1에 대해 명확히 수렴하고, a < 1에 대해 발산합니다. a = 1일 때, 응집 변환은 다음 급수를 제공합니다:

\sum n^{-b}(\log n)^{-c}

.

로그는 '왼쪽으로 이동합니다'. 그래서 a = 1일 때, 우리는 b > 1에 대해 수렴, b < 1에 대해 발산을 가집니다. b = 일 때, c의 값이 입력됩니다.

이 결과는 쉽게 일반화됩니다: 응집 테스트는, 반복적으로 적용되어, $k=1,2,3,\ldots$ 에 대해, 일반화된 베르트랑 급수

$\sum _{n\geq N}{\frac {1}{n\cdot \log n\cdot \log \log n\cdots \log ^{\circ (k-1)}n\cdot (\log ^{\circ k}n)^{\alpha }}}\quad \quad (N=\lfloor \exp ^{\circ k}(0)\rfloor +1)$

가 $\alpha >1$ 에 대해 수렴하고 $0<\alpha \leq 1$ 에 대해 발산함을 보이기 위해 사용될 수 있습니다.^[1] 여기서 $f^{\circ m}$ 는 다음

$f^{\circ m}(x):={\begin{cases}f(f^{\circ (m-1)}(x)),&m=1,2,3,\ldots ;\\x,&m=0.\end{cases}}$

이 되도록 함수 $f$ 의 m번째 합성적 반복(iterate)을 나타냅니다. 합의 아래쪽 극한, $N$ 은 급수의 모든 항이 양수가 되도록 선택되었습니다. 특히, 이들 급수는 임의적으로 느리게 수렴 또는 발산하는 무한 합의 예제를 제공합니다. 예를 들어, $k=2$ 및 $\alpha =1$ 의 경우에서, 부분 합은 $10^{10^{100}}$ (a 구골플렉스(googolplex)) 항 이후에 오직 10을 초과합니다; 그럼에도 불구하고 급수는 여전히 발산합니다.