Rolle's theorem

If a real-valued function $f$ is continuous on a closed interval $[a, b]$ , differentiable on the open interval $(a, b)$ , and $f (a) = f (b)$ , then there exists a $c$ in the open interval $(a, b)$ such that $f'(c) = 0$ .

미적분학(calculus)에서, 롤의 정리(Rolle's theorem) 또는 롤의 보조정리(Rolle's lemma)는 두 구별되는 점에서 같은 값에 도달하는 임의의 실수-값 미분-가능한 함수(differentiable function)는 그들 사이의 어딘가에 적어도 하나의 정류 점(stationary point)—즉, 일차 도함수 (함수의 그래프에 대한 접선의 기울기)가 영인 점—을 반드시 가져야 한다고 본질적으로 말합니다. 정리는 미셸 롤(Michel Rolle)의 이름을 따서 지어졌습니다.

Standard version of the theorem

만약 실수(real)-값 함수 f가 적절한 닫힌 구간(closed interval) [a, b] 위에 연속(continuous)이고, 열린 구간 (a, b) 위에 미분-가능(differentiable)이고, f(a) = f(b)이면, 다음을 만족하는 열린 구간(open interval) (a, b) 안에 적어도 하나의 c가 존재합니다:

f'(c)=0

.

롤의 정리의 이 버전은 평균 값 정리(mean value theorem)를 입증하기 위해 사용되며, 롤의 정리는 사실 그것의 특별한 경우입니다. 그것은 테일러의 정리(Taylor's theorem)의 증명에 대해 역시 기본입니다.

History

인도의 수학자 바스카라 II(Bhāskara II) (1114-1185)는 롤의 정리에 대한 지식을 믿었습니다.^[1] 비록 정리는 미셸 롤(Michel Rolle)의 이름을 따서 지어졌지만, 롤의 1691년 증명은 오직 다항 함수의 경우를 덮었습니다. 그의 증명은 미분 미적분학의 방법을 사용하지 않았으며, 그의 인생의 그 시점에서 그는 그것을 그릇된 것으로 여겼습니다. 그 정리는 1823년 평균 값 정리(mean value theorem)의 증명의 따름정리로 코시에 의해 처음으로 입증되었습니다.^[2] 이름 "롤의 정리"는 1834년 독일의 모리츠 빌헬름 드로비슈(Moritz Wilhelm Drobisch)와 1846년 이탈리아의 쥬스토 벨라비데스(Giusto Bellavitis)에 의해 처음으로 사용되었습니다.^[3]

Examples

First example

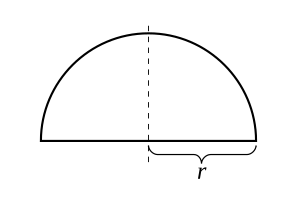
반지름 r > 0에 대해, 다음 함수를 생각해 보십시오:

$f(x)={\sqrt {r^{2}-x^{2}}},\quad x\in [-r,r].$

그것의 그래프는 원점에 중심을 둔 위쪽 반원입니다. 이 함수는 닫힌 간격 [−r,r] 위에 연속이고 열린 구간 (−r,r) 안에 미분-가능이지만, 끝점 −r 및 r에서 미분-가능이지 않습니다. f(−r) = f(r)이므로, 롤의 정리가 적용되고, 실제로, f의 도함수가 영이 되는 점이 있습니다. 정리는 심지어 함수가 끝점에서 미분-가능이지 않을 때 적용되는데 왜냐하면 그것이 오직 열린 구간 안에 미분-가능이 되는 함수를 요구하기 때문인 것에 주목하십시오.

Second example

만약 미분-가능성이 구간의 내부 점에서 실패하면, 롤의 정리의 결론은 유지되지 않을 수 있을 것입니다. 다음 절댓값(absolute value) 함수를 생각해 보십시오:

f(x)=|x|,\qquad x\in [-1,1].

그런-다음 $f (-1) = f (1)$ 이지만, $f'(c)$ 가 영인 것에 대해 −1과 1 사이에 $c$ 가 없습니다. 이것은 해당 함수가, 비록 연속이지만, $x = 0$ 에서 미분-가능이 아니기 때문입니다. $f$ 의 도함수가 $x = 0$ 에서 그의 부호를 바꾸지만, 값 0에 도달할 수 없음에 주목하십시오. 정리는 이 함수에 절대 적용될 수 없는데 왜냐하면 그것은 열린 간격 안의 모든 각 $x$ 에 대해 반드시 미분-가능이어야 하는 조건을 만족시키지 못하기 때문입니다. 어쨌든, 미분-가능성 요구-사항이 롤의 정리로부터 떨어지면, $f$ 는 여전히 열린 구간 $(a, b)$ 안의 임계 숫자(critical number)를 가질 것이지만, 그것은 (그래프에 표시된 절댓값의 경우에서 처럼) 수평 접선을 산출하지 못할 수 있을 것입니다.

Generalization

두 번째 예제는 롤의 정리에 대한 다음 일반화를 설명합니다:

$f (a) = f (b)$ 를 갖는 닫힌 구간 $[a, b]$ 위에 실수-값, 연속 함수 $f$ 를 생각해 보십시오. 만약 열린 구간 (a, b) 안의 모든 각 $x$ 에 대해 오른쪽 극한(right-hand limit)

f'(x^{+}):=\lim _{h\to 0^{+}}{\frac {f(x+h)-f(x)}{h}}

및 왼쪽 극한

f'(x^{-}):=\lim _{h\to 0^{-}}{\frac {f(x+h)-f(x)}{h}}

이 확장된 실수 직선(extended real line) $[-\infty, \infty]$ 에서 존재하면, 두 극한

f'(c^{+})\quad {\text{and}}\quad f'(c^{-})

의 (확장된 실수 직선에서) 하나가 ≥ 0이고 나머지 하나는 ≤ 0을 만족하는 열린 구간 $(a, b)$ 안의 어떤 숫자 $c$ 가 있습니다. 만약 오른쪽 및 왼쪽 극한이 모든 각 $x$ 에 대해 일치하면, 그들은 특히 $c$ 에 대해 일치하므로, $f$ 의 도함수는 $c$ 에서 존재하고 영과 같습니다.

Remarks

만약 $f$ 가 볼록 또는 오목이면, 오른쪽 및 왼쪽 도함수는 모든 각 내부 점에서 존재하므로, 위의 극한은 존재하고 실수입니다.
정리의 이 일반화된 버전은, 한쪽 도함수가 단조롭게 증가(monotonically increasing)할 때, 볼록성(convexity)을 입증하기 위해 충분합니다:^[4]

f'(x^{-})\leq f'(x^{+})\leq f'(y^{-}),\qquad x<y.

Proof of the generalized version

롤의 정리와 일반화의 표준 버전에 대한 증명이 매우 비슷하므로, 우리는 일반화를 입증합니다.

증명의 아이디어는, 만약 $f (a) = f (b)$ 이면, $f$ 가 $a$ 와 $b$ 사이의 어딘가에, 말하자면 $c$ 에서, 최댓값 또는 최솟값(maximum or minimun) 중 하나에 반드시 도달하고, 함수는 $c$ 에서 증가에서 감소로 (또는 반대 방향으로) 반드시 바뀌는 것을 주장하는 것입니다. 특히, 만약 도함수가 존재하면, 그것은 $c$ 에서 반드시 영이어야 합니다.

가정에 의해, $f$ 가 $[a, b]$ 위에 연속이고, 극단 값 정리(extreme value theorem)에 의해 $[a, b]$ 안에 그의 최댓값과 그의 최솟값 둘 다에 도달합니다. 만약 이들이 $[a, b]$ 의 끝점에서 둘 다 도달되면, $f$ 는 $[a, b]$ 위에 상수(constant)이고 그래서 $f$ 의 도함수는 $(a, b)$ 안의 모든 각 점에서 영입니다.

그런-다음 최댓값이 $(a, b)$ 의 내부 점(interior point) $c$ 에서 얻어진다고 가정합니다 (최솟값에 대한 논증은 매우 유사하고, 단지 $- f$ 를 고려하십시오). 우리는 위의 오른쪽 및 왼쪽 극한을 별도로 검사해야 합니다.

$c + h$ 가 $[a, b]$ 안에 있는 것을 만족하는 실수 $h$ 에 대해, 값 $f (c + h)$ 는 $f (c)$ 보다 작거나 같은데, 왜냐하면 $f$ 는 $c$ 에서 그의 최댓값을 도달하기 때문입니다. 그러므로, 모든 각 $h > 0$ 에 대해,

{\frac {f(c+h)-f(c)}{h}}\leq 0,

따라서

f'(c+):=\lim _{h\to 0^{+}}{\frac {f(c+h)-f(c)}{h}}\leq 0,

여기서 극한은 가정에 의해 존재하며, 그것은 음의 무한대일 수 있을 것입니다.

비슷하게, 모든 각 $h < 0$ 에 대해, 부등식은 방향이 바뀌는데 왜냐하면 분모가 이제 음수이기 때문이고, 우리는 다음을 얻습니다:

{\frac {f(c+h)-f(c)}{h}}\geq 0,

따라서

f'(c-):=\lim _{h\to 0^{-}}{\frac {f(c+h)-f(c)}{h}}\geq 0,

여기서 극한은 양의 무한대일 수 있을 것입니다.

마지막으로, 위의 오른쪽- 및 왼쪽 극한이 일치할 때 (특히 $f$ 가 미분-가능일 때), $c$ 에서 $f$ 의 도함수는 반드시 영이어야 합니다.

(대안적으로, 우리는 직접 페르마의 정류 점의 정리(Fermat's stationary point theorem)를 적용할 수 있습니다.)

Generalization to higher derivatives

우리는, $f$ 가 같은 값과 더 큰 규칙성을 갖는 더 많은 점을 가지는 것을 요구함으로써, 롤의 정리를 역시 일반화할 수 있습니다. 구체적으로, 다음임을 가정합니다:

함수 $f$ 는 닫힌 구간 [a,b] 위에 $n - 1$ 번 연속적으로 미분-가능(continuously differentiable)이고 $n$ 번째 도함수는 열린 구간 $(a, b)$ 위에 존재하고,
1에서 $n$ 까지 모든 각 $k$ 에 대해 $f (a k) = f (b k)$ 를 만족하는 $[a, b]$ 안의 $a 1 < b 1 \leq a 2 < b 2 \leq \dots \leq a n < b n$ 에 의해 제공되는 $n$ 구간이 있습니다. 그런-다음 $c$ 에서 $f$ 의 $n$ 번째 도함수가 영을 만족하는 $(a, b)$ 안의 숫자 $c$ 가 있습니다.

$f$ 의 $n$ 번째 도함수에 관하여 요구-사항은 위의 일반화에서 처럼 약화될 수 있으며, $f$ 의 자리에 $f (n - 1)$ 를 갖는 위에 정의된 오른쪽 및 왼쪽 극한에 대해 대응하는 (아마도 더 약한) 역설을 제공합니다.

특별히, 정리의 이 버전은 만약 충분한 횟수의 미분-가능한 함수가 $n$ 근을 가지면 (그래서 그것들은 같은 값, 즉 0을 가지면), $f (n - 1)$ 이 사라지는 내부 점이 있음을 주장합니다.

Proof

증명은 수학적 귀납법(mathematical induction)을 사용합니다. 경우 $n = 1$ 은 단순히 롤의 정리의 표준 버전입니다. $n > 1$ 에 대해, 일반화가 $n - 1$ 에 대해 참이라고 귀납법 가설을 취하십시오. 우리는 $n$ 에 대해 그것을 입증하기를 원합니다. 함수 $f$ 는 정리의 가설을 만족시키는 것으로 가정합니다. 롤의 정리의 표준 버전에 의해, 1에서 $n$ 까지 모든 각 정수 $k$ 에 대해, $f'(c k) = 0$ 를 만족하는 열린 구간 $(a k, b k)$ 안에 $c k$ 가 있습니다. 그러므로, 일차 도함수는 $n - 1$ 닫힌 구간 $[c 1, c 2], \dots, [c n - 1, c n]$ 위에 가정을 만족시킵니다. 귀납법 가설에 의해, $c$ 에서 $f'$ 의 $(n - 1)$ 차 도함수가 영을 만족하는 $c$ 가 있습니다.

Generalizations to other fields

롤의 정리는 실수에 걸쳐 미분-가능한 함수의 속성이며, 이것은 순서화 필드(ordered field)입니다. 이를테면, 그것은 다른 필드(fields)에 대해 일반화하지는 않지만, 다음과 같은 따름정리가 있습니다: 만약 실수 다항식이 실수에 걸쳐 인수화되면 (그의 모든 근을 가지면), 그의 도함수도 마찬가지입니다. 우리는 필드의 이 속성을 롤의 속성( Rolle's property)으로 부를 수 있을 것입니다.^{[citation needed]} 보다 일반적인 필드는 항상 미분-가능 함수를 가지지는 않지만, 그들은 항상 다항식을 가지며, 이것은 기호적으로 미분-가능이 될 수 있습니다. 비슷하게, 보다 일반적인 필드는 차수를 가지지 않을 수 있을 것이지만, 우리는 그것은 필드 안에 놓이는 다항식의 근의 개념을 가집니다.

따라서 롤의 정리는 실수가 롤의 속성을 가지고 있음을 보입니다. 복소수(complex numbers)와 같은 임의의 대수적으로 닫힌 필드는 롤의 속성을 가집니다. 어쨌든, 유리수는 그렇지 않습니다 – 예를 들어, $x 3 - x = x (x - 1)(x + 1)$ 는 유리수에 걸쳐 인수화되지만, 다음의 그의 도함수 그렇지 않습니다.

3x^{2}-1=3\left(x-{\tfrac {1}{\sqrt {3}}}\right)\left(x+{\tfrac {1}{\sqrt {3}}}\right),

어떤 필드가 롤의 속성을 만족시키는가에 대한 질문이 (Kaplansky 1972)에서 제기되었습니다.^[5] 유한 필드(finite field)에 대해, 그 답은 오직 $F 2$ 및 $F 4$ 이 롤의 속성을 가지는 것입니다.^[6]^[7]

복소수 버전에 대해, 베어호에 인덱스(Voorhoeve index)를 참조하십시오.

References

^ Gupta, R. C. Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures. p. 156.
^ Besenyei, A. (September 17, 2012). "A brief history of the mean value theorem" (PDF).
^ See Cajori, Florian. A History of Mathematics. p. 224.
^ Artin, Emil (1964) [1931], The Gamma Function, translated by Butler, Michael, Holt, Rinehart and Winston, pp. 3–4
^ Kaplansky, Irving (1972), Fields and Rings
^ Craven, Thomas; Csordas, George (1977), "Multiplier sequences for fields", Illinois J. Math., 21 (4): 801–817
^ Ballantine, C.; Roberts, J. (January 2002), "A Simple Proof of Rolle's Theorem for Finite Fields", The American Mathematical Monthly, 109 (1), Mathematical Association of America: 72–74, doi:10.2307/2695770, JSTOR 2695770

External links

"Rolle theorem", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Rolle's and Mean Value Theorems at cut-the-knot.
Mizar system proof: http://mizar.org/version/current/html/rolle.html#T2

[1] Gupta, R. C. Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures. p. 156.

[2] Besenyei, A. (September 17, 2012). "A brief history of the mean value theorem" (PDF).

[3] See Cajori, Florian. A History of Mathematics. p. 224.

[4] Artin, Emil (1964) [1931], The Gamma Function, translated by Butler, Michael, Holt, Rinehart and Winston, pp. 3–4

[5] Kaplansky, Irving (1972), Fields and Rings

[6] Craven, Thomas; Csordas, George (1977), "Multiplier sequences for fields", Illinois J. Math., 21 (4): 801–817

[7] Ballantine, C.; Roberts, J. (January 2002), "A Simple Proof of Rolle's Theorem for Finite Fields", The American Mathematical Monthly, 109 (1), Mathematical Association of America: 72–74, doi:10.2307/2695770, JSTOR 2695770

[1]

[2]

[3]

[4]

[5]

[6]

[7]