Real coordinate space

수학(mathematics)에서, 차원(dimension) $n$ 의 실수 좌표 공간(real coordinate space)은, $R n$ (/ɑːrˈɛn/ ar-EN) 또는 $\mathbb {R} ^{n}$ 으로 표시되며, 실수의 $n$ -튜플( $n$ -tuples)의 집합, 즉, $n$ 실수의 모든 수열의 집합입니다. 성분-별 덧셈과 스칼라 곱셈과 함께, 그것은 실수 벡터 공간(real vector space)이고, 그것의 원소는 좌표 벡터(coordinate vectors)라고 불립니다.

실수 벡터 공간의 원소의 기저(basis)에 걸쳐 좌표(coordinates)는 벡터 공간의 차원과 같은 차원의 실수 좌표 공간을 형성합니다. 유사하게, 차원 $n$ 의 유클리드 공간(Euclidean space)의 점의 데카르트 좌표(Cartesian coordinates)는 차원 $n$ 의 실수 좌표 공간을 형성합니다.

벡터, 점 및 좌표 벡터 사이의 이들 일-대-일 대응(one to one correspondences)은 좌표 공간과 좌표 벡터의 이름을 설명합니다. 그것은 실수 좌표 공간을 연구하기 위해 기하학적 용어와 방법을 사용할 수 있고, 반대로, 기하학에서 미적분(calculus)의 방법을 사용할 수 있습니다. 기하학의 이러한 접근은 17세기 르네 데카르트(René Descartes)에 의해 도입되었습니다. 그것은 유클리드 공간에서 점을 찾고 이를 사용하여 계산할 수 있으므로 널리 사용됩니다.

Definition and structures

임의의 자연수 $n$ 에 대해, 집합(set) $R n$ 은 실수 ( $R$ )의 모든 $n$ -튜플로 구성됩니다. 그것은 " $n$ -차원 실수 공간" 또는 "실수 $n$ -공간"이라고 불립니다.

$R n$ 의 원소는 따라서 $n$ -튜플이고, 다음으로 씁니다: $(x_{1},x_{2},\ldots ,x_{n})$ 여기서 각 $x i$ 는 실수입니다. 따라서, 다변수 미적분(multivariable calculus)에서, 여러 실수 변수의 함수의 도메인(domain)과 실수 벡터-값 함수(vector valued function)의 코도메인은 일부 $n$ 에 대해 $R n$ 의 부분집합(subsets)입니다.

실수 $n$ -공간은 특히 다음과 같은 몇 가지 추가적인 속성을 가집니다:

구성 성분-별(componentwise) 덧셈과 스칼라 곱셈(scalar multiplication)과 함께, 그것은 실수 벡터 공간(real vector space)입니다. 모든 각 $n$ -차원 실수 벡터 공간은 그것과 동형적(isomorphic)입니다.
점 곱(dot product, 성분의 항별 곱의 합)과 함께, 그것은 안의 곱 공간(inner product space)입니다. 모든 각 $n$ -차원 실수 안의 곱 공간은 그것과 동형적입니다.
모든 각 안의 곱 공간으로서, 그것은 토폴로지적 공간(topological space)이고, 토폴로지적 벡터 공간(topological vector space)입니다.
그것은 유클리드 공간(Euclidean space)과 실수 아핀 공간(affine space)이고, 모든 각 유클리드 또는 아핀 공간은 그것과 동형적입니다.
그것은 해석적 매니폴드(analytic manifold)이고, 정의에 의해, 매니폴드(manifolds)가, 각 점 근처에서, $R n$ 의 열린 부분집합(open subset)과 동형일 때, 모든 매니폴드의 원형으로 고려될 수 있습니다.
그것은 대수적 다양체(algebraic variety)이고, 모든 각 실수 대수적 다양체(real algebraic variety)는 $R n$ 의 부분-집합입니다.

$R n$ 의 이들 속성과 구조는 거의 모든 수학의 영역과 통계, 확률 이론, 및 물리학의 많은 부분과 같은 그것들의 응용 도메인에서 기본이 됩니다.

The domain of a function of several variables

$n$ 실수 변수의 임의의 함수 $f (x 1, x 2, ..., x n)$ 는 $R n$ 위에 (즉, 그것의 도메인으로 $R n$ 을 갖는) 함수로 고려될 수 있습니다. 개별적으로 고려되는 여러 변수 대신 실수 $n$ -공간의 사용은 표기법을 단순화하고 합리적인 정의를 제안할 수 있습니다. $n = 2$ 에 대해, 다음 형식의 함수 합성(function composition)을 생각해 보십시오: $F(t)=f(g_{1}(t),g_{2}(t)),$ 여기서 함수 $g 1$ 와 $g 2$ 는 연속(continuous)입니다. 만약 다음이면

$\forall x 1 \in R : f (x 1, \cdot)$ is continuous (by $x 2$ )
$\forall x 2 \in R : f (\cdot, x 2)$ is continuous (by $x 1$ )

$F$ 는 반드시 연속이 아닙니다. 연속성은 더 강력한 조건입니다: 자연 $R 2$ 토폴로지 (아래에 설명됨)에서 $f$ 의 연속성은, 역시 다변수 연속성이라고 불리며, 이는 합성 $F$ 의 연속성에 대해 충분입니다.

Vector space

좌표 공간 $R n$ 은 선형성(linearity)의 구조의 덧셈을 갖는 실수 필드(field)에 걸쳐 $n$ -차원 벡터 공간(vector space)을 형성하고, 종종 여전히 $R n$ 으로 표시됩니다. 벡터 공간으로서 $R n$ 위에 연산은 전형적으로 다음에 의해 정의됩니다: $\mathbf {x} +\mathbf {y} =(x_{1}+y_{1},x_{2}+y_{2},\ldots ,x_{n}+y_{n})$ $\alpha \mathbf {x} =(\alpha x_{1},\alpha x_{2},\ldots ,\alpha x_{n}).$ 영 벡터(zero vector)는 다음에 의해 제공됩니다: $\mathbf {0} =(0,0,\ldots ,0)$ 그리고 벡터 $x$ 의 덧셈 역(additive inverse)은 다음에 의해 제공됩니다: $-\mathbf {x} =(-x_{1},-x_{2},\ldots ,-x_{n}).$

이 구조는 임의의 $n$ -차원 실수 벡터 공간이 벡터 공간 $R n$ 과 동형적이기 때문에 중요합니다.

Matrix notation

표준 행렬(matrix) 표기법에서, $R n$ 의 각 원소는 전형적으로 다음 열 벡터(column vector)로 작성됩니다: $\mathbf {x} ={\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{bmatrix}}$ 그리고 때때로 행 벡터(row vector)로 쓰입니다: $\mathbf {x} ={\begin{bmatrix}x_{1}&x_{2}&\cdots &x_{n}\end{bmatrix}}.$

좌표 공간 $R n$ 은 그런-다음 덧셈과 스칼라 곱셈(scalar multiplication)의 보통의 행렬 연산을 갖는 모든 $n \times 1$ 열 벡터(column vectors), 또는 모든 $1 \times n$ 행 벡터(row vectors)의 공간으로 해석될 수 있습니다.

$R n$ 에서 $R m$ 으로의 선형 변환(Linear transformations)은 ( $R n$ 의 원소가 열 벡터일 때) 왼쪽(left) 곱셈을 통해 $R n$ 의 원소에 작용하고 (그것들이 열 벡터일 때) 오른쪽 곱셈을 통해 $R m$ 의 원소에 작용하는 $m \times n$ 행렬로 쓸 수 있습니다. 행렬 곱셈(matrix multiplication)의 특별한 경우, 왼쪽 곱셈에 대해 공식은 다음과 같습니다: $(A{\mathbf {x} })_{k}=\sum _{l=1}^{n}A_{kl}x_{l}$

임의의 선형 변환은 연속 함수(continuous function)입니다 (아래 참조하십시오). 역시, 행렬은 $R n$ 에서 $R m$ 로의 열린 맵(open map)을 정의하는 것과 행렬의 랭크(rank of the matrix)가 $m$ 과 같은 것은 필요충분 조건입니다.

Standard basis

좌표 공간 $R n$ 은 표준 기저로 제공됩니다: ${\begin{aligned}\mathbf {e} _{1}&=(1,0,\ldots ,0)\\\mathbf {e} _{2}&=(0,1,\ldots ,0)\\&{}\;\;\vdots \\\mathbf {e} _{n}&=(0,0,\ldots ,1)\end{aligned}}$

이것이 기저임을 확인하기 위해, $R n$ 에서 임의적인 벡터는 다음 형식으로 고유하게 쓸 수 있음을 주목하십시오: $\mathbf {x} =\sum _{i=1}^{n}x_{i}\mathbf {e} _{i}.$

Geometric properties and uses

Orientation

많은 다른 필드와 달리, 실수가 순서화된 필드(ordered field)를 구성한다는 사실은 $R n$ 위에 방향 구조(orientation structure)를 산출합니다. $R n$ 에서 자체로의 완전한-랭크(full-rank) 선형 맵은 그것의 행렬의 행렬식(determinant)의 부호(sign)에 따라 공간의 방향을 보존하거나 반대로 바꿉니다. 만약 우리가 좌표 (또는, 다시 말해서, 기저의 원소)를 순열(permutes)하면, 결과 방향은 순열의 패리티(parity of the permutation)에 따라 달라질 것입니다.

$R n$ 또는 그 안의 도메인의 미분-동형(Diffeomorphisms)은, 영 야코비(Jacobian)를 피하기 위한 미덕에 의해, 방향-보존하고 방향-역전하는 것으로 분류됩니다. 그것은 응용이 전기-동역학(electrodynamics)을 포함하는 미분 형식(differential forms)의 이론에 중요한 결과를 가져옵니다.

이 구조의 또 다른 징후는 $R n$ 에서 점 반사(point reflection)가 $n$ 의 짝수성(evenness of $n$ )에 따라 다른 속성을 가진다는 것입니다. 짝수 $n$ 에 대해, 그것은 방향을 보존하고, 반면에 홀수 $n$ 에 대해 반전됩니다 (부적절한 회전(improper rotation)을 참조하십시오).

Affine space

아핀 공간으로 이해되는 $R n$ 은 벡터 공간으로서의 $R n$ 이 평행이동(translations)에 의해 동작(acts)하는 같은 공간입니다. 반대로, 벡터는 "두 점 사이의 차이"로 이해되어야 하며, 보통 두 점을 연결하는 방향화된 선분에 의해 표시됩니다. 구별은 원점(origin)이 어디에서나 평행이동될 수 있기 때문에 아핀 $n$ -공간에서 어디로 가야 하는지에 대한 정식의(canonical) 선택이 없다고 말합니다.

Convexity

The n-simplex (see below) is the standard convex set, that maps to every polytope, and is the intersection of the standard $(n + 1)$ affine hyperplane (standard affine space) and the standard $(n + 1)$ orthant (standard cone).

$R n$ 과 같은 실수 벡터 공간에서, 벡터의 모든 비-음의 선형 조합을 포함하는 볼록한 원뿔(cone)을 정의할 수 있습니다. 아핀 공간에서 대응하는 개념은 볼록 조합 (합이 1이 되는 비-음의 선형 조합)만 허용하는 볼록 집합(convex set)입니다.

보편 대수(universal algebra)의 언어에서, 벡터 공간은 벡터의 유한 합에 대응하는 계수의 유한 수열의 보편 벡터 공간 $R \infty$ 에 걸쳐 대수이고, 반면에 아핀 공간은 (합해서 1인 유한 수열의) 이 공간에서 보편 아핀 초평면에 걸쳐 대수이고, 원뿔은 (비-음의 숫자의 유한 수열의) 보편 수직분면(orthant)에 걸쳐 대수이고, 볼록 집합은 (합해서 1인 비-음의 숫자의 유한 수열의) 보편 심플렉스(simplex)에 걸쳐 대수입니다. 이것은 "좌표 위에 (가능한) 제한을 갖는 합"이라는 측면에서 공리를 기하학화합니다.

볼록 해석학의 또 다른 개념은 $R n$ 에서 실수로의 볼록 함수(convex function)로, 점(points)의 볼록 조합 위에 그것의 값과 같은 계수를 갖는 점의 값의 합 사이의 부등식(inequality)을 통해 정의됩니다.

Euclidean space

다음 점 곱(dot product)은 $\mathbf {x} \cdot \mathbf {y} =\sum _{i=1}^{n}x_{i}y_{i}=x_{1}y_{1}+x_{2}y_{2}+\cdots +x_{n}y_{n}$ 벡터 공간 $R n$ 위에 노름(norm) $| x | = \sqrt x \cdot x$ 을 형성합니다. 만약 모든 각 벡터가 유클리드 노름(Euclidean norm)을 가지면, 임의의 점의 쌍에 대해 다음 거리는 아핀 구조 외에 $R n$ 위에 메트릭 공간(metric space) 구조를 제공하여 정의됩니다: $d(\mathbf {x} ,\mathbf {y} )=\|\mathbf {x} -\mathbf {y} \|={\sqrt {\sum _{i=1}^{n}(x_{i}-y_{i})^{2}}}$ 벡터 공간 구조에 대해, 점 곱과 유클리드 거리가 보통 특별한 설명 없이 $R n$ 에 존재한다고 가정됩니다. 어쨌든, 실수 $n$ -공간과 유클리드 $n$ -공간은 엄밀하게 말하자면 별개의 대상입니다. 임의의 유클리드 $n$ -공간은 점 곱과 유클리드 거리가 위에 표시된 데카르트(Cartesian)라고 불리는 형식을 가지는 좌표 시스템(coordinate system)을 가집니다. 그러나 유클리드 공간 위에 많은 데카르트 좌표 시스템이 있습니다.

반대로, 유클리드 메트릭에 대해 위의 공식은 $R n$ 위에 표준 유클리드 구조를 정의하지만, 그것이 유일하게 가능한 것은 아닙니다. 실제로, 임의의 양수-한정 이차 형식(positive-definite quadratic form) $q$ 는 자체 "거리" $\sqrt q (x - y)$ 를 정의하지만, 다음과 같은 의미에서 유클리드 형식과 크게 다르지 않습니다: $\exists C_{1}>0,\ \exists C_{2}>0,\ \forall \mathbf {x} ,\mathbf {y} \in \mathbb {R} ^{n}:C_{1}d(\mathbf {x} ,\mathbf {y} )\leq {\sqrt {q(\mathbf {x} -\mathbf {y} )}}\leq C_{2}d(\mathbf {x} ,\mathbf {y} ).$ 메트릭의 그러한 변경은 일부 그것의 속성, 예를 들어 완비 메트릭 공간(complete metric space)이라는 속성을 보존합니다. 이것은 역시 $R n$ 의 완전한-랭크 선형 변환, 또는 그것의 아핀 변환(affine transformation)이 일부 고정된 $C 2$ 에 의한 것보다 더 거리를 확대하지 않고, 거리를 $1 / C 1$ 배수보다 더 작게, 고정된 유한 숫자 배수보다 더 작게 만들지 않음을 의미합니다.

앞서 언급된 메트릭 함수의 동등성은 $\sqrt q (x - y)$ 가 $M (x - y)$ 로 대체되면 유지되며, 여기서 $M$ 은 차수 1의 임의의 볼록 양의 동차 함수, 즉, 벡터 노름입니다 (유용한 예제에 대해 민코프스키 거리를 참조하십시오). $R n$ 위에 임의의 "자연스러운" 메트릭이 유클리드 메트릭과 특별히 다르지 않다는 사실 때문에, $R n$ 은 전문적인 수학적 연구에서도 항상 유클리드 $n$ -공간과 구별되지 않습니다.

In algebraic and differential geometry

매니폴드(manifold)의 정의가 그것의 모델 공간이 $R n$ 이어야 할 필요는 없지만, 이 선택은 미분 기하학(differential geometry)에서 가장 공통적이고, 거의 배타적인 선택입니다.

다른 한편으로, 휘트니 삽입 정리(Whitney embedding theorems)는 임의의 실수 미분-가능 $m$ -차원 매니폴드가 $R 2 m$ 에 삽입(embedded)될 수 있다고 명시합니다.

Other appearances

$R n$ 위에 고려되는 다른 구조는 유사-유클리드 공간, 상징적 구조(symplectic structure) (짝수 $n$ ), 및 접촉 구조 (홀수 $n$ ) 중 하나를 포함합니다. 모든 이들 구조는, 좌표-없는 방식으로 정의될 수 있지만, 좌표에서 표준 (및 합리적으로 단순한) 형식을 허용합니다.

$R n$ 은 역시 복소수 켤레(complex conjugation)에 불변인 $C n$ 의 실수 벡터 부분공간입니다; 역시 복잡화(complexification)를 참조하십시오.

Polytopes in Rⁿ

임의의 $n$ 에 대해 $R n$ 공간에서 간단한 표현을 가지고, 실수 $n$ -공간에서 임의의 아핀 좌표 시스템을 시각화하기 위해 사용될 수 있는 세 가지 폴리토프(polytopes)의 가족이 있습니다. 초-입방체(hypercube)의 꼭짓점은 좌표 $(x 1, x 2, ..., x n)$ 를 가지며 여기서 각 $x k$ 는 전형적으로 0 또는 1의 두 값 중 하나를 취합니다. 어쨌든, 0과 1 대신에 예를 들어 −1과 1와 같은 임의의 두 숫자가 선택될 수 있습니다. $n$ -초입방체는 실수 직선 위에 $n$ 개의 동일한 구간 (예를 들어, 단위 구간 $[0,1]$ )의 데카르트 곱으로 생각될 수 있습니다. $n$ -차원 부분집합으로서, 그것은 다음과 같은 $2 n$ 부등식의 시스템으로 설명될 수 있습니다: $[0,1]$ 에 대해, ${\begin{matrix}0\leq x_{1}\leq 1\\\vdots \\0\leq x_{n}\leq 1\end{matrix}}$ 그리고 $[-1,1]$ 에 대해,

${\begin{matrix}|x_{1}|\leq 1\\\vdots \\|x_{n}|\leq 1\end{matrix}}$

교차-폴리토프(cross-polytope)의 각 꼭짓점은, 어떤 $k$ 에 대해, (그것이 부호까지 $k$ 번째 표준 기저 벡터임을 만족하는) ±1과 같은 $x k$ 좌표를 가지고 모든 다른 좌표는 0과 같습니다. 이것은 초입방체의 이중 폴리토프(dual polytope)입니다. $n$ -차원 부분집합으로서, 그것은 절댓값(absolute value) 연산을 사용하는 단일 부등식으로 설명될 수 있습니다: $\sum _{k=1}^{n}|x_{k}|\leq 1\,,$ 그러나 이것은 마찬가지로 $2 n$ 선형 부등식 시스템으로 표현될 수 있습니다.

간단하게 열거할 수 있는 좌표를 갖는 세 번째 폴리토프는 그것의 꼭짓점 $n$ 표준 기저 벡터와 원점 $(0, 0, ..., 0)$ 인 표준 심플렉스(standard simplex)입니다. $n$ -차원 부분집합으로서, 그것은 $n + 1$ 선형 부등식의 시스템으로 설명됩니다: ${\begin{matrix}0\leq x_{1}\\\vdots \\0\leq x_{n}\\\sum \limits _{k=1}^{n}x_{k}\leq 1\end{matrix}}$ 모든 "≤"를 "<"로 대체함은 이들 폴리토프의 내부를 제공합니다.

Topological properties

$R n$ 의 토폴로지적 구조(topological structure) (표준 토폴로지, 유클리드 토폴로지, 또는 보통의 토폴로지라고 불림)는 데카르트 곱에서만 얻을 수 있는 것은 아닙니다. 그것은 역시 위에서 논의한 유클리드 메트릭에 의해 유도된 자연 토폴로지(natural topology)와 동일합니다: 집합이 유클리드 토폴로지에서 열린 것과 그것은 각 점 주위에 열린 공 을 포함하는 것은 필요충분(iff) 조건입니다. 역시, $R n$ 은 선형 토폴로지적 공간 (위의 선형 맵의 연속성을 참조)이고, 선형 구조와 호환되는 가능한 (비-자명한) 토폴로지는 단 하나뿐입니다. 등거리-변환(isometries)이 아닌 $R n$ 에서 자체로의 많은 열린 선형 맵이 있기 때문에, 같은 토폴로지에 해당하는 $R n$ 위에 많은 유클리드 구조가 있을 수 있습니다. 실제로, 그것은 선형 구조에도 크게 의존하지 않습니다: $R n$ 을 자체 위로의, 또는 유클리드 열린 공이나 초입방체의 내부와 같은 그것의 부분 위로의 많은 비-선형 미분-동형 (및 기타 위상-동형)이 있습니다.

$R n$ 은 토폴로지적 차원 $n$ 을 가집니다. $R n$ 의 토폴로지 위에 중요한 결과는, 즉 피상적인 것과 거리가 먼, 브라우어(Brouwer)의 도메인의 불변성(invariance of domain)입니다. $R n$ 의 또 다른 열린 부분집합과 위상-동형인 (그것의 부분공간 토폴로지를 갖는) $R n$ 의 임의의 부분집합은 자체로 열린 것입니다. 이것의 즉각적인 결과는 $m \neq n$ 이면 $R m$ 이 $R n$ 과 위상-동형이 아니라는 것입니다 – 그럼에도 불구하고 증명하기 어려운 직관적으로 "명백한" 결과입니다.

토폴로지적 차원에서 차이에도 불구하고, 소박한 인식과는 달리, 더 작은 차원의 실수 공간을 $R n$ 위로의 연속적이고 전사적으로 매핑하는 것이 가능합니다. (매끄럽지는 않지만) 연속적인 공간-채우는 곡선 ( $R 1$ 의 이미지)이 가능합니다.

Examples

Empty column vector,
the only element of

R 0

R 1

n ≤ 1

$0 \leq n \leq 1$ 의 경우는 어떤 새로운 것을 제공하지 않습니다: $R 1$ 은 실수 직선(real line)이고, 반면 $R 0$ (빈 열 벡터를 포함하는 공간)은 영 벡터 공간(zero vector space)으로 이해되는 한원소(singleton)입니다. 어쨌든, 다른 $n$ 을 설명하는 이론의 자명한(trivial) 사례로 이들을 포함하는 것이 유용합니다.

n = 2

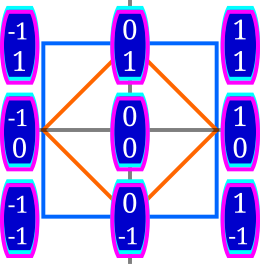
n = 3

n = 4

$R 4$ 는 각 $x k$ 가 0 또는 1인 16개 점 $(x 1, x 2, x 3, x 4)$ 이 테서랙트(tesseract) (그림), 4-초입방체 (위를 참조)의 꼭짓점이라는 사실을 사용하여 상상할 수 있습니다.

$R 4$ 의 첫 번째 주요 용도는 시공간 모델입니다: 3개의 공간 좌표와 1개의 시간 좌표입니다. 4차원은 갈릴레이(Galilei) 이후로 그러한 모델에 사용되었지만, 이것은 보통 상대성 이론(theory of relativity)과 관련이 있습니다. 그러나 이론의 선택은 다른 구조로 이어집니다: 갈릴레이의 상대성에서 $t$ 좌표가 특권이지만, 아인슈타인의 상대성에서 그렇지 않습니다. 특수 상대성은 민코프스키 공간(Minkowski space)에서 설정됩니다. 일반 상대성은 가장 실용적인 목적을 위해 곡선화된 메트릭(curved metric)을 갖는 $R 4$ 로 생각될 수 있는 곡선화된 공간을 사용합니다. 이들 구조 중 어느 것도 $R 4$ 위에 (양수-한정) 메트릭을 제공하지 않습니다.

유클리드 $R 4$ 는 역시 예를 들어 쿼터니언, 4-차원 실수 대수 자체와의 관계로 인해 수학자들의 관심을 끌고 있습니다. 일부 정보에 대해 4-차원 유클리드 공간에서 회전을 참조하십시오.

미분 기하학에서, $n = 4$ 는 $R n$ 이 비-표준 미분 구조(differential structure)를 인정하는 유일한 경우입니다: 이국적인 R⁴를 참조하십시오.

Norms on $R n$

우리는 벡터 공간(vector space) $R n$ 위에 많은 노름을 정의할 수 있습니다. 몇 가지 공통적인 예제는 다음과 같습니다:

p-노름, 모든 $\mathbf {x} \in \mathbb {R} ^{n}$ 에 대해 ${\textstyle \|\mathbf {x} \|_{p}:={\sqrt[{p}]{\sum _{i=1}^{n}|x_{i}|^{p}}}}$ 에 의해 정의되며 여기서 $p$ 는 양의 정수입니다. 경우 $p=2$ 는 매우 중요한데, 왜냐하면 그것은 정확하게 유클리드 노름(Euclidean norm)이기 때문입니다.
$\infty$ -노름 또는 최대 노름(maximum norm), 모든 $\mathbf {x} \in \mathbb {R} ^{n}$ 에 대해 $\|\mathbf {x} \|_{\infty }:=\max\{x_{1},\dots ,x_{n}\}$ 에 의해 정의됩니다. 이것은 모든 p-노름의 극한입니다: ${\textstyle \|\mathbf {x} \|_{\infty }=\lim _{p\to \infty }{\sqrt[{p}]{\sum _{i=1}^{n}|x_{i}|^{p}}}}$ .

정말 놀랍고 도움이 되는 결과는 $R n$ 위에 정의된 모든 각 노름이 동등하다(equivalent)는 것입니다. 이것은 $R n$ 위에 두 개의 임의적인 노름 $\|\cdot \|$ 와 $\|\cdot \|'$ 에 대해, 모든 $\mathbf {x} \in \mathbb {R} ^{n}$ 에 대해 다음을 만족하는 항상 양의 실수 $\alpha ,\beta >0$ 을 찾을 수 있음을 의미합니다: $\alpha \cdot \|\mathbf {x} \|\leq \|\mathbf {x} \|'\leq \beta \cdot \|\mathbf {x} \|$ 이것은 $R n$ 위의 모든 노름의 집합에 대한 동치 관계(equivalence relation)를 정의합니다. 이 결과와 함께 $R n$ 에서 벡터의 수열이 $\|\cdot \|$ 로 수렴하는 것과 그것이 $\|\cdot \|'$ 으로 수렴하는 것은 필요충분 조건임을 확인할 수 있습니다.

다음은 이 결과의 증명이 어떻게 생겼는지에 대한 스케치입니다:

동치 관계(equivalence relation) 때문에, $R n$ 위의 모든 각 노름이 유클리드 노름(Euclidean norm) $\|\cdot \|_{2}$ 와 동등하는 것을 보여주는 것으로 충분합니다. $\|\cdot \|$ 를 $R n$ 위에 임의적인 노름이라고 놓습니다. 증명은 두 단계로 나뉩니다:

모든 $\mathbf {x} \in \mathbb {R} ^{n}$ 에 대해 $\|\mathbf {x} \|\leq \beta \cdot \|\mathbf {x} \|_{2}$ 임을 만족하는 $\beta >0$ 가 존재함을 보여줍니다. 이 단계에서, 모든 각 $\mathbf {x} =(x_{1},\dots ,x_{n})\in \mathbb {R} ^{n}$ 은 표준 기저: ${\textstyle \mathbf {x} =\sum _{i=1}^{n}e_{i}\cdot x_{i}}$ 의 선형 조합으로 표현될 수 있다는 사실을 사용합니다. 그런-다음 코시-슈바르츠 부등식(Cauchy–Schwarz inequality)과 함께 $\|\mathbf {x} \|=\left\|\sum _{i=1}^{n}e_{i}\cdot x_{i}\right\|\leq \sum _{i=1}^{n}\|e_{i}\|\cdot |x_{i}|\leq {\sqrt {\sum _{i=1}^{n}\|e_{i}\|^{2}}}\cdot {\sqrt {\sum _{i=1}^{n}|x_{i}|^{2}}}=\beta \cdot \|\mathbf {x} \|_{2},$ 여기서 ${\textstyle \beta :={\sqrt {\sum _{i=1}^{n}\|e_{i}\|^{2}}}}$ .
이제 모든 $\mathbf {x} \in \mathbb {R} ^{n}$ 에 대해 $\alpha \cdot \|\mathbf {x} \|_{2}\leq \|\mathbf {x} \|$ 임을 만족하는 $\alpha >0$ 을 찾아야 합니다. 그러한 $\alpha$ 가 없다고 가정합니다. 그런-다음 모든 각 $k\in \mathbb {N}$ 에 대해, $\|\mathbf {x} _{k}\|_{2}>k\cdot \|\mathbf {x} _{k}\|$ 임을 만족하는 $\mathbf {x} _{k}\in \mathbb {R} ^{n}$ 이 존재합니다. 두 번째 수열 $({\tilde {\mathbf {x} }}_{k})_{k\in \mathbb {N} }$ 을 ${\textstyle {\tilde {\mathbf {x} }}_{k}:={\frac {\mathbf {x} _{k}}{\|\mathbf {x} _{k}\|_{2}}}}$ 으로 정의합니다. 이 수열은 $\|{\tilde {\mathbf {x} }}_{k}\|_{2}=1$ 이기 때문에 경계집니다. 따라서 볼차노–바이어슈트라스 정리(Bolzano–Weierstrass theorem) 때문에 극한 $\mathbf {a} \in$ $R n$ 을 갖는 수렴하는 부분수열 $({\tilde {\mathbf {x} }}_{k_{j}})_{j\in \mathbb {N} }$ 이 존재합니다. 이제 우리는 $\|\mathbf {a} \|_{2}=1$ 이지만 $\mathbf {a} =\mathbf {0}$ 임을 보여주며, 이는 모순입니다. $\|\mathbf {a} -{\tilde {\mathbf {x} }}_{k_{j}}\|\to 0$ 와 $0\leq {\frac {\|\mathbf {x} _{k_{j}}\|}{\|\mathbf {x} _{k_{j}}\|_{2}}}<{\frac {1}{k_{j}}}$ 이므로, ${\frac {\|\mathbf {x} _{k_{j}}\|}{\|\mathbf {x} _{k_{j}}\|_{2}}}\to 0$ 이기 때문에, 다음입니다: $\|\mathbf {a} \|\leq \left\|\mathbf {a} -{\tilde {\mathbf {x} }}_{k_{j}}\right\|+\left\|{\tilde {\mathbf {x} }}_{k_{j}}\right\|\leq \beta \cdot \left\|\mathbf {a} -{\tilde {\mathbf {x} }}_{k_{j}}\right\|_{2}+{\frac {\|\mathbf {x} _{k_{j}}\|}{\|\mathbf {x} _{k_{j}}\|_{2}}}\ {\overset {j\to \infty }{\longrightarrow }}\ 0,$ 이것은 $\|\mathbf {a} \|=0$ 을 의미하므로, $\mathbf {a} =\mathbf {0}$ 입니다. 다른 한편으로, $\|\mathbf {a} \|_{2}=\left\|\lim _{j\to \infty }{\tilde {\mathbf {x} }}_{k_{j}}\right\|_{2}=\lim _{j\to \infty }\left\|{\tilde {\mathbf {x} }}_{k_{j}}\right\|_{2}=1$ 이기 때문에 $\|\mathbf {a} \|_{2}=1$ 입니다. 이것은 참일 수 없으므로, 가정은 거짓이고 그러한 $\alpha >0$ 가 존재합니다.