Area of a circle

기하학에서, 반지름(radius) $r$ 의 원(circle)에 의해 둘러싸인 넓이(area)는 $π r 2$ 입니다. 여기서 그리스 문자 $π$ 는 임의의 원의 둘레(circumference)와 그것의 지름(diameter)의 상수(constant) 비율을 나타내며, 대략적으로 3.1416과 같습니다.

아르키메데스(Archimedes)에서 유래된, 이 공식을 유도하는 한 가지 방법은 원을 정규 다각형(regular polygon)의 수열의 극한(limit)으로 보는 것입니다. 정규 다각형의 넓이는 그것의 둘레(perimeter)와 그것의 중심에서 그것의 변까지의 거리를 곱한 것의 절반이고, 해당 공식 – 넓이는 둘레의 절반 곱하기 반지름 – 즉 $A = 1 / 2 \times 2π r \times r$ 은 원에 대해 극한에서 유지됩니다.

비록 비공식적 문액에서 종종 원의 넓이라고 참조될지라도, 엄밀하게 말하면 용어 디스크(disk)가 원의 내부 영역(region)을 참조하고, 반면에 원은 곡선(curve)이고 영역 자체를 포함하지 않는 오직 경계에 대해 예약되어 있습니다. 그러므로, 디스크의 넓이가 원에 의해 둘러싸인 넓이에 대해 보다 정확한 표현입니다.

History

현대 수학은 적분 미적분(integral calculus) 또는 그것의 더 정교한 자손, 실수 해석학(real analysis)의 방법을 사용하여 넓이를 얻을 수 있습니다. 어쨌든, 디스크의 넓이는 고대 그리스인들(Ancient Greeks)에 의해 연구되었습니다. 기원전 5세기 크니도스의 에우독소스(Eudoxus of Cnidus)는 디스크의 넓이는 반지름의 제곱에 비례한다는 것을 발견했습니다.^[1] 아르키메데스(Archimedes)는 유클리드 기하학(Euclidean geometry)의 도구를 그의 책 Measurement of a Circle에서 원 안의 넓이가 그것의 밑변이 원의 둘레의 길이를 가지고 그것의 높이가 원의 반지름과 같은 직각 삼각형(right triangle)의 넓이와 같음을 보이기 위해 사용했습니다. 원주는 2 $π$ r이고, 삼각형의 넓이는 밑변 곱하기 높이의 절반이며, 디스크에 대해 넓이 $π$ r²를 산출합니다. 아르키메데스 이전에, 키오스의 히포크라테스(Hippocrates of Chios)는 히포크라테스의 달(Lune of Hippocrates)의 그의 구적법의 일부로서 디스크의 넓이가 그것의 지름의 제곱에 비례한다는 것을 처음으로 보여주었지만,^[2] 비례 상수(constant of proportionality)는 식별하지 못했습니다.

Historical arguments

다양한 논즌이 수학적 엄밀함의 정도에 따라 방정식 $A=\pi r^{2}$ 을 수립하기 위해 역사적으로 발전해 왔습니다. 이들 중 가장 유명한 것은 극한(limit)의 수학적 개념의 최초의 사용 중 하나이자 실수 시스템(real number system)의 표준 해석적 처리의 일부로 남아 있는 아르키메데스 공리(Archimedes' axiom)의 기원, 아르키메데스의 소진의 방법(method of exhaustion)입니다. 아르키메데스의 원래 증명은 현대 표준에 의해 엄격하지 않는데, 왜냐하면 그것은 우리가 원의 호의 길이를 가름선과 접선의 길이와 비교할 수 있다고 가정하고, 기하학적으로 분명하듯이 넓이에 대한 유사한 명제를 가정하기 때문입니다.

Using polygons

정규 다각형의 넓이는 그것의 둘레 곱하기 아포팀(apothem)의 절반입니다. 정규 다각형의 변의 개수가 증가할수록, 다각형은 원으로, 아포팀은 반지름으로 경향이 있습니다. 이것은 디스크의 넓이가 경계하는 원의 둘레 곱하기 반지름의 절반임을 시사합니다.^[3]

Archimedes's proof

The Measurement of a Circle (c. 260 BCE)에서 아르키메데스의 논증에 따르면, 원으로 둘러싸인 넓이를 그것의 밑변이 원의 둘레의 길이를 가지고 그것의 높이가 원의 반지름과 같은 직각 삼각형과 비교하십시오. 만약 원의 넓이가 삼각형의 넓이와 같지 않으면, 그것은 더 크거나 작아야 합니다. 우리는 상등을 유일한 가능성으로 남겨두고 모순에 의해 이들 각각을 제거합니다. 우리는 같은 방법에서 정규 다각형(regular polygon)을 사용합니다.

Not greater

원으로 둘러싸인 넓이 C가 삼각형의 넓이 T = ¹⁄₂cr보다 크다고 가정합니다. E가 초과 총양을 나타낸다고 놓습니다. 그것의 네 모서리가 원 위에 놓이도록 원에 정사각형을 내접(Inscribe)시킵니다. 정사각형과 원 사이에는 넷의 분절이 있습니다. 만약 그것들 틈의 총 넓이 G₄가 E보다 크면, 각 호를 절반으로 나눕니다. 이것은 내접된 정사각형을 내접된 팔각형으로 만들고, 더 작은 총 틈을 갖는 여덟 분절 G₈을 생성합니다. 전체 틈 넓이 G_n이 E보다 작을 때까지 계속 분할합니다. 이제 내접된 다각형의 넓이 P_n = C − G_n은 삼각형의 넓이보다 커야 합니다.

{\begin{aligned}E&{}=C-T\\&{}>G_{n}\\P_{n}&{}=C-G_{n}\\&{}>C-E\\P_{n}&{}>T\end{aligned}}

그러나 이것은 다음과 같이 모순을 일으킵니다. 중심에서 다각형의 한 변의 중간점까지 수직선을 그립니다; 그것의 길이 h는 원 반지름보다 작습니다. 역시, 다각형의 각 변이 길이 s로 갖는다고 놓습니다; 그런-다음 변의 합, ns는 원의 둘레보다 작습니다. 다각형 넓이는 높이 h와 밑변 s를 갖는 n 같은 삼각형으로 구성되고, 따라서 ¹⁄₂nhs와 같습니다. 그러나 h < r와 ns < c이므로, 다각형 넓이는 삼각형 넓이 ¹⁄₂cr보다 작아야 하므로, 모순입니다. 그러므로, C가 T보다 클 수 있다는 우리의 가정은 적절하지 않은 것입니다.

Not less

원에 의해 둘러싸인 넓이가 삼각형의 넓이 T보다 작다고 가정합니다. D가 부족 총양을 나타낸다고 놓습니다. 각 모서리의 중간점이 원 위에 놓이도록 정사각형에 외접합니다. 만약 정사각형과 원 사이의 총 넓이 틈 G₄가 D보다 크면 원 접선으로 모서리를 잘라 외접 팔각형을 만들고 틈 넓이가 D보다 작을 때까지 계속 잘라냅니다. 다각형의 넓이, P_n은 T보다 작아야 합니다.

{\begin{aligned}D&{}=T-C\\&{}>G_{n}\\P_{n}&{}=C+G_{n}\\&{}<C+D\\P_{n}&{}<T\end{aligned}}

이것, 역시, 모순을 불러일으킵니다. 각 다각형 변의 중간점에 수선은 길이 r의 반지름이기 때문입니다. 그리고 총 변의 길이가 원주보다 크기 때문에, 다각형은 총 넓이가 T보다 큰 n 동일한 삼각형으로 구성됩니다. 다시 한 번 우리는 모순을 가지므로, C가 T보다 작을 수 있다는 우리의 가정도 역시 틀려야 합니다.

그러므로, 그것은 원에 의해 둘러싸인 넓이가 삼각형의 넓이와 정확하게 같은 경우여야 합니다. 이것으로 증명을 마칩니다.

Rearrangement proof

사토 모슌(Satō Moshun) (Smith & Mikami 1914, pp. 130–132)와 Leonardo da Vinci (Beckmann 1976, p. 19)에 따르면, 우리는 내접된 정규 다각형을 다른 방법에서 사용할 수 있습니다. 우리가 육각형(hexagon)을 내접한다고 가정합니다. 육각형을 중심에서 분할함으로써 6개의 삼각형으로 자릅니다. 두 개의 반대 삼각형은 둘 다 두 개의 공통 지름에 닿습니다; 방사형 가장자리가 인접하도록 하나를 따라 밀어 넣습니다. 그것들은 이제 육각형 변이 둘의 반대 가장자리를 만드는 평행사변형(parallelogram)을 형성하며, 그 중 하나는 밑변 s입니다. 둘의 방사형 가장자리는 경사진 변을 형성하고, 높이 h는 그것의 아포팀(apothem)과 같습니다 (아르키메데스 증명에서와 같이). 사실, 우리는 연속적인 쌍을 서로 옆에 놓음으로써 모든 삼각형을 하나의 큰 평행사변형으로 모을 수도 있습니다. 같은 것은 만약 그것을 8 변으로 늘리도 참이고 이런 식으로 계속됩니다. 2n 변을 갖는 다각형에 대해, 평행사변형은 길이 ns의 밑변과 높이 h를 가질 것입니다. 변의 수가 증가함에 따라, 평행사변형 밑면의 길이는 원 둘레의 절반에 가까워지고, 그것의 높이는 원 반지름에 가까워집니다. 극한에서, 평행사변형은 너비 $π$ r이고 높이 r을 갖는 직사각형이 됩니다.

**Unit disk area by rearranging n polygons.**
n	side	base	height	area
polygon		parallelogram
4	1.4142136	2.8284271	0.7071068	2.0000000
6	1.0000000	3.0000000	0.8660254	2.5980762
8	0.7653669	3.0614675	0.9238795	2.8284271
10	0.6180340	3.0901699	0.9510565	2.9389263
12	0.5176381	3.1058285	0.9659258	3.0000000
14	0.4450419	3.1152931	0.9749279	3.0371862
16	0.3901806	3.1214452	0.9807853	3.0614675
96	0.0654382	3.1410320	0.9994646	3.1393502
∞	1/∞	$π$	1	$π$

Modern proofs

상수 $π$ 의 다양한 등가 정의가 있습니다. 미적분학-이전 기하학에서 전통적인 정의는 원의 둘레와 그 지름의 비율입니다:

\pi ={\frac {C}{D}}.

어쨌든, 원의 둘레는 원시 해석적 개념이 아니기 때문에, 이 정의는 현대의 엄격한 처리에서 적합하지 않습니다. 표준 현대 정의는 $π$ 가 코사인(cosine) 함수의 최소 양수 근의 두 배 또는, 동등하게 사인(sine) (또는 코사인) 함수의 반-주기와 같다는 것입니다. 코사인 함수는 거듭제곱 급수(power series) 또는 특정 미분 방정식(differential equation)의 해로 정의될 수 있습니다. 이것은 원주와 원의 넓이에 대한 $π$ 의 관계에 대한 명제는 정의라기 보다는 실제로 정리가 되도록, "넓이"와 "원주"와 같은 개념의 해석적 정의를 따르도록 $π$ 의 정의에서 원에 대한 임의의 참조를 피합니다.

해석적 정의는 만약 원의 둘레가 다음 적분(integral)을 수단으로 정류-가능 곡선(rectifiable curve)으로 측정됨에 동의하면 동등한 것으로 봅니다:

C=2\int _{-R}^{R}{\frac {R\,dx}{\sqrt {R^{2}-x^{2}}}}=2R\int _{-1}^{1}{\frac {dx}{\sqrt {1-x^{2}}}}.

오른쪽에 나타나는 적분은 그것의 값이 $π$ 와 같은 사인(sine) 함수의 반-주기인 아벨 적분(abelian integral)입니다. 따라서 $C=2\pi R=\pi D$ 는 정리로 참인 것으로 보입니다.

다음의 몇 가지 명제는 $A=\pi r^{2}$ 공식을 재현하기 위해 기본 미적분학에서 개념만을 사용하지만, 이것을 실제 증명으로 고려하는 많은 경우에서, 그것들은 기하학과의 관계와 완전히 독립적인 방법에서 삼각 함수와 기본 상수 $π$ 를 개발할 수 있다는 사실에 암묵적으로 의존합니다. 우리는 적절한 곳에서 이들 각 증명을 모든 삼각법과 완전히 독립적으로 만들어질 수 있지만, 일부 경우에는 기본 미적분학에 의해 제공되는 것보다 더 정교한 수학적 아이디어를 요구한다는 것을 표시했습니다.

Onion proof

미적분학을 사용하여, 우리는 디스크를 양파의 층과 같은 얇은 동심원으로 분할하여 면적을 점진적으로 합할 수 있습니다. 이것은 이-차원에서의 쉘 적분(shell integration)의 방법입니다. 반지름 t의 "양파"의 무한소적으로 얇은 고리에 대해, 누적된 넓이는 2 $π$ t dt, 고리의 원주 길이 곱하기 무한소적인 너비를 곱한 값입니다 (너비=2 $π$ t와 높이=dt를 갖는 직사각형에 의해 이 고리를 근사할 수 있습니다). 이것은 반지름 r의 디스크에 대해 기본 적분을 제공합니다.

{\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{r}2\pi t\,dt\\&{}=2\pi \left[{\frac {t^{2}}{2}}\right]_{0}^{r}\\&{}=\pi r^{2}.\end{aligned}}

극좌표에서 다변수 치환 규칙(multivariate substitution rule)에 의해 엄격하게 정당화됩니다. 즉, 넓이가 디스크 자체에 걸쳐 상수 함수 1의 이중 적분(double integral)에 의해 제공됩니다. 만약 D가 디스크를 나타내면, 이중 적분은 다음과 같이 극좌표(polar coordinates)에서 계산될 수 있습니다:

{\begin{aligned}\mathrm {Area} (r)&{}=\iint _{D}1\ d(x,y)\\&{}=\iint _{D}t\ dt\ d\theta \\&{}=\int _{0}^{r}\int _{0}^{2\pi }t\ d\theta \ dt\\&{}=\int _{0}^{r}\left[t\theta \right]_{0}^{2\pi }dt\\&{}=\int _{0}^{r}2\pi t\,dt\\\end{aligned}}

이것은 위에서 얻어진 것과 같은 결과입니다.

삼각법의 특수 좌표에 의존없이, 동등한 엄격한 정당화는 공동넓이 공식(coarea formula)을 사용합니다. 함수 $\rho :\mathbb {R} ^{2}\to \mathbb {R}$ 를 $\rho (x,y)={\sqrt {x^{2}+y^{2}}}$ 에 의해 정의합니다. ρ가 그것의 그래디언트(gradient)가 단위 벡터 $|\nabla \rho |=1$ (거의 모든 곳(almost everywhere))인 립시츠 함수(Lipschitz function)임을 주목하십시오. D를 $\mathbb {R} ^{2}$ 에서 디스크 $\rho <1$ 라고 놓습니다. 우리는 ${\mathcal {L}}^{2}(D)=\pi$ 임을 보일 것이며, 여기서 ${\mathcal {L}}^{2}$ 는 $\mathbb {R} ^{2}$ 에서 이-차원 르베그 측정입니다. 우리는 원 $\rho =r$ 의 일-차원 하우스도르프 측정(Hausdorff measure)가 $2\pi r$ , 반지름 r의 원의 원주임을 가정해야 합니다. (이것은 원주의 정의로 취할 수 있습니다.) 그런-다음 공동넓이 공식에 의해,

{\begin{aligned}{\mathcal {L}}^{2}(D)&=\iint _{D}|\nabla \rho |\,d{\mathcal {L}}^{2}\\&=\int _{\mathbb {R} }{\mathcal {H}}^{1}(\rho ^{-1}(r)\cap D)\,dr\\&=\int _{0}^{1}{\mathcal {H}}^{1}(\rho ^{-1}(r))\,dr\\&=\int _{0}^{1}2\pi r\,dr=\pi .\end{aligned}}

Triangle proof

위에서 설명한 양파 증명과 유사하게, 우리는 디스크의 넓이에 대해 공식에 도달하기 위해 다른 방법에서 미적분학을 이용할 수 있습니다. 동심원을 직선 스트립으로 푸는 것을 생각해 보십시오. 이것은 그것의 높이 r과 그것의 밑변 2 $π$ r (양파의 바깥쪽 조각임)을 갖는 직각 삼각형을 형성할 것입니다.

이 삼각형의 넓이를 찾는 것은 디스크의 넓이를 제공할 것입니다:

{\begin{aligned}{\text{Area}}&{}={\frac {1}{2}}\cdot {\text{base}}\cdot {\text{height}}\\&{}={\frac {1}{2}}\cdot 2\pi r\cdot r\\&{}=\pi r^{2}\end{aligned}}

이 삼각형에 대해 반대쪽과 인접 각도는 각각 각도에서 9.0430611..., 80.956939... 및 라디안에서 OEIS: A233527, 1.4129651...OEIS: A233528입니다.

명시적으로, 우리는 원을 삼각형으로 나누는 것을 상상하며, 각 삼각형은 높이가 원의 반지름과 같고 밑변이 무한소적으로 작은 것입니다. 이들 삼각형 각각의 넓이는 $1/2\cdot r\cdot du$ 와 같습니다. 이들 삼각형의 모든 넓이를 합 (적분)함으로써, 우리는 원의 넓이에 대해 공식에 도달합니다:

{\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{2\pi r}{\frac {1}{2}}r\,du\\&{}=\left[{\frac {1}{2}}ru\right]_{0}^{2\pi r}\\&{}=\pi r^{2}.\end{aligned}}

그것은 역시 적분의 순서(order of integration)를 반대로 하고 위의 반복된 적분에서 변수의 변경을 사용함으로써 디스크에 걸쳐 상수 함수 1의 이중 적분으로 정당화될 수 있습니다:

{\begin{aligned}\mathrm {Area} (r)&{}=\iint _{D}1\ d(x,y)\\&{}=\iint _{D}t\ dt\ d\theta \\&{}=\int _{0}^{2\pi }\int _{0}^{r}t\ dt\ d\theta \\&{}=\int _{0}^{2\pi }{\frac {1}{2}}r^{2}\ d\theta \\\end{aligned}}

치환 $u=r\theta ,\ du=r\ d\theta$ 을 만들면 적분을 다음으로 변환합니다:

{\begin{aligned}\int _{0}^{2\pi r}{\frac {1}{2}}{\frac {r^{2}}{r}}du=\int _{0}^{2\pi r}{\frac {1}{2}}r\ du\end{aligned}}

이것은 위의 결과와 같습니다.

삼각형 증명은 삼각법과 상수 $π$ 의 모든 언급을 피하는 방법에서 유량-발산 형식 (즉, 발산 정리(divergence theorem)의 이-차원 버전)에서 그린의 정리(Green's theorem)의 적용으로 다시 공식화될 수 있습니다. 평면에서 벡터 필드(vector field) $\mathbf {r} =x\mathbf {i} +y\mathbf {j}$ 를 생각해 보십시오. 따라서 r의 발산(divergence)은 2와 같고, 따라서 디스크 D의 넓이는 다음과 같습니다:

A={\frac {1}{2}}\iint _{D}\operatorname {div} \mathbf {r} \,dA.

그린의 정리에 의해, 이것은 원 경계 D를 가로지르는 r의 바깥쪽 유량과 같습니다:

A={\frac {1}{2}}\oint _{\partial D}\mathbf {r} \cdot \mathbf {n} \,ds

여기서 n은 호 단위 법선이고 ds는 호 길이 측정입니다. 원점에 중심을 둔 반지름 R의 원에 대해, 우리는 $|\mathbf {r} |=R$ 와 $\mathbf {n} =\mathbf {r} /R$ 를 가지므로, 위의 상등은 다음입니다:

A={\frac {1}{2}}\oint _{\partial D}\mathbf {r} \cdot {\frac {\mathbf {r} }{R}}\,ds={\frac {R}{2}}\oint _{\partial D}\,ds.

전체 원 $\partial D$ 에 걸쳐 ds의 적분은 그것의 원주인 단지 호 길이이므로, 이것은 원에 의해 둘러싸인 넓이 A가 $R/2$ 곱하기 원의 원주와 같음을 보여줍니다.

삼각형을 사용하는 또 다른 증명은 원으로 둘러싸인 넓이를 무한한 숫자의 삼각형 (즉, 삼각형 각각은 원의 중심에서 $d θ$ 의 각도를 가집니다), (삼각형의 넓이에 대해 표현: $1 / 2 \cdot a \cdot b \cdot sin θ = 1 / 2 \cdot r \cdot r \cdot sin(d θ) = 1 / 2 \cdot r 2 \cdot d θ$ 에서 유도된) 각각이 $1 / 2 \cdot r 2 \cdot d θ$ 의 넓이를 갖는 삼각형으로 구성된 원에 의해 둘러싸인 넓이를 고려합니다. $sin(d θ)$ ≈ $d θ$ 는 작은 각도 근사(small angle approximation)에 기인함을 주목하십시오. 삼각형의 넓이를 합하는 것을 통해, 원의 넓이에 대해 표현은 따라서 다음과 같이 구할 수 있습니다: ${\begin{aligned}\mathrm {Area} &{}=\int _{0}^{2\pi }{\frac {1}{2}}r^{2}\,d\theta \\&{}=\left[{\frac {1}{2}}r^{2}\theta \right]_{0}^{2\pi }\\&{}=\pi r^{2}.\end{aligned}}$

Semicircle proof

반지름 r의 반원의 넓이는 적분 $\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx$ 에 의해 계산될 수 있음을 주목하십시오.

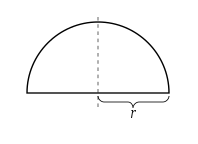
삼각 치환(trigonometric substitution)에 의해, 우리는 $x=r\sin \theta$ , 따라서 $dx=r\cos \theta \,d\theta$ 를 대체합니다.

\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx

=\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}{\sqrt {r^{2}(1-\sin ^{2}\theta )}}\cdot r\cos \theta \,d\theta

=2r^{2}\int _{0}^{\frac {\pi }{2}}\cos ^{2}\theta \,d\theta

={\frac {\pi r^{2}}{2}}.

마지막 단계는 삼각 함등식 $\cos(\theta )=\sin(\pi /2-\theta )$ 이 $\cos ^{2}\theta$ 와 $\sin ^{2}\theta$ 가 치환에 의한 적분(integration by substitution)을 사용하여 구간 $[0,\pi /2]$ 에 걸쳐 같은 적분을 가짐을 의미하기 때문에 비롯됩니다. 그러나 다른 한편으로, $\cos ^{2}\theta +\sin ^{2}\theta =1$ 이기 때문에, 두 적분의 합은 $\pi /2$ 인 해당 구간의 길이입니다. 결과적으로, $\cos ^{2}\theta$ 의 적분은 $\pi /4$ 인 해당 구간의 절반 길이와 같습니다.

그러므로, 반-원의 두 배 넓이인 반지름 r의 원의 넓이는 $2\cdot {\frac {\pi r^{2}}{2}}=\pi r^{2}$ 와 같습니다.

이 특정 증명은 다음과 같은 질문을 하는 것처럼 보일 수 있습니다: 만약 삼각 치환에 포함된 사인과 코사인 함수가 원과 관련해서 정의된 것으로 고련되면. 어쨌든, 이전에 언급했듯이, 삼각법과 완전히 독립적인 방법에서 사인, 코사인, 및 $π$ 를 정의하는 것이 가능하며, 이 경우에서 그 증명은 변수 변경의 공식(change of variables formula)과 푸비니의 정리(Fubini's theorem)에 의해 유효하며, 사인과 코사인의 기본 속성을 가정합니다 (이것은 역시 원과의 그것들 관계에 대한 어떠한 가정없이 증명될 수 있습니다).

Isoperimetric inequality

원은 최대 넓이를 둘러싸는 최소 둘레의 닫힌 곡선입니다. 이것은 같은-둘레 부등식(isoperimetric inequality)으로 알려져 있으며, 만약 유클리드 평면에서 정류-가능 조르당 곡선이 둘레 C를 가지고 넓이 A를 둘러싸면 (조르당 곡선 정리(Jordan curve theorem)에 의해), 다음임을 말합니다:

4\pi A\leq C^{2}.

더욱이, 상등이 이 부등식에서 유지되는 것과 그 곡선이 원인 것, 이 경우에서 $A=\pi r^{2}$ 와 $C=2\pi r$ 인 것은 필요충분 조건입니다.

Fast approximation

아르키메데스에 의해 그 넓이를 수치적으로 근사하기 위해 사용된 계산은 힘들고, 그는 96 변의 다각형에서 멈췄습니다. 더 빠른 방법은 Gerretsen & Verdenduin (1983, pp. 243–250)에 설명된 빌러브로어트 스넬(Willebrord Snell) (Cyclometricus, 1621)의 아이디어를 사용하고, 나아가서 크리스티안 하위헌스(Christiaan Huygens) (De Circuli Magnitudine Inventa, 1654)에 의해 개발되었습니다.

Archimedes' doubling method

원이 주어지면, u_n를 내접된 정규 n-각형의 둘레(perimeter)로 놓고, U_n를 둘레-접된 정규 n-각형의 둘레로 놓습니다. 그런-다음 u_n과 U_n은 n이 증가함에 따라 점점 더 날카로워지는 원의 둘레에 대해 아래쪽과 위쪽 경계이고, 그것들의 평균 (u_n + U_n)/2은 원주에 대한 특히 좋은 근사입니다. 큰 n에 대해 u_n과 U_n을 계산하기 위해, 아르키메데스는 다음과 같은 두-배 공식을 도출했습니다:

u_{2n}={\sqrt {U_{2n}u_{n}}}

(기하 평균(geometric mean)), 및

U_{2n}={\frac {2U_{n}u_{n}}{U_{n}+u_{n}}}

(조화 평균(harmonic mean)).

아르키메데스는 육각형에서 시작하여 두 배된 n을 네 번 곱하여 96각형을 얻었고, 이것은 그에게 원의 둘레에 대한 좋은 근사를 제공했습니다.

현대 표기법에서, 우리는 다음처럼 그의 계산 (및 더 나아가서)을 재생산할 수 있습니다. 단위 원에 대해, 내접된 육각형은 u₆ = 6을 가지고, 둘레접된 육각형은 U₆ = 4√3을 가집니다. 두 배를 일곱 번 하면 다음을 산출합니다:

**Archimedes doubling seven times; n = 6×2^k.**
k	n	u_n	U_n	u_n + U_n/4
0	6	6.0000000	6.9282032	3.2320508
1	12	6.2116571	6.4307806	3.1606094
2	24	6.2652572	6.3193199	3.1461443
3	48	6.2787004	6.2921724	3.1427182
4	96	6.2820639	6.2854292	3.1418733
5	192	6.2829049	6.2837461	3.1416628
6	384	6.2831152	6.2833255	3.1416102
7	768	6.2831678	6.2832204	3.1415970

(여기서 u_n + U_n/2는 단위 원의 원주를 근사하며, 이것은 2 $π$ 이므로, u_n + U_n/4는 $π$ 를 근사화합니다.)

테이블의 마지막 엔트리는 그것의 최상의 유리수 근사(best rational approximations) 중 하나로 ³⁵⁵⁄₁₁₃를 가집니다; 즉, 분모 113까지를 갖는 유리수 중에서 더 나은 근사는 없습니다. 숫자 ³⁵⁵⁄₁₁₃은 $π$ 에 대한 훌륭한 근사이기도 하며, 16604보다 작은 분모를 갖는 임의의 다른 유리수보다 우수합니다. ^[4]

The Snell–Huygens refinement

스넬은 아르키메데스보다 더 엄격한 경계를 제안했습니다 (그리고 하위헌스가 입증했습니다):

n{\frac {3\sin {\frac {\pi }{n}}}{2+\cos {\frac {\pi }{n}}}}<\pi <n\left(2\sin {\frac {\pi }{3n}}+\tan {\frac {\pi }{3n}}\right).

이것은 n = 48에 대해 아르키메데스의 방법 n = 768에 대한 것보다 더 좋은 근사 (약 3.14159292)를 제공합니다.

Derivation of Archimedes' doubling formulae

내접된 정규 n-각형의 한 변이 길이 s_n를 가지고 점 A와 B에서 원에 닿는다고 놓습니다. A′을 A′A이 지름이고, A′AB가 지름에 내접된 삼각형이 되도록 원 위에 A와 반대편 점이라고 놓습니다. 탈레스의 정리(Thales' theorem)에 의해, 이것은 B에서 직각을 갖는 직각 삼각형입니다. A′B의 길이를 c_n이라고 놓고, 이것을 s_n의 여라고 놓습니다; 따라서 c_n²+s_n² = (2r)²입니다. C를 A에서 B로 호를 이등분하고, C′을 원 위에 C와 반대편 점이라고 놓습니다. 따라서 CA의 길이는 s_2n, C′A의 길이는 c_2n이고, C′CA는 지름 C′C 위에 직각 삼각형 자체입니다. C가 A에서 B로 호를 이등분하기 때문에, C′C는 말하자면 P에서 A에서 B로 현을 수직으로 이등분합니다. 삼각형 C′AP는 따라서 직각 삼각형이고, 그것들이 C′에서 각도를 공유하기 때문에 C′CA와 닮았(similar)습니다. 따라서 모든 셋의 대응하는 변은 같은 비례에 있습니다; 특히, 우리는 C′A : C′C = C′P : C′A 및 AP : C′A = CA : C′C를 가집니다. 원의 중심 O는 A′A를 이등분하므로, 우리는 역시 A′B의 절반 길이 OP를 갖는 A′AB와 닮은 삼각형 OAP를 가집니다. 변 길이 관점에서, 이것은 우리에게 다음을 제공합니다:

{\begin{aligned}c_{2n}^{2}&{}=\left(r+{\frac {1}{2}}c_{n}\right)2r\\c_{2n}&{}={\frac {s_{n}}{s_{2n}}}.\end{aligned}}

첫 번째 방정식에서 C′P는 C′O+OP, 길이 r+¹⁄₂c_n이고, C′C는 지름, 2r입니다. 단위 원에 대해 우리는 루돌프 반 세울렌(Ludolph van Ceulen)의 유명한 두 배하는 방정식을 가집니다,

c_{2n}={\sqrt {2+c_{n}}}.

만약 우리가 이제 AB와 평행한 변 A″B″를 갖는 정규 n-각형을 외접하면, OAB와 OA″B″가 A″B″ : AB = OC : OP를 갖는 닮은 삼각형입니다. 외접된 변을 S_n이라고 부릅니다; 그런-다음 이것은 S_n : s_n = 1 : ¹⁄₂c_n입니다. (우리는 OP가 A′B 절반 길이라는 것을 다시 사용했습니다.) 따라서 우리는 다음을 얻습니다:

c_{n}=2{\frac {s_{n}}{S_{n}}}.

내접된 둘레를 u_n = ns_n, 둘레접된 둘레를 U_n = nS_n이라고 부릅니다. 그런-다음 방정식을 결합하면, 우리는 다음이 되도록

u_{2n}^{2}=u_{n}U_{2n},

다음을 가집니다:

c_{2n}={\frac {s_{n}}{s_{2n}}}=2{\frac {s_{2n}}{S_{2n}}}.

이것은 기하 평균(geometric mean) 방정식을 가집니다.

우리는 역시 다음임을 추론할 수 있습니다:

2{\frac {s_{2n}}{S_{2n}}}{\frac {s_{n}}{s_{2n}}}=2+2{\frac {s_{n}}{S_{n}}},

또는

{\frac {2}{U_{2n}}}={\frac {1}{u_{n}}}+{\frac {1}{U_{n}}}.

이것은 조화 평균(harmonic mean) 방정식을 제공합니다.

Dart approximation

넓이를 찾는 보다 효율적인 방법은 유용하지 않을 때, 우리는 "다트 던지기"에 의존할 수 있습니다. 이 몬테-카를로 방법(Monte Carlo method)은 만약 무작위 표본이 디스크가 있는 정사각형의 표면에 걸쳐 균등하게 흩어져 있게 취해지면, 디스크에 부딪힌 표본의 비례가 디스크의 넓이와 정사각형의 넓이의 비율에 근사한다는 사실을 사용합니다. 이것은 유용한 정확도를 얻기 위해 엄청난 숫자의 표본이 요구되기 때문에 디스크 (또는 임의의 모양)의 넓이를 계산하기 위한 최후의 방법으로 고려되어야 합니다; 10⁻ⁿ에 대한 좋은 추정은 약 100ⁿ 무작위 표본을 요구합니다 (Thijssen 2006, p. 273).

Finite rearrangement

우리는 디스크를 무한한 숫자의 조각으로 분할함으로써 조각을 직사각형으로 재조립할 수 있음을 보았습니다. 비교적 최근에 발견된 놀라운 사실 (Laczkovich 1990)은 디스크를 크지만 유한한 숫자의 조각으로 분할하고 그런-다음 조각을 같은 넓이의 정사각형으로 재조립할 수 있다는 것입니다. 이것은 타르스키의 원-제곱화 문제(Tarski's circle-squaring problem)라고 불립니다. 라츠코비치(Laczkovich)의 증명의 본질은 그러한 분할 (사실상, 그러한 많은 분할 중)의 존재를 입증하지만 임의의 특정 분할도 나타내지 않음을 만족한다는 것입니다.

Non-Euclidean circles

원은 비-유클리드 기하학(non-Euclidean geometry), 및 특히 쌍곡선(hyperbolic)과 타원(elliptic) 평면에서 정의될 수 있습니다.

예를 들어, 단위 구(unit sphere) $S^{2}(1)$ 은 이-차원 타원 평면에 대해 모델입니다. 그것은 측지선(geodesic) 길이를 측정함으로써 발생하는 본질적 메트릭(intrinsic metric)을 전달합니다. 측지 원은 측지 좌표 시스템(geodesic coordinate system)에서 평행입니다.

보다 정확하게, 우리가 천정(zenith)에 위치하는 점 $\mathbf {z} \in S^{2}(1)$ 을 고정합니다. 그 천정과 결합된 것은 측지 극 좌표 시스템 $(\phi ,\theta )$ , $0\leq \phi \leq \pi$ , $0\leq \theta <2\pi$ 이며, 여기서 z는 점 $\phi =0$ 입니다. 이들 좌표에서, z에서 좌표 $(\phi ,\theta )$ 를 가지는 임의의 다른 점 $\mathbf {x} \in S^{2}(1)$ 까지의 측지선 거리는 x에서 $\phi$ 의 값입니다. 구형 원은 천정 점 z에서 측지 거리 R까지의 점 집합입니다. 동등하게, $\mathbb {R} ^{3}$ 에 고정된 삽입과 함께, z에 중심을 둔 반지름 $R\leq \pi$ 의 구형 원은 $\mathbf {x} \cdot \mathbf {z} =\cos R$ 를 만족하는 $S^{2}(1)$ 에서 x의 집합입니다.

우리는 역시 구 위의 본질적 표면 넓이 측정을 사용하여 구형 원 내에 둘러싸인 구형 디스크의 넓이를 측정할 수 있습니다. 반지름 R의 디스크의 넓이는 그런-다음 다음에 의해 주어집니다:

A=\int _{0}^{2\pi }\int _{0}^{R}\sin(\phi )d\phi \,d\theta =2\pi (1-\cos R).

보다 일반적으로, 만약 구 $S^{2}(\rho )$ 가 곡률 $\rho$ 의 반지름을 가지면, 반지름 R의 디스크의 넓이는 다음에 의해 제공됩니다:

A=2\pi \rho ^{2}(1-\cos(R/\rho )).

로피탈의 규칙(L'Hôpital's rule)을 적용할 때, 이것은 평평한 극한 $\rho \to \infty$ 에서 유클리드 넓이 $\pi R^{2}$ 에 이르는 경향이 있음을 관찰합니다.

쌍곡선의 경우는 다음에 의해 주어진 (상수 곡률 $-1$ ) 쌍곡선 평면에서 본질적 반지름 R의 디스크의 넓이를 갖는 것과 유사합니다.

A=2\pi (1-\cosh R)

여기서 cosh는 쌍곡 코사인(hyperbolic cosine)입니다. 보다 일반적으로, 상수 곡률 $-k$ 쌍곡선 평면에 대해, 그 답은 다음입니다:

A=2\pi k^{-2}(1-\cosh(kR)).

이들 항등식은 기하학에서 비교 부등식에 대해 중요합니다. 예를 들어, 평평한 공간에서 반지름 R의 원에 의해 둘러싸인 넓이는 항상 구형 원의 넓이보다 크고 쌍곡선 원보다 작은데, 모든 셋의 원이 같은 (본질적) 반지름을 가진다는 조건으로 그렇습니다. 즉, 모든 $R>0$ 에 대해,

2\pi (1-\cos R)<\pi R^{2}<2\pi (1-\cosh R)

직관적으로, 이것은 구가 자체적으로 뒤로 구부러져 평면에 있는 것보다 작은 넓이의 원을 산출하는 경향이 있고, 반면에 쌍곡선 평면은 공간에 잠겨 있을 때 추가적인 넓이를 생성하는 변두리를 발현하기 때문입니다. 고정된 반지름 R의 원의 넓이는 곡률의 엄격하게 감소하는 함수라는 것이 더 일반적으로 참입니다.

모든 경우에서, 만약 $k$ 가 곡률 (상수, 양수 또는 음수)이면, 넓이 A와 둘레 L을 갖는 도메인에 대해 같은-둘레 부등식(isoperimetric inequality)은 다음입니다:

L^{2}\geq 4\pi A-kA^{2}

여기서 상등은 원에 대해 정확하게 달성됩니다.^[5]

Generalizations

우리는 디스크를 타원(ellipse)을 형성하기 위해 늘릴 수 있습니다. 이 늘림은 평면의 선형 변환(linear transformation)이기 때문에, 그것은 넓이를 변경하지만 넓이의 비율을 유지하는 왜곡 인수를 가집니다. 이 관찰은 단위 원의 넓이에서 임의적인 타원의 넓이를 계산하기 위해 사용될 수 있습니다.

변 길이 2의 정사각형에 의해 둘레접된 단위 원을 생각해 보십시오. 변환은 수평과 수직 지름을 타원의 주요 축과 보조 축으로 늘리거나 줄임으로써 원을 타원으로 보냅니다. 정사각형은 타원을 둘레접하는 사각형으로 보냅니다. 정사각형에 대한 원의 넓이 비율은 $π$ /4이며, 이것은 타원과 직사각형의 비율도 $π$ /4임을 의미합니다. a와 b가 타원의 주요 축과 보조 축의 길이라고 가정합니다. 직사각형의 넓이는 ab이므로, 타원의 넓이는 $π$ ab/4입니다.

우리는 역시 더 높은 차원에서 유사한 측정을 고려할 수 있습니다. 예를 들어, 우리는 구 내부의 부피를 찾고 싶을 수 있습니다. 우리는 표면 넓이에 대해 공식을 가질 때, 우리는 디스크에 대해 사용했던 종류의 "양파" 접근 방식을 사용할 수 있습니다.

Bibliography

Archimedes (1897), "Measurement of a circle", in Heath, T. L. (ed.), The Works of Archimedes, Cambridge University Press
(Originally published by Cambridge University Press, 1897, based on J. L. Heiberg's Greek version.)
Beckmann, Petr (1976), A History of Pi, St. Martin's Griffin, ISBN 978-0-312-38185-1
Gerretsen, J.; Verdenduin, P. (1983), "Chapter 8: Polygons and Polyhedra", in H. Behnke; F. Bachmann; K. Fladt; H. Kunle (eds.), Fundamentals of Mathematics, Volume II: Geometry, translated by S. H. Gould, MIT Press, pp. 243–250, ISBN 978-0-262-52094-2
(Originally Grundzüge der Mathematik, Vandenhoeck & Ruprecht, Göttingen, 1971.)
Laczkovich, Miklós (1990), "Equidecomposability and discrepancy: A solution to Tarski's circle squaring problem", Journal für die reine und angewandte Mathematik, 1990 (404): 77–117, doi:10.1515/crll.1990.404.77, MR 1037431, S2CID 117762563
Lang, Serge (1985), "The length of the circle", Math! : Encounters with High School Students, Springer-Verlag, ISBN 978-0-387-96129-3
Smith, David Eugene; Mikami, Yoshio (1914), A history of Japanese mathematics, Chicago: Open Court Publishing, pp. 130–132, ISBN 978-0-87548-170-8
Thijssen, J. M. (2006), Computational Physics, Cambridge University Press, p. 273, ISBN 978-0-521-57588-1

References

^ Stewart, James (2003). Single variable calculus early transcendentals (5th. ed.). Toronto ON: Brook/Cole. pp. 3. ISBN 0-534-39330-6. However, by indirect reasoning, Eudoxus (fifth century B.C.) used exhaustion to prove the familiar formula for the area of a disk: $A=\pi r^{2}.$
^ Heath, Thomas L. (2003), A Manual of Greek Mathematics, Courier Dover Publications, pp. 121–132, ISBN 0-486-43231-9.
^ Hill, George. Lessons in Geometry: For the Use of Beginners, page 124 (1894).
^ Not all best rational approximations are the convergents of the continued fraction!
^ Isaac Chavel (2001), Isoperimetric inequalities, Cambridge University Press

External links

Science News on Tarski problem

[1] Stewart, James (2003). Single variable calculus early transcendentals (5th. ed.). Toronto ON: Brook/Cole. pp. 3. ISBN 0-534-39330-6. However, by indirect reasoning, Eudoxus (fifth century B.C.) used exhaustion to prove the familiar formula for the area of a disk: $A=\pi r^{2}.$

[heath-2] Heath, Thomas L. (2003), A Manual of Greek Mathematics, Courier Dover Publications, pp. 121–132, ISBN 0-486-43231-9.

[3] Hill, George. Lessons in Geometry: For the Use of Beginners, page 124 (1894).

[4] Not all best rational approximations are the convergents of the continued fraction!

[5] Isaac Chavel (2001), Isoperimetric inequalities, Cambridge University Press

[1]

[2]

[3]

[4]

[5]