Multivariable calculus

다변수 미적분학(Multivariable calculus, 역시 다변량 미적분학(multivariate calculus)이라고 알려져 있음)은 한 변수(variable)에서 미적분학(calculus)을 여러 변수의 함수를 갖는 미적분학으로 확장입니다: 단지 하나가 아닌 여러 변수 (다변수)를 포함하는 함수의 미분과 적분입니다.^[1]

다변수 미적분학은 고급 미적분학의 기본 부분으로 생각될 수 있습니다. 고급 미적분에 대해, 유클리드 공간 위의 미적분(calculus on Euclidean space)을 참조하십시오. 삼 차원 공간에서 미적분학의 특수한 경우는 종종 벡터 미적분학(vector calculus)이라고 불립니다.

Typical operations

Limits and continuity

다변수 미적분학에서 극한(limits)과 연속성(continuity)에 대한 연구는 단일-변수 함수에 의해 시연되지 않은 많은 직관에 반하는 결과를 산출합니다.^[1]^: 19–22 예를 들어, 서로 다른 경로를 따라 접근할 때 서로 다른 극한을 제공하는 도메인에 점을 갖는 두 변수의 스칼라 함수가 있습니다. 예를 들어, 다음 함수는

f(x,y)={\frac {x^{2}y}{x^{4}+y^{2}}}

Plot of the function $f (x, y) = (x ²y)/(x 4 + y 2)$

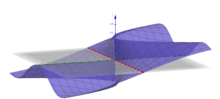
점 $(0,0)$ 이 원점을 통과하는 직선 ( $y=kx$ )을 따라 접근할 때마다 영에 접근합니다. 어쨌든, 포물선(parabola) $y=\pm x^{2}$ 를 따라 원점에 접근할 때, 함수 값은 $\pm 1/2$ 의 극한을 가집니다. 같은 점을 향해 다른 경로를 취하면 다른 극한 값이 생성되므로, 일반적인 극한은 존재하지 않습니다.

다변수 연속성(multivariate continuity)에 충분하지 않은 각 인수에서 연속성은 다음 예제에서도 볼 수 있습니다.^[1]^: 17–19 특히, 두 개의 실수-값 매개변수를 갖는 실수-값 함수, $f(x,y)$ 에 대해, 고정된 $y$ 에 대해 $x$ 에서 $f$ 의 연속성과 고정된 $x$ 에 대해 $y$ 에서 $f$ 의 연속성이 $f$ 의 연속성을 의미하지 않습니다.

다음을 생각해 보십시오:

f(x,y)={\begin{cases}{\frac {y}{x}}-y&{\text{if}}\quad 0\leq y<x\leq 1\\{\frac {x}{y}}-x&{\text{if}}\quad 0\leq x<y\leq 1\\1-x&{\text{if}}\quad 0<x=y\\0&{\text{everywhere else}}.\end{cases}}

이 함수가 사각형 $(0,1)\times (0,1)$ 의 경계와 외부에서 정의에 의해 영인지 쉽게 확인할 수 있습니다. 게다가, 상수 $x$ 와 $y$ 와 $0\leq a\leq 1$ 에 대해 다음에 의해 정의된 함수는 연속입니다:

g_{a}(x)=f(x,a)\quad

and

\quad h_{a}(y)=f(a,y)\quad

구체적으로,

g_{0}(x)=f(x,0)=h_{0}(0,y)=f(0,y)=0

for all

x

and

y

.

어쨌든, 수열 $f\left({\tfrac {1}{n}},{\tfrac {1}{n}}\right)$ (자연수 $n$ 에 대해)은 $\lim _{n\to \infty }f\left({\tfrac {1}{n}},{\tfrac {1}{n}}\right)=1$ 으로 수렴하여, 함수를 $(0,0)$ 에서 불연속으로 렌더링합니다. $x$ -축과 $y$ -축에 평행하지 않고 원점에 접근하면 이 불연속성이 드러납니다.

Continuity of function composition

만약 $f(x,y)$ 가 $(a,b)$ 에서 연속이고, $g$ 가 $f(a,b)$ 에서 연속적인 단일 변수 함수이면, $h(x,y)=g(f(x,y))$ 에 의해 정의된 합성 함수 $h=g\circ f$ 는 $(a,b)$ 에서 연속입니다.

예를 들어, $\exp(x-y)$ 와 $\ln(1+xy-4x+10y).$

Properties of continuous functions

만약 $f(x,y)$ 와 $g(x,y)$ 가 둘 다 $(a,b)$ 에서 연속이면,

(i) $f(x,y)\pm g(x,y)$ 는 $(a,b)$ 에서 연속입니다.

(ii) $cf(x,y)$ 는 임의의 상수 $c$ 에 대해 $(a,b)$ 에서 연속입니다.

(iii) $f(x,y)$ $.$ $g(x,y)$ 는 점 $(a,b)$ 에서 연속입니다.

(iv) ${\frac {f(x,y)}{g(x,y)}}$ 는 $g(a,b)\neq 0$ 이면 $(a,b)$ 에서 연속입니다.

(v) $\mid f(x,y)\mid$ 는 $(a,b)$ 에서 연속입니다.

Partial differentiation

부분 도함수는 도함수의 개념을 더 높은 차원으로 일반화합니다. 다변수 함수의 부분 도함수는 모든 다른 변수가 일정하게 유지되는 한 변수에 관한 도함수입니다.^[1]^: 26ff

부분 도함수는 흥미로운 방법으로 조합되어 도함수의 더 복잡한 표현을 만들 수 있습니다. 벡터 미적분(vector calculus)에서, 델(del) 연산자 ( $\nabla$ )는 부분 도함수의 관점에서 그래디언트(gradient), 다이버전스(divergence), 및 컬(curl)의 개념을 정의하기 위해 사용됩니다. 부분 도함수의 행렬, 야코비(Jacobian) 행렬은 임의적인 차원의 두 공간 사이의 함수의 도함수를 나타내기 위해 사용될 수 있습니다. 따라서 도함수는 함수의 도메인에서 점마다 직접적으로 달라지는 선형 변환(linear transformation)으로 이해될 수 있습니다.

부분 도함수를 포함하는 미분 방정식(Differential equations)은 부분 미분 방정식(partial differential equations) 또는 PDE라고 불립니다. 이들 방정식은 일반적으로 단 하나의 변수에 관한 도함수를 포함하는 보통의 미분 방정식(ordinary differential equations)보다 풀기가 더 어렵습니다.^[1]^: 654ff

Multiple integration

다중 적분은 적분의 개념을 여러 변수의 함수로 확장합니다. 이중 적분과 삼중 적분은 평면과 공간에서 영역의 넓이와 부피를 계산하기 위해 사용될 수 있습니다. 푸비니의 정리(Fubini's theorem)는 적분 도메인 전체에서 피적분이 연속적인 한 다중 적분을 반복된 적분(repeated integral 또는 iterated integral)으로 평가될 수 있음을 보장합니다.^[1]^: 367ff

표면 적분(surface integral)과 선 적분(line integral)은 표면(surfaces)과 곡선(curves)과 같은 곡선화된 매니폴드(manifolds)에 걸쳐 적분하기 위해 사용됩니다.

Fundamental theorem of calculus in multiple dimensions

단일-변수 미적분에서, 미적분의 기본 정리(fundamental theorem of calculus)는 도함수와 적분 사이의 연결을 수립합니다. 다변수 미적분학에서 도함수와 적분 사이의 연결은 벡터 미적분의 적분 정리에 의해 구체화됩니다:^[1]^: 543ff

다변수 미적분학에 대한 보다 발전된 연구에서, 이들 네 가지 정리는 매니폴드(manifolds)에 걸쳐 미분 형식(differential forms)의 적분에 적용되는 보다 일반적인 정리, 일반화된 스토크스의 정리(Stokes' theorem)의 구체적인 화신임을 알 수 있습니다.^[2]

Applications and uses

다변수 미적분학의 기술은 물질 세계에서 많은 관심 대상을 연구하기 위해 사용됩니다. 특히,

	Type of functions	Applicable techniques
곡선	$f:\mathbb {R} \to \mathbb {R} ^{n}$ for $n>1$	곡선의 길이, 선 적분(line integrals), 및 곡률(curvature).
표면	$f:\mathbb {R} ^{2}\to \mathbb {R} ^{n}$ for $n>2$	표면의 넓이(Areas), 표면 적분(surface integrals), 표면을 통한 플럭스(flux), 및 곡률.
스칼라 필드	$f:\mathbb {R} ^{n}\to \mathbb {R}$	최대와 최소, 라그랑주 곱셈수(Lagrange multipliers), 방향 도함수(directional derivative), 수준 집합(level sets).
벡터 필드	$f:\mathbb {R} ^{m}\to \mathbb {R} ^{n}$	그래디언트(gradient), 다이버전스(divergence), 및 컬(curl)을 포함하는 벡터 미적분(vector calculus)의 연산의 어떤 것.

다변수 미적분학은 여러 자유도(degrees of freedom)를 가지는 결정론적 시스템(deterministic systems)을 분석하기 위해 적용될 수 있습니다. 각 자유도에 해당하는 독립 변수(independent variables)를 갖는 함수는 종종 이들 시스템을 모델링하기 위해 사용되고, 다변수 미적분은 시스템 동역학(system dynamics)을 특성화하는 데 도구를 제공합니다.

다변수 미적분은 연속 시간 동역학적 시스템(dynamic systems)의 최적 제어(optimal control)에 사용됩니다. 그것은 다양한 경험적 데이터(empirical data)의 집합 사이의 관계를 추정하기 위한 공식을 도출하기 위해 회귀 분석(regression analysis)에 사용됩니다.

다변수 미적분은 결정론적 행동을 나타내는 고-차원 시스템을 모델링하고 연구하기 위해 자연 과학(natural science)과 사회 과학(social science) 및 공학(engineering)의 많은 분야에서 사용됩니다. 경제학에서, 예를 들어, 다양한 재화에 대한 소비자 선택과 사용할 다양한 투입물과 생산할 산출물에 대한 생산자 선택은 다변수 미적분학으로 모델링됩니다.

비-결정적 또는 확률적(stochastic) 시스템은 확률적 미적분(stochastic calculus)과 같은 다른 종류의 수학을 사용하여 연구될 수 있습니다.

References

^ ^a ^b ^c ^d ^e ^f ^g Richard Courant; Fritz John (14 December 1999). Introduction to Calculus and Analysis Volume II/2. Springer Science & Business Media. ISBN 978-3-540-66570-0.
^ Spivak, Michael (1965). Calculus on Manifolds. New York: W. A. Benjamin, Inc. ISBN 9780805390216.

External links

UC Berkeley video lectures on Multivariable Calculus, Fall 2009, Professor Edward Frenkel
MIT video lectures on Multivariable Calculus, Fall 2007
Multivariable Calculus: A free online textbook by George Cain and James Herod
Multivariable Calculus Online: A free online textbook by Jeff Knisley
Multivariable Calculus – A Very Quick Review, Prof. Blair Perot, University of Massachusetts Amherst
Multivariable Calculus, Online text by Dr. Jerry Shurman

[CourantJohn1999-1] ^ ^a ^b ^c ^d ^e ^f ^g Richard Courant; Fritz John (14 December 1999). Introduction to Calculus and Analysis Volume II/2. Springer Science & Business Media. ISBN 978-3-540-66570-0.

[2] Spivak, Michael (1965). Calculus on Manifolds. New York: W. A. Benjamin, Inc. ISBN 9780805390216.

[1]

[2]