Ratio test

Original article: w:Ratio test

수학(mathematics)에서, 비율 테스트(ratio test)는 급수(series)의 수렴(convergence)에 대해 테스트(test) (또는 "기준")입니다:

$\sum _{n=1}^{\infty }a_{n},$

여기서 각 항은 실수(real) 또는 복소수(complex number)이고 a_n은 n이 클 때 비-영입니다. 테스트는 최초로 장 르 롱 달랑베르(Jean le Rond d'Alembert)에 의해 발표되었고 때때로 달랑베르의 비율 테스트(d'Alembert's ratio test) 또는 코시 비율 테스트(Cauchy ratio test)로 알려져 있습니다.

The test

Decision diagram for the ratio test

테스트의 보통 형식은 극한(limit)의 사용을 만듭니다:

$L=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|.$

(1)

비율 테스트는 다음임을 말합니다:

• 만약 L < 1이면, 급수는 절대적으로 수렴(converges absolutely)입니다;
• 만약 L > 1이면, 급수는 발산(divergent)입니다;
• 만약 L = 1 또는 극한이 존재하지 않으면, 테스트는 결정적이지 않은데, 왜냐하면 이 경우를 만족시키는 수렴 및 발산하는 급수 둘 다가 존재합니다.

만약 극한 상부(limit superior)와 극한 하부(limit inferior)가 사용되면, 극한 L이 존재하지 않는 특정 경우에 적용가능한 비율 테트스를 만드는 것이 가능합니다. 테스트 기준은, 테스트가 심지어 L = 1일 때 때때로 결정적이도록 역시 세분화될 수 있습니다. 보다 구체적으로, 다음을 놓습니다:

$R=\lim \sup \left|{\frac {a_{n+1}}{a_{n}}}\right|$

$r=\lim \inf \left|{\frac {a_{n+1}}{a_{n}}}\right|$.

그런-다음 비율 테스트는 다음임을 말합니다:

• 만약 R < 1이면, 급수는 절대적으로 수렴합니다;
• 만약 r > 1이면, 급수는 발산합니다;
• 만약 모든 큰 n에 대해 (r의 값에 관계없이) $\left|{\frac {a_{n+1}}{a_{n}}}\right|\geq 1$이면, 급수는 역시 발산합니다; 이것은 $|a_{n}|$이 비-영이고 증가하는 것이고 따라서 a_n이 영에 접근하지 않기 때문입니다;
• 테스트는 그렇지 않으면 결정적이지 않습니다.

만약 극한 L이 (1)에서 존재하면, 우리는 L = R = r을 가져야 합니다. 그래서 원래 비율 테스트는 세련된 것의 더 약한 버전입니다.

Examples

Convergent because L < 1

다음 급수를 생각해 보십시오:

$\sum _{n=1}^{\infty }{\frac {n}{e^{n}}}$

비율 테스트를 적용하면, 우리는 다음 극한을 계산합니다:

$L=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|=\lim _{n\to \infty }\left|{\frac {\frac {n+1}{e^{n+1}}}{\frac {n}{e^{n}}}}\right|={\frac {1}{e}}<1.$

이 극한은 1보다 작으므로, 급수는 수렴합니다.

Divergent because L > 1

다음 급수를 생각해 보십시오:

$\sum _{n=1}^{\infty }{\frac {e^{n}}{n}}.$

이것을 비율 테스트에 넣으면:

$L=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|=\lim _{n\to \infty }\left|{\frac {\frac {e^{n+1}}{n+1}}{\frac {e^{n}}{n}}}\right|=e>1.$

따라서 급수는 발산합니다.

Inconclusive because L = 1

세 급수를 생각해 보십시오:

$\sum _{n=1}^{\infty }1,$

$\sum _{n=1}^{\infty }{\frac {1}{n^{2}}},$

$\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}.$

첫 번째 급수 (1 + 1 + 1 + 1 + ⋯)는 발산이며, 두 번째 것 (바젤 문제(Basel problem)에 하나의 중심)은 절대적으로 수렴하고 세 번째 것 (교대하는 조화 급수(alternating harmonic series))은 조건적으로 수렴합니다. 어쨌든, 세 번째 급수의 항별로 크기 비율 $\left|{\frac {a_{n+1}}{a_{n}}}\right|$은 각각 $1,$   ${\frac {n^{2}}{(n+1)^{2}}}$    및   ${\frac {n}{n+1}}$입니다. 그래서, 모든 세 경우에서, 우리는 극한 $\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|$이 1과 같음을 가집니다. 이것은 L = 1일 때를 묘사하고, 급수는 수렴 또는 발산할 수 있고, 따라서 원래 비율 테스트는 결정적이지 않습니다. 그러한 경우에서, 보다 세련된 테스트가 수렴 또는 발산을 결정하기 위해 요구됩니다.

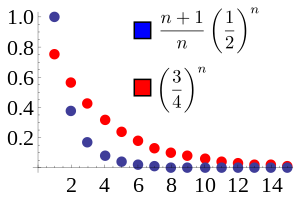
Proof

In this example, the ratio of adjacent terms in the blue sequence converges to L=1/2. We choose r = (L+1)/2 = 3/4. Then the blue sequence is dominated by the red sequence r^k for all n ≥ 2. The red sequence converges, so the blue sequence does as well.

아래는 원래 비율 테스트의 유효성의 증명입니다.

$L=\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|<1$임을 가정합니다. 우리는 그런-다음 그의 항이 결국 특정 수렴하는 기하 급수(geometric series)의 항보다 작아짐을 보여줌으로써 급수가 절대적으로 수렴함을 보일 수 있습니다. 이것을 하기 위해, $r={\frac {L+1}{2}}$로 놓습니다. 그런-다음 r은 L과 1 사이에 엄격하고, 충분하게 큰 n; 말하자면, N보다 더 큰 모든 n에 대해 $|a_{n+1}|<r|a_{n}|$입니다; 따라서 각 n > N 및 i > 0에 대해 $|a_{n+i}|<r^{i}|a_{n}|$이고, 그래서

$\sum _{i=N+1}^{\infty }|a_{i}|=\sum _{i=1}^{\infty }\left|a_{N+i}\right|<\sum _{i=1}^{\infty }r^{i}|a_{N}|=|a_{N}|\sum _{i=1}^{\infty }r^{i}=|a_{N}|{\frac {r}{1-r}}<\infty .$

즉, 급수는 절대적으로 수렴입니다.

다른 한편으로, 만약 L > 1이면, 더해지는-숫자의 극한이 비-영이 되도록, 충분하게 큰 n에 대해 $|a_{n+1}|>|a_{n}|$입니다. 따라서 급수는 발산입니다.

Extensions for L = 1

앞의 예에서 볼 수 있듯이, 비율 테스트는 비율의 극한이 1일 때 결정적이지 않을 수 있습니다. 비율 테스트에 대한 확장은, 어쨌든, 때때로 이 경우를 처리하기 위해 허용합니다.

아래의 모든 테스트에서, 우리는 Σa_n이 양의 a_n을 갖는 합임을 가정합니다. 이들 테스트는 음의 항의 유한 숫자를 갖는 임의의 급수에 역시 적용될 수 있습니다. 임의의 그러한 급수는 다음으로 쓸 수 있습니다:

$\sum _{n=1}^{\infty }a_{n}=\sum _{n=1}^{N}a_{n}+\sum _{n=N+1}^{\infty }a_{n}$

여기서 a_N은 가장-높은-인데스된 음의 항입니다. 오른쪽에서 첫 번째 표현은 유한일 수 있는 부분 합이고, 그래서 전체 급수의 수렴은 오른쪽에서 두 번째 표현의 수렴 속성에 의해 결정될 것이며, 이것은 n=1에서 시작하는 모든 양의 항의 급수를 형성하기 위해 다시-인덱스될 수 있을 것입니다.

각 테스트는 테스트 매개-변수 (ρ_n)을 정의하며 이것은 수렴 또는 발산을 수립하는 것에 필요한 해당 매개-변수의 동작을 지정합니다. 각 테스트에 대해, 테스트의 더 약한 형식은 존재하며 이것은 대신 lim_n->∞ρ_n에 대한 제한을 놓을 것입니다.

테스트의 모두는 영역을 가지며 이것에서 그들은 ∑a_n의 수렴 속성을 설명하지 못합니다. 실제로, 수렴 테스트는 급수의 수렴 속성을 완전히 설명할 수 없습니다. 이것은 만약 ∑a_n이 수렴하면, 두 번째 수렴하는 급수 ∑b_n은 더 느리게 수렴하는 것으로 발견될 수 있기 때문입니다: 즉, 그것은 lim_n->∞ (b_n/a_n) = ∞인 속성을 가집니다. 게다가, 만약 ∑a_n이 발산이면, 두 번째 발산하는 급수 ∑b_n는 더 느리게 발산하는 것으로 발견될 수 있습니다: 즉, 그것은 lim_n->∞ (b_n/a_n) = 0인 속성을 가집니다. 수렴 테스트는 a_n의 일부 특정 가족에 대한 비교 테스트를 본질적으로 사용하고, 더 느리게 수렴 또는 발산하는 수열에 대해 실패합니다.

De Morgan hierarchy

오거스터스 드 모르간(Auguscus De Morgan)은 비율-유형 테스트의 계층-구조을 제안했습니다:

아래의 비율 테스트 매개-변수 ($\rho _{n}$)는 모두 일반적으로 형식 $D_{n}a_{n}/a_{n+1}-D_{n+1}$의 항을 포함합니다. 이 항은 $a_{n+1}/a_{n}$을 곱하여 $D_{n}-D_{n+1}a_{n+1}/a_{n}$을 산출할 것입니다. 이 항은 테스트 매개 변수의 정의에서 이전 항을 대체할 수 있고 도출된 결론은 같게 남을 수 있습니다. 그에 따라서, 테스트 매개-변수의 하나 또는 나머지 하나 형식을 사용하는 참조 사이에 구별이 없을 것입니다.

1. d’Alembert’s ratio test

드 모르간 계층의 첫 번째 테스트는 위에서 묘사된 비율 테스트입니다.

2. Raabe's test

이 확장은 요셉 루드비히 하베(Joseph Ludwig Raabe)에 기인합니다. 다음 (및 여분의 항)을 정의합니다:

$\rho _{n}\equiv n\left({\frac {a_{n}}{a_{n+1}}}-1\right)$

(알리(Ali), 블랙번(Blackburn), 펠드(Feld), 두리스(Duris) (none), 두리수2(Duris2)를 참조하십시오)

급수는 다음일 것입니다:

• 모든 n>N에 대해 $\rho _{n}\geq c$를 만족하는 c>1이 존재할 때 수렴합니다.
• 모든 n>N에 대해 $\rho _{n}\leq 1$일 때 발산합니다.
• 그렇지 않으면, 테스트는 결정적이지 않습니다.

극한 버전에 대해, 급수는 다음일 것입니다:

• 만약 $\rho =\lim _{n\to \infty }\rho _{n}>1$ (이것은 경우 ρ = ∞를 포함합니다)이면, 수렴합니다.
• 만약 $\lim _{n\to \infty }\rho _{n}<1$이면, 발산합니다.
• 만약 ρ = 1이면, 테스트는 결정적이지 않습니다.

위의 극한이 존재하지 않을 때, 극한 상부 및 하부가 사용하는 것이 가능할 수 있을 것입니다. 급수는 다음일 것입니다:

• 만약 $\liminf _{n\to \infty }\rho _{n}>1$이면 수렴합니다.
• 만약 $\limsup _{n\rightarrow \infty }\rho _{n}<1$이면, 발산합니다.
• 그렇지 않으면, 테스트는 결정적이지 않습니다.

Proof of Raabe's test

$\rho _{n}\equiv n\left({\frac {a_{n}}{a_{n+1}}}-1\right)$를 정의하면, 우리는 극한이 존재한다고 가정할 필요가 없습니다; 만약 $\limsup \rho _{n}<1$이면, $\sum a_{n}$은 발산하지만, 만약 $\liminf \rho _{n}>1$이면 합은 수렴합니다.

증명은 본질적으로 $\sum 1/n^{R}$과 비교하여 진행됩니다. 먼저 $\limsup \rho _{n}<1$임을 가정합니다. 물론 만약 $\limsup \rho _{n}<0$이면, 큰 $n$에 대해 $a_{n+1}\geq a_{n}$이므로, 합은 발산합니다; 그런-다음 $0\leq \limsup \rho _{n}<1$임을 가정합니다. 모든 $n\geq N$에 대해 $\rho _{n}\leq R$를 만족하는 $R<1$이 존재하며, 이것은 $a_{n}/a_{n+1}\leq \left(1+{\frac {R}{n}}\right)\leq e^{R/n}$임을 말하는 것입니다. 따라서 $a_{n+1}\geq a_{n}e^{-R/n}$이며, 이것은 $n\geq N$에 대해 $a_{n+1}\geq a_{N}e^{-R(1/N+\dots +1/n)}\geq ca_{N}e^{-R\log(n)}=ca_{N}/n^{R}$임을 의미합니다; $R<1$이므로 이것은 $\sum a_{n}$가 발산함을 보입니다.

나머지 반의 증명은, 대부분의 불등식이 단순히 반대인 것과 함께, 전적으로 유사합니다. 우리는 위에서 사용했었던 간단한 $1+t<e^{t}$의 위치에서 사용하기 위한 예비 부등식이 필요합니다: $R$ 및 $N$을 수정합니다. $\log \left(1+{\frac {R}{n}}\right)={\frac {R}{n}}+O\left({\frac {1}{n^{2}}}\right)$임을 주목하십시오. 그래서 $\log \left(\left(1+{\frac {R}{N}}\right)\dots \left(1+{\frac {R}{n}}\right)\right)=R\left({\frac {1}{N}}+\dots +{\frac {1}{n}}\right)+O(1)=R\log(n)+O(1)$입니다; 따라서 $\left(1+{\frac {R}{N}}\right)\dots \left(1+{\frac {R}{n}}\right)\geq cn^{R}$입니다.

이제 $\liminf \rho _{n}>1$임을 가정합니다. 첫 번째 문단에서 처럼 주장하면, 이전 문단에서 수립했던 부등식을 사용하여, 우리는 $n\geq N$에 대해 $a_{n+1}\leq ca_{N}n^{-R}$를 만족하는 $R>1$가 존재함을 알 수 있습니다; $R>1$이므로, 이것은 $\sum a_{n}$가 수렴함을 보입니다.

3. Bertrand’s test

이 확장은 조제프 베르트랑(Joseph Bertrand)과 오거스터스 드 모르간(Augustus De Morgan)에 의한 것입니다.

다음을 정의합니다:

$\rho _{n}\equiv n\ln n\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\ln n$

베르트랑의 테스트는 급수가 다임일 것임을 주장합니다:

• 모든 n>N에 대해 $\rho _{n}\geq c$를 만족하는 c>1이 존재할 때 수렴합니다.
• 모든 n>N에 대해 $\rho _{n}\leq 1$일 때 발산합니다.
• 그렇지 않으면, 테스트는 비-결정적입니다.

극한 버전에 대해, 급수는 다음일 것입니다:

• 만약 $\rho =\lim _{n\to \infty }\rho _{n}>1$ (이것은 경우 ρ = ∞를 포함합니다)이면 수렴합니다.
• 만약 $\lim _{n\to \infty }\rho _{n}<1$이면 발산합니다.
• 만약 ρ = 1이면, 테스트는 비-결정적입니다.

위의 극한이 존재하지 않을 때, 극한 상부 및 하부를 사용하는 것이 가능성이 있을 것입니다. 급수는 다음일 것입니다:

• 만약 $\liminf \rho _{n}>1$이면 수렴합니다.
• 만약 $\limsup \rho _{n}<1$이면 발산합니다.
• 그렇지 않으면, 테스트는 비-결정적입니다.

4. Extended Bertrand’s test

이 확장은 에서 처음으로 등장했습니다. 기술적인 가정이 없는 더 간단한 증명은 .

$K\geq 1$를 정수로 놓고, $\ln _{(K)}(x)$가 자연 로그(natural logarithm)의 $K$번째 반복(iteration), 즉, $\ln _{(1)}(x)=\ln(x)$ 및 임의의 $2\leq k\leq K$에 대해, $\ln _{(k)}(x)=\ln _{(k-1)}(\ln(x))$를 나타내는 것으로 놓습니다.

비율 $a_{n}/a_{n+1}$은, $n$가 클 때, 다음 형식에서 표시됨을 가정합니다:

${\frac {a_{n}}{a_{n+1}}}=1+{\frac {1}{n}}+{\frac {1}{n}}\sum _{i=1}^{K-1}{\frac {1}{\prod _{k=1}^{i}\ln _{(k)}(n)}}+{\frac {\rho _{n}}{n\prod _{k=1}^{K}\ln _{(k)}(n)}},\quad K\geq 1.$

(빈 합은 0으로 가정됩니다. $K=1$과 함께, 테스트는 베르트랑의 테스트로 줄어듭니다.)

값 $\rho _{n}$은 다음 형식에서 명시적으로 표시될 수 있습니다:

$\rho _{n}=n\prod _{k=1}^{K}\ln _{(k)}(n)\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\sum _{j=1}^{K}\prod _{k=1}^{j}\ln _{(K-k+1)}(n).$

확장된 베르트랑의 테스트는 급수가 다음임을 주장합니다:

• 모든 $n>N$에 대해 $\rho _{n}\geq c$를 만족하는 $c>1$가 존재할 때 수렴합니다.
• 모든 $n>N$에 대해 $\rho _{n}\leq 1$일 때 발산합니다.
• 그렇지 않으면, 테스트는 비-결정적입니다.

극한 버전에 대해, 급수는 다음입니다:

• 만약 $\rho =\lim _{n\to \infty }\rho _{n}>1$ (이것은 경우 $\rho =\infty$를 포함합니다)이면, 수렴합니다.
• 만약 $\lim _{n\to \infty }\rho _{n}<1$이면, 발산합니다.
• 만약 $\rho =1$이면, 테스트는 비-결정적입니다.

위의 극한이 존재하지 않을 때, 극한 상부 및 하부를 사용하는 것이 가능할 것입니다. 급수는 다음입니다:

• 만약 $\liminf \rho _{n}>1$이면 수렴입니다.
• 만약 $\limsup \rho _{n}<1$이면 발산입니다.
• 그렇지 않으면, 테스트는 비-결정적입니다.

확장된 베르트랑의 테스트에 대해 출생-사망 과정(Birth-death process)를 참조하십시오.

5. Gauss’s test

이 확장은 카를 프리드리히 가우스(Carl Friedrich Gauss)에 의한 것입니다.

a_n > 0 및 r > 1을 가정하며, 만약 경계진 수열 C_n은 모든 n에 대해 다음을 만족하도록 구할 수 있으면:

${\frac {a_{n}}{a_{n+1}}}=1+{\frac {\rho }{n}}+{\frac {C_{n}}{n^{r}}}$

급수는 다음일 것입니다:

• 만약 $\rho >1$이면, 수렴합니다.
• 만약 $\rho \leq 1$이면, 발산합니다.

6. Kummer’s test

이 확장은 에른스트 쿠머(Ernst Kummer)에 의한 것입니다.

ζ_n를 양의 상수의 보조 수열로 놓습니다. 다음을 정의합니다:

$\rho _{n}\equiv \left(\zeta _{n}{\frac {a_{n}}{a_{n+1}}}-\zeta _{n+1}\right)$

쿠마의 테스트는 급수가 다음일 것임을 말합니다:

• 만약 모든 n>N에 대해 $\rho _{n}\geq c$를 만족하는 $c>0$가 존재하면 수렴합니다.

(이것은 $\rho _{n}>0$를 말함과 같지 않음에 주목하십시오)

• 만약 모든 n>N에 대해 $\rho _{n}\leq 0$이고 $\sum _{n=1}^{\infty }1/\zeta _{n}$가 발산하면 발산합니다.

극한 버전에 대해, 급수는 다음일 것입니다:

• 만약 $\lim _{n\to \infty }\rho _{n}>0$ (이것은 경우 ρ = ∞를 포함합니다)이면 수렴합니다.
• 만약 $\lim _{n\to \infty }\rho _{n}<0$이고 $\sum _{n=1}^{\infty }1/\zeta _{n}$가 발산하면 발산합니다.
• 그렇지 않으면, 테스트는 비-결정적입니다.

위의 극한이 존재하지 않을 때, 극한 상부 및 하부를 사용하는 것이 가능할 수 있을 것입니다. 급수는 다음일 것입니다:

• 만약 $\liminf _{n\to \infty }\rho _{n}>0$이면 수렴합니다.
• 만약 $\limsup _{n\to \infty }\rho _{n}<0$이고 $\sum 1/\zeta _{n}$가 발산하면 발산합니다.

Special cases

가우스의 테스트를 제외한 드 모르간 계층에서 모든 테스트는 쿠마의 테스트의 특수한 경우로 쉽게 보일 수 있습니다:

• 비율 테스트에 대해, ζ_n=1를 놓습니다. 그런-다음

$\rho _{Kummer}=\left({\frac {a_{n}}{a_{n+1}}}-1\right)=1/\rho _{Ratio}-1$

• 하베의 테스트에 대해, ζ_n=n를 놓습니다. 그런-다음:

$\rho _{Kummer}=\left(n{\frac {a_{n}}{a_{n+1}}}-(n+1)\right)=\rho _{Raabe}-1$

• 베르트랑의 테스트에 대해, ζ_n=n ln(n)를 놓습니다. 그런-다음:

$\rho _{Kummer}=n\ln(n)\left({\frac {a_{n}}{a_{n+1}}}\right)-(n+1)\ln(n+1)$

$\ln(n+1)=\ln(n)+\ln(1+1/n)$를 사용하고 큰 n에 대해 $\ln(1+1/n)\rightarrow 1/n$ (이것은 다른 항들과 비교해서 무시할 수 있습니다)를 근사하여(approximating), $\rho _{Kummer}$는 다음으로 쓸 수 있을 것입니다:

$\rho _{Kummer}=n\ln(n)\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\ln(n)-1=\rho _{Bertrand}-1$

• 확장된 베르트랑의 테스트에 대해, $\zeta _{n}=n\prod _{k=1}^{K}\ln _{(k)}(n)$를 놓습니다. 큰 $n$에 대해 테일러 급수(Taylor series) 전개로부터 우리는 근사(approximation)에 도착합니다:

$\ln _{(k)}(n+1)=\ln _{(k)}(n)+{\frac {1}{n\prod _{j=1}^{k-1}\ln _{(j)}(n)}}+O\left({\frac {1}{n^{2}}}\right),$

여기서 빈 곱은 1로 가정됩니다. 그런-다음,

$\rho _{Kummer}=n\prod _{k=1}^{K}\ln _{(k)}(n){\frac {a_{n}}{a_{n+1}}}-(n+1)\left[\prod _{k=1}^{K}\left(\ln _{(k)}(n)+{\frac {1}{n\prod _{j=1}^{k-1}\ln _{(j)}(n)}}\right)\right]+o(1)=n\prod _{k=1}^{K}\ln _{(k)}(n)\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\sum _{j=1}^{K}\prod _{k=1}^{j}\ln _{(K-k+1)}(n)-1+o(1).$

따라서,

$\rho _{Kummer}=\rho _{ExtendedBertrand}-1.$

이들 네 테스트에 대해, 그들이 드 모르간 계층에서 더 높을수록, $1/\zeta _{n}$ 급수가 더 느리게 발산함을 주목하십시오.

Proof of Kummer's test

만약 $\rho _{n}>0$이면 양수 $0<\delta <\rho _{n}$를 수정하십시오. 모든 각 $n>N$에 대해 다음을 만족하는 자연수 $N$가 존재합니다:

$\delta \leq \zeta _{n}{\frac {a_{n}}{a_{n+1}}}-\zeta _{n+1}.$

$a_{n+1}>0$이므로, 모든 각 $n>N$에 대해 다음입니다:

$0\leq \delta a_{n+1}\leq \zeta _{n}a_{n}-\zeta _{n+1}a_{n+1}.$

특히 모든 $n\geq N$에 대해 $\zeta _{n+1}a_{n+1}\leq \zeta _{n}a_{n}$이며 이것은 인덱스 $N$로부터 시작함을 의미하며 수열 $\zeta _{n}a_{n}>0$이 단조적으로 감소하고 양수이며 이것은 특히 그것이 0에 의해 아래로 경계짐을 의미합니다. 그러므로, 극한

$\lim _{n\to \infty }\zeta _{n}a_{n}=L$은 존재합니다.

이것은 양의 망원 급수(telescoping series)

$\sum _{n=1}^{\infty }\left(\zeta _{n}a_{n}-\zeta _{n+1}a_{n+1}\right)$

가 수렴하고, 모든 $n>N$에 대해, 양의 급수에 대해 직접 비교 테스트(direct comparison test)에 의해

$\delta a_{n+1}\leq \zeta _{n}a_{n}-\zeta _{n+1}a_{n+1}$

이므로, 급수 $\sum _{n=1}^{\infty }\delta a_{n+1}$가 수렴함을 의미합니다.

다른 한편으로, 만약 $\rho <0$이면, $\zeta _{n}a_{n}$가 $n>N$에 대해 증가함을 만족하는 N이 있습니다. 특히, 모든 $n>N$에 대해 $\zeta _{n}a_{n}>\epsilon$인 것에 대해 $\epsilon >0$가 존재하고, 그래서 $\sum _{n}a_{n}=\sum _{n}{\frac {a_{n}\zeta _{n}}{\zeta _{n}}}$가 $\sum _{n}{\frac {\epsilon }{\zeta _{n}}}$를 갖는 비교에 의해 발산합니다.

Second ratio test

보다 세련된 비율 테스트는 이차 비율 테스트입니다: $a_{n}>0$에 대해 정의합니다:

$L_{0}\equiv \lim _{n\rightarrow \infty }{\frac {a_{2n}}{a_{n}}}$

$L_{1}\equiv \lim _{n\rightarrow \infty }{\frac {a_{2n+1}}{a_{n}}}$

$L\equiv \max(L_{0},L_{1})$

이차 비율 테스트에 의해 급수는 다음일 것입니다:

• 만약 $L<{\frac {1}{2}}$이면 수렴합니다.
• 만약 $L>{\frac {1}{2}}$이면 발산합니다.
• 만약 $L={\frac {1}{2}}$이면 테스트는 비-결정적입니다.

만약 위의 극한이 존재하지 않으면, 극한 상부 및 하부를 사용하는 것이 가능할 수 있을 것입니다. 다음을 정의합니다:

$L_{0}\equiv \limsup _{n\rightarrow \infty }{\frac {a_{2n}}{a_{n}}}$		$L_{1}\equiv \limsup _{n\rightarrow \infty }{\frac {a_{2n+1}}{a_{n}}}$
$\ell _{0}\equiv \liminf _{n\rightarrow \infty }{\frac {a_{2n}}{a_{n}}}$		$\ell _{1}\equiv \liminf _{n\rightarrow \infty }{\frac {a_{2n+1}}{a_{n}}}$
$L\equiv \max(L_{0},L_{1})$		$\ell \equiv \min(\ell _{0},\ell _{1})$

그런-다음 급수는 다음일 것입니다:

• 만약 $L<{\frac {1}{2}}$이면 수렴합니다.
• 만약 $\ell >{\frac {1}{2}}$이면 발산합니다.
• 만약 $\ell \leq {\frac {1}{2}}\leq L$이면 테스트는 비-결정적입니다.

이차 비율 테스트는 m-번째 비율 테스트로 일반화될 수 있지만, 더 높은 차수는 유용함을 찾을 수 없습니다.

See also

• Root test
• Radius of convergence

References

• d'Alembert, J. (1768), Opuscules, vol. V, pp. 171–183.
• Apostol, Tom M. (1974), Mathematical analysis (2nd ed.), Addison-Wesley, ISBN 978-0-201-00288-1: §8.14.
• Knopp, Konrad (1956), Infinite Sequences and Series, New York: Dover Publications, Bibcode:1956iss..book.....K, ISBN 978-0-486-60153-3: §3.3, 5.4.
• Rudin, Walter (1976), Principles of Mathematical Analysis (3rd ed.), New York: McGraw-Hill, Inc., ISBN 978-0-07-054235-8: §3.34.
• "Bertrand criterion", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• "Gauss criterion", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• "Kummer criterion", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Watson, G. N.; Whittaker, E. T. (1963), A Course in Modern Analysis (4th ed.), Cambridge University Press, ISBN 978-0-521-58807-2: §2.36, 2.37.