Determinant

Original article: w:Determinant

This article is about mathematics. For determinants in epidemiology, see Risk factor. For determinants in immunology, see Epitope.

수학(mathematics)에서, 행렬식(determinant)은 정사각 행렬(square matrix)의 엔트리의 함수(function)인 스칼라 값(scalar value)입니다. 그것은 행렬의 일부 속성과 행렬로 표시되는 선형 맵(linear map)을 특성화합니다. 특히, 행렬식이 비-영인 것과 행렬이 역가능(invertible)이고 행렬에 의해 표현된 선형 맵이 동형(isomorphism)인 것은 필요충분(iff) 조건입니다. 행렬의 곱의 행렬식은 그것들의 행렬식의 곱입니다 (이전 속성은 이 속성의 따름정리입니다). 행렬 A의 행렬식은 det(A), det A, 또는 |A|로 표시됩니다.

2 × 2 행렬의 행렬식은 다음과 같습니다:

${\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc,$

그리고 3 × 3 행렬의 행렬식은 다음과 같습니다:

${\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=aei+bfg+cdh-ceg-bdi-afh.$

n × n 행렬의 행렬식은 몇 가지 동등한 방법으로 정의될 수 있습니다. 라이프니츠 공식(Leibniz formula)은 각 피합수가 n개의 다른 엔트리의 곱이고, 이들 피합수의 개수는 $n!,$ n의 팩토리얼 (처음 n개의 양의 정수의 곱)임을 만족하는 행렬 엔트리의 부호화된 곱의 합으로 행렬식을 표현합니다. 라플라스 전개(Laplace expansion)는 n × n 행렬의 행렬식을 $(n-1)\times (n-1)$ 부분행렬의 행렬식의 선형 조합(linear combination)으로 표현합니다. 가우스 소거법(Gaussian elimination)은 행렬식을 연속적인 기본 행 연산(elementary row operations)으로 얻은 대각 행렬(diagonal matrix)의 대각 엔트리의 곱으로 표현합니다.

행렬식은 일부 그것들의 속성에 의해 정의될 수도 있습니다: 행렬식은 다음 네 가지 속성을 가지는 n × n 행렬 위에 정의된 고유한 함수입니다. 항등 행렬(identity matrix)의 행렬식은 1입니다; 두 행 (또는 두 열)의 교환은 행렬식에 −1을 곱합니다; 행 (또는 열)에 숫자를 곱하는 것은 행렬식에 이 숫자가 곱해집니다; 그리고 행 (또는 열)에 또 다른 행 (또는 열)의 배수를 더하는 것은 행렬식을 변경하지 않습니다.

행렬식은 수학 전체에서 발생합니다. 예를 들어, 행렬은 종종 선형 방정식의 시스템에서 계수(coefficients)를 나타내기 위해 사용되고, 행렬식은 이들 방정식을 풀기 위해 사용될 수 있지만 (크라메르의 규칙), 다른 해결 방법이 계산적으로 훨씬 더 효율적입니다. 행렬식은 고윳값(eigenvalues)을 근으로 하는 행렬의 특성 다항식(characteristic polynomial)을 정의하는 데 사용됩니다. 기하학(geometry)에서, n-차원 평행육면체(parallelepiped)의 부호화된 n-차원 부피(volume)는 행렬식에 의해 표현됩니다. 이것은 특히 다중 적분(multiple integrals)에서 변수의 변경(changes of variables)에 대해 외부 미분 형식(exterior differential forms) 및 야코비 행렬식(Jacobian determinant)과 함께 미적분학(calculus)에서 사용됩니다.

Two by two matrices

2 × 2 행렬 ${\begin{pmatrix}a&b\\c&d\end{pmatrix}}$의 행렬식은 "det" 또는 행렬 주변에 수직 막대에 의해 표시되고, 다음과 같이 정의됩니다:

$\det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.$

예를 들어,

$\det {\begin{pmatrix}3&7\\1&-4\end{pmatrix}}={\begin{vmatrix}3&7\\1&{-4}\end{vmatrix}}=3\cdot (-4)-7\cdot 1=-19.$

First properties

행렬식은 $2\times 2$-행렬에 대한 정의의 직접 평가에 의해 입증될 수 있고, 더 큰 행렬의 행렬식에 대해 계속 유지되는 몇 가지 주요 속성을 가집니다. 그들은 다음과 같습니다: 첫째, 항등 행렬(identity matrix) ${\begin{pmatrix}1&0\\0&1\end{pmatrix}}$의 행렬식은 1입니다. 둘째, 행렬식은 두 행이 같으면 영입니다:

${\begin{vmatrix}a&b\\a&b\end{vmatrix}}=ab-ba=0.$

이것은 유사하게 만약 두 열이 같으면 유지됩니다. 게다가,

${\begin{vmatrix}a&b+b'\\c&d+d'\end{vmatrix}}=a(d+d')-(b+b')c={\begin{vmatrix}a&b\\c&d\end{vmatrix}}+{\begin{vmatrix}a&b'\\c&d'\end{vmatrix}}.$

마지막으로, 만약 임의의 열에 어떤 숫자 $r$을 곱하면 (즉, 해당 열에서 모든 엔트리에 해당 숫자를 곱하면), 행렬식에도 해당 숫자를 곱합니다:

${\begin{vmatrix}r\cdot a&b\\r\cdot c&d\end{vmatrix}}=rad-brc=r(ad-bc)=r\cdot {\begin{vmatrix}a&b\\c&d\end{vmatrix}}.$

Geometric meaning

The area of the parallelogram is the absolute value of the determinant of the matrix formed by the vectors representing the parallelogram's sides.

만약 행렬 엔트리가 실수이면, 행렬 A는 두 개의 선형 맵(linear maps)을 나타내기 위해 사용될 수 있습니다: 하나는 표준 기저(standard basis) 벡터를 A의 행에 매핑하고, 다른 하나는 그것들을 A의 열에 매핑합니다. 두 경우 모두에서, 기저 벡터의 이미지는 매핑 아래에서 단위 정사각형(unit square)의 이미지를 나타내는 평행사변형(parallelogram)을 형성합니다. 위 행렬의 행에 의해 정의된 평행사변형은 첨부된 그림과 같이 (0, 0), (a, b), (a + c, b + d), 및 (c, d)에 꼭짓점을 갖는 평행사변형입니다.

ad − bc의 절댓값은 평행사변형의 넓이이고, 따라서 넓이가 A에 의해 변환되는 스케일 인수를 나타냅니다. (A의 열에 의해 형성된 평행사변형은 일반적으로 다른 평행사변형이지만, 행렬식이 행과 열에 관해 대칭적이기 때문에, 넓이는 같을 것입니다.)

행렬식의 절댓값은 부호와 함께 평행사변형의 방향화된 넓이(oriented area)가 됩니다. 방향화된 넓이는 평행사변형을 정의하는 첫 번째 벡터에서 두 번째 벡터로의 각도가 시계 방향 (항등 행렬에 대해 얻는 방향과 반대임)으로 회전할 때 음수라는 점을 제외하면 보통의 넓이(area)와 같습니다.

ad − bc가 부호화된 넓이임을 보여주기 위해, 평행사변형의 변을 나타내는 두 벡터 u ≡ (a, b)와 v ≡ (c, d)를 포함하는 행렬을 고려할 수 있습니다. 부호화된 넓이는 벡터 사이의 각도 θ에 대해 |u| |v| sin θ로 표현할 수 있으며, 이는 단순히 밑변 곱하기 높이, 한 벡터의 길이 곱하기 다른 벡터의 수직 성분입니다. 사인(sine)으로 인해, 이것은 이미 부호화된 넓이이지만, 그것은 수직 벡터에 대한 보완 각도 (보각)의 코사인(cosine)을 사용하여 더 편리하게 표현할 수 있으며, 예를 들어, |u^⊥| |v| cos θ′가 되도록 u^⊥ = (−b, a)이며, 이는 스칼라 곱(scalar product)의 패턴에 의해 ad − bc와 같다고 결정될 수 있습니다:

${\text{Signed area}}=|{\boldsymbol {u}}|\,|{\boldsymbol {v}}|\,\sin \,\theta =\left|{\boldsymbol {u}}^{\perp }\right|\,\left|{\boldsymbol {v}}\right|\,\cos \,\theta '={\begin{pmatrix}-b\\a\end{pmatrix}}\cdot {\begin{pmatrix}c\\d\end{pmatrix}}=ad-bc.$

The volume of this parallelepiped is the absolute value of the determinant of the matrix formed by the columns constructed from the vectors r1, r2, and r3.

따라서 행렬식은 스케일 인수와 $A$로 표시되는 매핑에 의해 유도된 방향을 제공합니다. 행렬식이 일과 같을 때, 행렬에 의해 정의된 선형 매핑은 같은-넓이(equi-areal) 및 방향-보존하는 것입니다.

이중벡터(bivector)로 알려진 대상은 이들 아이디어와 관련이 있습니다. 2D에서, 그것은 각각 원점 (0, 0)과 좌표 (a, b)와 (c, d)를 갖는 두 벡터를 상상함으로써 형성된 방향화된 평면 구획(oriented plane segment)으로 해석될 수 있습니다. 이중-벡터 크기 ((a, b) ∧ (c, d)로 표시됨)는 부호화된 넓이이며, 이는 역시 행렬식 ad − bc이기도 합니다.

만약 n × n 실수(real) 행렬 $A$가 그것의 열 벡터 $A=\left[{\begin{array}{c|c|c|c}\mathbf {a} _{1}&\mathbf {a} _{2}&\cdots &\mathbf {a} _{n}\end{array}}\right]$의 관점에서 쓰이면, 다음과 같습니다:

$A{\begin{pmatrix}1\\0\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{1},\quad A{\begin{pmatrix}0\\1\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{2},\quad \ldots ,\quad A{\begin{pmatrix}0\\0\\\vdots \\1\end{pmatrix}}=\mathbf {a} _{n}.$

이것은 $A$가 단위 n-입방체를 벡터 $\mathbf {a} _{1},\mathbf {a} _{2},\ldots ,\mathbf {a} _{n}$에 의해 정의된 n-차원 평행다면체(parallelotope), 영역 $P=\left\{c_{1}\mathbf {a} _{1}+\cdots +c_{n}\mathbf {a} _{n}\mid 0\leq c_{i}\leq 1\ \forall i\right\}$로 매핑함을 의미합니다.

행렬식은 이 평행다면체의 부호화된 n-차원 부피, $\det(A)=\pm {\text{vol}}(P)$를 제공하고, 따라서 $A$에 의해 생성된 선형 변환(linear transformation)의 n-차원 부피 스케일링 인수를 보다 일반적으로 설명합니다. (그 부호는 변환이 방향을 유지하거나 반대로 바꾸는지 여부를 보여줍니다.) 특히, 행렬식이 영이면, 이 평행다면체는 부피 영을 가지고 완전히 n-차원이 아니며, 이는 $A$의 이미지의 차원이 n보다 작음을 나타냅니다. 이것은 $A$가 위로의(onto)도 아니고 일대일(one-to-one)도 아닌 선형 변환을 생성하고, 따라서 역가능이 아님을 의미합니다.

Definition

$A$를 n 행과 n 열을 갖는 정사각 행렬(square matrix)이라고 놓으면, 다음과 같이 쓸 수 있습니다:

$A={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{bmatrix}}.$

엔트리 $a_{1,1}$ 등은, 많은 목적을 위해, 실수 또는 복소수입니다. 아래에서 설명하는 것처럼, 행렬식은 엔터리가 교환 링(commutative ring)에 있는 행렬에 대해서도 정의됩니다.

$A$의 행렬식은 det($A$)로 표시하거나, 대괄호 대신 둘러싸는 막대를 쓺으로써 행렬 엔트리의 관점에서 직접 표시될 수 있습니다:

${\begin{vmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{vmatrix}}.$

정사각 행렬 $A$, 즉, 같은 수의 행과 열을 갖는 행렬의 행렬식을 정의하기 위한 여러 동등한 방법이 있습니다: 행렬식은 라이프니츠 공식(Leibniz formula), 행렬의 특정 엔트리의 곱의 합을 포함하는 명시적 공식을 통해 정의될 수 있습니다. 행렬식은 특정 속성을 만족시키는 행렬의 엔트리에 따라 고유한 함수로 특징지을 수도 있습니다. 이 접근 방식은 역시 문제에서 행렬을 단순화함으로써 행렬식을 계산하기 위해 사용될 수 있습니다.

Leibniz formula

Main article: Leibniz formula for determinants

3 × 3 matrices

3 × 3 행렬의 행렬식에 대해 라이프니츠 공식은 다음과 같습니다:

${\begin{aligned}{\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a(ei-fh)-b(di-fg)+c(dh-eg)\\&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}$

Rule of Sarrus

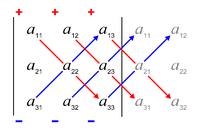
사뤼스의 규칙(rule of Sarrus)은 이 행렬식의 확장된 형식에 대한 기억법입니다: 그림과 같이 행렬의 처음 두 열의 복사본이 그 옆에 쓰일 때 행렬 원소의 3개의 대각선 북서쪽에서 남동쪽 선의 곱의 합에서 원소의 3개의 대각선 남서쪽에서 북동쪽 선의 곱의 합을 뺀 값. 3 × 3 행렬의 행렬식을 계산하기 위한 이 스킴은 더 높은 차원으로 이월되지 않습니다.

n × n matrices

더 높은 차원에서, 라이프니츠 공식은 $n\times n$-행렬의 행렬식을 순열(permutations)과 그것들의 시그니처(signatures)를 포함하는 표현식으로 표현합니다. 집합 $\{1,2,\dots ,n\}$의 순열은 이 정수의 집합을 재정렬하는 함수(function) $\sigma$입니다. 재정렬화 $\sigma$ 후 $i$-번째 위치에서 값은 아래에 $\sigma _{i}$에 의해 표시됩니다. 대칭 그룹(symmetric group)이라고 불리는 모든 그러한 순열의 집합은 공통적으로 $S_{n}$으로 표시됩니다. 순열 $\sigma$의 시그니처 $\operatorname {sgn} (\sigma )$는 순열이 두 엔트리의 짝수 교환으로 얻을 수 있으면 $+1$입니다; 그렇지 않으면, 그것은 $-1$입니다.

다음과 같은 행렬이 주어졌을 때,

$A={\begin{bmatrix}a_{1,1}\ldots a_{1,n}\\\vdots \qquad \vdots \\a_{n,1}\ldots a_{n,n}\end{bmatrix}},$

그것의 행렬식에 대한 라이프니츠 공식은, 시그마 표기법(sigma notation)을 사용하여, 다음과 같습니다:

$\det(A)={\begin{vmatrix}a_{1,1}\ldots a_{1,n}\\\vdots \qquad \vdots \\a_{n,1}\ldots a_{n,n}\end{vmatrix}}=\sum _{\sigma \in S_{n}}\operatorname {sgn} (\sigma )a_{1,\sigma _{1}}\cdots a_{n,\sigma _{n}}.$

파이 표기법(pi notation)을 사용하여, 이것은 다음으로 단축될 수 있습니다:

$\det(A)=\sum _{\sigma \in S_{n}}\left(\operatorname {sgn} (\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}\right)$.

레비-치비타 기호(Levi-Civita symbol) $\varepsilon _{i_{1},\ldots ,i_{n}}$은 $\{1,\ldots ,n\}$에 있는 정수의 n-튜플에서 두 정수가 같으면 0으로 정의되고, 그렇지 않으면, 정수의 튜플에 의해 정의된 순열의 시그니처로 정의됩니다. 레비-치비타 기호와 함께, 라이프니츠 공식은 다음과 같이 쓸 수 있습니다:

$\det(A)=\sum _{i_{1},i_{2},\ldots ,i_{n}}\varepsilon _{i_{1}\cdots i_{n}}a_{1,i_{1}}\cdots a_{n,i_{n}},$

여기서 합은 $\{1,\ldots ,n\}$에 있는 정수의 모든 n-튜플에 걸쳐 취합니다.

Properties of the determinant

Characterization of the determinant

행렬식은 다음 세 가지 주요 속성으로 특징지을 수 있습니다. 이를 설명하기 위해, $n\times n$-행렬 $A$를 $n$개의 열로 구성된 것으로 여기는 것이 편리하므로, 다음과 같이 표시됩니다:

$A={\big (}a_{1},\dots ,a_{n}{\big )},$

여기서 열 벡터(column vector) $a_{i}$ (각 i에 대해)는 i-번째 열에 있는 행렬의 엔트리로 구성됩니다.

2. $\det \left(I\right)=1$, 여기서 $I$는 항등 행렬(identity matrix)입니다.
4. 행렬식은 다중선형(multilinear)입니다: 만약 행렬 $A$의 j-번째 열이 두 개의 열 벡터(column vectors) $v$와 $w$와 숫자 $r$의 선형 조합(linear combination) $a_{j}=r\cdot v+w$로 쓰면, $A$의 행렬식은 유사한 선형 조합으로 표현할 수 있습니다:

   ${\begin{aligned}|A|&={\big |}a_{1},\dots ,a_{j-1},r\cdot v+w,a_{j+1},\dots ,a_{n}|\\&=r\cdot |a_{1},\dots ,v,\dots a_{n}|+|a_{1},\dots ,w,\dots ,a_{n}|\end{aligned}}$

6. 행렬식은 교대하는(alternating) 것입니다: 행렬의 두 열이 동일할 때마다, 그것의 행렬식은 0입니다:

   $|a_{1},\dots ,v,\dots ,v,\dots ,a_{n}|=0.$

만약 형렬식이 위와 같이 라이프니츠 공식을 사용하여 정의되면, 이들 세 가지 속성은 그 공식을 직접 살펴보면서 입증될 수 있습니다. 일부 저자는 역시 이들 세 가지 속성을 사용하여 행렬식에 직접 접근합니다: 임의의 $n\times n$ 행렬 $A$에 이들 세 가지 속성을 충족하는 숫자를 할당하는 정확하게 하나의 함수가 있음을 보여줄 수 있습니다. 이것은 역시 행렬식에 대한 이러한 보다 추상적인 접근 방식이 라이프니츠 공식을 사용하는 것과 같은 정의를 생성한다는 것을 보여줍니다.

이를 확인하기 위해, 각 열이 표준 기저(standard basis) 벡터인 행렬의 행렬식의 (거대한) 선형 조합으로 열에서 다중-선형성에 의해 행렬식을 확장하는 것으로 충분합니다. 이들 행렬식은 (속성 9에 의해) 0 또는 (아래 속성 1 및 12에 의해) ±1이므로, 선형 조합은 레비-치비타 기호의 관면에서 위의 표현을 제공합니다. 덜 기술적이지만, 이 특성화는 행렬식을 정의하는 데 라이프니츠 공식을 완전히 대체할 수 없는데, 왜냐하면 이 공식 없이 적절한 함수의 존재가 명확하지 않기 때문입니다.

Immediate consequences

이들 규칙은 몇 가지 추가 결과를 가집니다:

• 행렬식은 동차 방정식(homogeneous function)이며, 즉, $$\det(cA)=c^{n}\det(A)$$ (여기서 $A$는 $n\times n$ 행렬입니다).
• 행렬의 열의 쌍을 교환하는 것은 행렬식에 −1을 곱합니다. 이것은 행렬식이 다중선형이고 교대하는 것임을 따릅니다 (위의 속성 2와 3): $$|a_{1},\dots ,a_{j},\dots a_{i},\dots ,a_{n}|=-|a_{1},\dots ,a_{i},\dots ,a_{j},\dots ,a_{n}|.$$ 이 공식은 여러 열이 교체될 때 반복적으로 적용될 수 있습니다. 예를 들어, $$|a_{3},a_{1},a_{2},a_{4}\dots ,a_{n}|=-|a_{1},a_{3},a_{2},a_{4},\dots ,a_{n}|=|a_{1},a_{2},a_{3},a_{4},\dots ,a_{n}|.$$ 보다 일반적으로, 열의 임의의 순열은 행렬식에 순열의 부호(sign)를 곱합니다.
• 만약 일부 열은 다른 열의 선형 조합으로 표현될 수 있으면 (즉, 행렬의 열이 선형적으로 종속 집합을 형성하면), 그 행렬 식은 0입니다. 특별한 경우로, 여기에는 다음이 포함됩니다: 만약 어떤 열이 모든 그 엔트리가 영임을 만족하면, 해당 행렬의 행렬식은 0입니다.
• 한 열의 스칼라 배수를 또 다른 열에 더하는 것은 행렬식의 값을 변경하지 않습니다. 이것은 다중선형성의 결과이고 교대하게 됩니다: 다중선형성에 의해 행렬식은 두 개의 같은 열을 갖는 행렬의 행렬식의 배수만큼 변경되는데, 이는 행렬식이 영이며, 왜냐하면 행렬식이 교대하는 것이기 때문입니다.
• 만약 $A$가 삼각 행렬(triangular matrix), 즉, $i>j$일 때마다, 또는, 대안적으로 $i<j$일 때마다, $a_{ij}=0$이면, 행렬식은 대각 엔트리의 곱과 같습니다: $$\det(A)=a_{11}a_{22}\cdots a_{nn}=\prod _{i=1}^{n}a_{ii}.$$ 실제로, 그러한 행렬은 더 적은 비-영 엔트리를 갖는 열의 배수를 더 많은 비-영 엔트리를 갖는 열에 적절하게 더함으로써 (행렬식을 변경 없이) 대각 행렬(diagonal matrix)로 줄일 수 있습니다. 그러한 행렬에 대해, 각 열에서 선형성을 사용하는 것은 항등 행렬로 축소되며, 이 경우에서 명시된 공식은 행렬식의 속성을 첫 번째로 특징-지음으로써 유지합니다. 대안적으로, 이 공식은 역시 라이프니츠 공식에서 추론될 수 있는데, 왜냐하면 비-영 기여도를 제공하는 유일한 순열 $\sigma$는 항등 순열이기 때문입니다.

Example

위에 나열된 이들 특성과 그 결과는 모두 이론적으로 중요하지만, 역시 구체적 행렬에 대해 행렬식을 계산하기 위해 사용될 수 있습니다. 실제로, 가우스 소거법(Gaussian elimination)은 임의의 행렬을 위쪽 삼각 형식으로 가져오기 위해 적용될 수 있고, 이 알고리듬에서 단계는 제어된 방법으로 행렬식에 영향을 줍니다. 다음의 구체적인 예제는 해당 방법을 사용하여 행렬 $A$의 행렬식의 계산을 묘사합니다:

$A={\begin{bmatrix}-2&-1&2\\2&1&4\\-3&3&-1\end{bmatrix}}.$

Computation of the determinant of matrix $A$

행렬	$B={\begin{bmatrix}-3&-1&2\\3&1&4\\0&3&-1\end{bmatrix}}$	$C={\begin{bmatrix}-3&5&2\\3&13&4\\0&0&-1\end{bmatrix}}$	$D={\begin{bmatrix}5&-3&2\\13&3&4\\0&0&-1\end{bmatrix}}$	$E={\begin{bmatrix}18&-3&2\\0&3&4\\0&0&-1\end{bmatrix}}$
연산에 의해 얻음	두 번째 열을 첫 번째 열에 더함	세 번째 열을 3배해서 두 번째에 더함	처음 두 열을 서로 바꿈	두 번째 열에 $-{\frac {13}{3}}$배해서 첫 번째 열에 더함
행렬식	$|A|=|B|$	$|B|=|C|$	$|D|=-|C|$	$|E|=|D|$

이들 상등을 결합하는 것은 $|A|=-|E|=-(18\cdot 3\cdot (-1))=54$을 제공합니다.

Transpose

$A$의 전치(transpose)의 행렬식은 $A$의 행렬식과 같습니다:

$\det \left(A^{\textsf {T}}\right)=\det(A)$.

이것은 라이프니츠 공식을 검사함으로써 입증될 수 있습니다. 이것은 위에서 언급된 모든 속성에서, "열"이라는 단어가 전체에 걸쳐 "행"으로 대체될 수 있음을 의미합니다. 예를 들어, n × n 행렬을 n개의 행으로 구성된 것으로 보면 행렬식은 n-선형 함수입니다.

Multiplicativity and matrix groups

행렬식은 곱셈 맵(multiplicative map)입니다, 즉, 같은 크기의 정사각 행렬 $A$와 $B$에 대해, 행렬 곱(matrix product)의 행렬식은 그것들 행렬식의 곱과 같습니다:

$\det(AB)=\det(A)\det(B)$

이 핵심 사실은 고정된 행렬 $B$에 대해, 방정식의 양쪽 변이 $A$의 열에 의존하는 함수로서 교대하는 것이고 다중선형임을 관찰함으로써 입증될 수 있습니다. 게다가, 그것들 둘 다는 $A$가 항등 행렬일 때 값 $\det B$를 취합니다. 따라서 위에서-언급된 교대하는 다중선형 맵의 고유한 특성은 이러한 주장을 보여줍니다.

필드(field)에서 엔트리를 갖는 행렬 $A$는 그것의 행렬식이 비-영이면 정확하게 역가능(invertible)입니다. 이것은 행렬식의 곱셈성과 아래에 언급된 수반 행렬을 포함하는 역에 대한 공식에서 따릅니다. 이 경우에서, 역의 행렬식은 다음과 같이 주어집니다:

$\det \left(A^{-1}\right)={\frac {1}{\det(A)}}=[\det(A)]^{-1}$.

특히, 비-영 행렬식 (각각 행렬식 일)을 갖는 행렬의 곱과 역은 여전히 이 속성을 가집니다. 따라서, (필드 $K$에 걸쳐 고정된 크기 $n$의) 그러한 행렬의 집합은 일반 선형 그룹 $\operatorname {GL} _{n}(K)$으로 알려진 그룹을 형성합니다 (각각, 특수 선형 그룹 $\operatorname {SL} _{n}(K)\subset \operatorname {GL} _{n}(K)$라고 불리는 부분그룹을 형성합니다). 보다 일반적으로, "특수"라는 단어는 행렬식 일의 행렬의 또 다른 행렬 그룹의 부분그룹을 나타냅니다. 예를 들면 특수 직교 그룹 (n이 2 또는 3이면 모든 회전 행렬로 구성됨) 및 특수 유니태리 그룹이 있습니다.

행렬식은 곱셈과 역을 존중하기 때문에, 그것은 사실 $\operatorname {GL} _{n}(K)$에서 $K$의 비-영 원소의 곱셈 그룹 $K^{\times }$로의 그룹 준동형(group homomorphism)입니다. 이 준동형은 전사적이고 그것의 커널은 $\operatorname {SL} _{n}(K)$ (행렬식 일을 갖는 행렬)입니다. 따라서, 첫 번째 동형 정리(first isomorphism theorem)에 의해, 이것은 $\operatorname {SL} _{n}(K)$가 $\operatorname {GL} _{n}(K)$의 정규 부분그룹(normal subgroup)이고, 몫 그룹(quotient group) $\operatorname {GL} _{n}(K)/\operatorname {SL} _{n}(K)$가 $K^{\times }$와 동형적임을 보여줍니다.

코시–비네 공식(Cauchy–Binet formula)은 직사각 행렬에 대한 곱 공식의 일반화입니다. 이 공식은 그 엔트리가 주어진 행렬의 모든 이차 부분행렬의 행렬식인 복합 행렬(compound matrices)에 대한 곱셈 공식으로 재구성될 수도 있습니다.

Laplace expansion

라플라스 전개(Laplace expansion)는 행렬 $A$의 행렬식을 소행렬식(minors)으로 알려진 더 작은 행렬의 행렬식의 관점에서 표현합니다. 소행렬식 $M_{i,j}$는 $i$-번째 행과 $j$-번째 열을 제거함으로써 $A$에서 생성되는 $(n-1)\times (n-1)$-행렬의 행렬식으로 정의됩니다. 표현식 $(-1)^{i+j}M_{i,j}$는 여인수(cofactor)로 알려져 있습니다. 모든 각 $i$에 대해, 다음 상등을 가집니다:

$\det(A)=\sum _{j=1}^{n}(-1)^{i+j}a_{ij}M_{ij},$

이는 i-번째 행을 따라 라플라스 전개라고 불립니다. 예를 들어, 첫 번째 행 ($i=1$)을 따라 라플라스를 전개는 다음 공식을 제공합니다:

${\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=a{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c{\begin{vmatrix}d&e\\g&h\end{vmatrix}}$

이들 $2\times 2$-행렬의 행렬식을 풀면 위에서 언급된 라이프니츠 공식을 다시 제공합니다. 마찬가지로, $j$-번째 열을 따라 라플라스 전개는 다음과 같은 상등입니다:

$\det(A)=\sum _{i=1}^{n}(-1)^{i+j}a_{ij}M_{ij}.$

라플라스 전개는 행렬식 계산에 반복적으로 사용될 수 있지만, 이 접근 방식은 큰 행렬에 대해 비효율적입니다. 어쨌든, 그것은 방데르몽드 행렬(Vandermonde matrix)과 같은 고도로 대칭 행렬의 행렬식을 계산하는 데 유용합니다: $${\begin{vmatrix}1&1&1&\cdots &1\\x_{1}&x_{2}&x_{3}&\cdots &x_{n}\\x_{1}^{2}&x_{2}^{2}&x_{3}^{2}&\cdots &x_{n}^{2}\\\vdots &\vdots &\vdots &\ddots &\vdots \\x_{1}^{n-1}&x_{2}^{n-1}&x_{3}^{n-1}&\cdots &x_{n}^{n-1}\end{vmatrix}}=\prod _{1\leq i<j\leq n}\left(x_{j}-x_{i}\right).$$ 이 행렬식은, 예를 들어, 초월적 숫자(transcendental numbers)의 이론에서 베이커의 정리(Baker's theorem)의 증명에서 적용되어 왔습니다.

Adjugate matrix

수반 행렬(adjugate matrix) $\operatorname {adj} (A)$는 여인수의 행렬의 전치입니다, 즉,

$(\operatorname {adj} (A))_{ij}=(-1)^{i+j}M_{ji}.$

모든 각 행렬에 대해, 다음을 가집니다:

$(\det A)I=A\operatorname {adj} A=(\operatorname {adj} A)\,A.$

따라서 수반 행렬은 비-특이 행렬(nonsingular matrix)의 역을 표현하는 데 사용될 수 있습니다:

$A^{-1}={\frac {1}{\det A}}\operatorname {adj} A.$

Block matrices

위의 $2\times 2$-행렬의 행렬식에 대한 공식은 블록 행렬(block matrix), 즉, 각각 차원 $m\times m$, $m\times n$, $n\times m$, 및 $n\times n$의 네 개의 부분행렬 $A,B,C,D$로 구성된 행렬에 대해 적절한 추가 가정 아래에서 계속 유지됩니다. 라이프니츠 공식이나 슈어 여(Schur complement)를 포함하는 인수분해를 사용하여 입증될 수 있는 가장 쉬운 그런 공식은 다음과 같습니다:

$\det {\begin{pmatrix}A&0\\C&D\end{pmatrix}}=\det(A)\det(D)=\det {\begin{pmatrix}A&B\\0&D\end{pmatrix}}.$

만약 $A$가 역가능(invertible)이면, 그것은 다음이라는 곱셈성에 대한 섹션에서 결과를 따릅니다:

${\begin{aligned}\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}&=\det(A)\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}\underbrace {\det {\begin{pmatrix}A^{-1}&-A^{-1}B\\0&I_{n}\end{pmatrix}}} _{=\,\det(A^{-1})\,=\,(\det A)^{-1}}\\&=\det(A)\det {\begin{pmatrix}I_{m}&0\\CA^{-1}&D-CA^{-1}B\end{pmatrix}}\\&=\det(A)\det(D-CA^{-1}B),\end{aligned}}$

이는 $D$가 $1\times 1$-행렬일 때 $\det(A)(D-CA^{-1}B)$로 단순화됩니다.

유사한 결과는 $D$가 역가능일 때 유지됩니다. 즉,

${\begin{aligned}\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}&=\det(D)\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}\underbrace {\det {\begin{pmatrix}I_{m}&0\\-D^{-1}C&D^{-1}\end{pmatrix}}} _{=\,\det(D^{-1})\,=\,(\det D)^{-1}}\\&=\det(D)\det {\begin{pmatrix}A-BD^{-1}C&BD^{-1}\\0&I_{n}\end{pmatrix}}\\&=\det(D)\det(A-BD^{-1}C).\end{aligned}}$

두 결과를 결합하여 실베스터의 행렬식 정리(Sylvester's determinant theorem)를 도출할 수 있으며, 이 정리도 아래에 설명되어 있습니다.

만약 블록이 같은 크기의 정사각 행렬이면 추가 공식이 유지됩니다. 예를 들어, $C$와 $D$가 교환하면 (즉, $CD=DC$이면), 다음과 같습니다:

$\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}=\det(AD-BC).$

이 공식은 다시 개별 블록 사이의 적절한 교환성 조건 아래에서 $2\times 2$ 블록보다 많은 것으로 구성된 행렬로 일반화되어 왔습니다.

$A=D$와 $B=C$에 대해, 다음 공식이 유지됩니다 (심지어 $A$와 $B$가 교환하지 않더라도)

$\det {\begin{pmatrix}A&B\\B&A\end{pmatrix}}=\det(A-B)\det(A+B).$

Sylvester's determinant theorem

실베스터의 행렬식 정리(Sylvester's determinant theorem)는, $A$, m × n 행렬이고, $B$, n × m 행렬에 대해 다음임을 말합니다 (여기서 $A$와 $B$는 정사각 행렬을 형성하는 어느 순서로든 곱할 수 있는 차원을 가집니다):

$\det \left(I_{\mathit {m}}+AB\right)=\det \left(I_{\mathit {n}}+BA\right),$

여기서 $I_{m}$과 $I_{n}$은 각각 m × m과 n × n 항등 행렬입니다.

이 일반적인 결과로부터 몇 가지 결과가 뒤따릅니다:

1. 각 m 구성 요소를 갖는 열 벡터 c와 행 벡터 r의 경우에 대해, 공식은 랭크 1의 행렬에 의해 항등 행렬과 다른 행렬의 행렬식의 빠른 계산을 허용합니다:

   $\det \left(I_{\mathit {m}}+cr\right)=1+rc.$

2. 보다 일반적으로, 임의의 역가능 m × m 행렬 X에 대해,
   $\det(X+AB)=\det(X)\det \left(I_{\mathit {m}}+BX^{-1}A\right),$
3. 위와 같은 열과 행 벡터에 대해:
   $\det(X+cr)=\det(X)\det \left(1+rX^{-1}c\right)=\det(X)+r\,\operatorname {adj} (X)\,c.$
4. 같은 크기의 정사각 행렬 $A$와 $B$에 대해, 행렬 $AB$와 $BA$는 같은 특성 다항식을 가집니다 (따라서 같은 고윳값을 가집니다).

Sum

같은 크기의 두 정사각 행렬의 합 $A+B$의 행렬식은 일반적으로 $A$와 $B$의 행렬식의 관점에서 표현할 수 없습니다. 어쨌든, 같은 크기의 양수 반한정 행렬(positive semidefinite matrices) $A$, $B$, 및 $C$에 대해, $$\det(A+B+C)+\det(C)\geq \det(A+C)+\det(B+C){\text{,}}$$ 다음과 같은 따름정리를 가집니다: $$\det(A+B)\geq \det(A)+\det(B){\text{.}}$$ 반대로, 만약 $A$와 $B$가 에르미트(Hermitian), 양수-한정이고, 크기 $n\times n$이면, 행렬식은 오목 $n$^번째 근을 가집니다; 이것은 동차성에 의해 다음임을 의미합니다: $${\sqrt[{n}]{\det {\!(A+B)}}}\geq {\sqrt[{n}]{\det {\!(A)}}}+{\sqrt[{n}]{\det {\!(B)}}}$$

Sum identity for 2×2 matrices

복소수 엔트리를 갖는 $2\times 2$ 행렬의 특수한 경우에 대해, 합의 행렬식은 다음 항등식에서 행렬식과 대각합의 관점에서 쓸 수 있습니다:

$\det(A+B)=\det(A)+\det(B)+{\text{tr}}(A){\text{tr}}(B)-{\text{tr}}(AB).$

Proof of identity

이것은 구성 요소 $A_{ij},B_{ij}$에서 각 항을 쓺으로써 표시할 수 있습니다. 왼쪽 변은 다음과 같습니다:

$(A_{11}+B_{11})(A_{22}+B_{22})-(A_{12}+B_{12})(A_{21}+B_{21}).$

전개하여,

$A_{11}A_{22}+B_{11}A_{22}+A_{11}B_{22}+B_{11}B_{22}-A_{12}A_{21}-B_{12}A_{21}-A_{12}B_{21}-B_{12}B_{21}.$

$A$에서 이차인 항은 $\det(A)$로 보이고, $B$에 대해 유사하므로, 표현식은 다음으로 쓸 수 있습니다:

$\det(A)+\det(B)+A_{11}B_{22}+B_{11}A_{22}-A_{12}B_{21}-B_{12}A_{21}.$

그런-다음 교차-항을 다음으로 쓸 수 있습니다:

$(A_{11}+A_{22})(B_{11}+B_{22})-(A_{11}B_{11}+A_{12}B_{21}+A_{21}B_{12}+A_{22}B_{22})$

이는 다음으로 인식될 수 있습니다:

${\text{tr}}(A){\text{tr}}(B)-{\text{tr}}(AB).$

이로써 증명을 완료합니다.

이것은 $2\times 2$ 행렬 대수로의 응용을 가집니다. 예를 들어, 복소수를 행렬 대수로 생각해 보십시오. 복소수는 다음 형식의 행렬로 표현됩니다: $$aI+b\mathbf {i} :=a{\begin{pmatrix}1&0\\0&1\end{pmatrix}}+b{\begin{pmatrix}0&-1\\1&0\end{pmatrix}}$$ 이때 $a$와 $b$는 실수입니다. ${\text{tr}}(\mathbf {i} )=0$이기 때문에, 위의 항등식에서 $A=aI$와 $B=b\mathbf {i}$로 취하는 것은 다음을 제공합니다:

$\det(aI+b\mathbf {i} )=a^{2}\det(I)+b^{2}\det(\mathbf {i} )=a^{2}+b^{2}.$

이 결과는 바로 ${\text{tr}}(\mathbf {i} )=0$와 $\det(I)=\det(\mathbf {i} )=1$에서 나온 것입니다.

Properties of the determinant in relation to other notions

Eigenvalues and characteristic polynomial

행렬식은 선형 대수의 두 가지 다른 중심 개념, 행렬의 고윳값(eigenvalues)과 특성 다항식(characteristic polynomial)과 밀접한 관련이 있습니다. $A$를 복소수 엔트리를 갖는 $n\times n$-행렬이라고 놓습니다. 그런-다음, 대수학의 기본 정리에 의해, $A$는 정확하게 n개의 고윳값 $\lambda _{1},\lambda _{2},\ldots ,\lambda _{n}$을 가져야 합니다. (여기서 대수적 중복도(algebraic multiplicity) μ를 갖는 고윳값은 이 목록에서 μ번 발생한다는 것으로 이해합니다.) 그런-다음, A의 행렬식은 이들 고윳값의 곱과 같다는 것이 밝혀졌습니다:

$\det(A)=\prod _{i=1}^{n}\lambda _{i}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.$

모든 비-영 고윳값의 곱은 유사-행렬식(pseudo-determinant)이라고 참조됩니다.

이것으로부터, 행렬 $A$의 행렬식이 영인 것과 $0$이 $A$의 고윳값임은 필요충분 조건임을 즉시 알 수 있습니다. 다시 말해서, $A$가 역가능인 것과 $0$이 $A$의 고윳값이 아닌 것은 필요충분 조건입니다.

특성 다항식은 다음과 같이 정의됩니다:

$\chi _{A}(t)=\det(t\cdot I-A).$

여기서, $t$는 다항식의 불확정(indeterminate)이고 $I$는 $A$와 같은 크기의 항등 행렬입니다. 이 다항식을 수단으로, 행렬식은 행렬 $A$의 고윳값(eigenvalues)을 찾기 위해 사용될 수 있습니다: 그것들은 정확하게 이 다항식의 근(roots), 즉, 그것들은 다음임을 만족하는 복소수 $\lambda$입니다:

$\chi _{A}(\lambda )=0.$

에르미트 행렬(Hermitian matrix)은 모든 그것의 고윳값이 양수이면 양수 한정(positive definite)입니다. 실베스터의 기준(Sylvester's criterion)은 이것이 $1$과 $n$ 사이의 모든 $k$에 대해 양수인 다음 부분행렬의 행렬식과 동등하다고 주장합니다:

$A_{k}:={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,k}\\a_{2,1}&a_{2,2}&\cdots &a_{2,k}\\\vdots &\vdots &\ddots &\vdots \\a_{k,1}&a_{k,2}&\cdots &a_{k,k}\end{bmatrix}}$

Trace

대각합(trace) tr($A$)는 정의에 의해 $A$의 대각 엔트리의 합이고 역시 고윳값의 합과 같습니다. 따라서, 복소수 행렬 $A$에 대해,

$\det(\exp(A))=\exp(\operatorname {tr} (A))$

또는, 실수 행렬 $A$에 대해,

$\operatorname {tr} (A)=\log(\det(\exp(A))).$

여기서 exp($A$)는 $A$의 행렬 지수(matrix exponential)를 나타내는데, 왜냐하면 $A$의 모든 각 고윳값 λ는 exp($A$)의 고윳값 exp(λ)에 해당하기 때문입니다. 특히, $A$의 임의의 로그(logarithm), 즉, 다음을 만족시키는 임의의 행렬 L이 주어졌을 때,

$\exp(L)=A$

$A$의 행렬식은 다음에 의해 주어집니다:

$\det(A)=\exp(\operatorname {tr} (L)).$

예를 들어, 각각 n = 2, n = 3, 및 n = 4에 대해,

${\begin{aligned}\det(A)&={\frac {1}{2}}\left(\left(\operatorname {tr} (A)\right)^{2}-\operatorname {tr} \left(A^{2}\right)\right),\\\det(A)&={\frac {1}{6}}\left(\left(\operatorname {tr} (A)\right)^{3}-3\operatorname {tr} (A)~\operatorname {tr} \left(A^{2}\right)+2\operatorname {tr} \left(A^{3}\right)\right),\\\det(A)&={\frac {1}{24}}\left(\left(\operatorname {tr} (A)\right)^{4}-6\operatorname {tr} \left(A^{2}\right)\left(\operatorname {tr} (A)\right)^{2}+3\left(\operatorname {tr} \left(A^{2}\right)\right)^{2}+8\operatorname {tr} \left(A^{3}\right)~\operatorname {tr} (A)-6\operatorname {tr} \left(A^{4}\right)\right).\end{aligned}}$

비고. 케일리-해밀턴 정리(Cayley–Hamilton theorem). 그러한 표현은 조합론적 논증, 뉴턴의 항등식(Newton's identities), 또는 파데예프–르베리에 알고리듬(Faddeev–LeVerrier algorithm)에서 추론할 수 있습니다. 즉, 일반적인 n에 대해, detA = (−1)ⁿc₀ 특성 다항식(characteristic polynomial)의 부호화된 상수, 다음에서 재귀적으로 결정됩니다:

$c_{n}=1;~~~c_{n-m}=-{\frac {1}{m}}\sum _{k=1}^{m}c_{n-m+k}\operatorname {tr} \left(A^{k}\right)~~(1\leq m\leq n)~.$

일반적인 경우에서, 이것은 역시 다음에서 얻을 수 있습니다:

$\det(A)=\sum _{\begin{array}{c}k_{1},k_{2},\ldots ,k_{n}\geq 0\\k_{1}+2k_{2}+\cdots +nk_{n}=n\end{array}}\prod _{l=1}^{n}{\frac {(-1)^{k_{l}+1}}{l^{k_{l}}k_{l}!}}\operatorname {tr} \left(A^{l}\right)^{k_{l}},$

여기서 합은 다음 방정식을 만족시키는 모든 정수 k_l ≥ 0의 집합에 걸쳐 취합니다:

$\sum _{l=1}^{n}lk_{l}=n.$

공식은 n 인수 s_l = −(l – 1)! tr(A^l)의 완비 지수 벨 다항식(Bell polynomial)의 관점에서 다음처럼 표현될 수 있습니다:

$\det(A)={\frac {(-1)^{n}}{n!}}B_{n}(s_{1},s_{2},\ldots ,s_{n}).$

이 공식은 역시 다중차원 인덱스 I = (i₁, i₂, …, i_r)와 J = (j₁, j₂, …, j_r)를 갖는 행렬 A^I_J의 행렬식을 찾기 위해 사용될 수 있습니다. 그러한 행렬의 곱과 대각합은 다음과 같이 자연스러운 방법에서 정의됩니다:

$(AB)_{J}^{I}=\sum _{K}A_{K}^{I}B_{J}^{K},\operatorname {tr} (A)=\sum _{I}A_{I}^{I}.$

중요한 임의적인 차원 n 항등식은 전개가 수렴할 때 로그의 메르카토르 급수(Mercator series) 전개에서 얻을 수 있습니다. 만약 $A$의 모든 각 고윳값이 절댓값에서 1보다 작으면,

$\det(I+A)=\sum _{k=0}^{\infty }{\frac {1}{k!}}\left(-\sum _{j=1}^{\infty }{\frac {(-1)^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,$

여기서 I는 항등 행렬입니다. 보다 일반적으로, 만약 다음이

$\sum _{k=0}^{\infty }{\frac {1}{k!}}\left(-\sum _{j=1}^{\infty }{\frac {(-1)^{j}s^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,$

s에서 형식적 거듭제곱 급수로 전개되면, m > n에 대해 s^m의 모든 계수는 영이고 남아있는 다항식은 det(I + sA)입니다.

Upper and lower bounds

양수 한정 행렬 A에 대해, 대각합 연산자는 로그 행렬식에 다음과 같은 단단한 아래쪽 경계와 위쪽 경계를 제공합니다:

$\operatorname {tr} \left(I-A^{-1}\right)\leq \log \det(A)\leq \operatorname {tr} (A-I)$

이때 등호인 것과 A = I인 것은 필요충분 조건입니다. 이 관계는 두 다변수 정규(multivariate normal) 분포 사이의 쿨백-라이블러 발산(Kullback–Leibler divergence) 공식을 통해 유도될 수 있습니다.

역시,

${\frac {n}{\operatorname {tr} \left(A^{-1}\right)}}\leq \det(A)^{\frac {1}{n}}\leq {\frac {1}{n}}\operatorname {tr} (A)\leq {\sqrt {{\frac {1}{n}}\operatorname {tr} \left(A^{2}\right)}}.$

이들 부등식은 고윳값의 관점에서 대각합과 행렬식을 표현함으로써 입증될 수 있습니다. 이를테면, 그것들은 조화 평균(harmonic mean)이 기하 평균(geometric mean)보다 작다는 잘 알려진 사실을 나타내며, 기하 평균은 산술 평균(arithmetic mean)보다 작으며, 산술 평균은 차례로 제곱근 평균 제곱(root mean square)보다 작습니다.

Derivative

라이프니츠 공식은 실수 (또는 복소수에 대해 유사하게) 제곱 행렬의 행렬식이 $\mathbf {R} ^{n\times n}$에서 $\mathbf {R}$로의 다항(polynomial) 함수임을 보여줍니다. 특히, 그것은 모든 곳에서 미분-가능(differentiable)입니다. 그 도함수는 야코비의 공식(Jacobi's formula)을 사용하여 표현할 수 있습니다:

${\frac {d\det(A)}{d\alpha }}=\operatorname {tr} \left(\operatorname {adj} (A){\frac {dA}{d\alpha }}\right).$

여기서 $\operatorname {adj} (A)$는 $A$의 수반(adjugate)을 나타냅니다. 특히, 만약 $A$가 역-가능이면, 다음을 가집니다:

${\frac {d\det(A)}{d\alpha }}=\det(A)\operatorname {tr} \left(A^{-1}{\frac {dA}{d\alpha }}\right).$

$A$의 엔트리의 관점에서 표현되면, 이것들은 다음과 같습니다:

${\frac {\partial \det(A)}{\partial A_{ij}}}=\operatorname {adj} (A)_{ji}=\det(A)\left(A^{-1}\right)_{ji}.$

또 다른 동등한 공식은 큰 O 표기법(big O notation)을 사용하여 다음과 같습니다:

$\det(A+\epsilon X)-\det(A)=\operatorname {tr} (\operatorname {adj} (A)X)\epsilon +O\left(\epsilon ^{2}\right)=\det(A)\operatorname {tr} \left(A^{-1}X\right)\epsilon +O\left(\epsilon ^{2}\right)$,

$A=I$가 항등 행렬인 특수한 경우는 다음을 산출합니다:

$\det(I+\epsilon X)=1+\operatorname {tr} (X)\epsilon +O\left(\epsilon ^{2}\right).$

이 항등식은 특정 행렬 리 그룹(Lie groups)과 결합된 리 대수(Lie algebras)를 설명하는 데 사용됩니다. 예를 들어, 특수 선형 그룹 $\operatorname {SL} _{n}$은 방정식 $\det A=1$에 의해 정의됩니다. 위의 공식은 리 대수가 대각합 영을 가지는 행렬로 구성된 특수 선형 리 대수(special linear Lie algebra) ${\mathfrak {sl}}_{n}$임을 보여줍니다.

$3\times 3$-행렬을 $A={\begin{bmatrix}a&b&c\end{bmatrix}}$로 쓰면, 여기서 $a,b,c$는 길이 3의 열 벡터이며, 세 벡터 중 하나에 걸쳐 그래디언트는 다른 두 벡터의 교차 곱(cross product)으로 쓸 수 있습니다:

${\begin{aligned}\nabla _{\mathbf {a} }\det(A)&=\mathbf {b} \times \mathbf {c} \\\nabla _{\mathbf {b} }\det(A)&=\mathbf {c} \times \mathbf {a} \\\nabla _{\mathbf {c} }\det(A)&=\mathbf {a} \times \mathbf {b} .\end{aligned}}$

History

역사적으로, 행렬식은 행렬보다 오래 전에 사용되었습니다: 행렬식은 원래 선형 방정식의 시스템의 속성으로 정의되었습니다. 행렬식은 시스템이 고유한 해를 가지는지 여부를 "결정"합니다 (해는 만약 행렬식이 비-영이면 정확히 발생합니다). 이런 의미에서, 행렬식은 중국 수학 교과서 The Nine Chapters on the Mathematical Art (九章算術, 중국 학자들, 기원전 3세기경)에서 처음 사용되었습니다. 유럽에서, 두 방정식의 선형 시스템의 해는 1545년 카르다노(Cardano)에 의해 행렬식-같은 엔터티로 표현되었습니다.

적절한 행렬식은 1683년 일본에서 세키 타카카즈(Seki Takakazu)의 연구와 동시에 1693년 라이프니츠(Leibniz)의 연구에서 비롯되었습니다. Cramer (1750)는, 증명 없이, 크라메르의 규칙을 말했습니다. 크라메르와 Bezout (1779)은 둘 다 주어진 점의 집합을 통과하는 평면 곡선(plane curves)의 문제에 의해 행렬식으로 이어졌습니다.

방데르몽드 (1771)는 처음으로 독립 함수로 행렬식을 인식했습니다. Laplace (1772)는 보완적인 소행렬식(minors)의 관점에서 행렬식을 전개하는 일반적인 방법을 제시했습니다: 방데르몽드는 이미 특별한 경우를 제시해 왔습니다. 바로 이어서, Lagrange (1773)는 2차 및 3차 행렬식을 처리했고 그것을 소거 이론(elimination theory)의 문제에 적용했습니다; 그는 일반적인 항등식의 많은 특별한 경우를 입증했습니다.

가우스 (1801)는 그 다음 발전을 이루었습니다. 라그랑주와 마찬가지로, 그는 숫자의 이론에서 행렬식을 많이 사용했습니다. 그는 "determinant" (라플라스는 "resultant"를 사용함)라는 단어를 도입했으며, 현재의 의미에서는 아니지만, 정량적(quantic)의 판별식(discriminant)에 적용했습니다. 가우스는 역시 역수 (역) 행렬식의 개념에 도달했고, 곱셈 정리에 매우 근접했습니다.

다음으로 중요한 기여자는 비네 (1811, 1812)로, 그는 m 열과 n 행의 두 행렬의 곱과 관련된 정리를 형식적으로 언급했으며, 이는 m = n의 특수한 경우에 대해 곱셈 정리로 축소됩니다. 같은 날 (1812년 11월 30일) 비네가 학술원에 논문을 발표한 날, 코시도 그 주제에 관한 논문을 발표했습니다. (코시–비네 공식 참조.) 여기에서 그는 "determinant"라는 단어를 현재의 의미로 사용했고, 그 주제에 대해 당시 알려진 것을 요약하고 단순화하고, 표기법을 개선하고, 비네의 증명보다 더 만족스러운 증명으로 곱셈 정리를 제공했습니다. 그와 함께 이론의 일반성이 시작됩니다.

Jacobi (1841)는 실베스터가 나중에 야코비(Jacobian)라고 부른 함수형 행렬식을 사용했습니다. 1841년 Crelle's Journal의 회고록에서 그는 이 주제와 실베스터가 교대(alternants)라고 부른 교대 함수의 클래스를 특별히 다룹니다. 야코비의 마지막 회고록이 나올 무렵 실베스터 (1839)와 케일리가 그들의 연구를 시작했습니다. Cayley 1841은 수직 막대를 사용하여 행렬식에 대한 현대 표기법을 도입했습니다.

행렬식의 특별한 형식에 대한 연구는 일반 이론의 완성에 따른 자연스러운 결과였습니다. 축대칭 행렬식은 르베그, 헤세, 및 실베스터에 의해 연구되었습니다; 실베스터와 한켈의 부대칭 행렬식; 카탈랑, 스포티스우드, 글레이셔, 및 스콧에 의한 순환; 케일리에 의한 직교 변환 이론과 관련하여 반-대칭 행렬식 및 Pfaffians; 실베스터에 의한 지속성; Christoffel과 Frobenius에 의한 (역시 Wronskians (Muir에 의해 그렇게 불림); Sylvester, Reiss, 및 Picquet의 복합 행렬식; Sylvester에 의한 야코비와 헤세; 및 Trudi에 의한 대칭 고쉬 행렬식이 연구되었습니다. 주제에 관한 교과서 중에서 Spottiswoode의 것이 첫 번째였습니다. 미국에서, Hanus(1886), Weld(1893), 및 Muir/Metzler (1933)가 논문을 발표했습니다.

Applications

Cramer's rule

행렬식은 $Ax=b$와 같이 행렬 형식으로 쓴 선형 방정식의 시스템의 해를 설명하기 위해 사용될 수 있습니다. 이 방정식이 고유한 해 $x$를 가지는 것과 $\det(A)$가 비-영인 것은 필요충분 조건입니다. 이 경우에서, 해는 크라메르의 규칙(Cramer's rule)에 의해 제공됩니다:

$x_{i}={\frac {\det(A_{i})}{\det(A)}}\qquad i=1,2,3,\ldots ,n$

여기서 $A_{i}$는 $A$의 $i$-번째 열을 열 벡터 $b$로 대체함으로써 형성된 행렬입니다. 이것은 행렬식의 열 전개, 즉, 다음에 의해 즉시 따릅니다:

$\det(A_{i})=\det {\begin{bmatrix}a_{1}&\ldots &b&\ldots &a_{n}\end{bmatrix}}=\sum _{j=1}^{n}x_{j}\det {\begin{bmatrix}a_{1}&\ldots &a_{i-1}&a_{j}&a_{i+1}&\ldots &a_{n}\end{bmatrix}}=x_{i}\det(A)$

여기서 벡터 $a_{j}$는 $A$의 열입니다. 그 규칙은 역시 다음 항등식에 의해 암시됩니다:

$A\,\operatorname {adj} (A)=\operatorname {adj} (A)\,A=\det(A)\,I_{n}.$

크라메르의 규칙은 $\operatorname {O} (n^{3})$ 시간에 구현될 수 있으며, 이는 LU, QR, 또는 특이값 분해(singular value decomposition)와 같은 선형 방정식의 시스템을 푸는 보다 공통적인 방법과 유사합니다.

Linear independence

행렬식은 선형적으로 종속 벡터를 특성화하기 위해 사용될 수 있습니다: $\det A$가 영인 것과 행렬 $A$의 열 벡터 (또는, 동등하게, 행 벡터)가 선형적으로 종속인 것은 필요충분 조건입니다. 예를 들어, 2개의 선형 독립 벡터 $v_{1},v_{2}\in \mathbf {R} ^{3}$가 주어지면, 세 번째 벡터 $v_{3}$는 만약 3개의 벡터로 구성된 $3\times 3$-행렬의 행렬식이 영이면 정확하게 이전의 두 벡터에 의해 스팬된 평면에 놓입니다. 같은 아이디어가 미분 방정식(differential equations)의 이론에서도 사용됩니다: 함수 $f_{1}(x),\dots ,f_{n}(x)$가 주어지면 ($n-1$번 미분-가능인 것으로 가정됨), 론스키언(Wronskian)은 다음으로 정의됩니다:

$W(f_{1},\ldots ,f_{n})(x)={\begin{vmatrix}f_{1}(x)&f_{2}(x)&\cdots &f_{n}(x)\\f_{1}'(x)&f_{2}'(x)&\cdots &f_{n}'(x)\\\vdots &\vdots &\ddots &\vdots \\f_{1}^{(n-1)}(x)&f_{2}^{(n-1)}(x)&\cdots &f_{n}^{(n-1)}(x)\end{vmatrix}}.$

그것이 지정된 구간에서 (일부 $x$에 대해) 비-영인 것과 주어진 함수와 차수 $n-1$까지의 모든 그것들의 도함수가 선형적으로 독립인 것은 필요충분 조건입니다. 만약 론스키언이 구간의 모든 곳에서 영이라고 표시될 수 있으면, 해석적 함수(analytic functions)의 경우에서, 이것은 주어진 함수가 선형적으로 종속임을 의미합니다. 로스키언과 선형 독립을 참조하십시오. 행렬식의 또 다른 그러한 사용은 두 개의 다항식(polynomials)이 공통 근(root)을 가질 때 기준을 제공하는 결과식(resultant)입니다.

Orientation of a basis

Main article: Orientation (vector space)

행렬식은 그 열이 주어진 벡터인 정사각 행렬을 사용함으로써, Rⁿ에서 n 벡터의 모든 각 순서열(sequence)에 숫자를 할당하는 것으로 생각될 수 있습니다. 행렬식이 비-영이 아닐 것과 벡터의 순서열이 Rⁿ에서 기저인 것은 필요충분 조건입니다. 해당 경우에서, 행렬식의 부호는 기저의 방향(orientation)이 표준 기저(standard basis)의 방향과 일치하는지 또는 반대인지를 결정합니다. 직교 기저의 경우에서, 행렬식의 크기는 기저 벡터 길이의 곱과 같습니다. 예를 들어, Rⁿ에서 엔트리를 갖는 직교 행렬(orthogonal matrix)은 유클리드 공간(Euclidean space)에서 직교정규 기저(orthonormal basis)를 나타내고, 따라서 ±1의 행렬식을 가집니다 (왜냐하면 모든 벡터가 길이 1을 가지기 때문입니다). 행렬식이 +1인 것과 기저가 같은 방향을 가지는 것은 필요충분 조건입니다. 그것이 −1인 것과 기저가 반대 방향을 가지는 것은 필요충분 조건입니다.

보다 일반적으로, $A$의 행렬식이 양수이면, $A$는 방향-보존하는 선형 변환을 나타내지만 ($A$가 직교 2 × 2 또는 3 × 3 행렬이면, 이것은 회전임), 그것이 음수이면, $A$는 기저의 방향을 전환합니다.

Volume and Jacobian determinant

위에서 지적한 바와 같이, 실수 벡터의 행렬식의 절댓값은 해당 벡터에 의해 스팬된 평행육면체(parallelepiped)의 부피와 같습니다. 결과로써, 만약 $f:\mathbf {R} ^{n}\to \mathbf {R} ^{n}$이 행렬 $A$와의 곱셈에 의해 주어진 선형 맵이고, $S\subset \mathbf {R} ^{n}$이 임의의 측정-가능한 부분집합이면, $f(S)$의 부피는 $|\det(A)|$ 곱하기 $|\det(A)|$의 부피에 의해 주어집니다. 보다 일반적으로, 만약 선형 맵 $f:\mathbf {R} ^{n}\to \mathbf {R} ^{m}$가 $m\times n$-행렬 $A$로 표시되면, $f(S)$의 $n$-차원 부피는 다음과 같이 제공됩니다:

$\operatorname {volume} (f(S))={\sqrt {\det \left(A^{\textsf {T}}A\right)}}\operatorname {volume} (S).$

네 점으로 둘러싸인 사면체(tetrahedron)의 부피를 계산함으로써, 그것들은 꼬인 직선(skew lines)을 식별하기 위해 사용될 수 있습니다. 꼭짓점 $a,b,c,d$가 주어지면, ${\frac {1}{6}}\cdot |\det(a-b,b-c,c-d)|$, 또는 꼭짓점에 걸쳐 스패닝 트리(spanning tree)를 형성하는 꼭짓점 쌍의 임의의 다른 조합.

A nonlinear map $f\colon \mathbf {R} ^{2}\to \mathbf {R} ^{2}$ sends a small square (left, in red) to a distorted parallelogram (right, in red). The Jacobian at a point gives the best linear approximation of the distorted parallelogram near that point (right, in translucent white), and the Jacobian determinant gives the ratio of the area of the approximating parallelogram to that of the original square.

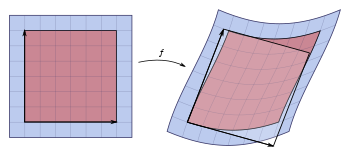
일반적인 미분-가능 함수(differentiable function)에 대해, 위의 대부분은 f의 야코비 행렬(Jacobian matrix)을 고려함으로써 수행됩니다. 다음에 대해,

$f:\mathbf {R} ^{n}\rightarrow \mathbf {R} ^{n},$

야코비 행렬은 그 엔트리가 다음 부분 도함수(partial derivatives)로 제공되는 n × n 행렬입니다:

$D(f)=\left({\frac {\partial f_{i}}{\partial x_{j}}}\right)_{1\leq i,j\leq n}.$

그것의 행렬식, 야코비 행렬식(Jacobian determinant)은 치환에 의한 적분(integration by substitution)의 고-차원 버전에서 나타납니다: 적합한 함수 f 및 Rⁿ (f의 도메인)의 열린 부분집합 U에 대해, 일부 다른 함수 φ : Rⁿ → R^m의 f(U)에 걸쳐 적분은 다음과 같이 제공됩니다:

$\int _{f(U)}\phi (\mathbf {v} )\,d\mathbf {v} =\int _{U}\phi (f(\mathbf {u} ))\left|\det(\operatorname {D} f)(\mathbf {u} )\right|\,d\mathbf {u} .$

야코비는 역시 역 함수 정리(inverse function theorem)에서 나타납니다.

지도-제작(Cartography)의 분야에 적용될 때, 행렬식은 극 근처 지도의 확장의 율을 측정하기 위해 사용될 수 있습니다.

Abstract algebraic aspects

Determinant of an endomorphism

곱의 행렬식과 행렬의 역에 관한 위의 항등식은 닮은 행렬(similar matrices)이 같은 행렬식을 가진다는 것을 의미합니다: 두 행렬 A와 B는 만약 A = X⁻¹BX임을 만족하는 역-가능 행렬 X가 존재하면 닮았습니다. 실제로, 위의 항등식을 반복적으로 적용하면 다음을 산출합니다:

$\det(A)=\det(X)^{-1}\det(B)\det(X)=\det(B)\det(X)^{-1}\det(X)=\det(B).$

행렬식은 따라서 닮음 불변(similarity invariant)이라고도 불립니다. 일부 유한-차원 벡터 공간(vector space) V에 대해 다음 선형 변환(linear transformation)의 행렬식은

$T:V\to V$

V에서 기저(basis)의 임의적인 선택에 관해 그것을 설명하는 행렬의 행렬식으로 정의됩니다. 닮음 불변에 의해, 이 행렬식은 V에 대한 기저의 선택과 독립이고 따라서 자기-사상(endomorphism) T에만 의존합니다.

Square matrices over commutative rings

라이프니츠 규칙을 사용하는 행렬식의 위의 정의는 행렬의 엔트리가 실수 또는 복소수의 필드(field)와 반대로 정수 $\mathbf {Z}$와 같은 교환 링(commutative ring) $R$의 원소일 때 더 일반적으로 작동하도록 유지됩니다. 더욱이, $\det(I)=1$을 만족시키는 고유한 교대 다중선형 맵으로서 행렬식의 특성화는 해당 특성화로부터 결과인 모든 속성과 마찬가지로 여전히 유지됩니다.

행렬 $A\in \operatorname {Mat} _{n\times n}(R)$은 (그 엔터리가 $R$에 있는 역행렬이 있다는 의미에서) 역가능인 것과 그것의 행렬식이 $R$에 있는 역가능 원소(invertible element)인 것은 필요충분 조건입니다. $R=\mathbf {Z}$에 대해, 이것은 행렬식이 +1 또는 −1임을 의미합니다. 그러한 행렬은 유니모듈러(unimodular)라고 불립니다.

행렬식은 곱셈적이므로, 그것은 일반 선형 그룹 ($R$에서 엔트리를 갖는 역가능 $n\times n$-행렬의 그룹)과 $R$에서 단위의 곱셈 그룹(multiplicative group) 사이의 다음과 같은 그룹 준동형(group homomorphism)을 정의합니다:

$\operatorname {GL} _{n}(R)\rightarrow R^{\times },$

그것이 두 그룹에서 곱셈을 존중하기 때문에, 이 맵은 그룹 준동형(group homomorphism)입니다.

The determinant is a natural transformation.

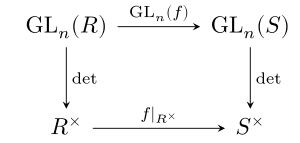
링 준동형(ring homomorphism) $f:R\to S$가 주어졌을 때, $R$에 있는 모든 엔트리를 $f$ 아래의 그 이미지로 대체함으로써 제공되는 맵 $\operatorname {GL} _{n}(f):\operatorname {GL} _{n}(R)\to \operatorname {GL} _{n}(S)$가 있습니다. 행렬식은 이들 맵을 존중하며, 즉, 다음 항등식을 유지합니다:

$f(\det((a_{i,j})))=\det((f(a_{i,j})))$

다시 말해서, 표시된 교환 다이어그램이 교환합니다.

예를 들어, 복소수 행렬의 복소수 켤레(complex conjugate)의 행렬식 (이는 켤레 전치의 행렬식이기도 함)은 행렬식의 복소수 켤레이고, 정수 행렬에 대해: 그러한 행렬의 행렬식의 축소 모듈로 $m$은 행렬 축소된 모듈로 $m$의 행렬식과 같습니다 (후자 행렬식은 모듈러 산술을 사용하여 계산됩니다). 카테고리 이론(category theory)의 언어에서, 행렬식은 두 함수자 $\operatorname {GL} _{n}$과 $(-)^{\times }$ 사이의 자연스러운 변환(natural transformation)입니다. 추상화의 또 다른 계층을 추가하면, 이것은 행렬식이 일반적인 선형 그룹에서 곱셈 그룹(multiplicative group)에 이르는 대수적 그룹(algebraic groups)의 사상이라고 말함으로써 포착됩니다:

$\det :\operatorname {GL} _{n}\to \mathbb {G} _{m}.$

Exterior algebra

See also: Exterior algebra § Linear algebra

$n$-차원 벡터 공간 $V$의 선형 변환 $T:V\to V$, 또는 보다 일반적으로 교환 링 $R$에 걸쳐 (유한) 랭크(rank) $n$의 자유 모듈(free module)의 행렬식은 $V$의 $n$-번째 외부 거듭제곱(exterior power) $\bigwedge ^{n}V$를 고려함으로써 좌표-없는 방식으로 형식화될 수 있습니다. 맵 T는 다음과 같은 선형 맵을 유도합니다:

${\begin{aligned}\bigwedge ^{n}T:\bigwedge ^{n}V&\rightarrow \bigwedge ^{n}V\\v_{1}\wedge v_{2}\wedge \dots \wedge v_{n}&\mapsto Tv_{1}\wedge Tv_{2}\wedge \dots \wedge Tv_{n}.\end{aligned}}$

$\bigwedge ^{n}V$는 1차원이기 때문에, 맵 $\bigwedge ^{n}T$은 어떤 스칼라, 즉, $R$에서 원소를 곱함으로써 제공됩니다. (Bourbaki 1998)와 같은 일부 저자는 이 사실을 사용하여 행렬식을 (모든 $v_{i}\in V$에 대해) 다음 항등식을 만족시키는 $R$에서 원소로 정의합니다:

$\left(\bigwedge ^{n}T\right)\left(v_{1}\wedge \dots \wedge v_{n}\right)=\det(T)\cdot v_{1}\wedge \dots \wedge v_{n}.$

이 정의는 보다 구체적인 좌표-종속 정의와 일치합니다. 이것은 $R^{n}$에서 벡터의 $n$-튜플 위에 다중-선형 교대하는 형식의 고유성을 사용하여 표시될 수 있습니다. 이러한 이유로, 가장 높은 비-영 외부 거듭제곱 $\bigwedge ^{n}V$ (자기사상과 결합된 행렬식과 반대)는 때때로 $V$의 행렬식이라고도 불리고 벡터 공간의 벡터 다발(vector bundles) 또는 체인 복합체(chain complexes)와 같은 더 관련된 대상에 대해서도 유사합니다. 행렬의 소행렬식은 $k<n$을 갖는 더 낮은 교대하는 형식 $\bigwedge ^{k}V$를 고려함으로써 이 설정에서 캐스팅될 수도 있습니다.

Generalizations and related notions

위에서 취급된 행렬식은 몇 가지 변형을 허용합니다: 라이프니츠 규칙에서 발생하는 인수 $\operatorname {sgn} (\sigma )$가 생략된다는 점을 제외하고 행렬의 퍼머넌트(permanent)는 행렬식으로 정의됩니다. 임머넌트(immanant)는 라이프니츠의 규칙에서 대칭 그룹(symmetric group) $S_{n}$의 캐릭터(character)를 도입함으로써 둘 다 일반화합니다.

Determinants for finite-dimensional algebras

필드 $F$에 걸쳐 벡터 공간으로 유한-차원인 임의의 결합 대수(associative algebra) $A$에 대해, 다음과 같은 행렬식 맵이 있습니다:

$\det :A\to F.$

이 정의는 행렬식과 독립적으로 특성 다항식을 수립하고, 행렬식을 이 다항식의 최하위 항으로 정의함으로써 진행됩니다. 이 일반적인 정의는 행렬 대수(matrix algebra) $A=\operatorname {Mat} _{n\times n}(F)$에 대한 행렬식을 복구하지만, 쿼터니언(quaternion)의 행렬식을 포함하여 몇 가지 추가 사례도 포함합니다:

$\det(a+ib+jc+kd)=a^{2}+b^{2}+c^{2}+d^{2}$,

필드 확장(field extension)의 노름(norm) $N_{L/F}:L\to F$, 마찬가지로 반-대칭 행렬의 파피안(Pfaffian)과 중앙 단순 대수의 축소된 노름(reduced norm)도 이 구성의 특수한 경우로 발생합니다.

Infinite matrices

무한한 개수의 행과 열을 갖는 행렬에 대해, 결정자에 대한 위의 정의가 직접 적용되지 않습니다. 예를 들어, 라이프니츠 공식에서, 무한 합 (모든 항이 무한 곱임)이 계산되어야 합니다. 함수형 해석(Functional analysis)은 그러한 무한-차원 상황에 대해 행렬식의 다양한 확장을 제공하며, 이는 어쨌든 특정 종류의 연산자에 대해서만 작동합니다.

프레드홀름 행렬식(Fredholm determinant)은 공식의 적절한 일반화를 통해 대각합 클래스 연산자(trace class operators)로 알려진 연산자에 대한 행렬식을 정의합니다:

$\det(I+A)=\exp(\operatorname {tr} (\log(I+A))).$

행렬식의 또 다른 무한-차원 개념은 함수형 행렬식(functional determinant)입니다.

Operators in von Neumann algebras

유한 요인(factor)의 연산자에 대해, 정식의 대각합을 사용하여 푸글레데−카디슨 행렬식(Fuglede−Kadison determinant)이라고 불리는 양의 실수-값 행렬식을 정의할 수 있습니다. 사실, 폰 노이만 대수(von Neumann algebra) 위에 모든 각 대각합 상태(tracial state)에 해당하는푸글레데−카디슨 행렬식의 개념이 있습니다.

Related notions for non-commutative rings

비-교환 링에 걸쳐 행렬에 대해, 다중-선형성과 교대하는 속성은 n ≥ 2에 대해 호환되지 않으므로, 이 설정에서 행렬식에 대한 좋은 정의가 없습니다.

비-교환 링에서 엔트리를 갖는 정사각 행렬에 대해, 교환 링에 대한 것과 유사하게 행렬식을 정의하는 데 여러 가지 어려움이 있습니다. 하나의 의미는 곱에 대한 차수가 지정되고, 행렬식의 다른 정의에 대해서도 유사하게 지정된다는 조건으로 하여 라이프니츠 공식에 부여될 수 있지만, 비-교환성은 그런-다음 곱셈 속성 또는 행렬식이 행렬의 전치 아래에서 변경되지 않는다와 같은 행렬식의 많은 토대적인 속성의 손실로 이어집니다. 비-교환 링에 걸쳐, 다중선형 형식에 대한 합리적인 개념이 없습니다 (일부 인수의 쌍의 값으로 R의 정규 원소(regular element)를 갖는 비-영 쌍선형 형식(bilinear form)의 존재는 R이 교환적임을 의미합니다). 그럼에도 불구하고, 비-교환 행렬식의 다양한 개념은 행렬식, 특히 준행렬식(quasideterminants), 및 디외도네 행렬식(Dieudonné determinant)의 속성 중 일부를 보존하도록 형식화되어 왔습니다. 비-교환 원소를 갖는 일부 행렬의 클래스에 대해, 행렬식을 정의하고 교환 아날로그와 매우 유사한 선형 대수 정리를 입증할 수 있습니다. 예를 들면 양자 그룹에 대한 q-행렬식, 카펠리 행렬에 대한 카펠리 행렬식(Capelli determinant), 초월행렬 (즉, 그 엔트리가 $\mathbb {Z} _{2}$-등급화된 링(graded rings)의 원소인 행렬)에 대한 비리이즘(Berezinian)이 있습니다. 마닌 행렬(Manin matrices)은 교환 원소를 갖는 행렬에 가장 가까운 클래스를 형성합니다.

Calculation

행렬식은 주로 이론적 도구로 사용됩니다. 역가능을 확인하고 고윳값을 찾는 것과 같은 응용에 대해 행렬식은 대부분 다른 기술로 대체되어 온 수치 선형 대수(numerical linear algebra)에서 그것들은 명시적으로 드물게 계산됩니다. 계산 기하학(Computational geometry)은, 어쨌든, 행렬식과 관련된 계산을 자주 사용합니다.

행렬식은 라이프니츠 규칙을 사용하여 직접 계산될 수 있지만, 이 접근 방법은 큰 행렬에 대해 매우 비효율적인데, 왜냐하면 해당 공식은 $n\times n$-행렬에 대해 $n!$ ($n$ 팩토리얼) 곱을 요구하기 때문입니다. 따라서, 필요한 연산의 수는 매우 빠르게 증가합니다: 그것의 차수는 $n!$입니다. 라플라스 전개도 비슷하게 비효율적입니다. 그러므로, 행렬식을 계산하기 위해 더 많은 관련 기술이 개발되어 왔습니다.

Decomposition methods

일부 방법은 행렬식을 더 쉽게 계산할 수 있는 행렬의 곱으로 행렬을 작성함으로써 $\det(A)$를 계산합니다. 그러한 기술은 분해 방법이라고 참조됩니다. 예로는 LU 분해, QR 분해, 또는 (양수 한정 행렬에 대해) 숄레스키 분해(Cholesky decomposition)가 있습니다. 이들 방법은 $\operatorname {O} (n^{3})$ 차수이며, 이는 $\operatorname {O} (n!)$보다 크게 개선되었습니다.

예를 들어, LU 분해는 $A$를 다음의 곱으로 표현합니다:

$A=PLU.$

여기서 $P$는 순열 행렬(permutation matrix) (이는 각 열에 정확하게 단일 1이 있고, 그렇지 않으면 영들을 가짐), $L$은 아래쪽 삼각 행렬이고, $U$는 위쪽 삼각 행렬입니다. 두 삼각 행렬 $L$과 $U$의 행렬식은 빠르게 계산될 수 있는데, 왜냐하면 그것들은 각 대각선 엔트리의 곱이기 때문입니다. $P$의 행렬식은 해당 순열의 부호 $\varepsilon$일 뿐입니다 (이는 순열의 짝수에 대해 $+1$이고 순열의 홀수에 대해 $-1$입니다). 일단 그러한 LU 분해가 $A$에 대해 알려져 있으면, 그 행렬식은 다음과 같이 쉽게 계산됩니다:

$\det(A)=\varepsilon \det(L)\cdot \det(U).$

Further methods

분해 방법으로 도달한 차수 $\operatorname {O} (n^{3})$는 다른 방법에 의해 개선되어 왔습니다. 만약 차수 $n$의 두 행렬은 시간 $M(n)$에서 곱할 수 있으면, 여기서 일부 $a>2$에 대해 $M(n)\geq n^{a}$이며, 시간 $M(n)\geq n^{a}$에서 행렬식을 계산하는 알고리듬이 있습니다. 이것은, 예를 들어, 코퍼스미스-위노그라드 알고리듬(Coppersmith–Winograd algorithm)을 기반으로 행렬식을 계산하는 $\operatorname {O} (n^{2.376})$ 알고리듬이 존재함을 의미합니다. 이 지수는, 2016년 당시, 2.373으로 더 낮아졌습니다.

알고리듬의 복잡성 외에도, 알고리듬을 비교하기 위해 추가 기준을 사용할 수 있습니다. 특히 링에 걸쳐 행렬과 관련된 응용에 대해, 임의의 나눗셈 없이 행렬식을 계산하는 알고리듬이 존재합니다. (대조적으로, 가우스 소거법은 나눗셈이 필요합니다.) 복잡도 $\operatorname {O} (n^{4})$를 가지는 그러한 알고리듬 중 하나는 다음 아이디어를 기반으로 합니다: 순열 (라이프니츠 규칙에서와 같이)을 여러 항목이 반복될 수 있는 소위 닫힌 순서화된 걸음(closed ordered walks)으로 대체합니다. 결과 합은 라이프니츠 규칙보다 더 많은 항을 가지지만, 그 과정에서 이들 곱 중 여러 개는 재사용될 수 있으며, 라이프니츠 규칙으로 소박하게 계산하는 것보다 더 효율적입니다. 알고리듬은 비트 복잡성(bit complexity), 즉, 계산에서 발생하는 중간 값을 저장하기 위해 필요한 정확도 비트 수에 따라 평가될 수도 있습니다. 예를 들어, 가우스 소거법 (또는 LU 분해) 방법은 $\operatorname {O} (n^{3})$ 차수이지만, 중간 값의 비트 길이는 지수적으로 길어질 수 있습니다. 이에 비해, 버라이스 알고리듬(Bareiss algorithm)은 정확한-나눗셈 방법 (그래서 그것은 나눗셈을 사용하지만, 이들 나눗셈은 나머지 없이 수행될 수 있는 경우에만)은 같은 차수이지만, 비트 복잡도는 대략 행렬에서 원래 엔트의 비트 크기에 $n$을 곱한 값입니다.

만약 $A$의 행렬식과 $A$의 역이 이미 계산되어 있으면, 행렬 행렬식 보조정리(matrix determinant lemma)는 A + uv^T의 행렬식을 빠른 계산을 허용하며, 여기서 $u$와 $v$는 열 벡터입니다.

Charles Dodgson (예를 들어, Alice's Adventures in Wonderland 명성의 Lewis Carroll)은 도지슨 응집(Dodgson condensation)이라고 불리는 행렬식을 계산하는 방법을 발명했습니다. 불행하게도 이 흥미로운 방법이 항상 원래 형식으로 작동하는 것은 아닙니다.

See also

• Cauchy determinant
• Cayley–Menger determinant
• Dieudonné determinant
• Slater determinant
• Determinantal conjecture

References

See also: Linear algebra § Further reading

• Anton, Howard (2005), Elementary Linear Algebra (Applications Version) (9th ed.), Wiley International
• Axler, Sheldon Jay (2015). Linear Algebra Done Right (3rd ed.). Springer. ISBN 978-3-319-11079-0.
• Bareiss, Erwin (1968), "Sylvester's Identity and Multistep Integer-Preserving Gaussian Elimination" (PDF), Mathematics of Computation, 22 (102): 565–578, doi:10.2307/2004533, JSTOR 2004533, archived (PDF) from the original on 2012-10-25
• de Boor, Carl (1990), "An empty exercise" (PDF), ACM SIGNUM Newsletter, 25 (2): 3–7, doi:10.1145/122272.122273, S2CID 62780452, archived (PDF) from the original on 2006-09-01
• Bourbaki, Nicolas (1998), Algebra I, Chapters 1-3, Springer, ISBN 9783540642435
• Bunch, J. R.; Hopcroft, J. E. (1974). "Triangular Factorization and Inversion by Fast Matrix Multiplication". Mathematics of Computation. 28 (125): 231–236. doi:10.1090/S0025-5718-1974-0331751-8.
• Dummit, David S.; Foote, Richard M. (2004), Abstract algebra (3rd ed.), Hoboken, NJ: Wiley, ISBN 9780471452348, OCLC 248917264
• Fisikopoulos, Vissarion; Peñaranda, Luis (2016), "Faster geometric algorithms via dynamic determinant computation", Computational Geometry, 54: 1–16, doi:10.1016/j.comgeo.2015.12.001
• Garibaldi, Skip (2004), "The characteristic polynomial and determinant are not ad hoc constructions", American Mathematical Monthly, 111 (9): 761–778, arXiv:math/0203276, doi:10.2307/4145188, JSTOR 4145188, MR 2104048
• Habgood, Ken; Arel, Itamar (2012). "A condensation-based application of Cramer's rule for solving large-scale linear systems" (PDF). Journal of Discrete Algorithms. 10: 98–109. doi:10.1016/j.jda.2011.06.007. Archived (PDF) from the original on 2019-05-05.
• Harris, Frank E. (2014), Mathematics for Physical Science and Engineering, Elsevier, ISBN 9780128010495
• Kleiner, Israel (2007), Kleiner, Israel (ed.), A history of abstract algebra, Birkhäuser, doi:10.1007/978-0-8176-4685-1, ISBN 978-0-8176-4684-4, MR 2347309
• Kung, Joseph P.S.; Rota, Gian-Carlo; Yan, Catherine (2009), Combinatorics: The Rota Way, Cambridge University Press, ISBN 9780521883894
• Lay, David C. (August 22, 2005), Linear Algebra and Its Applications (3rd ed.), Addison Wesley, ISBN 978-0-321-28713-7
• Lombardi, Henri; Quitté, Claude (2015), Commutative Algebra: Constructive Methods, Springer, ISBN 9789401799447
• Mac Lane, Saunders (1998), Categories for the Working Mathematician, Graduate Texts in Mathematics 5 (2nd ed.), Springer-Verlag, ISBN 0-387-98403-8
• Meyer, Carl D. (February 15, 2001), Matrix Analysis and Applied Linear Algebra, Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0-89871-454-8, archived from the original on 2009-10-31
• Muir, Thomas (1960) [1933], A treatise on the theory of determinants, Revised and enlarged by William H. Metzler, New York, NY: Dover
• Poole, David (2006), Linear Algebra: A Modern Introduction (2nd ed.), Brooks/Cole, ISBN 0-534-99845-3
• G. Baley Price (1947) "Some identities in the theory of determinants", American Mathematical Monthly 54:75–90 MR0019078
• Horn, Roger Alan; Johnson, Charles Royal (2018) [1985]. Matrix Analysis (2nd ed.). Cambridge University Press. ISBN 978-0-521-54823-6.
• Lang, Serge (1985), Introduction to Linear Algebra, Undergraduate Texts in Mathematics (2 ed.), Springer, ISBN 9780387962054
• Lang, Serge (1987), Linear Algebra, Undergraduate Texts in Mathematics (3 ed.), Springer, ISBN 9780387964126
• Lang, Serge (2002). Algebra. Graduate Texts in Mathematics. New York, NY: Springer. ISBN 978-0-387-95385-4.
• Leon, Steven J. (2006), Linear Algebra With Applications (7th ed.), Pearson Prentice Hall
• Rote, Günter (2001), "Division-free algorithms for the determinant and the Pfaffian: algebraic and combinatorial approaches" (PDF), Computational discrete mathematics, Lecture Notes in Comput. Sci., vol. 2122, Springer, pp. 119–135, doi:10.1007/3-540-45506-X_9, ISBN 978-3-540-42775-9, MR 1911585, archived from the original (PDF) on 2007-02-01, retrieved 2020-06-04
• Trefethen, Lloyd; Bau III, David (1997), Numerical Linear Algebra (1st ed.), Philadelphia: SIAM, ISBN 978-0-89871-361-9

Historical references

• Bourbaki, Nicolas (1994), Elements of the history of mathematics, translated by Meldrum, John, Springer, doi:10.1007/978-3-642-61693-8, ISBN 3-540-19376-6
• Cajori, Florian (1993), A history of mathematical notations: Including Vol. I. Notations in elementary mathematics; Vol. II. Notations mainly in higher mathematics, Reprint of the 1928 and 1929 originals, Dover, ISBN 0-486-67766-4, MR 3363427
• Bezout, Étienne (1779), Théorie générale des equations algébriques, Paris
• Cayley, Arthur (1841), "On a theorem in the geometry of position", Cambridge Mathematical Journal, 2: 267–271
• Cramer, Gabriel (1750), Introduction à l'analyse des lignes courbes algébriques, Genève: Frères Cramer & Cl. Philibert, doi:10.3931/e-rara-4048
• Eves, Howard (1990), An introduction to the history of mathematics (6 ed.), Saunders College Publishing, ISBN 0-03-029558-0, MR 1104435
• Grattan-Guinness, I., ed. (2003), Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences, vol. 1, Johns Hopkins University Press, ISBN 9780801873966
• Jacobi, Carl Gustav Jakob (1841), "De Determinantibus functionalibus", Journal für die reine und angewandte Mathematik, 1841 (22): 320–359, doi:10.1515/crll.1841.22.319, S2CID 123637858
• Laplace, Pierre-Simon, de (1772), "Recherches sur le calcul intégral et sur le systéme du monde", Histoire de l'Académie Royale des Sciences (seconde partie), Paris: 267–376{{citation}}: CS1 maint: multiple names: authors list (link)

External links

• Suprunenko, D.A. (2001) [1994], "Determinant", Encyclopedia of Mathematics, EMS Press
• Weisstein, Eric W. "Determinant". MathWorld.
• O'Connor, John J.; Robertson, Edmund F., "Matrices and determinants", MacTutor History of Mathematics archive, University of St Andrews.
• Determinant Interactive Program and Tutorial
• Linear algebra: determinants. Archived 2008-12-04 at the Wayback Machine Compute determinants of matrices up to order 6 using Laplace expansion you choose.
• Determinant Calculator Calculator for matrix determinants, up to the 8th order.
• Matrices and Linear Algebra on the Earliest Uses Pages
• Determinants explained in an easy fashion in the 4th chapter as a part of a Linear Algebra course.