Jump to content

History of mathematics

This is a fully translated article. Click here for more information.
From DawoumWiki, the free Mathematics self-learning
Original article: w:History of mathematics
A proof from Euclid's Elements, widely considered the most influential textbook of all time.[1]
Table of numerals

수학의 역사(history of mathematics)로 알려진 연구의 분야는 주로 수학(mathematics)에서 발견의 기원에 대한 조사이고, 더 작은 범위에서, 과거의 수학적 방법과 표기법에 대한 조사입니다. 현대 시대(modern age)와 지식의 세계적인 확산 전에, 새로운 수학적 개발에 대한 서면 예제는 오직 몇 가지 지역에서 밝혀져 왔습니다. 기원전 3000년부터 수메르(Sumer)의 메소포타미아(Mesopotamian) 주(states), 아카드(Akkad) 및 아시리아(Assyria), 고대 이집트(Ancient Egypt)와 에블라(Ebla)와 함께 과세, 상업, 무역의 목적에 대해, 그리고 역시 천문학(astronomy)의 분야에서 달력(calendars)을 공식화하고 시간을 기록하기 위해 산술(arithmetic), 대수(algebra), 및 기하학(geometry)을 사용하기 시작했습니다.

가장 오래된 수학 텍스트는 메소포타미아(Mesopotamia)와 이집트(Egypt) – 플림프턴 322(Plimpton 322) (Babylonian c. 1900 BC),[2] 린드 수학적 파피루스(Rhind Mathematical Papyrus) (Egyptian c. 2000–1800 BC)[3] 및 모스크바 수학적 파피루스(Moscow Mathematical Papyrus) (Egyptian c. 1890 BC)로부터 유용합니다. 이들 텍스트의 모두는 소위 피타고라스 세-쌍(Pythagorean triple:티라고라스 삼조)을 언급했고, 그래서, 추론에 의해, 피타고라스의 정리(Pythagorean theorem)가, 기본 산술과 기하학 후에, 가장 고전적이고 광범위한 수학적 개발인 것으로 보입니다.

"논증할 수 있는 훈련"으로서의 수학에 대한 연구는 기원전 6세기에 피타고라스주의와 함께 시작하는데, 피타고라스주의(Pythagoreans)는 "교육의 주제(subject of instruction")을 의미하는 고대 그리스어(Greek) μάθημα (mathema)로부터, 용어 "수학"을 만들어 냅니다.[4] 그리스 수학(Greek mathematics)은 (특히 증명(proofs)에서 연역적 추론과 수학적 엄격함(mathematical rigor)을 도입을 통해) 방법을 크게 정제했고 수학의 소재를 확장했습니다.[5] 비록 그들이 이론적 수학(theoretical mathematics)에 사실상 기여하지는 않았지만, 고대 로마인(ancient Romans)은 측량(surveying), 구조 공학(structural engineering), 기계 공학(mechanical engineering), 부기(bookkeeping), 음력(lunar) 및 양력 달력(solar calendar)의 생성, 그리고 심지어 예술 및 공예(arts and crafts)에서 응용 수학을 사용했습니다. 중국 수학(Chinese mathematics)은 자리 값 시스템(place value system)과 음수(negative numbers)의 첫 번째 사용을 포함하여 초기에 공헌을 만들었습니다.[6][7] 힌두–아라비아 숫자 시스템(Hindu–Arabic numeral system)과 오늘날 전 세계적으로 사용에서 그의 연산의 사용에 대한 규칙은 인도(India)에서 첫 번째 밀레니엄 AD의 과정에 걸쳐 진화되었고 무하마드 이븐 무사 알-콰리즈미(Muḥammad ibn Mūsā al-Khwārizmī)의 업적으로 인하여 이슬람 수학(Islamic mathematics)을 통해 서방 세계(Western world)로 전달되었습니다.[8][9] 이슬람 수학은, 차례로, 이들 문명에 알려진 수학을 발전시키고 확장시켰습니다.[10] 동시대이지만 이들 전통과 독립적으로 멕시코(Mexico)와 중미(Central America)의 마야 문명(Maya civilization)에 의해 수학은 개발되었으며, 여기서 영(zero)의 개념은 마야 숫자 시스템(Maya numerals)에서 표준 기호로 제공되었습니다.

수학에 관한 많은 그리스어 및 아랍어 텍스트가 12세기 이후 라틴어로 번역되어, 중세 유럽(Medieval Europe)에서 수학의 뒤따른 발전을 이끌었습니다. 고대 시대부터 중세(Middle Ages)에 이르기까지, 수학적 발견의 기간은 수세기 동안 계속 침체되었습니다. 15세기에서 르네상스(Renaissance) 이탈리아(Italy)에서 시작하여, 새로운 과학적 발견과 상호 작용하는 새로운 수학적 발전이 오늘날까지 계속되는 증가하는 속도(increasing pace)로 만들어져 왔습니다. 이것은 17세기 동안 무한소 미적분학(calculus)의 개발에서 아이작 뉴턴(Isaac Newton)과 고트프리트 빌헬름 라이프니츠(Gottfried Wilhelm Leibniz) 둘 다의 획기적인 업적을 포함합니다. 19세기 말에 수학자의 국제 회의(International Congress of Mathematicians)가 창립되었고 이 분야에서 선두에서 발전을 계속합니다.[citation needed]

Prehistoric

수학적 사고의 기원은 숫자(number), 크기(magnitude) 및 형태(form)의 개념에 있습니다.[11] 동물 인식에 대한 현대의 연구는 이들 개념이 인간에게 유일한 것이 아니라는 것을 보여 왔습니다. 그러한 개념은 사냥꾼-채집자 사회에서 일상 생활의 일부였을 것입니다. 시대에 걸쳐 점진적으로 진화하는 "숫자"의 개념의 아이디어는 "하나", "둘" 및 "다수" 사이의 구별을 유지하지만 2보다 큰 숫자의 것은 없는 언어의 존재에 의해 뒷받침됩니다.[11]

2만년 이상된, 아프리카에서 발견된 선사시대(Prehistoric) 유물(artifacts)은 시간을 정량화(quantify)하려는 초기 시도를 시사합니다.[not in citation given] 나일(Nile) 강 (콩고 북동쪽)의 상류 가까이에서 발견된, 이시고 뼈(Ishango bone)는 2만년이 넘었을 수 있었고 뼈의 길이를 따라 세 개의 기둥에서 조각된 일련의 자국으로 이루어져 있습니다. 공통적인 해석은 이시고 뼈가 소수(prime number)[12]의 수열(sequence)에 대한 최초의 알려진 시연의 탈리(tally), 또는 육-개월 음력 달력중 하나를 보여주는 것입니다.[13] 피터 루드만(Peter Rudman)은 소수 개념의 발전은 나눗셈의 개념 후에 오직 발생했을 것이라고 주장했습니다. 그는 나눗셈에 대해 기원전 1만년 후로 거슬로 올라가고, 기원전 500년경까지 소수와 함께 아마도 이해하지 못했을 것이라고 주장했습니다. 그는 "왜 어떤 것의 탈리가 2의 배수, 10과 20 사이의 소수, 그리고 거의 10의 배수가 되는 일부 숫자를 보여주어야 하는지에 대해서는 설명하려고 만들어진 시도는 없습니다"라고 역시 썼습니다.[14] 학자 알렉산더 마샥(Alexander Marshack)에 따르면, 이시고 뼈는, 이시고 뼈의 일부 엔트리처럼, 이집트 산술이 2에 의한 곱셈의 사용을 역시 만들었을 때, 이집트에서 수학의 후기 발전에 영향을 미쳤을 것입니다; 이것은 어쨌든, 논쟁의 여지가 있습니다.[15]

기원전 5천년의 왕조시대-이전 이집트(Predynastic Egypt)인은 기하학적(geometric) 디자인을 그림으로 묘사했습니다. 기원전 3천년부터 시작된, 잉글랜드와 스코틀랜드의 거석(megalith) 기념물에서 원(circle), 타원(ellipse), 그들 디자인에서 피타고라스 세-쌍(Pythagorean triple)과 같은 기하학적 아이디어를 반영하고 있었다고 주장해 왔습니다.[16] 위의 모든 것들은 논쟁의 여지가 있고, 어쨌든 현재 가장 오래된 논쟁이 없는 수학적 문서는 바빌로니아와 왕조 이집트 원천들입니다.[citation needed]

Babylonian

Main article: Babylonian mathematics
See also: Plimpton 322

바빌로니아(Babylonia)의 수학은 초기 수메르(Sumer)의 시대부터 헬레니즘 기간(Hellenistic period)를 거쳐 거의 기독교(Christianity)의 새벽에 이르기까지 메소포타미아(Mesopotamia) (현대 이라크)의 사람들의 임의의 수학을 가리킵니다.[17] 바빌로니아의 수학적 업적의 대부분은 2개의 광범위하게 분리된 기간: 두 번째 밀레니엄 BC (오래된 바빌론 기간)의 처음 몇 백년, 그리고 첫 번째 밀레니엄 BC (셀레우시드(Seleucid) 기간)의 마지막 몇 세기에서 옵니다.[18] 그것은 연구의 장소일 때 바빌론(Babylon)의 중심 역할에 기인하여 바빌로니아의 수학이라고 이름지어졌습니다. 나중에 아랍 제국(Arab Empire) 아래에서, 메소포타미아, 특히 바그다드(Baghdad)는 다시 한번 이슬람 수학(Islamic mathematics)에 대해 연구의 중요한 중심이 되었습니다.

Geometry problem on a clay tablet belonging to a school for scribes; Susa, first half of the 2nd millennium BCE

이집트의 수학(Egyptian mathematics)에서 출처의 희박성과는 달리, 바빌로니아의 수학에 대한 우리의 지식은 1850년대 이래 발굴된 400개 이상의 점토 태블릿에서 유래됩니다.[19] 설형 문자 스크립트(Cuneiform script)로 쓰인, 태블릿은 점토가 약간 젖어 있는 동안 쓰이고, 오븐 또는 태양열로 열심히 구워졌습니다. 이들 중 일부는 점수가 매겨진 숙제인 것으로 보입니다.[20]

기록된 수학에 대한 가장 초기의 흔적은 메소포타미아에서 최초의 문명을 건설했던, 고대 수메르(Sumer) 사람으로 거슬러 올라갑니다. 그들은 기원전 3000년부터 도량형학(metrology)의 복잡한 시스템을 개발했습니다. 기원전 2500년경부터, 수메르 사람은 점토 태블릿에 곱셈 테이블(multiplication table)을 썼었고 기하학적(geometrical) 연습과 나눗셈(division) 문제를 다루었습니다. 바빌로니아의 숫자 시스템의 흔적은 역시 이시기로 거슬러 올라갑니다.[21]

The Babylonian mathematical tablet Plimpton 322, dated to 1800 BC.

바빌로니아의 수학은 육십진수(sexagesimal) (밑수-60) 숫자 시스템(numeral system)을 사용하여 작성되었습니다.[19] 이것으로부터 분에서 60초, 시간에서 60분, 원에서 360 (60 x 6)도의 현대적인 사용법, 마찬가지로 각도의 분수를 나타내기 위한 호의 초와 분을 사용이 유래합니다. 60은 2, 3, 4, 5, 6, 10, 12, 15, 20 및 30에 의해 균등하게 나누어질 수 있기 때문에 육십진수 시스템이 선택되었을 가능성이 있습니다.[19] 역시, 이집트, 그리스, 및 로마 사람들과 달리, 바빌로니아 사람은 참된 자리-값 시스템을 가졌었고, 여기서 왼쪽 열에서 기록된 자릿수는 십진법(decimal) 시스템에서 처럼 더 큰 값을 나타냅니다.[18] 바빌로니아 표기법 시스템의 거듭제곱은 분수를 정수만큼 쉽게 표현하기 위해 사용될 수 있다는 것을 의미합니다; 따라서 분수를 포함하는 두 숫자를 곱하는 것은, 우리의 현대 표기법과 유사하게, 정수를 곱하는 것과 다르지 않았습니다.[18] 바빌로니아의 표기법 시스템은 르네상스(Renaissance)까지 임의의 문명 중에서 최고였고,[22] 그의 거듭제곱은 놀랄만한 계산 정확도와 동력을 얻는 것을 허용했습니다; 예를 들어, 바빌로니아의 태블릿 YBC 7289는 소수점 이하 다섯 자리까지 √2의 근삿값을 제공합니다.[22] 바빌로니아 사람은, 어쨌든, 소수점과 동등한 것이 없었고, 그래서 기호의 장소 값은 종종 문맥으로부터 추론되어야 했습니다.[18] 셀레우시드 기간에 의해, 바빌로니아 사람은 빈 위치에 대해 자리 표시자로 영 기호를 개발했었습니다; 어쨌든 그것은 단지 중간 위치에 대해 사용되었습니다.[18] 이 영 기호는 끝 위치에 나타나지 않았고, 따라서 바빌로니아 사람은 접근했었지만 참된 장소 값 시스템을 개발하지는 못했습니다.[18]

바빌로니아의 수학에 의해 다루어진 다른 주제는 분수, 대수, 이차 및 삼차 방정식, 및 규칙적(regular) 역수(reciprocal) 쌍(pairs)의 계산을 포함합니다.[23] 태블릿은 그 시대에 대해 주목할만한 성취, 선형(linear), 이차 방정식(quadratic equation) 및 삼차 방정식(cubic equation)을 푸는 것에 대해 곱셈 테이블과 방법을 역시 포함합니다.[24] 오래된 바빌로니아 기간으로부터 태블릿은 피타고라스의 정리(Pythagorean theorem)에 대한 최초의 알려진 명제를 역시 포함합니다.[25] 어쨌든, 이집트의 수학과 마찬가지로, 바빌로니아의 수학은 정확한 해와 근접한 해 사이의 차이의 인식, 또는 문제의 해결 가능성을 보여주지 않았고, 가장 중요하게, 증명(proofs) 또는 논리적 원리에 대해 명시적 명제를 보여주지는 못했습니다.[20]

Egyptian

Main article: Egyptian mathematics
Image of Problem 14 from the Moscow Mathematical Papyrus. The problem includes a diagram indicating the dimensions of the truncated pyramid.

이집트(Egypt)의 수학은 이집트의 언어(Egyptian language)로 서면 수학을 가리킵니다. 헬레니즘 기간(Hellenistic period)으로부터, 그리스어(Greek)는 이집트의(Egyptian) 학자의 서면 언어로 이집트어를 대체했습니다. 이집트(Egypt)에서 수학적 연구는 이후, 아랍어(Arabic)가 이집트 학자의 서면 언어가 될 때, 이슬람 수학(Islamic mathematics)의 일부로 아랍 제국(Arab Empire)에서 계속되었습니다.

가장 광범위한 이집트의 수학 텍스트는 (때때로 그의 저자 후에 아머스 파피루스라고 역시 불리는) 린드 파피루스(Rhind papyrus)가 기원전 c. 1650에 확인되었지만, 기원전 약 2000–1800의 중간 왕국(Middle Kingdom)으로부터 더 오래된 문서의 사본일 가능성이 있습니다.[26] 그것은 산술 및 기하학에서 학생들에 대해 지침서입니다. 곱셈, 나누기 및 단위 분수로 작업하는 넓이 수식 및 방법을 제공하는 것 외에도, 그것은 합성수(composite) 및 소수(prime number); 산술(arithmetic), 기하(geometric) 및 조화 평균(harmonic mean); 그리고 에라토스테네스의 체(Sieve of Eratosthenes)와 완전 숫자 이론(perfect number theory) (즉, 숫자 6의 그것)의 단순한 이해를 포함하는, 또 다른 수학적 지식의 증거를 역시 포함합니다.[27][28] 그것은 일차 선형 방정식(linear equation)뿐만 아니라 산술(arithmetic) 및 기하 급수(geometric series)를 해결하는 방법을 역시 보여줍니다.[29][30]

또 다른 중요한 이집트의 수학 텍스트는 기원전 c. 1890로 확인되는, 역시 중간 왕국(Middle Kingdom) 기간으로부터 모스코우 파피루스(Moscow papyrus)입니다.[31] 그것은 오락 거리로 분명히 의도된, 오늘날 단어 문제 또는 이야기 문제라고 불리는 것들로 구성됩니다. 한 가지 문제는 절두체(frustum) (잘린 피라미드)의 부피를 찾는 방법을 제공하기 때문에 특히 중요한 것으로 여겨집니다.

마침내, 베를린 파피루스 6619(Berlin Papyrus 6619) (기원전 c. 1800)는 고대 이집트인이 이차 대수 방정식(algebraic equation)을 풀 수 있음을 보여줍니다.[32]

Greek

Main article: Greek mathematics
The Pythagorean theorem. The Pythagoreans are generally credited with the first proof of the theorem.

그리스 수학은 밀레토스의 탈레스(Thales of Miletus) 시대 (기원전 ~600)로부터 529년에서 아테네의 아카데미(Academy of Athens)의 폐쇄까지 그리스 언어(Greek language)로 쓰인 수학을 가리킵니다.[33] 그리스 수학자는 이탈리아에서 북아프리카까지 전체 동부 지중해에 퍼져있는 도시에 살았지만, 문화와 언어에 의해 통일되었습니다. 다음의 알렉산더 대왕(Alexander the Great) 기간의 그리스 수학은 헬레니즘(Hellenistic) 수학을 때때로 불립니다.[34]

그리스 수학은 이전 문화에 의해 개발되어 왔던 수학보다 훨씬 정교했습니다. 그리스-이전 수학의 모든 살아남은 기록은 귀납적 추론, 즉 무지의 법칙을 확립하기 위해 사용되는 반복된 관찰의 사용을 보여줍니다. 그리스 수학자는, 반면에, 연역적 추론을 사용했습니다. 그리스인은 정의와 공리로부터 결론을 유도하기 위해 논리를 사용했고, 그들을 입증하기 위해 수학적 엄격함(mathematical rigor)을 사용했습니다.[35]

그리스 수학은 밀레토스의 탈레스(Thales of Miletus) (기원전 c. 624–c.546)와 사모스의 피타고라스(Pythagoras of Samos) (기원전 c. 582–c. 507)로 시작된 것으로 생각됩니다. 비록 그 영향의 범위는 논쟁의 여지가 있을지라도, 그들은 아마도 이집트(Egyptian)와 바빌로니아의 수학(Babylonian mathematics)에 의해 영감을 얻었을 것입니다. 전설에 따르면, 피타고라스는 이집트 제사장으로부터 수학, 기하학, 및 천문학을 배우기 위해 이집트로 여행했습니다.

탈레스는 피라미드(pyramids)의 높이와 해안으로부터 배의 거리를 계산하는 것과 같은 문제를 해결하기 위해 기하학(geometry)을 사용했습니다. 그는, 네 개의 추론을 탈레스의 정리(Thales' Theorem)로 유도함으로써, 기하학에 적용되는 연역적 추론의 첫 번째 사용으로 인정됩니다. 결과적으로, 그는 최초의 참된 수학자이고 수학적 발견을 기인한 최초의 알려진 개인으로 환영받아 왔습니다.[36] 피타고라스(Pythagoras)는 피타고라스 학파(Pythagorean School)를 설립했으며, 그들의 주의는 수학이 우주를 통치하고 그의 모토는 "모두 것은 숫자"라는 것입니다.[37] 피타고라스 학파는 용어 "수학"을 만들어 냈었고, 수학 자체의 목적에 대해 수학의 연구를 시작했습니다. 피타고라스 학파는, 비록 정리의 명제가 무리수(irrational numbers)의 존재의 증명과 함께 오랜 역사를 가질지라도,[38][39] 피타고라스의 정리(Pythagorean theorem)[40]의 첫 번째 증명으로 인정됩니다. 비록 그가 바빌로니아(Babylonians)와 중국(Chinese)에 의해 선해되었음에도 불구하고,[41] 네오피타고라스(Neopythagorean)의 수학자 니코마코스(Nicomachus) (60–120 AD)는 최초의 그리스-로마(Greco-Roman) 곱셈 테이블(multiplication table) 중 하나를 제공했으며, 반면에 가장 오래된 현존하는 그리스 곱셈 테이블은 1세기에 나온 왁스 테이블에서 발견되었습니다 (현재 대영 박물관(British Museum)에서 보관됨).[42] 네오피타고라스와 곱셈 테이블의 서구 발명의 연관성은 그의 후기 중세(Medieval) 이름: mensa Pythagorica에서 분명히 나타납니다.[43]

플라톤(Plato) (기원전 428/427 – 348/347)은 다른 사람들에게 영감을 불어 넣어주고 안내하는 수학의 역사에서 중요합니다.[44] 아테네(Athens)에서, 그의 플라톤 아카데미(Platonic Academy)는 기원전 4세기에서 세상의 수학적 중심지가 되었고, 이 학교에서 당시의 유명한, 크니두스의 유독소스(Eudoxus of Cnidus)와 같은, 수학자가 나왔습니다.[45] 플라톤은 수학의 토대에 대해 역시 논의했고,[46] 정의의 일부 (예를 들어, "폭이 없는 길이"와 같은 선의 그것)를 밝히고, 가정을 재구성했습니다.[47] 해석적 방법(analytic method)은 플라톤(Plato)에 속하는 것으로 생각되고, 반면에 피타고라스의 세-쌍을 얻기 위한 공식은 그의 이름을 따릅니다.[45]

에우독소스(Eudoxus) (기원전 408–c. 355)는 현대 적분(integration)의 선구자, 소진의 방법(method of exhaustion)을 개발했었고,[48] 비-정수비율가능 크기(incommensurable magnitudes)의 문제를 피하는 비율 이론을 개발했었습니다.[49] 전자는 곡선형 그림의 넓이와 부피의 계산을 허용하고,[50] 반면에 후자는 기하학에서 중요한 발전을 만들기 위해 후속 기하학자를 활성화했습니다. 비록 그가 특정한 기술적인 수학적 발견을 만들지 않았을지라도, 아리스토델레스(Aristotle) (기원전 384–c. 322)는 논리(logic)의 토대를 마련함으로써 수학의 발전에 크게 기여했습니다.[51]

One of the oldest surviving fragments of Euclid's Elements, found at Oxyrhynchus and dated to circa AD 100. The diagram accompanies Book II, Proposition 5.[52]

기원전 3세기에서, 수학 교육과 연구의 최고의 중심은 알렉산드리아(Alexandria)의 무슬림(Musaeum)이었습니다.[53] 유클리드(Euclid) (기원전 c. 300)가 가르쳤고, 모든 시간 중 가장 성공적이고 영향력 있는 교과서로 널리 여겨지는 원론(Elements:원론)을 썼다는 것이 그곳이었습니다.[1] 그 원론은 공리적 방법(axiomatic method)을 통해 수학적 엄격함(mathematical rigor)을 도입했었고 오늘날 수학에서 여전히 사용되는 형식, 정의, 공리, 정리 및 증명의 최초의 예제입니다. 비록 원론의 대부분의 내용이 이미 알려졌었지만, 유클리드는 그들을 하나의, 일관된 논리적 프레임워크로 정리했습니다.[54] 원론은 서구의 모든 교육받은 사람들에게 20세기 중반까지 알려졌었고 그 내용은 오늘날도 기하학 수업에서 여전히 가르쳐집니다.[55] 유클리드 기하학(Euclidean geometry)의 익숙한 정리 외에도, 원론은 숫자 이론(number theory:수론), 대수학(algebra) 및 입체 기하학(solid geometry)과 같은, 시간의 모든 수학적 주제에 대한 입문 교과서로서 의미가 있으며,[54] 이의 제곱근이 무리수인 것 그리고 무한히 많은 소수가 있는 것의 증명을 포함합니다. 유클리드는 역시 원뿔 단면(conic sections), 광학(optics), 구형 기하학(spherical geometry), 및 역학과 같은 또 다른 주제를 광범위하게 썼지만, 그의 글의 오직 절반 정도가 잔존해 있습니다.[56]

Archimedes used the method of exhaustion to approximate the value of pi.

고대의 가장 위대한 수학자로 널리 여겨지는,[57] 시러큐스(Syracuse)의 아르키메데스(Archimedes) (기원전 c. 287–212)는, 현대 미적분학과 크게 다른 방식이 아닌 방식으로, 포물선(parabola)의 호 아래의 넓이(area)를 무한 급수의 합으로 계산하기 위해 소진의 방법(method of exhaustion)을 사용했습니다.[58] 그는 원하는 만큼의 정밀도로 π의 값을 계산하기 위해 소진의 방법을 사용할 수 있고, 그 때 알려진 π의 가장 정확한 값, 310/71 < π < 310/70을 얻을 수 있음을 역시 보여주었습니다.[59] 그는 그의 이름이 새겨진 나선형(spiral)을 역시 연구했고, 회전의 표면(surfaces of revolution) (포물면체, 타원면체, 쌍곡면체)의 부피(volume)에 대해 공식,[58] 그리고 매우 큰 숫자를 표현하는 것에 대해 지수화(exponentiation)의 독창적인 방법을 얻었습니다.[60] 그는 물리학 및 여러 가지 고급 기계적 장치에 대한 그의 기여에 대해 역시 알려지는 동안, 아르키메데스는 자신의 생각과 일반적인 수학적 원리의 산물에 훨씬 더 큰 가치를 스스로 부여했습니다.[61] 그는 구체의 표면 넓이와 부피를 찾은 것을 자신의 가장 큰 업적으로 여겼는데, 그가 이들을 증명함으로써 획득한 그것은 구체에 외접하는 실린더의 표면 넓이와 부피의 2/3입니다.[62]

Apollonius of Perga made significant advances in the study of conic sections.

페르게의 아폴로니우스(Apollonius of Perga) (기원전 c. 262–190)는 원뿔 단면(conic sections)의 연구에 상당한 발전을 만들었었고, 이중-입힌 원뿔을 자르는 평면의 각도를 변화시킴으로써 원뿔 단면의 세 가지 종류를 모두 얻을 수 있음을 보였습니다.[63] 그는 원뿔 단면에 대해 오늘날 사용하는 용어, 즉 포물선(parabola) ("옆에 놓기" 또는 "비교"), "타원" ("부족"), "쌍곡선" ("저편에 던지기")을 역시 만들었습니다.[64] 그의 업적 Conics는 고대에서 가장 잘 알려지고 보존된 수학적 연구 중 하나이고, 그것에서 그는 아이작 뉴턴과 같은 행성 운동을 연구하는 천문학자와 후기 수학자에게 매우 귀중한 입증되어지는 원뿔 단면과 관련된 많은 정리를 도출합니다.[65] 아폴로니우스 또는 다른 그리스 수학자는 기하학을 통합하기 위한 도약을 만들지는 않았지만, 곡선의 아폴로니우스의 취급법은 어떤 방법에서 현대의 취급법과 유사하고, 그의 업적 중 일부는 약 1800년 후 데카르트에 의해 해석적 기하학의 개발을 앞질러 한 것으로 보입니다.[66]

대충 같은 시기에, 키레네의 에라토스테네스 (기원전 c. 276–194)는 소수(prime numbers)를 찾는 것에 대해 에라토스테네스의 체(Sieve of Eratosthenes)를 고안했습니다.[67] 기원전 3세기는 일반적으로 그리스 수학의 "황금 시대"로 여겨지고, 순수 수학의 진보와 함께 그 때 이후 상대적으로 쇠퇴합니다.[68] 그럼에도 불구하고, 수세기에 걸쳐 따르는 중요한 진보는 응용 수학, 주로 천문학자의 요구를 해결하기 위해, 특히 주목할만한 삼각법에서 만들어졌습니다.[68] 니케아의 히파르쿠스(Hipparchus of Nicaea) (기원전 c. 190–120)는 처음으로 알려진 삼각법 테이블을 편집한 것에 대해 삼각법의 창시자로 여겨지고, 그에게 360 각도 원의 체계적인 사용을 역시 기인입니다.[69] 알렉산드리아의 헤론(Heron of Alexandria) (기원후 c. 10–70)은 부등변 삼각형의 넓이를 찾는 것에 대해 헤론의 공식(Heron's formula)과 제곱 근을 소유되는 음수의 가능성을 처음으로 인식한 것으로 인정됩니다.[70] 알렉산드리아의 메넬라우스(Menelaus of Alexandria) (기원후 c. 100)는 메넬라우스의 정리(Menelaus' theorem)를 통해 구형 삼각법(spherical trigonometry)을 개척했습니다.[71] 고대의 가장 완전하고 영향력 있는 삼각법의 업적은 프톨레마이오스(Ptolemy) (기원후 c. 90–168)의 Almagest로서, 이 역사상 획기적인 천문학 논문에서 그의 삼각법 테이블은 다음 천 년에 대해 천문학자들에 의해 사용되었을 것입니다.[72] 프톨레마이오스는 삼각법적 양을 도출하는 것에 대해 프톨레마이오스의 정리(Ptolemy's theorem)를 역시 만들었었고, 중세 기간까지 중국 외부에서 π의 가장 정확한 값, 3.1416을 얻었습니다.[73]

Title page of the 1621 edition of Diophantus' Arithmetica, translated into Latin by Claude Gaspard Bachet de Méziriac.

프톨레마이오스 이후 정체기의 다음의 기간, 기원후 250년과 350년 사이의 기간은 그리스 수학의 "은의 시대"("Silver Age")로 때때로 지칭됩니다.[74] 이 기간 동안, 디오판토스(Diophantus)는 대수학(algebra), "디오판토스 해석"으로 역시 알려진, 특히 불확정 해석(indeterminate analysis)에서 중요한 발전을 만들었습니다.[75] 디오판토스 방정식(Diophantine equations)과 디오판토스 근사(Diophantine approximations)의 연구는 오늘날까지 연구의 중요한 영역입니다. 그의 주요 업적은, 확정 및 불확정 방정식(indeterminate equation)에 대한 정확한 해를 다루는 150개의 대수 문제 모음, Arithmetica였습니다.[76] Arithmetica는 피에르 드 페르마(Pierre de Fermat)와 같은 후기 수학자들에게 중요한 영향을 미쳤는데, 페르마는 Arithmetica에서 읽었던 문제 (제곱을 두 개의 제곱으로 나누는 것)를 일반화하려고 시도한 후에 그의 유명한 마지막 정리(Last Theorem)에 이르렀습니다.[77] 디오판토스는 역시 표기법에서 상당한 발전을 만들었고, Arithmetica는 대수적 상징주의와 중략의 첫 번째 사례가 되었습니다.[76]

The Hagia Sophia was designed by mathematicians Anthemius of Tralles and Isidore of Miletus.

그리스의 마지막 위대한 수학자 중에는 알렉산드리아의 파푸스(Pappus of Alexandria) (기원후 4세기)가 있습니다. 그는 파푸스 구성(Pappus configuration)과 파푸스 그래프(Pappus graph)뿐 아니라, 그의 육각형 정리(hexagon theorem)와 도형-중심 정리(centroid theorem)에 대해 알려집니다. 그의 Collection은, 그것의 대부분이 현존하기 때문에, 그리스 수학에 대한 지식의 주요 원천입니다.[78] 파푸스는 그리스 수학에서 마지막 주요 혁신가로 여젹지고, 이후 작업은 주로 초기 업적에 대한 논평으로 구성됩니다.

역사에 기록된 최초의 여성 수학자는 알렉산드리아의 히파티아(Hypatia) (기원후 350–415)였습니다. 그녀는 대 도서관에서 사서로 그의 아버지 (알렉산드리아의 테온(Theon of Alexandria))의 자리를 계승하였고[citation needed] 응용 수학에 관한 많은 저서를 저술했습니다. 정치적 분쟁때문에, 알렉산드리아에서 기독교 공동체(Christian community)기독교 공동체는 그녀를 공개적으로 박탈해 왔었고 처형했습니다.[79] 그녀의 죽음은, 비록 업적은 프로크로스(Proclus), 심플리키우스(Simplicius) 및 유토시우스(Eutocius)와 같은 인물들과 함께 또 다른 수세기에 대해 아테네에서 계속되었을지라도, 알렉산드리아인 그리스 수학 시대의 끝으로 때때로 받아들여졌습니다.[80] 비록 프로크로스와 심플리키우스가 수학자보다는 철학자였을지라도, 초기 업적에 대한 그들 논평은 그리스 수학에 대한 가치있는 원천입니다. 기원후 529년에서 황제 유스티니아누스(Justinian)에 의한 네오-플라톤 아테네 아카데미(Academy of Athens)의 폐쇄는, 비록 그리스 전통이 트랄레스의 아테미우스(Anthemius of Tralles)와 밀레토스의 이시도르(Isidore of Miletus), 아퍄 소피아(Hagia Sophia)의 건축가와 같은 수학자들과 함께 비잔틴 제국(Byzantine empire)에서 꺾이지 않고 계속되었을지라도, 그리스 수학 시대의 끝을 표시하는 것으로 전통적으로 유지됩니다.[81] 그럼에도 불구하고, 비잔틴 수학은 주로 논평으로 구성되었으며, 혁신의 방식은 거의 없었고, 수학 혁신의 중심은 이 시기에서 다른 곳에서 발견되었을 것입니다.[82]

Roman

Further information: Roman abacus and Roman numerals
Equipment used by an ancient Roman land surveyor (gromatici), found at the site of Aquincum, modern Budapest, Hungary

비록 그리스계(ethnic Greek) 수학자들이 로마 공화국(Roman Republic)과 그 뒤의 로마 제국(Roman Empire)의 통치 아래에서 계속되었을지라도, 비교하여 주목할만한 라틴 출신(native Latin) 수학자는 없었습니다.[83][84] 그리스에서 수학을 연구했던 영향력 있는 로마의 정치가, 키케로(Cicero) (기원전 106–43)와 같은 고대 로마인(Ancient Romans)은 로마의 측량사(surveyor)와 계산자(calculators)는 그리스인에 의해 존중받았던 이론적 수학(theoretical mathematics)과 기하학보다 응용 수학(applied mathematics)에서 훨씬 더 관심이 있다고 믿었습니다.[85] 그것은 로마인이 그리스의 전례로부터 직접 또는, 지금 투스카니(Tuscany), 중부 이탈리아(central Italy)에서 중심인 에투루스칸 문명(Etruscan civilization)에 의해 사용된 에트루리아 숫자 시스템(Etruscan numerals)으로부터 그들의 숫자 시스템을 처으믕로 도출했는지 여부는 명확하지 않습니다.[86]

계산을 사용하여, 로마인은 재무부(treasury)에 대해 세금을 관리(managing taxes)하는 것과 마찬가지로 금융 사기(fraud)를 선동하는 것 그리고 탐지하는 것 둘 다에 숙달했었습니다.[87] 로마의 gromatici (즉, 토지 측량사)중 하나, 시쿨루스 플라쿠스(Siculus Flaccus)는, 로마 측량사가 할당된 토지 및 영토의 표면 넓이(surface area)를 측정하는 것에서 도움이 되는 Categories of Fields를 작성했습니다.[88] 무역 및 세금 관리 외에도, 로마인은 다리(bridges), 도로-건설(road-building), 및 군대 캠페인에 대해 준비와 같은 건축물(architecture)의 건설을 포함하여 공학(engineering)에서 문제를 해결하기 위해 수학을 정기적으로 적용했습니다.[89] 이전 그리스 디자인(Greek designs)에서 영감을 얻은, 로마 모자이크(Roman mosaic)와 같은 예술과 공예품(Arts and crafts)은 환상의 기하학적 패턴과 각 테세라(tessera) 타일, 8 밀리미터 정사각형을 측정하는 평균에 대한 오푸스 테셀레이텀(opus tessellatum) 조각, 그리고 4 밀리미터 정사각형의 평균 표면을 가지는 더 정밀한 오푸스 버메이큘레이텀(opus vermiculatum) 조각에 대해 정확한 측정을 요구하는 풍부하고 상세한 장면을 만들었습니다.[90][91]

로마 달력(Roman calendar)의 창조는 기초 수학을 역시 필요로 했습니다. 첫 번째 달력은 주장한 바에 의하면 로마 왕국(Roman Kingdom) 동안 기원전 8세기로 거슬러 올라가고 모든 각 다른 년마다 356일에 덧붙여 윤년(leap year)을 포함했습니다.[92] 대조적으로, 공화당 연대의 음력 달력(lunar calendar)은 2월 23일 이후 달력에 추가 달을 더함으로써 해결되는 불일치, 태양 년(solar year)보다 약 10-과-1/4 일 더 짧은 355일을 포함했습니다.[93] 이 달력은 율리우스 카이사르(Julius Caesar) (기원전 100–44)에 의해 조직되고 알산드리아의 소시젠스(Sosigenes of Alexandria)에 의해 365-일 주기에서 모든 각 4년마다 윤일(leap day)을 포함하도록 고안된 태양 달력(solar calendar:양력), 율리우스 달력(Julian calendar)에 의해 대체되었습니다.[94] 11분 14초의 오류를 포함하고 있는, 이 달력은, 사실상 국제 표준 달력으로 현대에서 사용되는 같은 태양 달력, 교황 그레고리오 13세(Pope Gregory XIII) (r. 1572–1585)에 의해 조직된 그레고리 달력(Gregorian calendar)에 의해 나중에 수정되었습니다.[95]

대략 같은 시간에서, 한 왕조의 중국인(Han Chinese) 그리고 로마인 둘 다는 여행한 거리(distance)를 측정하기 위해 바퀴 달린 주행거리계(odometer) 장치를 발명했으며, 로마 모델은 로마의 토목 기사이고 건축가 비트루비우스(Vitruvius) (기원전 c. 80–15)에 의해 최초로 묘사되었습니다.[96] 그 장치는 적어도 황제 콤모두스(Commodus) (기원후 177–192)의 통치 기간까지 사용되었지만, 그의 디자인은, 실험이 서유럽에서 15세기 동안 만들어질 때까지 손실되어 온 것으로 보입니다.[97] 아마도 안티키티라 메커니즘(Antikythera mechanism)에서 발견된 비슷한 기어-작업 및 기술(technology)에 의존하는, 비트루비우스의 주행거리계는 일 로마 마일(Roman mile) (대략 4590 피트/1400 미터)에서 400번 회전하는 지름에서 4 피트 (1.2 미터)를 측정하는 전차 바퀴의 특색을 이루었습니다. 각 회전과 함께, 핀-과-축 장치는, 여행한 일 마일을 표현하는 각 자갈을 상자에 떨어뜨리는 책임을 지는 두 번째 기어를 돌리는 400-이빨 톱니 바퀴(cogwheel)를 서로 맞물립니다.[98]

Chinese

Main article: Chinese mathematics
Further information: Book on Numbers and Computation
The Tsinghua Bamboo Slips, containing the world's earliest decimal multiplication table, dated 305 BC during the Warring States period

초기 중국 수학의 분석은, 전적으로 독립적인 개발을 가정하는 것으로 학자들을 이끄는, 전 세계의 다른 지역과 비교하여 독특한 발전을 논증해 왔습니다.[99] 중국에서 가장 오래된 현존하는 수학 텍스트는, 비록 전국 시대 기간 동안 기원전 약 300년의 날짜가 합리적으로 보일지라도, 기원전 1200년과 기원전 100년 사이에 다양하게 기원되는, Zhoubi Suanjing입니다.[100] 어쨌든, (비록 고대 바빌로니아 사람이 육십의 밑수를 가진 곱셈 테이블을 가졌을지라도) 최초의 알려진|십진수(decimal)]] 곱셈 테이블(multiplication table)을 포함하는, 칭화 뱀부 슬립(Tsinghua Bamboo Slips)은 기원전 약 305년경 기원되고 아마도 중국의 가장 오래 현존하는 수학적 텍스트일 것입니다.[41]

Counting rod numerals

특히 주목할 점은 중국 수학에서 십진수 위치적 표기법 시스템, 즉 구별되는 암호가 1에서 10 사이의 숫자에 대해 사용되고, 십의 거듭제곱에 대해 추가적인 암호가 사용되는, 소위 "막대 숫자(rod numbers)"의 사용입니다.[101] 따라서 숫자 123은 "1"에 대한 기호, 뒤이어 "100"에 대해 기호, 그런 다음 "2"에 대한 기호 뒤이어 "10"에 대한 기호, 뒤이어 "3"에 대한 기호를 사용하여 쓰일 것입니다. 이것은 당시 세계에서 가장 진보된 숫자 시스템였으며, 공통적인 시대 이전의 수세기와 인도 숫자 시스템의 개발 충분히 이전에 분명히 사용되었습니다.[102] 막대 숫자(Rod numerals)는 원하는 만큼 큰 숫자의 표현을 허용했었고 사안 판(suan pan), 또는 중국 주판에서 계산을 수행할 수 있도록 허용했습니다. 사안 판의 발명의 날짜는 확실하지 않지만, 가장 오래된 서면 언급은 허이 요우(Xu Yue)의 Supplementary Notes on the Art of Figures에서, 기원후 190년에 날짜를 기입합니다.

중국에서 기하학(geometry)에 대한 가장 오래된 현존하는 업적은, 묵자(Mozi) (기원전 470–390)의 추종자들에 의해 편집되는, 기원전 c. 300년 철학적인 모히스트(Mohist)의 캐논에서 비롯된 것입니다. 모 징(Mo Jing)은 물리적 과학과 관련된 많은 분야의 다양한 관점을 설명하고, 마찬가지로 기하학적 정리의 몇 개를 제공했습니다.[103] 그것은 원주(circumference), 지름(diameter), 반지름(radius), 및 부피(volume)의 개념을 역시 정의했습니다.[104]

The Nine Chapters on the Mathematical Art, one of the earliest surviving mathematical texts from China (2nd century AD).

기원전 212년에서, 황제 진시황(Qin Shi Huang)은 공식적으로 승인된 것 이외에는 진 제국(Qin Empire)의 모든 책을 불태워야 한다고 명령했습니다. 이 법령은 보편적으로 순종되지 않았지만, 이 명령의 결과로 이 날짜 이전의 고대 중국 수학에 대해 거의 알려져 있지 않습니다. 기원전 212년의 책 태움(book burning:분서갱유) 후에, 한 왕조(Han dynasty) (기원전 202–기원후 220)는, 아마도 지금은 잃어버린 작품을 확장하는, 수학 작품을 만들었습니다. 이들의 가장 중요한 것은 The Nine Chapters on the Mathematical Art로써, 기원후 179에 의해 전체 제목이 등장했지만, 앞서 다른 제목 아래에 부분적으로 존재했습니다. 그것은 농업, 사업, 중국 퍼고다(Chinese pagoda) 탑에 대해 높이 범위와 넓이 비율을 묘사하는 것에 대한 기하학의 적용, 공학, 측량(surveying)을 포함하는 246 단어 문제로 구성되고, 직각 삼각형에 관한 자료를 포함합니다.[100] 그것은 피타고라스의 정리(Pythagorean theorem)에 대한 수학적 증명[105]과 가우스 소거법(Gaussian elimination)에 대한 수학적 공식을 만들었습니다.[106] 이 논문은, 중국 수학자들이 류 신(Liu Xin) (기원후 d. 23)이 3.1457의 계산을 제공할 때까지 3으로 원래 근사하고, 이후 장 형(Zhang Heng) (78–139)이 pi를 3.1724,[107] 마찬가지로 10의 제곱근(square root)을 취함으로써 3.162로 근사하는,[108][109] π의 값을 역시 제공합니다.[100] 류 휘(Liu Hui)는 서기 3세기에 Nine Chapters에 주석을 달았고 소수점 5 자리 (즉, 3.14159)로 정확한 π 값을 기록했습니다.[110][111] 비록 이론적 통찰력보다 계산적 내구력의 문제가 더 많았을지라도, 기원후 5세기 조충지(Zu Chongzhi)는 π의 값을 소수점 7자리 (즉, 3.141592)로 계산했으며, 이것은 거의 다음 1000년 동안 가장 정확한 π의 값을 유지했습니다.[110][112] 그는 나중에 구체(sphere)의 부피를 찾기 위한 나중에 카발리에리의 원리(Cavalieri's principle)라고 불리는 방법을 역시 확립했습니다.[113]

중국 수학의 최고봉은 송 왕조(Song dynasty) (960–1279) 후반기 동안 13세기에서 중국 대수학의 발전과 함께 일어났습니다. 그 시기로부터 가장 중요한 텍스트는 한 경(Zhu Shijie) (1249–1314)에 의한 Precious Mirror of the Four Elements이며, 호너의 방법(Horner's method)과 비슷한 방법을 사용하여 동시에 일어나는 높은 차수 대수적 방정식의 해를 다룹니다.[110] 귀중한 거울(Precious Mirror)은, 비록 둘 다 1100년 전에 중국 작품에 나타났을지라도, 8차 거듭제곱에 걸쳐 이항 전개의 계수와 함께 파스칼의 삼각형(Pascal's triangle)의 다이어그램을 역시 포함합니다.[114] 중국은, 고대 시대에 묘사되고 양 휘(Yang Hui) (기원후 1238–1298)에 의해 완성된, 마법의 사각형(magic square:마방진)과 마법의 원(magic circles)으로 알려진 복잡한 조합론적 다이어그램의 사용을 역시 만들었습니다.[114]

심지어 유럽 수학이 르네상스(Renaissance) 동안 번성하기 시작한 후에도, 유럽과 중국 수학은, 13세기 이후부터 쇠퇴에서 중요한 중국 수학 결과와 함께, 별개의 전통이었습니다. 마테오 리치(Matteo Ricci)와 같은 예수회(Jesuit) 선교사들은, 비록 이 시점에서 훨씬 더 많은 수학적 아이디어가 중국에서 나오는 것보다 들어갔을지라도, 16세기에서 18세기까지 두 문화 사이에서 수학적 아이디어를 이리저리 나랐습니다.[114]

일본 수학(Japanese mathematics), 한국 수학(Korean mathematics), 및 베트남 수학(Vietnamese mathematics)은 중국 수학에서 유래하는 것 그리고 유교(Confucian)-기반 동아시아 문화권(East Asian cultural sphere)에 속하는 것으로 전통적으로 보입니다.[115] 한국과 일본의 수학은 중국의 송 왕조 동안 생성된 대수적 작품에 의해 크게 영향을 받았으며, 반면에 베트남 수학은 중국의 명 왕조(Ming dynasty) (1368–1644)의 유명한 작품에 크게 빚졌습니다.[116] 예를 들어, 비록 베트남의 수학 논문이 중국어(Chinese) 또는 토착 베트남어 쯔 놈(Chữ Nôm) 스크립트로 작성되었을지라도, 그들의 모두는 문제를 해결하는 것에 대해 알고리듬(algorithm), 뒤이은 수치적 대답과 함께 문제의 모음을 소개하는 것의 중국 형식을 따랐습니다.[117] 베트남과 한국에서 수학은 주로 수학자와 천문학자의 전문적인 궁정 관료와 관련이 있으며, 반면에 일본에서 그것은 사립 학교(private school)의 영역에서 더 널리 퍼졌습니다.[118]

Indian

Main article: Indian mathematics
See also: History of the Hindu–Arabic numeral system
The numerals used in the Bakhshali manuscript, dated between the 2nd century BCE and the 2nd century CE.
Numerals evolution in India
Indian numerals in stone and copper inscriptions[119]
Brahmi numerals
Ancient Brahmi numerals in a part of India

인도 아대륙에 대한 최초의 문명은 인더스 강(Indus river) 유역에서 번영했던 인더스 골짜기 문명(Indus Valley Civilization) (성숙한 단계: 기원전 2600–1900)입니다. 그들의 도시는 기하학적 규칙성과 함께 배치되었지만, 알려진 수학적 문서는 이 문명으로부터 현존하는 것이 없습니다.[120]

인도로부터 가장 오래된 현존하는 수학 기록은 (기원전 8세기와 기원후 2세기 사이에 여러 가지로 기록되는), 정사각형, 직사각형, 평행사변형, 및 다른 것과 같은 다양한 모양의 제단을 건설하는 간단한 규칙을 제공하는 종교적인 텍스트에 대한 부록,[121] 술바 수트라스(Sulba Sutras)입니다.[122] 이집트와 마찬가지로, 성전 기능에 대한 선입관은 종교적인 의식에서 수학의 기원을 가리킵니다.[122] 술바 수트라스는 주어진 사각형과 거의 같은 넓이를 갖는 원을 구성하는 방법을 제공하는데, 이것은 π 값의 몇 가지 다른 근삿값을 의미합니다.[123][124][a] 게다가, 그들은 여러 집진 자리의 2의 제곱근(square root)을 계산하고, 피타고라스의 세-쌍을 나열하고, 피타고라스의 정리(Pythagorean theorem)의 명제를 제공합니다.[124] 이들 결과의 모두는, 메소포타미아의 영향을 나타내는, 바빌로니아 수학에 건네집니다.[122] 술바 수트라스가 나중에 인도 수학자들에게 어느 정도 영향을 미치는지는 알려져 있지 않습니다. 중국에서 처럼, 인도 수학에서 연속성의 부족이 있습니다; 중대한 진보는 비-활동의 긴 기간에 의해 구분됩니다.[122]

파니니(Pāṇini) (기원전 c. 5세기)는 산스크리트 문법(Sanskrit grammar)에 대해 규칙을 공식화했습니다.[125] 그의 표기법은 현대의 수학 표기법과 유사했고, 메타-규칙(metarules), 변환(transformations), 재귀(recursion)를 사용했습니다.[126] 운율(prosody)의 그의 논문에서 핀갈라(Pingala) (대략 기원전 3–1세기)는 이진 숫자 시스템(binary numeral system)에 해당하는 장치를 사용합니다.[127][128] 박자(meters)의 조합론(combinatorics)에 대한 그의 논의는 이항 정리(binomial theorem)의 기본 버전에 해당합니다. 핀갈라의 작품은 (mātrāmeru라고 불리는) 피보나치 숫자(Fibonacci number)의 기본 아이디어를 역시 포함합니다.[129]

술바 수트라스 이후의 인도로부터 다음 중요한 수학적 문서는 강한 헬레니즘 영향을 보여주는 기원후 4세기와 5세기 (굽타 기간(Gupta period))로부터 천문학 논문, 시타한타스(Siddhantas)입니다.[130] 그들은 프톨레마이오스 삼각법의 경우였던 것처럼, 전체 현이라기 보다는, 현대의 삼각법에서 경우인 것처럼, 반-현에 기초한 삼각법적 관계의 첫 번째 예제를 포함하는 것에서 그들은 중요합니다.[131] 일련의 번역 오류를 통해, 단어 "사인(sine)"과 "코사인(cosine)"은 산스크리트어 "지아(jiya)"와 "코지아(kojiya)"에서 파생됩니다.[131]

Explanation of the sine rule in Yuktibhāṣā

기원후 약 500년, 아리아바타(Aryabhata)는, 비록 논리 또는 연연적 방법론에 대해 전혀 느낌이 없을지라도, 천문학 및 수학적 측정에서 사용된 계산의 규칙을 보완하려는 의도에서, 운문으로 쓰인, 아주 작은 권수의, 아리아바티아(Aryabhatiya)를 썼습니다.[132] 비록 엔터디의 약 절반이 틀렸을지라도, 아리아바티아에서 십진 자리-값 시스템이 처음으로 나타납니다. 수세기 후에, 이슬람 수학자(Muslim mathematician) 아부 라힘 비루니(Abu Rayhan Biruni)는 아리아바티아를 "공통적인 자갈과 값 비싼 크리스탈의 혼합"으로 묘사했습니다.[133]

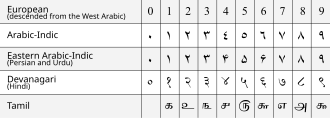
7세기에서, 브라마굽타(Brahmagupta)는 브라마굽타 정리(Brahmagupta theorem)와 브라마굽타의 항등식(Brahmagupta's identity), 및 브라마굽타의 공식(Brahmagupta's formula)을 식별하고, 처음으로, 브라마-스푸타-싯단타(Brahma-sphuta-siddhanta)에서, 그는 자리-표시자와 십진 자릿수(decimal digit) 둘 다에서 영(zero)을 사용을 명쾌하게 설명했고, 힌두–아라비아 숫자 시스템(Hindu–Arabic numeral system)을 설명했습니다.[134] 그것은 수학에 대한 이 인도 텍스트의 번역본으로부터 였었는데 (c. 770) 이슬람 수학자들은 이 숫자 시스템에 도입되었으며, 그들은 이것을 아라비아 숫자 시스템(Arabic numerals)으로 개조했습니다. 이슬람 학자들은 12세기에서 이 숫자 시스템에 대한 지식을 유럽에 전달했고, 그것은 이제 전 세계를 통해 모든 구 숫자 시스템을 대체해 왔습니다. 다양한 기호 집합이 힌두–아라비아 숫자 시스템에서 숫자를 나타내기 위해 사용되며, 그것의 모두는 브라흐미 숫자 시스템(Brahmi numeral)에서 진화했습니다. 인도의 대략 12개 주요 스크립트의 각각은 그 자체의 고유한 숫자 시스템 글리프를 가집니다. 10세기에서, 핀갈라(Pingala)의 작품에 대한 하라유다(Halayudha)의 주석은 피보나치 수열(Fibonacci sequence)과 파스칼의 삼각형(Pascal's triangle)의 연구를 포함하고, 행렬(matrix)의 형성을 기술합니다.[citation needed]

12세기에서, 바스카라 II(Bhāskara II)[135]는 인도 남부에 살았었고 그 때에 알려진 모든 수학의 가지에 대해 광범위하게 글을 썼습니다. 그의 작품은 무한소, 도함수, 평균값 정리(the mean value theorem) 및 사인 함수의 미분과 동등 또는 거의 대략적으로 동등한 수학적 대상을 포함합니다. 그가 미적분학의 발명을 어느 정도까지 예상했을 것은 수학의 역사가들 사이에서 논란의 대상입니다.[136]

14세기에서, 이른바 수학의 케랄라 학교(Kerala School of Mathematics)의 설립자, 산가마그라마의 마드하바(Madhava of Sangamagrama)는 마드하바–라이프니츠 급수(Madhava–Leibniz series)를 발견했었고, 21항을 사용하여, π의 값을 3.14159265359로 계산했습니다. 마드하바는 아크탄젠트를 구하기 위해 마하드바-그레고리 급수(the Madhava-Gregory series), 사인 및 코사인을 결정하기 위해 마하드바-뉴턴 거듭제곱 급수 그리고 사인 및 코사인 함수에 대해 테일러 근사(the Taylor approximation)를 발견했습니다.[137] 16세기에서, 지드데바(Jyesthadeva)는 Yukti-bhāṣā에서 케랄라 학교의 발달과 정리의 많은 것을 통합했습니다.[138] 어쨌든, 케랄라 학교는 미분(differentiation)과 적분(integration)에 대한 시스템적 이론을 공식화하지 않았고, 그들의 결과를 케랄라 밖으로 전달된 것에 대해 어떤 직접적인 증거도 없습니다.[139][140][141][142]

Islamic empire

Main article: Mathematics in medieval Islam
See also: History of the Hindu–Arabic numeral system
Page from The Compendious Book on Calculation by Completion and Balancing by Muhammad ibn Mūsā al-Khwārizmī (c. AD 820)

8세기에서, 페르시아(Persia), 중동(Middle East), 중앙 아시아(Central Asia), 북 아프리카(North Africa), 이베리아(Iberia), 및 인도(India) 일부 지역에 설립된 이슬람 제국(Islamic Empire)은 수학에 상당한 공헌을 만들었습니다. 비록 수학에 관한 대부분의 이슬람 텍스트는 아랍어(Arabic)로 작성되었지만, 그들의 대부분은 아랍인(Arab)에 의해 쓰이지 않았는데, 왜냐하면 헬레니즘 시대에서 그리스인의 지위와 상당히 비슷하기 때문에, 아랍어는 당시에 이슬람 세계 전역에서 비-아랍인 학자들의 서면 언어로 사용되었습니다. 페르시아인(Persians)은 아랍인과 함께 수학의 세계에 기여했습니다.

9세기에서, 페르시아(Persian) 수학자 무하마드 이븐 무사 알-콰리즈미(Muḥammad ibn Mūsā al-Khwārizmī)는 힌두–아라비아 숫자와 방정식을 푸는 방법에 관한 몇 가지 중요한 책을 썼습니다. 알-킨디(Al-Kindi)의 작품과 함께, 825년경에 쓰인, 그의 책 On the Calculation with Hindu Numerals는 인도 수학(Indian mathematics)과 인도 숫자 시스템(Indian numerals)을 서구에 널리 알리는 데 수단이 되었습니다. 단어 알고리듬(algorithm)은 그의 이름의 라틴어화, Algoritmi로부터 유래되고, 단어 대수(algebra)는 그의 작품중 하나, Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala (The Compendious Book on Calculation by Completion and Balancing)의 제목으로부터 유래됩니다. 그는 양의 근을 가진 이차 방정식의 대수적 해에 대해 철저한 설명을 제공했고,[143] 그는 초등 형태(elementary form)에서 그 자체를 위해서 처음으로 대수학을 가르쳤습니다.[144] 그는 "축소(reduction)"와 "균형"의 가본적인 방법을 논의했는데, 이것은 뺄셈된 항을 방정식의 다른 변에 대해 전치, 즉, 방정식의 반대쪽 변에 대한 동류항의 상쇄를 언급했습니다. 이것은 알-꽈리즈미가 원래 al-jabr으로 묘사했던 연산입니다.[145] 그의 대수는 또한 더 이상 "해결해야 할 일련의 문제들과 관련이 없지만, 그 시간부터 명백하게 연구의 진정한 대상을 구성하는, 그 조합들이 방정식에 대해 가능한 모든 프로토타입을 반드시 제공해야 하는 원시적 항으로 시작하는 전시(exposition)였습니다." 그는 역시 그 자체로 방정식을 연구했고 "문제를 해결하는 과정에서 단순히 나타나지는 않지만, 문제의 무한 클래스를 정의하기 위해 특별히 불리는 한 일반적인 방식으로 연구했습니다."[146]

이집트에서, 아부 카밀(Abu Kamil)은 대수를, 이차 방정식에 대한 해와 계수로 제곱근과 네제곱근을 받아들이는, 무리수(irrational numbers)의 집합으로 확장했습니다. 그는 세 개의 미지수를 갖는 세 개의 비-선형 연립 방정식을 풀기 위해 사용되는 기술을 역시 개발했습니다. 그의 작품 중 하나의 독특한 특징은, 그가 2676개의 해를 찾았던 문제를 포함하여, 그의 문제의 일부에 대한 모든 가능한 해를 찾으려고 시도했습니다.[147] 그의 작품은 대수학의 발전에 대해 중요한 기초를 형성했고 알-카라지(Al-Karaji)와 피보나치와 같은 후기 수학자들에게 영향을 주었습니다.

대수학에서 뒤따른 발전은 알-카라지(Al-Karaji)에 의해 그의 논문 al-Fakhri에서 만들어졌는데, 여기서 그는 미지수 양의 정수 거듭제곱와 정수 근을 통합하기 위해 방법론을 확장했습니다. 수학적 귀납법(mathematical induction)에 의한 증명(proof)에 가까운 어떤 것은 기원후 약 1000년경에 알-카라지에 의해 쓰인 책에서 나타나고, 그는 이항 정리(binomial theorem), 파스칼의 삼각형(Pascal's triangle), 적분(integral) 큐브(cubes)의 합을 증명하기 위해 그것을 사용했습니다.[148] 수학의 역사학자(historian), 프란즈 웨프커는 "대수적 미적분학(calculus)의 이론(theory)을 도입한 첫 번째 사람"으로 알-카라지를 칭찬했습니다.[149] 또한 10세기에서, 아불 와파(Abul Wafa)는 디오판토스(Diophantus)의 연구를 아랍어로 번역했습니다. 이븐 알-하이삼(Ibn al-Haytham)은 임의의 정수 거듭제곱의 합에 대해 일반 공식을 결정하기 위해 손쉽게 일반화할 수 있는 방법을 사용하여, 네-번째 거듭제곱의 합에 대해 공식을 유도한 최초의 수학자였습니다. 그는 포물면체(paraboloid)의 부피를 찾기 위해 적분을 수행했고, 다항식(polynomial)의 적분에 대한 그의 결과를 사차(foruth degree)까지 일반화할 수 있었습니다. 그는 따라서 다항식의 적분(integral)에 대해 일반적인 공식을 찾는데 거의 다가 갔지만, 그는 사차보다 큰 임의의 다항식에 대해서는 관심이 없었습니다.[150]

11세기 후반에서, 오마르 하이얌(Omar Khayyam)은 유클리드의 원론(Euclid's Elements)의 결점, 특히 평행 공준(parallel postulate)으로 인식한 것에 관한 책, Discussions of the Difficulties in Euclid을 썼습니다. 그는 삼차 방정식(cubic equation)에 대한 일반적인 기하학적 해를 처음으로 역시 발견했습니다. 그는 달력 개정(calendar reform)에 역시 많은 영향을 주었습니다.[151]

13 세기에서, 나시르 알-딘 알-투시(Nasir al-din al-Tusi) (Nasireddin)는 구형 삼각법(spherical trigonometry)에서 발전을 만들었습니다. 그는 유클리드(Euclid)의 평행 공준(parallel postulate)에 대한 영향력있는 작품을 역시 썼습니다. 15세기에서, 잠시드 알-캐시(Ghiyath al-Kashi)는 π의 값을 소수점 16자리까지 계산했습니다. 캐시는 n-번째 근을 계산하는 알고리듬을 역시 가지고 있었으며, 이것은 수세기 후 루피니(Ruffini)와 호너(Horner)에 의해 제공된 방법의 특별한 경우였습니다.

이 기간 동안 이슬람 수학자의 다른 업적은 아라비아 숫자 시스템(Arabic numerals)에 소수점(decimal point) 표기법의 추가, 사인 외에 모든 현대적인 삼각 함수(trigonometric function)의 발견, 암호해독(cryptanalysis) 및 빈도 분석(frequency analysis)의 알-킨디(Al-Kindi)의 도입, 이븐 알-하이삼(Ibn al-Haytham)에 의한 해석 기하학(analytic geometry)의 개발, 오마르 하이얌(Omar Khayyam)에 의한 대수 기하학(algebraic geometry)의 시작과 알-칼라스사디(al-Qalasādī)에 의한 대수 표기법(algebraic notation)의 개발을 포함합니다.[152]

15세기로부터 오스만 제국(Ottoman Empire)과 사파비 제국(Safavid Empire)의 시기 동안, 이슬람 수학의 발전은 정체되었습니다.

Maya

The Maya numerals for numbers 1 through 19, written in the Maya script

콜럼버스 아메리카-이전(Pre-Columbian Americas)에서, 기원후 첫 번째 천년 동안 멕시코(Mexico)와 중앙 아메리카(Central America)에서 번성했던 마야 문명(Maya civilization)은 지리적 고립으로 인해 기존의 유럽, 이집트 및 아시아 수학과는 완전히 독립적인 수학의 독특한 전통을 발전시켰습니다.[153] 마야 숫자 시스템(Maya numerals)은 대부분의 현대 문화에서 사용되는 십진(decimal) 시스템의 기초를 형성하는 십의 진수 대신, 밑수 20(vigesimal) 시스템, 20의 진수(base)를 사용했습니다.[153] 마야는 마야 달력(Maya calendar)을 생성하고 마찬가지로 그들의 토착 마야 천문학(Maya astronomy)에서 천문적 현상을 예측하기 위해 수학을 사용했습니다.[153] 영(zero)의 개념은 많은 현대 문화의 수학에서 추론되어야 했지만, 마야는 그것에 대해 표준 기호를 개발했습니다.[153]

Medieval European

Further information: Category:Medieval European mathematics, List of medieval European scientists, and European science in the Middle Ages
See also: Latin translations of the 12th century

중세 유럽의 수학에 대한 관심은 현대 수학자들의 관심사와는 상당히 다른 관심사에 의해 이끌어졌습니다. 하나의 추진 요소는 수학이 자연의 창조된 질서를 이해하는데 핵심을 제공했다는 믿음이었는데, 플라톤(Plato)의 Timaeus와 하나님은 모든 것을 측정, 그리고 숫자, 그리고 무게를 지시하셨습니다라는 성경의 (지혜서(Book of Wisdom)에 있는) 악절에 의해 자주 정당화되었습니다.[154]

보에티우스(Boethius)는 산술, 기하학, 천문학, 및 음악의 연구를 설명하기 위해 용어 quadrivium를 만들 때 6세기 커리큘럼에서 수학에 대해 자리를 제공했습니다. 그는 니코마코스(Nicomachus)의 Introduction to Arithmetic의 그리스어로부터 무료 번역, De institutione arithmetica; 그리스 원천으로부터 역시 파생된, De institutione musica; 유클리드(Euclid)의 원론(Elements)으로부터 일련의 발췌들을 썼습니다. 그의 작품은 실용적이라기보다는 이론적이었고, 그리스어와 아랍어 수학 작품을 복원할 때까지 수학 공부의 기초였습니다.[155][156]

12세기에서, 유럽의 학자들은 체스터의 로버트(Robert of Chester)에 의해 라틴어로 번역된, 알-콰리즈미(al-Khwārizmī)의 The Compendious Book on Calculation by Completion and Balancing, 배스의 아델라드(Adelard of Bath), 카린티아의 허먼(Herman of Carinthia), 및 크레모나의 제라드(Gerard of Cremona)에 의해 다양한 버전으로 번역된, 유클리드의 원론(Euclid's Elements)에 대한 완전한 텍스트를 포함하여, 과학적 아랍어 텍스트를 찾는 스페인과 시실리로 여행을 갔습니다.[157][158] 이것들과 다른 새로운 원천은 수학의 갱신을 촉발시켰습니다.

지금 피보나치(Fibonacci)로 알려진, 피사의 레오나르도는 그의 상인 아버지와 함께 지금의 알제리(Algeria), 베자이아(Béjaïa)에 대한 여행에서 힌두–아라비아 숫자 시스템(Hindu–Arabic numerals)에 대해 우연찮게 배우게 되었습니다. (유럽은 여전히 로마 숫자 시스템(Roman numerals)을 사용하고 있었습니다.) 거기에서, 그는 힌두–아라비아 숫자 시스템의 위치적 표기법(positional notation)으로 인해 훨씬 효율적이고 상업을 굉장히 용이하게 하는 산술(arithmetic) 시스템 (특히 알고리듬)을 관찰했습니다. 레오나르도는 1202년에 유럽에 대한 기술을 소개하고 그것을 대중화하는 것의 긴 기간을 시작하는 Liber Abaci (1254년에 업데이트 됨)을 썼습니다. 그 책은 텍스트 내에 눈에 띄지 않는 예제로서 사용된 (수백년 전에 인도의 수학자들에게 알려진) 피보나치 수열(Fibonacci sequence)로 지금 알려진 것을 유럽에 역시 가져왔습니다.

14세기는 문제의 광범위한 영역을 조사하기 위해 새로운 수학 개념의 개발을 보였습니다.[159] 한 가지 중요한 공헌은 지역 운동의 수학 발전이었습니다.

토머스 브래드워딘(Thomas Bradwardine)은 저항 (R)에 대한 힘 (F)의 비율이 기하학적 비율로 증가할 때 속도 (V)는 산술 비율로 증가한다고 제안했습니다. 브래드워딘은 일련의 구체적인 예제에 의해 이것을 표현했지만, 비록 로그가 아직 잉태되지는 않았을지라도, 우리는 다음과 같이 작성함으로써, 시대는 맞지 않지만, 그의 결론을 표현할 수 있습니다: V = log (F/R).[160] 브래드워딘의 해석학은 다른 물리적 문제에 대한 복합적 처치의 본성을 정량화하기 위해 빌라노바의 아르날드(Arnald of Villanova)와 알-킨디(al-Kindi)에 의해 사용된 수학적 기법을 전달하는 사례입니다.[161]

Nicole Oresme (1323–1382), shown in this contemporary illuminated manuscript with an armillary sphere in the foreground, was the first to offer a mathematical proof for the divergence of the harmonic series.[162]

14세기에 미분학(differential calculus)과 극한(limits)의 개념이 결여되어 있는, 옥스포드 계산기(Oxford Calculators) 중 하나, 윌리엄 헤이테스버리(William Heytesbury)는, "만약 ... 그것이 주어진 순간에 움직이는 것과 같은 속도로 균일하게 움직였다면, [몸체]에 의해 묘사되어질 수 있는 경로에 의해" 순간 속도를 측정할 것을 제안했습니다.[163]

헤이테스버리와 다른 것들은 (오늘날 적분(integration)에 의해 해결되는) 균일하게 가속되는 동작을 겪고있는 몸체에 의해 도달되는 거리를 수학적으로 결정했습니다. "[속도의] 증분으로 균일하게 획득 또는 잃게 되는 움직이는 몸체는, 만약 그것이 [속도의] 평균 정도와 함께 같은 시간을 통해 연속적으로 움직였다면, 어떤 주어진 시간에서 그것이 지나갈 것과 완전하게 같은 [거리를] 지나갈 것"이라고 말했습니다.[164]

파리 대학(University of Paris)의 니콜 오렘(Nicole Oresme)와 이탈리아 지오바니 디 카살리(Giovanni di Casali)는, 일정한 가속도를 묘사하는 선 아래의 넓이가 전체 주행 거리를 나타내는 것이라고 주장하는 이 관계의 그래픽적 논증을 독립적으로 제공했습니다.[165] 나중에 유클리드의 원론에 대한 수학적 논평에서, 오렘은, 몸체가 홀수만큼 증가하는 임의의 질의 증분을 시간의 연속적인 증분에서 획득될 수 있다는 것을 논증한 것에서 보다 자세한 일반적인 해석을 만들었습니다. 유클리드가 홀수의 합이 제곱수임을 논증했기 때문에, 몸체에 의해 획득된 전체 질은 시간의 제곱으로 증가합니다.[166]

Renaissance

Further information: Mathematics and art

르네상스(Renaissance) 동안, 수학과 회계(accounting)의 발전이 서로 얽히게 되있습니다.[167] 대수학과 회계 사이에는 직접적인 관계가 없었지만, 과목 및 책의 가르침은 종종 (플랜더스(Flanders)와 독일(Germany)에서) 계산 학교 또는 (이탈리아에서 abbaco로 알려진) 주판 학교(abacus school)에 보내진 상인의 자녀를 대상으로 하며, 무역 및 상거래에 유용한 기술을 배웠습니다. 부기(bookkeeping) 연산을 수행하는 것에서 대수학이 필요하지 않을 수도 있지만, 복잡한 물물 교환 연산 또는 복리(compound interest) 계산에 대해, 산술의 기본 지식이 필수적이고 대수학의 지식이 매우 유용했습니다.

피에로 델라 프란체스카(Piero della Francesca) (c. 1415–1492)는, De Prospectiva Pingendi (그림에 대한 관점에서), Trattato d’Abaco (주판 논문), 및 De corporibus regularibus (정다면체)를 포함하여, 강체 기하학(solid geometry) 및 선형 관점(linear perspective)에 대한 책을 썼습니다.[168][169][170]

Portrait of Luca Pacioli, a painting traditionally attributed to Jacopo de' Barbari, 1495, (Museo di Capodimonte).

루카 파치올리(Luca Pacioli)의 Summa de Arithmetica, Geometria, Proportioni et Proportionalità (이탈리아어: "산술(arithmetic), 기하(geometry), 비율(ratio) and 비례(Proportion)의 검토")는 1494년 베네치아(Venice)에서 처음 인쇄되고 출판되었습니다. 이 책은 27 페이지의 부기(bookkeeping)에 대한 논문(treatise), "Particularis de Computis et Scripturis" (이탈리아어: "계산 및 기록의 세부 사항")을 포함합니다. 그것은 주로 책을 참고 문헌, 그것에 포함된 수학적 퍼즐(mathematical puzzles)에서 기쁨의 원천으로 사용한 상인들에게, 그리고 그들의 자녀 교육을 돕기 위해 주로 쓰였고 판매되었습니다.[171] Summa Arithmetica에서, 파치올리는 이탈리아 르네상스 수학에서 표준 표기법이 된 기호, 인쇄된 책에서 처음으로 더하기 및 빼기(plus and minus)에 대해 기호를 도입했습니다. Summa Arithmetica은 이탈리아에서 대수(algebra)를 포함하여 인쇄된 최초의 알려진 책이었습니다. 파치올리는 그가 표절한 피에로 델라 프란체스카(Piero Della Francesca)로부터 자신의 아이디어 중 많은 것을 얻었습니다.

이탈리아에서, 16세기 상반기 동안, 시피오네 델 페로(Scipione del Ferro)와 니콜로 폰타나 타르탈리아(Niccolò Fontana Tartaglia)가 삼차 방정식(cubic equation)에 대한 해를 발견했습니다. 제롤라모 카르다노(Gerolamo Cardano)는 그의 학생 로도비코 페라리(Lodovico Ferrari)에 의해 발견된, 사차 방정식(quartic equation)에 대한 해와 함께, 그의 1545년 책 Ars Magna에서 그것을 발표했습니다. 1572년에서, 라파엘 봄벨리(Rafael Bombelli)는 삼차 방정식을 푸는 카르다노의 공식에서 나타날 수 있는 허수 양(imaginary quantities)을 다루는 방법을 보여주는, 그의 L'Algebra를 출판했습니다.

시몬 스테빈(Simon Stevin)의 책 De Thiende ('the art of tenths')는 1585년 네덜란드에서 최초로 출판되었으며, 실수 시스템(real number system)에 대한 이후 모든 작품에 영향을 미치는, 십진 표기법(decimal notation)의 최초의 체계적인 처리를 포함합니다.

항해의 수요와 큰 넓이의 정확한 지도에 대해 증가하는 필요에 의해 박차를 가한, 삼각법(trigonometry)은 수학의 주요 가지로 성장했습니다. 바르톨로메오 피티쿠스(Bartholomaeus Pitiscus)는 1595년에 Trigonometria를 출판하여, 그 단어를 처음으로 사용했습니다. 레기오몬타누스(Regiomontanus)의 사인과 코사인 테이블은 1533년에 출판되었습니다.[172]

르네상스 동안 자연의 세계를 현실적으로 나타내기 위한 예술가의 열망은, 그리스인의 철학과 재발견과 함께, 예술가들로 하여금 수학을 공부하게 했습니다. 그들은 또한 당시 공학자이자 건축가였었고, 그래서 어떤 경우에도 수학의 필요성을 느꼈습니다. 원근법에서 회화의 예술, 및 그것과 관련되는 기하학에서 발달은, 강렬하게 연구되었습니다.[173]

Mathematics during the Scientific Revolution

17th century

Gottfried Wilhelm Leibniz.

17세기에는 유럽 전역의 수학적 그리고 과학적 아이디어의 전례없는 증가를 보였습니다. 갈릴레오(Galileo)는 네덜란드에서 수입한 장난감을 기반으로 망원경을 사용하여 지구에 관한 궤도에서 목성의 달을 관측했습니다. 튀코 브라헤(Tycho Brahe)는 하늘에서 행성의 위치를 설명하는 엄청난 양의 수학적 데이터를 수집했습니다. 브라헤의 조수로 그의 위치에 의해, 요하네스 케플러(Johannes Kepler)는 행성 운동의 주제에 처음 접하게 되었고 심각하게 상호 작용했습니다. 케플러의 계산은 존 네이피어(John Napier)와 요스트 뷔르기(Jost Bürgi)에 의해 로그의 동시 발명에 의해 더 간단해졌습니다. 케플러는 행성 운동의 수학적 법칙을 공식화하는 데 성공했습니다.[174] 르네 데카르트(René Descartes) (1596-1650)가 개발된 해석적 기하학(analytic geometry)은 그들 궤도를 데카르트 좌표(Cartesian coordinates)에서 그래프 위에 그려지는 것을 허용했습니다.

많은 이전 연구가에 의해 초기 작업을 토대로, 아이작 뉴턴(Isaac Newton)은 케플러의 법칙(Kepler's Laws)을 설명하는 물리학의 법칙을 발견하고, 지금 미적분학(calculus)으로 알려진 개념을 모았습니다. 독립적으로, 고트프리트 빌헬름 라이프니츠(Gottfried Wilhelm Leibniz)는, 틀림없이 17세기의 가장 중요한 수학자 중 한 명으로, 미적분과 지금 여전히 사용하는 많은 미적분 표기법을 개발했습니다. 과학과 수학은 국제적인 노력으로 자리를 잡았었고, 곧 전 세계에 걸쳐 퍼져 나갔을 것입니다.[175]

하늘의 연구에 수학을 적용하는 것 외에도, 응용 수학(applied mathematics)은 피에르 드 페르마(Pierre de Fermat)와 블레즈 파스칼(Blaise Pascal)의 서신과 함께 새로운 영역으로 확장되기 시작했습니다. 파스칼과 페르마는 겜블링(gambling)의 게임에 대한 논의에서 확률 이론(probability theory)의 조사와 조합론(combinatorics)의 해당 규칙에 대해 토대를 마련했습니다. 그의 내기(wager)와 함께, 파스칼은 비록 성공 확률이 적을지라도, 보상은 무한할 수 있다는 것을 근거로, 새롭게 개발된 확률 이론을 종교에 헌신하는 삶에 대해 논쟁하기 위해 사용하려고 시도했습니다. 어떤 의미에서, 이것은 18–19세기에서 효용 이론(utility theory)의 발전을 예고했습니다.

18th century

Leonhard Euler by Emanuel Handmann.

18세기의 가장 영향력있는 수학자는 틀림없이 레온하르트 오일러(Leonhard Euler)였습니다. 그의 공헌은 쾨니히스베르크의 일곱 개 다리(Seven Bridges of Königsberg) 문제와 함께 그래프 이론(graph theory)의 연구를 창안하는 것부터 현대의 많은 수학적 용어와 표기법을 표준화하는 것에 이르기까지 다양합니다. 예를 들어, 그는 음의 1의 제곱근을 기호 i로 명명했고, 그리스 문자 를 사용하여 원의 원주에 대한 지름의 비율을 나타내는 것을 대중화했습니다. 그는 토폴로지, 그래프 이론, 미적분학, 조합론 및 복소수 해석학에 대한 수많은 공헌을 했으며, 그의 이름으로 명명된 많은 정리 및 표기법에 의해 입증되었습니다.

18세기의 또 다른 중요한 유럽 수학자는 숫자 이론, 대수학, 미분학, 변화의 계산법에서 선구자적 연구를 담당했던, 조제프 루이 라그랑주(Jose Louis Lagrange)를 포함하며, 그리고 나폴레옹(Napoleon) 시대에서, 라플라스(Laplace)는 천체 역학(celestial mechanics)과 통계학(statistics)의 기초에 중요한 연구를 했습니다.

Modern

19th century

Carl Friedrich Gauss.

19세기 전반에 걸쳐 수학은 점점 추상화되었습니다. 카를 프리드리히 가우스(Carl Friedrich Gauss) (1777–1855)는 이러한 추세를 요약합니다. 그는 복소수 변수(complex variable)의 함수(functions), 기하학(geometry), 급수(series)의 수렴에 대한 혁명적인 작업을 수행했고, 과학에 대한 많은 기여를 제쳐두고 떠났습니다. 그는 대수학의 기본 정리(fundamental theorem of algebra)와 이차 상호 법칙(quadratic reciprocity law)에 대한 최초의 만족스러운 증명을 역시 제공했습니다.

Behavior of lines with a common perpendicular in each of the three types of geometry

이 세기는 비-유클리드 기하학(non-Euclidean geometry)의 두 가지 형태의 개발을 보였으며, 여기서 유클리드 기하학(Euclidean geometry)의 평행 공준(parallel postulate)은 더 이상 유지되지 않습니다. 러시아의 수학자 니콜라이 이바노비치 로바쳅스키(Nikolai Ivanovich Lobachevsky)와 그의 경쟁자, 헝가리의 수학자 보여이 야노시(János Bolyai)는 쌍곡 기하학(hyperbolic geometry)을 독립적으로 정의하고 연구했으며, 여기서 평행의 유일성은 더 이상 유지되지 않습니다. 이 기하학에서 삼각형에서 각도의 합은 180° 이하입니다. 타원 기하학(Elliptic geometry)은 독일 수학자 베른하르트 리만(Bernhard Riemann)에 의해 19세기 후반에 개발되었습니다; 여기서는 평행은 찾아질 수 없고 삼각형에서 각들은 합해져서 180° 이상입니다. 리만은 역시 리만 기하학(Riemannian geometry)을 개발했으며, 기하학의 세 가지 형태를 통합하고 광범위하게 일반화했고, 곡선(curve)과 곡면(surfaces)의 아이디어를 일반화하는 매니폴드(manifold)의 개념을 정의했습니다.

19세기는 대단한 추상 대수학(abstract algebra)의 시작을 보였습니다. 독일에서 헤르만 그라스만(Hermann Grassmann)은 벡터 공간(vector space)의 첫 번째 버전을 제공했고, 아일랜드에서 윌리엄 로언 해밀턴(William Rowan Hamilton)은 비-교환가능 대수(noncommutative algebra:비가환 대수)를 개발했습니다. 영국의 수학자 조지 부울(George Boole)은 대수학을 고안하여 지금 부울 대수(Boolean algebra)이라고 불리는 것으로 곧 발전시켰는데, 그것에서 오직 숫자는 0과 1이었습니다. 부울 대수는 수학적 논리(mathematical logic)의 출발점이고 컴퓨터 과학(computer science)에서 중요한 응용을 가집니다.

오귀스탱-루이 코시(Augustin-Louis Cauchy), 베른하르트 리만(Bernhard Riemann), 카를 바이어슈트라스(Karl Weierstrass)는 미적분을 보다 엄격한 방식으로 재구성했습니다.

또한, 처음으로, 수학의 한계가 탐구되었습니다. 노르웨이 사람, 닐스 헨리크 아벨(Niels Henrik Abel)과 프랑스 사람, 에바리스트 갈루아(Évariste Galois)는 4보다 큰 차수의 다항 방정식을 풀기 위한 일반적인 대수적 방법이 없다는 것을 증명했습니다 (아벨–루피니 정리). 또 다른 19세기의 수학자들은, 직선자와 컴퍼스 단독으로 임의의 각도를 삼등분하는 것(trisect an arbitrary angle), 주어진 육면체의 부피의 두 배의 육면체를 구성하는 것이 충분하지 않고, 주어진 원에 대한 넓이와 같은 정사각형을 구성하는 것이 불가능하다는 그들 증명에서 이것을 활용했습니다. 수학자들은 고대 그리스 시대 이후로 이들 모든 문제를 해결하기 위해 헛되이 시도했습니다. 반면에, 기하학에서 삼 차원(dimension)의 한계는 매개변수 공간(parameter space)과 초복소수(hypercomplex number)의 고려를 통해 19세기에 더 커졌습니다.

다양한 다항 방정식의 해법에 대한 아벨과 갈루아의 조사는 그룹 이론(group theory)의 뒤따른 발전과 추상 대수학(abstract algebra)의 관련 분야에 대한 토대를 마련했습니다. 20세기에서 물리학자와 또 다른 과학자들은 그룹 이론을 대칭(symmetry)을 연구하는 이상적인 방법으로 여겼습니다.

19세기 후반에서, 게오르크 칸토어(Georg Cantor)는 무한 개념의 엄격한 처리를 가능하게 하고 거의 모든 수학의 공통 언어가 된 집합 이론(set theory)의 첫 번째 기초를 수립했습니다. 칸토어의 집합 이론, 그리고 페아노(Peano), 브라우어르(L.E.J. Brouwer), 다비트 힐베르트(David Hilbert), 버트런드 러셀(Bertrand Russell), 화이트헤드(A.N. Whitehead)의 손에서 수학적 논리(mathematical logic)의 등장은 수학의 기초(foundations of mathematics)에 대한 장기 토론을 시작했습니다.

19세기는 여러 가지 국가 수학적 사회의 창립을 보였습니다; 1865년에 London Mathematical Society, 1872년에 Société Mathématique de France, 1884년에 Circolo Matematico di Palermo, 1883년에 Edinburgh Mathematical Society, 그리고 1888년에 American Mathematical Society를 설립되었습니다. 최초의 국제적, 특별-관심 협회, 쿼터니언 협회(Quaternion Society)는 벡터 논쟁(vector controversy)의 맥락에서 1899년에 형성되었습니다.

1897년에, 헨젤은 p-진수 숫자(p-adic number)를 도입했습니다.

20th century

20세기는 수학이 중요한 직업이 되는 것을 보였습니다. 매년, 수학에서 수천 명의 새로운 박사들이 수여되었고, 직업은 강의와 산업 둘 다에서 유효했습니다. 수학의 분야 및 응용을 카탈로그하기 위한 노력이 클라인의 백과사전(Klein's encyclopedia)에서 수행되었습니다.

수학자의 국제 회의(International Congress of Mathematicians)의 1900년 연설에서, 다비트 힐베르트(David Hilbert)는 수학에서 해결되지 않은 23가지 문제의 목록을 설정했습니다. 수학의 많은 분야에 걸친 이들 문제는 20세기 수학의 많은 부분에 대해 중점을 형성했습니다. 오늘날, 10개가 해결되었으며, 7개는 부분적으로 해결되었고, 2개는 여전히 열려 있습니다. 남아있는 4개는 너무 느슨하게 공식화되어 해결할 수 있는지에 대해 말해지지 않습니다.

A map illustrating the Four Color Theorem

주목할만한 역사적인 추측이 마침내 입증되었습니다. 1976년에, 볼프강 하켄(Wolfgang Haken)과 케네스 아펠(Kenneth Appel)은 네 가지 색깔 정리(four color theorem)를 증명했는데, 그 당시에 그렇게 하기 위해 컴퓨터의 사용에 대해 논쟁의 여지가 있었습니다. 앤드루 와일스(Andrew Wiles)는 다른 사람들의 작업을 기반으로 1995년 페르마의 마지막 정리(Fermat's Last Theorem)를 증명했습니다. 폴 코언(Paul Cohen)과 쿠르트 괴델(Kurt Gödel)은 연속체 가설(continuum hypothesis)은 집합 이론의 표준 공리와는 (그것으로부터 증명될 수도 없거나 반증을 들 수도 없는) 독립(independent)적이라는 것을 증명했습니다. 1998년에 토머스 캘리스터 헤일즈(Thomas Callister Hales)는 케플러 추측(Kepler conjecture)을 증명했습니다.

전례없는 크기와 범위의 수학적 공동 작업이 진행되었습니다. 예제는 ("거대한 정리"라고 역시 불리는) 유한 단순 그룹의 분류(classification of finite simple groups)이며, 1955년과 1983년 사이의 그의 증명은 약 100 명의 저자에 의해 500 여개의 동떨어진 저널 기사를 요구하고, 수만 페이지를 채우는 것이었습니다. 가명(pseudonym) "니콜라 부르바키"라는 이름으로 출판하는, 장 디외도네(Jean Dieudonné)와 앙드레 베유(André Weil)를 포함한 프랑스 수학자 그룹은 모든 알려진 수학을 일관된 엄격한 전체로서 노출하기 위해 시도했습니다. 그 결과로 수십 권이 수학 교육에 대한 논란의 영향을 끼쳐오고 있습니다.[176]

Newtonian (red) vs. Einsteinian orbit (blue) of a lone planet orbiting a star, with relativistic precession of apsides

미분 기하학(Differential geometry)은 아인슈타인(Einstein)이 일반 상대성(general relativity)에서 사용했을 때 그 자체로 나타났습니다. 수학적 논리(mathematical logic), 토폴로지(topology) 및 존 폰 노이만(John von Neumann)의 게임 이론(game theory)과 같은 완전히 새로운 수학 영역은 수학적 방법으로 대답할 수 있는 질문의 종류를 변경했습니다. 구조(structures)의 모든 종류는 공리와 거리 공간(metric space), 토폴로지적 공간(topological space) 등과 같은 주어진 이름을 사용하여 추상화되었습니다. 수학자들이 행할 때, 추상적 구조의 개념은 자체로 추상화되었고 카테고리 이론(category theory)으로 이어졌습니다. 그로텐디크(Grothendieck)와 세르(Serre)는 층 이론(sheaf theory)을 사용하여 대수 기하학(algebraic geometry)을 다시 만들었습니다. 큰 발전은 푸앵카레(Poincaré)가 1890년대에 시작했었던 동역학 시스템(dynamical systems)의 질적 연구에서 만들어졌습니다. 측정 이론(Measure theory)은 19세기 후반과 20세기 초반에 개발되었습니다. 측정의 응용은 르베그 적분(Lebesgue integral), 확률 이론(probability theory)의 콜모고로프(Kolmogorov)의 공리주의, 그리고 에르고딕성 이론(ergodic theory)을 포함합니다. 매듭 이론(Knot theory)은 크게 확장되었습니다. 양자 역학(Quantum mechanics)은 함수형 해석학(functional analysis)의 발전으로 이어졌습니다. 다른 새로운 분야는 로랑 슈바르츠(Laurent Schwartz)의 분포 이론(distribution theory), 고정 점 이론(fixed point theory), 특이점 이론(singularity theory) 및 르네 톰(René Thom)의 급변 이론(catastrophe theory), 모델 이론(model theory), 그리고 망델브로(Mandelbrot)의 프랙탈(fractals)을 포함합니다. 리 그룹(Lie group)과 리 대수(Lie algebras)와 함께 리 이론(Lie theory)은 주요 연구 분야 중 하나가 되었습니다.

에이브러햄 로빈슨(Abraham Robinson)에 의해 소개된, 비-표준 해석학(Non-standard analysis)은 실수의 필드를 무한소와 무한대 양을 포함하는 초실수(Hyperreal number)로 확장함으로써, 극한(limits) 이론의 편애에서 나쁜 평판에 빠뜨려 왔던 미적분학에 대한 무한소(infinitesimal) 접근법을 회복시켰습니다. 심지어 더 큰 숫자 시스템, 초현실수(surreal number)는 조합론적 게임(combinatorial game)과 관련하여 존 호턴 콘웨이(John Horton Conway)에 의해 발견되었습니다.

첫 번째 기계적 아날로그 기계와 그 후 디지털 전자 기계에서, 컴퓨터(computer)의 개발 및 지속적인 개선은 대량 생산 및 유통 및 통신을 용이하게 하기 위해 더 많은 양의 데이터를 처리하는 것을 산업(industry)에 허용했고, 수학의 새로운 영역은 이 문제를 다루기 위해 개발되었습니다: 앨런 튜링(Alan Turing)의 계산가능성 이론(computability theory); 복잡성 이론(complexity theory); 뒤따른 숫자 이론과 이론 및 루카스-레머 테스트(Lucas-Lehmer test)에 대한 에니악(ENIAC)의 데릭 헨리 레머(Derrick Henry Lehmer)의 사용; 로저 페테르(Rózsa Péter)의 재귀 함수 이론(recursive function theory); 클로드 섀넌(Claude Shannon)의 정보 이론(information theory); 신호 처리(signal processing); 데이터 분석(data analysis); 최적화(optimization) 및 운영 연구(operations research:운영 과학)의 다른 영역. 이후 수세기에서 미적분(calculus)과 연속 함수에 대한 많은 수학적 초점이 있었지만, 컴퓨팅 및 통신 네트워크의 부상으로 이산(discrete) 개념의 중요성의 증가하고 그래프 이론(graph theory)을 비롯한 조합론(combinatorics)의 확장으로 이어졌습니다. 컴퓨터의 속도 및 데이터 처리 능력은 연필 및 종이 계산에 의해 다루어지기에 너무 많은 시간이 소요되는, 수치 해석(numerical analysis) 및 기호 계산(symbolic computation)과 같은 영역으로 이르는 수학적 문제를 처리하는 것을 역시 활성화했습니다. 20세기의 가장 중요한 방법과 알고리듬의 몇 가지는 심플렉스 알고리듬(simplex algorithm), 고속 푸리에 변환(Fast Fourier Transform), 오류-정정 코드(error-correcting code), 제어 이론(control theory)으로부터 칼만 필터(Kalman filter) 그리고 공개-키 암호화(public-key cryptography)의 RSA 알고리듬(RSA algorithm)입니다.

동시대에서, 깊은 통찰력은 수학에 대한 한계에 대해 만들어졌습니다. 1929년과 1930년에, 자연수(natural number) 더하기 덧셈 및 곱셈 중 하나에 대한 공식화된 모든 명제의 진실 또는 거짓은 결정 가능(decidable), 즉 일부 알고리듬에 의해 결정될 수 있음을 입증되었습니다. 1931년에, 쿠르트 괴델(Kurt Gödel)은 이것이 자연수 더하기 덧셈 및 곱셈 둘 다에 해당하지 않는다는 것을 발견했습니다; 페아노 산술(Peano arithmetic)로 알려진 이 시스템은 사실 불완전성(incompletable)이었습니다. (페아노 산술은 소수(prime number)의 개념을 포함하여 많은 숫자 이론(number theory)의 좋은 정책에 적합합니다.) 괴델의 두 가지 불완전성 정리(incompleteness theorem)의 결과는 (모든 해석학(analysis) 및 기하학(geometry)을 포함하여) 페아노 산술을 포함하는 임의의 수학적 시스템에서, 진리는 필연적으로 증명의 한도를 넘어섬, 즉, 시스템 내에서 입증될 수 없는 진리 명제가 있다는 것입니다. 따라서 수학은 수학적 논리로 절대 축소될 수 없고, 모든 수학을 완전하고 일관성있게 만드는 다비트 힐베르트(David Hilbert)의 꿈은 재구성되어야 했습니다.

The absolute value of the Gamma function on the complex plane.

20세기 수학에서 더 다채로운 인물 중 하나는, 고도합성수(highly composite number)의 속성, 분할 함수(partition function)와 그의 점근선(asymptotics), 그리고 모조 세타 함수(mock theta functions)를 포함하여 3000개 이상의 정리를 추측하거나 증명한 인도의 독학자(autodidact), 쉬리니바사 아이영거 라마누젼(Srinivasa Aiyangar Ramanujan) (1887-1920)이었습니다. 그는 감마 함수(gamma function), 모듈러 형태(modular form), 발산 급수(divergent series), 초기하학 급수(hypergeometric series) 및 소수(prime number) 이론의 영역에서 주요 조사를 역시 만들었습니다.

팔 에르되시(Paul Erdős)는 역사상 다른 수학자보다 더 많은 논문을 발표하여, 수백 명의 공동 작업자와 일했습니다. 수학자는 케빈 베이컨 게임(Kevin Bacon Game)과 동등한 게임을 가지고 있는데, 그것은 수학자의 에르되스 숫자(Erdős number)를 유도합니다. 이것은, 수학 논문의 공동 저작자에 의해 측정될 때, 한 사람과 팔 에르되시 사이의 "협력적 거리"를 묘사합니다.

에미 뇌터(Emmy Noether)는 수학의 역사에서 가장 중요한 여성으로 많은 사람들에 의해 묘사되어 왔습니다.[177] 그녀는 링(rings), 필드(fields), and 대수(algebras)의 이론을 연구했습니다.

대부분의 연구 분야에서와 마찬가지로, 과학 시대에서 지식 폭발은 전문화를 이끌어 왔습니다: 세기말에는 수학에서 수백 개의 전문 분야가 있었고 수학 주제 분류(Mathematics Subject Classification)는 수십 페이지에 이릅니다.[178] 점점 더 많은 수학 저널(mathematical journal)이 출판되었고, 세기말에 월드 와이드 웹(World Wide Web)의 개발은 온라인 출판으로 이어졌습니다.

21st century

See also: List of unsolved problems in mathematics § Problems solved since 1995

2000년에, 클레이 수학 연구소(Clay Mathematics Institute)는 일곱 개 밀레니엄 프라이즈 문제(Millennium Prize Problems)를 발표했고, 2003년에 푸앵카레 추측(Poincaré conjecture)은 그리고리 페렐만(Grigori Perelman)에 의해 해결되었습니다 (그는 수학 설립에 대해 비판적이었기 때문에 상을 수락하지 않았습니다).

대부분의 수학 저널은 이제 온라인 버전과 마찬가지로 인쇄 버전이 있고, 많은 온라인-전용 저널이 출시됩니다. arXiv에 의해 첫 번째 대중화된, 열린 접근 출판(open access publishing)에 대한 요구가 커지고 있습니다.

Future

Main article: Future of mathematics

수학에서 많은 주목할만한 트렌드가 있습니다. 가장 주목할만한 것은 그 주제가 점점 더 커지고 있다는 것, 컴퓨터가 더욱 중요하고 강력해지는 것, 생물 정보학에 대한 수학의 응용은 급속하게 확대되는 것, 과학 및 산업에 의한 생산된, 컴퓨터에 의해 용이하게 된 데이터의 크기는, 폭발적으로 확대되고 있는 것입니다.[citation needed]

See also

Notes

  1. ^ The approximate values for π are 4 x (13/15)2 (3.0044...), 25/8 (3.125), 900/289 (3.11418685...), 1156/361 (3.202216...), and 339/108 (3.1389)
  1. ^ a b (Boyer 1991, "Euclid of Alexandria" p. 119) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  2. ^ J. Friberg, "Methods and traditions of Babylonian mathematics. Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations", Historia Mathematica, 8, 1981, pp. 277–318.
  3. ^ Neugebauer, Otto (1969) [1957]. The Exact Sciences in Antiquity (2 ed.). Dover Publications. ISBN 978-0-486-22332-2. Chap. IV "Egyptian Mathematics and Astronomy", pp. 71–96.
  4. ^ Heath (1931). "A Manual of Greek Mathematics". Nature. 128 (3235): 5. Bibcode:1931Natur.128..739T. doi:10.1038/128739a0.
  5. ^ Sir Thomas L. Heath, A Manual of Greek Mathematics, Dover, 1963, p. 1: "In the case of mathematics, it is the Greek contribution which it is most essential to know, for it was the Greeks who first made mathematics a science."
  6. ^ George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics, Penguin Books, London, 1991, pp. 140–48
  7. ^ Georges Ifrah, Universalgeschichte der Zahlen, Campus, Frankfurt/New York, 1986, pp. 428–37
  8. ^ Robert Kaplan, "The Nothing That Is: A Natural History of Zero", Allen Lane/The Penguin Press, London, 1999
  9. ^ "The ingenious method of expressing every possible number using a set of ten symbols (each symbol having a place value and an absolute value) emerged in India. The idea seems so simple nowadays that its significance and profound importance is no longer appreciated. Its simplicity lies in the way it facilitated calculation and placed arithmetic foremost amongst useful inventions. the importance of this invention is more readily appreciated when one considers that it was beyond the two greatest men of Antiquity, Archimedes and Apollonius." – Pierre Simon Laplace http://www-history.mcs.st-and.ac.uk/HistTopics/Indian_numerals.html
  10. ^ A.P. Juschkewitsch, "Geschichte der Mathematik im Mittelalter", Teubner, Leipzig, 1964
  11. ^ a b (Boyer 1991, "Origins" p. 3) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  12. ^ Williams, Scott W. (2005). "The Oldest Mathematical Object is in Swaziland". Mathematicians of the African Diaspora. SUNY Buffalo mathematics department. Retrieved 2006-05-06.
  13. ^ Marshack, Alexander (1991): The Roots of Civilization, Colonial Hill, Mount Kisco, NY.
  14. ^ Rudman, Peter Strom (2007). How Mathematics Happened: The First 50,000 Years. Prometheus Books. p. 64. ISBN 978-1-59102-477-4.
  15. ^ Marshack, A. 1972. The Roots of Civilization: the Cognitive Beginning of Man’s First Art, Symbol and Notation. New York: McGraw-Hil
  16. ^ Thom, Alexander, and Archie Thom, 1988, "The metrology and geometry of Megalithic Man", pp. 132–51 in C.L.N. Ruggles, ed., Records in Stone: Papers in memory of Alexander Thom. Cambridge University Press. ISBN 0-521-33381-4.
  17. ^ (Boyer 1991, "Mesopotamia" p. 24) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  18. ^ a b c d e f (Boyer 1991, "Mesopotamia" p. 26) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  19. ^ a b c (Boyer 1991, "Mesopotamia" p. 25) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  20. ^ a b (Boyer 1991, "Mesopotamia" p. 41) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  21. ^ Duncan J. Melville (2003). Third Millennium Chronology, Third Millennium Mathematics. St. Lawrence University.
  22. ^ a b (Boyer 1991, "Mesopotamia" p. 27) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  23. ^ Aaboe, Asger (1998). Episodes from the Early History of Mathematics. New York: Random House. pp. 30–31.
  24. ^ (Boyer 1991, "Mesopotamia" p. 33) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  25. ^ (Boyer 1991, "Mesopotamia" p. 39) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  26. ^ (Boyer 1991, "Egypt" p. 11) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  27. ^ Egyptian Unit Fractions at MathPages
  28. ^ Egyptian Unit Fractions
  29. ^ Egyptian Papyri
  30. ^ Egyptian Algebra – Mathematicians of the African Diaspora
  31. ^ (Boyer 1991, "Egypt" p. 19) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  32. ^ Egyptian Mathematical Papyri – Mathematicians of the African Diaspora
  33. ^ Howard Eves, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0
  34. ^ (Boyer 1991, "The Age of Plato and Aristotle" p. 99) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  35. ^ Martin Bernal, "Animadversions on the Origins of Western Science", pp. 72–83 in Michael H. Shank, ed., The Scientific Enterprise in Antiquity and the Middle Ages, (Chicago: University of Chicago Press) 2000, p. 75.
  36. ^ (Boyer 1991, "Ionia and the Pythagoreans" p. 43) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  37. ^ (Boyer 1991, "Ionia and the Pythagoreans" p. 49) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  38. ^ Kurt Von Fritz (1945). "The Discovery of Incommensurability by Hippasus of Metapontum". The Annals of Mathematics. {{cite journal}}: Invalid |ref=harv (help)
  39. ^ James R. Choike (1980). "The Pentagram and the Discovery of an Irrational Number". The Two-Year College Mathematics Journal. {{cite journal}}: Invalid |ref=harv (help)
  40. ^ Eves, Howard, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0.
  41. ^ a b Jane Qiu (7 January 2014). "Ancient times table hidden in Chinese bamboo strips". Nature. doi:10.1038/nature.2014.14482. Retrieved 15 September 2014.
  42. ^ David E. Smith (1958), History of Mathematics, Volume I: General Survey of the History of Elementary Mathematics, New York: Dover Publications (a reprint of the 1951 publication), ISBN 0-486-20429-4, pp. 58, 129.
  43. ^ David E. Smith (1958), History of Mathematics, Volume I: General Survey of the History of Elementary Mathematics, New York: Dover Publications (a reprint of the 1951 publication), ISBN 0-486-20429-4, p. 129.
  44. ^ (Boyer 1991, "The Age of Plato and Aristotle" p. 86) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  45. ^ a b (Boyer 1991, "The Age of Plato and Aristotle" p. 88) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  46. ^ Calian, George F. (2014). "One, Two, Three… A Discussion on the Generation of Numbers" (PDF). New Europe College. Archived from the original (PDF) on 2015-10-15. {{cite web}}: Unknown parameter |deadurl= ignored (|url-status= suggested) (help)
  47. ^ (Boyer 1991, "The Age of Plato and Aristotle" p. 87) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  48. ^ (Boyer 1991, "The Age of Plato and Aristotle" p. 92) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  49. ^ (Boyer 1991, "The Age of Plato and Aristotle" p. 93) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  50. ^ (Boyer 1991, "The Age of Plato and Aristotle" p. 91) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  51. ^ (Boyer 1991, "The Age of Plato and Aristotle" p. 98) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  52. ^ Bill Casselman. "One of the Oldest Extant Diagrams from Euclid". University of British Columbia. Retrieved 2008-09-26.
  53. ^ (Boyer 1991, "Euclid of Alexandria" p. 100) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  54. ^ a b (Boyer 1991, "Euclid of Alexandria" p. 104) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  55. ^ Howard Eves, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0 p. 141: "No work, except The Bible, has been more widely used...."
  56. ^ (Boyer 1991, "Euclid of Alexandria" p. 102) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  57. ^ (Boyer 1991, "Archimedes of Syracuse" p. 120) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  58. ^ a b (Boyer 1991, "Archimedes of Syracuse" p. 130) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  59. ^ (Boyer 1991, "Archimedes of Syracuse" p. 126) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  60. ^ (Boyer 1991, "Archimedes of Syracuse" p. 125) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  61. ^ (Boyer 1991, "Archimedes of Syracuse" p. 121) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  62. ^ (Boyer 1991, "Archimedes of Syracuse" p. 137) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  63. ^ (Boyer 1991, "Apollonius of Perga" p. 145) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  64. ^ (Boyer 1991, "Apollonius of Perga" p. 146) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  65. ^ (Boyer 1991, "Apollonius of Perga" p. 152) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  66. ^ (Boyer 1991, "Apollonius of Perga" p. 156) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  67. ^ (Boyer 1991, "Greek Trigonometry and Mensuration" p. 161) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  68. ^ a b (Boyer 1991, "Greek Trigonometry and Mensuration" p. 175) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  69. ^ (Boyer 1991, "Greek Trigonometry and Mensuration" p. 162) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  70. ^ S.C. Roy. Complex numbers: lattice simulation and zeta function applications, p. 1 [1]. Harwood Publishing, 2007, 131 pages. ISBN 1-904275-25-7
  71. ^ (Boyer 1991, "Greek Trigonometry and Mensuration" p. 163) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  72. ^ (Boyer 1991, "Greek Trigonometry and Mensuration" p. 164) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  73. ^ (Boyer 1991, "Greek Trigonometry and Mensuration" p. 168) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  74. ^ (Boyer 1991, "Revival and Decline of Greek Mathematics" p. 178) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  75. ^ (Boyer 1991, "Revival and Decline of Greek Mathematics" p. 180) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  76. ^ a b (Boyer 1991, "Revival and Decline of Greek Mathematics" p. 181) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  77. ^ (Boyer 1991, "Revival and Decline of Greek Mathematics" p. 183) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  78. ^ (Boyer 1991, "Revival and Decline of Greek Mathematics" pp. 183–90) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  79. ^ Medieval Sourcebook: Socrates Scholasticus: The Murder of Hypatia (late 4th Cent.) from Ecclesiastical History, Bk VI: Chap. 15
  80. ^ (Boyer 1991, "Revival and Decline of Greek Mathematics" pp. 190–94) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  81. ^ (Boyer 1991, "Revival and Decline of Greek Mathematics" p. 193) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  82. ^ (Boyer 1991, "Revival and Decline of Greek Mathematics" p. 194) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  83. ^ (Goodman 2016, p. 119)
  84. ^ (Cuomo 2001, pp. 194, 204–06)
  85. ^ (Cuomo 2001, pp. 192–95)
  86. ^ (Goodman 2016, pp. 120–21)
  87. ^ (Cuomo 2001, p. 196)
  88. ^ (Cuomo 2001, pp. 207–08)
  89. ^ (Goodman 2016, pp. 119–20)
  90. ^ (Tang 2005, pp. 14–15, 45)
  91. ^ (Joyce 1979, p. 256)
  92. ^ (Gullberg 1997, p. 17)
  93. ^ (Gullberg 1997, pp. 17–18)
  94. ^ (Gullberg 1997, p. 18)
  95. ^ (Gullberg 1997, pp. 18–19)
  96. ^ (Needham & Wang 2000, pp. 281–85)
  97. ^ (Needham & Wang 2000, p. 285)
  98. ^ (Sleeswyk 1981, pp. 188–200)
  99. ^ (Boyer 1991, "China and India" p. 201) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  100. ^ a b c (Boyer 1991, "China and India" p. 196) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  101. ^ Katz 2007, pp. 194–99
  102. ^ (Boyer 1991, "China and India" p. 198) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  103. ^ (Needham & Wang 1995, pp. 91–92)
  104. ^ (Needham & Wang 1995, p. 94)
  105. ^ (Needham & Wang 1995, p. 22)
  106. ^ (Straffin 1998, p. 164)
  107. ^ (Needham & Wang 1995, pp. 99–100)
  108. ^ (Berggren, Borwein & Borwein 2004, p. 27)
  109. ^ (Crespigny 2007, p. 1050)
  110. ^ a b c (Boyer 1991, "China and India" p. 202) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  111. ^ (Needham & Wang 1995, pp. 100–01)
  112. ^ (Berggren, Borwein & Borwein 2004, pp. 20, 24–26)
  113. ^ Zill, Dennis G.; Wright, Scott; Wright, Warren S. (2009). Calculus: Early Transcendentals (3 ed.). Jones & Bartlett Learning. p. xxvii. ISBN 978-0-7637-5995-7. Extract of p. 27
  114. ^ a b c (Boyer 1991, "China and India" p. 205) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  115. ^ (Volkov 2009, pp. 153–56)
  116. ^ (Volkov 2009, pp. 154–55)
  117. ^ (Volkov 2009, pp. 156–57)
  118. ^ (Volkov 2009, p. 155)
  119. ^ Development Of Modern Numerals And Numeral Systems: The Hindu-Arabic system, Encyclopaedia Britannica, Quote: "The 1, 4, and 6 are found in the Ashoka inscriptions (3rd century bce); the 2, 4, 6, 7, and 9 appear in the Nana Ghat inscriptions about a century later; and the 2, 3, 4, 5, 6, 7, and 9 in the Nasik caves of the 1st or 2nd century CE – all in forms that have considerable resemblance to today’s, 2 and 3 being well-recognized cursive derivations from the ancient = and ≡."
  120. ^ (Boyer 1991, "China and India" p. 206) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  121. ^ Puttaswamy, T.K. (2000). "The Accomplishments of Ancient Indian Mathematicians". In Selin, Helaine; D'Ambrosio, Ubiratan (eds.). Mathematics Across Cultures: The History of Non-western Mathematics. Springer. pp. 411–12. ISBN 978-1-4020-0260-1. {{cite book}}: Invalid |ref=harv (help)
  122. ^ a b c d (Boyer 1991, "China and India" p. 207) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  123. ^ Kulkarni, R.P. (1978). "The Value of π known to Śulbasūtras" (PDF). Indian Journal of History of Science. 13 (1): 32–41. Archived from the original (PDF) on 2012-02-06.
  124. ^ a b Connor, J.J.; Robertson, E.F. "The Indian Sulbasutras". Univ. of St. Andrew, Scotland.
  125. ^ Bronkhorst, Johannes (2001). "Panini and Euclid: Reflections on Indian Geometry". Journal of Indian Philosophy. 29 (1–2): 43–80. doi:10.1023/A:1017506118885. {{cite journal}}: Invalid |ref=harv (help)
  126. ^ Kadvany, John (2008-02-08). "Positional Value and Linguistic Recursion". Journal of Indian Philosophy. 35 (5–6): 487–520. CiteSeerX 10.1.1.565.2083. doi:10.1007/s10781-007-9025-5. ISSN 0022-1791.
  127. ^ Sanchez, Julio; Canton, Maria P. (2007). Microcontroller programming : the microchip PIC. Boca Raton, Florida: CRC Press. p. 37. ISBN 978-0-8493-7189-9.
  128. ^ W.S. Anglin and J. Lambek, The Heritage of Thales, Springer, 1995, ISBN 0-387-94544-X
  129. ^ Hall, Rachel W. (2008). "Math for poets and drummers" (PDF). Math Horizons. 15 (3): 10–11. doi:10.1080/10724117.2008.11974752.
  130. ^ (Boyer 1991, "China and India" p. 208) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  131. ^ a b (Boyer 1991, "China and India" p. 209) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  132. ^ (Boyer 1991, "China and India" p. 210) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  133. ^ (Boyer 1991, "China and India" p. 211) harv error: multiple targets (2×): CITEREFBoyer1991 (help)
  134. ^ Boyer (1991). "The Arabic Hegemony". History of Mathematics. p. 226. By 766 we learn that an astronomical-mathematical work, known to the Arabs as the Sindhind, was brought to Baghdad from India. It is generally thought that this was the Brahmasphuta Siddhanta, although it may have been the Surya Siddhanata. A few years later, perhaps about 775, this Siddhanata was translated into Arabic, and it was not long afterwards (ca. 780) that Ptolemy's astrological Tetrabiblos was translated into Arabic from the Greek.
  135. ^ Plofker 2009 182–207
  136. ^ Plofker 2009 pp. 197–98; George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics, Penguin Books, London, 1991 pp. 298–300; Takao Hayashi, Indian Mathematics, pp. 118–30 in Companion History of the History and Philosophy of the Mathematical Sciences, ed. I. Grattan.Guinness, Johns Hopkins University Press, Baltimore and London, 1994, p. 126
  137. ^ Plofker 2009 pp. 217–53
  138. ^ P.P. Divakaran, The first textbook of calculus: Yukti-bhāṣā, Journal of Indian Philosophy 35, 2007, pp. 417–33.
  139. ^ Pingree, David (December 1992). "Hellenophilia versus the History of Science". Isis. 83 (4): 554–563. Bibcode:1992Isis...83..554P. doi:10.1086/356288. JSTOR 234257. One example I can give you relates to the Indian Mādhava's demonstration, in about 1400 A.D., of the infinite power series of trigonometrical functions using geometrical and algebraic arguments. When this was first described in English by Charles Whish, in the 1830s, it was heralded as the Indians' discovery of the calculus. This claim and Mādhava's achievements were ignored by Western historians, presumably at first because they could not admit that an Indian discovered the calculus, but later because no one read anymore the Transactions of the Royal Asiatic Society, in which Whish's article was published. The matter resurfaced in the 1950s, and now we have the Sanskrit texts properly edited, and we understand the clever way that Mādhava derived the series without the calculus; but many historians still find it impossible to conceive of the problem and its solution in terms of anything other than the calculus and proclaim that the calculus is what Mādhava found. In this case the elegance and brilliance of Mādhava's mathematics are being distorted as they are buried under the current mathematical solution to a problem to which he discovered an alternate and powerful solution.
  140. ^ Bressoud, David (2002). "Was Calculus Invented in India?". College Mathematics Journal. 33 (1): 2–13. doi:10.2307/1558972. JSTOR 1558972. {{cite journal}}: Cite has empty unknown parameter: |month= (help)
  141. ^ Plofker, Kim (November 2001). "The 'Error' in the Indian "Taylor Series Approximation" to the Sine". Historia Mathematica. 28 (4): 293. doi:10.1006/hmat.2001.2331. It is not unusual to encounter in discussions of Indian mathematics such assertions as that 'the concept of differentiation was understood [in India] from the time of Manjula (... in the 10th century)' [Joseph 1991, 300], or that 'we may consider Madhava to have been the founder of mathematical analysis' (Joseph 1991, 293), or that Bhaskara II may claim to be 'the precursor of Newton and Leibniz in the discovery of the principle of the differential calculus' (Bag 1979, 294).... The points of resemblance, particularly between early European calculus and the Keralese work on power series, have even inspired suggestions of a possible transmission of mathematical ideas from the Malabar coast in or after the 15th century to the Latin scholarly world (e.g., in (Bag 1979, 285)).... It should be borne in mind, however, that such an emphasis on the similarity of Sanskrit (or Malayalam) and Latin mathematics risks diminishing our ability fully to see and comprehend the former. To speak of the Indian 'discovery of the principle of the differential calculus' somewhat obscures the fact that Indian techniques for expressing changes in the Sine by means of the Cosine or vice versa, as in the examples we have seen, remained within that specific trigonometric context. The differential 'principle' was not generalized to arbitrary functions – in fact, the explicit notion of an arbitrary function, not to mention that of its derivative or an algorithm for taking the derivative, is irrelevant here
  142. ^ Katz, Victor J. (June 1995). "Ideas of Calculus in Islam and India" (PDF). Mathematics Magazine. 68 (3): 163–74. Bibcode:1975MathM..48...12G. doi:10.2307/2691411. JSTOR 2691411.
  143. ^ (Boyer 1991, "The Arabic Hegemony" p. 230) harv error: multiple targets (2×): CITEREFBoyer1991 (help) "The six cases of equations given above exhaust all possibilities for linear and quadratic equations having positive root. So systematic and exhaustive was al-Khwārizmī's exposition that his readers must have had little difficulty in mastering the solutions."
  144. ^ Gandz and Saloman (1936), The sources of Khwarizmi's algebra, Osiris i, pp. 263–77: "In a sense, Khwarizmi is more entitled to be called "the father of algebra" than Diophantus because Khwarizmi is the first to teach algebra in an elementary form and for its own sake, Diophantus is primarily concerned with the theory of numbers".
  145. ^ (Boyer 1991, "The Arabic Hegemony" p. 229) harv error: multiple targets (2×): CITEREFBoyer1991 (help) "It is not certain just what the terms al-jabr and muqabalah mean, but the usual interpretation is similar to that implied in the translation above. The word al-jabr presumably meant something like "restoration" or "completion" and seems to refer to the transposition of subtracted terms to the other side of an equation; the word muqabalah is said to refer to "reduction" or "balancing" – that is, the cancellation of like terms on opposite sides of the equation."
  146. ^ Rashed, R.; Armstrong, Angela (1994). The Development of Arabic Mathematics. Springer. pp. 11–12. ISBN 978-0-7923-2565-9. OCLC 29181926.
  147. ^ Sesiano, Jacques (1997). "Abū Kāmil". Encyclopaedia of the history of science, technology, and medicine in non-western cultures. Springer. pp. 4–5.
  148. ^ (Katz 1998, pp. 255–59)
  149. ^ F. Woepcke (1853). Extrait du Fakhri, traité d'Algèbre par Abou Bekr Mohammed Ben Alhacan Alkarkhi. Paris.
  150. ^ Katz, Victor J. (1995). "Ideas of Calculus in Islam and India". Mathematics Magazine. 68 (3): 163–74. doi:10.2307/2691411. JSTOR 2691411.
  151. ^ Alam, S (2015). "Mathematics for All and Forever" (PDF). Indian Institute of Social Reform & Research International Journal of Research.
  152. ^ O'Connor, John J.; Robertson, Edmund F., "Abu'l Hasan ibn Ali al Qalasadi", MacTutor History of Mathematics archive, University of St Andrews.
  153. ^ a b c d (Goodman 2016, p. 121)
  154. ^ Wisdom, 11:21
  155. ^ Caldwell, John (1981) "The De Institutione Arithmetica and the De Institutione Musica", pp. 135–54 in Margaret Gibson, ed., Boethius: His Life, Thought, and Influence, (Oxford: Basil Blackwell).
  156. ^ Folkerts, Menso, "Boethius" Geometrie II, (Wiesbaden: Franz Steiner Verlag, 1970).
  157. ^ Marie-Thérèse d'Alverny, "Translations and Translators", pp. 421–62 in Robert L. Benson and Giles Constable, Renaissance and Renewal in the Twelfth Century, (Cambridge: Harvard University Press, 1982).
  158. ^ Guy Beaujouan, "The Transformation of the Quadrivium", pp. 463–87 in Robert L. Benson and Giles Constable, Renaissance and Renewal in the Twelfth Century, (Cambridge: Harvard University Press, 1982).
  159. ^ Grant, Edward and John E. Murdoch (1987), eds., Mathematics and Its Applications to Science and Natural Philosophy in the Middle Ages, (Cambridge: Cambridge University Press) ISBN 0-521-32260-X.
  160. ^ Clagett, Marshall (1961) The Science of Mechanics in the Middle Ages, (Madison: University of Wisconsin Press), pp. 421–40.
  161. ^ Murdoch, John E. (1969) "Mathesis in Philosophiam Scholasticam Introducta: The Rise and Development of the Application of Mathematics in Fourteenth Century Philosophy and Theology", in Arts libéraux et philosophie au Moyen Âge (Montréal: Institut d'Études Médiévales), at pp. 224–27.
  162. ^ Pickover, Clifford A. (2009), The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics, Sterling Publishing Company, Inc., p. 104, ISBN 978-1-4027-5796-9, Nicole Oresme ... was the first to prove the divergence of the harmonic series (c. 1350). His results were lost for several centuries, and the result was proved again by Italian mathematician Pietro Mengoli in 1647 and by Swiss mathematician Johann Bernoulli in 1687.
  163. ^ Clagett, Marshall (1961) The Science of Mechanics in the Middle Ages, (Madison: University of Wisconsin Press), pp. 210, 214–15, 236.
  164. ^ Clagett, Marshall (1961) The Science of Mechanics in the Middle Ages, (Madison: University of Wisconsin Press), p. 284.
  165. ^ Clagett, Marshall (1961) The Science of Mechanics in the Middle Ages, (Madison: University of Wisconsin Press), pp. 332–45, 382–91.
  166. ^ Nicole Oresme, "Questions on the Geometry of Euclid" Q. 14, pp. 560–65, in Marshall Clagett, ed., Nicole Oresme and the Medieval Geometry of Qualities and Motions, (Madison: University of Wisconsin Press, 1968).
  167. ^ Heeffer, Albrecht: On the curious historical coincidence of algebra and double-entry bookkeeping, Foundations of the Formal Sciences, Ghent University, November 2009, p. 7 [2]
  168. ^ della Francesca, Piero. De Prospectiva Pingendi, ed. G. Nicco Fasola, 2 vols., Florence (1942).
  169. ^ della Francesca, Piero. Trattato d'Abaco, ed. G. Arrighi, Pisa (1970).
  170. ^ della Francesca, Piero. L'opera "De corporibus regularibus" di Pietro Franceschi detto della Francesca usurpata da Fra Luca Pacioli, ed. G. Mancini, Rome, (1916).
  171. ^ Alan Sangster, Greg Stoner & Patricia McCarthy: "The market for Luca Pacioli’s Summa Arithmetica" (Accounting, Business & Financial History Conference, Cardiff, September 2007) pp. 1–2
  172. ^ Grattan-Guinness, Ivor (1997). The Rainbow of Mathematics: A History of the Mathematical Sciences. W.W. Norton. ISBN 978-0-393-32030-5.
  173. ^ Kline, Morris (1953). Mathematics in Western Culture. Great Britain: Pelican. pp. 150–51.
  174. ^ Struik, Dirk (1987). A Concise History of Mathematics (3rd. ed.). Courier Dover Publications. p. 89. ISBN 978-0-486-60255-4.
  175. ^ Eves, Howard, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0, p. 379, "...the concepts of calculus...(are) so far reaching and have exercised such an impact on the modern world that it is perhaps correct to say that without some knowledge of them a person today can scarcely claim to be well educated."
  176. ^ Maurice Mashaal, 2006. Bourbaki: A Secret Society of Mathematicians. American Mathematical Society. ISBN 0-8218-3967-5, 978-0-8218-3967-6.
  177. ^ Alexandrov, Pavel S. (1981), "In Memory of Emmy Noether", in Brewer, James W; Smith, Martha K (eds.), Emmy Noether: A Tribute to Her Life and Work, New York: Marcel Dekker, pp. 99–111, ISBN 978-0-8247-1550-2.
  178. ^ Mathematics Subject Classification 2000

References

  • Berggren, Lennart; Borwein, Jonathan M.; Borwein, Peter B. (2004), Pi: A Source Book, New York: Springer, ISBN 978-0-387-20571-7
  • Boyer, C.B. (1991) [1989], A History of Mathematics (2nd ed.), New York: Wiley, ISBN 978-0-471-54397-8
  • Cuomo, Serafina (2001), Ancient Mathematics, London: Routledge, ISBN 978-0-415-16495-5
  • Goodman, Michael, K.J. (2016), An introduction of the Early Development of Mathematics, Hoboken: Wiley, ISBN 978-1-119-10497-1{{citation}}: CS1 maint: multiple names: authors list (link)
  • Gullberg, Jan (1997), Mathematics: From the Birth of Numbers, New York: W.W. Norton and Company, ISBN 978-0-393-04002-9
  • Joyce, Hetty (July 1979), "Form, Function and Technique in the Pavements of Delos and Pompeii", American Journal of Archaeology, 83 (3): 253–63, doi:10.2307/505056, JSTOR 505056.
  • Katz, Victor J. (1998), A History of Mathematics: An Introduction (2nd ed.), Addison-Wesley, ISBN 978-0-321-01618-8
  • Katz, Victor J. (2007), The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook, Princeton, NJ: Princeton University Press, ISBN 978-0-691-11485-9
  • Needham, Joseph; Wang, Ling (1995) [1959], Science and Civilization in China: Mathematics and the Sciences of the Heavens and the Earth, vol. 3, Cambridge: Cambridge University Press, ISBN 978-0-521-05801-8
  • Needham, Joseph; Wang, Ling (2000) [1965], Science and Civilization in China: Physics and Physical Technology: Mechanical Engineering, vol. 4 (reprint ed.), Cambridge: Cambridge University Press, ISBN 978-0-521-05803-2
  • Sleeswyk, Andre (October 1981), "Vitruvius' odometer", Scientific American, 252 (4): 188–200.
  • Straffin, Philip D. (1998), "Liu Hui and the First Golden Age of Chinese Mathematics", Mathematics Magazine, 71 (3): 163–81, doi:10.1080/0025570X.1998.11996627
  • Tang, Birgit (2005), Delos, Carthage, Ampurias: the Housing of Three Mediterranean Trading Centres, Rome: L'Erma di Bretschneider (Accademia di Danimarca), ISBN 978-88-8265-305-7.
  • Volkov, Alexei (2009), "Mathematics and Mathematics Education in Traditional Vietnam", in Robson, Eleanor; Stedall, Jacqueline (eds.), The Oxford Handbook of the History of Mathematics, Oxford: Oxford University Press, pp. 153–76, ISBN 978-0-19-921312-2

Further reading

General

  • Aaboe, Asger (1964). Episodes from the Early History of Mathematics. New York: Random House.
  • Bell, E.T. (1937). Men of Mathematics. Simon and Schuster.
  • Burton, David M. The History of Mathematics: An Introduction. McGraw Hill: 1997.
  • Grattan-Guinness, Ivor (2003). Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences. The Johns Hopkins University Press. ISBN 978-0-8018-7397-3.
  • Kline, Morris. Mathematical Thought from Ancient to Modern Times.
  • Struik, D.J. (1987). A Concise History of Mathematics, fourth revised edition. Dover Publications, New York.

Books on a specific period

Books on a specific topic

External links

Documentaries

Educational material

Bibliographies

Organizations

Journals

Directories

Retrieved from "https://dawoum.duckdns.org/w/index.php?title=History_of_mathematics&oldid=84633"