Improper integral

Original article: w:Improper integral

An improper integral of the first kind. The integral may need to be defined on an unbounded domain.

An improper Riemann integral of the second kind. The integral may fail to exist because of a vertical asymptote in the function.

수학적 해석학(mathematical analysis)에서, 부적절한 적분(improper integral)은 적분화의 구간의 끝점이 지정된 실수(real), $\infty$, $-\infty$에 접근할 때, 또는, 일부 예제에서, 양쪽 끝 점이 극한에 접근할 때 한정 적분(definite integral)의 극한(limit)입니다. 그러한 적분은 표준 한정 적분과 같이 기호적으로 종종 쓰이며, 어떤 경우에서 적분화의 극한으로 무한대를 가집니다.

구체적으로, 부적절한 적분은 다음 형식의 극한입니다:

$\lim _{b\to \infty }\int _{a}^{b}f(x)\,dx,\qquad \lim _{a\to -\infty }\int _{a}^{b}f(x)\,dx,$

또는

$\lim _{c\to b^{-}}\int _{a}^{c}f(x)\,dx,\quad \lim _{c\to a^{+}}\int _{c}^{b}f(x)\,dx,$

이것에서, 우리는 하나 또는 다른 (또는 때때로 양쪽) 끝점에 극한을 취합니다 (Apostol 1967, §10.23).

표기법의 남용(abuse of notation)에 의해, 부적절한 적분은, 아마도 적분화의 극한 사이에 무한대(infinity)를 갖는, 표준 한정 적분처럼 기호적으로 종종 쓰입니다. 한정 적분이 (리만 적분(Rieman integral) 또는 보다 진보된 르베그 적분(Lebesgue integral)의 의미에서) 존재할 때, 이 모호성은 적절한 및 부적절한 적분 둘 다가 값에서 일치할 때 해결됩니다.

종종 우리는, 심지어 함수가 전통적인 의미에서 (예를 들어, 리만 적분(Riemann integral)에서) 적분이 가능하지 않을 때, 부적절한 적분에 대해 값을 계산할 수 있는데, 왜냐하면 함수의 특이점 또는 적분화의 경계 중 하나가 무한이기 때문입니다.

Examples

리만 적분(Riemann integral)의 원래 정의는 구간 [1, ∞) 위에 $1/{x^{2}}$와 같은 함수에 적용하지 않는데, 왜냐하면 이런 경우에서 적분화의 도메인은 무경계(unbounded)이기 때문입니다. 어쨌든, 리만 적분은 연속성(continuity), 및 부적절한 적분을 다음 극한(limit)으로 대신 정의함으로써 종종 확장될 수 있습니다:

$\int _{1}^{\infty }{\frac {1}{x^{2}}}\,dx=\lim _{b\to \infty }\int _{1}^{b}{\frac {1}{x^{2}}}\,dx=\lim _{b\to \infty }\left(-{\frac {1}{b}}+{\frac {1}{1}}\right)=1.$

리만 적분의 좁은 정의는 구간 [0, 1] 위에 함수 $1/{\sqrt {x}}$를 역시 다루지 않습니다. 문제는 여기서 피적분이 적분화 도메인에서 무경계(ubounded)인 것입니다 (정의는 적분화와 피적분의 도메인 둘 다는 경계가 있는 것을 요구합니다). 어쨌든, 부적절한 적분은, 만약 다음 극한으로 이해되면, 존재합니다:

$\int _{0}^{1}{\frac {1}{\sqrt {x}}}\,dx=\lim _{a\to 0^{+}}\int _{a}^{1}{\frac {1}{\sqrt {x}}}\,dx=\lim _{a\to 0^{+}}(2-2{\sqrt {a}})=2.$

The improper integral
$\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi$
has unbounded intervals for both domain and range.

때때로 적분은 그들이 부적절한 곳에서 두 개의 특이점을 가질 수 있습니다. 예를 들어, (오른쪽에 보이는) 0에서 ∞까지 적분되는 함수 1/((x + 1)√x)를 생각해 보십시오. 아래쪽 경계에서, x가 0으로 갈 때 함수가 ∞로 가고, 비록 함수가 0으로 갈지라도, 위쪽 경계는 자체로 ∞입니다. 따라서 이것은 이중으로 부적절한 적분입니다. 말하자면, 1에서 3까지 적분된, 보통의 리만 합은 π/6의 결과를 산출하기에 충분합니다. 1에서 ∞까지 적분하기 위해, 리만 합은 가능하지 않습니다. 어쨌든, 임의의 유한 위쪽 경계, (t > 1를 갖는) 말하자면 t는 잘 정의된 결과, 2 arctan(√t) − π/2를 제공합니다. 이것은 t가 무한대로 갈 때 유한 극한, 즉 π/2를 가집니다. 비슷하게, 1/3에서 1까지 적분은 마찬가지로 리만 합을 허용하며, 우연히 다시 π/6를 생성합니다. 임의의 양의 값 (s < 1를 갖는) s에 의해 1/3을 대체하는 것은 똑같이 안전하며, π/2 − 2 arctan(√s)을 제공합니다. 이것은, 또한, s가 영으로 갈 때 유한 극한, 즉 π/2를 가집니다. 두 단편의 극한을 결합하여, 이 부적절한 적분의 결과는 다음입니다:

${\begin{aligned}\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}&{}=\lim _{s\to 0^{+}}\int _{s}^{1}{\frac {dx}{(x+1){\sqrt {x}}}}+\lim _{t\to \infty }\int _{1}^{t}{\frac {dx}{(x+1){\sqrt {x}}}}\\&{}=\lim _{s\to 0^{+}}\left({\frac {\pi }{2}}-2\arctan {\sqrt {s}}\right)+\lim _{t\to \infty }\left(2\arctan {\sqrt {t}}-{\frac {\pi }{2}}\right)\\&{}={\frac {\pi }{2}}+\left(\pi -{\frac {\pi }{2}}\right)\\&{}=\pi .\end{aligned}}$

이 과정이 성공을 보증하지는 않습니다; 극한은 존재하지 않거나, 무한일 수 있습니다. 예를 들어, 0에서 1까지 경계진 구간에 걸쳐 1/x의 적분은 수렴하지 않습니다; 그리고 1에서 ∞까지 무경계 구간에 걸쳐 1/√x의 적분은 수렴하지 않습니다.

The improper integral
$\int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}=6$
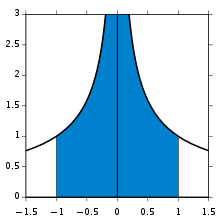
converges, since both left and right limits exist, though the integrand is unbounded near an interior point.

그것은 피적분이 내부 점 근처에서 무경계이면 역시 발생할 수 있으며, 이 경우에서 적분은 해당 점에서 반드시 분할되어야 합니다. 전체적으로 수렴하는 적분에 대해, 양쪽의 극한 적분이 반드시 존재하고 반드시 경계져야 합니다. 예를 들어:

${\begin{aligned}\int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}&{}=\lim _{s\to 0}\int _{-1}^{-s}{\frac {dx}{\sqrt[{3}]{x^{2}}}}+\lim _{t\to 0}\int _{t}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}\\&{}=\lim _{s\to 0}3(1-{\sqrt[{3}]{s}})+\lim _{t\to 0}3(1-{\sqrt[{3}]{t}})\\&{}=3+3\\&{}=6.\end{aligned}}$

그러나 비슷한 적분

$\int _{-1}^{1}{\frac {dx}{x}}$

은 이런 방식에서 값을 할당될 수 없는데, 왜냐하면 영 위 및 아래의 적분은 독립적으로 수렴하지 않기 때문입니다. (어쨌든, 코시 주요 값(Cauchy principal value)을 참조하십시오.)

Convergence of the integral

부적절한 적분은 만약 그것을 정의되는 극한이 존재하면 수렴합니다. 따라서 예를 들어 우리는 다음임을 말합니다: 부적절한 적분

$\lim _{t\to \infty }\int _{a}^{t}f(x)\,dx$

은, 만약 극한 아래의 적분이 모든 충분하게 큰 t에 대해 존재하고, 극한의 값이 L과 같으면, 존재하고 L과 같습니다.

그것은 무한대로 발산하는 부적절한 적분에 대해 역시 가능합니다. 해당 경우에서, 우리는 ∞ (또는 -∞)의 값을 적분에 할당할 수 있습니다. 예를 들어

$\lim _{b\to \infty }\int _{1}^{b}{\frac {1}{x}}\,dx=\infty .$

어쨌든, 다른 부적절한 적분은 특별한 방향없이, 다음에서 처럼, 단순히 발산할 수 있습니다:

$\lim _{b\to \infty }\int _{1}^{b}x\sin(x)\,dx,$

이것은, 심지어 확장된 실수(extended real number)일 때에도, 존재하지 않습니다. 이것은 진동에 의한 발산으로 불립니다.

부적절한 적분화의 기술의 한계는 극한이 한 번에 하나의 끝점에 관해 반드시 취해져야 한다는 것입니다. 따라서, 예를 들어, 다음 형식의 부적절한 적분

$\int _{-\infty }^{\infty }f(x)\,dx$

은 두 개의 분리된 극한을 취하는 것에 의해 정의될 수 있습니다; 즉,

$\int _{-\infty }^{\infty }f(x)\,dx=\lim _{a\to -\infty }\lim _{b\to \infty }\int _{a}^{b}f(x)\,dx$

은 이중 적분이 유한일 때 제공됩니다. 그것은 첫 번째 종류의 구별되는 부적절한 적분의 쌍으로 역시 정의될 수 있습니다:

$\lim _{a\to -\infty }\int _{a}^{c}f(x)\,dx+\lim _{b\to \infty }\int _{c}^{b}f(x)\,dx$

여기서 c는 적분화를 시작하기 것에서 임의의 편리한 점입니다. 이 정의는 이들 적분화의 하나가 무한일 때, 또는 만약 그들이 같은 부호를 가지면 둘 다일 때 역시 적용합니다.

양 끝점이 무한대인 부적절한 적분의 예제는 가우스 적분(Gaussian integral) $\int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}$입니다. 무한대에서 평가하는 예제는 $\int _{-\infty }^{\infty }e^{x}\,dx$입니다. 그러나 우리는 명백하게 이 종류의 다른 극한, $\int _{-\infty }^{\infty }x\,dx$와 같은 것을 절대 정의하지 못하는데, 왜냐하면 이중 적분이 무한이고 두-적분 방법

$\lim _{a\to -\infty }\int _{a}^{c}x\,dx+\lim _{b\to \infty }\int _{c}^{b}x\,dx$

은 $\infty -\infty$를 산출하기 때문입니다. 이 경우에서, 우리는 어쨌든 코시 주요 값(Cauchy principal value)의 의미에서 부적절한 적분을 정의할 수 있습니다:

$\operatorname {p.v.} \int _{-\infty }^{\infty }x\,dx=\lim _{b\to \infty }\int _{-b}^{b}x\,dx=0.$

우리가 부적절한 적분을 결정하는 것에서 반드시 다루어야 할 질문은 다음입니다:

• 극한이 존재합니까?
• 극한이 계산될 수 있습니까?

첫 번째 질문은 수학적 해석학(mathematical analysis)의 이슈입니다. 두 번째 것은 미적분 기법에 의해 다루어질 수 있지만, 역시 어떤 경우에서 윤곽 적분화(contour integration), 푸리에 변환(Fourier transform) 및 다른 보다 고급 방법으로 다루어질 수 있습니다.

Types of integrals

적분화(integration)의 하나보다 더 많은 이론이 있습니다. 미적분학의 관점에서, 리만 적분(Riemann integral) 이론은 보통 기본 이론으로 가정됩니다. 부적절한 적분을 사용함에서, 어떤 적분화 이론이 작용하는지가 중요할 수 있습니다.

• 리만 적분 (또는 그것과 동등한 다르부 적분(Darboux integral))에 대해, 부적절한 적분은 무경계 구간에 대해 (왜냐하면 우리는 구간을 유한 길이의 무한하게 많은 부분 구간으로 나눌 수 없기 때문입니다) 및 유한 적분을 갖는 무경계 함수에 대해 (왜냐하면, 그것이 위의 무경계 가정에 의해, 위쪽 적분은 무한일 수 있지만, 아래쪽 적분은 유한일 수 있기 때문입니다) 둘 다 필요됩니다.
• 르베그 적분(Lebesgue integral)은, 종종 부적절한 리만 적분으로 오직 존재하는 적분은, $\int _{1}^{\infty }{\frac {1}{x^{2}}}\,dx$와 같은, (적절한) 르베그 적분으로 존재하도록, 무경계 도메인과 무경계 함수를 다르게 다룹니다. 다른 한편으로, 부적절한 리만 적분을 가지지만, $\int _{0}^{\infty }{\frac {\sin x}{x}}\,dx$와 같은, (적절한) 르베그 적분을 가지지 않는 적분이 역시 있습니다. 르베그 이론은 결핍으로 이것을 보지 않습니다: 측정 이론(measure theory)의 관점에서, $\int _{0}^{\infty }{\frac {\sin x}{x}}\,dx=\infty -\infty$ 및 만족스럽게 정의될 수는 없습니다. 어떤 상황에서, 어쨌든, 예를 들어, 코시 주요 값(Cauchy principal value)을 정의할 때와 같이, 부적절한 르베그 적분을 사용하는 것이 편리할 수 있습니다. 르베그 적분은, 전체 실수 직선에 걸쳐 적분의 확장되는 사용을 갖는, 푸리에 변환(Fourier transform)의 이론적 처리에서 다소 필수적입니다.
• 헨스탁–쿠르즈베일 적분(Henstock–Kurzweil integral)에 대해, 부적절한 적분은 필요하지 않고, 이것은 이론의 힘으로 보입니다: 그것은 모든 르베그 적분-가능 및 부적절한 리만 적분-가능 함수를 포함합니다.

Improper Riemann integrals and Lebesgue integrals

Figure 1

Figure 2

어떤 경우에서, 적분

$\int _{a}^{c}f(x)\,dx$

은 다음 극한에 대한 참조없이 적분 (예를 들어 르베그 적분(Lebesgue integral))으로 정의될 수 있습니다:

$\lim _{b\to c^{-}}\int _{a}^{b}f(x)\,dx$

그러나 그렇지 않으면 편리하게 결코 계산될 수 없습니다. 이것은 a에서 c까지 적분된 함수 f가 c에서 수직 점근선(vertical asymptote)을 가질 때, 또는 만약 c = ∞이면, 종종 발생합니다 (그림 1과 2를 참조하십시오). 그러한 경우에서, 부적절한 리만 적분은 함수의 르베그 적분을 계산하는 것을 허용합니다. 구체적으로, 다음 정리가 유지됩니다 (Apostol 1974, Theorem 10.33):

• 만약 함수 f가 모든 b ≥ a에 대해 [a,b] 위에 리만 적분-가능이고, 부분 적분

$\int _{a}^{b}|f(x)|\,dx$

은 b → ∞로 경계지면, 부적절한 리만 적분

$\int _{a}^{\infty }f(x)\,dx,\quad {\text{and }}\int _{a}^{\infty }|f(x)|\,dx$

둘 다는 존재합니다. 게다가, f가 [a, ∞) 위에 르베그 적분 가능이고, 그의 르베그 적분은 그의 부적절한 리만 적분과 같습니다.

예를 들어, 적분

$\int _{0}^{\infty }{\frac {dx}{1+x^{2}}}$

은 다음 부적절한 적분으로 대안적으로 해석될 수 있습니다:

$\lim _{b\to \infty }\int _{0}^{b}{\frac {dx}{1+x^{2}}}=\lim _{b\to \infty }\arctan {b}={\frac {\pi }{2}},$

또는 그것은 집합 (0, ∞)에 걸쳐 르베그 적분(Lebesgue integral)으로 대신 해석될 수 있습니다. 적분의 이런 두 종류는 모두 일치하므로, 우리는, 심지어 우리가 궁극적으로 그것을 르베그 적분으로 여기기를 원한다고 할지라도, 적분의 값을 계산하기 위해 첫 번째 방법을 선택하는 것이 자유롭습니다. 따라서 부적절한 적분은 적분의 실제 값을 얻기 위한 명확하게 유용한 도구입니다.

다른 경우에서, 어쨌든, 유한 끝점 사이의 르베그 적분은 심지어 정의되지 않을 수 있는데, 왜냐하면 f의 양 및 음의 부분의 적분은 둘 다 무한하지만, 부적절한 리만 적분이 여전히 존재할 수 있기 때문입니다. 그러한 경우는 "적절하게 부적절한" 적분이며, 즉 그들의 값은 그러한 극한을 제외할 때 결코 정의될 수 없습니다. 예를 들어,

$\int _{0}^{\infty }{\frac {\sin(x)}{x}}\,dx$

은 르베그 적분으로 절대 해석될 수 없는데, 왜냐하면 다음이기 때문입니다:

$\int _{0}^{\infty }\left|{\frac {\sin(x)}{x}}\right|\,dx=\infty .$

그러나 $f(x)={\frac {\sin(x)}{x}}$는 그럼에도-불구하고 임의의 두 유한 끝점 사이에서 적분-가능이고, 0과 ∞ 사이의 그의 적분은 다음 적분의 극한으로 보통 이해됩니다:

$\int _{0}^{\infty }{\frac {\sin(x)}{x}}\,dx=\lim _{b\to \infty }\int _{0}^{b}{\frac {\sin(x)}{x}}\,dx={\frac {\pi }{2}}.$

Singularities

우리는 부적절한 적분의 특이점에 대해 말할 수 있으며, 극한이 사용되는 곳에서 확장된 실수 직선(extended real number line)의 그들 점을 의미합니다.

Cauchy principal value

Main article: Cauchy principal value

두 극한의 값에서 차이를 생각해 보십시오:

$\lim _{a\to 0^{+}}\left(\int _{-1}^{-a}{\frac {dx}{x}}+\int _{a}^{1}{\frac {dx}{x}}\right)=0,$

$\lim _{a\to 0^{+}}\left(\int _{-1}^{-a}{\frac {dx}{x}}+\int _{2a}^{1}{\frac {dx}{x}}\right)=-\ln 2.$

전자는 다르게 잘못-정의된 다음 표현의 코시 주요 값입니다:

$\int _{-1}^{1}{\frac {dx}{x}}{\ }\left({\text{which}}\ {\text{gives}}\ -\infty +\infty \right).$

비슷하게, 우리는 다음을 가집니다:

$\lim _{a\to \infty }\int _{-a}^{a}{\frac {2x\,dx}{x^{2}+1}}=0,$

그러나 다음을 가집니다:

$\lim _{a\to \infty }\int _{-2a}^{a}{\frac {2x\,dx}{x^{2}+1}}=-\ln 4.$

전자는 다르게 잘못-정의된 다음 표현의 주요 값입니다:

$\int _{-\infty }^{\infty }{\frac {2x\,dx}{x^{2}+1}}{\ }\left({\text{which}}\ {\text{gives}}\ -\infty +\infty \right).$

위의 극한의 모두는 불확정 형식(indeterminate form) ∞ − ∞의 경우들입니다.

이들 병리(pathologies)는 "르베그 적분-가능" 함수 즉, 그의 절댓값(absolute value)이 유한인 적분 함수에 영향을 미치지 않습니다.

Summability

부적절한 적분은 그것을 정의하는 극한이 존재하지 않을 수 있는 것의 의미에서 발산일 수 있습니다. 이 경우에서, 부적절한 적분에 대해 수렴 값을 생성할 수 있는 극한의 보다 정교한 정의가 있습니다. 이것은 합가능성(summability) 방법으로 불립니다.

푸리에 해석(Fourier analysis)에서 널리 쓰이는, 하나의 합가능성 방법은 체사로 합(Cesàro summation) 방법입니다. 적분

$\int _{0}^{\infty }f(x)\,dx$

은, 만약

$\lim _{\lambda \to \infty }\int _{0}^{\lambda }\left(1-{\frac {x}{\lambda }}\right)^{\alpha }f(x)\,dx$

이 존재하고 유한이면, 체사로 합가능 (C, α)입니다 (Titchmarsh 1948, §1.15). 이 극한의 값은, 그것이 존재해야만, 적분의 (C, α) 합입니다.

적분은, 그것이 부적절한 적분으로 존재할 때, 정확하게 (C, 0) 합가능입니다. 어쨌든, (리만 또는 르베그의 의미에서) 부적절한 적분으로 수렴을 실패하는 α > 0에 대해 (C, α) 합가능인 적분이 있습니다. 하나의 예제는 다음 적분입니다:

$\int _{0}^{\infty }\sin x\,dx$

이것은 부적절한 적분으로 존재하는 것이 실패하지만, 모든 각 α > 0에 대해 (C,α) 합가능입니다. 이것은 그란디의 급수(Grandi's series)의 적분 버전입니다.

Multivariable improper integrals

부적절한 적분은 여러 변수의 함수에 대해 역시 정의될 수 있습니다. 정의는, $\mathbb {R} ^{2}$와 같은, 무경계 도메인에 걸쳐 적분화를 요구하는지 여부, 또는 $f(x,y)=\log(x^{2}+y^{2})$와 같은, 특이점을 갖는 함수를 적분하는지 여부에 따라, 약간 다릅니다.

Improper integrals over arbitrary domains

만약 $f:\mathbb {R} ^{n}\to \mathbb {R}$가, $a>0$에 대해, 형식 $[-a,a]^{n}$의 모든 각 컴팩트 입방체에 걸쳐 리만 적분-가능인 비-음의 함수이면, $\mathbb {R} ^{n}$에 걸쳐 f의 부적절한 적분은, 다음 극한이 존재할 때, 그것으로 정의됩니다:

$\lim _{a\to \infty }\int _{[-a,a]^{n}}f$.

$\mathbb {R} ^{n}$에서 임의의 도메인 A 위의 함수는 A 밖의 영에 의해 $\mathbb {R} ^{n}$ 위의 함수 ${\tilde {f}}$로 확장됩니다:

${\tilde {f}}(x)={\begin{cases}f(x)&x\in A\\0&x\not \in A\end{cases}}$

경계진 도메인 A에 걸쳐 함수의 리만 적분은, 그런-다음, A를 포함하는 입방체 $[-a,a]^{n}$에 걸쳐 확장된 함수 ${\tilde {f}}$의 적분으로 정의됩니다:

$\int _{A}f=\int _{[-a,a]^{n}}{\tilde {f}}.$

보다 일반적으로, 만약 A가 무경계이면, $\mathbb {R} ^{n}$에서 임의의 도메인에 걸쳐 부적절한 리만 적분은 다음 극한으로 정의됩니다:

$\int _{A}f=\lim _{a\to \infty }\int _{A\cap [-a,a]^{n}}f=\lim _{a\to \infty }\int _{[-a,a]^{n}}{\tilde {f}}.$

Improper integrals with singularities

만약 f가 도메인 A에서 무경계 비-음의 함수이면, f의 부적절한 적분은 어떤 절단 M에서 f를 잘라내는 것, 결과 함수를 적분하는 것, 및 그런-다음 M이 무한대로 경향이 있을 때 극한을 취함으로써 정의됩니다. 즉 $M>0$에 대해, $f_{M}=\min\{f,M\}$으로 놓습니다. 그런-다음, 다음 극한이 존재할 때, 제공된 극한으로 정의합니다:

$\int _{A}f=\lim _{M\to \infty }\int _{A}f_{M}$.

Functions with both positive and negative values

이들 정의는 비-음수인 함수에 대해 적용합니다. 보다 일반적인 함수 f는 그의 양의 부분 $f_{+}=\max\{f,0\}$ 및 음의 부분 $f_{-}=\max\{-f,0\}$의 차이로 재구성될 수 있으므로, $f_{+}$와 $f_{-}$ 둘 다 비-음의 함수를 갖는 다음입니다:

$f=f_{+}-f_{-}$

함수 f는, 만약 $f_{+}$와 $f_{-}$의 각각이 하나를 가지면, 부적절한 리만 적분을 가지며, 이 경우에서 해당 부적절한 적분의 값은 다음에 의해 정의됩니다:

$\int _{A}f=\int _{A}f_{+}-\int _{A}f_{-}.$

이런 의미에서 존재하기 위해, 부적절한 적분은 반드시 절대적으로 수렴인데, 왜냐하면 다음이기 때문입니다:

$\int _{A}|f|=\int _{A}f_{+}+\int _{A}f_{-}.$

Bibliography

• Apostol, T (1974), Mathematical analysis, Addison-Wesley, ISBN 978-0-201-00288-1.
• Apostol, T (1967), Calculus, Vol. 1 (2nd ed.), Jon Wiley & Sons.
• Autar Kaw, Egwu Kalu (2008), Numerical Methods with Applications (1st ed.), autarkaw.com
• Titchmarsh, E (1948), Introduction to the theory of Fourier integrals (2nd ed.), New York, N.Y.: Chelsea Pub. Co. (published 1986), ISBN 978-0-8284-0324-5.
• Cooper, Jeffery (2005), Working analysis, Gulf Professional
• Ghorpade, Sudhir; Limaye, Balmohan (2010), A course in multivariable calculus and analysis, Springer

External links

• Numerical Methods to Solve Improper Integrals at Holistic Numerical Methods Institute
• Improper integrals – chapter from an online textbook