Complex number

복소수(complex number)는 형식 $a + bi$ 로 표현될 수 있는 숫자(number)입니다; 여기서 $a$ 와 $b$ 는 실수이고, $i$ 는 방정식 $x 2 = -1$ 의 해입니다. 이 방정식을 만족시키는 실수(real number)는 없기 때문에, $i$ 는 허수(imaginary number)로 불립니다. 복소수 $a + bi$ 에 대해, $a$ 는 실수 부분(real part)으로 불리고, $b$ 는 허수 부분(imaginary part)으로 불립니다. 역사적인 명명법 "상상의(imaginary)"에도 불구하고, 복소수는 수학적 과학에서 실수에서의 "실제의(real)"와 마찬가지로 여겨지고, 자연계의 과학적 묘사의 여러 관점에서 근본입니다.^{[note 1]}^[1]

복소수는 실수(real number)에서 해를 가지지 않는 특정 방정식에 대해 해를 허용합니다. 예를 들어 방정식

(x+1)^{2}=-9

은 실수 해를 가지지 않는데, 왜냐하면 실수의 제곱은 음의 값이 될 수 없기 때문입니다. 복소수는 이 문제에 대한 해를 제공합니다. 그 아이디어는, 앞의 방정식과 같은 것에 대한 해는 구할 수 있도록, 관계 $i 2 = -1$ 를 만족시키는 것으로 취해지는 (때때로 허수 단위(imaginary unit)로 불리는) 불확정수(indeterminate) $i$ 와 함께 실수를 확장(extend)하는 것입니다. 이 경우에서 해는 $-1 + 3 i$ 및 $-1 - 3 i$ 인데, 왜냐하면 $i 2 = -1$ 이라는 사실을 사용하여 검증될 수 있기 때문입니다:

((-1+3i)+1)^{2}=(3i)^{2}=\left(3^{2}\right)\left(i^{2}\right)=9(-1)=-9,

((-1-3i)+1)^{2}=(-3i)^{2}=(-3)^{2}\left(i^{2}\right)=9(-1)=-9.

대수학의 기본 정리(fundamental theorem of algebra)에 따라, 단일 변수에서 실수 또는 복소수 계수를 가진 모든 다항 방정식(polynomial equation)은 복소수에서 해를 가집니다. 대조적으로, 실수 계수를 가진 어떤 다항 방정식은 실수에서 해를 가지지 않습니다. 16세기 이탈리아 수학자 제롤라모 카르다노(Gerolamo Cardano)는 삼차 방정식(cubic equations)에 대한 해를 찾기 위한 시도에서 복소수를 도입한 것으로 공인됩니다.^[2]

공식적으로, 복소수 시스템은, 허수 $i$ 에 의한, 보통의 실수의 대수적 확장(algebraic extension)으로 정의될 수 있습니다.^[3] 이것은, 복소수가, 부과된 규칙 $i 2 = -1$ 과 함께, 변수 $i$ 에서 다항식으로, 더하고, 빼고, 곱해질 수 있음을 의미합니다. 게다가, 복소수는 비-영 복소수에 의해 역시 나뉠 수 있습니다. 전체로서, 복소수 시스템은 하나의 필드(field)입니다.

기하학적으로, 복소수는 실수 부분에 수평 축(horizontal axis)과 허수 부분에 수직 축(vertical axis)을 사용함으로써, 일-차원(one-dimensional) 숫자 직선(number line)의 개념을 이-차원(two-dimensional) 복소 평면(complex plane)으로 확장합니다. 복소수 $a + bi$ 는 복소 평면에서 점 $(a, b)$ 로 식별될 수 있습니다. 그의 실수 부분이 영인 복소수는 순수한 허수(imaginary)라고 말합니다; 이들 숫자에 대해 그 점은 복소 평면의 수직 축 위에 놓입니다. 그의 허수 부분이 영인 복소수는 실수로 보일 수 있습니다; 그 점은 복소 평면의 수평 축에 놓입니다. 복소수는 극 형식으로 역시 나타낼 수 있으며, 이것은 각 복소수를 원점으로부터의 거리 (그의 크기)와 이 복소수의 편각(argument)으로 알려진 특정 각도를 결합시킵니다.

유클리드 평면(Euclidean plane) ( $\mathbb {R} ^{2}$ )인, 복소 평면과 함께 복소수의 기하학적 식별은 그들의 구조를 분명한 실수 2-차원 벡터 공간(vector space)으로 만듭니다. 복소수의 실수 부분과 허수 부분은 정식의 표준 기저(standard basis)에 관한 벡터의 성분으로 취할 수 있습니다. 복소수의 덧셈은 따라서 보통 벡터의 성분-별 덧셈으로 즉시 묘사됩니다. 어쨌든, 복소수는 벡터 공간에서 반드시 유효한 것이 아닌, 추가적인 연산을 포함하는, 보다 풍부한 대수적 구조를 허용합니다; 예를 들어, 두 복소수의 곱셈은 항상 다시 복소수를 생성하고, 스칼라 곱셈(scalar multiplication), 스칼라 곱(scalar product) 또는 많은 벡터 공간에서 사용-가능한 다른 (반쌍)선형 형식(forms)와 같은, 벡터를 포함하는 보통 "곱"에 대해 잘못 판단해서는 안됩니다; 그리고 광범위하게 이용되는 벡터 곱(vector product)은 삼-차원에서 방향(orientation)-의존적 형태로 오직 존재합니다.

Definition

실수(real number)의 개념에 기초로 한, 복소수는 형식 $a + bi$ 의 숫자이며, 여기서 $a$ and $b$ 는 실수이고 $i$ 는 $i 2 = -1$ 을 만족시키는 불확정수입니다. 예를 들어, $2 + 3 i$ 는 복소수입니다.^[4]

이 방법으로, 복소수는 단일 불확정수 $i$ 에서 실수 계수를 가진 다항식(polynomial)으로 정의되며, 이것에 대해 관계 $i 2 + 1 = 0$ 이 부과됩니다. 이 정의에 기초하여, 복소수는 다항식에 대해 덧셈과 곱셈을 사용하여, 더해지거나 곱해질 수 있습니다. 관계 $i 2 + 1 = 0$ 은 방정식 $i 4 k = 1, i 4 k +1 = i, i 4 k +2 = -1,$ 및 $i 4 k +3 = - i$ 를 유도하며, 이것은 모든 정수 k에 대해 유지됩니다; 이것들은 복소수를 $i$ 에서 선형 다항식에 대한 덧셈과 곱셈으로부터, 다시 실수 계수 $a, b$ 를 갖는 형식 $a + bi$ 을 초래하는 임의의 다항식의 감소를 허용합니다

실수 $a$ 는 복소수 $a + bi$ 의 실수 부분으로 불립니다; 실수 $b$ 는 그의 허수 부분으로 불립니다. 강조하기 위해, 허수 부분은 인수 $i$ 를 포함하지 않습니다; 즉, 허수 부분은 $b$ 이지, $bi$ 가 아닙니다.^[5]^[6]

공식적으로, 복소수는 다항식 $i 2 + 1$ 에 의해 생성된 아이디얼(ideal)에 의해, 불확정수 $i$ 에서 다항식 링(polynomial ring)의 몫 링(quotient ring)으로 정의됩니다 (아래(below)를 참조하십시오).^[7]

Notation

실수 $a$ 는 그의 허수 부분이 0인 복소수 $a + 0 i$ 로 여길 수 있습니다. 순수한 허수(imaginary number) $bi$ 는 실수 부분이 영인 복소수 $0 + bi$ 입니다. 다항식과 마찬가지로, $a + 0 i$ 에 대해 $a$ 로, $0 + bi$ 에 대해 $bi$ 로 쓰는 것이 공통적입니다. 게다가, 허수 부분이 음수, 즉 $b = - |b| < 0$ 일 때, $a + (- |b|) i$ 대신에 $a - |b|i$ 를 쓰는 것이 공통적입니다; 예를 들어, $b = -4$ 에 대해, $3 - 4 i$ 는 $3 + (-4) i$ 대신에 쓸 수 있습니다.

실수 계수를 가진 다항식에서 불확정수 $i$ 와 실수의 곱셈은 교환적이므로, 다항식 $a + bi$ 는 $a + ib$ 로 쓸 수 있습니다. 이것은, 예를 들어, $b$ 가 근호적일 때, 표현에 의해 나타내는 허수 부분에 대해 종종 편리합니다.^[8]

복소수 $z$ 의 실수 부분은 $Re(z)$ 또는 $ℜ(z)$ 으로 나타냅니다; 복소수 $z$ 의 허수 부분은 $Im(z)$ 또는 $ℑ(z)$ 으로 나타냅니다. 예를 들어,

\operatorname {Re} (2+3i)=2\quad

및

\quad \operatorname {Im} (2+3i)=3.

모든 복소수의 집합(set)은 $\mathbf {C}$ (upright bold) 또는 $\mathbb {C}$ (blackboard bold)으로 나타냅니다.

일부 분야, 특히 전자기학(electromagnetism) 및 전기 공학(electrical engineering)에서, $j$ 가 $i$ 대신에 사용되는데 왜냐하면 $i$ 는 전류(electric current)를 나타내기 위해 자주 사용되기 때문입니다.^[9] 이들 경우에서, 복소수는 $a + bj$ 또는 $a + jb$ 로 쓰입니다.

Visualisation

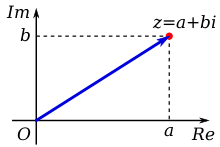
복소수 $z$ 는 따라서 실수의 순서 쌍(ordered pair) $(Re(z), Im(z))$ 으로 식별될 수 있으며, 이것은 차례로 이-차원 공간에서 점의 좌표로 해석될 수 있습니다. 가장 직접적 공간은 적절한 좌표와 함께 유클리드 평면이며, 장-로베르 아르강(Jean-Robert Argand)의 이름을 따서 지은, 아르강 다이어그램(Argand diagram) 또는 복소 평면(complex plane)이라고 불립니다.^[10]^[11] 좌표가 투영될 수 있는 또 다른 주요한 공간은 구의 이-차원 표면이며, 이것은 그런 다음 리만 구(Riemann sphere)라고 불립니다.

Cartesian complex plane

두 개의 임의의 실수 값을 포함하는 복소수의 정의는 복소 평면에서 데카르트 좌표의 사용을 즉시 제안합니다. 수평 (실수) 축은 일반적으로 오른쪽으로 증가하는 값을 갖는 실수 부분을 표시하기 위해 사용되고 위쪽으로 증가하는 값을 갖는 허수 부분은 수직 (허수) 축에 표시합니다.

도표화된 숫자는 좌표화된 점, 또는 원점에서 이 점까지의 위치 벡터(position vector)로 보일 수 있습니다. 복소수 $z$ 의 좌표 값은 데카르트, 직교 또는 대수적 형식을 제공한다고 말합니다.

특히, 덧셈과 곱셈의 연산은 복소수가 위치 벡터로 보일 때 매우 자연스러운 기하학적 특성을 취합니다: 덧셈은 벡터 덧셈(vector addition)에 해당하지만, 곱셈은 그들의 크기는 곱하는 것과 그들이 실수 축과 만드는 각도를 더하는 것에 해당합니다 (아래(below)를 참조하십시오). 이들 방법으로 볼 때, $i$ 에 의한 복소수의 곱셈은 원점에 대한 위치 벡터를 반-시계 방향(counterclockwise)으로 1/4 회전(turn) (90°)만큼 회전하는 것에 해당합니다.

(a+bi)\cdot i=ai+b(i)^{2}=-b+ai.

Polar complex plane

Modulus and argument

복소 평면에서 좌표에 대해 대안적인 선택은 원점(origin) (O)으로부터 점 $z$ 의 거리, 및 양의 실수 축(positive real axis)에서 반-시계-방향 의미에서 선분 Oz 사이의 각도를 사용하는 극 좌표 시스템(polar coordinate system)입니다. 이것은 복소수의 극 형식으로 이어집니다.

복소수 $z = x + yi$ 의 절댓값(absolute value) (또는 모듈러스(modulus) 또는 크기(magnitude))은 다음입니다:^[12]

r=|z|={\sqrt {x^{2}+y^{2}}}.

만약 $z$ 가 실수이면 (즉, 만약 $y = 0$ 이면), $r = | x |$ 입니다. 즉, 실수의 절댓값은 복소수에서 절댓값과 같습니다.

피타고라스의 정리(Pythagoras' theorem)에 의해, 복소수의 절댓값은 복소 평면(complex plane)에서 복소수를 나타내는 점의 원점에 대한 거리입니다.

$z$ 의 편각(argument) (많은 응용에서 "위상(phase)" $φ$ 로 언급됨)은 양의 실수 축과 함께 radius Oz의 각도이고, $\arg(z)$ 로 쓰입니다. 모듈러스와 마찬가지로, 편각은 실수에-의한-허수 부분의 몫에 대한 역 탄젠트를 적용함으로써 직교 형식 $x+yi$ ^[13]으로부터 구할 수 있습니다. 반-각 항등식을 사용함으로써 아크탄젠트의 단일 가지는 $arg$ -함수의 범위, $(-π, π]$ 로 다루기에 충분하고, 보다 미묘한 경우-별 해석을 피할 수 있습니다:

\varphi =\arg(x+yi)={\begin{cases}2\arctan \left({\dfrac {y}{{\sqrt {x^{2}+y^{2}}}+x}}\right)&{\text{if }}x>0{\text{ or }}y\neq 0,\\\pi &{\text{if }}x<0{\text{ and }}y=0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}

통상적으로, 위에서 주어진 것처럼, 구간 $(-π, π]$ 에서 주요 값(principal value)이 선택됩니다. 범위 $[0, 2π)$ 에서 값은, 만약 그 값이 음수이면, $2π$ 를 더함으로써 구해집니다. $φ$ 의 값은 이 기사에서 라디안(radian)으로 표현됩니다. 그것은 $2π$ 의 정수배만큼 증가할 수 있고 양의 실수 축의 반직선과 원점에서 z를 통과하는 반직선 사이의 형성된 것으로 보이는 같은 각도를 여전히 제공합니다. 따라서, 각(arg) 함수는 때때로 다중-값(multivalued)으로 고려됩니다. 복소수 0에 대해 극 각도는 미-결정이지만, 극 각도 0의 임의의 선택은 공통입니다.

$φ$ 의 값은 atan2의 결과와 같습니다:

\varphi =\operatorname {atan2} \left(\operatorname {Im} (z),\operatorname {Re} (z)\right).

함께, $r$ 과 $φ$ 는 복소수를 나타내는 또 다른 방법, 극 형식(polar form)을 제공하는데, 왜냐하면 모듈러스와 편각의 조합은 평면 위의 점의 위치를 완전히 지정하기 때문입니다. 극 형식으로부터 원래 직교 좌표를 복구하는 것은 삼각법 형식(trigonometric form)으로 불리는 공식에 의해 행해집니다:

z=r(\cos \varphi +i\sin \varphi ).

오일러의 공식(Euler's formula)을 사용하여, 이것은 다음으로 쓸 수 있습니다:

z=re^{i\varphi }.

cis 함수를 사용하여, 이것은 때때로 다음으로 축약됩니다:

z=r\operatorname {cis} \varphi .

각 표기법(angle notation)에서, 진폭 $r$ 과 위상 $φ$ 와 함께 페이저(phasor)를 나타내기 위해 전자공학(electronics)에서 종종 사용되며, 그것은 다음으로 쓰입니다:^[14]

z=r\angle \varphi .

Complex graphs

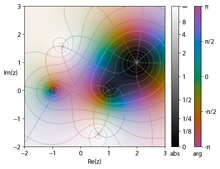
A color wheel graph of the expression $(z 2 - 1)(z - 2 - i) 2 / z 2 + 2 + 2 i$

복소 함수(complex functions)를 시각화할 때, 복소수 입력과 출력 둘 다가 필요합니다. 각 복소수는 이-차원으로 표현되기 때문에, 복소 함수를 시각적으로 그래프로 나타내는 것은, 오직 투영에서 가능한, 사-차원 공간(four dimensional space)의 인식이 요구됩니다. 이것 때문에, 복소 함수를 시각화하는 다른 방법들이 설계되어 왔습니다.

도메인 색칠(Domain coloring)에서, 출력 차원은, 각각, 색깔과 밝기로 표현됩니다. 도메인으로 복소 평면에서 각 점은 장식되는데(ornated), 전형적으로 색깔(color)은 복소수의 인수를 나타내고, 밝기(brightness)는 크기를 나타내는 것입니다. 어두운 점은 모듈러스를 0 근처에 표시하고, 밝은 점은 원점에서 더 멀어지며, 점층법(gradation)은 불연속적이지만, 단조적으로 가정됩니다. 색깔은 빨강, 노랑, 초록, 청록, 파랑에서, 마젠타까지 $0$ 에서 $2 π$ 까지 $π$ /3의 단계에서 종종 변합니다. 이들 그래프는 색깔 바퀴 그래프(color wheel graphs)로 불립니다. 이것은 정보 손실없이 함수를 시각화하는 간단한 방법을 제공합니다. 그림은 $\pm1, (2+i)$ 에 대해 영점 및 $\pm \sqrt -2-2i$ 에서 극점을 보여줍니다.

리만 곡면(Riemann surface)은 복소 함수를 시각화하는 또 다른 방법입니다.^{[further explanation needed]} 리만 곡면은 복소 평면의 변형(deformations)으로 생각될 수 있습니다; 수평 축들은 실수 및 허수 입력을 나타내지만, 단일 수직 축은 실수 또는 허수 출력 중 오직 하나를 나타냅니다. 어쨌든, 리만 곡면은 180도 회전하면 허수 출력을 보여주고, 그 반대도 마찬가지인 그러한 방법으로 세워집니다. 도메인 색칠과 달리, 리만 곡면은 ${\sqrt {z}}$ 와 같은 다중-값 함수(multivalued function)를 나타낼 수 있습니다.

History

일반적인 삼차 방정식(cubic equation)의 (삼각 함수(trigonometric functions)없이) 제곱근(radicals)에서 해는 세 근이 모두 실수일 때 음수(negative numbers)의 제곱근을 포함하며, 인수화에 의해 절대 교정될 수 없는 이 상황은, 만약 삼차가 기약(irreducible) (소위 기약 경우(casus irreducibilis))이면 유리 근 테스트(rational root test)에 의해 지원됩니다. 이 수수께끼는, 비록 그의 생각이 초보적일지라도, 약 1545년에 이탈리아 수학자 제롤라모 카르다노(Gerolamo Cardano)를 복소수의 상상으로 이끕니다.^[15]

일반적인 다항식의 문제에 대한 연구는 궁극적으로 대수학의 기본 정리(fundamental theorem of algebra)로 이어졌으며, 이것은 복소수 계수를 갖는 일차 이상의 모든 각 다항(polynomial) 방정식에 대한 해가 존재함을 보여줍니다. 복소수는 따라서 대수적으로 닫힌 필드(algebraically closed field)를 형성하며, 여기서 임의의 다항(polynomial) 방정식은 근(root)을 가집니다.

많은 수학자들이 복소수의 개발에 기여했습니다. 복소수의 덧셈, 뺄셈, 곱셈 및 근 추출에 대해 규칙은 이탈리아 수학자 라파엘 봄벨리(Rafael Bombelli)에 의해 개발되었습니다.^[16] 복소수에 대해 보다 추상적인 형식주의는 아일랜드 수학자 윌리엄 로언 해밀턴(William Rowan Hamilton)에 의해 더욱 발전되었는데, 그는 이 추상화를 쿼터니언(quaternions)의 이론으로 확장했습니다.

음수(negative number)의 제곱근(square root)에 대한 가장 초기의 잠깐 동안의 참조는 아마도 기원후(AD) 1세기의 그리스 수학자(Greek mathematician) 알렉산드리아의 히이로(Hero of Alexandria)의 연구에서 발생한 것이라고 말할 수 있으며, 여기서 그의 Stereometrica에서, 비록 음수는 헬레니즘 수학(Hellenistic mathematics)에서 인식되지 않았고 히이로는 단순히 그것을 양수 ( ${\sqrt {144-81}}=3{\sqrt {7}}$ )로 대체했을지라도, 그는 계산에서 피라미드(pyramid)의 불가능한 절두체(frustum)의 부피가 항 ${\sqrt {81-144}}=3i{\sqrt {7}}$ 에 도달한다고, 분명하게 오류로, 고려합니다.^[17]

복소수를 자체에서 주제로 연구하려는 원동력은 16세기에 삼차(cubic) 및 사차(quartic) 다항식(polynomial)의 근에 대해 대수적 해(algebraic solution)가 이탈리아 수학자들에 의해 발견되었을 때 처음으로 생겼습니다 (니콜로 폰타나 타르탈리아(Niccolò Fontana Tartaglia), 제롤라모 카르다노(Gerolamo Cardano)를 참조하십시오). 이들 공식은, 비록 우리가 실수 해에 오직 관심이 있었을지라도, 음수의 제곱근의 조작을 때때로 요구된다는 사실을 곧 깨달았습니다 (그러나 훨씬 후에 입증되었습니다).^[18] 예제에서 처럼, 형식 $x^{3}=px+q$ ^{[note 2]}의 삼차 방정식에 대해 타르탈리아의 공식은 다음으로 방정식 $x 3 = x$ 에 대한 해를 제공합니다:

{\tfrac {1}{\sqrt {3}}}\left(\left({\sqrt {-1}}\right)^{1/3}+\left({\sqrt {-1}}\right)^{-1/3}\right).

언뜻보기에, 이것은 말도 안되는 것처럼 보입니다. 어쨌든 복소수를 갖는 공식적인 계산은 방정식 $z 3 = i$ 이 해 $- i$ , ${\tfrac {\sqrt {3}}{2}}+{\tfrac {1}{2}}i$ 및 ${\tfrac {-{\sqrt {3}}}{2}}+{\tfrac {1}{2}}i$ 를 가짐을 보입니다. 타르탈리아의 삼차 공식에서 ${{\sqrt {-1}}^{1/3}}$ 에 대해 차례로 이들을 대체하고 단순화하면, 우리는 $x 3 - x = 0$ 의 해로 0, 1 및 –1을 얻습니다. 물론 이 특정 방정식은 한 눈에 풀 수 있지만 일반적인 공식이 실수 근을 갖는 삼차 방정식을 풀기 위해 사용될 때, 나중에 수학자들이 엄격하게 보여 주듯이,^[18] 복소수의 사용은 피할 수 없는 것을 묘사합니다. 라파엘 봄벨리(Rafael Bombelli)는 삼차 방정식의 이들 겉보기에 역설적 해를 명시적으로 해결한 최초의 인물이고 이들 문제를 해결하기 위한 시도하여 복소수 산술에 대해 규칙을 개발했습니다.

이들 양에 대해 용어 "허수(imaginary)"가, 비록 그가 그들의 허수 본성을 강조하기 위해 애쓰고 있었을지라도, 1637년에 르네 데카르트(René Descartes)에 의해 만들어졌습니다:^[19]

[...] 때때로 오직 허수, 즉, 누군가 각 방정식에서 내가 말한 만큼 상상할 수 있지만, 때때로 우리가 상상하는 것과 일치하는 양이 없습니다. ([...] quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune quantité qui corresponde à celle qu'on imagine.)

혼란의 또 다른 원인은 방정식 ${\sqrt {-1}}^{2}={\sqrt {-1}}{\sqrt {-1}}=-1$ 가 대수적 항등식 ${\sqrt {a}}{\sqrt {b}}={\sqrt {ab}}$ 과 변덕스럽게 일관되지 않은 것처럼 보이는 것이었으며, 이것은 비-음의 실수 $a$ 와 $b$ 에 대해 유효하고, $a$ , $b$ 의 하나가 양수이고 다른 하나가 음수와 함께 복소수 계산에서 역시 사용되었습니다. 이 항등식 (및 관련된 항등식 ${\tfrac {1}{\sqrt {a}}}={\sqrt {\tfrac {1}{a}}}$ ))의 부정확한 사용은 $a$ 와 $b$ 둘 다가 음수일 때 그 경우에서, 심지어 오일러를 몹시 괴롭혔습니다. 이 어려움은 결국 이 잘못을 막기 위해 √−1의 위치에 특수 기호 $i$ 를 사용하는 관례로 이어졌습니다.^{[citation needed]} 그럼에도 불구하고, 오일러는 우리가 오늘날 하는 것보다 훨씬 더 일찍 복소수를 학생들에게 소개하는 것이 당연하다고 생각했습니다. 그의 기본 대수학 교과서, Elements of Algebra에서, 그는 이들 숫자를 거의 동시에 소개했고 그런-다음 그들을 도처에서 자연스러운 방법에서 사용합니다.

18세기에서 복소수가 더 널리 사용되었는데, 왜냐하면 복소 표현의 공식적인 조작이 삼각 함수를 포함하는 계산을 단순화하기 위해 사용될 수 있음을 알게 되었기 때문입니다. 예를 들어, 1730년에 아브라암 드 무아브르(Abraham de Moivre)는 각도의 정수 배수의 삼각 함수와 해당 각도의 삼각 함수의 거듭-제곱과 관련된 복잡한 항등식이 그의 이름, 드 무아브르의 공식(de Moivre's formula)을 낳은 다음의 잘-알려진 공식에 의해 간단히 다시-표현될 수 있음을 언급했습니다:

(\cos \theta +i\sin \theta )^{n}=\cos n\theta +i\sin n\theta .

1748년에 레온하르트 오일러(Leonhard Euler)는 더 나아갔고 복소 거듭제곱 급수(power series)를 공식적으로 조작함으로써 복소 해석학(complex analysis)의 오일러의 공식(Euler's formula)을 얻었습니다:

\cos \theta +i\sin \theta =e^{i\theta }

그리고 이 공식은 임의의 삼각 항등식을 훨씬 더 간단한 지수 항등식으로 줄이기 위해 사용될 수 있음을 관찰했습니다.

복소 평면 (위쪽(above))에서 점으로 복소수의 아이디어는, 비록 월러스의(Wallis's) De Algebra tractatus에서 1685년 초에 예상되었을지라도, 1799년에 캐스퍼 비슬(Caspar Wessel)에 의해 처음 설명되었습니다.

비슬의 회고록은 코펜하겐 아카데미(Copenhagen Academy)의 의사록에 실렸지만 크게 눈에-띄지 않았습니다. 1806년에 장-로베르 아르강(Jean-Robert Argand)은 독립적으로 복소수에 대한 팜플렛을 발행하고 대수학의 기본 정리(fundamental theorem of algebra)의 엄격한 증명을 제공했습니다. 카를 프리드리히 가우스(Carl Friedrich Gauss)는 1797년에 그 이론의 본질적으로 토폴로지적(topological) 증명을 발표했지만, 그 당시에 "−1의 제곱근의 진정한 형이상학"에 대한 그의 의심을 표명했습니다. 1831년이 되기 전까지 그는 이들 의심을 극복했었고 복소 평면에서 점으로 복소수에 대한 그의 출판했었으며,^[20]^[21] 크게 현대의 표기법과 용어를 확립했습니다.

만약 누군가 이전에 이 주제를 틀린 관점에서 고려하고 신비한 어둠을 발견했다면, 이것은 서투른 용어에 큰 부분 기인한 것입니다. 누군가 +1, −1, √−1 양수, 음수, 또는 허수 (또는 심지어 불가능한) 단위라고 부르는 것이 아니라, 대신에, 직접, 역, 또는 측면 단위라고 말한 다음, 그러한 어둠에 대해서 거의 이야기할 수 없었습니다. - Gauss^[20]^[21]

19세기 초에서, 다른 수학자들: 뷰이(Buée), 무훼(Mourey), 워렌(Warren), 프앙쉐(Français) 및 그의 형제 벨라비떼스(Bellavitis)는 복소수의 기하학적 표현을 독립적으로 발견했습니다.^[22]

영국 수학자 고드프리 해럴드 하디(G.H. Hardy)는 가우스가 비록 닐스 헨리크 아벨(Niels Henrik Abel)과 카를 구스타프 야코프 야코비(Carl Gustav Jacob Jacobi)와 같은 수학자들이 가우스가 그의 1831년 논문을 발표하기 전에 일상적으로 그것들을 사용한 것이 필연적일지라도, '정말 확신하고 있고 과학적인 방법'에서 복소수를 사용한 최초의 수학자였다고 말했습니다.^[23]

오귀스탱-루이 코시(Augustin-Louis Cauchy)와 베른하르트 리만(Bernhard Riemann)은 복소 해석학(complex analysis)의 기본 아이디어를 1825년경부터 코시의 경우에서 시작하여 완성의 높은 상태로 만들었습니다.

이론에서 사용된 공통 용어는 주로 창립자에 기인입니다. 아르강은 $\cos \phi +i\sin \phi$ 를 방향 인수(direction factor), 및 $r={\sqrt {a^{2}+b^{2}}}$ 를 모듈러스(modulus)로 불렀습니다; 코시 (1828)는 $\cos \phi +i\sin \phi$ 를 감소된 형식(reduced form) (l'expression réduite)으로 불렀고 분명하게 용어 편각(argument)를 도입했습니다. 가우스는 ${\sqrt {-1}}$ 에 대해 $i$ 를 사용했었고 $a + bi$ 에 대해 용어 복소수(complex number)를 도입했고, $a 2 + b 2$ 를 노름(norm)으로 불렀습니다. $\cos \phi +i\sin \phi$ 에 대해 자주 사용되는, 표현 방향 계수(direction coefficient)는 한켈(Hankel) (1867)에 기인하고, 모듈러스에 대해 절댓값은 바이어슈트라스(Weierstrass)에 기인입니다.

일반적인 이론에 대한 후기 고전 저자는 리하르트 데데킨트(Richard Dedekind), 오토 횔더(Otto Hölder), 펠릭스 클라인(Felix Klein), 앙리 푸앵카레(Henri Poincaré), 헤르만 슈바르츠(Hermann Schwarz), 카를 바이어슈트라스(Karl Weierstrass) 및 많은 다른 사람들을 포함합니다.

Relations and operations

Equality

두 복소수가 같은 것과 그들의 실수 부분과 허수 부분 둘 다가 같은 것은 필요충분(iff) 조건입니다. 즉, 복소수 $z_{1}$ 과 $z_{2}$ 가 같은 것은 $\operatorname {Re} (z_{1})=\operatorname {Re} (z_{2})$ 과 $\operatorname {Im} (z_{1})=\operatorname {Im} (z_{2})$ 은 필요충분 조건입니다. 극 형식(polar form)에서 쓰인 비-영 복소수가 같은 것과 그들이 같은 크기를 가지고 그들의 편각이 $2 π$ 의 정수 배수만큼 다른 것은 필요충분 조건입니다.

Ordering

복소수는 이-차원 평면 위에 존재하는 것으로 자연적으로 생각되므로, 복소수의 집합에 대한 자연 선형 순서화(linear ordering)는 없습니다. 사실, 덧셈 및 곱셈과 호환되는 복소수에 대한 선형 순서화(linear ordering)가 없습니다 – 복소수는 순서화된 필드(ordered field)의 구조를 절대 가질 수 없습니다. 이것이 순서화된 필드에서 임의의 제곱이 적어도 0이지만, $i 2 = -1$ 이기 때문입니다.

Conjugate

복소수 $z = x + yi$ 의 복소 켤레(complex conjugate)는 $x - yi$ 에 의해 제공됩니다. ${\overline {z}}$ 또는 $z *$ 에 의해 표시됩니다.^[24] 복소수에 대한 이 단항 연산(unary operation)은 오직 그들의 기본 연산 덧셈, 뺄셈, 곱셈 및 나눗셈을 적용함으로써 표현될 수 없습니다.

기하학적으로, ${\overline {z}}$ 는 실수 축에 대한 $z$ 의 "반사(reflection)"입니다. 두 번 켤레화는 원래 복소수를 제공합니다:

{\overline {\overline {z}}}=z,

이것은 이 연산 인볼류션(involution)을 만듭니다. 반사는 실수 부분과 $z$ 의 크기 둘 다를 변경하지 않은 채 남겨두는데, 즉

\operatorname {Re} ({\overline {z}})=\operatorname {Re} (z)\quad

and

\quad |{\overline {z}}|=|z|.

허수 부분과 복소수 $z$ 의 편각은 켤레화 아래에서 그들의 부호를 바꿉니다:

\operatorname {Im} ({\overline {z}})=-\operatorname {Im} (z)\quad

및

\quad \operatorname {arg} ({\overline {z}})\equiv -\operatorname {arg} (z){\pmod {2\pi }}.

인수와 크기에 대한 자세한 내용에 대해, 극 형식(Polar form)에 대한 섹션을 참조하십시오.

복소수 $z=x+yi$ 와 그의 켤레의 곱은 항상 양의 실수이고 각각의 크기의 제곱과 같습니다:

z\cdot {\overline {z}}=x^{2}+y^{2}=|z|^{2}=|{\overline {z}}|^{2}.

이 속성은 주어진 분모의 켤레로 분수의 분자와 분모 둘 다에 전개함으로써 복소 분모를 가진 분수를 실수 분모를 가진 등가 분수로 변환하기 위해 사용할 수 있습니다. 이 과정은 때때로 (비록 마지막 표현에서 분모는 무리수 실수일 수 있을지라도) 분모의 "유리화(rationalization)"라고 불루는데, 왜냐하면 그것은 분모에서 단순 표현으로부터 근을 제거하는 방법과 유사하기 때문입니다.

복소수 $z$ 의 실수 및 허수 부분은 켤레화를 사용하여 추출될 수 있습니다:

\operatorname {Re} (z)={\dfrac {z+{\overline {z}}}{2}},\quad

및

\quad \operatorname {Im} (z)={\dfrac {z-{\overline {z}}}{2i}}.

게다가, 복소수가 실수인 것과 그것이 그 자신의 켤레와 같은 것은 필요충분 조건입니다.

켤레화는 기본 복소 산술 연산에 걸쳐 분배됩니다:

{\overline {z\pm w}}={\overline {z}}\pm {\overline {w}},

{\overline {z\cdot w}}={\overline {z}}\cdot {\overline {w}},\quad {\overline {z/w}}={\overline {z}}/{\overline {w}}.

켤레화는 한 직선에 대한 것보다 보다 일반적인 반사를 연구하는 기하학의 가지, 역 기하학(inversive geometry)에서 역시 사용됩니다. 전기 회로의 네트워크 분석(network analysis of electrical circuits)에서, 복소 켤레는, 최대 전력 전송 정리(maximum power transfer theorem)가 찾아질 때, 등가 임피던스를 찾는 것에서 사용됩니다.

Addition and subtraction

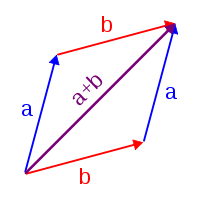
두 복소수 $a$ 와 $b$ 는 피합수의 그들의 실수 부분과 허수 부분을 개별적으로 더함으로써 가장 쉽게 더해질(added) 수 있습니다. 다시 말해서:

a+b=(x+yi)+(u+vi)=(x+u)+(y+v)i.

비슷하게, 뺄셈(subtraction)은 다음으로 수행될 수 있습니다:

a-b=(x+yi)-(u+vi)=(x-u)+(y-v)i.

복소 평면에서 복소수의 시각화를 사용하여, 덧셈은 다음 기하학적 해석을 가집니다: 복소 평면에서 점으로 해석되는, 두 복소수 $a$ 와 $b$ 의 합은 세 꼭짓점 $O$ , 및 (그들이 한 직선 위에 있지 않은 것으로 제공되는) $a$ 와 $b$ 로 이름-붙인 화살표의 점으로부터 평행사변형(parallelogram)을 만듦으로써 얻어진 점입니다. 동등하게, 이들 점 $A,\;B,$ 와 평행사변형 $X$ 의 네 번째 점을 각각 호출하면, 삼각형(triangle) $OAB$ 및 $XBA$ 는 일치(congruent)합니다. 뺄셈의 시각화는 음의 감수(subtrahend)의 덧셈을 고려함으로써 달성될 수 있습니다.

Multiplication

복소수에서 실수 부분, 허수 부분, 및 불확정 $i$ 는 자체에서 숫자로 모두 여겨지며, $z=x+yi$ and $w=u+vi$ 와 같이 주어지면, 두 복소수는 다음 방법에서 분배 속성(distributive property), 교환 속성(commutative properties) 및 정의하는 속성 $i^{2}=-1$ 의 규칙 아래에서 곱해집니다:

{\begin{aligned}z\cdot w&=(x+yi)\cdot (u+vi)&\\&=x(u+vi)+yi(u+vi)&&{\text{by the (right) distributive law}}\\&=xu+xvi+yiu+yivi&&{\text{by the (left) distributive law}}\\&=xu+yivi+xvi+yiu&&{\text{by the commutativity of addition}}\\&=xu+yvi^{2}+xvi+yui&&{\text{by the commutativity of multiplication}}\\&=(xu+yvi^{2})+(xvi+yui)&&{\text{by the associativity of addition}}\\&=(xu-yv)+(xvi+yui)&&{\text{by the defining property of }}i\\&=(xu-yv)+(xv+yu)i&&{\text{by the distributive law}}.\end{aligned}}

Reciprocal and division

켤레화를 사용하여, 비-영 복소수 $z = x + yi$ 의 역수(reciprocal)는 항상 다음으로 나누어 쓸 수 있습니다:

{\frac {1}{z}}={\frac {\overline {z}}{z{\overline {z}}}}={\frac {\overline {z}}{|z|^{2}}}={\frac {\overline {z}}{x^{2}+y^{2}}}={\frac {x}{x^{2}+y^{2}}}-{\frac {y}{x^{2}+y^{2}}}i,

왜냐하면 비-영은 $x^{2}+y^{2}$ 가 영보다 큼을 의미하기 때문입니다.

이것은 다음으로 비-영 복소수 $z$ 로 임의의 복소수 $w=u+vi$ 의 나눗셈을 표현하기 위해 사용될 수 있습니다:

{\frac {w}{z}}=w\cdot {\frac {1}{z}}=(u+vi)\cdot \left({\frac {x}{x^{2}+y^{2}}}-{\frac {y}{x^{2}+y^{2}}}i\right)={\frac {1}{x^{2}+y^{2}}}\left((ux+vy)+(vx-uy)i\right).

Multiplication and division in polar form

곱셈, 나눗셈 및 지수화에 대해 공식은 데카르트 좌표에서 해당하는 공식보다 극 형식에서 더 단순화됩니다. 두 복소수 $z 1 = r 1 (cos φ 1 + i sin φ 1)$ 와 $z 2 = r 2 (cos φ 2 + i sin φ 2)$ 가 주어지면, 다음 삼각 항등식 때문에:

\cos(a)\cos(b)-\sin(a)\sin(b)=\cos(a+b)

\cos(a)\sin(b)+\sin(a)\cos(b)=\sin(a+b)

우리는 다음을 유도할 수 있습니다:

z_{1}z_{2}=r_{1}r_{2}(\cos(\varphi _{1}+\varphi _{2})+i\sin(\varphi _{1}+\varphi _{2})).

달리 말해서, 절댓값은 곱해지고 편각은 더해져서 곱의 극 형식을 산출합니다. 예를 들어, $i$ 를 곱하면 반-시계 방향으로 1/4-회전(turn)에 해당하며, 이것은 $i 2 = -1$ 을 반환합니다. 오른쪽 그림은 다음의 곱셈을 묘사합니다:

(2+i)(3+i)=5+5i.

$5 + 5 i$ 의 실수 및 허수 부분이 같으므로, 해당 숫자의 편각은 45도, 또는 (라디안(radian)에서) π/4입니다. 다른 한편으로, 역시 빨간색과 파란색 삼각형의 원점에서 각도의 합은 각각 아크탄젠트(arctan) (1/3)과 아크탄젠트 (1/2)입니다. 따라서, 공식

{\frac {\pi }{4}}=\arctan \left({\frac {1}{2}}\right)+\arctan \left({\frac {1}{3}}\right)

은 유지됩니다. 아크탄젠트(arctan) 함수는 매우 효율적으로 근사될 수 있으므로, 매친-계열 공식(Machin-like formulas)으로 알려진 이와 같은 공식은 π의 고-정밀 근사에 사용됩니다.

비슷하게, 나눗셈은 다음에 의해 제공됩니다:

{\frac {z_{1}}{z_{2}}}={\frac {r_{1}}{r_{2}}}\left(\cos(\varphi _{1}-\varphi _{2})+i\sin(\varphi _{1}-\varphi _{2})\right).

Square root

( $b \neq 0$ 을 갖는) $a + bi$ 의 제곱근은 $\pm (\gamma +\delta i)$ 이며, 여기서

\gamma ={\sqrt {\frac {a+{\sqrt {a^{2}+b^{2}}}}{2}}}

및

\delta =\operatorname {sgn} (b){\sqrt {\frac {-a+{\sqrt {a^{2}+b^{2}}}}{2}}},

여기서 sgn는 시그넘(signum) 함수입니다. 이것은 $a + bi$ 를 얻기 위해 $\pm (\gamma +\delta i)$ 를 제곱함으로써 보일 수 있습니다.^[25]^[26] 여기서 ${\sqrt {a^{2}+b^{2}}}$ 는 $a + bi$ 의 모듈러스(modulus)로 불리고, 제곱근 부호는 비-음 실수 부분을 갖는 제곱근을 가리키고, 주요 제곱근으로 불립니다; 역시 ${\sqrt {a^{2}+b^{2}}}={\sqrt {z{\overline {z}}}}$ 이며, 여기서 $z=a+bi$ 입니다.^[27]

Exponential function

지수 함수(exponential function) $\exp(z)$ 는 거듭제곱 급수(power series)에 의해 모든 각 복소수에 대해 정의될 수 있습니다:

\exp(z)=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}},

이것은 수렴의 무한 반지름(radius of convergence)을 가집니다.

지수 함수의 $1$ 에서 값은 오일러의 숫자(Euler's number)입니다:

e=\exp(1)=\sum _{n=1}^{\infty }{\frac {1}{n!}}\approx 2.71828.

만약 $z$ 가 실수이면, 우리는 $\exp(z)=e^{z}$ 을 가집니다. 해석적 연속(Analytic continuation)은 $z$ 의 모든 각 복소 값에 대해 이 상등을 확장하고, 따라서 다음으로 밑수 $e$ 를 갖는 복소 지수화를 정의하는 것을 허용합니다:

e^{z}=\exp(z).

Functional equation

지수 함수는 다음 함수 방정식(functional equation) $e^{z+t}=e^{z}e^{t}$ 을 만족시킵니다. 이것은 양 쪽 구성원의 거듭제곱 급수 전개를 비교하는 것 또는 실수 인수로 방정식의 제한으로부터 해석적 연속(analytic continuation)을 적용함으로써 입증될 수 있습니다.

Euler's formula

오일러의 공식(Euler's formula)은 임의의 실수 $x$ 에 대해, 다음임을 말합니다:

e^{ix}=\cos x+i\sin x.

함수의 방정식은 따라서 만약 $x$ 와 $y$ 가 실수이면 우리는 다음을 가짐을 의미합니다:

e^{x+iy}=e^{x}\cos y+ie^{x}\sin y,

이것은 실수 및 허수 부분으로 지수 함수의 분해입니다.

Exponentiation

만약 $x > 0$ 이 실수이고 $z$ 가 복소수이면, 지수화는 다음으로 정의됩니다:

x^{z}=e^{z\ln x},

여기서 $ln$ 은 자연 로그를 나타냅니다.

이 공식을 $x$ 의 복소수 값으로 확장하는 것은 자연스러워 보이지만, 복소 로그가 실제로 함수가 아니라, 다중-값 함수(multivalued function)라는 사실로 인해 일부 어려움이 있습니다.

Complex logarithm

실수 경우에서, 자연 로그(natural logarithm)는 지수 함수의 역(inverse)으로 정의될 수 있습니다. 이것을 복소 도메인으로 확장하는 것에 대해, 우리는 오일러의 공식으로부터 시작할 수 있습니다. 그것은 만약 복소수 $z$ 가 극 형식(polar form)에서 다음으로 쓰이면,

z=r(\cos \varphi +i\sin \varphi ),

그의 복소 로그(complex logarithm)는 다음이어야 함을 의미합니다:

\ln(z)=\ln(r)+\varphi i.

어쨌든, 코사인과 사인은 주기 함수이기 때문에, $\varphi$ 에 $2 π$ 의 정수 배수의 덧셈은 $z$ 를 변경하지 않습니다. 예를 들어, $e^{i\pi }=e^{3i\pi }=-1$ 이므로, $i\pi$ 와 $3i\pi$ 둘 다는 $-1$ 의 자연 로그에 대해 가능한 값입니다.

그러므로 복소 로그는 다중-값 함수(multivalued function)로 정의되어야 합니다:

\ln(z)=\left\{\ln(r)+\varphi i+2\pi ki\mid k\in \mathbb {Z} \right\}.

대안적으로, 가지 자름(branch cut)은 참 함수를 정의하기 위해 사용될 수 있습니다. 만약 $z$ 가 음의 실수가 아니면, 복소 로그의 주요 값(principal value)은 $-\pi <\varphi <\pi$ 와 함께 얻습니다. 이것은 음의 실수 외부의 해석적 함수(analytic function)이지만, 임의의 음의 실수에서 연속인 함수로 절대 연장될 수 없습니다.

그것은 만약 $z$ 가 위와 처럼이면, 및 만약 $t$ 가 또 다른 복소수이면, 지수화는 다중-값 함수임을 따릅니다:

z^{t}=\left\{e^{t\ln r}\,(\cos(\varphi t+2\pi kt)+i\sin(\varphi t+2\pi kt))\}\mid k\in \mathbb {Z} \right\}

Integer and fractional exponents

만약, 이전 공식에서, $t$ 가 정수이면, 사인과 코사인은 $k$ 와 독립입니다. 따라서, 만약 지수 $n$ 이 정수이면, $z^{n}$ 은 잘 정의되고, 지수화 공식은 드 무아브로의 공식(de Moivre's formula)으로 단순화됩니다:

z^{n}=(r(\cos \varphi +i\sin \varphi ))^{n}=r^{n}\,(\cos n\varphi +i\sin n\varphi ).

복소수 $z$ 의 $n$ $n$ 번째 근( $n$ th roots)은 $0 \leq k \leq n - 1$ 에 대해 다음에 의해 제공됩니다:

z^{1/n}={\sqrt[{n}]{r}}\left(\cos \left({\frac {\varphi +2k\pi }{n}}\right)+i\sin \left({\frac {\varphi +2k\pi }{n}}\right)\right)

(여기서 ${\sqrt[{n}]{r}}$ 는 보통 양의 실수 $r$ 의 (양의) $n$ 번째 근입니다.) 사인과 코사인이 주기적이기 때문에, $k$ 의 다른 정수 값은 다른 값을 제공하지 않습니다.

양의 실수 $r$ 의 $n$ 번째 근은 $c n = r$ 을 만족시키는 양의 실수 $c$ 로 선택되지만, 복소수의 하나의 특정 복소수 $n$ 번째 근을 구별하는 자연스러운 방법은 없습니다. 그러므로, $n$ 번째 근은 $z$ 의 $n$ -값 함수( $n$ -valued function)입니다. 이것은, 양의 실수의 경우와 달리, 우리가 다음을 가짐을 의미합니다:

(z^{n})^{1/n}\neq z,

왜냐하면 왼쪽 변은 $n$ 값으로 구성되고, 오른쪽 변은 단일 값이기 때문입니다.

Properties

Field structure

복소수의 집합 C는 필드(field)입니다.^[28] 간단히 말해서, 이것은 다음 사실이 유지됨을 의미합니다: 첫째, 두 복소수는 또 다른 복소수를 산출하기 위해 더해지고 곱해질 수 있습니다. 둘째, 임의의 복소수 $z$ 에 대해, 그것의 덧셈의 역원(additive inverse) $- z$ 도 복소수입니다; 그리고 셋째, 모든 각 비-영 복소수는 역수(reciprocal) 복소수를 가집니다. 게다가, 이들 연산은 법칙의 많은 숫자, 예를 들어 임의의 두 복소수 $z 1$ 및 $z 2$ 에 대해 덧셈과 곱셈의 교환-특성(commutativity)의 법칙을 만족시킵니다:

z_{1}+z_{2}=z_{2}+z_{1},

z_{1}z_{2}=z_{2}z_{1}.

필드에 대한 이들 두 법칙과 다른 요구-사항은 위에 주어진 공식에 의해 입즈이될 수 있으며, 실수 자체가 필드를 형성하는 사실을 사용합니다.

실수와 달리, C는 순서화 필드(ordered field)가 아닙니다. 다시 말해서, 덧셈 및 곱셈에 호환되는 관계 $z 1 < z 2$ 를 정의하는 것이 가능하지 않습니다. 사실, 임의의 순서화 필드에서, 임의의 원소의 제곱은 필연적으로 양수이므로, $i 2 = -1$ 은 C에 대한 순서화(ordering)의 존재를 배제합니다.^[29]

수학적 주제 또는 구성에 대해 놓여-있는 필드가 복소수의 필드일 때, 주제의 이름은 보통 해당 사실을 반영하기 위해 수정됩니다. 예를 들어: 복소 해석학(complex analysis), 복소 행렬(matrix), 복소 다항식(polynomial), 및 복소 리 대수(Lie algebra)가 있습니다.

Solutions of polynomial equations

임의의 복소수 (계수(coefficient)로 불리는) $a 0, ..., a n$ 가 주어지면, 방정식

a_{n}z^{n}+\dotsb +a_{1}z+a_{0}=0

은 적어도 하나의 복소 해 z를 가지며, 더 높은 계수 $a 1, ..., a n$ 의 적어도 하나가 비-영인 조건으로 제공됩니다.^[30] 이것이 카를 프리드리히 가우스(Carl Friedrich Gauss) 및 장 르 롱 달랑베르(Jean le Rond d'Alembert)의 대수학의 기본 정리(fundamental theorem of algebra)의 명제입니다. 이 사실때문에, C는 대수적으로 닫힌 필드(algebraically closed field)로 불립니다. 이 속성은 유리수의 필드(field of rational numbers) Q (다항식 $x 2 - 2$ 은 유리 근을 가지지 않는데, 왜냐하면 √2는 유리수가 아니기 때문입니다) 및 실수 R (다항식 $x 2 + a$ 은 $a > 0$ 에 대해 실수 근을 가지지 않는데, 왜냐하면 $x$ 의 제곱은 임의의 실수 $x$ 에 대해 양수이기 때문입니다)에 대해 유지되지 않습니다

이 정리의 증명, 리우빌의 정리(Liouville's theorem)와 같은 해석적 방법, 또는 감김 숫자(winding number)와 같은 토폴로지적(topological) 방법, 또는 갈루아 이론(Galois theory)과 홀수 차수의 임의의 실수 다항식이 적어도 하나의 실수 근을 가지는 사실을 결합한 증명 등의 다양한 증명이 있습니다.

이 사실때문에, 임의의 대수적으로 닫힌 필드에 대해에 대해 유지되는 정리는 C에 적용됩니다. 예를 들어, 임의의 비-빈 복소 정사각 행렬(square matrix)은 적어도 하나의 (복소) 고윳값(eigenvalue)을 가집니다.

Algebraic characterization

필드 C는 다음 세 속성을 가집니다: 첫째, 그것은 특성(characteristic) 0를 가집니다. 이것은 피합수의 임의의 숫자에 대해 $1 + 1 + \dots + 1 \neq 0$ 임을 의미합니다 (그것의 모두가 일과 같습니다). 둘째, Q에 걸쳐 그것의 초월 차수(transcendence degree), C의 소수 필드(prime field)는 연속체의 카디널리티(cardinality of the continuum)입니다. 셋째, 그것은 대수적으로 닫힘입니다 (위를 참조하십시오). 이들 속성을 갖는 임의의 필드는 C에 대해 (필드로서) 동형(isomorphic)임을 보일 수 있습니다. 예를 들어, Q_p의 대수적 클로저(algebraic closure)는 역시 이들 세 속성을 만족시키므로, 이들 두 필드는 동형 (필드로서 토폴로지적 필드는 아님)입니다.^[31] 역시, C는 복소 푸죄 급수(Puiseux series)의 필드에 대한 동형입니다. 어쨌든, 동형사상을 명시하는 것은 선택의 공리(axiom of choice)를 요구합니다. 이 대수적 특성화의 또 다른 결과는 C가 C와 동형인 많은 적절한 부분-필드를 포함한다는 것입니다.

Characterization as a topological field

C의 전술한 특성화는 오직 C의 대수적 관점을 설명합니다. 다시 말해서, 해석학(analysis) 및 토폴로지(topology)와 같은 영역에서 중요한 근접성(nearness) 및 연속성(continuity)의 속성은 다루지 않습니다. 토폴로지적 필드(topological field) (즉, 수렴의 개념을 허용하는 토폴로지(topology)를 갖는 갖춰진 필드)로서 C의 다음 설명은 토폴로지적 속성을 고려합니다. C는 다음 세 조건을 만족시키는 비-영 원소의 부분-집합 $P$ (즉, 양의 실수의 집합)를 포함합니다:

$P$ 는 덧셈, 곱셈 및 역을 취하는 아래에서 닫혀 있습니다.
만약 $x$ 와 $y$ 는 $P$ 의 구별되는 원소이면, $x - y$ 또는 $y - x$ 중의 하나는 $P$ 안에 있습니다.
만약 $S$ 는 $P$ 의 비-빈 부분-집합이면, C 안에 일부 $x$ 에 대해 $S + P = x + P$ 입니다.

게다가, C는 $x x *$ 가, C 안에 임의의 비-영 $x$ 에 대해 $P$ 안에 있는 것을 만족하는, 비-자명한 인볼루션(involutive) 자기-동형(automorphism)을 가집니다.

이들 속성을 갖는 임의의 필드 $F$ 는 집합 $B (x, p) = {y | p - (y - x)(y - x)* \in P}$ 을 기저(base)로 취함으로써 토폴로지가 부여될 수 있으며, 여기서 $x$ 는 필드에 걸쳐 범위이고 $p$ 는 $P$ 에 걸쳐 범위입니다. 이 토폴로지와 함께 $F$ 는 토폴로지적 필드를 C로 동형입니다.

오직 연결된(connected) 지역적으로 컴팩트(locally compact) 토폴로지적 필드(topological fields)는 R과 C입니다. 이것은 C를 토폴로지 필드로 또 다른 특성화를 제공하며, C는 R로부터 식별될 수 있는데 왜냐하면 비-영 복소수가 연결된(connected) 것이지만, 비-영 실수가 연결되지 않기 때문입니다.^[32]

Formal construction

Construction as ordered pairs

윌리엄 로언 해밀턴(William Rowan Hamilton)은 복소수의 집합 $C$ 를 실수의 집합의 순서화된 쌍(ordered pair) $(a, b)$ 의 집합 $R 2$ 를 정의하기 위한 접근 도입했으며,^[33] 이것에서 덧셈 및 곱셈에 대해 다음 규칙이 부과됩니다:^[34]

{\begin{aligned}(a,b)+(c,d)&=(a+c,b+d)\\(a,b)\cdot (c,d)&=(ac-bd,bc+ad).\end{aligned}}

그런-다음 $(a, b)$ 를 $a + bi$ 로 표현하기 위한 단지 표기법의 문제일 뿐입니다.

Construction as a quotient field

비록 이 낮은-수준 구성이 복소수의 구조를 정확하게 묘사할지라도, 다음 동등한 정의는 $C$ 의 대수적 본성을 보다 즉시 드러냅니다. 이 특성화는 필드와 다항식의 개념에 의존합니다. 필드는 말하자면 유리수로부터 익숙한 것처럼 행동하는 덧셈, 뺄셈, 곱셈 및 나눗셈 연산을 부여하는 집합입니다. 예를 들어, 분배 법칙(distributive law)

(x+y)z=xz+yz

은 필드의 임의의 세 원소 $x$ , $y$ 및 $z$ 에 대해 반드시 유지됩니다. 실수의 집합 $R$ 은 필드를 형성합니다. 실수 계수(coefficient)를 갖는 다항식 $p (X)$ 는 다음 형식의 표현입니다:

a_{n}X^{n}+\dotsb +a_{1}X+a_{0},

여기서 $a 0, ..., a n$ 는 실수입니다. 다항식의 보통의 덧셈과 곱셈은 링(ring) 구조를 갖는 모든 그러한 다항식의 집합 $R [X]$ 을 부여합니다. 이 링은 실수에 걸쳐 다항식 링(polynomial ring)으로 불립니다.

복소수의 집합은 몫 링(quotient ring) $R [X]/(X 2 + 1)$ 으로 정의됩니다.^[35] 이 확장 필드는 $-1$ 의 두 제곱근, 즉, 각각 $X$ 와 $- X$ (의 코셋(coset))을 포함합니다. $1$ 과 $X$ (의 코셋)은 실수 벡터 공간(vector space)으로 $R [X]/(X 2 + 1)$ 의 기저를 형성하며, 이것은 확장 필드의 각 원소가 이들 두 원소에서 선형 조합(linear combination)으로 고유하게 쓸 수 있음을 의미합니다. 동등하게, 확장 필드의 원소는 실수의 순서 쌍 $(a, b)$ 으로 쓸 수 있습니다. 몫 링은 필드인데, 왜냐하면 $X 2 + 1$ 는 $R$ 에 걸쳐 기약(irreducible)이므로, 그것을 생성하는 아이디얼은 최대(maximal)입니다.

링 $R [X]$ , 모듈로 관계 $X 2 = -1$ 에서 덧셈과 곱셈에 대해 공식은 순서 쌍으로 정의된 복소수의 덧셈과 곱셈에 대해 공식에 해당합니다. 따라서 필드 $C$ 의 두 정의는 (필드로) 동형(isomorphic)입니다.

$C$ 가 대수적으로 닫힌 것으로 수용하면, 그것이 이 접근에서 $R$ 의 대수적 확장(algebraic extension)이므로, $C$ 는 따라서 $R$ 의 대수적 클로저(algebraic closure)입니다.

Matrix representation of complex numbers

복소수 $a + bi$ 는 다음 형식을 가지는 $2 \times 2$ 행렬(matrices)에 의해 역시 표현될 수 있습니다:

{\begin{pmatrix}a&-b\\b&\;\;a\end{pmatrix}}

여기서 엔트리 $a$ 와 $b$ 는 실수입니다. 두 그러한 행렬의 합과 곱은 다시 이 형식이고, 복소수의 합과 곱은 그러한 행렬의 합과 곱(product)에 해당하며, 곱은 다음입니다:

{\begin{pmatrix}a&-b\\b&\;\;a\end{pmatrix}}{\begin{pmatrix}c&-d\\d&\;\;c\end{pmatrix}}={\begin{pmatrix}ac-bd&-ad-bc\\bc+ad&\;\;-bd+ac\end{pmatrix}}

복소수의 곱셈의 기하학적 설명은 복소수와 그러한 행렬 사이의 이 대응을 사용함으로써 회전 행렬(rotation matrices)의 관점에서 역시 표현될 수 있습니다. 게다가, 행렬로 표현된 복소수의 절댓값의 제곱은 해당 행렬의 행렬식(determinant)과 같습니다:

|z|^{2}={\begin{vmatrix}a&-b\\b&a\end{vmatrix}}=a^{2}+b^{2}.

켤레 ${\overline {z}}$ 는 행렬의 전치(transpose)에 해당합니다.

비록 행렬과 함께 복소수의 이 표현이 가장 공통일지라도, 많은 다른 표현이 항등 행렬(identity matrix)의 음수를 제곱하는 ${\bigl (}{\begin{smallmatrix}0&-1\\1&0\end{smallmatrix}}{\bigr )}$ 이외의 행렬로부터 발생합니다. 복소수의 다른 표현에 대해 2 × 2 실수 행렬(2 × 2 real matrices)에 대한 기사를 참조하십시오.

Complex analysis

Color wheel graph of $sin(1/ z)$ . Black parts inside refer to numbers having large absolute values.

복소 변수의 함수의 연구는 복소 해석학(complex analysis)으로 알려져 있고 응용 수학(applied mathematics)에서 마찬가지로 수학의 다른 가지에서 거대한 실용적인 사용을 가집니다. 종종, 실수 해석학(real analysis) 또는 심지어 숫자 이론(number theory)에서 명제에 대해 가장 자연스러운 증명은 복소 해석학으로부터 기법을 사용합니다 (예를 들어 소수 정리(prime number theorem)를 참조하십시오). 공통적으로 이-차원 그래프로 표현되는, 실수 함수와 달리, 복소 함수(complex function)는 사-차원 그래프를 가지고 사-차원을 제안하기 위한 삼-차원 그래프(three-dimensional graph)를 색깔-코딩함으로써 또는 복소 평면의 복소 함수의 동적 변환에 애니메이팅함으로써 유용하게 설명될 수 있습니다.

Complex exponential and related functions

(실수) 해석학에서 수렴 급수(convergent series) 및 연속 함수(continuous function)의 개념은 복소 해석학에서 자연스러운 아날로그를 가집니다. 복소수의 수열 이 수렴한다고 말하는 것과 그의 실수와 허수 부분이 수렴(converge)하는 것은 필요충분 조건입니다. 이것은 극한의 (ε, δ)-정의((ε, δ)-definition of limit)와 동등하며, 여기서 실수의 절댓값은 복소수의 하나에 의해 대체됩니다. 보다 추상적인 관점으로부터, 메트릭(metric)

\operatorname {d} (z_{1},z_{2})=|z_{1}-z_{2}|

과 함께 부여된, C는 완전 메트릭 공간(metric space)이며, 이것은 임의의 두 복소수 $z 1$ 및 $z 2$ 에 대해, 삼각형 부등식(triangle inequality)을 특히 포함합니다:

|z_{1}+z_{2}|\leq |z_{1}|+|z_{2}|

.

실수 해석학에서 처럼, 수렴의 이 개념은 많은 초등 함수(elementary function)를 구성하기 위해 사용됩니다: $e z$ 로 역시 쓰이는, 지수 함수(exponential function) $exp(z)$ 는 무한 급수(infinite series)로 정의됩니다:

\exp(z):=1+z+{\frac {z^{2}}{2\cdot 1}}+{\frac {z^{3}}{3\cdot 2\cdot 1}}+\cdots =\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}.

실수 삼각 함수 사인(sine)과 코사인(cosine), 마찬가지로 쌍곡선 함수(hyperbolic functions) 쌍곡-사인(sinh) 및 쌍곡-코사인(cosh)을 정의하는 급수는 변경없이 복소수 인수로 이어집니다. 탄젠트(tangent)와 같은, 다른 삼각 및 쌍곡선 함수에 대해, 그런 일은 약간 더 복잡한데, 왜냐하면 정의하는 급수는 모든 복소수 값에 대해 수렴하지 않기 때문입니다. 그러므로, 우리는 그들을 사인, 코사인 및 지수, 또는 동등하게, 해석적 연속(analytic continuation)의 방법을 사용함으로써, 정의해야 합니다.

오일러의 공식(Euler's formula)은, 임의의 실수 φ에 대해, 말합니다:

\exp(i\varphi )=\cos(\varphi )+i\sin(\varphi )

특히

\exp(i\pi )=-1

실수의 환경에서와 달리, 임의의 복소수 $w \neq 0$ 에 대해, 방정식

\exp(z)=w

의 복소 해 $z$ 의 무한(infinitude)이 있습니다. $w$ 의 복소 로그(complex logarithm)로 불리는 임의의 그러한 해 $z$ 는 다음을 만족시킴을 보일 수 있습니다:

\log(w)=\ln |w|+i\arg(w),

여기서 arg는 위에서(above) 정의된 편각(argument)이고, ln은 (실수) 자연 로그(natural logarithm)입니다. arg는 다중-값 함수(multivalued function)이므로, 오직 2π의 배수까지(up to) 고유하며, log는 역시 다중-값입니다. log의 주요 값(principal value)은 허수 부분을 구간(interval) $(-π, π]$ 로 제한함으로써 종종 취합니다.

복소 지수(exponentiation) $z ω$ 는 다음으로 정의됩니다:

z^{\omega }=\exp(\omega \log z),

그리고 $\omega$ 가 정수일 때를 제외하고 다중-값입니다. $ω = 1 / n$ 에 대해, 어떤 자연수 $n$ 에 대해, 이것은 위에서 언급된 $n$ 번째 근의 비-고유성을 회복합니다.

복소수는, 자연수와 달리, 비-수정된 거듭제곱과 로그 항등식, 특히 단일-값 함수로 소박히 처리될 때, 일반적으로 만족시키지 못합니다; 거듭제곱과 로그 항등식의 실패(failure of power and logarithm identities)를 참조하십시오. 예를 들어, 그들은 다음을 만족시키지 않습니다:

a^{bc}=\left(a^{b}\right)^{c}.

방정식의 양쪽 변은 여기저 주어진 복소 지수화의 정의에 의해 다중-값이고, 왼쪽에 대한 값은 오른쪽에 대한 그들의 부분-집합입니다.

Holomorphic functions

함수 f : C → C는 만약 그것이 코시–리만 방정식(Cauchy–Riemann equations)을 만족시키면 정칙(holomorphic)으로 불립니다. 예를 들어, 임의의 R-선형(R-linear) 맵 C → C은 복소 계수 $a$ 와 $b$ 를 갖는 다음 형식에서 쓸 수 있습니다:

f(z)=az+b{\overline {z}}

이 맵이 정칙인 것과 $b = 0$ 인 것은 필요충분(iff) 조건입니다. 두 번째 피합수 $b{\overline {z}}$ 는 실수-미분가능이지만, 코시–리만 방정식(Cauchy–Riemann equations)을 만족시키지 않습니다.

복소 해석학은 실수 해석학에서 명백하지 않은 일부 특징을 보여줍니다. 예를 들어, C의 임의의 작은 열린 부분-집합(open subset)과 일치하는 임의의 두 정칙 함수 $f$ 와 $g$ 는 어디에서나 필연적으로 일치합니다. 유리형 함수(Meromorphic function), 정칙 함수 $f$ 를 갖는 $f (z)/(z - z 0) n$ 로 지역적으로 쓸 수 있는 함수는 정칙 함수의 특징의 일부를 여전히 공유합니다. 다른 함수는, $z = 0$ 에서 $sin(1/ z)$ 와 같은 본질적인 특이점(essential singularities)을 가집니다.

Applications

복소수는 신호 처리(signal processing), 제어 이론(control theory), 전자기학(electromagnetism), 유체 역학(fluid dynamics), 양자 역학(quantum mechanics), 지도학(cartography), 및 진동 분석(vibration analysis)을 포함한 많은 과학 분야에서 응용을 가집니다. 이러한 응용의 일부는 아래에 묘사됩니다.

Geometry

Shapes

평면에서 세 비-같은-직선(non-collinear) 점 $u,v,w$ 은 삼각형 $\{u,v,w\}$ 의 모양(shape)을 결정합니다. 복소 평면에서 점을 위치시키면, 삼각형의 이 모양은 다음으로 복소수에 의해 표현될 수 있습니다:

S(u,v,w)={\frac {u-w}{u-v}}.

삼각형의 모양 $S$ 는, 복소 평면이 모양의 직관적인 개념에 대응하고, 닮음(similarity)을 나타내는, 평행-이동 또는 (아핀 변환(affine transformation)에 의해) 팽창으로 변환될 때, 같은 것으로 유지될 것입니다. 따라서 각 삼각형 $\{u,v,w\}$ 은 같은 모양을 갖는 닮음 클래스(similarity class) 안에 있습니다.^[36]

Fractal geometry

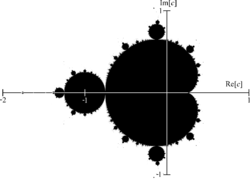
망델브로 집합(Mandelbrot set)은 복소 평면 위에 형성된 프랙탈의 인기있는 예제입니다. 그것은 모든 각 위치 $c$ 를 그림으로써 정의되며 여기서 수열 $f_{c}(z)=z^{2}+c$ 을 반복하는 것은 무한하게 반복(iterated)될 때 발산(diverge)하지 않습니다. 유사하게, 줄리아 집합(Julia set)은 같은 규칙을 가지며, $c$ 가 상수로 유지되는 것을 제외합니다.

Triangles

모든 각 삼각형은 고유한 슈타이너 내접-타원(Steiner inellipse)을 가집니다 – 내접-타원(ellipse)은 삼각형 내부에 있고 삼각형의 세 변의 중점에 접합니다. 삼각형의 슈타이너 내접-타원의 초점(foci)은 마든의 정리(Marden's theorem)에 따라 다음처럼 찾아질 수 있습니다:^[37]^[38] 복소 평면에서 삼각형의 꼭짓점을 $a = x A + y A i$ , $b = x B + y B i$ , 및 $c = x C + y C i$ 으로 나타냅니다. 삼차 방정식(cubic equation) $\scriptstyle (x-a)(x-b)(x-c)=0$ 을 쓰고, 그의 도함수을 취하고 (이차) 도함수을 영과 같게 합니다. 마든의 정리(Marden's Theorem)는 이 방정식의 해가 슈타이너 내접-타원의 두 초점의 위치를 나타내는 복소수임을 말합니다.

Algebraic number theory

Construction of a regular pentagon using straightedge and compass.

위에서 언급했듯이, (복소 계수에서) 임의의 비-상수 다항 방정식은 C에서 해를 가집니다. 포티오라이, 같은 것은 만약 그 방정식이 유리 계수를 가지면 참입니다. 그러한 방정식의 근은 대수적 숫자(algebraic numbers)로 불립니다 – 그들은 대수적 숫자 이론(algebraic number theory)에서 연구의 주요 대상입니다. 역시 모든 대수적 숫자를 포함하는 Q의 대수적 클로저, Q와 비교하여, C는 기하학적 용어로 쉽게 이해될 수 있는 이점을 가집니다. 이런 방법에서, 대수적 방법은 기하학적 질문을 연구하기 위해 사용될 수 있고 그 반대도 마찬가지입니다. 대수적 방법과 함께, 단위의 근(roots of unity)을 포함하는 숫자 필드(number field)에 필드 이론(field theory)의 기계를 구체적으로 적용하면, 오직 나침반과 직선자를 사용하여 – 순수한 기하학적 문제 – 정규 구각형(nonagon)을 구성하는 것이 가능하지 않음을 보여줄 수 있습니다.

또 다른 예제는 가우스 정수(Gaussian integer), 즉, 형식 $x + iy$ 의 숫자이며, 여기서 $x$ 와 $y$ 는 정수이며, 이것은 제곱의 합(sums of squares)을 분류하기 위해 사용될 수 있습니다.

Analytic number theory

해석적 숫자 이론은 그들이 복소수로 여길 수 있다는 사실의 이점을 취함으로써, 종종 정수 또는 유리수, 숫자를 연구하며, 이것에서 해석적 방법이 사용될 수 있습니다. 이것은 복소-값 함수에서 숫자-이론적 정보를 인코딩함으로써 행해집니다. 예를 들어, 리만 제타 함수(Riemann zeta function) $ζ(s)$ 는 소수(prime number)의 분포와 관련됩니다.

Improper integrals

응용 분야에서, 복소수는 복소-값 함수에 의해 특정 실수-값 부적절한 적분(improper integral)을 계산하기 위해 종종 사용됩니다. 여러 방법이 이것을 하기 위해 존재합니다; 윤곽 적분화의 방법(methods of contour integration)을 참조하십시오.

Dynamic equations

미분 방정식(differential equation)에서, 선형 미분 방정식(linear differential equation) 또는 방정식 시스템의 특성 방정식(characteristic equation)의 모든 복소 근 $r$ 을 먼저 찾은 다음 형식 $f (t) = e rt$ 의 초등 함수의 관점에서 시스템을 풀려고 시도하는 것이 공통입니다. 마찬가지로, 차이 방정식(difference equations)에서, 차이 방정식 시스템의 특성 방정식의 복소 근 $r$ 은 형식 $f (t) = r t$ 의 초등 함수의 관점에서 시스템을 풀려고 시도하기 위해 사용됩니다.

In applied mathematics

Control theory

제어 이론(control theory)에서, 시스템은 라플라스 변환(Laplace transform)을 사용하여 시간 도메인(time domain)에서 주파수 도메인(frequency domain)으로 종종 변환됩니다. 시스템의 영점과 극점(zeros and poles)은 그런-다음 복소 평면에서 분석됩니다. 근 자취(root locus), 나이퀴스트 선도(Nyquist plot) 및 니콜스 선도(Nichols plot) 기법은 모두 복소 평면을 사용합니다.

근 자취 방법에서, 영점과 극점이 왼쪽 또는 오른쪽 반 평면에 있는지 여부, 즉, 영보다 큰 또는 작은 실수 부분을 가지는지 여부가 중요합니다. 만약 선형, 시간-불변 (LTI) 시스템은 다음인 극점을 가집니다:

오른쪽 반 평면에서, 그것은 불안정(unstable)이 될 것입니다.
왼쪽 반 평면에 있는 모두는, 안정(stable)이 될 것입니다.
허수 축 위에, 그것은 한계 안정성(marginal stability)을 가질 것입니다.

만약 시스템이 오른쪽 반 평면에 영점을 가지면, 그것은 비-최소 위상(nonminimum phase) 시스템입니다.

Signal analysis

복소수는 신호 해석(signal analysis) 및 다른 필드에서 주기적으로 변하는 신호에 대해 편리한 설명을 위해 사용됩니다. 실제 물리적 양을 나타내는 주어진 실수 함수에 대해, 종종 사인과 코사인의 관점에서, 대응하는 복소 함수는 실수 부분이 원래의 양인 것으로 고려됩니다. 주어진 주파수(frequency)의 사인파(sine wave)에 대해, 해당하는 $z$ 의 절댓값 $| z |$ 은 진폭(amplitude)이고 편각(argument) $arg(z)$ 는 위상(phase)입니다.

만약 푸리에 해석(Fourier analysis)은 주어진 실수-값 신호를 주기적 함수의 합으로 쓰기 위해 사용되며, 이들 주기적 함수는 다음 형식의 복소 값 함수로 종종 쓰입니다:

x(t)=\operatorname {Re} \{X(t)\}

및

X(t)=Ae^{i\omega t}=ae^{i\phi }e^{i\omega t}=ae^{i(\omega t+\phi )}

여기서 ω는 각 진동수(angular frequency)이고 복소수 A는 위에 설명된 것처럼 위상과 진폭을 인코딩합니다.

이 사용은 디지털 신호 처리(digital signal processing) 및 디지털 이미지 처리(digital image processing)로 역시 확장되며, 이것은 전송, 압축(compress), 복원 및 디지털(digital) 오디오(audio) 신호, 정지 이미지, 및 비디오(video) 신호를 다른 방법의 처리하기 위해 푸리에 해석 (및 웨이블릿(wavelet) 해석)의 디지털 버전을 사용합니다.

AM 라디오의 진폭 변조(amplitude modulation)의 두 사이드 밴드와 관련된, 또 다른 예제는 다음입니다:

{\begin{aligned}\cos((\omega +\alpha )t)+\cos \left((\omega -\alpha )t\right)&=\operatorname {Re} \left(e^{i(\omega +\alpha )t}+e^{i(\omega -\alpha )t}\right)\\&=\operatorname {Re} \left(\left(e^{i\alpha t}+e^{-i\alpha t}\right)\cdot e^{i\omega t}\right)\\&=\operatorname {Re} \left(2\cos(\alpha t)\cdot e^{i\omega t}\right)\\&=2\cos(\alpha t)\cdot \operatorname {Re} \left(e^{i\omega t}\right)\\&=2\cos(\alpha t)\cdot \cos \left(\omega t\right).\end{aligned}}

In physics

Electromagnetism and electrical engineering

전기 공학(electrical engineering)에서, 푸리에 변환(Fourier transform)은 변하는 전압(voltage) 및 전류(currents)를 분석하기 위해 사용됩니다. 저항기(resistor), 축전기(capacitor), 및 유도자(inductor)의 처리는 그런-다음 후자 둘에 대해 허수, 주파수-종속 저항을 도입하고 임피던스(impedance)라는 단일 복소수에서 모든 셋을 결합함으로써 통합될 수 있습니다. 이 접근은 페이저(phasor) 미적분학으로 불립니다.

전기 공학에서, 허수 단위는 전류(electric current)를 나타내기 위해 일반적으로 사용되는 $I$ , 또는 보다 특별히, 순간 전류를 나타내기 위해 일반적으로 사용되는 $i$ 와 혼동을 피하기 위해, $j$ 로 표시됩니다.

AC 회로(circuit)에서 전압(voltage)은 진동하므로, 다음으로 나타낼 수 있습니다:

V(t)=V_{0}e^{j\omega t}=V_{0}\left(\cos \omega t+j\sin \omega t\right),

측정-가능 양을 얻기 위해, 실수 부분은 취합니다:

v(t)=\mathrm {Re} (V)=\mathrm {Re} \left[V_{0}e^{j\omega t}\right]=V_{0}\cos \omega t.

복소-값 신호 $V(t)$ 는 실수-값, 측정-가능 신호 $v(t)$ 의 해석적(analytic) 표현으로 불립니다. ^[39]

Fluid dynamics

유체 동역학(fluid dynamics)에서, 복소 함수는 이차원에서 퍼텐셜 유동(potential flow in two dimensions)을 설명하기 위해 사용됩니다.

Quantum mechanics

복소수 필드는 양자 역학의 수학적 공식화(mathematical formulations of quantum mechanics)에 내재되어 있으며, 여기서 복소 힐베르트 공간(Hilbert space)은 편리하고 아마도 가장 표준적인 하나의 그러한 공식화에 대해 문맥을 제공합니다. 양자 역학의 원래의 기초 공식 – 슈뢰딩거 방정식(Schrödinger equation)과 하이젠베르크의 행렬 역학(matrix mechanics) – 은 복소수를 사용합니다.

Relativity

특수(special) 및 일반 상대성-이론(general relativity)에서, 시공간(spacetime)에 대한 메트릭에 대해 일부 공식은 만약 우리가 시공간 연속체의 시간 성분을 허수인 것으로 취하면 더 단순하게 됩니다. (이 접근은 고전 상대성-이론에서 더 이상 표준이 아니지만, 양자 필드 이론(quantum field theory)에서 필수적인 방법으로 사용됩니다.) 복소수는 스피너(spinor)에 필수적이며, 이것은 상대성-이론에 사용되는 텐서(tensor)의 일반화입니다.

Generalizations and related notions

실수의 필드 R을 C로 확장하는 과정은 케일리–딕슨 구성(Cayley–Dickson construction)으로 알려져 있습니다. 그것은 더 큰 차원으로 더 운반될 수 있으며, (실수 벡터 공간으로) 각각 차원 4 및 8인 쿼터니언(quaternion) H 및 옥토니언(octonion) O를 산출합니다. 이 문맥에서 복소수는 바이내리언(binarions)으로 불립니다.^[40]

구성을 실수에 적용함으로써 순서화(ordering)의 속성을 잃어버린 것처럼, 실수와 복소수로부터 익숙한 속성은 각 확장과 함께 사라집니다. 쿼터니언은 교환서을 잃어버리며, 즉, 일부 쿼터니언 $x, y$ 에 대해, $x \cdot y \neq y \cdot x$ 이며, 쿼터니언의 곱셈은, 추가적으로 교환적이지 않기 위해, 결합적인 것에 실패합니다: 일부 옥토니언 $x, y, z$ 에 대해 $(x \cdot y)\cdot z \neq x \cdot(y \cdot z)$ 입니다.

실수, 복소수, 쿼터니언 및 옥토니언은 R에 걸쳐 모든 정규화 나눗셈 대수(normed division algebra)입니다. 후르비츠의 정리(Hurwitz's theorem)에 의해, 그들은 오직 하나입니다: 세데니언(sedenion), 케일리–딕슨 구성에서 다음 단계는 이 구성을 가짐에 실해합니다.

케일리–딕슨 구성은, 기저 $(1, i)$ 와 관련하여, R-algebra (곱셈과 함께 R-벡터 공간)으로 생각하는, C의 정규 표현(regular representation)에 밀접하게 관련됩니다. 이것은 다음을 의미합니다: 일부 고정된 복소수 $w$ 에 대해, R-선형 맵

\mathbb {C} \rightarrow \mathbb {C} ,z\mapsto wz

은 $2 \times 2$ 행렬에 의해 표현될 수 있습니다 (일단 기저가 선택되어 왔습니다). 기저 $(1, i)$ 에 관하여, 이 행렬은 다음입니다:

{\begin{pmatrix}\operatorname {Re} (w)&-\operatorname {Im} (w)\\\operatorname {Im} (w)&\;\;\operatorname {Re} (w)\end{pmatrix}}

,

즉, 위의 복소수의 행렬 표현에 대한 섹션에서 언급된 하나입니다. 이것은 2 × 2 실수 행렬(2 × 2 real matrices)에서 C의 선형 표현(linear representation)이지만, 유일한 것은 아닙니다. 임의의 행렬

J={\begin{pmatrix}p&q\\r&-p\end{pmatrix}},\quad p^{2}+qr+1=0

은 그의 정사각 행렬이 항등 행렬: $J 2 = - I$ 의 부정인 속성을 가집니다. 그런-다음

\{z=aI+bJ:a,b\in \mathbf {R} \}

은 필드 C에 역시 동형이고, R² 위에 대안적인 복소 구조를 제공합니다. 이것은 선형 복소 구조(linear complex structure)의 개념에 의해 일반화됩니다.

초-복소수(Hypercomplex number)는 R, C, H, 및 O를 일반화합니다. 예를 들어, 이 개념은 분할-복소수(split-complex number)를 포함하며, 이것은 ( $R [x]/(x 2 + 1)$ 와 반대로) 링 $R [x]/(x 2 - 1)$ 의 원소입니다. 이 링에서, 방정식 $a 2 = 1$ 은 네 해를 가집니다.

필드 R은 보통 절댓값(absolute value) 메트릭(metric)에 관한 유리수(rational number)의 필드, Q의 완비입니다. Q 위에 메트릭(metrics)의 다른 선택은 (임의의 소수(prime number) p에 대해) p-진수 숫자(p-adic numbers)의 필드 Q_p로 이어지며, 이것은 그것에-의하여 R에 아날로그입니다. 오스트롭스키 정리(Ostrowski's theorem)에 의해, R과 Q_p보다 Q를 완비화의 다른 비-자명한 방법이 없습니다. Q_p의 대수적 클로저 ${\overline {\mathbf {Q} _{p}}}$ 는 여전히 노름을 나르지만, (C와 달리) 그것에 관해 완비가 아닙니다. ${\overline {\mathbf {Q} _{p}}}$ 의 완비 $\mathbf {C} _{p}$ 는 대수적으로 닫힌 것으로 밝혀집니다. 이 필드는 아날로그에 의해 p-진수 복소수라고 불립니다.

필드 R과 Q_p 및 C를 포함하는 그들의 유한 필드 확장은 지역 필드(local field)입니다.

Notes

^ For an extensive account of the history, from initial skepticism to ultimate acceptance, See (Bourbaki 1998), pages 18-24.
^ In modern notation, Tartaglia's solution is based on expanding the cube of the sum of two cube roots: $\left({\sqrt[{3}]{u}}+{\sqrt[{3}]{v}}\right)^{3}=3{\sqrt[{3}]{uv}}\left({\sqrt[{3}]{u}}+{\sqrt[{3}]{v}}\right)+u+v$ With $x={\sqrt[{3}]{u}}+{\sqrt[{3}]{v}}$ , $p=3{\sqrt[{3}]{uv}}$ , $q=u+v$ , $u$ and $v$ can be expressed in terms of $p$ and $q$ as $u=q/2+{\sqrt {(q/2)^{2}-(p/3)^{3}}}$ and $v=q/2-{\sqrt {(q/2)^{2}-(p/3)^{3}}}$ , respectively. Therefore, $x={\sqrt[{3}]{q/2+{\sqrt {(q/2)^{2}-(p/3)^{3}}}}}+{\sqrt[{3}]{q/2-{\sqrt {(q/2)^{2}-(p/3)^{3}}}}}$ . When $(q/2)^{2}-(p/3)^{3}$ is negative (casus irreducibilis), the second cube root should be regarded as the complex conjugate of the first one.

References

^ Penrose, Roger (2016). The Road to Reality: A Complete Guide to the Laws of the Universe (reprinted ed.). Random House. pp. 72–73. ISBN 978-1-4464-1820-8. Extract of p. 73: "complex numbers, as much as reals, and perhaps even more, find a unity with nature that is truly remarkable. It is as though Nature herself is as impressed by the scope and consistency of the complex-number system as we are ourselves, and has entrusted to these numbers the precise operations of her world at its minutest scales."
^ Burton, David M. (1995), The History of Mathematics (3rd ed.), New York: McGraw-Hill, p. 294, ISBN 978-0-07-009465-9
^ Bourbaki, Nicolas. "VIII.1". General topology. Springer-Verlag.
^ Axler, Sheldon (2010). College algebra. Wiley. p. 262.
^ Spiegel, M.R.; Lipschutz, S.; Schiller, J.J.; Spellman, D. (14 April 2009), Complex Variables (2nd Edition), Schaum's Outline Series, McGraw Hill, ISBN 978-0-07-161569-3
^ Aufmann, Richard N.; Barker, Vernon C.; Nation, Richard D. (2007), "Chapter P", College Algebra and Trigonometry (6 ed.), Cengage Learning, p. 66, ISBN 978-0-618-82515-8
^ Bourbaki, Nicolas. "VIII.1". General topology. Springer-Verlag.
^ See (Ahlfors 1979) harv error: multiple targets (2×): CITEREFAhlfors1979 (help).
^ Brown, James Ward; Churchill, Ruel V. (1996), Complex variables and applications (6th ed.), New York: McGraw-Hill, p. 2, ISBN 978-0-07-912147-9, In electrical engineering, the letter j is used instead of i.
^ Pedoe, Dan (1988), Geometry: A comprehensive course, Dover, ISBN 978-0-486-65812-4
^ See (Solomentsev 2001): "The plane $\R^2$ whose points are identified with the elements of $\C$ is called the complex plane"... "The complete geometric interpretation of complex numbers and operations on them appeared first in the work of C. Wessel (1799). The geometric representation of complex numbers, sometimes called the "Argand diagram" , came into use after the publication in 1806 and 1814 of papers by J.R. Argand, who rediscovered, largely independently, the findings of Wessel".
^ See (Apostol 1981), page 18.
^ Kasana, H.S. (2005), "Chapter 1", Complex Variables: Theory And Applications (2nd ed.), PHI Learning Pvt. Ltd, p. 14, ISBN 978-81-203-2641-5
^ Nilsson, James William; Riedel, Susan A. (2008), "Chapter 9", Electric circuits (8th ed.), Prentice Hall, p. 338, ISBN 978-0-13-198925-2
^ Kline, Morris. A history of mathematical thought, volume 1. p. 253.
^ Katz, Victor J. (2004), "9.1.4", A History of Mathematics, Brief Version, Addison-Wesley, ISBN 978-0-321-16193-2
^ Nahin, Paul J. (2007), An Imaginary Tale: The Story of √−1, Princeton University Press, ISBN 978-0-691-12798-9, retrieved 20 April 2011
^ ^a ^b Confalonieri, Sara (2015). The Unattainable Attempt to Avoid the Casus Irreducibilis for Cubic Equations: Gerolamo Cardano's De Regula Aliza. Springer. pp. 15-16 (note 26). ISBN 3658092750. It has been proved that imaginary numbers have necessarily to appear in the cubic formula when the equation has three real, different roots by Pierre Laurent Wantzel in 1843, Vincenzo Mollame in 1890, Otto Hölder in 1891 and Adolf Kneser in 1892. Paolo Ruffini also provided an incomplete proof in 1799.
^ Descartes, René (1954) [1637], La Géométrie | The Geometry of René Descartes with a facsimile of the first edition, Dover Publications, ISBN 978-0-486-60068-0, retrieved 20 April 2011
^ ^a ^b Gauss, C.F. (1831). "Anzeige von Theoria residuorum biquadraticorum, commentatio secunda (Notice on the Theory of Biquadratic Residues, second treatise)". Göttingische gelehrte Anzeigen. p. 638. Retrieved 18 March 2020.
^ ^a ^b Ewald, William B. (1996). "From Kant to Hilbert: A Source Book in the Foundations of Mathematics". Oxford University Press. p. 313. Retrieved 18 March 2020.
^ Caparrini, Sandro (2000), "On the Common Origin of Some of the Works on the Geometrical Interpretation of Complex Numbers", in Kim Williams (ed.), Two Cultures, Birkhäuser, p. 139, ISBN 978-3-7643-7186-9 Extract of page 139 Archived 2 December 2016 at the Wayback Machine
^ Hardy, G.H.; Wright, E.M. (2000) [1938], An Introduction to the Theory of Numbers, OUP Oxford, p. 189 (fourth edition), ISBN 978-0-19-921986-5
^ For the former notation, See (Apostol 1981), pages 15–16.
^ Abramowitz, Milton; Stegun, Irene A. (1964), Handbook of mathematical functions with formulas, graphs, and mathematical tables, Courier Dover Publications, p. 17, ISBN 978-0-486-61272-0, archived from the original on 23 April 2016, retrieved 16 February 2016, Section 3.7.26, p. 17 Archived 10 September 2009 at the Wayback Machine
^ Cooke, Roger (2008), Classical algebra: its nature, origins, and uses, John Wiley and Sons, p. 59, ISBN 978-0-470-25952-8, archived from the original on 24 April 2016, retrieved 16 February 2016, Extract: page 59 Archived 23 April 2016 at the Wayback Machine
^ See (Ahlfors 1979) harv error: multiple targets (2×): CITEREFAhlfors1979 (help), page 3.
^ See (Apostol 1981), pages 15–16.
^ See (Apostol 1981), page 25.
^ Bourbaki, Nicolas. "VIII.1". General topology. Springer-Verlag.
^ Marker, David (1996), "Introduction to the Model Theory of Fields", in Marker, D.; Messmer, M.; Pillay, A. (eds.), Model theory of fields, Lecture Notes in Logic, vol. 5, Berlin: Springer-Verlag, pp. 1–37, ISBN 978-3-540-60741-0, MR 1477154
^ Bourbaki, Nicolas. "VIII.4". General topology. Springer-Verlag.
^ Corry, Leo (2015). A Brief History of Numbers. Oxford University Press. pp. 215–16.
^ See (Apostol 1981), pages 15–16.
^ Bourbaki, Nicolas. "VIII.1". General topology. Springer-Verlag.
^ Lester, J.A. (1994), "Triangles I: Shapes", Aequationes Mathematicae, 52: 30–54, doi:10.1007/BF01818325
^ Kalman, Dan (2008a), "An Elementary Proof of Marden's Theorem", American Mathematical Monthly, 115 (4): 330–38, doi:10.1080/00029890.2008.11920532, ISSN 0002-9890, archived from the original on 8 March 2012, retrieved 1 January 2012
^ Kalman, Dan (2008b), "The Most Marvelous Theorem in Mathematics", Journal of Online Mathematics and its Applications, archived from the original on 8 February 2012, retrieved 1 January 2012
^ Grant, I.S.; Phillips, W.R. (2008), Electromagnetism (2 ed.), Manchester Physics Series, ISBN 978-0-471-92712-9
^ Kevin McCrimmon (2004) A Taste of Jordan Algebras, pp 64, Universitext, Springer ISBN 0-387-95447-3 MR2014924

Works cited

Ahlfors, Lars (1979), Complex analysis (3rd ed.), McGraw-Hill, ISBN 978-0-07-000657-7
Apostol, Tom (1981). Mathematical analysis. Addison-Wesley.{{cite book}}: CS1 maint: ref duplicates default (link)
Solomentsev, E.D. (2001) [1994], "Complex number", Encyclopedia of Mathematics, EMS Press