Integration by parts

Original article: w:Integration by parts

미적분학(calculus), 및 보다 일반적으로 수학적 해석학(mathematical analysis)에서, 부분에 의한 적분(integration by parts) 또는 부분적인 적분(partial integration)은 그들의 도함수와 역도함수의 곱의 적분의 관점에서 함수의 곱(product)의 적분(integral)을 찾는 과정입니다. 그것은 함수의 곱의 역도함수를 해가 보다 쉽게 구할 수 있는 역도함수로 변환하기 위해 자주 사용됩니다. 규칙은 미분화(differentiation)의 곱 규칙(product rule)의 적분 버전으로 생각될 수 있습니다.

만약 u = u(x)와 du = u′(x) dx이지만, v = v(x)와 dv = v′(x) dx이면, 부분에 의한 적분화는 다음임을 말합니다:

${\begin{aligned}\int _{a}^{b}u(x)v'(x)\,dx&\ =\ {\Big [}u(x)v(x){\Big ]}_{a}^{b}-\int _{a}^{b}u'(x)v(x)\,dx\\&\ =\ u(b)v(b)-u(a)v(a)-\int _{a}^{b}u'(x)v(x)\,dx\end{aligned}}$

또는 보다 간결하게:

$\int u\,dv\ =\ uv-\int v\,du.$

수학자 브룩 테일러(Brook Taylor)는 부분에 의한 적분화를 발견했으며, 1715년에 처음으로 그 아이디어를 발표했습니다. 부분에 의한 적분화의 보다 일반적인 공식화는 리만–스틸티어스(Riemann–Stieltjes) 및 르베그–스틸티어스 적분(Lebesgue–Stieltjes integrals)에 대해 존재합니다. 수열에 대해 이산 아날로그는 부분에 의한 합(summation by parts)으로 불립니다.

Theorem

Product of two functions

정리는 다음으로 유도될 수 있습니다. 두 연속적으로 미분-가능(continuously differentiable) 함수(functions) u(x)와 v(x)에 대해, 곱 규칙은 다음임을 말합니다:

${\Big (}u(x)v(x){\Big )}'\ =\ v(x)u'(x)+u(x)v'(x).$

양쪽 변에 x에 관해 적분하고,

$\int {\Big (}u(x)v(x){\Big )}'\,dx\ =\ \int u'(x)v(x)\,dx+\int u(x)v'(x)\,dx,$

부정 적분(indefinite integral)이 역도함수임을 주목하면 다음을 제공합니다:

$u(x)v(x)\ =\ \int u'(x)v(x)\,dx+\int u(x)v'(x)\,dx,$

여기서 우리는 적분화의 상수(constant of integration)를 쓰는 것을 무시합니다. 이것은 부분에 의한 적분화에 대해 공식을 산출합니다:

$\int u(x)v'(x)\,dx\ =\ u(x)v(x)-\int u'(x)v(x)\,dx,$

또는 미분(differentials) $\ du=u'(x)\,dx,\ \ dv=v'(x)\,dx$의 관점에서 공식을 제공합니다:

$\int u(x)\,dv\ =\ u(x)v(x)-\int v(x)\,du.$

이것은 각 변에 더해지는 지정되지-않은 상수를 갖는 함수의 상등으로 이해됩니다. 두 값 x = a 및 x = b 사이의 각 변의 차이를 취하고 미적분의 기본 정리(fundamental theorem of calculus)를 적용하면 한정 적분 버전을 제공합니다:

$\int _{a}^{b}u(x)v'(x)\,dx\ =\ u(b)v(b)-u(a)v(a)-\int _{a}^{b}u'(x)v(x)\,dx.$

원래 적분 ∫ uv′ dx은 도함수(derivative) v′을 포함합니다; 정리를 적용하기 위해, 우리는 반드시 v, v'의 역도함수(antiderivative)를 찾아야 하며, 그런-다음 결과 적분 ∫ vu′ dx을 평가합니다.

Validity for less smooth functions

그것은 u와 v에 대해 연속적으로 미분-가능인 것을 요구하지 않습니다. 부분에 의한 적분화는, 만약 u가 절대적으로 연속(absolutely continuous)이고 v′을 가리킨 함수가 르베그 적분 가능(Lebesgue integrable)이면 (그러나 반드시 연속일 필요는 없는), 작동합니다. (만약 v′가 불연속성의 점을 가지면 그것의 역도함수 v는 해당 점에서 도함수를 가지지 않을 수 있습니다.)

만약 적분화의 구간이 컴팩트(compact)가 아니면, 그것은 전체 구간에서 절대적으로 연속이 되는 u에 대해 또는 구간에서 르베그 적분 가능이 되는 v′에 대해 요구되지 않습니다. 몇 가지 예제 (이것에서 u와 v는 연속이고 연속적으로 미분-가능입니다)가 보일 것입니다. 예를 들어, 만약 다음이면,

$u(x)=\exp(x)/x^{2},\,v'(x)=\exp(-x)$

u는 구간 [1, ∞) 위의 절대적으로 연속이 아니지만, 그럼에도-불구하고 $\left[u(x)v(x)\right]_{1}^{\infty }$가 $L\to \infty$일 때 $u(L)v(L)-u(1)v(1)$의 극한을 의미하는 것으로 취해지는 한 및 오른쪽 변의 두 항이 유한한 한, 다음입니다:

$\int _{1}^{\infty }u(x)v'(x)\,dx={\Big [}u(x)v(x){\Big ]}_{1}^{\infty }-\int _{1}^{\infty }u'(x)v(x)\,dx$

이것은, 만약 우리가 $v(x)=-\exp(-x)$를 선택하면, 오직 참입니다. 비슷하게, 만약 다음이면:

$u(x)=\exp(-x),\,v'(x)=x^{-1}\sin(x)$

v'는 구간 [1, ∞) 위의 르베그 적분-가능이 아니지만, 그럼에도-불구하고 같은 해석과 함께, 다음입니다:

$\int _{1}^{\infty }u(x)v'(x)\,dx={\Big [}u(x)v(x){\Big ]}_{1}^{\infty }-\int _{1}^{\infty }u'(x)v(x)\,dx$

우리는 u와 v가 연속적으로 미분-가능이 아닌 것에서 유사한 예제를 역시 쉽게 얻을 수 있습니다.

게다가, 만약 $f(x)$가 구간 $[a,b]$ 위에 경계진 변화의 함수이고 $\varphi (x)$가 $[a,b]$ 위에 미분-가능이면, 다음입니다:

$\int _{a}^{b}f(x)\varphi '(x)\,dx=-\int _{-\infty }^{\infty }{\widetilde {\varphi }}(x)\,d({\widetilde {\chi }}_{[a,b]}(x){\widetilde {f}}(x)),$

여기서 $d(\chi _{[a,b]}(x){\widetilde {f}}(x))$는 경계진 변화 $\chi _{[a,b]}(x)f(x)$의 함수에 해당하는 부호화된 측정을 나타내고, 함수 ${\widetilde {f}},{\widetilde {\varphi }}$는 $\mathbb {R}$에 대한 $f,\varphi$의 확장이며, 이것은 경계진 변화 및 미분-가능의 각각입니다.

Product of many functions

세 개의 곱해진 함수, u(x), v(x), w(x)에 대해 곱 규칙을 적분하는 것은 비슷한 결과를 제공합니다:

$\int _{a}^{b}uv\,dw\ =\ {\Big [}uvw{\Big ]}_{a}^{b}-\int _{a}^{b}uw\,dv-\int _{a}^{b}vw\,du.$

일반적으로, n 인수에 대해

$\left(\prod _{i=1}^{n}u_{i}(x)\right)'\ =\ \sum _{j=1}^{n}u_{j}'(x)\prod _{i\neq j}^{n}u_{i}(x),$

이것은 다음으로 이어집니다:

$\left[\prod _{i=1}^{n}u_{i}(x)\right]_{a}^{b}\ =\ \sum _{j=1}^{n}\int _{a}^{b}u_{j}'(x)\prod _{i\neq j}^{n}u_{i}(x).$

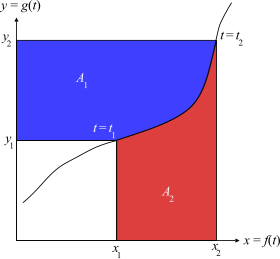
Visualization

Graphical interpretation of the theorem. The pictured curve is parametrized by the variable t.

(x, y) = (f(t), g(t))에 의한 매개변수화 곡선을 생각해 보십시오. 곡선은 지역적으로 일-대-일(one-to-one) 및 적분-가능(integrable)음을 가정하며, 우리는 다음임을 정의할 수 있습니다:

$x(y)=f(g^{-1}(y))$

$y(x)=g(f^{-1}(x))$

파란색 영역의 넓이는 다음입니다:

$A_{1}=\int _{y_{1}}^{y_{2}}x(y)\,dy$

비슷하게, 붉은색 영역의 넓이는 다음입니다:

$A_{2}=\int _{x_{1}}^{x_{2}}y(x)\,dx$

전체 넓이 A₁ + A₂는 큰 사각형의 넓이, x₂y₂, 빼기 작은 사각형의 넓이, x₁y₁와 같습니다:

$\overbrace {\int _{y_{1}}^{y_{2}}x(y)\,dy} ^{A_{1}}+\overbrace {\int _{x_{1}}^{x_{2}}y(x)\,dx} ^{A_{2}}\ =\ {\biggl .}x\cdot y(x){\biggl |}_{x_{1}}^{x_{2}}\ =\ {\biggl .}y\cdot x(y){\biggl |}_{y_{1}}^{y_{2}}.$

또는, t의 관점에서,

$\int _{t_{1}}^{t_{2}}x(t)\,dy(t)+\int _{t_{1}}^{t_{2}}y(t)\,dx(t)\ =\ {\biggl .}x(t)y(t){\biggl |}_{t_{1}}^{t_{2}}$

또는 부정 적분의 관점에서, 이것은 다음으로 쓸 수 있습니다:

$\int x\,dy+\int y\,dx\ =\ xy$

재정렬하여 다음입니다:

$\int x\,dy\ =\ xy-\int y\,dx$

따라서 부분에 의한 적분화는 직사각형의 넓이와 붉은색 영역의 넓이로부터 파란색 영역의 넓이를 유도하는 것으로 생각될 수 있습니다.

이 시각화는 왜 부분에 의한 적분화가, 함수 f(x)의 적분이 알려져 있을 때, 역함수 f⁻¹(x)의 적분을 찾는 데 도움이 될 수 있는 이유를 역시 설명합니다. 사실, 함수 x(y)와 y(x)는 역이고, 적분 ∫ x dy는 적분 ∫ y dx를 아는 것으로부터 위에서 처럼 계산될 수 있습니다. 특히, 이것은 로그(logarithm) 및 역 삼각 함수(inverse trigonometric function)를 적분하기 위한 부분에 의한 적분화의 사용을 설명합니다.

Applications

Finding antiderivatives

부분에 의한 적분화는 적분을 해결하기 위한 기계적인 과정이 아니라 휴리스틱(heuristic)입니다; 적분하기 위한 단일 함수가 주어지면, 전형적인 전략은 이 단일 함수를 부분에 의한 적분화 공식으로부터 남게 되는 적분이 단일 함수보다 평가하기 더 쉬운 것을 만족하는 두 함수 u(x)v(x)의 곱으로 조심스럽게 떼어놓는 것입니다. 다음 형식은 취하기 위한 최선의 전략을 묘사하는 것에서 유용합니다.

$\int uv\ dx=u\int v\ dx-\int \left(u'\int v\ dx\right)\ dx.$

오른쪽 변에서, u는 미분되고 v는 적분됩니다; 결과적으로 그것은 미분될 때 단순화되는 함수로 u를 선택하는 것, 또는 적분될 때 단순화되는 함수로 v를 선택하는 것이 유용합니다. 간단한 예제로, 다음을 생각해 보십시오:

$\int {\frac {\ln(x)}{x^{2}}}\ dx\ .$

ln(x)의 도함수는 1/x이므로, 우리는 (ln(x))를 부분 u으로 만드는데; 왜냐하면 1/x²의 역도함수는 −1/x이기 때문이며, 우리는 1/x² dx를 부분 dv로 만듭니다. 공식은 이제 다음을 산출합니다:

$\int {\frac {\ln(x)}{x^{2}}}\ dx=-{\frac {\ln(x)}{x}}-\int {\biggl (}{\frac {1}{x}}{\biggr )}{\biggl (}-{\frac {1}{x}}{\biggr )}\ dx\ .$

−1/x²의 역도함수는 거듭제곱 규칙(power rule)과 함께 구할 수 있고 1/x입니다.

대안적으로, 우리는 곱 u′ (∫v dx)가 약분에 의해 단순화되는 것을 만족하는 u와 v를 선택할 수 있을 것입니다. 예를 들어, 우리가 다음을 적분하기를 원한다고 가정합니다:

$\int \sec ^{2}(x)\cdot \ln {\Big (}{\bigl |}\sin(x){\bigr |}{\Big )}\ dx.$

만약 우리가 u(x) = ln(|sin(x)|) 및 v(x) = sec²x을 선택하면, u는 체인 규칙(chain rule)을 사용하여 1/ tan x로 미분되고 v는 tan x로 적분됩니다; 그래서 공식은 다음을 제공합니다:

$\int \sec ^{2}(x)\cdot \ln {\Big (}{\bigl |}\sin(x){\bigr |}{\Big )}\ dx=\tan(x)\cdot \ln {\Big (}{\bigl |}\sin(x){\bigr |}{\Big )}-\int \tan(x)\cdot {\frac {1}{\tan(x)}}\,dx\ .$

피적분은 1로 단순화되므로, 역도함수는 x입니다. 단순화 조합을 찾는 것은 종종 실험을 포함합니다.

일부 응용에서, 부분에 의한 적분화로 생성된 적분이 간단한 형식을 갖도록 보증하기 위해 필요한 것은 아닐 것입니다; 예를 들어, 수치 해석(numerical analysis)에서, 그것이 작은 크기를 가지고 그래서 오직 작은 오차 항에 기여하는 것으로 충분할 것입니다. 일부 다른 특수 기법이 아래 예제에서 시연됩니다.

Polynomials and trigonometric functions

다음을 계산하기 위해

$I=\int x\cos(x)\ dx\ ,$

다음으로 놓습니다:

$u=x\ \Rightarrow \ du=dx$

$dv=\cos(x)\ dx\ \Rightarrow \ v=\int \cos(x)\ dx=\sin(x)$

그런-다음:

${\begin{aligned}\int x\cos(x)\ dx&=\int u\ dv\\&=u\cdot v-\int v\,du\\&=x\sin(x)-\int \sin(x)\ dx\\&=x\sin(x)+\cos(x)+C,\end{aligned}}$

여기서 C는 적분화의 상수(constant of integration)입니다.

x의 더 높은 거듭제곱에 대해 다음 형식에서

$\int x^{n}e^{x}\ dx,\ \int x^{n}\sin(x)\ dx,\ \int x^{n}\cos(x)\ dx\ ,$

반복적으로 부분에 의한 적분화를 사용하면 다음에서 처럼 적분을 평가할 수 있습니다; 정리의 각 적용은 x의 거듭제곱을 1씩 낮춥니다.

Exponentials and trigonometric functions

부분에 의한 적분화의 동작을 검사하기 위해 공통적으로 사용되는 예제는 다음입니다:

$I=\int e^{x}\cos(x)\ dx.$

여기서, 부분에 의한 적분화는 두-번 수행됩니다. 먼저 다음을 놓습니다:

$u=\cos(x)\ \Rightarrow \ du=-\sin(x)\ dx$

$dv=e^{x}\ dx\ \Rightarrow \ v=\int e^{x}\ dx=e^{x}$

그런-다음 다음입니다:

$\int e^{x}\cos(x)\ dx=e^{x}\cos(x)+\int e^{x}\sin(x)\ dx.$

이제, 남아있는 적분을 평가하기 위해, 우리는, 다음과 함께, 다시 부분에 의한 적분화를 사용합니다:

$u=\sin(x)\ \Rightarrow \ du=\cos(x)\ dx$

$dv=e^{x}\ dx\ \Rightarrow \ v=\int e^{x}\ dx=e^{x}.$

그런-다음 다음입니다:

$\int e^{x}\sin(x)\ dx=e^{x}\sin(x)-\int e^{x}\cos(x)\ dx.$

이들을 함께 대입하면, 다음입니다:

$\int e^{x}\cos(x)\ dx=e^{x}\cos(x)+e^{x}\sin(x)-\int e^{x}\cos(x)\ dx.$

같은 적분이 이 방정식의 양쪽 변에 나타납니다. 적분은 다음을 얻기 위해 양쪽에 단순히 더해질 수 있습니다:

$2\int e^{x}\cos(x)\ dx=e^{x}{\bigl (}\sin(x)+\cos(x){\bigr )}+C$

이것은 다음으로 재정렬됩니다:

$\int e^{x}\cos(x)\ dx={\frac {e^{x}{\bigl (}\sin(x)+\cos(x){\bigr )}}{2}}+C'$

여기서 다시 C (및 C′ = C/2)는 적분화의 상수(constant of integration)입니다.

비슷한 방법은 시컨트 세제곱의 적분(integral of secant cubed)을 찾기 위해 사용됩니다.

Functions multiplied by unity

잘 알려진 두 예제는 부분에 의한 적분화가 1과 자체의 곱으로 표현된 함수에 적용될 때입니다. 이것은, 만약 함수의 도함수가 알려져 있고, 이 도함수의 적분 곱하기 x가 역시 알려져 있으면, 작동합니다.

첫 번째 예제는 ∫ ln(x) dx입니다. 우리는 이것을 다음으로 씁니다:

$I=\int \ln(x)\cdot 1\ dx\ .$

다음을 놓습니다:

$u=\ln(x)\ \Rightarrow \ du={\frac {dx}{x}}$

$dv=dx\ \Rightarrow \ v=x$

그런-다음 다음입니다:

${\begin{aligned}\int \ln(x)\ dx&=x\ln(x)-\int {\frac {x}{x}}\ dx\\&=x\ln(x)-\int 1\ dx\\&=x\ln(x)-x+C\end{aligned}}$

여기서 C는 적분화의 상수(constant of integration)입니다.

두 번째 에제는 역 탄젠트(inverse tangent) 함수 arctan(x)입니다:

$I=\int \arctan(x)\ dx.$

이것을 다음으로 다시-씁니다:

$\int \arctan(x)\cdot 1\ dx.$

이제 다음을 놓습니다:

$u=\arctan(x)\ \Rightarrow \ du={\frac {dx}{1+x^{2}}}$

$dv=dx\ \Rightarrow \ v=x$

그런-다음 다음입니다:

${\begin{aligned}\int \arctan(x)\ dx&=x\arctan(x)-\int {\frac {x}{1+x^{2}}}\ dx\\[8pt]&=x\arctan(x)-{\frac {\ln(1+x^{2})}{2}}+C\end{aligned}}$

역 체인 규칙 방법(inverse chain rule method) 및 자연 로그 적분 조건(natural logarithm integral condition)의 조합을 사용합니다.

LIATE rule

엄지의 규칙(rule of thumb)이 제안되어 왔으며, 다음 목록에서 먼저 오는 함수를 u로 선택하여 구성합니다:

L – 로그 함수(logarithmic function): $\ln(x),\ \log _{b}(x),$ 등등.

I – 역 삼각 함수(inverse trigonometric function): $\arctan(x),\ \operatorname {arcsec} (x),$ 등등.

A – algebraic functions(대수적 함수): $x^{2},\ 3x^{50},$ 등등.

T – 삼각 함수(trigonometric functions): $\sin(x),\ \tan(x),$ 등등.

E – 지수 함수(exponential function): $e^{x},\ 19^{x},$ 등등.

dv가 될 함수는 목록에서 마지막에 오는 것입니다: 목록에서 더 낮은 함수는 그것들 위의 함수보다 더 쉬운 역도함수(antiderivative)를 가집니다. 그 규칙은 때때로 "DETAIL"로 작성되며 여기서 D는 dv를 나타냅니다.

LIATE 규칙을 시연하기 위해, 다음 적분을 생각해 보십시오:

$\int x\cdot \cos(x)\,dx.$

LIATE 규칙에 따라, u = x, 및 dv = cos(x) dx이므로, du = dx, 및 v = sin(x)이며, 이것은 적분을 다음이 되게 만듭니다:

$x\cdot \sin(x)-\int 1\sin(x)\,dx,$

이것은 다음과 같습니다:

$x\cdot \sin(x)+\cos(x)+C.$

일반적으로, 우리는 du는 u보다 더 간단하고 dv는 적분하는 것이 쉬운 것을 만족하는 u와 dv를 선택하기 위해 시도합니다. 만약 대신에 cos(x)가 u로 선택되고, x dx가 dv로 선택되면, 우리는 다음 적분을 가질 것입니다:

${\frac {x^{2}}{2}}\cos(x)+\int {\frac {x^{2}}{2}}\sin(x)\,dx,$

이것은, 부분에 의한 적분화 공식의 재귀적인 적용 후에, 무한 재귀를 명백하게 초래하고 아무 데도 이어지지 않습니다.

비록 유용한 엄지의 규칙일지라도, LIATE 규칙에 대한 예외가 있습니다. 공통적인 대안은 대신에 "ILATE" 순서에서 규칙을 고려하는 것입니다. 역시, 일부 경우에서, 다항 항은 비-자명한 방법으로 나눌 필요가 있습니다. 예를 들어, 다음을 적분하기 위해

$\int x^{3}e^{x^{2}}\,dx,$

우리는 다음이 되도록:

$du=2x\,dx,\quad v={\frac {e^{x^{2}}}{2}}$,

다음을 정할 것입니다:

$u=x^{2},\quad dv=x\cdot e^{x^{2}}\,dx$.

그런-다음, 다음입니다:

$\int x^{3}e^{x^{2}}\,dx=\int (x^{2})\left(xe^{x^{2}}\right)\,dx=\int u\,dv=uv-\int v\,du={\frac {x^{2}e^{x^{2}}}{2}}-\int xe^{x^{2}}\,dx.$

마지막으로, 이것은 다음을 초래합니다:

$\int x^{3}e^{x^{2}}\,dx={\frac {e^{x^{2}}(x^{2}-1)}{2}}+C.$

부분에 의한 적분화는 수학적 해석학(mathematical analysis)에서 정리를 입증하기 위한 도구로 종종 사용됩니다.

Gamma function identity

감마 함수(gamma function)는 z > 0에 대해 부적절한 적분(improper integral)으로 정의된 특수 함수(special function)의 예제입니다. 부분에 의한 적분화는 그것을 팩토리얼(factorial)의 확장인 것으로 묘사합니다:

${\begin{aligned}\Gamma (z)&=\int _{0}^{\infty }e^{-x}x^{z-1}\,dx\\&=-\int _{0}^{\infty }x^{z-1}\,d\left(e^{-x}\right)\\&=-\left[e^{-x}x^{z-1}\right]_{0}^{\infty }+\int _{0}^{\infty }e^{-x}\,d\left(x^{z-1}\right)\\&=0+\int _{0}^{\infty }\left(z-1\right)x^{z-2}e^{-x}\,dx\\&=(z-1)\Gamma (z-1).\end{aligned}}$

왜냐하면, 정수 z에 대해, 다음이며,

$\Gamma (1)=\int _{0}^{\infty }e^{-x}\,dx=1,$

이 공식을 반복적으로 적용하면 팩토리얼(factorial)을 제공합니다:

$\Gamma (z+1)=z!$

Use in harmonic analysis

부분에 의한 적분화는 종종 조화 해석학(harmonic analysis), 특히 푸리에 해석학(Fourier analysis)에서, 충분히 매끄러운 피적분을 갖는 빠르게 진동하는 적분은 빠르게 감쇠함을 보이기 위해 종종 사용됩니다. 이것의 가장 공통적인 예제는 함수의 푸리에 변환의 감쇠가, 아래 설명된 것처럼, 해당 함수의 매끄러움에 달려 있음을 보이는 것에서 그것의 사용입니다.

Fourier transform of derivative

만약 f가 k-번 연속적으로 미분-가능 함수이고 k번째 것까지 모든 도함수가 무한대에서 0으로 감쇠하면, 그것의 푸리에 변환(Fourier transform)은 다음을 만족시킵니다:

$({\mathcal {F}}f^{(k)})(\xi )=(2\pi i\xi )^{k}{\mathcal {F}}f(\xi ),$

여기서 f^(k)는 f의 k번째 도함수입니다. (오른쪽에서 정확한 상수는 사용된 푸리에 변환의 협약에 의존합니다.) 이것은 다음임을 주목함으로써 입증됩니다:

${\frac {d}{dy}}e^{-2\pi iy\xi }=-2\pi i\xi e^{-2\pi iy\xi },$

그래서 도함수의 푸리에 변환에 대한 부분에 의한 적분화를 사용하여 우리는 다음을 얻습니다:

${\begin{aligned}({\mathcal {F}}f')(\xi )&=\int _{-\infty }^{\infty }e^{-2\pi iy\xi }f'(y)\,dy\\&=\left[e^{-2\pi iy\xi }f(y)\right]_{-\infty }^{\infty }-\int _{-\infty }^{\infty }(-2\pi i\xi e^{-2\pi iy\xi })f(y)\,dy\\[5pt]&=2\pi i\xi \int _{-\infty }^{\infty }e^{-2\pi iy\xi }f(y)\,dy\\[5pt]&=2\pi i\xi {\mathcal {F}}f(\xi ).\end{aligned}}$

이것을 귀납적으로(indectively) 적용하면 일반적인 k에 대해 결과를 제공합니다. 비슷한 방법은 함수의 도함수의 라플라스 변환(Laplace transform)을 찾기 위해 사용될 수 있습니다.

Decay of Fourier transform

위의 결과는 우리에게 푸리에 변환의 감쇠에 대해 말해주는데, 왜냐하면 그것은 만약 f와 f^(k)가 적분-가능이면 다음임을 따르기 때문입니다:

$\vert {\mathcal {F}}f(\xi )\vert \leq {\frac {I(f)}{1+\vert 2\pi \xi \vert ^{k}}},{\text{ where }}I(f)=\int _{-\infty }^{\infty }{\Bigl (}\vert f(y)\vert +\vert f^{(k)}(y)\vert {\Bigr )}\,dy.$

달리 말해서, 만약 f가 이들 조건을 만족시키면 그것의 푸리에 변환은 무한대에서 적어도 1/|ξ|^k만큼 빠르게 감쇠합니다. 특히, 만약 k ≥ 2이면, 푸리에 변환은 적분-가능입니다.

증명은 푸리에 변환의 정의로부터 즉각적인 다음이라는 사실을 사용합니다:

$\vert {\mathcal {F}}f(\xi )\vert \leq \int _{-\infty }^{\infty }\vert f(y)\vert \,dy.$

이 서브섹션의 시작에서 말했던 상등에 대한 같은 아이디어를 사용하여 다음을 제공합니다:

$\vert (2\pi i\xi )^{k}{\mathcal {F}}f(\xi )\vert \leq \int _{-\infty }^{\infty }\vert f^{(k)}(y)\vert \,dy.$

이들 두 부등식을 합하고 그런-다음 1 + |2πξ^k|로 나누면 말했던 부등식을 제공합니다.

Use in operator theory

연산자 이론(operator theory)에서 부분에 의한 적분화의 하나의 사용은 그것이 −∆ (여기서 ∆는 라플라스 연산자(Laplace operator)입니다)는 L² 위의 양의 연산자(positive operator)임을 보여 주는 것입니다 (L^p 공간을 참조하십시오). 만약 f가 매끄럽고 컴팩트하게 지원된 것이면, 부분에 의한 적분화를 사용하여, 우리는 다음을 가집니다:

${\begin{aligned}\langle -\Delta f,f\rangle _{L^{2}}&=-\int _{-\infty }^{\infty }f''(x){\overline {f(x)}}\,dx\\[5pt]&=-\left[f'(x){\overline {f(x)}}\right]_{-\infty }^{\infty }+\int _{-\infty }^{\infty }f'(x){\overline {f'(x)}}\,dx\\[5pt]&=\int _{-\infty }^{\infty }\vert f'(x)\vert ^{2}\,dx\geq 0.\end{aligned}}$

Other applications

• 스튀름–리우빌 이론(Sturm–Liouville theory)에서 경계 조건(boundary condition)을 결정하는 것
• 변화의 계산법(calculus of variations)에서 오일러–라그랑주 방정식(Euler–Lagrange equation)을 도출하는 것

Repeated integration by parts

부분적인 적분에 대해 공식의 왼쪽-변에 대한 적분에서 $v$의 이차 도함수를 고려하면 오른쪽-변에 대한 적분에 반복된 적용을 제안합니다:

$\int uv''\,dx=uv'-\int u'v'\,dx=uv'-\left(u'v-\int u''v\,dx\right).$

반복된 부분적인 적분화의 이 개념을 차수 n의 도함수로 확장하면 다음으로 이어집니다:

${\begin{aligned}\int u^{(0)}v^{(n)}\,dx&=u^{(0)}v^{(n-1)}-u^{(1)}v^{(n-2)}+u^{(2)}v^{(n-3)}-\cdots +(-1)^{n-1}u^{(n-1)}v^{(0)}+(-1)^{n}\int u^{(n)}v^{(0)}\,dx.\\[5pt]&=\sum _{k=0}^{n-1}(-1)^{k}u^{(k)}v^{(n-1-k)}+(-1)^{n}\int u^{(n)}v^{(0)}\,dx.\end{aligned}}$

이 개념은 $v^{(n)}$의 연속적인 적분이 손-쉽게 이용할 수 있을 때 (예를 들어, 라플라스(Laplace) 또는 푸리에 변환(Fourier transform)에서 처럼, 일반 지수 또는 사인과 코사인) 및 $u$의 n번째 도함수가 사라질 때 (예를 들어, 차수 $(n-1)$을 갖는 다항 함수일 때) 유용할 것입니다. 후자의 조건은 부분적인 적분의 반복을 중단하는데 왜냐하면 오른쪽-변의 적분이 사라지기 때문입니다.

부분적인 적분의 위의 반복 과정에서 다음 적분

$\int u^{(0)}v^{(n)}\,dx\quad$ and $\quad \int u^{(\ell )}v^{(n-\ell )}\,dx\quad$ and $\quad \int u^{(m)}v^{(n-m)}\,dx\quad {\text{ for }}1\leq m,\ell \leq n$

이 관련됩니다. 이것은 피적분 안에서 $v$와 $u$ 사이의 임의적으로 "평행-이동하는" 도함수로 해석될 수 있고, 역시 유용함을 입증할 수 있습니다 (로드리게스의 공식(Rodrigues' formula)을 참조하십시오).

Tabular integration by parts

위의 공식의 필수적인 과정은 테이블에서 요약될 수 있습니다: 결과적인 방법은 "테이블 적분화"로 불리고 영화 Stand and Deliver에서 소개되었습니다.

예를 들어, 다음 적분을 생각해 보십시오:

$\int x^{3}\cos x\,dx\quad$ and take $\quad u^{(0)}=x^{3},\quad v^{(n)}=\cos x.$

함수 $u^{(0)}=x^{3}$ 및 그의 후속 도함수 $u^{(i)}$가 영에 도달할 때까지 A 열에 나열하는 것으로 시작하십시오. 그런-다음 함수 $v^{(n)}=\cos x$ 및 그의 후속 적분 $v^{(n-i)}$가 열 B의 크기가 열 A의 크기와 같아질 때까지 열 B에 나열하십시오. 그 결과는 다음에서 처럼입니다:

# i	Sign	A: derivatives u(i)	B: integrals v(n−i)
0	+	$x^{3}$	$\cos x$
1	−	$3x^{2}$	$\sin x$
2	+	$6x$	$-\cos x$
3	−	$6$	$-\sin x$
4	+	$0$	$\cos x$

행 i에서 각각 부호와 함께 열 A와 B의 엔트리의 곱은 반복된 부분에 의한 적분화의 과정에서 단계 i에 관련된 적분을 제공합니다. 단계 i = 0은 원래 적분을 산출합니다. 단계 i > 0에서 완전한 결과에 대해 i번째 적분은 주어진 j번째 부호를 갖는 열 A의 j번째 엔트리와 열 B의 (j + 1)번째 엔트리의 모든 이전 곱 (0 ≤ j < i) (즉, 열 A의 첫 번째 엔트리와 열 B의 두 번째 엔트리를 곱하고, 열 A의 두 번째 엔트리와 열 B의 세 번째 엔트리를 곱하고, 등등 ...)에 더해져야 합니다. 이 과정은 적분을 산출하는 곱이 0일 때 (이 예제에서 i = 4), 자연스럽게 멈춥니다. 전체 결과는 (각 항에서 교대하는 부호를 갖는) 다음의 것입니다:

$\underbrace {(+1)(x^{3})(\sin x)} _{j=0}+\underbrace {(-1)(3x^{2})(-\cos x)} _{j=1}+\underbrace {(+1)(6x)(-\sin x)} _{j=2}+\underbrace {(-1)(6)(\cos x)} _{j=3}+\underbrace {\int (+1)(0)(\cos x)\,dx} _{i=4:\;\to \;C}.$

이것은 다음을 산출합니다:

$\underbrace {\int x^{3}\cos x\,dx} _{\text{step 0}}=x^{3}\sin x+3x^{2}\cos x-6x\sin x-6\cos x+C.$

반복된 부분적인 적분화는, 함수 $u^{(i)}$와 $v^{(n-i)}$를 각각 미분화하고 적분화하는 과정에서 그들의 곱이 원래 피적분의 배수를 초래할 때, 역시 유용한 것으로 밝혀집니다. 이 경우에서, 반복은 이 인덱스 i로 역시 종료될 수 있습니다. 이것은, 예상대로, 지수 및 삼각 함수와 함께 발생할 수 있습니다. 예제로 다음을 생각해 보십시오:

$\int e^{x}\cos x\,dx.$

# i	Sign	A: derivatives u(i)	B: integrals v(n−i)
0	+	$e^{x}$	$\cos x$
1	−	$e^{x}$	$\sin x$
2	+	$e^{x}$	$-\cos x$

이 경우에서 인덱스 i = 2에 대해 적절한 부호를 갖는 열 A와 B에서 항의 곱은 원래 피적분의 음수를 산출합니다 (행 i = 0와 i = 2를 비교하십시오).

$\underbrace {\int e^{x}\cos x\,dx} _{\text{step 0}}=\underbrace {(+1)(e^{x})(\sin x)} _{j=0}+\underbrace {(-1)(e^{x})(-\cos x)} _{j=1}+\underbrace {\int (+1)(e^{x})(-\cos x)\,dx} _{i=2}.$

오른쪽-변에 대한 적분은 그 자체 적분화 $C'$를 가질 수 있음을 관찰하고, 다른 변에 추상적인 적분을 가져오면, 다음을 제공합니다:

$2\int e^{x}\cos x\,dx=e^{x}\sin x+e^{x}\cos x+C',$

및 마침내 다음입니다:

$\int e^{x}\cos x\,dx={\frac {1}{2}}\left(e^{x}(\sin x+\cos x)\right)+C,$

여기서 C = C′/2.

Higher dimensions

부분에 의한 적분화는 미적분학의 기본 정리의 버전을 적절한 곱 규칙에 적용함으로써 여러 변수의 함수로 확장될 수 있습니다. 스칼라-값 함수 u 및 벡터-값 함수 (벡터 필드) V를 포함하는, 다변수 미적분학에서 가능한 여러 그러한 쌍의-연결이 있습니다.

발산에 대해 곱 규칙(product rule for divergence)은 다음임을 말합니다:

$\nabla {\cdot }(u\mathbf {V} )\ =\ u\,\nabla {\cdot }\mathbf {V} \ +\ \nabla u\cdot \mathbf {V} .$

$\Omega$는 조각마다 매끄러운(piecewise smooth) 경계(boundary) $\Gamma =\partial \Omega$를 갖는 $\mathbb {R} ^{n}$의 열린(open) 경계진 부분-집합(bounded subset)인 것으로 가정합니다. 표준 부피에 관한 $\Omega$에 걸쳐 적분하는 것은 $d\Omega$를 형성하고, 발산 정리(divergence theorem)를 적용하면, 다음을 제공합니다:

$\int _{\Gamma }u\mathbf {V} \cdot {\hat {\mathbf {n} }}\,d\Gamma \ =\ \int _{\Omega }\nabla \cdot (u\mathbf {V} )\,d\Omega \ =\ \int _{\Omega }u\,\nabla {\cdot }\mathbf {V} \,d\Omega \ +\ \int _{\Omega }\nabla u\cdot \mathbf {V} \,d\Omega ,$

여기서 ${\hat {\mathbf {n} }}$는 표준 리만 부피 형식 $d\Gamma$에 관해 적분된, 경계에 대한 외부 단위 법선 벡터입니다. 재정렬하면 다음을 제공합니다:

$\int _{\Omega }u\,\nabla {\cdot }\mathbf {V} \,d\Omega \ =\ \int _{\Gamma }u\mathbf {V} \cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }\nabla u\cdot \mathbf {V} \,d\Omega ,$

또는 다른 단어에서

$\int _{\Omega }u\,\operatorname {div} (\mathbf {V} )\,d\Omega \ =\ \int _{\Gamma }u\mathbf {V} \cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }\operatorname {grad} (u)\cdot \mathbf {V} \,d\Omega .$

정리의 정칙성(regularity) 요구-사항은 완화될 수 있습니다. 예를 들어, 경계 $\Gamma =\partial \Omega$는 오직 립시츠 연속(Lipschitz continuous)인 것으로 요구되고, 함수 u, v는 오직 소볼레프 공간(Sobolev space) H¹(Ω)에 놓이는 것으로 요구됩니다.

First Green's identity

연속적으로 미분-가능 벡터 필드 $\mathbf {U} =u_{1}\mathbf {e} _{1}+\cdots +u_{n}\mathbf {e} _{n}$ 및 $v\mathbf {e} _{1},\ldots ,v\mathbf {e} _{n}$를 생각해 보십시오, 여기서 $\mathbf {e} _{i}$는 $i=1,\ldots ,n$에 대해 i-번째 표준 기저 벡터입니다. 이제 위의 부분에 의한 적분화를 각 $u_{i}$ 곱하기 벡터 필드 $v\mathbf {e} _{i}$에 적용하십시오:

$\int _{\Omega }u_{i}{\frac {\partial v}{\partial x_{i}}}\,d\Omega \ =\ \int _{\Gamma }u_{i}v\,\mathbf {e} _{i}\cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }{\frac {\partial u_{i}}{\partial x_{i}}}v\,d\Omega .$

i에 걸쳐 합하는 것은 새로운 부분에 의한 적분화 공식을 제공합니다:

$\int _{\Omega }\mathbf {U} \cdot \nabla v\,d\Omega \ =\ \int _{\Gamma }v\mathbf {U} \cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }v\,\nabla {\cdot }\mathbf {U} \,d\Omega .$

$u\in C^{2}({\bar {\Omega }})$인, 경우 $\mathbf {U} =\nabla u$는 첫 번째 그린의 항등식(first Green's identity)으로 알려져 있습니다:

$\int _{\Omega }\nabla u\cdot \nabla v\,d\Omega \ =\ \int _{\Gamma }v\,\nabla u\cdot {\hat {\mathbf {n} }}\,d\Gamma -\int _{\Omega }v\,\nabla ^{2}\!u\,d\Omega .$

See also

• Integration by parts for the Lebesgue–Stieltjes integral
• Integration by parts for semimartingales, involving their quadratic covariation.
• Integration by substitution
• Legendre transformation

Further reading

• Louis Brand (10 October 2013). Advanced Calculus: An Introduction to Classical Analysis. Courier Corporation. pp. 267–. ISBN 978-0-486-15799-3.
• Hoffmann, Laurence D.; Bradley, Gerald L. (2004). Calculus for Business, Economics, and the Social and Life Sciences (8th ed.). pp. 450–464. ISBN 0-07-242432-X.
• Willard, Stephen (1976). Calculus and its Applications. Boston: Prindle, Weber & Schmidt. pp. 193–214. ISBN 0-87150-203-8.
• Washington, Allyn J. (1966). Technical Calculus with Analytic Geometry. Reading: Addison-Wesley. pp. 218–245. ISBN 0-8465-8603-7.

External links

• "Integration by parts", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Integration by parts—from MathWorld