Exponentiation

Original article: w:Exponentiation

"Exponent" redirects here. For other uses, see Exponent (disambiguation).

Graphs of y = b^x for various bases b:   base 10,   base e,   base 2,   base 1/2. Each curve passes through the point (0, 1) because any nonzero number raised to the power of 0 is 1. At x = 1, the value of y equals the base because any number raised to the power of 1 is the number itself.

지수화(Exponentiation)은, 두 숫자, 밑수(base) b와 지수(exponent) 또는 거듭제곱(power) n을 포함하는, bⁿ으로 쓰이는 수학적(mathematical) 연산(operation)이고, "b에 올려진 n의 거듭제곱"이라고 발음합니다. n이 양의 정수(integer)일 때, 지수화는 밑수의 반복되는 곱셈(multiplication)에 해당합니다: 즉, bⁿ은 n 밑수를 곱하는 곱(product)입니다:

$b^{n}=\underbrace {b\times \dots \times b} _{n\,{\textrm {times}}}.$

지수는 밑수의 오른쪽에 위첨자(superscript)로 보통 보입니다. 그 경우에서, bⁿ은 "b에 올려진 n번째 거듭제곱", "b에 올려진 n의 거듭제곱", "b의 n번째 거듭제곱", "b에 n-번째 거듭제곱", 또는 가장 간단하게 "b에 n번째"으로 불립니다.

우리는 b¹ = b을 가지고, 임의의 양의 정수 m과 n에 대해, 우리는 bⁿ ⋅ b^m = b^n+m를 가집니다. 이 속성을 비-양의 정수 지수로 확장하기 위해, b⁰은 1로 정의되고, (양의 정수 n과 비-영 b와 함께) b⁻ⁿ은 1/bⁿ로 정의됩니다. 특히, b⁻¹은 1/b, b의 역수(reciprocal)와 같습니다.

지수화의 정의는 임의의 실수 또는 복소수(complex) 지수를 허용하기 위해 확장될 수 있습니다. 정수 지수에 의한 지수화는 역시 행렬(matrices)을 포함하여 대수적 구조의 광범위한 종류에 대해 정의될 수 있습니다.

지수화는 복리(compound interest), 인구 성장(population growth), 화학 반응 속도론(chemical reaction kinetics), 파동(wave) 행태, 및 공개-키 암호(public-key cryptography)와 같은 응용을 갖는, 경제학(economics), 생물학(biology), 화학(chemistry), 물리학(physics), 및 컴퓨터 과학(computer science)을 포함한, 많은 분야에서 널리 사용됩니다.

History of the notation

용어 거듭제곱(power, Latin: potentia, potestas, dignitas)은 직선의 제곱에 대해, 키오스의 히포크라테스(Hippocrates of Chios) 다음의, 그리스(Greek) 수학자 유클리드(Euclid)에 의해 사용된 고대 그리스어(ancient Greek) δύναμις (dúnamis, 여기서: "amplification")의 잘못된-번역입니다. 아르키메데스(Archimedes)는 10의 거듭제곱을 조작하기 위해 필요한, 지수의 법칙 10^a ⋅ 10^b = 10^a+b을 발견하고 증명했습니다. 9세기에, 페르시아 수학자 무하마드 이븐 무사 알-콰리즈미(Muhammad ibn Mūsā al-Khwārizmī)는 제곱(square)에 대해 용어 مَال (māl, "possessions", "property")—무슬림, "그 당시와 이전 시대의 대부분의 수학자처럼, 제곱된 숫자를 넓이, 특히 토지의 묘사, 따라서 재산으로 생각"—과 세제곱(cube)에 대해 كَعْبَة (kaʿbah, "cube")를 사용했으며, 이후 이슬람(Islamic) 수학자들은, 압바스 알-하산 이븐 알리 알-칼라스사디(Abū al-Hasan ibn Alī al-Qalasādī)의 연구에서 보이는 것처럼, 15세기까지, 각각 문자 mīm (m)과 kāf (k)로 수학 표기법(mathematical notation)에서 표현했습니다.

16세기 후반에, 요스트 뷔르기(Jost Bürgi)는 지수에 대해 로마 숫자-표시를 사용했습니다.

니콜라스 추케(Nicolas Chuquet)는 15세기에 지수 표기법의 형식을 사용했으며, 나중에 16세기에 하인리히 슈라이버(Heinrich Schreiber)와 미카엘 스티펠(Michael Stifel)에 의해 사용되었습니다. 단어 "exponent(지수)"는 1544년에 미카엘 스티펠에 의해 만들어졌습니다. 사무엘 제이크(Samuel Jeake)는 1696년에 용어 indices을 도입했습니다. 16세기에, 로버트 레코드(Robert Recorde)는 용어 square, cube, zenzizenzic (네 번째 거듭제곱), supersolid (다섯 번째), zenzicube (여섯 번째), second supersolid (일곱 번째), 및 zenzizenzizenzic (여덟 번째)를 사용했습니다. Biquadrate는 마찬가지로 네 번째 거듭제곱을 참조하기 위해 사용되어 왔습니다.

17세기 초에, 우리의 현대 지수 표기법의 첫 번째 형식은 La Géométrie의 제목인 그의 책에서 르네 데카르트(Rene Descartes)에 의해 도입되었습니다; 그것에서, 그 표기법은 제 I권에 소개되어 있습니다.

일부 수학자 (예를 들어, 아이작 뉴턴(Isaac Newton))는 오직 2보다 큰 거듭제곱에 대해 지수를 사용했으며, 제곱을 반복된 곱셈으로 표시하는 것을 선호했습니다. 따라서 그들은 다항식(polynomial)을, 예를 들어, ax + bxx + cx³ + d으로, 썼을 것입니다.

또 다른 역사적인 동의어, involution은 지금은 드물고 그것의 보다 공통적인 의미(인볼루션)과 혼동되어서는 안됩니다.

1748년에 레온하르트 오일러(Leonhard Euler)는 썼습니다:

"지수 자체가 변수인 지수 또는 거듭제곱을 생각해 보십시오. 그것들에서 지수는 반드시 상수이기 때문에, 이런 종류의 양은 대수적 함수(algebraic function)가 아닌 것이 분명합니다."

초월적 함수(transcendental function)의 이 도입과 함께, 오일러는 자연 지수 함수(natural exponential function), f(x) = e^x에 대해 역함수(inverse function)로 자연 로그(natural logarithm)의 현대 도입에 대한 기초를 마련했습니다.

Terminology

표현 b² = b ⋅ b은 "b의 제곱(square)" 또는 "제곱된 b"라고 불리는데, 왜냐하면 변-길이 b를 갖는 정사각형(square)의 넓이는 b²이기 때문입니다.

유사하게, 표현 b³ = b ⋅ b ⋅ b은 "b의 세제곱(cube)" 또는 "세제곱된 b"라고 불리는데, 왜냐하면 변-길이 b를 갖는 정육면체(cube)의 부피는 b³이기 때문입니다.

지수가 양의 정수(positive integer)일 때, 지수는 함께 곱해지는 밑수의 사본이 몇개인지를 나타냅니다. 예를 들어, 3⁵ = 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 243입니다. 지수가 5이기 때문에, 밑수 3은 반복된 곱셈에서 5번 나타납니다. 여기서, 243은 3의 5번째 거듭제곱(5th power of 3), 또는 3에 올려진 5번째 거듭제곱(3 raised to the 5th power)입니다.

단어 "올려진"은 보통 생략되고, 때때로 "거듭제곱"도 마찬가지로 생략되므로, 3⁵은 간단히 "3의 5번째", 또는 "3에 5"로 읽을 수 있습니다. 그러므로, 지수화 bⁿ은 "b에 n의 거듭제곱", "b에 n번째 거듭제곱", "b에 n번째", 또는 가장 간략하게 "b에 n"로 표현될 수 있습니다.

3⁵⁷ (이것은 3⁽⁵⁷⁾를 의미하고 (3⁵)⁷가 아닙니다)과 같은 중첩된 지수를 갖는 수식은 거듭제곱의 탑(tower of powers) 또는 단순히 탑이라고 불립니다.

Integer exponents

정수 지수를 가진 지수화 연산은 기초 산술 연산(arithmetic operation)에서 직접 정의될 수 있습니다.

Positive exponents

양의 정수 지수를 갖는 거듭제곱은 다음의 기본 경우와 재귀 관계에 의해 정의될 수 있습니다:

기본 경우

$b^{1}=b$

및 재귀 관계(recurrence relation)

$b^{n+1}=b^{n}\cdot b.$

곱셈의 결합성(associativity)은 임의의 양의 정수 m과 n에 대해 다음임을 의미합니다:

$b^{m+n}=b^{m}\cdot b^{n}.$

Zero exponent

임의의 비-영 숫자에 올려진 0 거듭제곱은 1입니다:

$b^{0}=1.$

그러한 거듭제곱의 한 가지 해석은 빈 곱(empty product)입니다.

0⁰의 경우는 더 복잡하고, 그것에 값을 할당할지 여부와 무슨 값을 할당할지는 문맥에 따라 다를 수 있습니다. 더 자세한 내용에 대해, 영에 영의 거듭제곱(Zero to the power of zero)을 참조하십시오.

Negative exponents

다음 항등식은 임의의 정수 n과 비-영 b에 대해 유지됩니다:

$b^{-n}={\frac {1}{b^{n}}}.$

0에 음의 지수를 올리는 것은 정의되지 않지만, 일부 환경에서, 그것은 무한대 (∞)로 해석될 수 있습니다.

위의 항등식은 지수의 범위를 음의 정수로 확장하려는 목적을 가진 정의를 통해 유도될 수 있습니다.

비-영 b와 양의 n에 대해, 위의 재귀 관계는 다음으로 다시 쓸 수 있습니다:

$b^{n}={\frac {b^{n+1}}{b}},\quad n\geq 1.$

이 관계를 모든 정수 n과 비-영 b에 대해 유효한 것으로 정의함으로써, 그것은 다음임을 따릅니다:

${\begin{aligned}b^{0}&={\frac {b^{1}}{b}}=1,\\[3pt]b^{-1}&={\frac {b^{0}}{b}}={\frac {1}{b}},\end{aligned}}$

그리고 보다 일반적으로 임의의 비-영 b와 임의의 비-음의 정수 n에 대해,

$b^{-n}={\frac {1}{b^{n}}}.$

이것은 그런-다음 모든 각 정수 n에 대해 참으로 쉽게 보입니다.

Identities and properties

다음 항등식(identities)은 모든 정수 지수에 대해 유지되며, 밑수가 비-영인 것으로 조건 아래에서 제공됩니다:

${\begin{aligned}b^{m+n}&=b^{m}\cdot b^{n}\\\left(b^{m}\right)^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b^{n}\cdot c^{n}\end{aligned}}$

덧셈과 곱셈과 달리:

• 지수화는 교환적(commutative)이 아닙니다. 예를 들어, 2³ = 8 ≠ 3² = 9.
• 지수화는 결합적(associative)이 아닙니다. 예를 들어, (2³)⁴ = 8⁴ = 4096이고, 반면에 2⁽³⁴⁾ = 2⁸¹ = 2417851639229258349412352입니다. 괄호없이, 위첨자 표기법에서 연속 지수화(serial exponentiation)에 대해 전통적인 연산의 순서(order of operations)는, 상향식 (또는 왼쪽-결합적)이 아닌, 하향식 (또는 오른쪽-결합적)입니다. 즉,

  $b^{p^{q}}=b^{\left(p^{q}\right)},$

  이것은, 일반적으로, 다음과 다릅니다:

  $\left(b^{p}\right)^{q}=b^{pq}.$

Powers of a sum

합의 거듭제곱은 통상적으로 이항 공식(binomial formula)에 의해 피합수의 거듭제곱으로부터 계산될 수 있습니다:

$(a+b)^{n}=\sum _{i=0}^{n}{\binom {n}{i}}a^{i}b^{n-i}=\sum _{i=0}^{n}{\frac {n!}{i!(n-i)!}}a^{i}b^{n-i}.$

어쨌든, 이 공식은 오직 피합수가 교환될 때 (즉, ab = ba일 때) 참이며, 이것은 그것들이 교환적(commutative)인 구조(structure)에 속함을 의미합니다. 그렇지 않으면, 만약 a와 b가, 말하자면, 같은 크기의 정사각 행렬(square matrices)이면, 이 공식은 사용될 수 없습니다. 그것은 컴퓨터 대수학(computer algebra)에서, 정수 지수를 포함하는 많은 알고리듬(algorithm)은 지수화 밑수가 교환되지 않을 때 변경되어야 함을 따릅니다. 일부 일반적인 컴퓨터 대수 시스템(computer algebra system)은 비-교환하는 밑수를 갖는 지수화를 위해 다른 표기법 (때때로 ^ 대신 ^^)을 사용하며, 이것은 그때에 비-교환 지수화라고 불립니다.

Combinatorial interpretation

See also: Exponentiation over sets

비-음의 정수 n과 m에 대해, n^m의 값은 m 원소의 집합(set)에서 n 원소의 집합으로의 함수(functions)의 개수입니다 (세는-숫자 지수화(cardinal exponentiation)를 참조하십시오). 그러한 함수는 n-원소 집합에서 m-튜플(tuple)로 (또는 n-문자 알파벳에서 m-문자 단어로) 표현될 수 있습니다. m과 n의 특정 값에 대해 일부 예제가 다음 테이블에서 제공됩니다:

nm	집합 {1,...,n}에서 원소의 nm 가능한 m-튜플
$0^{5}=0$	none
$1^{4}=1$	$(1,1,1,1)$
$2^{3}=8$	$(1,1,1),(1,1,2),(1,2,1),(1,2,2),(2,1,1),(2,1,2),(2,2,1),(2,2,2)$
$3^{2}=9$	$(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)$
$4^{1}=4$	$(1),(2),(3),(4)$
$5^{0}=1$	$()$

Particular bases

Powers of ten

See also: Scientific notation

Main article: Power of 10

밑수 십 (십진수(decimal)) 숫자 시스템에서, 10의 정수 거듭제곱은 지수의 부호와 크기에 의해 결정되는 영들의 숫자에 의해 뒤에 오는 또는 앞에 오는 자릿수 1로 쓰입니다. 예를 들어, 10³ = 1000 및 10⁻⁴ = 0.0001.

밑수 10을 갖는 지수화는 과학 표기법(scientific notation)에서 큰 또는 작은 숫자를 나타내기 위해 사용됩니다. 예를 들어, (진공에서 빛의 속력(speed of light), 초당 미터(metres per second)에서) 299792458 m/s는 2.99792458×10⁸ m/s로 쓸 수 있고, 그런-다음 2.998×10⁸ m/s로 근사화(approximated)될 수 있습니다.

10의 거듭제곱에 기초한 SI 접두사(SI prefix)는 역시 작은 또는 큰 양을 나타내기 위해 사용됩니다. 예를 들어, 접두사 킬로(kilo)는 10³ = 1000이므로, 1 킬로미터는 1000 m입니다.

Powers of three

Main article: Power of three

Powers of two

Main article: Power of 2

2의 첫 번째 음의 거듭제곱은 공통적으로 사용되고, 특별한 이름, 예를 들어: 절반(half) 및 4분의 일(quarter)을 가집니다.

2의 거듭제곱은 집합 이론에 나타나는데, 왜냐하면 n 구성원을 가진 집합은 거듭제곱 집합(power set), 그것의 부분집합(subset)의 모두의 집합을 가지며, 2ⁿ 구성원을 가집니다.

2의 정수 거듭제곱은 컴퓨터 과학(computer science)에서 중요합니다. 양의 정수 거듭제곱 2ⁿ은 n-비트(bit) 정수 이진 숫자(binary number)에 대해 가능한 값의 숫자를 제공합니다; 예를 들어, 일 바이트(byte)는 2⁸ = 256개의 서로 다른 값을 취할 수 있습니다. 이진 숫자 시스템(binary number system)은 2의 거듭제곱의 합으로 임의의 숫자를 표현하고, 그것을 이진 점(binary point)에 의해 분리되는, 0과 1의 수열로 나타내며, 여기서 1은 합에서 나타나는 2의 거듭제곱을 가리킵다; 지수는 이것 1의 위치에 의해 결정됩니다: 비-음의 지수는 그 점의 왼쪽에 있는 (0부터 시작) 1의 순위이고, 음의 지수는 그 점의 오른쪽에 있는 순위에 의해 결정됩니다.

Powers of one

일의 거듭제곱은 모두 일입니다: 1ⁿ = 1.

Powers of zero

만약 지수 n가 양수 (n > 0)이면, 영의 n번째 거듭제곱은 영입니다: 0ⁿ = 0.

만약 지수 n가 음수 (n < 0)이면, 영의 n번째 거듭제곱 0ⁿ은 정의되지 않는데, 왜냐하면 그것은 -n > 0을 갖는 $1/0^{-n}$와 반드시 같고, 이것은 위에 따라 $1/0$이 될 것이기 때문입니다.

표현 0⁰은 1로 정의되거나, 또는 정의되지 않은 채 남겨집니다 (영에 영 거듭제곱(Zero to the power of zero)을 참조하십시오).

Powers of negative one

만약 n이 짝수 정수이면, (−1)ⁿ = 1.

만약 n이 홀수 정수이면, (−1)ⁿ = −1.

이것 때문에, −1의 거듭제곱은 교대하는 수열(sequence)을 표현하는 것에 유용합니다. 복소수 i의 거듭제곱의 비슷한 논의에 대해, § Powers of complex numbers을 참조하십시오.

Large exponents

일보다 큰 숫자의 거듭제곱의 수열의 극한(limit of a sequence)은 발산합니다: 달리 말해서, 극한은 경계없이 증가합니다:

b > 1일 때, n → ∞일 때 bⁿ → ∞입니다.

이것은 "b가 일보다 클 때, n이 무한대로 가는 경향이 있을 때 b의 n 거듭제곱은 +∞로 가는 경향이 있습니다"로 읽을 수 있습니다.

일보다 작은 절댓값을 가진 숫자의 거듭제곱은 영으로 가는 경향이 있습니다:

|b| < 1일 때, n → ∞일 때 bⁿ → 0입니다.

일의 임의의 거듭제곱은 항상 일입니다:

만약 b = 1이면, 모든 n에 대해 bⁿ = 1입니다.

–1의 거듭제곱은 n이 짝수와 홀수를 교대시킬 때 1과 –1 두 값 사이를 교대하고, 따라서 n이 증가할 때 임의의 극한으로 가는 경향이 없습니다.

만약 b < –1이면, bⁿ은 n이 짝수와 홀수를 교대시킬 때 아주 큰 양의 숫자와 음의 숫자를 교대하고, 따라서 n이 증가할 때 임의의 극한으로 가는 경향이 없습니다.

만약 지수화된 숫자가, 지수가 무한대로 가는 경향이 있을 때, 1로 가는 경향 동안 변하면, 극한은 위의 것 중의 하나일 필요는 없습니다. 특히 중요한 경우는 다음입니다:

n → ∞일 때 (1 + 1/n)ⁿ → e

아래의 § The exponential function를 참조하십시오.

다른 극한들, 특히 불확정 형식(indeterminate form)을 취하는 표현의 극한은 아래의 § Limits of powers에서 설명되어 있습니다.

Power functions

Power functions for $n=1,3,5$

Power functions for $n=2,4,6$

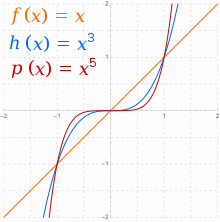
$c\neq 0$인 형식 $f(x)=cx^{n}$의 실수 함수는 때때로 거듭제곱 함수라고 불립니다. $n$이 정수(integer)이고 $n\geq 1$일 때, 둘의 주요 가족이: 짝수 $n$에 대해 및 홀수 $n$에 대해 존재합니다. 일반적으로 $c>0$에 대해, $n$이 짝수일 때 $f(x)=cx^{n}$은 증가하는 $x$와 함께 양의 무한대(infinity)로 향하는 경향이 있고, 역시 감소하는 $x$와 함께 양의 무한대로 향하는 경향이 있습니다. 짝수 거듭제곱 함수의 가족에서 모든 그래프는 $y=cx^{2}$의 일반적인 모양을 가지며, $n$이 증가할 때 중간에서 더 평평해집니다. 이런 종류의 대칭(symmetry) ($f(-x)=f(x)$)을 갖는 함수는 짝수 함수(even functions)라고 불립니다.

$n$이 홀수일 때, $f(x)$의 점근적(asymptotic) 행동은 양의 $x$에서 음의 $x$로 뒤집힙니다. $c>0$에 대해, $f(x)=cx^{n}$은 역시 증가하는 $x$와 함께 양의 무한대(infinity)로 향하는 경향일 것이지만, 감소하는 $x$와 함께 음의 무한대로 향하는 경향일 것입니다. 홀수 거듭제곱 함수의 가족으로부터 모든 그래프는 $y=cx^{3}$의 일반적인 모양을 가지며, $n$이 증가할 때 중간에서 더 평평하게 되고 $n=1$에 대해 모든 평평함을 잃어버리고 직선이 됩니다. 이런 종류의 대칭 ($f(-x)=-f(x)$)을 가진 함수는 홀수 함수(odd functions)라고 불립니다.

$c<0$에 대해, 반대 점근적 행동은 각 경우에서 참입니다.

List of whole-number powers

n	n2	n3	n4	n5	n6	n7	n8	n9	n10
2	4	8	16	32	64	128	256	512	1024
3	9	27	81	243	729	2187	6561	19683	59049
4	16	64	256	1024	4096	16384	65536	262144	1048576
5	25	125	625	3125	15625	78125	390625	1953125	9765625
6	36	216	1296	7776	46656	279936	1679616	10077696	60466176
7	49	343	2401	16807	117649	823543	5764801	40353607	282475249
8	64	512	4096	32768	262144	2097152	16777216	134217728	1073741824
9	81	729	6561	59049	531441	4782969	43046721	387420489	3486784401
10	100	1000	10000	100000	1000000	10000000	100000000	1000000000	10000000000

Rational exponents

Main article: nth root

From top to bottom: x^1/8, x^1/4, x^1/2, x¹, x², x⁴, x⁸.

숫자(number) b의 n번째 근(nth root)은 xⁿ = b을 만족하는 숫자 x입니다:

만약 b가 양의 실수이고 n이 양의 정수이면, xⁿ = b에 대한 정확히 하나의 양의 실수 해가 있습니다. 이 해는 b의 주요 n-번째 근(principal nth root)이라고 불립니다. 그것은 ⁿ√b으로 표시되며, 여기서 √  은 제곱근 기호(symbol)입니다; 대안적으로, b의 주요 n-번째 근은 b^1/n로 쓸 수 있습니다. 예를 들어: 9^1/2 = √9 = 3 및 8^1/3 = ³√8 = 2.

$x=b^{1/n}$은 $x^{n}=b$를 푼다는 사실은 다음에 나타내는 것을 따릅니다:

${\begin{aligned}x^{n}&=\left(b^{\frac {1}{n}}\right)^{n}=\underbrace {b^{\frac {1}{n}}\times b^{\frac {1}{n}}\times \cdots \times b^{\frac {1}{n}}} _{n\,{\textrm {times}}}\\&=b^{\underbrace {\left({\frac {1}{n}}+{\frac {1}{n}}+\cdots +{\frac {1}{n}}\right)} _{n\,{\textrm {times}}}}=b^{\frac {n}{n}}=b^{1}=b.\end{aligned}}$

만약 b가 0과 같으면, 방정식 xⁿ = b는 x = 0인 하나의 해를 가집니다.

만약 n이 짝수(even)이고 b가 양수이면, xⁿ = b는 둘의 실수 해를 가지며, 그것은 b의 양과 음의 n번째 근, 즉, b^1/n > 0 및 -(b^1/n) < 0입니다.

만약 n이 짝수이고 b가 음수이면, 방정식은 실수에서 해를 가지지 않습니다.

만약 n이 홀수이면, xⁿ = b은 정확히 하나의 실수 해를 가지며, 만약 b가 양수이면 해는 양수 (b^1/n > 0)이고, 만약 b가 음수이면 해는 음수 (b^1/n < 0)입니다.

양의 실수 b에, u가 정수이고 v가 양의 정수인, 유리(rational) 지수 u/v를 취하고, 오직 주요 근을 고려했을 때, 다음을 산출합니다:

$b^{\frac {u}{v}}=\left(b^{u}\right)^{\frac {1}{v}}={\sqrt[{v}]{b^{u}}}=\left(b^{\frac {1}{v}}\right)^{u}=\left({\sqrt[{v}]{b}}\right)^{u}.$

음의 실수 b에 u/v가 가장 낮은 항인, 유리수 거듭제곱 u/v를 취하면, 만약 u가 짝수이면 양의 실수 결과를 산출하고, 따라서 v가 홀수인데, 왜냐하면 그때에 b^u는 양수이기 때문입니다; 그리고 만약 u와 v가 둘 다 홀수이면, 음의 실수 결과를 산출하는데, 왜냐하면 그때에 b^u는 음수이기 때문입니다. 짝수 v (및, 따라서, 홀수 u)의 경우는, x^2k = −1를 만족하는 실수 x가 없기 때문에, 실수 내에서 이런 방식으로 절대 처리될 수 없으며, 이 경우에서 b^u/v의 값은, 섹션 § 복소수의 거듭제곱에서 보다 완전히 묘사된 것처럼, 허수 단위(imaginary unit) i를 반드시 사용합니다.

따라서 우리는 (−27)^1/3 = −3와 (−27)^2/3 = 9를 가집니다. 숫자 4는 둘의 3/2번째 거듭제곱, 즉 8과 −8을 가집니다; 어쨌든, 관례에 의해 표기법 4^3/2는 주요 근을 채택하고, 8을 결과로 초래합니다. v-번째 근을 채택하는 것에 대해, u/v-번째 거듭제곱은 역시 u/v-번째 근이라고 불리고, 짝수 v에 대해 용어 주요 근(principal root)은 역시 양의 결과를 나타냅니다.

이 부호 모호성은 거듭제곱 항등식을 적용할 때 반드시 주의를 기울여야 합니다. 예를 들어, 다음은 분명히 틀렸습니다:

$-27=(-27)^{\left(\left({\frac {2}{3}}\right)\left({\frac {3}{2}}\right)\right)}=\left((-27)^{\frac {2}{3}}\right)^{\frac {3}{2}}=9^{\frac {3}{2}}=27$

그 문제는 본질적으로 모호한 상황–짝수 근에 대해 묻는 것–에 대해 표준 표기법을 도입함으로써 첫 번째 상등에서 이미 시작되었고 단순히 오직 한 가지, 즉 관례적(conventional) 또는 주요한(principal) 해석에 잘못 의존하는 것입니다. 같은 문제는 역시 부적절하게 도입된 무리수-표기법에서 발생하여, 본질적으로 양의 결과를 강제합니다:

$\left((-27)^{\frac {2}{3}}\right)^{\frac {3}{2}}={\sqrt {\left({\sqrt[{3}]{(-27)^{2}}}\right)^{3}}}={\sqrt {(-27)^{2}}}\neq -27$

대신에

$\left((-27)^{\frac {2}{3}}\right)^{\frac {3}{2}}=-{\sqrt {\left({\sqrt[{3}]{(-27)^{2}}}\right)^{3}}}=-{\sqrt {(-27)^{2}}}=-27.$

일반적으로 같은 종류의 문제가 섹션 § Failure of power and logarithm identities에서 설명된 것처럼 복소수에 대해 발생합니다.

Real exponents

양의 실수의 실수 거듭제곱에 대한 지수화는 유리수 거듭제곱을 연속성에 의해 실수로 확장함으로써, 또는 보다 일반적으로 아래 § Powers via logarithms에 주어진 것에 의해 정의될 수 있습니다. 그 결과는 항상 양의 실수이고, 정수 지수에 대해 위에 표시된 항등식과 속성(identities and properties)은 마찬가지로 비-정수 지수를 갖는 양의 실수 밑수에 대해 참입니다.

다른 한편으로, 음의 실수의 실수 거듭제곱에 대한 지수화는 일관되게 정의하기가 훨씬 더 어려운데, 왜냐하면 그것은 비-실수일 수 있고 여러 값을 가질 수 있기 때문입니다 (§ Real exponents with negative bases을 참조하십시오). 우리는 주요 값(principal value)이라고 불리는, 이들 값 중 하나를 선택할 수 있지만, 다음 식이 참을 만족하는 항등식에 대해 주요 값의 선택이 없습니다; § Failure of power and logarithm identities을 참조하십시오:

$\left(b^{r}\right)^{s}=b^{r\cdot s}$

그러므로, 양의 실수가 아닌 밑수를 갖는 지수화는 일반적으로 다중-값 함수(multivalued function)로 바라봅니다.

Limits of rational exponents

Because the exponential function is continuous we find $\lim _{n\to \infty }e^{x_{n}}=e^{\lim _{n\to \infty }x_{n}}$ for convergent sequences (x_n). This is shown here for x_n = 1/n.

임의의 무리수(irrational number)는 유리수의 수열의 극한(limit of a sequence)으로 표현될 수 있기 때문에, 임의적인 실수 지수 x를 갖는 양의 실수 b의 지수화는 다음 규칙과 함께 연속성(continuity)에 의해 정의될 수 있습니다:

$b^{x}=\lim _{r(\in \mathbb {Q} )\to x}b^{r}\quad (b\in \mathbb {R} ^{+},\,x\in \mathbb {R} ),$

여기서 극한은 r이 x에 가까워질 때 r의 오직 유리수 값에 대해 취합니다. 이 극한은 오직 양의 b에 대해 존재합니다. 극한의 (ε, δ)-정의((ε, δ)-definition of limit)가 사용됩니다; 이것은 결과 b^x의 임의의 원하는 정확도에 대해 우리가 x 주위의 충분하게 작은 구간을 선택하므로 구간에서 모든 유리수 거듭제곱이 원하는 정확도 내에 있음을 보여주는 것과 관련합니다.

예를 들어, 만약 x = π이면, 비-종결하는 십진 표현 π = 3.14159...은 유리수 거듭제곱에 의해 경계진 구간을 얻기 위해 (유리수 거듭제곱의 엄격한 단조성에 기초하여) 사용될 수 있습니다:

$\left[b^{3},b^{4}\right]$, $\left[b^{3.1},b^{3.2}\right]$, $\left[b^{3.14},b^{3.15}\right]$, $\left[b^{3.141},b^{3.142}\right]$, $\left[b^{3.1415},b^{3.1416}\right]$, $\left[b^{3.14159},b^{3.14160}\right]$, $\ldots$

경계진 구간은 유일한 실수로 수렴하며, $b^{\pi }$에 의해 표시됩니다. 이 기법은 임의의 무리수 지수에 대해 양의 실수 b의 거듭제곱을 얻기 위해 사용될 수 있습니다. 함수 f_b(x) = b^x는 따라서 임의의 실수 x에 대해 정의됩니다.

The exponential function

Main article: Exponential function

중요한 수학 상수 e는, 때때로 오일러의 숫자(Euler's number)라고 불리며, 2.718과 근사적으로 같고 자연 로그(natural logarithm)의 밑수입니다. 비록 e의 지수화가, 원칙적으로, 임의의 다른 실수의 지수화와 같게 취급될 수 있을지라도, 그러한 지수는 특히 휼륭하고 유용한 속성을 가지는 것으로 밝혀집니다. 다른 것들 사이에서, 이들 속성은 e의 지수화를, 유리수 지수를 갖는 지수화의 익숙한 의미와 일치하면서, 복소수 또는 심지어 행렬과 같은, 지수의 다른 유형에 자연스러운 방법에서 일반화될 수 있음을 허용합니다.

결과적으로, 표기법 e^x는 보통 지수 함수(exponential function), exp(x)라고 불리는, 일반화된 지수화 함수 정의를 나타내고, 예를 들어, 다음에 의해 많은 동등한 방법에서 정의될 수 있습니다:

$\exp(x)=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}.$

다른 속성 사이에서, exp는 다음 지수 항등식을 만족시킵니다:

$\exp(x+y)=\exp(x)\cdot \exp(y).$

지수 함수는 x의 모든 정수, 분수, 실수, 및 복소수(complex) 값에 대해 정의됩니다. 사실, 행렬 지수(matrix exponential)는 정사각형 행렬(square matrix)에 대해 잘-정의되어 있고 (이런 경우에 이 지수 항등식은 오직 x와 y가 교환될 때 유지됩니다), 선형 미분 방정식(linear differential equation)의 시스템을 푸는 것에 대해 유용합니다.

exp(1)은 e와 같고, exp(x)는 이 지수 항등식을 만족하기 때문에, exp(x)는 정수 x에 대해 e^x의 반복된-곱셈 정의와 일치하는 것을 즉시 따르고, 역시 유리수 거듭제곱이 보통처럼 (양의) 근을 나타내므로, exp(x)는 연속성에 대해 모든 실수 x에 대해 이전 섹션에서 e^x 정의와 일치하는 것을 따릅니다.

Powers via logarithms

e^x가 지수 함수로 정의될 때, b^x는, e^x의 관점에서, 다른 양의 실수 b에 대해 정의될 수 있습니다. 구체적으로 특별히, 자연 로그(natural logarithm) ln(x)는 지수 함수 e^x의 역(inverse)입니다. 그것은 b > 0에 대해 정의되고, 다음을 만족시킵니다:

$b=e^{\ln b}.$

만약 b^x가 로그와 지수 규칙을 보존하는 것이면, 우리는 각 실수 x에 대해 반드시 다음을 가집니다:

$b^{x}=\left(e^{\ln b}\right)^{x}=e^{x\cdot \ln b}$.

이것은 실수 거듭제곱 b^x의 대안적인 정의로 사용될 수 있고 유리수 지수 및 연속성을 사용하여 위에 주어진 정의와 일치합니다. 로그를 사용하는 지수화의 정의는, 아래에 논의된 것처럼, 복소수의 문맥에서 보다 공통적입니다.

Real exponents with negative bases

양의 실수의 거듭제곱은 항상 양의 실수입니다. x² = 4의 해는, 어쨌든, 2 또는 –2일 수 있습니다. 4^1/2의 주요 값은 2이지만, −2도 역시 유효한 제곱근입니다. 만약 실수의 지수화의 정의가 음의 결과를 허용하는 것으로 확장되면, 그 결과는 더 이상 잘-행동되지 않습니다.

로그 방법 또는 유리수 지수 방법 어떤 것도 음의 실수 b와 임의의 실수 r에 대해 실수로 b^r을 정의하기 위해서 사용될 수 없습니다. 실제로, e^r은 모든 각 실수 r에 대해 양수이므로, ln(b)는 b ≤ 0에 대해 실수로서 정의되지 않습니다.

유리수 지수 방법은 b의 음수 값에 대해 절대 사용될 수 없는데, 왜냐하면 그것은 연속성(continuity)에 의존하기 때문입니다. 함수 f(r) = b^r은, 각 b > 0에 대해, 유리수에서 실수로의 고유한 연속 확장을 가집니다. 그러나 b < 0일 때, 함수 f는 그것이 정의된 유리수 r의 집합 위에서 심지어 연속이 아닙니다.

예를 들어, b = −1을 생각해 보십시오. −1의 n번째 근은 모든 각 홀수 자연수 n에 대해 −1입니다. 그래서 만약 n이 홀수 양의 정수이면, m이 홀수이면, (−1)^(m/n) = −1이고, m이 짝수이면, (−1)^(m/n) = 1입니다. 따라서 (−1)^q = 1에 대해 유리수 q의 집합은, (−1)^q = −1에 대해 q의 집합과 마찬가지로, 유리수에서 조밀(dense)입니다. 이것은 함수 (−1)^q가 그것이 정의된 임의의 유리수 q에서 연속적이지 않음을 의미합니다.

다른 한편으로, 음수 b의 임의의 복소수 거듭제곱(complex powers)은 b의 복소수 로그(complex logarithm)를 선택함으로써 정의될 수 있습니다.

Irrational exponents

Main article: Gelfond–Schneider theorem

만약 b가 양의 실수 대수적 숫자(algebraic number)이고, x가 유리수이면, b^x는 대수적 숫자라는 것을 위에서 보여왔습니다. b^x가 모두 대수적인 여러 가지 값 (유한한 숫자, 아래를 참조)을 취할 수 있는 단지 차이와 함께, 이것이 비록 우리가 b에 대해 임의의 대수적 숫자를 수용할지라도, 참으로 남습니다. 겔폰트–슈나이더 정리는 x가 무리수(irrational)일 때 (즉, 유리수가 아닐 때), b^x의 본질에 대한 일부 정보를 제공합니다. 그것은 말합니다:

만약 b가 0과 1과 다른 대수적 숫자이고, x가 무리적 대수적 숫자이면, b^x의 모든 값 (무한하게 많이 있음)은 초월적(transcendental)입니다 (즉, 대수적이 아닙니다).

Complex exponents with a positive real base

만약 b가 양의 실수이고, z가 임의의 복소수(complex number)이면, 거듭제곱 b^z는 다음에 의해 정의됩니다:

$b^{z}=e^{(z\ln b)},$

여기서 x = ln(b)는 방정식 e^x = b에 대한 고유한 실수 해이고, e의 복소수 거듭제곱은 지수 함수(exponential function)에 의해 정의되며, 이것은 그의 도함수와 같고 x = 0에 대해 값 1을 취하는 복소 변수의 유일한 함수(function of a complex variable)입니다.

일반적으로, b^z는 실수가 아니기 때문에, (b^z)^w와 같은 표현은 이전 정의에 의해 정의되지 않습니다. 그것은 복소수의 거듭제곱(powers of complex numbers)에 대해 규칙을 통해 반드시 해석되어야 하고, 만약 z가 실수가 아니거나 w가 정수가 아니면, 누군가는 기대할 수도 있는, 일반적으로 b^zw와 같지 않습니다.

다양한 지수 함수의 정의(definitions of the exponential function)가 있지만 그것들은 복소수에 대해 호환되게 확장되고 지수 속성을 만족시킵니다. 임의의 복소수 z와 w에 대해, 지수 함수는 $e^{z+w}=e^{z}e^{w}$를 만족시킵니다. 특히, 임의의 복소수 $z=x+iy$에 대해

$e^{z}=e^{x+iy}=e^{x}\cdot e^{iy},$

두 번째 항 $e^{iy}$는 오일러의 공식(Euler's formula)에 의해 제공된 값을 가집니다:

$e^{iy}=\cos y+i\sin y.$

이 공식은 삼각법(trigonometry)과 대수학에서 문제를 연결합니다.

그러므로, 임의의 복소수 $z=x+iy$에 대해,

$e^{z}=e^{x+iy}=e^{x}\cdot e^{iy}=e^{x}(\cos y+i\sin y).$

피타고라스 삼각 항등식(Pythagorean trigonometric identity)때문에, $\cos y+i\sin y$의 절댓값은 1입니다. 그러므로, 실수 인수 $e^{x}$는 $e^{z}$의 절댓값(absolute value)이고 지수의 허수 부분 $y$는 복소수 $e^{z}$의 편각(argument) (각도)으로 식별됩니다.

Series definition

그의 도함수와 같고 $e^{0}=1$을 만족하는 지수 함수에 대해, 그것의 테일러 급수(Taylor series)는 다음이어야 합니다:

$e^{z}=\sum _{n=0}^{\infty }{z^{n} \over n!}=1+z+{\frac {z^{2}}{2!}}+{\frac {z^{3}}{3!}}+{\frac {z^{4}}{4!}}+\cdots .$

이 무한 급수(infinite series)는, 종종 임의적인 복소 지수에 대해 지수 함수 e^z의 정의로 취해지며, 모든 복소수 z에 대해 절대적 수렴(absolutely convergent)입니다.

z가 순수한 허수(imaginary), 즉, 실수 y에 대해 z = iy일 때, 위의 급수는 다음이 됩니다:

$e^{iy}=1+iy+{\frac {(iy)^{2}}{2!}}+{\frac {(iy)^{3}}{3!}}+{\frac {(iy)^{4}}{4!}}+\cdots ,$

이것은 (그것이 절대적으로 수렴하기 때문에) 다음으로 다시 정리될 수 있습니다:

$e^{iy}=\left(1-{\frac {y^{2}}{2!}}+{\frac {y^{4}}{4!}}-{\frac {y^{6}}{6!}}+\cdots \right)+i\left(y-{\frac {y^{3}}{3!}}+{\frac {y^{5}}{5!}}-\cdots \right).$

이 표현의 실수와 허수 부분은, 오일러의 공식을 암시하는, 영에 중심을 둔, 각각 사인과 코사인의 테일러 전개(Taylor expansions of cosine and sine)입니다:

$e^{iy}=\cos y+i\sin y.$

Limit definition

This animation shows by repeated multiplications in the complex plane for values of n (denoted as N in the picture), increasing from 1 to 100, how $(1+i\pi /n)^{n}$ approaches −1. The values of $(1+i\pi /n)^{k},$ for k = 0 ... n, are the vertices of a polygonal path whose leftmost endpoint is $(1+i\pi /k)^{k}$ for the actual k. It can be seen that as k gets larger $(1+i\pi /k)^{k}$ approaches the limit −1, illustrating Euler's identity: $e^{i\pi }=-1.$

지수 함수 $e^{z}$의 또 다른 특성화는, n이 무한대로 접근할 때, $(1+z/n)^{n}$의 극한(limit)입니다. 이 정의에서 n번째 거듭제곱을 극 형식(polar form)에서 반복된 곱셈으로 생각함으로써, 오일러의 공식을 시각적으로 설명하기 위해 사용될 수 있습니다. 임의의 복소수는 극 형식에서 $(r,\theta )$으로 나타낼 수 있으며, 여기서 r은 절댓값이고 θ는 그것의 편각입니다. 두 복소수 $(r_{1},\theta _{1})$와 $(r_{2},\theta _{2})$의 곱은 $(r_{1}r_{2},\theta _{1}+\theta _{2})$입니다.

꼭짓점으로 $0$, $1$, 및 $1+ix/n$을 가지는 복소 평면(complex plane)에서 직각 삼각형(right triangle)을 생각해 보십시오. n의 큰 값에 대해, 삼각형은 거의 1의 반지름을 갖고 $x/n$ 라디안(radian)과 같은 작은 중심각을 갖는 부채꼴(circular sector)입니다. $1+ix/n$은 그때에 극 형식 $(1,x/n)$을 갖는 숫자로 근사화될 수 있습니다. 따라서, n이 무한대에 접근할 때 극한에서, $(1+ix/n)^{n}$은 $(1,x/n)^{n}=(1^{n},nx/n)=(1,x)$에 접근하며, 양의 실수 축(positive real axis)으로부터 그것의 각이 x 라디안인 단위 원(unit circle) 위의 점입니다. 이 점의 데카르트 좌표(Cartesian coordinate)는 $(\cos x,\sin x)$이므로, $e^{ix}=\cos x+i\sin x$입니다; 이것은 다시 오일러의 공식인며, 급수 정의와 함께 정교해짐에 따라 삼각 함수에 대한 같은 연결을 허용합니다.

Periodicity

방정식 $e^{z}=1$에 대한 해는 $2\pi i$의 정수배입니다:

$\left\{z:e^{z}=1\right\}=\{2k\pi i:k\in \mathbb {Z} \}$

따라서, 만약 $v$가 $e^{v}=w$를 만족하는 복소수이면, 역시 $e^{z}=w$를 만족하는 모든 각 $z$는 $e^{z}=e^{v}\cdot 1=e^{v+i2k\pi }$, 즉 $v$에 대한 $2\pi i$의 임의적인 정수 배를 더함으로써 구할 수 있습니다:

$\left\{z:e^{z}=w\right\}=\{v+2k\pi i:k\in \mathbb {Z} \}$

즉, 임의의 정수 k에 대해 복소수 지수 함수 $e^{z}=\exp(z)=\exp(z+2k\pi i)$는 주기 $2\pi i$를 갖는 주기 함수(periodic function)입니다.

Examples

${\begin{aligned}2^{i}&=e^{i\ln(2)}=\cos {\big (}\ln(2){\big )}+i\sin {\big (}\ln(2){\big )}\approx 0.76924+0.63896i,\\e^{i}&=\cos(1)+i\sin(1)\approx 0.54030+0.84147i,\\\left(e^{2\pi }\right)^{i}&=e^{i\ln(e^{2\pi })}=e^{i(2\pi )}=\cos(2\pi )+i\sin(2\pi )=1.\end{aligned}}$

Powers of complex numbers

비-영 복소수의 정수 거듭제곱은 위에서 처럼 반복된 곱셈 또는 나눗셈에 의해 정의됩니다. 만약 i가 허수 단위(imaginary unit)이고 n이 정수이면, iⁿ은, 정수 n이 0, 1, 2 또는 3 모듈로 4와 일치하는지 여부에 따라, 1, i, −1, 또는 −i와 같습니다. 이것 때문에, i의 거듭제곱은 주기 4(period 4)의 수열(sequence)을 나타내는 것에 유용합니다.

양의 실수의 복소수 거듭제곱은 위의 섹션 양의 실수 밑수를 가진 복소수 지수에서 e^x를 통해 정의됩니다. 이것들은 연속 함수입니다.

이들 함수를 양의 실수가 아닌 복소수의 비정수 거듭제곱의 일반적인 경우로 확대하려는 시도는 어려움으로 이어집니다. 우리는 불연속 함수 또는 다중-값 함수(multivalued function)를 정의합니다. 이들 선택사항의 어느 것도 완전히 만족스럽지는 않습니다.

복소수의 유리수 거듭제곱은 대수적 방정식에 대한 해이어야 합니다. 그러므로, 그것은 항상 가능한 값의 유한한 숫자를 가집니다. 예를 들어, w = z^1/2는 방정식 w² = z에 대한 해이어야 합니다. 그러나 만약 w가 해이면, −w도 마찬가지로 해가 되는데, 왜냐하면 (−1)² = 1이기 때문입니다. 주요 값(principal value)으로 불리는 유일하지만 다소 임의적인 해는 역시 비유리수 거듭제곱에 대해 적용되는 일반적인 규칙을 사용하여 선택될 수 있습니다.

복소수 거듭제곱 및 로그는 리만 곡면(Riemann surface) 위에 단일 값 함수로 보다 자연스럽게 처리됩니다. 단일 값 버전은 판(sheet)을 선택함으로써 정의됩니다. 그 값은 가지 자름(branch cut)을 따라 불연속을 가집니다. 주요 값으로 많은 해 중에서 하나를 선택하는 것은 연속이 아닌 함수를 우리에게 남겨주고, 거듭제곱을 조작하는 것에 대해 보통 규칙들은 우리를 방황으로 이끌 수 있습니다.

복소수의 임의의 비유리수 거듭제곱은 복소수 로그(complex logarithm)의 다중-값 본성 때문에 가능한 값의 무한한 숫자를 가집니다. 주요 값은, 그것의 다른 속성 중에서도, 양의 실수 부분과 영 허수 부분을 갖는 복소수의 거듭제곱이 해당하는 실수 밑수에 대해 위에 정의된 규칙에서 행한 것처럼 같은 값을 제공하는 것이 보장되는, 규칙에 의해 이것들에서 선택되는 하나의 단일 값입니다.

실수에 복소수 거듭제곱을 지수화하는 것은 공식적으로 해당 복소수에 대한 것으로부터 다른 연산입니다. 어쨌든, 양의 실수의 공통적인 경우에서 주요 값은 같습니다.

비음의 실수의 거듭제곱은 항상 정의되는 것은 아니고 심지어 정의된 곳에서 불연속입니다. 사실, 그것들은, 지수가 홀수인 분모를 갖는 유리수일 때 오직 정의됩니다. 복소수를 다룰 때, 복소수 연산이 통상적으로 대신 사용됩니다.

Complex exponents with complex bases

w ≠ 0인 복소수 w와 z에 대해, 표기법 w^z는 log w인 것과 같은 의미에서 모호합니다.

w^z의 값을 얻기 위해, 먼저 w의 로그를 선택하십시오; 그것을 log w라고 부릅니다. 그러한 선택은 주요 값(principal value) Log w (만약 다른 명세가 주어지지 않으면, 기본값) 또는 아마도 미리 고정된 어떤 다른 log w의 가지(branch of log w)에 의해 주어진 값일 수 있습니다. 그런-다음, 복소수 지수 함수를 사용하여, 우리는 다음을 정의합니다:

$w^{z}=e^{z\log w}$

왜냐하면 이것은 w가 양의 실수이고 log w의 (실수) 주요 값이 사용되는 경우에서 이전 정의(earlier definition)와 일치하기 때문입니다.

만약 z가 정수(integer)이면, w^z의 값은 log w의 선택과 독립이고, 정수 지수를 가진 지수화의 이전 정의와 일치합니다.

만약 z가 z > 0을 가진 가장 낮은 항에서 유리수(rational number) m/n이면, log w의 셀-수-있는 무한하게(countably infinite) 많은 선택은 w^z에 대해 오직 n개의 다른 값을 산출합니다; 이들 값은 방정식 sⁿ = w^m에 대한 n개의 복소수 해 s입니다.

만약 z가 무리수(irrational number)이면, log w의 셀-수-있는 무한하게 많은 선택은 w^z에 대해 무한하게 많은 구별되는 값으로 이어집니다.

복소수 거듭제곱의 계산은, 아래에서 상세히 설명하는 것처럼, 밑수 w를 극 형식(polar form)으로 변환함으로써 용이하게 됩니다.

비슷한 구조가 쿼터니언(quaternions)에서 사용됩니다.

Complex roots of unity

Main article: Root of unity

The three 3rd roots of 1

양의 정수 n에 대해 wⁿ = 1을 만족하는 복소수 w는 단위원의 n번째 근(nth root of unity)입니다. 기하학적으로, 단위원의 n번째 근은 실수 1 위에 하나의 꼭짓점을 갖는 정규 n-각형의 꼭짓점에서 복소 평면의 단위 원 위에 놓입니다.

만약 0 < k < n을 만족하는 모든 자연수 k에 대해 wⁿ = 1이지만 w^k ≠ 1이면, w는 단위원의 원시 n번째 근(primitive nth root of unity)이라고 불립니다. 음의 단위 −1은 단위원의 유일한 원시 제곱근입니다. 허수 단위(imaginary unit) i는 단위원의 둘의 원시 4번째 근 중 하나입니다; 다른 하나는 −i입니다.

숫자 e^2πi/n는 가장 작은 양의 편각(argument)을 갖는 단위원의 원시 n번째 근입니다. (비록 이 용어는 보편적이 아니고, ⁿ√1의 주요 값(principal value), 1과 절대 혼동되어서 안될지라도, 때때로 단위원의 주요 n번째 근(principal nth root of unity)이라고 불립니다.)

단위원의 다른 n번째 근들은 2 ≤ k ≤ n에 대해 다음에 의해 주어집니다:

$\left(e^{{\frac {2}{n}}\pi i}\right)^{k}=e^{{\frac {2}{n}}\pi ik}$

Roots of arbitrary complex numbers

비록 일반적인 복소수 로그에 대해 무한하게 많은 가능한 값이 있을지라도, q = 1/n과 n이 양의 정수인 중요하게 특별한 경우에서 거듭제곱 w^q에 대해 값의 오직 유한한 숫자가 있습니다. 이것들은 w의 n번째 근들입니다; 그것들은 방정식 zⁿ = w의 해입니다. 실수 근과 마찬가지로, 두 번째 근은 제곱근이라고 역시 불리고 세 번째 근은 역시 세제곱근라고 불립니다.

수학에서 근의 주요 값(principal value)으로 w^1/n을 정의하는 것이 보통이며, 관례적으로, 그것의 편각이 가장 작은 절댓값(absolute value)을 가지는 n번째 근입니다. w가 양의 실수일 때, 이것은 고유한 양의 실수 n번째 근으로 w^1/n을 정의하는 것의 보통 관례와 일치합니다. 다른 한편으로, w가 음의 실수이고, n이 홀수 정수일 때, 고유한 실수 n번째 근은 그의 편각이 가장 작은 절댓값을 가지는 둘의 n번째 근 중 하나가 아닙니다. 이런 경우에서, w^1/n의 의미는 문맥에 따라 다를 수 있고, 일부 주의가 오류를 피하기 위해 필요할 수 있습니다.

복소수 w의 n번째 근의 집합은 단위원의 n번째 근들 각각에 의해 주요 값 w^1/n을 곱함으로써 얻습니다. 예를 들어, 16의 네 번째 근은 2, −2, 2i, 및 −2i인데, 왜냐하면 16의 네 번째 근의 주요 값은 2이고 단위의 네 번째 근은 1, −1, i, 및 −i이기 때문입니다.

Computing complex powers

극 형식(polar form)에서 지수화되는 숫자를 씀으로써 복소수 거듭제곱을 계산하는 것이 종종 더 쉽습니다. 모든 각 복소수 z는 극 형식에서 다음으로 쓸 수 있습니다:

$z=re^{i\theta }=e^{\ln(r)+i\theta },$

여기서 r은 비음의 실수이고 θ는 z의 (실수) 편각(argument)입니다. 극 형식은 간단한 기하학적 해석을 가집니다: 만약 복소수 u + iv가 데카르트 좌표(Cartesian coordinates)를 사용하여 복소 평면(complex plane)에서 점 (u, v)을 나타내는 것으로 생각되면, (r, θ)는 극 좌표(polar coordinates)에서 같은 점입니다. 즉, r은 "반지름" r² = u² + v²이고 θ는 "각도" θ = atan2(v, u)입니다. 극 각도 θ는 모호한데, 왜냐하면 2π의 임의의 정수 배는 점의 위치의 변경없이 θ에 더해질 수 있기 때문입니다. θ의 각 선택은 일반적으로 거듭제곱의 다른 가능한 값을 제공합니다. 가지 자름(branch cut)은 특정 값을 선택하기 위해 사용될 수 있습니다. 주요 값 (가장 공통적인 가지 자름)은 구간 (−π, π]에서 선택된 θ에 해당합니다. 양의 실수 부분과 영 허수 부분을 갖는 복소수에 대해 주요 값을 사용하는 것은 해당하는 실수를 사용하는 것처럼 같은 결과를 제공합니다.

복소수 거듭제곱 w^z를 계산하기 위해, w를 극 형식에서 다음과 같이 씁니다:

$w=re^{i\theta }.$

그런-다음

$\log(w)=\ln(r)+i\theta ,$

따라서

$w^{z}=e^{z\log(w)}=e^{z(\ln(r)+i\theta )}.$

만약 z가 c + di로 분해되면, w^z에 대해 공식은 다음과 같이 더 명확하게 쓸 수 있습니다:

$(r^{c}e^{-d\theta })e^{i(d\ln(r)+c\theta )}=(r^{c}e^{-d\theta }){\big [}\cos {\big (}d\ln(r)+c\theta {\big )}+i\sin {\big (}d\ln(r)+c\theta {\big )}{\big ]}.$

이 최종 공식은 복소수 거듭제곱을 밑수를 극 형식과 지수를 데카르트 형식으로의 분해로부터 쉽게 계산되는 것을 허용합니다. 그것은 (오일러의 항등식을 통해) 극 형식과 데카르트 형식에서 둘 다를 여기서 보입니다.

다음 예제는, 주요 값, θ를 구간 (−π, π] 내에 있도록 하는 가지 자름을 사용합니다. iⁱ를 계산하기 위해, i를 다음과 같이 극 형식과 데카르트 형식으로 씁니다:

${\begin{aligned}i&=1\cdot e^{{\frac {1}{2}}i\pi },\\i&=0+1i.\end{aligned}}$

그런-다음 r = 1, θ = π/2, c = 0, 및 d = 1을 갖는, 위의 공식은 다음을 산출합니다:

$i^{i}=\left(1^{0}e^{-{\frac {1}{2}}\pi }\right)e^{i\left[1\cdot \ln(1)+0\cdot {\frac {1}{2}}\pi \right]}=e^{-{\frac {1}{2}}\pi }\approx 0.2079.$

비슷하게, (−2)^{3 + 4i}를 찾기 위해, −2의 극 형식을 다음과 같이 계산합니다:

$-2=2e^{i\pi }$

그리고 위의 공식을 사용하여 다음을 계산합니다:

$(-2)^{3+4i}=(2^{3}e^{-4\pi })e^{i[4\ln(2)+3\pi ]}\approx (2.602-1.006i)\cdot 10^{-5}.$

복소수 거듭제곱의 값은 사용된 가지에 따라 다릅니다. 예를 들어, 만약 극 형식 i = 1e^5πi/2가 iⁱ를 계산하기 위해 사용되면, 거듭제곱은 e^−5π/2로 나타납니다; 위에서 계산된, iⁱ의 주요 값은 e^−π/2입니다. iⁱ에 대해 모든 가능한 값의 집합은 다음과 같이 주어집니다:

${\begin{aligned}i&=1\cdot e^{{\frac {1}{2}}i\pi +i2\pi k}\mid k\in \mathbb {Z} ,\\i^{i}&=e^{i\left({\frac {1}{2}}i\pi +i2\pi k\right)}\\&=e^{-\left({\frac {1}{2}}\pi +2\pi k\right)}.\end{aligned}}$

그래서 iⁱ의 값에 대해 가능한 후보인, 각각의 정수 k에 대해 하나씩, 값의 무한대 개수가 있습니다. 그것들 모두는 영 허수 부분을 가지므로, 우리는 iⁱ는 유효한 실수 값의 무한대를 가진다고 말할 수 있습니다.

Failure of power and logarithm identities

양의 실수에 대해 거듭제곱과 로그에 대해 일부 항등식은, 복소수 거듭제곱과 복소수 로그가 단일-값 함수로 어떻게 정의되더라도, 복소수에 대해 실패할 것입니다. 예를 들어:

• 항등식 log(b^x) = x ⋅ log b는 b가 양의 실수이고 x가 실수일 때마다 유지됩니다. 그러나 복소수 로그의 주요 가지(principal branch)에 대해 우리는 다음을 가집니다:

  $i\pi =\log(-1)=\log \left[(-i)^{2}\right]\neq 2\log(-i)=2\left(-{\frac {i\pi }{2}}\right)=-i\pi$

  로그의 어떤 가지가 사용되는지에 상관없이, 항등식의 유사한 실패가 존재할 것입니다. 말할 수 있는 최선 (오직 이 결과를 사용하면)은 다음인 것입니다:

  $\log(w^{z})\equiv z\cdot \log(w){\pmod {2\pi i}}$

  이 항등식은 심지어 다중-값 함수로 로그를 고려할 때에도 유지되지 않습니다. log(w^z)의 가능한 값은 부분집합으로 z ⋅ log w의 값을 포함합니다. log(w)의 주요 값과 양쪽 변의 임의의 정수 가능한 값으로 m, n에 대해 Log(w)를 사용하는 것은 다음입니다:

  ${\begin{aligned}\left\{\log(w^{z})\right\}&=\left\{z\cdot \operatorname {Log} (w)+z\cdot 2\pi in+2\pi im\right\}\\\left\{z\cdot \log(w)\right\}&=\left\{z\cdot \operatorname {Log} (w)+z\cdot 2\pi in\right\}\end{aligned}}$

• 항등식 (bc)^x = b^xc^x과 (b/c)^x = b^x/c^x는 b와 c는 양의 실수이고 x는 실수일 때 유효합니다. 그러나 주요 가지를 사용하여 계산은 다음임을 보여줍니다
  $1=(-1\cdot -1)^{\frac {1}{2}}\not =(-1)^{\frac {1}{2}}(-1)^{\frac {1}{2}}=-1$

  및

  $i=(-1)^{\frac {1}{2}}=\left({\frac {1}{-1}}\right)^{\frac {1}{2}}\not ={\frac {1^{\frac {1}{2}}}{(-1)^{\frac {1}{2}}}}={\frac {1}{i}}=-i$

  다른 한편으로, x가 정수일 때, 항등식은 모든 비-영 복소수에 대해 유효합니다.

  만약 지수화가 다중-값 함수로 고려되면, (−1 ⋅ −1)^1/2의 가능한 값들은 {1, −1}입니다. 항등식은 유지되지만, {1} = {(−1 ⋅ −1)^1/2}을 말하는 것은 틀렸습니다.
• 항등식 (e^x)^y = e^xy은 실수 x와 y에 대해 유지되지만, 복소수에 대해 그의 진리를 가정하는 것은 클라우센(Clausen)에 의해 1827년에 발견된 다음의 역설(paradox)로 이어집니다: 임의의 정수 n에 대해, 우리는 다음을 가집니다:
  1. $e^{1+2\pi in}=e^{1}e^{2\pi in}=e\cdot 1=e$
  2. $\left(e^{1+2\pi in}\right)^{1+2\pi in}=e\qquad$ (양쪽 변의 $(1+2\pi in)$-번째 거듭제곱을 취하여)
  3. $e^{1+4\pi in-4\pi ^{2}n^{2}}=e\qquad$ ($(e^{x})^{y}=e^{xy}$를 사용하고 지수를 전개하여)
  4. $e^{1}e^{4\pi in}e^{-4\pi ^{2}n^{2}}=e\qquad$ ($e^{x+y}=e^{x}e^{y}$를 사용하여)
  5. $e^{-4\pi ^{2}n^{2}}=1\qquad$ (e로 나누어서)
  그러나 이것은 정수 n이 비영일 때 실패입니다. 그 오류는 다음입니다: 정의에 의해, $e^{y}$는 참 함수, $\exp(y)$에 대한 표기법이고, $x^{y}$은 다중-값 함수인 $\exp(y\log x)$에 대한 표기법입니다. 따라서 표기법은 x = e일 때 모호합니다. 여기서, 지수를 전개하기 전에, 두 번째 줄은 반드시 다음이어야 합니다:

  $\exp \left((1+2\pi in)\log \exp(1+2\pi in)\right)=\exp(1+2\pi in).$

  그러므로, 지수를 전개할 때, 우리는 z의 복소수 값에 대해 $\log \exp z=z$임을 암묵적으로 가정해 왔는데, 이것은 틀린 것으로써, 왜냐하면 복소수 로그는 다중-값이기 때문입니다. 달리 말해서, 잘못된 항등식 (e^x)^y = e^xy은 다음의 항등식으로 반드시 대체되어야 합니다:

  $\left(e^{x}\right)^{y}=e^{y\log e^{x}},$

  이것은 다중-값 함수 사이에서 참 항등식입니다.

Generalizations

Monoids

정수 지수를 갖는 지수화는 임의의 곱셈 모노이드(monoid)에서 정의될 수 있습니다. 모노이드는 집합 X와 결합 법칙(associative law)과, 1로 표시되는, 곱셈의 항등원(multiplicative identity)을 만족시키는 합성 ("곱셈")에 대해 규칙과 함께 집합 X로 구성하는 대수적 구조(algebraic structure)입니다. 지수화는 다음에 의해 귀납적으로 정의됩니다:

• 모든 $x\in X$에 대해 $x^{0}=1$,
• 모든 $x\in X$와 비-음의 정수 n에 대해 $x^{n+1}=x^{n}x$,
• 만약 n이 음의 정수이면 $x^{n}$은 $x$가 X에서 역을 가지면 오직 정의됩니다.

모노이드는, 그룹(groups)과 (곱셈 아래에서) 링(rings)을 포함하여, 수학에서 중요한 많은 구조를 포함하고, 후자의 보다 구체적인 예제는 행렬 링(matrix ring)과 필드(fields)입니다.

Matrices and linear operators

만약 A가 정사각 행렬이면, A 그 자체를 n번 곱한 것은 행렬 거듭제곱(matrix power)이라고 불립니다. 역시 $A^{0}$은 항등 행렬이라고 정의되고, 만약 A의 역-가능이면, $A^{-n}=(A^{-1})^{n}$입니다.

행렬 거듭제곱은 종종 이산 동역학적 시스템(discrete dynamical system)의 문맥에서 나타나며, 여기서 행렬 A는 어떤 시스템의 상태 벡터 x에서 시스템의 다음 상태 Ax로의 전이를 표현합니다. 예를 들어 이것은 마르코프 체인(Markov chain)의 표준 해석입니다. 그런-다음 $A^{2}x$은 두 시간 단계 후에 시스템의 상태이고, 이런 식으로 계속됩니다: $A^{n}x$는 n 시간 단계 후에 시스템의 상태입니다. 행렬의 거듭제곱 $A^{n}$은 현재 상태와 미래에서 시간 n 단계에서 상태 사이의 전이 행렬입니다. 따라서 행렬 거듭제곱을 계산하는 것은 동역학적 시스템의 진화를 푸는 것과 동등합니다. 많은 경우에서, 행렬 거듭제곱은 고윳값과 고유벡터(eigenvalues and eigenvectors)를 사용함으로써 편리하게 계산될 수 있습니다.

행렬을 제외하고, 보다 일반적인 선형 연산자(linear operator)가 역시 지수화될 수 있습니다. 예제는 미적분학의 도함수(derivative) 연산자, $d/dx$이며, 이것은 새로운 함수 $(d/dx)f(x)=f'(x)$를 얻기 위해 함수 $f(x)$에 작용하는 선형 연산자입니다. 미분 연산자의 n-번째 거듭제곱은 n-번째 도함수입니다:

$\left({\frac {d}{dx}}\right)^{n}f(x)={\frac {d^{n}}{dx^{n}}}f(x)=f^{(n)}(x).$

이들 예제는 선형 연산자의 이산 지수에 대한 것이지만, 많은 환경에서 연속 지수를 갖는 그러한 연산자의 거듭제곱을 정의하는 것이 역시 바람직합니다. 이것은 반그룹(semigroups)의 수학적 이론의 출발점입니다. 마치 이산 지수를 가진 행렬 거듭제곱을 계산하는 것은 이산 동역학적 시스템을 푸는 것처럼, 연속 지수를 가진 행렬 거듭제곱을 계산하는 것은 연속 동역학을 가진 시스템을 푸는 것입니다. 예제는 열 방정식(heat equation), 슈뢰딩거 방정식(Schrödinger equation), 파동 방정식(wave equation), 및 시간 진화를 포함하는 다른 부분 미분 방정식을 풀기 위한 접근법을 포함합니다. 도함수 연산자를 비-정수 거듭제곱으로 지수화하는 특수한 경우는, 분수적 도함수(fractional derivative)로 불리고, 이것은, 분수적 적분(fractional integral)과 함께, 분수적 미적분학(fractional calculus)의 기본 연산 중 하나입니다.

Finite fields

필드(field)는 곱셈, 덧셈, 뺄셈, 및 나눗셈이 모두 잘-정의되고 그것들의 익숙한 속성을 만족시키는 대수적 구조입니다. 예를 들어, 실수는, 복소수와 유리수가 그런 것처럼, 필드를 형성합니다. 모두 무한 집합(infinite set)인, 필드의 이들 익숙한 예제와 달리, 일부 필드는 오직 유한하게 많은 원소를 가집니다. 가장 간단한 예제는 $0+1=1+0=1$과 $0+0=1+1=0$에 의해 정의된 덧셈, 및 $0\cdot 0=1\cdot 0=0\cdot 1=0$과 $1\cdot 1=1$에 의해 정의된 곱셈을 갖는 두 원소 $F_{2}=\{0,1\}$를 가진 필드입니다.

유한 필드에서 지수화는 공개 키 암호화(public key cryptography)에서 응용을 가집니다. 예를 들어, 디피–헬먼 키 교환(Diffie–Hellman key exchange)은 지수화가 유한 필드에서 계산적으로 저렴하고, 반면에 이산 로그(discrete logarithm) (지수화의 역함수)는 계산적으로 비싸다는 사실을 사용합니다.

임의의 유한 필드 F는 F에서 모든 x에 대해 $px=0$을 만족하는 유일한 소수(prime number) p가 있다는 속성을 가집니다; 즉, x 자체를 p번 더한 것은 영입니다. 예를 들어, $F_{2}$에서, 소수 p = 2는 이 속성을 가집니다. 이 소수는 필드의 특성(characteristic)이라고 불립니다. F가 특성 p의 필드라고 가정하고, F의 각 원소에 거듭제곱 p를 올리는 함수 $f(x)=x^{p}$를 생각해 보십시오. 이것은 F의 플로베니우스 자기-동형(Frobenius automorphism)이라고 불립니다. 그것은 신입생의 꿈(Freshman's dream) 항등식 $(x+y)^{p}=x^{p}+y^{p}$때문에 필드의 자기-동형입니다. 플로베니우스 자기-동형은 숫자 이론(number theory_에 중요한데, 왜냐하면 그것은 그것의 소수 부분필드에 걸쳐 F의 갈루아 그룹(Galois group)을 생성하기 때문입니다.

In abstract algebra

정수 지수에 대해 지수화는 추상 대수학(abstract algebra)에서 꽤 일반적인 구조에 대해 정의될 수 있습니다.

X를 곱셈적으로 쓰인 거듭제곱-결합(power-associative) 이항 연산(binary operation)을 갖는 집합(set)으로 놓습니다. 그런-다음 xⁿ은 X의 임의의 원소 x와 임의의 비-영 자연수(natural number) n에 대해 x의 n 사본의 곱으로 정의되며, 이것은 재귀적으로 다음에 의해 정의됩니다:

${\begin{aligned}x^{1}&=x,\\x^{n}&=x^{n-1}x\quad {\text{for }}n>1.\end{aligned}}$

우리는 다음 속성을 가집니다:

${\begin{aligned}(x^{i}x^{j})x^{k}&=x^{i}(x^{j}x^{k}),&&{\text{(power-associative property)}}\\x^{m+n}&=x^{m}x^{n},\\(x^{m})^{n}&=x^{mn}.\end{aligned}}$

만약 연산이 양-측 항등원(identity element) 1을 가지면, x⁰는 임의의 x에 대해 1과 같도록 정의됩니다:

${\begin{aligned}x1&=1x=x,&&{\text{(two-sided identity)}}\\x^{0}&=1.\end{aligned}}$

만약 연산이 역시 양-측 역원(inverses)을 가지고 결합적이면, 마그마(magma)는 그룹(group)입니다. x의 역은 x⁻¹에 의해 표시될 수 있고 지수에 대해 모든 보통 규칙을 따릅니다:

${\begin{aligned}xx^{-1}&=x^{-1}x=1,&&{\text{(two-sided inverse)}}\\(xy)z&=x(yz),&&{\text{(associative)}}\\x^{-n}&=(x^{-1})^{n},\\x^{m-n}&=x^{m}x^{-n}.\end{aligned}}$

만약 곱셈 연산이 교환적(commutative)이면 (예를 들어 아벨 그룹(abelian group)에서 처럼), 다음이 유지됩니다:

$(xy)^{n}=x^{n}y^{n}.$

만약 이항 연산이 덧셈적으로 쓰이면, 아벨 그룹(abelian groups)에 대해 종종 그런 것처럼, "지수화는 반복된 곱셈임"은 "곱셈(multiplication)은 반복된 덧셈(addition)임"으로 재해석될 수 있습니다. 따라서, 위의 지수화의 법칙의 각각은 곱셈의 법칙들 사이에서 아날로그(analogue)를 가집니다.

하나의 집합 위에 정의된 여러 가지 거듭제곱-결합적 이항 연산이 있을 때, 그 중 임의의 하나가 반복될 수 있으며, 연산이 위첨자에서 그것의 기호를 배치함으로써 반복되는 것임을 나타내는 것이 공통적입니다. 따라서, x^∗n은 x ∗ ... ∗ x이고, 반면에 x^#n은 x # ... # x이며, 연산 * 및 #이 무엇이든지 상관없습니다.

위첨자 표기법은 역시, 특히 그룹 이론(group theory)에서, 켤레(conjugation)를 나타내기 위해 사용됩니다. 즉, g^h = h⁻¹gh이며, 여기서 g와 h는 일부 그룹(group)의 원소입니다. 비록 켤레가 지수화처럼 같은 법칙의 일부를 따르지만, 임의의 의미에서 반복된 곱셈의 예제가 아닙니다. 퀀들(quandle)은 켤레의 이들 법칙이 중심 역할을 하는 대수적 구조(algebraic structure)입니다.

Over sets

Main article: Cartesian product

만약 n이 자연수이고 그리고 A가 임의적인 집합이면, 표현 Aⁿ은 종종 A의 원소의 순서화된 n-튜플(n-tuple)의 집합을 나타내기 위해 사용됩니다. 이것은 Aⁿ을 집합 {0, 1, 2, ..., n−1}에서 집합 A로의 함수의 집합으로 놓는 것과 동등합니다; n-튜플 (a₀, a₁, a₂, ..., a_n−1)은 i를 a_i로 보내는 함수를 설명합니다.

무한 세는-숫자(cardinal number) κ와 집합 A에 대해, 표기법 A^κ는 역시 크기 κ의 집합에서 A로의 모든 함수의 집합을 나타내기 위해 사용됩니다. 이것은 때때로, 아래에서 정의되는, 그것을 세는-숫자 지수화로부터 구별하기 위해 ^κA로 쓰입니다.

이 일반화된 지수는 역시 집합 위에 연산에 대해 또는 여분의 구조(structure)를 가진 집합에 대해 정의될 수 있습니다. 예를 들어, 선형 대수에서, 그것은 임의적인 인덱스 집합에 걸쳐 벡터 공간(vector space)의 직접 합(direct sum)을 인덱스하기 위한 의미를 만듭니다. 즉, 우리는 다음을 말할 수 있습니다:

$\bigoplus _{i\in \mathbb {N} }V_{i},$

여기서 각 V_i는 벡터 공간입니다.

그런-다음 만약 각 i에 대해 V_i = V이면, 결과의 직접 합은 직접 합이 기본이라는 이해와 함께 V^⊕N, 또는 간단히 V^N으로 지수 표기법에서 쓸 수 있습니다. 비록 카디널리티 n을 갖는 특정 표준 집합을 선택하는 것이 없을지라도, 우리는 Vⁿ을 얻기 위해 세는-숫자 n을 갖는 집합 N을 다시 대체할 수 있으며, 이것은 오직 동형(isomorphism)까지(up to) 정의됩니다. V를 (자체에 걸쳐 벡터 공간으로 생각된) 실수의 필드(field) R 및 n을 일부 자연수(real number)로 취하면, 우리는 선형 대수에서 가장 공통적으로 연구되는 벡터 공간, 실수 벡터 공간 Rⁿ을 얻습니다.

만약 지수화 연산의 밑수가 집합이면, 달리 말하지 않은 한, 지수화 연산은 데카르트 곱(Cartesian product)입니다. 다중 데카르트 곱은, 적절한 카디널리티의 집합 위에 함수로 표현될 수 있는, n-튜플(tuple)을 생성하기 때문에, S^N은 단순히 이 경우에서 N에서 S로의 단순히 모든 함수(function)의 집합이 됩니다:

$S^{N}\equiv \{f\colon N\to S\}.$

이것은 세는-숫자의 지수화(exponentiation of cardinal numbers)에 적합한데, 그런 의미에서 |S^N| = |S|^|N|이며, 여기서 |X|는 X의 카디널리티입니다. "2"가 {0, 1}로 정의될 때, 우리는 |2^X| = 2^|X|을 가지며, 여기서 보통 P(X)로 표시되는, 2^X는 X의 거듭제곱 집합(power set)입니다; X의 각 부분집합(subset) Y는 x ∈ Y에 대해 값 1을 취하고 x ∉ Y에 대해 0을 취하는 X 위에 함수와 유일하게 대응합니다.

In category theory

Main article: Cartesian closed category

데카르트 닫힌 카테고리(Cartesian closed category)에서, 지수(exponential) 연산은 임의적인 대상을 또 다른 대상의 거듭제곱으로 올리기 위해 사용될 수 있습니다. 이것은 집합의 카테고리에서 데카르트 곱(Cartesian product)을 일반화합니다. 만약 0이 데카르트 닫힌 카테고리에서 초기 대상(initial object)이면, 지수 대상(exponential object) 0⁰은 임의의 끝 대상 1과 동형적입니다.

Of cardinal and ordinal numbers

Main articles: cardinal arithmetic and ordinal arithmetic

집합 이론(set theory)에서, 세는-숫자(cardinal)와 순서-숫자(ordinal)에 대해 지수 연산이 있습니다.

만약 κ와 λ가 세는-숫자이면, 표현 κ^λ는 카디널리티 λ의 임의의 집합에서 카디널리티 κ의 임의의 집합으로의 함수의 집합의 카디널리티를 나타냅니다. 만약 κ와 λ가 유한이면, 이것은 보통의 산술 지수 연산과 일치합니다. 예를 들어, 2-원소 집합으로부터 원소의 3-튜플의 집합은 카디널리티 8 = 2³을 가집니다. 세는-숫자 산술에서, κ⁰은 항상 1입니다 (심지어 κ가 무한 세는-숫자 또는 영임에도 불구하고 그렇습니다).

세는-숫자의 지수화는 순서-숫자의 지수화로부터 구별되며, 이것은 초월유한 귀납법(transfinite induction)을 포함하는 극한(limit) 과정에 의해 정의됩니다.

Repeated exponentiation

Main articles: Tetration and Hyperoperation

마치 자연수의 지수화가 반복된 곱셈에 의해 동기 부여되는 것처럼, 반복된 지수화를 기반으로 연산을 정의하는 것이 가능합니다; 이 연산은 때때로 하이퍼-4(hyper-4) 또는 테트레이션(tetration)이라고 불립니다. 반복하는 테트레이션은 또 다른 연산, 및 곧 초연산(hyperoperation)이라 명명된 개념으로 이어집니다. 연산의 이 수열은 아커만 함수(Ackermann function)와 커누스의 윗-화살표 표기법(Knuth's up-arrow notation)에 의해 표현됩니다. 마치 지수화가 덧셈보다 빠르게-증가하는 곱셈보다 빠르게 증가하는 것처럼, 테트레이션은 지수화보다 빠르게 증가합니다. (3, 3)에서 평가된, 함수 덧셈, 곱셈, 지수화, 및 테트레이션은, 각각, 6, 9, 27, 및 7625597484987 (= 3²⁷ = 3³³ = ³3)입니다.

Limits of powers

영에 영의 거듭제곱(Zero to the power of zero)은 불확정 형식(indeterminate form) 0⁰인 극한의 다수의 예제를 제공합니다. 이들 예제에서 극한은 존재하지만, 다른 값을 가지며, 둘의-변수 함수 x^y는 점 (0, 0)에서 극한을 가지지 않음을 보입니다. 우리는 무슨 점에서 이 함수가 극한을 가지는지 고려할 수 있습니다.

보다 정확하게, D = {(x, y) ∈ R² : x > 0} 위에 정의된 함수 f(x, y) = x^y를 생각해 보십시오. 그런-다음 D는 R²의 부분집합으로 보일 수 있으며 (즉, 확장된 실수 직선(extended real number line) R = [−∞, +∞]에 속하는 x, y를 갖는 모든 쌍 (x, y)의 집합은, 곱 토폴로지(product topology)를 부여합니다), 이것은 함수 f가 극한을 가지는 것에서 점을 포함할 것입니다.

사실, f는 (0, 0), (+∞, 0), (1, +∞) 및 (1, −∞)을 제외하고, D의 모든 누적 점(accumulation point)에서 극한을 가집니다. 그에 따라서, 이것은, 불확정 형식으로 남아있는, 0⁰, (+∞)⁰, 1^+∞ 및 1^−∞을 제외한, 0 ≤ x ≤ +∞, −∞ ≤ y ≤ +∞일 때마다 연속성에 의해 거듭제곱 x^y를 정의하는 것을 허용합니다.

연속성에 의한 이 정의 아래에서, 우리는 다음을 얻습니다:

• 1 < x ≤ +∞일 때, x^+∞ = +∞ 및 x^−∞ = 0.
• 0 ≤ x < 1일 때, x^+∞ = 0 및 x^−∞ = +∞.
• 0 < y ≤ +∞일 때, 0^y = 0 및 (+∞)^y = +∞.
• −∞ ≤ y < 0일 때, 0^y = +∞ 및 (+∞)^y = 0.

이들 거듭제곱은 x의 양의 값에 대해 x^y의 극한을 취함으로써 얻습니다. 이 방법은, x < 0일 때, x^y의 정의를 허용하지 않는데, 왜냐하면 x < 0을 갖는 쌍 (x, y)는 D의 누적 점이 아니기 때문입니다.

다른 한편으로, n이 정수일 때, 거듭제곱 xⁿ은, 음수 값을 포함하는, x의 모든 값에 대해 이미 의미가 있습니다. 이것은, n이 홀수일 때, 문제의 음의 n에 대해 위에서 얻은 정의 0ⁿ = +∞를 만들 수 있는데, 왜냐하면 이 경우에서 x가 양의 값을 통해 0으로 접근할 때 xⁿ → +∞이지만, 음의 값에 대해 그렇지 않기 때문입니다.

Efficient computation with integer exponents

반복된 곱셈을 사용하여 bⁿ을 계산하는 것은 n − 1 곱셈 연산이 필요하지만, 다음 예제에서 묘사되는 것처럼, 그것은 반복된 곱셈보다 더 효율적으로 계산될 수 있습니다. 2¹⁰⁰을 계산하기 위해, 100 = 64 + 32 + 4을 주목하십시오. 다음에 보이는 순서대로 계산하십시오:

1. 2² = 4
2. (2²)² = 2⁴ = 16
3. (2⁴)² = 2⁸ = 256
4. (2⁸)² = 2¹⁶ = 65,536
5. (2¹⁶)² = 2³² = 4,294,967,296
6. (2³²)² = 2⁶⁴ = 18,446,744,073,709,551,616
7. 2⁶⁴ 2³² 2⁴ = 2¹⁰⁰ = 1,267,650,600,228,229,401,496,703,205,376

이 일련의 단계는 99 대신에 오직 8 곱셈 연산을 필요로 합니다 (위의 마지막 곱셈은 2 곱셈을 취합니다).

일반적으로, bⁿ을 계산하기 위해 요구된 곱셈 연산의 숫자는 제곱화에 의한 지수화(exponentiation by squaring) 또는 (보다 일반적으로) 덧셈-체인 지수화(addition-chain exponentiation)를 사용함으로써 Θ(log n)으로 줄어들 수 있습니다. bⁿ에 대해 곱셈의 최소 수열 (지수에 대해 최소-길이 덧셈 체인)을 찾는 것은, 효율적인 알고리듬이 현재 알려지지 않은 어려운 문제이지만 (부분집합 합 문제(Subset sum problem)를 참조하십시오), 많은 합리적으로 효율적인 휴리스틱 알고리듬이 유효합니다.

Exponential notation for function names

마치 함수가 거듭제곱에 올려질 수 있는 것처럼, 함수의 이름 또는 기호 뒤에 정수 위첨자를 배치하는 것은 공통적으로 반복된 곱셈이 아니라 반복된 함수 합성(function composition)을 참조합니다. 따라서, f³(x)는 f(f(f(x)))를 의미할 것입니다; 특히, f⁻¹(x)는 보통 f의 역함수(inverse function)를 나타냅니다. 이 표기법은 한스 하인리히 뷔르만(Hans Heinrich Bürmann)과 존 프레더릭 윌리엄 허셜(John Frederick William Herschel)에 의해 도입되었습니다. 반복된 함수(Iterated function)는 프랙탈(fractal)과 동역학적 시스템(dynamical systems)의 연구에서 관심이 있습니다. 배비지(Babbage)는 함수형 제곱근(functional square root) f^1/2(x)을 찾는 문제를 처음으로 연구한 것이었습니다.

지수화를 함수 합성으로부터 구별하기 위해, 공통적인 사용법은 함수의 인수를 둘러싼 괄호 뒤에 지수화의 지수를 쓰는 것입니다; 즉, f(x)³는 (f(x))³을 의미하고, f(x)^–1은 1/f(x)을 의미합니다.

역사적인 이유에 대해, 및 인수를 괄호로 묶지 않아서 초래하는 모호성때문에, 삼각 함수(trigonometric)와 쌍곡선(hyperbolic) 함수에 구체적으로 적용된 함수 이름 뒤에 위첨자는 일탈적인 의미를 가집니다: 함수의 약어에 적용된 양의 지수는 결과가 해당 거듭제곱을 올리게 됨을 의미하고, 반면에 −1의 지수는 여전히 역함수를 나타냄을 의미합니다. 즉, sin² x는 단지 괄호 사용없이 (sin x)² = sin(x)²를 쓰기 위한 속기 방법이고, 반면에 sin⁻¹ x는 사인(sine)의 역함수를 참조하며, 역시 arcsin x라고 불립니다. 각각의 삼각과 쌍곡선 함수는 역수 (예를 들어, 1/(sin x) = (sin x)⁻¹ = sin(x)⁻¹ = csc x), 그것의 역 (예를 들어, cosh⁻¹ x = arcosh x)에 대해 둘 다 그 자신의 이름과 약어를 가집니다. 비슷한 관례가 로그에 적용되며, 여기서 오늘날 log² x는 보통 log log x가 아니라 (log x)²을 의미합니다.

모호성을 피하기 위해, 일부 수학자는 ∘을 합성적 의미를 나타내기 위해 사용하며, 예를 들어, f(f(f(x)))을 의미하는 f^∘3(x)에서 처럼, 함수 f(x)의 n-번째 반복에 대해 f^∘n(x)를 씁니다. 같은 목적에 대해, f^[n](x)가 벤저민 퍼스(Benjamin Peirce)에 의해 사용되었고, 반면에 알프레트 프링스하임(Alfred Pringsheim)과 주르 모르크(Jules Molk)는 대신에 ⁿf(x)를 제안했습니다.

In programming languages

프로그래밍 언어(Programming language)는 일반적으로 지수 연산자를 중위 연산자 또는 (접두사) 함수로 표현하는데, 왜냐하면 그들은 위첨자를 지원하지 않는 선형 표기법이기 때문입니다:

• x ↑ y: Algol, Commodore BASIC, TRS-80 Level II/III BASIC.
• x ^ y: AWK, BASIC, J, MATLAB, Wolfram Language (Mathematica), R, Microsoft Excel, Analytica, TeX (and its derivatives), TI-BASIC, bc (for integer exponents), Haskell (for nonnegative integer exponents), Lua and most computer algebra systems. Conflicting uses of the symbol ^ include: XOR (in POSIX Shell arithmetic expansion, AWK, C, C++, C#, D, Go, Java, JavaScript, Perl, PHP, Python, Ruby and Tcl), indirection (Pascal), and string concatenation (OCaml and Standard ML).
• x ^^ y: Haskell (for fractional base, integer exponents), D.
• x ** y: Ada, Z shell, KornShell, Bash, COBOL, CoffeeScript, Fortran, FoxPro, Gnuplot, Groovy, JavaScript, OCaml, F#, Perl, PHP, PL/I, Python, Rexx, Ruby, SAS, Seed7, Tcl, ABAP, Mercury, Haskell (for floating-point exponents), Turing, VHDL.
• pown x y: F# (for integer base, integer exponent).
• x⋆y: APL.

많은 다른 프로그래밍 언어는 지수에 대한 구문 지원이 부족하지만, 라이브러리 함수를 제공합니다:

• pow(x, y): C, C++.
• Math.Pow(x, y): C#.
• math:pow(X, Y): Erlang.
• Math.pow(x, y): Java.
• [Math]::Pow(x, y): PowerShell.
• (expt x y): Common Lisp.

특정 지수에 대해, 일반적인 지수화를 통한 것보다 훨씬 더 빠른 x^y 계산하기 위한 특별한 방법이 있습니다. 이들 경우는 작은 양의 정수와 음의 정수 (x²보다 x · x를 선호함; x⁻¹보다 1/x을 선호함)와 근 (x^0.5 보다 sqrt(x)을 선호함; x^1/3보다 cbrt(x)를 선호함)을 포함합니다.

모든 프로그래밍 언어가 지수에 대해 같은 결합 관례를 준수하는 것은 아닙니다: 반면 울프럼 언어(Wolfram language), 구글 검색(Google Search) 및 다른 것은 오른쪽-결합을 사용합니다 (즉, a^b^c는 a^(b^c)로 평가됩니다). 마이크로소프트 오피스 액셀(Microsoft Office Excel) 및 매트랩(Matlab)과 같은 많은 컴퓨터 프로그램은 왼쪽에 결합됩니다 (즉, a^b^c는 (a^b)^c로 평가됩니다).

See also

• Double exponential function
• Exponential decay
• Exponential field
• Exponential growth
• List of exponential topics
• Modular exponentiation
• Scientific notation
• Unicode subscripts and superscripts
• x^y = y^x
• Zero to the power of zero

External links

• Laws of Exponents with derivation and examples