Calculus

미적분학(Calculus)은, 원래 무한소 미적분학(infinitesimal calculus), 또는 "무한소의 미적분학"으로 불리며, 연속적인 변화의 수학적(mathematical) 연구이며, 같은 방법에서, 기하학(geometry)은 형상에 대한 연구이고 대수학(algebra)은 산술 연산(arithmetic operations)의 일반화의 연구입니다.

그것은 두 가지 주요한 가지, 미분 미적분학(differential calculus) 및 적분 미적분학(integral calculus)을 가집니다; 전자는 순간 변화율, 및 곡선의 기울기와 관련되지만, 적분 미적분학은 양의 축적과 곡선 아래 또는 사이의 넓이와 관련됩니다. 이들 두 가지는 미적분학의 기본 정리(fundamental theorem of calculus)에 의해 서로 관련되고, 그들은 무한 수열(inifinite sequence)과 잘-정의된 극한(limit)에 의한 무한 급수(infinite series)의 수렴(convergence)의 기본적인 개념을 사용합니다.^[1]

무한소 미적분학은 아이작 뉴턴(Isaac Newton)과 고트프리트 빌헬름 라이프니츠(Gottfried Wilhelm Leibniz)에 의해 17세기에 독립적으로 개발되었습니다.^[2]^[3] 오늘날, 미적분학은 과학(science), 공학(engineering), 및 경제학(economics)에서 광범위하게 사용되어 왔습니다.^[4]

수학 교육(mathematics education)에서, 미적분학은 기본 수학적 해석학(mathematical analysis)의 과정을 나타내며, 이것은 함수(functions)와 극한의 연구에 주로 전념됩니다. 단어 calculus (복수형 calculi)는 라틴어(Latin) 단어이며, 원래 "작은 조약돌"을 의미합니다 (이 의미는 의학에서 유지됩니다). 그러한 조약돌은 계산에 대해 사용되었기 때문에, 단어의 의미는 진화되어 왔고 오늘날 보통 계산의 방법을 의미합니다. 그것은, 따라서, 명제 계산법(propositional calculus), 리치 계산법(Ricci calculus), 변화의 계산법(calculus of variations), 람다 계산법(lambda calculus), 및 공정 계산법(process calculus)과 같은, 계산의 특정 방법 및 관련된 이론을 이름-짓는 것에 사용됩니다.

History

현대 미적분학은 17-세기 유럽에서 아이작 뉴턴(Isaac Newton)과 고트프리트 빌헬름 라이프니츠(Gottfried Wilhelm Leibniz) (서로 독립적으로, 같은 시기에 최초로 출판됨)에 의해 개발되었지만 그의 요소는 고대 그리스, 그 후 중국과 중동에서 나타나고, 중세 유럽과 인도에서 나중에 다시 등장합니다.

Ancient

고대 시대에는 적분학(integral calculus)을 이끌어내는 몇 가지 아이디어가 소개되었으나, 이러한 아이디어를 엄격하고 체계적인 방법으로 개발하지는 않은 것으로 보입니다. 적분법의 한 목표, 부피(volume)와 넓이(area)의 계산은 이집트의 모스코우 파피루스(Moscow papyrus) (13번째 왕조, c. 1820 BC)에서 발견될 수 있지만, 수식은, 방법에 대한 설명이 없는, 간단한 지침이고, 그들의 일부는 주요 구성 요소가 없습니다.^[5]

그리스 수학의 시대로부터, 에우독소스(Eudoxus) (c. 408–355 BC)는, 극한의 개념을 예고한, 넓이와 부피를 계산하기 위해서, 소진의 방법(method of exhaustion)을 사용했지만, 아르키메데스(Archimedes) (c. 287–212 BC)는, 적분학의 방법을 닮은 휴리스틱(heuristics)을 발명하여, 이 아이디어를 더 발전시켰습니다.^[6]

소진의 방법(method of exhaustion)은 서기 3세기에 원의 넓이를 구하기 위해 류 혜(Liu Hui)에 의해 중국(China)에서 독자적으로 나중에 발견되었습니다.^[7] 서기 5세기에서, 조충지(Zu Chongzhi)의 아들인, 조긍지(Zu Gengzhi)는, 나중에 구(sphere)의 부피를 찾기 위한 카발리에리의 원리(Cavalieri's principle)라고 불리는 방법^[8]^[9]을 확립했습니다.

Medieval

Alhazen, 11th century Arab mathematician and physicist

중동에서, 알하젠(Alhazen) (c. 965 – c. 1040 CE)으로 라틴어화된, 하산 이븐 알-하이삼(Hasan Ibn al-Haytham)은 네 번째 거듭제곱(fourth power)의 합에 대해 공식을 도출했습니다. 그는 지금 이 함수의 적분(integration)으로 불리는 것을 수행하기 위해 결과를 사용했으며, 여기서 적분 제곱과 네 번째 거듭제곱의 합에 대한 공식은 그에게 포물면체(paraboloid)의 부피를 계산하는 것을 허용했습니다.^[10]

14세기에서, 인도 수학자들은, 일부 삼각 함수에 적용할 수 있는, 미분화를 닮은, 비-엄격한 방법을 제시했습니다. 산가마그라마의 마드하바(Madhava of Sangamagrama)와 천문학과 수학의 케랄라 학교(Kerala school of astronomy and mathematics)는 미적분학의 구성 요소를 그 수단으로 말했습니다. 이러한 구성 요소를 포괄하는 완전한 이론은 지금 서양 세계에서 테일러 급수(Taylor series) 또는 무한 급수(infinite series) 근사로 잘-알려져 있습니다.^[11] 어쨌든, 그들은 "도함수와 적분의 두 가지 통일하는 주제 아래에서 많은 다른 아이디어를 결합하고, 둘 사이의 연결을 보여 주고, 그리고 미적분학을 오늘날 우리가 가진 큰 문제-해결 도구로 전환"할 수는 없었습니다.^[10]

Modern

"The calculus was the first achievement of modern mathematics and it is difficult to overestimate its importance. I think it defines more unequivocally than anything else the inception of modern mathematics, and the system of mathematical analysis, which is its logical development, still constitutes the greatest technical advance in exact thinking."

—John von Neumann^[12]

유럽에서, 기초적인 작업은 보나벤투라 카발리에리(Bonaventura Cavalieri)에 의해 쓰인 논문이었는데, 그는 부피와 넓이는 무한소적으로 얇은 횡단면의 부피와 넓이로 계산해야 한다고 주장했습니다. 이 아이디어는 The Method에서 아르키메데스의 방법과 유사하지만, 이 논문은 13세기에 잃어버린 것으로 믿어져 왔고, 20세기 초반에 단지 재발견되었으며, 카발리에리에게는 알려지지 않았을 것입니다. 카발리에리의 업적은 그의 방법이 잘못된 결과를 초래할 수 있기 때문에 존경받지 못했으며, 그가 소개한 무한소 양은 처음에는 평판이 나빴습니다.

미적분학에 대한 공식적인 연구는 같은 시기에 유럽에서 개발된 유한한 차이의 미적분학(calculus of finite differences)과 함께 카발리에리의 무한소를 함께 가져왔습니다. 그가 디오판투스(Diophantus)로부터 빌려 왔다고 주장하는, 피에르 드 페르마(Pierre de Fermat)는 타당성(adequality) 개념을 도입했으며, 이것은 무한소 오류 항까지 같음을 나타냅니다.^[13] 이 결합은 존 월리스(John Wallis), 아이작 배로(Isaac Barrow), 및 제임스 그레고리(James Gregory)에 의해 이루어졌으며, 후자의 두 사람은 1670년경의 미적분학의 두 번째 기본 정리(second fundamental theorem of calculus)를 증명했습니다.

Isaac Newton developed the use of calculus in his laws of motion and gravitation.

곱 규칙(product rule)과 체인 규칙(chain rule),^[14] 고차원 도함수(higher derivative)와 테일러 급수(Taylor series)의 개념,^[15] 및 해석적 함수(analytic function)^{[citation needed]}의 개념은 특이한 표기법으로 아이작 뉴턴(Isaac Newton)에 의해 소개되었으며, 그는 이것을 수학적 물리학(mathematical physics)의 문제를 해결하기 위해서 사용했습니다. 그의 업적에서, 뉴턴은 시간의 수학적 관용구에 맞도록 그의 아이디어를 바꿔 말하고, 비난을 넘어서는 것으로 여겨졌던 동등한 기하학적 논증에 의해 계산을 무한소로 대체했습니다. 그는 행성 운동의 문제, 회전하는 유체의 표면의 모양, 지구의 타원율, 사이클로이드(cycloid) 위에 미끄러지는 무게의 움직임, 및 그의 Principia Mathematica (1687)에서 논의된 많은 다른 문제를 해결하기 위해 미적분학의 방법을 사용했습니다. 다른 업적에서, 그는, 분수와 무리수 거듭제곱을 포함하는, 함수에 대해 수열 전개를 발전시켰고, 그것은 그가 테일러 급수(Taylor series)의 원리를 이해했다는 것을 분명히 했습니다. 그는 모든 이러한 발견을 발표하지 않았으며, 이 시기에는 무한소 방법은 여전히 불명예스러운 것으로 여겨졌습니다.

이들 아이디어는 고트프리트 빌헬름 라이프니츠(Gottfried Wilhelm Leibniz)에 의한 무한소의 참 미적분학으로 조정되었으며, 그는 원래 뉴턴에 의한 표절(plagiarism)의 혐의로 고소당했습니다.^[16] 그는 이제 미적분학의 독립적 발명가이자 공로자로 여겨집니다. 그의 기여는 무한소 양과 함께 동작하는 것에 대해 규칙의 분명한 집합을 제공하는 것이며, 이차 및 고차 도함수를 계산하는 것을 허용하고, 그들 미분과 적분 형식에서, 곱 규칙(product rule)과 체인 규칙(chain rule)을 제공합니다. 뉴턴과는 달리, 라이프니츠는 형식주의에 많은 관심을 기울였으며, 종종 개념에 대해 적절한 기호를 결정하는 것에 며칠을 소비했습니다.

오늘날, 라이프니츠(Leibniz)와 뉴턴(Newton)은 보통 미적분학을 독립적으로 발명하고 개발하는 것에 대해 둘 다 인정을 받았습니다. 뉴턴은 일반 물리학(physics)에 미적분학을 처음 적용했으며 라이프니츠는 오늘날 미적분학에서 사용되는 많은 표기법을 개발했습니다. 뉴턴과 라이프니츠가 제공한 기본 통찰력은 미분화와 적분화의 법칙, 이차와 고차 도함수, 및 다항식 급수를 근사하는 것의 개념이었습니다. 뉴턴의 시간에서, 미적분학의 기본 정리가 알려졌습니다.

뉴턴과 라이프니츠가 처음으로 결과를 발표했을 때, 수학자 (및 따라서 어느 나라)가 신용을 받을 자격이 있는지에 대한 큰 논란이 있었습니다. 뉴턴은 그의 결과를 처음으로 끌어냈고 (나중에 그의 Method of Fluxions에서 출판되어짐), 라이프니츠는 그의 "Nova Methodus pro Maximis et Minimis"를 먼저 출판했습니다. 뉴턴은 라이프니츠가 그의 출판되지 않은 노트로부터 아이디어를 훔쳤다고 주장했으며, 그것은 뉴턴이 왕립 학회의 몇 명에게 공유한 것입니다. 이 논쟁은 수년 동안 대륙 유럽 수학자들로부터, 영어 수학에 해가 되는, 영어를-말하는 수학자들을 나누었습니다.^{[citation needed]} 라이프니츠와 뉴턴의 논문에 대한 주의 깊은 검사는, 라이프니츠가 적분과 뉴턴은 미분화와 함께 처음에 시작했다는 것, 및 서로 독립적으로 그들 결과에 도달했다는 것을 보여줍니다. 어쨌든, 새로운 학문에 이름을 부여한 것은 라이프니츠입니다. 뉴턴은 그의 미적분학을 "유율의 과학(the science of fluxions)"이라고 불렀습니다.

라이프니츠와 뉴턴 시대부터, 많은 수학자들이 미적분학의 발전에 지속적으로 기여해 왔습니다. 무한소와 적분학(integral calculus) 둘 다에 대한 최초이자 가장 완벽한 작품 중 하나는 마리아 가에타나 아녜지(Maria Gaetana Agnesi)에 의해 1748년에 쓰였습니다.^[17]^[18]

Foundations

미적분학에서, 토대(foundations)는 공리(axiom)와 정의로부터 주제의 엄격한(rigorous) 발전을 의미합니다. 초기 미적분학에서 무한소(infinitesimal) 양의 사용은 비-엄격한 것으로 여겨졌고, 가장 주목할만한 미셸 롤(Michel Rolle)과 주교 버클리(Bishop Berkeley)와 같은, 많은 저자들에 의해 맹렬히 비난되었습니다. 버클리는 1734년 그의 저서 The Analyst에서 떠난 양의 유령으로 무한소를 유명하게 묘사했습니다. 미적분학에 대해 엄격한 토대의 성취는 뉴턴과 라이프니츠를 따르는 세기의 많은 부분에 수학자들이 종사했으며, 오늘날에도 여전히 어느 정도 연구의 활동 영역입니다.

매클로린(Maclaurin)을 포함하는, 여러 수학자들은 무한소를 사용하는 것의 건전함을 증명하려 애썼지만, 코시(Cauchy)와 바이어슈트라스(Weierstrass)의 연구로 인해, 무한하게 적은 양의 단순한 "개념"을 피할 수 있는 하나의 방법이 발견되는 150년 후까지 그렇지 못했습니다.^[19] 미분 미적분과 적분 미적분의 토대가 놓여져 왔습니다. 코시의 Cours d'Analyse에서, 우리는 무한소의 관점에서 연속성(continuity)의 정의와 미분화의 정의에서 극한의 (ε, δ)-정의의 (다소 부정확한) 프로토타입을 포함하는, 광범위한 토대 접근을 발견합니다.^[20] 그의 연구에서 바이어슈트라스는 극한(limit)의 개념을 공식화하고 (비록 그의 정의는 실제로 제곱영(nilsquare)의 무한소를 유효성을 검사할지라도) 무한소를 제거했습니다. 바이어슈트라스의 업적에 따라서, 그것은 결국, 비록 주제가 여전히 때때로 "무한소 미적분학(infinitesimal calculus)"이라고 불리지만, 무한소 양 대신에 극한 위에 미적분학을 근거하는 것이 보편적으로 되었습니다. 베른하르트 리만(Bernhard Riemann)은 이들 아이디어를 사용하여 적분의 정확한 정의를 제시했습니다. 그것으로부터 미적분학의 아이디어가 유클리드 공간(Euclidean space)과 복소 평면(complex plane)으로 일반화된 것이 이 시기 동안에 이루어졌습니다.

현대 수학에서, 미적분학의 토대는 실 해석학(real analysis)의 분야에 포함되고, 이것은 미적분학의 정리의 완전한 정의와 증명(proof)을 포함합니다. 미적분의 범위도 역시 크게 확장되어 왔습니다. 앙리 르베그(Henri Lebesgue)는 측정 이론(measure theory)을 발명했고 그것을 가장 병리적(pathological) 함수를 제외한 모든 함수의 적분을 정의하기 위해서 사용했습니다. 로랑 슈바르츠(Laurent Schwartz)는 분포(distribution)를 도입했으며, 이것은 임의의 함수가 무엇이든지 도함수를 취하는 것에 사용될 수 있습니다.

극한은 미적분학의 토대에 대해 유일한 엄격한 접근이 아닙니다. 또 다른 방법은 에이브러햄 로빈슨(Abraham Robinson)의 비-표준 해석학(non-standard analysis)을 사용하는 것입니다. 1960년대에 개발된, 로빈슨의 접근은, 원래의 뉴턴-라이프니츠 개념에서와 같이, 수학적 논리(mathematical logic)로부터 무한소(infinitesimal) 및 무한한(infinite) 숫자와 함께 실수 시스템을 증가시키는 것까지 기술 기계를 사용합니다. 결과 숫자는 초실수(hyperreal number)라 불리고, 그들은 미적분학의 보통 규칙의 라이프니츠-같은 개발을 제공하기 위해서 사용될 수 있습니다. 도함수 중에 더 높은 거듭제곱의 무한소를 무시해야 한다는 점에서 비-표준 해석학과는 다른 매끄러운 무한소 해석학(smooth infinitesimal analysis)도 있습니다.

Significance

미적분학의 많은 아이디어가 그리스(Greece), 중국(China), 인도(India), 이라크, 페르시아(Iraq, Persia), 일본(Japan)에서 초기에 개발되어 오는 동안, 미적분학의 사용은, 17세기에 유럽에서, 아이작 뉴턴(Isaac Newton)과 고트프리트 빌헬름 라이프니츠(Gottfried Wilhelm Leibniz)가 초기 수학자들의 그것의 기본 원칙을 소개하기 위해 이 작업을 수행했을 때, 시작되었습니다. 미적분학의 발전은 순간 운동의 초기 개념과 곡선 아래의 넓이에 기초하여 작성되었습니다.

미적분학의 응용은 속도(velocity)와 가속도(acceleration), 곡선의 기울기(slope), 및 최적화(optimization)를 포함하는 계산을 포함합니다. 적분학의 응용은 넓이, 부피(volume), 호 길이(arc length), 질량의 중심(center of mass), 일(work), 및 압력(pressure)을 포함하는 계산을 포함합니다. 보다 진보된 응용은 거듭제곱 급수(power series)과 푸리에 급수(Fourier series)를 포함합니다.

미적분학은 공간, 시간, 및 운동의 본성의 보다 정확한 이해를 얻기 위해 역시 사용됩니다. 수세기 동안, 수학자들과 철학자들은 영에 의한 나눗셈(division by zero) 또는 무한하게 많은 숫자의 합을 포함하는 역설과 씨름했습니다. 이러한 질문은 운동(motion)과 넓이의 연구에서 발생합니다. 고대 그리스 철학자 엘레아의 제논(Zeno of Elea)은 그러한 역설의 여러가지 유명한 예제를 제공했습니다. 미적분학은 역설을 해결하는 도구, 특히 극한(limit)과 무한 급수(infinite series)를 도구로 제공합니다.

Principles

Limits and infinitesimals

미적분은 보통 매우 작은 양과 함께 작업하는 것에 의해 개발됩니다. 역사적으로, 그렇게 하는 첫 번째 방법은 무한소(infinitesimal)에 의한 것이었습니다. 이것들은 실수처럼 취급될 수 있지만, 어떤 의미에서, "무한히 작은" 것의 대상입니다. 예를 들어, 무한소 숫자는 영보다 클 수 있지만, 수열 1, 1/2, 1/3, ...에서 임의의 숫자보다 작고 따라서 임의의 양의 실수(real number)보다 작습니다. 이런 관점에서, 미적분은 무한소를 조작하는 것에 대해 기법의 모음입니다. 기호 $dx$ 와 $dy$ 는 무한소로 취해졌고, 도함수 $dy/dx$ 는 단순히 그들의 비율이었습니다.

정확한 무한소의 개념을 만드는 것이 어려웠기 때문에, 무한소 접근은 19세기에 호감을 잃었습니다. 어쨌든, 이 개념은 20 세기에 비-표준 해석학(non-standard analysis)과 매끄러운 무한소 해석학(smooth infinitesimal analysis)의 도입과 함께 되살아났으며, 이것은 무한소의 조작에 대해 견고한 토대를 제공했습니다.

19세기에서, 무한소가 극한(limit)에 대한 엡실론, 델타(epsilon, delta) 접근에 의해 대체되었습니다. 극한은 근처 입력에서 그의 값의 관점에서 특정 입력에서 함수(function)의 값을 나타냅니다. 그들은 실수 시스템의 맥락에서 소-규모 행동을 포착합니다. 이런 처리에서, 미적분은 특정 극한을 조작하는 것에 대해 기술의 모음입니다. 무한소는 매우 작은 숫자에 의해 대체되고, 함수의 무한하게 작은 동작은 점점 더 작아지는 숫자에 대해 극한하는 동작을 취하는 것에 의해 발견됩니다. 극한은 미적분학에 대해 엄격한 토대를 제공하는 첫 번째 방법이었고, 이러한 이유에 대해 그들은 표준 접근입니다.

Differential calculus

미분학은 미분 함수의 도함수(derivative)의 정의, 속성, 및 응용의 연구입니다. 도함수를 찾는 것의 프로세서는 미분화(differentiation)라고 불립니다. 도메인에서 함수와 한 점이 주어지면, 그 지점에서 도함수는 그 지점 근처의 함수의 소-규모 행동을 인코딩하는 방법입니다. 그의 도메인 내의 모든 점에서 함수의 도함수를 찾는 것에 의해, 그것은, 도함수 함수 또는 바로 원래 함수의 도함수라고 불리는, 새로운 함수를 생성하는 것으로 가능합니다. 공식적인 용어에서, 도함수는 그의 입력으로 함수를 취하고 그의 출력으로 두 번째 함수를 생성하는 선형 연산자(linear operator)입니다. 이것은, 함수가 보통 숫자를 입력하고 다른 숫자를 출력하는, 초등 대수학에서 연구된 많은 프로세스보다 더 추상적입니다. 예를 들어, 만약 두배하는 함수에 입력 3을 주면, 그것은 6을 출력하고, 만약 제곱하는 함수에 입력 3을 주면, 그것은 9를 출력합니다. 어쨌든, 도함수는 입력으로 제곱하는 함수를 취할 수 있습니다. 이것은 도함수가 제곱하는 함수의 모든 정보를 취하고—이는 사를 보내고, 삼은 구를 보내고, 사는 십육을 보내는, 등과 같은—다른 함수를 생성하기 위해 이 정보를 사용하는 것을 의미합니다. 제곱 함수를 유도하는 것에 의해 생성된 함수는 두배하는 함수로 판명됩니다.

보다 명확한 용어에서, "두배하는 함수"는 $g (x) = 2 x$ 로 표시되고 "제곱하는 함수"는 $f (x) = x 2$ 로 표시될 수 있습니다. 이제 "도함수"는, 입력으로, 그것의 모든 정보—이는 사를 보내고, 삼은 구를 보내고, 사는 십육을 보내고, 등과 같은— 표현 " $x 2$ "으로 정의되는, 함수 $f (x)$ 를 취하고, 이 정보를 다른 함수의 출력으로 사용하고, 함수 $g (x) = 2 x$ 와 같이 밝혀질 것입니다.

도함수에 대해 가장 공통적인 기호는 프라임(prime)이라고 부르는 아포스트로피(apostrophe)-같은 기호입니다. 따라서, $f$ 라고 부르는 함수의 도함수는 $f'$ 으로 표시되며, "f 프라임"이라고 발음합니다. 예를 들어, 만약 $f (x) = x 2$ 가 제곱하는 함수이면, $f' (x) = 2 x$ 는 그의 도함수 (위로부터 두배하는 함수 $g$ )입니다. 이 표기법은 라그랑주의 표기법(Lagrange's notation)으로 알려져 있습니다.

만약 함수의 입력이 시간을 나타내면, 도함수는 시간에 관한 변화를 나타냅니다. 예를 들어, 만약 $f$ 가 입력으로 시간을 취하고 출력으로 그 시간에 공의 위치를 제공하는 함수이면, $f$ 의 도함수는 위치가 시간에 대해 어떻게 변하는지이며, 즉, 그것은 공의 속도(velocity)입니다.

만약 함수가 선형(linear)이면 (즉, 만약 함수의 그래프(graph)가 직선이면), 함수는 $y = mx + b$ 로 쓸 수 있으며, 여기서 $x$ 는 독립 변수이고, $y$ 는 종속 변수이고, $b$ 는 y-절편, 그리고:

m={\frac {\text{rise}}{\text{run}}}={\frac {{\text{change in }}y}{{\text{change in }}x}}={\frac {\Delta y}{\Delta x}}.

이것은 직선의 기울기에 대해 정확한 값을 제공합니다. 만약 함수의 그래프가 직선이 아니라면, 어쨌든, $x$ 의 변화에 의해 나누어지는 $y$ 의 변화는 변합니다. 도함수는 입력의 변화에 관한 출력의 변화의 개념에 정확한 의미를 제공합니다. 구체적으로, $f$ 를 함수로 놓고, $f$ 의 도메인 내의 점 $a$ 를 고정합니다. $(a, f (a))$ 는 함수의 그래프 위의 점입니다. 만약 $h$ 가 영에 가까운 숫자이면, $a + h$ 는 $a$ 에 가까운 숫자입니다. 그러므로, $(a + h, f (a + h))$ 는 $(a, f (a))$ 에 가깝습니다. 이 두 점 사이의 기울기는

m={\frac {f(a+h)-f(a)}{(a+h)-a}}={\frac {f(a+h)-f(a)}{h}}.

이 표현은 차이 몫(difference quotient)이라고 불립니다. 곡선 위의 두 점을 지나는 직선을 할선이라고 불리므로, $m$ 은 $(a, f (a))$ 와 $(a + h, f (a + h))$ 사이의 할선의 기울기입니다. 할선은 $a$ 와 $a + h$ 사이에서 무슨 일이 일어나는지에 대해 설명하지 않기 때문에, 할선은 점 $a$ 에서 함수의 동작에 대한 단지 근사입니다. 이것은, 정의되지 않는, 영에 의한 나눗셈(dividing by zero)을 요구하기 때문에, 그것은 $h$ 를 영으로 설정하여 동작을 발견하는 것이 불가능합니다. 도함수는 $h$ 가 영으로 가는 경향일 때, 극한(limit)을 취하는 것에 의해 정의되며, 그것은 $h$ 의 모든 작은 값에 대해 $f$ 의 동작을 고려하고 $h$ 가 영과 같을 때의 경우에 대해 일관된 값을 추출하는 것을 의미합니다:

\lim _{h\to 0}{f(a+h)-f(a) \over {h}}.

기하학적으로, 도함수는 $a$ 에서 $f$ 의 그래프에 대한 접선(tangent line)의 기울기입니다. 접선은, 도함수가 차이 몫의 극한인 것처럼, 할선의 극한입니다. 이런 이유에 대해, 도함수는 때때로 함수 $f$ 의 기울기라고 불립니다.

이것은 특별한 예제이고, 입력 3에서 제곱하는 함수의 도함수입니다. $f (x) = x 2$ 를 제곱하는 함수라고 놓습니다.

The derivative $f' (x)$ of a curve at a point is the slope of the line tangent to that curve at that point. This slope is determined by considering the limiting value of the slopes of secant lines. Here the function involved (drawn in red) is $f (x) = x 3 - x$ . The tangent line (in green) which passes through the point (−3/2, −15/8) has a slope of 23/4. Note that the vertical and horizontal scales in this image are different.

{\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-3^{2} \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}

점 (3, 9)에서 제곱하는 함수에 대한 접선의 기울기는 6이며, 즉 말하자면, 그것은 그것이 오른쪽으로 가는 것보다 6배 빠르게 올라갑니다. 바로 위에 설명한 극한 프로세스는 제곱하는 함수의 도메인 내의 임의의 점에 대해 수행될 수 있습니다. 이것은 제곱 함수의 도함수 함수 또는 짧게 제곱하는 함수의 바로 도함수를 정의합니다. 위의 것과 유사한 계산은 제곱하는 함수의 도함수가 두배하는 함수임을 보여줍니다.

Leibniz notation

위의 예제에서, 라이프니츠에 의해 소개된, 도함수에 대해 공통적인 표기법은 다음과 같습니다:

{\begin{aligned}y&=x^{2}\\{\frac {dy}{dx}}&=2x.\end{aligned}}

극한에 기초한 접근에서, 기호 $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:.0 .1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:.1em .1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0 0,0 0,0 0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}dy/dx$ 는 두 개의 숫자의 몫이 아니라 위에서 계산된 극한의 약식으로 해석되어야 합니다. 어쨌든, 라이프니츠는, $x$ 에 적용되는 무한소적으로 작은 변화 $dx$ 에 의해 야기된, $y$ 내의 무한소적으로 작은 변화인 $dy$ 로, 두 무한소적으로 작은 숫자의 몫을 나타내기 위해 그것을 의도했습니다. 우리는 미분 연산자로 $d / dx$ 를 역시 생각할 수 있으며, 이것은 입력으로 함수를 취하고 출력으로 다른 함수, 도함수를 제공합니다. 예를 들어:

{\frac {d}{dx}}(x^{2})=2x.

이런 사용법에서, 분모에서 $dx$ 는 " $x$ 에 관한"으로 읽습니다. 정확한 표기법의 다른 예제는 다음과 같습니다:

${\begin{aligned}g(t)=t^{2}+2t+4\\\\{d \over dt}g(t)=2t+2\end{aligned}}$

비록 미적분학이 무한소라기 보다는 극한을 사용하여 개발되었다 할지라도, 그것은 $dx$ 와 $dy$ 와 같은 기호를 마치 실수인 것처럼 조작하는 것이 공통적입니다; 비록 그것은 그러한 조작을 피할 수 있을지라도, 그들은 때때로 전체 도함수(total derivative)와 같은 연산을 표현할 때 표기법으로 편리합니다.

Integral calculus

적분법(Integral calculus)은 두 가지 관련 개념, 부정 적분(indefinite integral)과 한정 적분(definite integral)의 정의, 속성, 및 응용의 연구입니다. 적분의 값을 찾는 과정은 적분화(integration)라고 불립니다. 기술 언어에서, 적분법은 두 개의 관련된 선형 연산자(linear operator)를 연구합니다.

역도함수(antiderivative)라고 역시 알려진, 부정 적분은 도함수에 대한 역 연산입니다. $F$ 는, $f$ 가 $F$ 의 도함수일 때, $f$ 의 부정 적분입니다. (함수와 그의 부정 적분에 대해 소문자와 대문자의 이 사용은 미적분학에서 공통적입니다.)

한정 적분은 함수를 입력하고 숫자를 출력하며, 이것은 입력의 그래프와 x-축 사이의 넓이의 대수적 합을 제공합니다. 한정 적분의 기술적인 정의는, 리만 합(Riemann sum)이라고 불리는, 직사각형 넓이의 합의 극한(limit)을 포함합니다.

동기 부여 예제는 주어진 시간 동안 이동한 거리입니다.

\mathrm {Distance} =\mathrm {Speed} \cdot \mathrm {Time}

만약 속력이 일정하면, 오직 곱셈이 요구되지만, 만약 속력이 변하면, 거리를 찾는 보다 강력한 방법이 필요합니다. 그러한 방법 중 하나는 시간을 여러 짧은 구간으로 나누어 이동한 거리를 근사적으로 계산한 다음, 각 구간에서 경과된 시간에 해당 구간의 속력을 곱한 다음, 각 구간에서 이동한 근사 거리의 합 (리만 합(Riemann sum))을 취하는 것입니다. 기본 아이디어는, 만약 단지 짧은 시간이 지나면, 속력은 아주 약간 달라질 수 있다는 것입니다. 어쨌든, 리만 합은 이동한 거리의 오직 근사치를 제공합니다. 우리는 이동한 정확한 거리를 찾기 위해 모든 그러한 리만 합의 극한을 반드시 취해야 합니다.

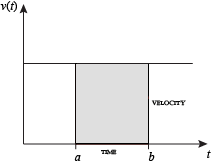
속도가 일정할 때, 주어진 시간 간격 동안 이동한 전체 거리는 속도와 시간을 곱하는 것에 의해 계산될 수 있습니다. 예를 들어, 3시간 동안 50 mph로 변하지 않고 계속 이동하면 전체 거리는 150마일이 됩니다. 왼쪽의 다이어그램에서, 일정한 속도와 시간이 그래프로 표시될 때, 이들 두 값은 경과된 시간과 같은 너비와 속도와 같은 높이를 갖는 직사각형을 형성합니다. 그러므로, 속도와 시간의 곱은 (일정한) 속도 곡선 아래의 직사각형 넓이를 역시 계산합니다. 곡선 아래의 넓이와 이동한 거리 사이의 이 연결은 주어진 시간 동안 변동하는 속도를 나타내는 임의의 불규칙한 모양의 넓이로 확장될 수 있습니다. 만약 오른쪽 다이어그램에서 $f (x)$ 가 시간에 따라 변화하는 속력을 나타내면, ( $a$ 와 $b$ 로 표시되는 시간 사이의) 이동한 거리는 음영처리된 영역 $s$ 의 넓이입니다.

그 넓이를 근사하기 위해, 직관적인 방법은 $a$ 와 $b$ 사이의 거리를 많은 같은 분할로 나누는 것이며, 각 분할의 길이는 기호 $Δ x$ 로 나타냅니다. 각각의 작은 분할에 대해, 우리는 함수 $f (x)$ 의 한 값을 선택할 수 있습니다. 그 값을 $h$ 라고 부릅니다. 그런-다음 밑변 $Δ x$ 와 높이 $h$ 를 가진 직사각형의 넓이는 해당 분할에서 (시간 $Δ x$ 와 속도 $h$ 에 의해 곱해진) 이동한 거리를 제공합니다. 각 분할과 결합된 $f (x) = h$ 인 함수의 평균값입니다. 모든 그러한 직사각형의 합은 축과 곡선 사이의 넓이의 근사를 제공하고, 이것은 이동한 전체 거리의 근사입니다. $Δ x$ 에 대해 더 작은 값은 더 많은 직사각형을 제공할 것이고 대부분의 경우에서 더 좋은 근사를 제공할 것입니니다. 그러나 정확한 답에 대해 우리는 $Δ x$ 가 영으로 접근할 때 극한을 취해야 합니다.

적분화의 기호는 $\int$ 이며, 길이가 긴 (S는 "sum"을 의미하는) S입니다. 한정 적분은 다음과 같이 쓰입니다:

\int _{a}^{b}f(x)\,dx.

그리고 "x에 관한 f-of-x의 a에서 b까지의 적분"이라고 읽습니다. 라이프니츠 표기법 $dx$ 는 그들 너비 $Δ x$ 가 무한소적으로 작은 $dx$ 가 되도록 곡선 아래의 넓이를 무한 숫자의 사각형으로 나누는 것을 제안하기 위한 의도입니다. 극한에 기초한 미적분학의 공식화에서, 다음 표기법은

\int _{a}^{b}\cdots \,dx

입력으로 함수를 취하고, 출력으로, 넓이, 숫자를 제공하는 연산자로 이해되는 것입니다. 종료하는 미분, $dx$ 는 숫자가 아니고, 비록, $Δ x$ 극한 정의를 상기하는 역할을 하는, 그것이 적분의 기호적 조작에서처럼 처리될 수 있을지라도, $f (x)$ 에 의해 곱해지는 것도 아닙니다. 공식적으로, 미분은 함수가 적분되는 것에 걸쳐 변수를 가리키고 적분화 연산자에 대해 닫히는 괄호의 역할을 합니다.

부정 적분, 또는 역도함수는 다음과 같이 쓰입니다:

\int f(x)\,dx.

오직 상수가 다른 함수는 같은 도함수를 가지고, 주어진 함수의 역도함수는 실제로 오직 상수가 다른 함수의 가족임을 보여줄 수 있습니다. 함수 $y = x 2 + C$ 의 도함수는, 여기서 $C$ 는 임의의 상수이며, $y' = 2 x$ 이므로, 후자의 역도함수는 다음에 의해 제공됩니다:

\int 2x\,dx=x^{2}+C.

부정 적분 또는 역도함수에 존재하는 불특정 상수 $C$ 는 적분의 상수(constant of integration)로 알려져 있습니다.

Fundamental theorem

미적분학의 기본 정리(fundamental theorem of calculus)는 미분화와 적분화가 역 연산임을 말합니다. 보다 정확하게, 그것은 역도함수의 값을 한정 적분과 관련 짓습니다. 그것은 한정 적분의 정의를 적용하는 것보다 역도함수를 계산하는 것이 보통 더 쉽기 때문에, 미적분학의 기본 정리는 한정 적분을 계산하는 실용적인 방법을 제공합니다. 그것은 역시 미분화가 적분화의 역이라는 사실에 대한 정확한 명제로 해석될 수 있습니다.

미적분학의 기본 정리는 말합니다: 만약 함수 $f$ 가 구간 $[a, b]$ 위에서 연속(continuous)이고 $F$ 가 구간 $(a, b)$ 위에서 그의 도함수가 $f$ 인 함수이면,

\int _{a}^{b}f(x)\,dx=F(b)-F(a).

게다가, 구간 $(a, b)$ 내의 모든 $x$ 에 대해,

{\frac {d}{dx}}\int _{a}^{x}f(t)\,dt=f(x).

아이작 배로(Isaac Barrow)의 초기 연구 결과를 기반으로 한, 뉴턴(Newton)과 라이프니츠(Leibniz)의 이러한 구현은, 그들 연구가 알려지게 된 후에, 분석적 결과의 확산에 대해 핵심적인 역할을 했습니다. 기본 정리는 역도함수(antiderivatives)에 대한 공식을 찾는 것에 의해—극한 프로세서를 수행하지 않고—많은 한정 적분 계산의 대수적 방법을 제공합니다. 그것은 역시 미분 방정식(differential equation)의 프로토타입 해입니다. 미분 방정식은 알려지지 않은 함수를 그의 도함수와 연관지으며, 과학에서 유비쿼터스입니다.

Applications

The logarithmic spiral of the Nautilus shell is a classical image used to depict the growth and change related to calculus.

미적분학은 물리적 과학, 보험수리적 과학, 컴퓨터 과학, 통계학, 공학, 경제학, 사업, 의학, 인구 통계학, 및 문제가 수학적 모델(mathematical model)이 되고 최적의(optimal) 해결책이 요구되는 어디든지 해당되는 다른 분야의 모든 가지에서 사용됩니다. 그것은 (비-상수) 변화율에서 전체 변화율로 또는 그 반대로 갈 수 있게 허용하고, 우리가 알고 있는 문제와 찾으려고 노력하는 문제를 연구하는 것에서 여러 번 반복하는 것을 허용합니다.

물리학(physics)은 미적분학의 사용을 특별하게 만듭니다; 고전 역학(classical mechanics)과 전자기학(electromagnetism)의 모든 개념은 미적분학을 통해 관련됩니다. 알려진 밀도(density)의 대상의 질량(mass), 대상의 관성 모멘트(moment of inertia), 마찬가지로 보존 필드 내의 대상의 전체 에너지는 미적분의 사용에 의해 발견될 수 있습니다. 역학에서 미적분학의 사용의 예제는 뉴턴의 운동의 두 번째 법칙입니다: 역사적으로 그것은 미분을 의미하는 용어 "운동의 변화"를 명시적으로 사용한다고 말합니다: 몸의 운동량의 변화는 몸에 작용하는 합력과 같고, 합력의 방향과 같은 방향입니다. 힘 = 질량 × 가속도로 오늘날 공통적으로 표현되는, 그것은 미적분을 의미하는데, 왜냐하면 가속도는 속도의 시간 도함수 또는 궤도 또는 공간적 위치의 이차 시간 도함수이기 때문입니다. 대상이 어떻게 가속화되는지를 아는 것으로 시작하여, 우리는 그의 경로를 유도하기 위해서 미적분학을 사용합니다.

전자기학(electromagnetism)의 맥스웰의 이론과 일반 상대성(general relativity)의 아인슈타인(Einstein)의 이론은 미분학의 언어에서 역시 표현됩니다. 화학은 반응 비율과 방사성 붕괴를 결정하기 위해 역시 미적분을 사용합니다. 생물학에서, 인구 동역학은 인구 변화를 모델하기 위해 재생과 사망 비율로 시작합니다.

미적분학은 다른 수학 분야와 연결해서 사용될 수 있습니다. 예를 들어, 그것은 도메인 내의 점의 집합에 대한 "가장 잘 맞는" 선형 근사를 찾기 위해서 선형 대수(linear algebra)과 함께 사용될 수 있습니다. 또는 그것은 가정된 밀도 함수로부터 연속 확률 변수의 확률을 결정하기 위해 확률 이론(probability theory)에서 사용될 수 있습니다. 해석적 기하학(analytic geometry), 함수의 그래프의 연구에서, 미적분학은 높은 점과 낮은 점 (최댓값들 그리고 최솟값들), 기울기, 오목(concavity)과 변곡점(inflection points)을 찾기 위해서 사용됩니다.

단순한 닫힌 곡선 C 주위의 곡선 적분과 C에 의해 경계된 평면 영역 D에 걸친 이중 적분 사이의 관계를 제공하는 그린의 정리(Green's Theorem)는 플래니미터(planimeter)로 알려진 기계 내에 적용되고, 플래니미터는 그림 위의 평평한 표면의 넓이를 계산하기 위해서 사용됩니다. 예를 들어, 그것은 불규칙적인 형상의 꽃 침대 또는 소유지 일부의 레이아웃을 디자인할 때 수영장에 의해 차지하는 넓이를 계산하기 위해서 사용됩니다.

단순한 닫힌 직사각형 곡선 C 주위의 함수의 이중 적분과 곡선의 가장자리를 따라 구석 점에서 역도함수의 값의 선형 결합을 제공하는, 이산 그린의 정리(Discrete Green's Theorem)는 직사각형 도메인 내의 값의 합의 빠른 계산을 허용합니다. 예를 들어, 특색을 빠르게 추출하고 대상을 탐지하기 위해, 그것은 이미지에서 직사각형 도메인의 합을 효율적으로 계산하기 위해서 사용될 수 있습니다; 사용될 수 있는 다른 알고리듬은 합쳐진 넓이 테이블(summed area table)입니다.

의학의 영역에서, 미적분학은 혈관의 최적의 분지 각도를 찾아 흐름을 최대화하기 위해 사용될 수 있습니다. 인체에서 특정 약물의 제거에 대한 붕괴 법칙(decay law)으로부터, 그것은 투약 법칙을 유도하기 위해서 사용됩니다. 핵 의학에서, 그것은 표적되는 종양 치료법에서 방사선 수송의 모델을 구축하기 위해서 사용됩니다.

경제학에서, 미적분학은 한계 비용(marginal cost)과 한계 수익(marginal revenue) 둘 다를 쉽게 계산하는 방법을 제공하는 것에 의해 최대 이익의 결정을 허용합니다.

미적분학은 방정식에 대한 근사 해를 찾기 위해서 역시 사용됩니다; 연습에서 그것은 미분 방정식을 풀고 대부분의 응용에서 근을 찾기 위해 수행하는 표준 방법입니다. 예제는 뉴턴의 방법(Newton's method), 고정된 점 반복(fixed point iteration), 및 선형 근사(linear approximation)와 같은 방법이 있습니다. 예를 들어, 우주선은 무중력 환경에서 곡선 진로를 근사하기 위해 오일러 방법(Euler method)의 변형을 사용합니다.

Varieties

수년에 걸쳐, 미적분학의 많은 재공식화는 다른 목적을 위해 조사되어 왔습니다.

Non-standard calculus

무한소에 대한 부정확한 계산은 1870년대에 시작하는 엄격한 극한의 (ε, δ)-정의로 넓게 대체되었습니다. 그 동안에, 무한소를 갖는 계산은 지속하고 종종 정확한 결과로 이끌어 냈습니다. 이것은 에이브러햄 로빈슨(Abraham Robinson)에게, 만약 미적분학의 정리가 여전히 유효한 것에 대해 무한소 양의 숫자 시스템을 개발 가능한지에 대해, 조사하게 만들었습니다. 1960년, 에드윈 휴잇(Edwin Hewitt)과 예르지 워시(Jerzy Łoś)의 작업을 바탕으로, 그는 비-표준 해석학(non-standard analysis)을 개발하는 것에 성공했습니다. 비-표준 해석학의 이론은 수학의 많은 가지에서 적용될 수 있을 정도로 풍부합니다. 그것에 따라, 미적분의 전통적인 정리에만 전적으로 헌정된 책과 기사는 종종 비-표준 미적분학이라는 제목으로 갑니다.

Smooth infinitesimal analysis

이것은 무한소(infinitesimal)의 관점에서 미적분학의 또 다른 재공식화입니다. 프랜시스 윌리엄 로비어(F. W. Lawvere)의 아이디어를 바탕으로 카테고리 이론(category theory)의 방법을 사용하여, 그것은 모든 함수를 연속(continuous)으로 바라보고 이산(discrete) 엔터디의 관점으로 표현할 수 없는 것으로 바라봅니다. 이 공식화의 한 측면은, 제외된 중간의 법칙(law of excluded middle)이 이 공식화에서 유지되지 않는다는 것입니다.

Constructive analysis

구성적 수학(Constructive mathematics)은 숫자, 함수, 또는 다른 수학적 대상의 존재에 대한 증명이 대상의 구성을 제공해야 한다고 주장하는 수학의 한 가지입니다. 그러한 구성적 수학은 역시 제외된 중간의 법칙(law of excluded middle)을 거부합니다. 구성적 프레임워크에서 미적분학의 재공식화는 일반적으로 구성적 해석학(constructive analysis)의 주제의 일부입니다.

^ DeBaggis, Henry F.; Miller, Kenneth S. (1966). Foundations of the Calculus. Philadelphia: Saunders. OCLC 527896.
^ Boyer, Carl B. (1959). The History of the Calculus and its Conceptual Development. New York: Dover. OCLC 643872.
^ Bardi, Jason Socrates (2006). The Calculus Wars : Newton, Leibniz, and the Greatest Mathematical Clash of All Time. New York: Thunder's Mouth Press. ISBN 1-56025-706-7.
^ Hoffmann, Laurence D.; Bradley, Gerald L. (2004). Calculus for Business, Economics, and the Social and Life Sciences (8th ed.). Boston: McGraw Hill. ISBN 0-07-242432-X.
^ Morris Kline, Mathematical thought from ancient to modern times, Vol. I
^ Archimedes, Method, in The Works of Archimedes ISBN 978-0-521-66160-7
^ Dun, Liu; Fan, Dainian; Cohen, Robert Sonné (1966). "A comparison of Archimdes' and Liu Hui's studies of circles". Chinese studies in the history and philosophy of science and technology. 130. Springer: 279. ISBN 0-7923-3463-9. {{cite journal}}: Cite journal requires |journal= (help),Chapter , p. 279
^ Katz, Victor J. (2008). A history of mathematics (3rd ed.). Boston, Mass.: Addison-Wesley. p. 203. ISBN 0-321-38700-7.
^ Zill, Dennis G.; Wright, Scott; Wright, Warren S. (2009). Calculus: Early Transcendentals (3 ed.). Jones & Bartlett Learning. p. xxvii. ISBN 0-7637-5995-3. Extract of page 27
^ ^a ^b Katz, V. J. 1995. "Ideas of Calculus in Islam and India." Mathematics Magazine (Mathematical Association of America), 68(3):163–174.
^ "Indian mathematics".
^ von Neumann, J., "The Mathematician", in Heywood, R. B., ed., The Works of the Mind, University of Chicago Press, 1947, pp. 180–196. Reprinted in Bródy, F., Vámos, T., eds., The Neumann Compendium, World Scientific Publishing Co. Pte. Ltd., 1995, ISBN 981-02-2201-7, pp. 618–626.
^ André Weil: Number theory. An approach through history. From Hammurapi to Legendre. Birkhauser Boston, Inc., Boston, MA, 1984, ISBN 0-8176-4565-9, p. 28.
^ Blank, Brian E.; Krantz, Steven George (2006). Calculus: Single Variable, Volume 1 (illustrated ed.). Springer Science & Business Media. p. 248. ISBN 978-1-931914-59-8. Extract of page 248
^ Ferraro, Giovanni (2007). The Rise and Development of the Theory of Series up to the Early 1820s (illustrated ed.). Springer Science & Business Media. p. 87. ISBN 978-0-387-73468-2. Extract of page 87
^ Leibniz, Gottfried Wilhelm. The Early Mathematical Manuscripts of Leibniz. Cosimo, Inc., 2008. Page 228. Copy
^ Allaire, Patricia R. (2007). Foreword. A Biography of Maria Gaetana Agnesi, an Eighteenth-century Woman Mathematician. By Cupillari, Antonella (illustrated ed.). Edwin Mellen Press. p. iii. ISBN 978-0-7734-5226-8.
^ Unlu, Elif (April 1995). "Maria Gaetana Agnesi". Agnes Scott College.
^ Russell, Bertrand (1946). History of Western Philosophy. London: George Allen & Unwin Ltd. p. 857. The great mathematicians of the seventeenth century were optimistic and anxious for quick results; consequently they left the foundations of analytical geometry and the infinitesimal calculus insecure. Leibniz believed in actual infinitesimals, but although this belief suited his metaphysics it had no sound basis in mathematics. Weierstrass, soon after the middle of the nineteenth century, showed how to establish the calculus without infinitesimals, and thus at last made it logically secure. Next came Georg Cantor, who developed the theory of continuity and infinite number. "Continuity" had been, until he defined it, a vague word, convenient for philosophers like Hegel, who wished to introduce metaphysical muddles into mathematics. Cantor gave a precise significance to the word, and showed that continuity, as he defined it, was the concept needed by mathematicians and physicists. By this means a great deal of mysticism, such as that of Bergson, was rendered antiquated.
^ Grabiner, Judith V. (1981). The Origins of Cauchy's Rigorous Calculus. Cambridge: MIT Press. ISBN 0-387-90527-8.

External links

"Calculus", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Weisstein, Eric W. "Calculus". MathWorld.
Topics on Calculus at PlanetMath.org.
Calculus Made Easy (1914) by Silvanus P. Thompson Full text in PDF
Calculus on In Our Time at the BBC
Calculus.org: The Calculus page at University of California, Davis – contains resources and links to other sites
COW: Calculus on the Web at Temple University – contains resources ranging from pre-calculus and associated algebra
Earliest Known Uses of Some of the Words of Mathematics: Calculus & Analysis
Online Integrator (WebMathematica) from Wolfram Research
The Role of Calculus in College Mathematics from ERICDigests.org
OpenCourseWare Calculus from the Massachusetts Institute of Technology
Infinitesimal Calculus – an article on its historical development, in Encyclopedia of Mathematics, ed. Michiel Hazewinkel.
Daniel Kleitman, MIT. "Calculus for Beginners and Artists".
Calculus Problems and Solutions by D.A. Kouba
Donald Allen's notes on calculus
Calculus training materials at imomath.com
(in English and Arabic) The Excursion of Calculus, 1772

[1] DeBaggis, Henry F.; Miller, Kenneth S. (1966). Foundations of the Calculus. Philadelphia: Saunders. OCLC 527896.

[2] Boyer, Carl B. (1959). The History of the Calculus and its Conceptual Development. New York: Dover. OCLC 643872.

[3] Bardi, Jason Socrates (2006). The Calculus Wars : Newton, Leibniz, and the Greatest Mathematical Clash of All Time. New York: Thunder's Mouth Press. ISBN 1-56025-706-7.

[4] Hoffmann, Laurence D.; Bradley, Gerald L. (2004). Calculus for Business, Economics, and the Social and Life Sciences (8th ed.). Boston: McGraw Hill. ISBN 0-07-242432-X.

[5] Morris Kline, Mathematical thought from ancient to modern times, Vol. I

[6] Archimedes, Method, in The Works of Archimedes ISBN 978-0-521-66160-7

[7] Dun, Liu; Fan, Dainian; Cohen, Robert Sonné (1966). "A comparison of Archimdes' and Liu Hui's studies of circles". Chinese studies in the history and philosophy of science and technology. 130. Springer: 279. ISBN 0-7923-3463-9. {{cite journal}}: Cite journal requires |journal= (help),Chapter , p. 279

[8] Katz, Victor J. (2008). A history of mathematics (3rd ed.). Boston, Mass.: Addison-Wesley. p. 203. ISBN 0-321-38700-7.

[9] Zill, Dennis G.; Wright, Scott; Wright, Warren S. (2009). Calculus: Early Transcendentals (3 ed.). Jones & Bartlett Learning. p. xxvii. ISBN 0-7637-5995-3. Extract of page 27

[katz-10] Katz, V. J. 1995. "Ideas of Calculus in Islam and India." Mathematics Magazine (Mathematical Association of America), 68(3):163–174.

[11] "Indian mathematics".

[12] von Neumann, J., "The Mathematician", in Heywood, R. B., ed., The Works of the Mind, University of Chicago Press, 1947, pp. 180–196. Reprinted in Bródy, F., Vámos, T., eds., The Neumann Compendium, World Scientific Publishing Co. Pte. Ltd., 1995, ISBN 981-02-2201-7, pp. 618–626.

[13] André Weil: Number theory. An approach through history. From Hammurapi to Legendre. Birkhauser Boston, Inc., Boston, MA, 1984, ISBN 0-8176-4565-9, p. 28.

[14] Blank, Brian E.; Krantz, Steven George (2006). Calculus: Single Variable, Volume 1 (illustrated ed.). Springer Science & Business Media. p. 248. ISBN 978-1-931914-59-8. Extract of page 248

[15] Ferraro, Giovanni (2007). The Rise and Development of the Theory of Series up to the Early 1820s (illustrated ed.). Springer Science & Business Media. p. 87. ISBN 978-0-387-73468-2. Extract of page 87

[leib-16] Leibniz, Gottfried Wilhelm. The Early Mathematical Manuscripts of Leibniz. Cosimo, Inc., 2008. Page 228. Copy

[17] Allaire, Patricia R. (2007). Foreword. A Biography of Maria Gaetana Agnesi, an Eighteenth-century Woman Mathematician. By Cupillari, Antonella (illustrated ed.). Edwin Mellen Press. p. iii. ISBN 978-0-7734-5226-8.

[18] Unlu, Elif (April 1995). "Maria Gaetana Agnesi". Agnes Scott College.

[19] Russell, Bertrand (1946). History of Western Philosophy. London: George Allen & Unwin Ltd. p. 857. The great mathematicians of the seventeenth century were optimistic and anxious for quick results; consequently they left the foundations of analytical geometry and the infinitesimal calculus insecure. Leibniz believed in actual infinitesimals, but although this belief suited his metaphysics it had no sound basis in mathematics. Weierstrass, soon after the middle of the nineteenth century, showed how to establish the calculus without infinitesimals, and thus at last made it logically secure. Next came Georg Cantor, who developed the theory of continuity and infinite number. "Continuity" had been, until he defined it, a vague word, convenient for philosophers like Hegel, who wished to introduce metaphysical muddles into mathematics. Cantor gave a precise significance to the word, and showed that continuity, as he defined it, was the concept needed by mathematicians and physicists. By this means a great deal of mysticism, such as that of Bergson, was rendered antiquated.

[20] Grabiner, Judith V. (1981). The Origins of Cauchy's Rigorous Calculus. Cambridge: MIT Press. ISBN 0-387-90527-8.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]